An Identity-Based Cross-Domain Authenticated Asymmetric Group Key Agreement

Abstract

Cross-domain authenticated asymmetric group key agreement allows group members in different domains to establish a secure group communication channel and the senders can be anyone. However, the existing schemes do not meet the requirement of batch verification in the group key negotiation phase, which makes the schemes have low efficiency. To address this problem, an identity-based cross-domain authenticated asymmetric group key agreement is proposed that supports batch verification. The performance analysis shows that this protocol is highly efficient. Finally, the proposed protocol is proved to be secure under the k-Bilinear Diffie–Hellman Exponent assumption.

1. Introduction

With the rapid proliferation of the mobile network, secure group communication is usually required in many emerging applications [1], such as teleconference, telemedicine, social group networks, ad hoc networks, and mobile cloud computing [2,3,4,5,6]. A popular approach is to employ the group key agreement (GKA) protocols. The conventional GKA protocols enable group members to exchange information confidentially by negotiating a shared symmetric key over an open network [7]. Nevertheless, this symmetric key is only known to the group members, which results in the problem of sender restriction. This problem means that if an outsider wants to broadcast secret messages to the group, he/she must join this group first. Motivated by the mentioned observation, Wu et al. [8] introduced an asymmetric group key agreement (AGKA) protocol that a common public encryption key (access to outsiders) is negotiated among group members and each member can respectively compute a private decryption key. This protocol is only proved secure to passive attackers who simply eavesdrop on the group communications. By considering active attacks, such as a man in the middle attack, Zhang et al. [9] designed an authenticated AGKA (AAGKA) protocol based on Public Key Infrastructure (PKI). To alleviate the overhead of complicated certificate management, an identity-based AAGKA protocol [10] is presented. However, the above studies only consider the scenarios in a single domain.

In cross-domain scenarios, such as telemedicine [11] and mobile cloud computing networks [12], members physically belong to different regions, clouds, institutions or networks. Each domain has its own domain administrator (DA), resources and members. When there is collaborative work between several domains, members in a domain may ask for resources in other domains [13]. For instance, in an electronic health social system, patients in different hospitals with the same symptoms need to form a group to securely share treatment or rehabilitation information [14] and get medical advice from outside experts. Another example in mobile cloud computing [12], group terminals distributed in different clouds or heterogeneous networks can also share resources with other groups when in collaborative work. In recent years, some cross-domain AAGKA protocols [11,12,15] have been proposed to establish a secure connection between different domains. In the literature [11,15], group members from different domains will authenticate each other with digital signatures before calculating the group session keys. Despite realizing mutual authentication, the digital signature schemes cannot support batch verification so that the number of complex operations (e.g., bilinear pairing) grows linearly with the number of group members. It seems inefficient and impractical that group members may be mobile terminals with limited energy, computation and communication resources. To reduce the computational overhead of group members, a semi-centered scheme [12] was proposed that DAs need to authenticate other group members for their domain members, while DAs may become the bottleneck [16] of the whole system.

Our Contributions

• Inspired by Zhang et al. [10], this work extends a hierarchical batch signature scheme [17] to a batch multi-signature scheme. Then, we apply it into the construction of the proposed identity-based cross-domain AAGKA (ID-CD-AAGKA) protocol, which is distributed without any trusted party and supports batch verification.
• The security proof is given that this protocol offers secrecy, known-key security and partial forward secrecy. Meanwhile, as the performance analysis shows, the IB-CD-AGAKA protocol is more efficient than existing works.

The remainder of this paper is organized as follows. Section 2 gives a brief review of the related works. Section 3 presents bilinear pairing and the complexity assumption. Our IB-CD-AAGKA protocol is described in Section 4. The proof of correctness is provided in Section 5, and the security aspect of the proposed protocol is analyzed in Section 6. Section 7 gives the performance comparison between the IB-CD-AAGKA protocol and the previous works. Finally, Section 8 concludes our work.

2. Related Works

Studies to secure group communications in cross-domain scenarios can be divided into two categories, i.e., conventional authenticated GKA protocol and AAGKA protocol.

2.1. Cross-Domain Conventional Authenticated GKA (CCAGKA) Protocols

In 2015, Guo et al. [18] first put forth a multi-participant cross-domain group password-based authenticated key exchange (MCGPAKE) protocol. In this protocol, a domain member shares passwords with trusted domain servers. A header is selected as a proxy of each domain to negotiate a cross-domain session key with other headers. If all the headers are malicious attackers, they can predetermine the session key. Subsequently, Zhu et al. [19] proposed a novel MCGPAKE protocol with explicit authentication and contributiveness in the universally composable (UC) framework. The scheme realizes $(\frac{n}{2},n)$ contributions that if the adversary corrupts less than half of the participants, the session key still cannot be predetermined. On the other hand, the communication rounds in the aforementioned works [18,19] are no less than eight rounds, which is not round-efficient. In 2016, Lan et al. [13] presented a one-round CCAGKA protocol in which group members use different cryptographic settings and signature schemes. An indistinguishability obfuscation program is published by a trusted third party to make all the participants have the uniform computation as the group session key. In 2018, Yang et al. [14] utilized a three-layer tree structure to construct a CCAGKA protocol with symptom-matching for an e-health system. In the group key agreement phase, a powerful patient is chosen to authenticate other group patients. In 2020, Luo et al. [20] pointed out Yang’s scheme does not meet the requirement that different domains may have different cryptographic system parameters. In this scheme, a group controller is set up to generate a group session key for all the participants. However, it may lead to single node failure when the group controller is corrupted. All the above CCAGKA protocols have the same shortcoming, i.e., sender restriction [21].

2.2. Cross-Domain AAGKA Protocols

In 2014, Qikun et al. [15] proposed a distributed cross-domain AAGKA protocol. Each domain member is assigned with a register key binding to his public key and the domain public key of the corresponding DA. The domain public keys lack an authentication mechanism. Thus, domain members need to store all the domain public keys. In the resource-constrained environment, terminals may not have enough memories to keep them. Besides, when a domain public key is updated, terminals in all domains also need to update this key. In 2018, Zheng et al. proposed a semi-centered scheme to solve the problems in [15] where DAs participate in the key agreement phase as intermediated nodes between users. All the messages received or sent by the group users must be authenticated and transferred by DAs. Moreover, DAs form a pair of alliance public/private keys to validate the domain public keys. In this way, each member only needs to store the corresponding domain public key. It will reduce the computational overhead of group users. Nevertheless, DAs can also compute the group session keys. If a DA fails, the group session keys and the previous group messages would be leaked, which is the single node failure to make DA become the system’s bottleneck [16]. In the same year, Qikun et al. [11] proposed a distributed cross-domain AAGKA protocol based on a new signature scheme in the above alliance structure. However, in the verification phase of this signature scheme, the number of bilinear pairings grows linearly with the number of group members. When the group size is large, the consumption of computing resources is considerable so that the resource-constrained terminals cannot afford it.

Then, we give the comparisons between the IB-CD-AAGKA protocol and the above schemes in Table 1.

Table 1. Comparison between the above cross-domain group key agreement protocols and the IB-CD-AAGKA protocol.

Schemes	Distributed	Sender-Unrestricted	Constant or No Bilinear Pairing of Each User
Guo et al. [18]	no	no	yes
Zhu et al. [19]	no	no	yes
Lan et al. [13]	no	no	yes
Yang et al. [14]	no	no	yes
Luo et al. [20]	no	no	yes
Zhang et al. [15]	yes	yes	no
Zheng et al. [12]	no	yes	yes
Zhang et al. [11]	yes	yes	no
The proposed protocol	yes	yes	yes

3. Preliminaries

3.1. Bilinear Pairing

As our protocol is constructed from bilinear pairing [22], we give a brief introduction of it in this section.

Let $G_1$ be an additive group and $G_2$ be a multiplicative group. Both of them have the same prime order q. $\widehat{e}:G_1\times G_1\to G_2$ is called a bilinear pairing if the following properties hold:

• Bilinearity: For all $P,Q\in G_1$ and $a,b\in Z_q^{*}$, there is $\widehat{e}(aP,bQ)=\widehat{e}{(P,Q)}^{ab}$.
• Nondegeneracy: There exists $P,Q\in G_1$, such that $\widehat{e}(P,Q)\ne 1$.
• Computability: For all $P,Q\in G_1$, there exists an efficient algorithm to compute $\widehat{e}(P,Q)\in G_2$.

3.2. Complexity Assumptions

The security of the proposed protocol bases on k-Bilinear Diffie–Hellman Exponent (BDHE) assumption [8,23], which is described as follows:

k-BDHE problem: Given $P,I$ and $t_{\phi }=a^{\phi }P(\phi =1,2,3,\cdots ,k,k+2,\cdots ,2k)$ as input, compute $\widehat{e}{(P,I)}^{a^{k+1}}$. As the input vector lacks the term $a^{k+1}P$, the bilinear pairing seems to be of no help in calculating $\widehat{e}{(P,I)}^{a^{k+1}}$.

k-BDHE assumption: Let $\mathcal{B}$ be an algorithm which has advantage

$$\begin{array}{c}\hfill Adv(\mathcal{B})=Pr[\mathcal{B}(P,I,t_1,\cdots ,t_k,t_{k+2},\cdots ,t_{2k})=\widehat{e}{(P,I)}^{a^{k+1}}]\end{array}$$

in solving the k-BDHE problem. The k-BDHE assumption is that $Adv(\mathcal{B})$ is negligible for any polynomial-time algorithm $\mathcal{B}$.

4. Our IB-CD-AAGKA Protocol

In this section, we present the proposed IB-CD-AAGKA protocol in detail.

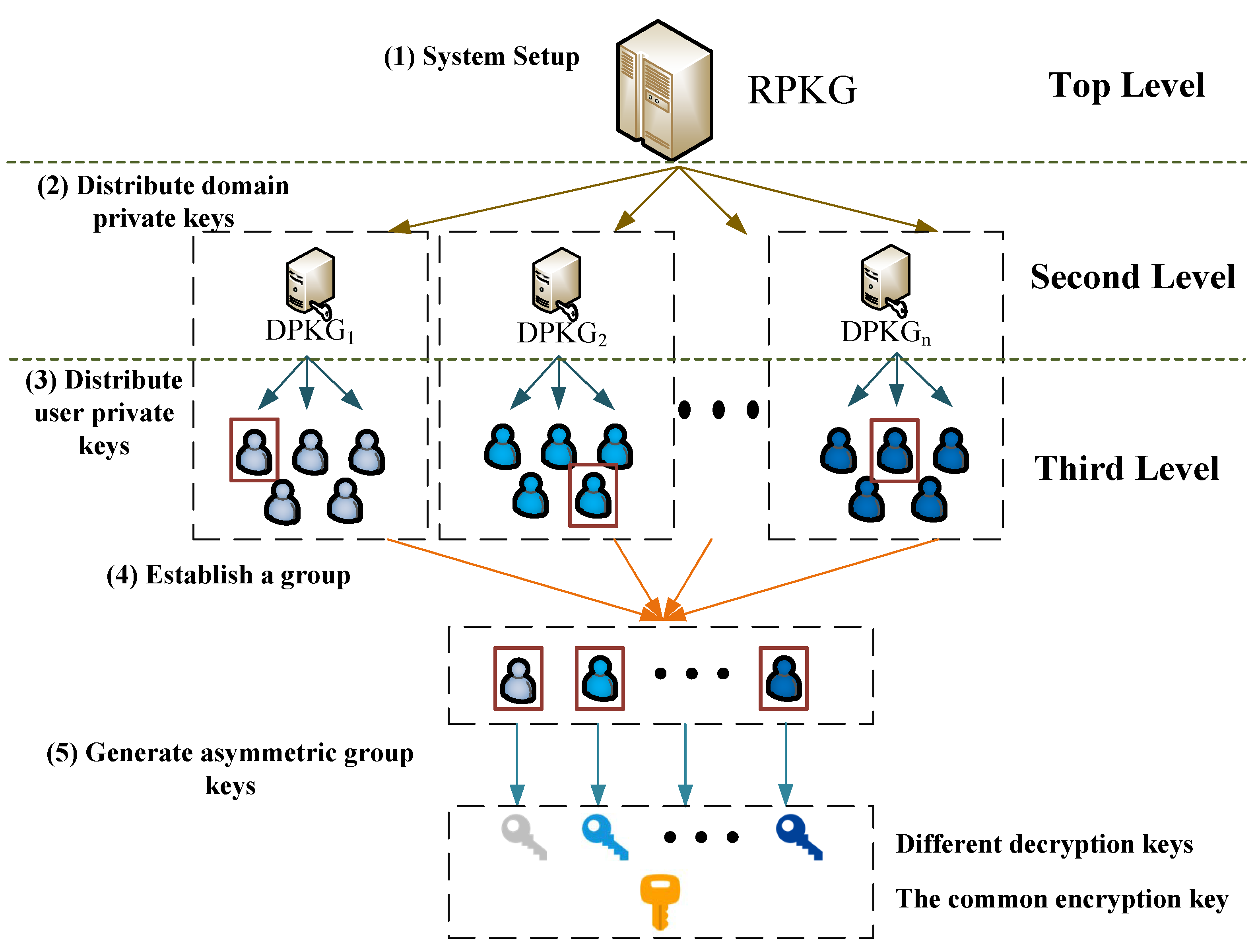
4.1. Network Architecture

The cross-domain network architecture used in this protocol is illustrated in Figure 1. There are three types of entities in this architecture. The root private key generator ($RPKG$) is at the top level. The domain private key generators ($DPKG$) are at the second level. The users are at the third level. A brief workflow of our protocol is as follows.

Figure 1. The three-layer cross-domain network architecture.

• The $RPKG$ generates a master private key, a master public key, and other system parameters. Then, the $RPKG$ keeps the master private key secret and publishes the master public key and the other system parameters.
• Each $DPKG$ manages a domain independently and registers to the $RPKG$. The $RPKG$ generates all the $DPKG$s’ private keys, and sends them to the $DPKG$s separately in a secure channel.
• When a user joins a domain, he/she registers to the corresponding $DPKG$. The $DPKG$ generates the user’s private key, which is sent to the user securely.
• When users from different domains want to establish a group, they generate and publish their parameters of group keys.
• The group members verify whether the received parameters of group keys are from other group members or not. If the verification passes, each group member can calculate his/her group decryption private key and a common group encryption public key.

An outside sender can encrypt the messages with the group encryption key and broadcast the ciphertexts to a group. Then, the group members can decrypt the ciphertexts with their group decryption keys.

4.2. Detailed Construction

Assume the number of group members in domain $D_i(1\le i\le n)$ is $m_i$, and $DPK{G}_i$ generates private keys for $D_i$’s domain users. Let $U_{i,j}(1\le i\le n,1\le j\le m_i)$ denote the jth domain member of $D_i$ in the group, who negotiates the asymmetric group keys with other group members. $I{D}_i,I{D}_{i,j}$ are identities of $DPK{G}_i$ and $U_{i,j}$, respectively. For simplicity, we also assume the number of group members in each domain is equal, i.e., $m_1=m_2=\cdots =m_n=m$. The group size is $N=n·m$.

In the following, we provide a detailed description of our proposed IB-CD-AAGKA protocol, which comprises three phases: system setup and private key distribution, cross-domain group key agreement, group encryption and group decryption.

• System setup and private key distribution.
  First, the $RPKG$ runs Setup to initialize the system parameters, including the master private key and master public key. Second, the $RPKG$ executes DPKG.Register to generate the private key for each $DPK{G}_i$. Third, each $DPK{G}_i$ generates private keys for $D_i$’s domain members by Member.Register.

  (a)

  Setup: On input a security parameter $1^{\lambda }$, the $RPKG$ generates system parameters $\{G_1$, $G_2$, q, P, Q, $\widehat{e}$, s, $P{K}_{root}\}$, where $G_1$ is an additive group, $G_2$ is a multiplicative group, q is the prime order of $G_1$ and $G_2$, P and Q are generators of $G_1$, $\widehat{e}$ denotes a bilinear pairing $G_1\times G_1\to G_2$, a random number $s\in Z_q^{*}$ is the master private key, and $P{K}_{root}=s·P$ is the master public key. The $RPKG$ chooses four hash functions $H_1,H_2,H_3:{\{0,1\}}^{*}\to Z_q^{*}$ and $H_4:G_2\to {\{0,1\}}^{\tau }$ ($\tau$ is the bit-length of plaintexts). Then, the $RPKG$ keeps s secret, and publishes the remaining system parameters and the hash functions.

  (b)

  DPKG.Register: When $DPK{G}_i$ registers to the $RPKG$, the $RPKG$ runs this algorithm to generate the public/private key pair for $DPK{G}_i$. The $RPKG$ first chooses a random number $r_i\in Z_q^{*}$ to compute $R_i=r_i·P$, ${\alpha }_i=H_1(I{D}_i\Vert R_i)$, and $S{K}_i=(r_i+{\alpha }_i·s)·Q$, where the tuple $(R_i,{\alpha }_i)$ is $DPK{G}_i$’s public key and $S{K}_i$ is $DPK{G}_i$’s private key. Then, the $RPKG$ transmits $(R_i,S{K}_i)$ to $DPK{G}_i$ over a secure channel.

  (c)

  Member.Register: When $U_{i,j}$ joins the $D_i$, $DPK{G}_i$ generates public/private key pair for $U_{i,j}$ in this algorithm. First, $DPK{G}_i$ randomly selects $r_{i,j}\in Z_q^{*}$. Second, $DPK{G}_i$ computes $R_{i,j}=r_{i,j}·P$, ${\alpha }_{i,j}=H_2(I{D}_i\Vert R_i\Vert I{D}_{i,j}\Vert R_{i,j})$, and $S{K}_{i,j}=S{K}_i+{\alpha }_{U_{i,j}}·r_{i,j}·Q$, where the tuple $(R_{i,j},{\alpha }_{i,j})$ is $U_{i,j}$’s public key and $S{K}_{i,j}$ is $U_{i,j}$’s private key. Third, $DPK{G}_i$ transmits $(I{D}_i,R_i,I{D}_{i,j},R_{i,j},{\alpha }_{i,j},$$S{K}_{i,j})$ to $U_i$ securely.

• Cross-domain group key agreement.
  All group members’ common encryption key and group decryption keys are generated in this phase. The process of cross-domain group key agreement involves four algorithms, namely GenKeyParams, BVerify, GenEncKey and GenDecKey, which are executed by $U_{i,j}$ sequentially. Let $U_{x,y}$$(1\le x\le n,1\le y\le m)$ symbolize the yth member of $D_x$ in the group and $\left\{U_{x,y}\right\}(1\le x\le n,1\le y\le m)$ represent a set of all the group members. $\{(x,y)\}(1\le x\le n,1\le y\le m)$ is a set of group indexes of $\left\{U_{x,y}\right\}(1\le x\le n,1\le y\le m)$.

  (a)

  GenKeyParams: $U_{i,j}$ executes this algorithm to generate the parameters of group keys which includes $U_{i,j}$’s signatures on all the group members’ indexes $\{(x,y)\}(1\le x\le n,1\le y\le m)$. $U_{i,j}$ chooses a random number ${\eta }_{i,j}\in Z_q^{*}$, computes $T_{i,j}={\eta }_{i,j}·P$. For $1\le x\le n,1\le y\le m$, $U_{i,j}$ computes $f_{x,y}=H_3(x\Vert y)$ and $S_{i,j}(x,y)=S{K}_{i,j}+f_{x,y}·{\eta }_{i,j}·Q$. So far, $U_{i,j}$ has generated his/her signatures on $\{(x,y)\}(1\le x\le n,1\le y\le m)$, which are $(R_i,R_{i,j},T_{i,j},\left\{S_{i,j}(x,y)\right\}(1\le x\le n,1\le y\le m))$. Note that, $\left\{S_{i,j}(x,y)\right\}(1\le x\le n,1\le y\le m)$ is a set including $S_{i,j}(i,j)$, when $x=i$ and $y=j$. Then, $U_{i,j}$ keeps $S_{i,j}(i,j)$ secret and broadcasts $M_{i,j}$ $=(R_i,I{D}_i,R_{i,j},I{D}_{i,j},T_{i,j},\left\{S_{i,j}(x,y)\right\}$ $(1\le x\le n,1\le y\le m,x\ne i$ or $y\ne j))$.

  (b)

  BVerify: $U_{i,j}$ receives $\{R_x,I{D}_x,R_{x,y},I{D}_{x,y},T_{x,y},S_{x,y}(i,j)\}(1\le x\le n,1\le y\le m,x\ne i$ or $y\ne j)$, where $\{R_x,R_{x,y},T_{x,y},S_{x,y}(i,j)\}(1\le x\le n,1\le y\le m,x\ne i$ or $y\ne j)$ are other group members’ signatures on $(i,j)$. Then, $U_{i,j}$ runs this algorithm to take a batch verification of the signatures. First, $U_{i,j}$ computes $f_{i,j}=H_3(i\Vert j)$. Second, for $1\le x\le n,1\le y\le m,x\ne i$ or $y\ne j$, $U_{i,j}$ computes ${\alpha }_x=H_1(I{D}_x\Vert R_x)$ and ${\alpha }_{x,y}=H_2(I{D}_x\Vert R_x\Vert I{D}_{x,y}\Vert R_{x,y})$. Then, $U_{i,j}$ checks Equation (1). If Equation (1) holds, $U_{i,j}$ ensures that the received messages are really from other group members.

  $$\begin{array}{cc}\hfill \widehat{e}(\sum _{x=1}^n\sum _{y=1}^m{S}_{x,y}(i,j),P)=\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m({\alpha }_x·P{K}_{root}+R_x+{\alpha }_{x,y}·& R_{x,y}+f_{i,j}·T_{x,y},Q)\hfill \\ & (x\ne iory\ne j)\hfill \end{array}$$

  (1)

  (c)

  GenEncKey: When someone wants to broadcast secret messages to the group, he/she runs this algorithm to calculate the group encryption public key $ek$. For $1\le x\le n,1\le y\le m$, the sender calculates $ek:(W,\Omega )$, in which $W=\sum _{x=1}^n\sum _{y=1}^m{T}_{x,y}$ and $\Omega =\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m({\alpha }_x·P{K}_{root}+R_x+{\alpha }_{x,y}·R_{x,y}),Q)$.

  (d)

  GenDecKey: This algorithm helps $U_{i,j}$ calculate his/her unique group private decryption key $d{k}_{i,j}=\sum _{x=1}^n\sum _{y=1}^m{S}_{x,y}(i,j)$. The parameters to generate all the group members’ decryption keys are listed in Table 2, in which $S_{i,j}(i,j)$ is kept secretly by $U_{i,j}$. $\left\{S_{x,y}(i,j)\right\}((1\le i\le n,1\le j\le m,1\le x\le n,1\le y\le m))$ in each column are utilized to compute $U_{i,j}$’s group decryption key.

  Table 2. The parameters to generate the group decryption key.

  Members	${\mathit{U}}_{1,1}$	⋯	${\mathit{U}}_{1,\mathit{m}}$	${\mathit{U}}_{2,1}$	⋯	${\mathit{U}}_{\mathit{n},\mathit{m}}$
  $U_{1,1}\Rightarrow$	$S_{1,1}(1,1)$	⋯	$S_{1,1}(1,m)$	$S_{1,1}(2,1)$	⋯	$S_{1,1}(n,m)$
  ⋮	⋮	⋱	⋮	⋮	⋱	⋮
  $U_{1,m}\Rightarrow$	$S_{1,m}(1,1)$	⋯	$S_{1,m}(1,m)$	$S_{1,m}(2,1)$	⋯	$S_{1,m}(n,m)$
  $U_{2,1}\Rightarrow$	$S_{2,1}(1,1)$	⋯	$S_{2,1}(1,m)$	$S_{2,1}(2,1)$	⋯	$S_{2,1}(n,m)$
  ⋮	⋮	⋱	⋮	⋮	⋱	⋮
  $U_{n,m}\Rightarrow$	$S_{n,m}(1,1)$	⋯	$S_{n,m}(1,m)$	$S_{n,m}(2,1)$	⋯	$S_{n,m}(n,m)$
  Keys	$d{k}_{1,1}$	⋯	$d{k}_{1,m}$	$d{k}_{2,1}$	⋯	$d{k}_{n,m}$

• Group encryption and group decryption.
  Once group members finish the above algorithms and establish a confidential group communication channel, any sender can send encrypted messages to the group in this phase.

  (a)

  Encryption: If someone wants to send a message $m^{*}$ secretly to the group, he/she should run this algorithm to encrypt it. The sender chooses a random number $\rho \in Z_q^{*}$ and computes $C_1=\rho ·P$, $C_2=\rho ·W$, $C_3=m^{*}\oplus H_4({\Omega }^{\rho })$. Then, the sender outputs the ciphertext $(C_1,C_2,C_3)$.

  (b)

  Decryption: When receiving the ciphertext $(C_1,C_2,C_3)$, $U_{i,j}$ runs this algorithm to decrypt it. $U_{i,j}$ computes $m^{*}$ in Equation (2).

  $$m^{*}=C_3\oplus H_4(\widehat{e}(d{k}_{i,j},C_1)·\widehat{e}(-f_{i,j}·Q,C_2)).$$

  (2)

5. Correctness Analysis

The correctness of this protocol depends on two conditions. Condition 1. $U_{i,j}$ ensures that the received group key parameters are from other legitimate group members with batch verification. Then, they can use the received parameters to calculate the proper pair of group encryption/decryption keys. To meet this condition, Equation (1) must hold. Condition 2. When receiving the ciphertext encrypted by the group encryption key, $U_{i,j}$ can use his/her decryption key to decrypt it and obtain the correct plaintext. To satisfy this condition, Equation (2) must hold.

• Equation (1) is proved as follows.

  $$\begin{array}{cc}\hfill & \widehat{e}(\sum _{x=1}^n\sum _{y=1}^m{S}_{x,y}(i,j),P)(x\ne iory\ne j)\hfill \\ & =\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m(S{K}_{x,y}+f_{i,j}·{\eta }_{x,y}·Q),P)(x\ne iory\ne j)\hfill \\ \hfill & =\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m(S{K}_x+{\alpha }_{x,y}·r_{x,y}·Q+f_{i,j}·{\eta }_{x,y}·Q),P)(x\ne iory\ne j)\hfill \\ \hfill & =\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m((r_x+{\alpha }_x·s)·Q+{\alpha }_{x,y}·r_{x,y}·Q+f_{i,j}·{\eta }_{x,y}·Q),P)(x\ne iory\ne j)\hfill \\ \hfill & =\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m((r_x+{\alpha }_x·s)·P+{\alpha }_{x,y}·r_{x,y}·P+f_{i,j}·{\eta }_{x,y}·P),Q)(x\ne iory\ne j)\hfill \\ \hfill & =\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m(R_x+{\alpha }_x·P{K}_{root}+{\alpha }_{x,y}·R_{x,y}+f_{i,j}·T_{x,y}),Q)(x\ne iory\ne j)\hfill \end{array}$$
• Equation (2) is proved as follows.

  $$\begin{array}{cc}\hfill & C_3\oplus H_4(\widehat{e}(d{k}_{i,j},C_1)·\widehat{e}(-f_{i,j}·Q,C_2))\hfill \\ \hfill & =C_3\oplus H_4(\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m{S}_{x,y}(i,j),\rho ·P)·\widehat{e}(-f_{i,j}·Q,\rho ·\sum _{x=1}^n\sum _{y=1}^m{T}_{x,y}))\hfill \\ \hfill & =C_3\oplus H_4(\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m(S{K}_{x,y}+f_{i,j}·{\eta }_{x,y}·Q),\rho ·P)·\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m-f_{i,j}·Q,\rho ·\sum _{x=1}^n\sum _{y=1}^m\hfill \\ & {\eta }_{x,y}·P))\hfill \\ \hfill & =C_3\oplus H_4(\widehat{e}(\sum _{x=1}^n\sum _{y=1}^{m}S{K}_{x,y},\rho ·P)·\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m{f}_{i,j}·{\eta }_{x,y}·Q,\rho ·P)·\widehat{e}(\sum _{x=1}^n\sum _{y=1}^m{f}_{i,j}·{\eta }_{x,y}\hfill \\ \hfill & {·Q,\rho ·P)}^{-1})\hfill \\ \hfill & =C_3\oplus H_4(\widehat{e}(\sum _{x=1}^n\sum _{y=1}^{m}S{K}_{x,y}+{\alpha }_{x,y}·r_{x,y}·Q,\rho ·P))\hfill \\ \hfill & =C_3\oplus H_4(\widehat{e}{(\sum _{x=1}^n\sum _{y=1}^m(r_x+{\alpha }_x·s)·P+{\alpha }_{x,y}·r_{x,y}·P,Q)}^{\rho })\hfill \\ \hfill & =C_3\oplus H_4(\widehat{e}{(\sum _{x=1}^n\sum _{y=1}^m(R_x+{\alpha }_x·P{K}_{root}+{\alpha }_{x,y}·R_{x,y}),Q)}^{\rho })\hfill \\ \hfill & =C_3\oplus H_4({\Omega }^{\rho })\hfill \\ \hfill & =m^{*}\oplus H_4({\Omega }^{\rho })\oplus H_4({\Omega }^{\rho })\hfill \\ \hfill & =m^{*}\hfill \end{array}$$

6. Security Analysis

This section gives the proofs that the proposed protocol achieves three security properties [10], i.e., the partial forward secrecy, the known key security, and the secrecy. The partial forward secrecy requires that even if some group members’ long term keys are leaked, the group decryption keys previously established by these group members would not be compromised. The known-key security ensures that if an adversary learns the encryption/decryption keys of some groups, he cannot calculate other groups’ decryption keys. The secrecy means that only the legitimate group members can decrypt the encrypted message under the corresponding group encryption key.

6.1. Known Key Security and Partial Forward Secrecy

Because $U_{i,j}$ needs to pick a random number ${\eta }_{i,j}$ to generate his/her group key parameters, the encryption/decryption keys of a group are generated independently to the corresponding keys of other groups. As a result, the decryption keys of a group cannot be computed even if all encryption/decryption keys of other groups are leaked, i.e., our protocol satisfies the known key security.

Furthermore, an attacker cannot recover the $S_{i,j}(i,j)$ without the knowledge of ${\eta }_{i,j}$, even if the $U_{i,j}$’s private key $S{K}_{i,j}$ is corrupted. Therefore, the proposed protocol satisfies the partial forward secrecy.

6.2. Secrecy

6.2.1. Security Model

In this model, secrecy means the indistinguishability of a message encrypted under the negotiated public encryption key from a random string in the ciphertext space [10]. Specifically, we construct a game between a challenger $\mathcal{C}$ and an adversary $\mathcal{A}$ who has full control of the communication channel to prove the secrecy of our protocol. This game has three phases, which are described as follows:

Initial: The challenger $\mathcal{C}$ initiates the system and transmits the system parameters to $\mathcal{A}$.

Training: $\mathcal{C}$ answers $\mathcal{A}$’s queries as follows:

• DPKG.Extract: $\mathcal{C}$ generates the $DPK{G}_i$’s public and private keys, then outputs the public key.
• Member.Extract: $\mathcal{C}$ generates the $U_{i,j}$’s public and private keys, then outputs the public key.
• Execute: $\mathcal{C}$ executes an asymmetric group key agreement.
• Test: $\mathcal{A}$ sends $m_1$ and $m_2$ ($\left|m_1\right|=\left|m_2\right|$) to $\mathcal{C}$. $\mathcal{C}$ randomly chooses a bit $b\in \{0,1\}$, and encrypts $m_b$ using $ek$. $\mathcal{A}$ can submit this query only once and this query is used to model secrecy.

Response: Finally, $\mathcal{A}$ returns a bit $b^{\prime }\in \{0,1\}$ as the guess. If $b=b^{\prime }$, $\mathcal{A}$ wins the game. The advantage of $\mathcal{A}$ is $Adv(\mathcal{A})=\left|Pr[b=b^{\prime }]-\frac{1}{2}\right|$. As defined in the literature [10], we consider that if $Adv(\mathcal{A})$ is negligible, our protocol is secure against semantically indistinguishable chosen identity and plaintext attacks (Ind-ID-CPA).

6.2.2. Security Proof

This section proves that if an adversary $\mathcal{A}$ can corrupt the secrecy of the proposed protocol with a non-negligible advantage, $\mathcal{C}$ can solve the k-BDHE problem with a non-negligible advantage.

Proof. 

Assume $N<k$ and given $(P,I,t_1,\cdots ,t_k,t_{k+2},\cdots ,t_{2k})$, $\mathcal{C}$ computes $\widehat{e}{(P,I)}^{a^{k+1}}$ is a k-BDHE problem, where $P,I$ are generators of $G_1$ and $t_{\phi }=a^{\phi }·P$ ($\phi =1,2,3,\cdots ,k,k+2,\cdots ,2k$) with an unknown $a\in Z_q^{*}$. In the following, we show the process that $\mathcal{C}$ computes $\widehat{e}{(P,I)}^{a^{k+1}}$.

Initial: At the beginning of the game, $\mathcal{C}$ chooses system parameters $\{G_1,G_2,\widehat{e},P,Q,P{K}_{root}\}$ where $P{K}_{root}=t_1=a·P$ and $Q=a^k·P$ and sends them to $\mathcal{A}$. Then, $\mathcal{C}$ randomly picks a $DPKG$’s identity $I{D}_{DPKG}^{*}$ and a group member’s identity $I{D}_U^{*}$ as challenge identities.

Training: In this phase, $\mathcal{C}$ answers $\mathcal{A}$’s queries as follows.

• $H_1$ query: $\mathcal{C}$ keeps an initially empty list $L_{H_1}$. On input $I{D}_i,R_i$$(1\le i\le n)$, $\mathcal{C}$ does the following:
  • If there is a tuple $(I{D}_i,R_i,{\alpha }_i)$ on $L_{H_1}$, $\mathcal{C}$ returns ${\alpha }_i$ as the answer;
  • Otherwise, $\mathcal{C}$ chooses a random number ${\alpha }_i\in Z_q^{*}$ and adds $(I{D}_i,R_i,{\alpha }_i)$ to $L_{H_1}$. Then, $\mathcal{C}$ returns ${\alpha }_i$ as the answer.
• $H_2$ query: $\mathcal{C}$ keeps an initially empty list $L_{H_2}$. On input $I{D}_i,R_i,I{D}_{i,j},R_{i,j}$$(1\le i\le n,1\le j\le m)$, $\mathcal{C}$ does the following:
  • If there is a tuple $(I{D}_i,R_i,I{D}_{i,j},R_{i,j},{\alpha }_{i,j})$ on $L_{H_2}$, $\mathcal{C}$ returns ${\alpha }_{i,j}$ as the answer.
  • Otherwise, $\mathcal{C}$ chooses a random number ${\alpha }_{i,j}\in Z_q^{*}$ and adds $(I{D}_i,R_i,I{D}_{i,j},R_{i,j},{\alpha }_{i,j})$ to $L_{H_2}$. Then $\mathcal{C}$ returns ${\alpha }_{i,j}$ as the answer.
• $H_3$ query: $\mathcal{C}$ keeps an initially empty list $L_{H_3}$. On input $x,y$$(1\le x\le n,1\le y\le m)$, $\mathcal{C}$ does the following:
  • If there is a tuple $(x,y,f_{x,y})$ on $L_{H_3}$, $\mathcal{C}$ returns $f_{x,y}$ as the answer.
  • Otherwise, $\mathcal{C}$ chooses a random number $f_{x,y}\in Z_q^{*}$ and adds $(x,y,f_{x,y})$ to $L_{H_3}$. Then, $\mathcal{C}$ returns $f_{x,y}$ as the answer.
• $H_4$ query: $\mathcal{C}$ keeps an initially empty list $L_{H_4}$. On input a message ℧, $\mathcal{C}$ does the following:
  • If there is a tuple $(\mho ,\varpi )$ on $L_{H_4}$, $\mathcal{C}$ returns $\varpi$ as the answer.
  • Otherwise, $\mathcal{C}$ chooses a random number string $\varpi \in {\{0,1\}}^{\tau }$ and adds $(\mho ,\varpi )$ to $L_{H_4}$. Then, $\mathcal{C}$ returns $\varpi$ as the answer.
• DPKG.Extract: $\mathcal{C}$ keeps an initially empty list $L_{DPKG}$. On input $I{D}_i$$(1\le i\le n)$, $\mathcal{C}$ does the following:
  • If there is a tuple $(I{D}_i,r_i,R_i,S{K}_i)$ on $L_{DPKG}$, $\mathcal{C}$ returns $R_i$ as the answer.
  • Otherwise, $\mathcal{C}$ randomly chooses ${\alpha }_i,r_i\in Z_q^{*}$ and proceeds as follows:

    (a)

    If $I{D}_i\ne I{D}_{DPKG}^{*}$, $\mathcal{C}$ computes $R_i=r_i·P-{\alpha }_i·P{K}_{root}$ and $S{K}_i=r_i·Q$.

    (b)

    Else, $\mathcal{C}$ computes $R_i={\alpha }_i·P$, and sets $S{K}_i=null$.

    Then, $\mathcal{C}$ adds $(I{D}_i,r_i,R_i,S{K}_i)$ to $L_{DPKG}$ and adds $(I{D}_i,R_i,{\alpha }_i)$ to $L_{H_1}$. Then $\mathcal{C}$ returns $R_i$ as the answer.
• Member.Extract: $\mathcal{C}$ keeps an initially empty list $L_{member}$. On input $(I{D}_i,I{D}_{i,j})$, $\mathcal{C}$ does the following:
  • If there is a tuple $(I{D}_i,R_i,I{D}_{i,j},r_{i,j},R_{i,j},S{K}_{i,j})$ on $L_{member}$, $\mathcal{C}$ returns $R_{i,j}$ as the answer.
  • Otherwise, $\mathcal{C}$ randomly chooses ${\alpha }_{i,j},r_{i,j}\in Z_q^{*}$ and proceeds as follows:

    (a)

    If $I{D}_i\ne I{D}_{DPKG}^{*}$, $\mathcal{C}$ computes $R_{i,j}=r_{i,j}·P$ and $S{K}_{i,j}=S{K}_i+{\alpha }_{i,j}·r_{i,j}·Q$.

    (b)

    Else, $\mathcal{C}$ does the following:

    i.

    If $I{D}_{i,j}\ne I{D}_U^{*}$, $\mathcal{C}$ computes $R_{i,j}={\alpha }_{i,j}^{-1}·(r_{i,j}·P-{\alpha }_i·P{K}_{root}-R_i)$ and $S{K}_{i,j}=r_{i,j}·Q$.

    ii.

    Else, $\mathcal{C}$ computes $R_{i,j}=r_{i,j}·P$, and sets $S{K}_{i,j}=null$.

    Subsequently, $\mathcal{C}$ adds $(I{D}_i,R_i,I{D}_{i,j},r_{i,j},R_{i,j},S{K}_{i,j})$ to $L_{member}$ and adds $(I{D}_i,R_i,$

    $I{D}_{i,j},R_{i,j},{\alpha }_{i,j})$ to $L_{H_2}$. Then, $\mathcal{C}$ returns $R_{i,j}$ as the answer.

• Execute: $\mathcal{C}$ keeps an initially empty list $L_{Execute}$. $\mathcal{C}$ does the following:
  • If $I{D}_i\ne I{D}_{DPKG}^{*}$ and $I{D}_{i,j}\ne I{D}_U^{*}$, or $I{D}_i=I{D}_{DPKG}^{*}$ and $I{D}_{i,j}\ne I{D}_U^{*}$:

    (a)

    $\mathcal{C}$ chooses a random number ${\eta }_{i,j}\in Z_q^{*}$ and computes $T_{i,j}=r_{i,j}·P+f_{x,y}^{-1}·t_{1-(i-1)·n-j}$.

    (b)

    For $1\le x\le n,1\le y\le m,x\ne i$ or $y\ne j$, $\mathcal{C}$ computes $S_{i,j}(x,y)=S{K}_{i,j}+f_{x,y}·r_{i,j}·Q+t_{k+1-(i-1)·n-j}$.

    (c)

    $\mathcal{C}$ adds $(I{D}_{i,j},{\eta }_{i,j},null)$ to $L_{Execute}$.

  • Else $I{D}_i=I{D}_{DPKG}^{*}$ and $I{D}_{i,j}=I{D}_U^{*}$:

    (a)

    $\mathcal{C}$ chooses a random number ${\eta }_{i,j}\in Z_q^{*}$ and computes $T_{i,j}=f_{x,y}^{-1}(r_{i,j}·P-{\displaystyle \sum _{h=1}^{N,h\ne (i-1)·n+j}}{t}_{k-h+1}-R_i-{\alpha }_i·P{K}_{root}-{\alpha }_{i,j}·P)$.

    (b)

    For $1\le x\le n,1\le y\le m,x\ne i$ or $y\ne j$, $\mathcal{C}$ calculates $S_{i,j}(x,y)=r_{i,j}·Q-{\displaystyle \sum _{h=1}^{N,h\ne (i-1)·n+j}}{t}_{2k-h+1}$.

    (c)

    $\mathcal{C}$ adds $(I{D}_{i,j},{\eta }_{i,j},null)$ to $L_{Execute}$.

    $\mathcal{C}$ publishes $M_{i,j}=(R_i,R_{i,j},T_{i,j},\left\{S_{i,j}(x,y)\right\}(1\le x\le n,1\le y\le m,x\ne i$ or $y\ne j))$
• Ek.Reveal: $\mathcal{C}$ returns $ek=(W,Q)$.
• Test: At some point, $\mathcal{A}$ chooses two messages $m_0,m_1(\left|m_1\right|=\left|m_2\right|)$ on which $\mathcal{A}$ wishes to be challenged and send these messages to $\mathcal{C}$. Then, $\mathcal{C}$ does the following:
  • For $1\le i\le n,1\le j\le m$, $\mathcal{C}$ obtains $(I{D}_i,r_i,R_i,S{K}_i)$ from L and $(I{D}_i,R_i,I{D}_{i,j},r_{i,j},$
    $R_{i,j},S{K}_{i,j})$ from $L_{member}$.
  • $\mathcal{C}$ obtains $({\eta }_{1,1},\cdots ,{\eta }_{1,m},\cdots ,{\eta }_{n,1},\cdots ,{\eta }_{n,m})$ from $L_{Send}$.
  • $\mathcal{C}$ computes the group public encryption key $ek=(W,\Omega )$. Then, $\mathcal{C}$ does as follows:

    (a)

    $W={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}{\eta }_{i,j}·P$.

    (b)

    $\Omega =\widehat{e}({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j}),Q)=\widehat{e}({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j}),a^k·P)$.

  • $\mathcal{C}$ generates the ciphertext $(C_1,C_2,C_3)$. Then, $\mathcal{C}$ does the following:

    (a)

    $\mathcal{C}$ sets $C_1=I$ and $C_2=I·({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}{\eta }_{i,j})$.

    (b)

    $\mathcal{C}$ chooses a random string $\Lambda \in {\{0,1\}}^{\tau }$ and $b\in \{0,1\}$. Then $\mathcal{C}$ computes $C_3=m_b\oplus \Lambda$.

  • $\mathcal{A}$ returns $(C_1,C_2,C_3)$ to $\mathcal{A}$. Note that, $\mathcal{A}$ cannot recognize that $(C_1,C_2,C_3)$ is not a proper ciphertext, unless $\mathcal{A}$ has executed an $H_4$ query on $D=\widehat{e}({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j})·a^k,I)$.

Response: $\mathcal{A}$ finishes querying and returns $b^{\prime }\in \{0,1\}$ as the guess. If $b=b^{\prime }$, $\mathcal{A}$ has recognized that $(C_1,C_2,C_3)$ is not a proper ciphertext and has executed an $H_4$ query on $D=\widehat{e}({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j})·a^k,I)$. Then, $\mathcal{C}$ randomly chooses a tuple $(\mho ,\varpi )$ from $L_{H_4}$.

Subsequently, $\mathcal{C}$ constructs another random number oracle $H_1^{\prime }$ which has the same probability distribution as $H_1$. $\mathcal{C}$ uses $H_1^{\prime }$ to replace $H_1$ and executes the game with $\mathcal{A}$ again. If $\mathcal{A}$ can also return the right guess, $\mathcal{A}$ has executed an $H_4$ query on $D^{\prime }=\widehat{e}({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i^{{}^{\prime }}·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j}·a^k),I)$. Then, $\mathcal{C}$ randomly chooses a tuple $({\mho }^{{}^{\prime }},{\varpi }^{{}^{\prime }})$ from $H_4$, and returns ${({\varpi }_{i,j}·{({\varpi }_{i,j}^{{}^{\prime }})}^{-1})}^{-{\displaystyle \sum _{i=1}^n}m·({\alpha }_i-{\alpha }_i^{{}^{\prime }})}$ as the answer to this k-BDHE challenge. Note that, only if $\varpi =D$ and ${\varpi }^{\prime }=D^{\prime }$, that the above answer ${({\varpi }_{i,j}·{({\varpi }_{i,j}^{{}^{\prime }})}^{-1})}^{-{\displaystyle \sum _{i=1}^n}m·({\alpha }_i-{\alpha }_i^{{}^{\prime }})}$ is equal to $\widehat{e}{(P,I)}^{a^{k+1}}$. The proof is as follows.

$$\begin{array}{cc}\hfill & {\varpi }_{i,j}·{({\varpi }_{i,j}^{{}^{\prime }})}^{-1}\hfill \\ \hfill & =N·{(N^{\prime })}^{-1}\hfill \\ \hfill & =\widehat{e}({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i·P{K}_{root}+R_i+{\alpha }_{U_{i,j}}·R_{i,j})·a^k,I)\hfill \\ & ·\widehat{e}{({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i^{{}^{\prime }}·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j})·a^k,I)}^{-1}\hfill \\ \hfill & =\widehat{e}({\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}({\alpha }_i·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j}-{\alpha }_i^{{}^{\prime }}·P{K}_{root}+R_i+{\alpha }_{i,j}·R_{i,j})·a^k,I)\hfill \\ \hfill & =\widehat{e}({\displaystyle \sum _{i=1}^n}m·({\alpha }_i·P{K}_{root}-{\alpha }_i^{{}^{\prime }}·P{K}_{root})·a^k,I)\hfill \\ \hfill & =\widehat{e}({\displaystyle \sum _{i=1}^n}m·({\alpha }_i·a·P-{\alpha }_i^{{}^{\prime }}·a·P)·a^k,I)\hfill \\ \hfill & =\widehat{e}({\displaystyle \sum _{i=1}^n}m·({\alpha }_i-{\alpha }_i^{{}^{\prime }})·a^{k+1}·P,I)\hfill \\ \hfill & =\widehat{e}{({\displaystyle \sum _{i=1}^n}{a}^{k+1}·P,I)}^{{\displaystyle \sum _{i=1}^n}m·({\alpha }_i-{\alpha }_i^{{}^{\prime }})}\hfill \end{array}$$

 □

7. Performance Analysis

In this section, the performance of the IB-CD-AAGKA protocol is analyzed. Due to the limited resources of mobile terminals, we adopt the following five metrics, i.e., the computational complexity, the computational cost, the communication complexity, the communication cost and the energy consumption. As mentioned in Section 2, most works have shortcomings in security or functionalities. Specifically, the CCAGKA protocols [13,18,19,20,24] have the limitation of sender restriction. In addition, the semi-centered AAGKA protocol [12] faces single node failure. To our best knowledge, only schemes [11,15] are distributed and sender-unrestricted. Thus, we take a performance comparison between the proposed protocol and the schemes [11,15].

7.1. Computational Complexity and Cost

The computational complexity relates to the number of cryptographic operations of a group member in the cross-domain group key agreement phase. The symbols $T_{mul}$, $T_{add}$, $T_{bp}$, and $T_h$ denote the computing time for a scalar multiplication in $G_1$, an addition in $G_1$, a bilinear pairing, and a hash function, respectively. The computational complexity is analyzed in the following.

The cross-domain group key agreement in the IB-CD-AAGKA protocol comprises four algorithms, namely GenKeyParams, BVerify, GenEncKey, and GenDecKey. The computational complexity of GenKeyParams is $(2N+1)T_{mul}+N·T_{add}+N·T_h$. The computational complexity of BVerify is $3(N-1)·T_{mul}+(5N-7)T_{add}+(2N-1)T_h+2T_{bp}$. The computational complexity of GenEncKey is $2T_{mul}+(N+2)T_{add}+2T_h+T_{bp}$. Because, the part of $\Omega$, which is ${\displaystyle \sum _{x=1}^n}{\displaystyle \sum _{y=1}^m}({\alpha }_x·P{K}_{root}+R_x+{\alpha }_{x,y}·R_{x,y})$$(x\ne i$ or $y\ne j)$, has been computed in BVerify. In GenDecKey, the computational complexity is $T_{add}$, because ${\displaystyle \sum _{x=1}^n}{\displaystyle \sum _{y=1}^m}{S}_{x,y}(i,j)$$(x\ne i$ or $y\ne j)$ has also been calculated in BVerify. The computational complexity of the IB-CD-AAGKA protocol is $5N·T_{mul}+(7N-4)T_{add}+3T_{bp}+(3N+1)T_h$. Moreover, as shown in the Table 3, the computational complexity of scheme [11] is $(3N+2)T_{mul}+2N·T_{bp}$ and the computational complexity of scheme [15] is $(N+4)T_{mul}+(2N-1)T_{add}+3N·T_{bp}$.

Table 3. The performance comparison between the proposed protocol and the schemes [11,15].

Performance Metrics	Proposed Protocol	Zhang et al. [11]	Zhang et al. [15]
Computational complexity	$5N·T_{mul}$ $+(7N-4)T_{add}$ $+3T_{bp}+(3N+1)T_h$	$(3N+2)T_{mul}$ $+2N·T_{bp}$	$(N+4)T_{mul}$ $+(2N-1)T_{add}+3N·T_{bp}$
Computational cost (ms)	$4.103N+16.743$	$13.621N+1.634$	$17.571N+3.266$
Length of sent messages	$(N+2)\left|G\right|+2l$	$N·\left|G\right|+2l$	$(N+3)\left|G\right|+l$
Length of received messages	$4(N-1)\left|G\right|$ $+2(N-1)l$	$2(N-1)\left|G\right|$${}^1$ $+2(N-1)l$	$5(N-1)\left|G\right|$${}^2$ $+(N-1)l$
Length of total messages	$(5N-2)\left|G\right|$ $+2N·l$	$(3N-2)\left|G\right|$ $+2N·l$	$(6N-2)\left|G\right|$ $+N·l$
Communication cost (bits)	$5440N-2048$	$3392N-2048$	$6304N-2048$
Energy Consumption (mJ)	$46.053N+141.190$	$121.810N+17.077$	$152.115N+35.694$

${}^1$ The authors of [15] believe, in their scheme, the number of parameters in received messages is $N+4$. However, the authors of [27] point out that this value is incorrect and give a new value, which is $4(N-1)$. We further recounted the number of parameters in received messages based on two types of parameters, i.e., identities, and points on group $G_1$ or $G_2$. The results are shown in the Table 3, which is $2(N-1)\left|G\right|+2(N-1)l$. The total number of parameters is $2(N-1)+2(N-1)=4(N-1)$, which is the same as the value provided by [27]; ${}^2$ In the schemes [11,15], each group member’s secret parameter of group keys is encrypted separately by other members’ public keys, and the encrypted parameters are published. The scheme [11] assumes that each group member only receives the parameters encrypted by his/her public key, while the scheme [15] assumes that group members receive all the encrypted parameters. For comparison, we adopt the assumption in the scheme [11] and recalculate the length of received messages in scheme [15]. Compared with [15], the recalculated length of received messages is smaller.

To calculate the computational cost, we adopt the values provided by the literature [25], where $T_{mul}=0.817$ ms, $T_{add}=0.002$ ms, $T_{bp}=5.5832$ ms, and $T_h=0.0012$ ms. Their experiment was run on a Windows 7 machine with an Intel I7-6700 processor ($3.40$ GHZ) and 8GB memory, and the cryptographic operations were implemented using the MIRACL [26] cryptographic library. The bilinear pairing $\widehat{e}:G_1\times G_1\to G_2$ is built on 80-bit security levels. q is the order of the additive group $G_1$. p is a generator of $G_1$ and it is a point on the super singular elliptic curve $y^2=x^3+x(modp)$ with the embedding degree 2. Moreover, p is a 512-bit prime number and q is a 160-bit Solinas prime number. Then, the computational cost of our protocol is $(5N)\times 0.817+(7N-4)\times 0.002+3\times 5.5832+(3N+1)\times 0.0012=(4.103N+16.743)$ ms. The computational cost of [11] is $(3N+2)\times 0.817+2N\times 5.5832=(13.621N+1.634)$ ms and the one of [15] is $(N+4)\times 0.817+(2N-1)\times 0.002+3N\times 5.5832=(17.571N+3.266)$ ms. As we can see, the number of bilinear pairing in our protocol is 3. By comparison, the ones in the schemes [11,15] are $2N$ and $3N$. The reason for this is that the proposed protocol employs batch verification while in other schemes, group members can only verify one signature at a time. Moreover, our protocol has less computational cost than that of [11,15], when $N\ge 2$ and $N\ge 1$, respectively.

7.2. Communication Complexity and Cost

The communication complexity is relevant to the length of sent messages, the length of received messages and the length of total messages in the group key agreement phase. We also employ the symbols and values from [25], in which $\left|G\right|=1024$ bits denotes the length of an element in $G_1$ or $G_2$, and $l=160$ bits is the length of an identity. The analysis of communication complexity and communication cost is as follows.

As for each group member $U_{i,j}$, his/her sent messages are $M_{i,j}$$=(R_i,I{D}_i,R_{i,j},I{D}_{i,j},T_{i,j},\left\{S_{i,j}(x,y)\right\}(1\le x\le n,1\le y\le m,x\ne i$, $y\ne j))$ and the received messages are $\{R_x,I{D}_x,R_{x,y},I{D}_{x,y},T_{x,y},S_{x,y}(i,j)\}(1\le x\le n,1\le y\le m,x\ne i$, $y\ne j)$, where $R_i,R_{i,j},T_{i,j},S_{i,j}(x,y),R_x,R_{x,y},T_{x,y},S_{x,y}(i,j)\in G_1$ and $I{D}_i,I{D}_{i,j},I{D}_x,I{D}_{x,y}$ are identities of $DPK{G}_i$, $U_{i,j}$, $DPK{G}_x$ and $U_{x,y}$. Thus, the length of sent messages is $(N+2)\left|G\right|+2l$ and the length of received messages is $4(N-1)\left|G\right|+2(N-1)l$. The length of total messages is $(5N-2)\left|G\right|+2N·l$. The communication cost is $(5N-2)\times 1024+(2N)\times 160=(5440N-2048)$ bits.

Moreover, as shown in the Table 3, the communication cost of scheme [11] is $(3392N-2048)$ bits and the one of scheme [15] is $(6304N-2048)$ bits. Thus, the proposed protocol has more communication cost than that of [11] and less communication cost in than [15]. However, we found that in the group key agreement phase of [11], a group member’s sent messages do not include his/her own public key and the corresponding domain key. Both of them are not known by other members in the group. The length of the two keys is $2\left|G\right|$. Then, we recompute the communication complexity of [11], where the length of sent messages is $(N+2)\left|G\right|+2l$, the length of received messages is $4(N-1)\left|G\right|+2(N-1)l$, the length of total messages is $(5N-2)\left|G\right|+2N·l$ and the communication cost is $(5444N-2048)$ bits. In this condition, the IB-CD-AAGKA protocol has the same communication complexity and communication cost.

7.3. Energy Consumption

The computational and communication costs are the main factors that impact the energy consumption. We adopt the energy consumption values of cryptographic operations and transmission data provided by Tan et al. [28] and Xu et al. [27], where a “Strong ARM” microprocessor running at 133 MHz performing a scalar multiplication, a point addition, hash function and bilinear pairing consumes $8.8$, $0.001085$, $0.000108$ and 47 mJ, respectively. An IEEE $802.11$ Spectrum24 WLAN card requires $0.00066$ mJ for the transmission of 1 bit and $0.00031$ mJ for the reception of 1 bit.

Then, we calculate the energy consumption of our protocol, which is $(5N)\times 8.8+(7N-4)\times 0.001085+3\times 47+(3N+1)\times 0.000108+((N+2)\times 1024+2\times 160)\times 0.00066+((5N-2)\times 1024+(2N)\times 160)\times 0.00031=(46.053N+141.190)$ mJ. From Table 3, the energy cost of the scheme in [11] is $(121.810N+17.077)$ mJ and the one of the scheme in [15] is $(152.115N+35.694)$ mJ. Our protocol is more efficient than [11,15], when $N\ge 2$ and $N\ge 1$. The reason is the same as explained in Section 7.2.

8. Conclusions

To solve the efficiency problem of the existing cross-domain AAGKA protocols, this paper proposed a distributed IB-CD-AAGKA protocol with batch verification. The security analysis shows that our work achieves some typical security properties, i.e., secrecy, known-key security, and partial forward secrecy. Furthermore, the performance analysis indicates that the IB-CD-AAGKA protocol has lower computational and energy costs than those of [11,15]. With strong security and efficient performance, the proposed protocol is suitable for some resource-constrained environments, e.g., mobile computing networks.