A Quaternion Gated Recurrent Unit Neural Network for Sensor Fusion
Abstract
:1. Introduction
2. Previous Work on Quaternion Neural Networks
3. Proposed Quaternion Gated Recurrent Unit
3.1. Real-valued GRU
3.2. Quaternion Algebraic Representation and Operations
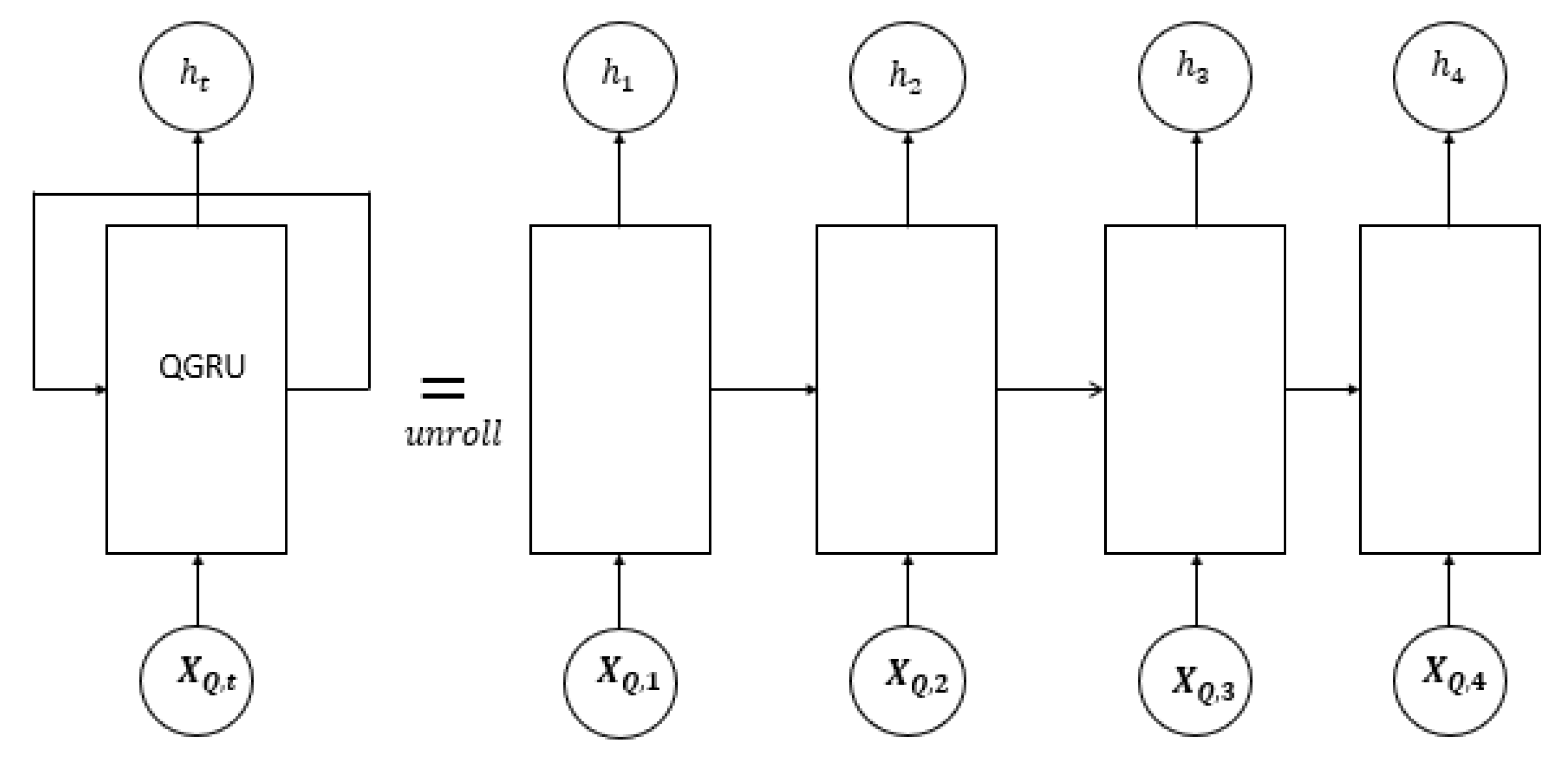
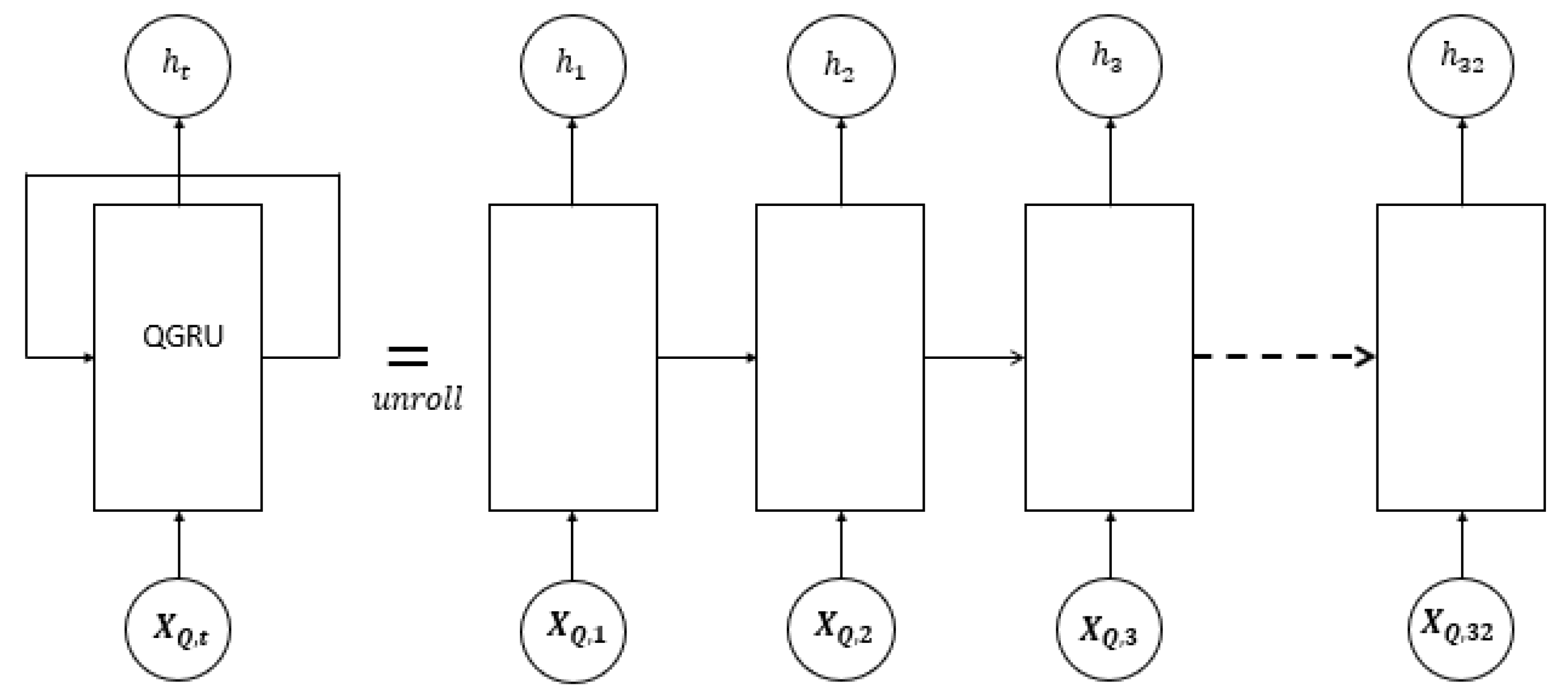
3.3. Quaternion-Valued Gated Recurrent Unit
3.3.1. Weight Initialisation
3.3.2. Gated Operations
3.3.3. Quaternion Backward Propagation through Time
4. QGRU Experiments on Sensor Fusion Applications
4.1. Vehicular Localisation Using Wheel Encoders
4.1.1. Dataset
4.1.2. Quaternion Features
4.2. Human Activity Recognition
4.2.1. Dataset
4.2.2. Quaternion Features
5. Results and Discussion
5.1. Challenging Vehicular Localisation Task
5.2. Human Activity Recognition (HAR) Task
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Purohit, H.; Tanabe, R.; Ichige, K.; Endo, T.; Nikaido, Y.; Suefusa, K.; Kawaguchi, Y. MIMII dataset: Sound dataset for malfunctioning industrial machine investigation and inspection. arXiv 2019, arXiv:1909.09347. [Google Scholar]
- Tsang, G.; Deng, J.; Xie, X. Recurrent neural networks for financial time-series modelling. In Proceedings of the International Conference on Pattern Recognition, Beijing, China, 20–24 August 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018; pp. 892–897. [Google Scholar] [CrossRef] [Green Version]
- El-Moneim, S.A.; Nassar, M.A.; Dessouky, M.I.; Ismail, N.A.; El-Fishawy, A.S.; Abd El-Samie, F.E. Text-independent speaker recognition using LSTM-RNN and speech enhancement. Multimed. Tools Appl. 2020, 79, 24013–24028. [Google Scholar] [CrossRef]
- Mao, W.; Wang, M.; Sun, W.; Qiu, L.; Pradhan, S.; Chen, Y.-C. RNN-based room scale hand motion tracking. In Proceedings of the 25th Annual International Conference on Mobile Computing and Networking, Los Cabos, Mexico, 21–25 October 2019; Association for Computing Machinery (ACM): New York, NY, USA, 2019; Volume 19, pp. 1–16. [Google Scholar] [CrossRef]
- Senturk, U.; Yucedag, I.; Polat, K. Repetitive neural network (RNN) based blood pressure estimation using PPG and ECG signals. In Proceedings of the ISMSIT 2018—2nd International Symposium on Multidisciplinary Studies and Innovative Technologies, Ankara, Turkey, 19–21 October 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Rajkomar, A.; Oren, E.; Chen, K.; Dai, A.M.; Hajaj, N.; Hardt, M.; Liu, P.J.; Liu, X.; Marcus, J.; Sun, M.; et al. Scalable and accurate deep learning with electronic health records. NPJ Digit. Med. 2018, 1, 18. [Google Scholar] [CrossRef] [PubMed]
- Nwe, T.L.; Dat, T.H.; Ma, B. Convolutional neural network with multi-task learning scheme for acoustic scene classification. In Proceedings of the 9th Asia-Pacific Signal and Information Processing Association Annual Summit and Conference, APSIPA ASC 2017, Kuala Lumpur, Malaysia, 12–15 December 2017; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018; pp. 1347–1350. [Google Scholar] [CrossRef]
- Susto, G.A.; Cenedese, A.; Terzi, M. Time-series classification methods: Review and Applications to power systems data. In Big Data Application in Power Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 179–220. ISBN 9780128119693. [Google Scholar]
- Nweke, H.F.; Teh, Y.W.; Al-garadi, M.A.; Alo, U.R. Deep learning algorithms for human activity recognition using mobile and wearable sensor networks: State of the art and research challenges. Expert Syst. Appl. 2018, 105, 233–261. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Peng, X.; Hu, L. Deep learning for sensor-based activity recognition: A survey. Pattern Recognit. Lett. 2019, 119, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Lu, X.; Markham, A.; Trigoni, N. IONet: Learning to cure the curse of drift in inertial odometry. arXiv 2018, arXiv:1802.02209. [Google Scholar]
- Dai, H.F.; Bian, H.W.; Wang, R.Y.; Ma, H. An INS/GNSS integrated navigation in GNSS denied environment using recurrent neural network. Def. Technol. 2019. [Google Scholar] [CrossRef]
- Fang, W.; Jiang, J.; Lu, S.; Gong, Y.; Tao, Y.; Tang, Y.; Yan, P.; Luo, H.; Liu, J. A LSTM algorithm estimating pseudo measurements for aiding INS during GNSS Signal outages. Remote Sens. 2020, 12, 256. [Google Scholar] [CrossRef] [Green Version]
- Brossard, M.; Barrau, A.; Bonnabel, S. AI-IMU dead-reckoning. IEEE Trans. Intell. Veh. 2020. [Google Scholar] [CrossRef]
- Onyekpe, U.; Palade, V.; Kanarachos, S. Learning to localise automated vehicles in challenging environments using Inertial Navigation Systems (INS). Appl. Sci. 2021, 11, 1270. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- Parcollet, T.; Morchid, M.; Linarès, G. A survey of quaternion neural networks. Artif. Intell. Rev. 2020, 53, 2957–2982. [Google Scholar] [CrossRef]
- Matsui, N.; Isokawa, T.; Kusamichi, H.; Peper, F.; Nishimura, H. Quaternion neural network with geometrical operators. J. Intell. Fuzzy Syst. 2004, 15, 149–164. [Google Scholar]
- Kusamichi, H.; Kusamichi, H.; Isokawa, T.; Isokawa, T.; Matsui, N.; Matsui, N.; Ogawa, Y.; Ogawa, Y.; Maeda, K.; Maeda, K. A new scheme for color night vision by quaternion neural network. In Proceedings of the 2nd International Conference on Autonomous Robots and Agents (ICARA2004), Palmerston North, New Zealand, 13–15 December 2004; pp. 101–106. [Google Scholar]
- Parcollet, T.; Ravanelli, M.; Morchid, M.; Linarès, G.; Trabelsi, C.; De Mori, R.; Bengio, Y. Quaternion Recurrent Neural Networks. 2019. Available online: https://github.com/Orkis-Research/Pytorch-Quaternion-Neural-Networks (accessed on 16 June 2020).
- Choi, J.; Wang, Z.; Venkataramani, S.; Chuang, P.I.-J.; Srinivasan, V.; Gopalakrishnan, K. PACT: Parameterized Clipping Activation for Quantized Neural Networks. arXiv 2018, arXiv:1805.06085. [Google Scholar]
- Isokawa, T.; Kusakabe, T.; Matsui, N.; Peper, F. Quaternion neural network and its application. In Proceedings of the Lecture Notes in Artificial Intelligence (Subseries of Lecture Notes in Computer Science); Springer: Berlin/Heidelberg, Germany, 2003; Voluem 2774, Part 2, pp. 318–324. [Google Scholar] [CrossRef]
- Parcollet, T.; Morchid, M.; Linares, G. Quaternion convolutional neural networks for heterogeneous image processing. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 8514–8518. [Google Scholar] [CrossRef] [Green Version]
- Moya-Sánchez, E.U.; Xambó-Descamps, S.; Sánchez Pérez, A.; Salazar-Colores, S.; Martínez-Ortega, J.; Cortés, U. A bio-inspired quaternion local phase CNN layer with contrast invariance and linear sensitivity to rotation angles. Pattern Recognit. Lett. 2020, 131, 56–62. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Li, G.; Shi, Y. A quaternion-embedded capsule network model for knowledge graph completion. IEEE Access 2020, 8, 100890–100904. [Google Scholar] [CrossRef]
- Özcan, B.; Kınlı, F.; Kıraç, F. Quaternion Capsule Networks. arXiv 2020. Available online: https://github.com/Boazrciasn/Quaternion-Capsule-Networks.git (accessed on 24 February 2021).
- Grassucci, E.; Comminiello, D.; Uncini, A. QUATERNION-VALUED VARIATIONAL AUTOENCODER. arXiv 2020, arXiv:2010.11647v1. [Google Scholar]
- Nguyen, D.Q.; Nguyen, T.D.; Phung, D. Quaternion graph neural networks. arXiv 2020. Available online: https://github.com/daiquocnguyen/QGNN (accessed on 24 February 2021).
- Parcollet, T.; Morchid, M.; Linares, G.; De Mori, R. Bidirectional quaternion long short-term memory recurrent neural networks for speech recognition. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 8519–8523. [Google Scholar]
- Onyekpe, U.; Kanarachos, S.; Palade, V.; Christopoulos, S.-R.G. Learning uncertainties in wheel odometry for vehicular localisation in GNSS deprived environments. In Proceedings of the International Conference on Machine Learning Applications (ICMLA), Miami, FL, USA, 14–17 December 2020; pp. 741–746. [Google Scholar]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. A public domain dataset for human activity recognition using smartphones. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 24–26 April 2013. [Google Scholar]
- Hirose, A.; Yoshida, S. Generalization characteristics of complex-valued feedforward neural networks in relation to signal coherence. IEEE Trans. Neural Networks Learn. Syst. 2012, 23, 541–551. [Google Scholar] [CrossRef]
- Nitta, T. On the critical points of the complex-valued neural network. In Proceedings of the ICONIP 2002 9th International Conference on Neural Information Processing: Computational Intelligence for the E-Age, Singapore, 18–22 November 2002; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2002; Volume 3, pp. 1099–1103. [Google Scholar] [CrossRef]
- Yao, W.; Zhou, D.; Zhan, L.; Liu, Y.; Cui, Y.; You, S.; Liu, Y. GPS signal loss in the wide area monitoring system: Prevalence, impact, and solution. Electr. Power Syst. Res. 2017, 147, 254–262. [Google Scholar] [CrossRef]
- Luo, L.; Feng, H.; Ding, L. Color image compression based on quaternion neural network principal component analysis. In Proceedings of the 2010 International Conference on Multimedia Technology, ICMT 2010, Ningbo, China, 29–31 October 2010. [Google Scholar] [CrossRef]
- Greenblatt, A.; Mosquera-Lopez, C.; Agaian, S. Quaternion neural networks applied to prostate cancer gleason grading. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2013, Manchester, UK, 13–16 October 2013; pp. 1144–1149. [Google Scholar] [CrossRef]
- Shang, F.; Hirose, A. Quaternion neural-network-based PolSAR land classification in poincare-sphere-parameter space. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5693–5703. [Google Scholar] [CrossRef]
- Parcollet, T.; Morchid, M.; Linares, G. Deep quaternion neural networks for spoken language understanding. In Proceedings of the 2017 IEEE Automatic Speech Recognition and Understanding Workshop, ASRU 2017, Okinawa, Japan, 16–20 December 2017; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018; pp. 504–511. [Google Scholar] [CrossRef] [Green Version]
- Parcollet, T.; Morchid, M.; Linarès, G. Quaternion Denoising Encoder-Decoder for Theme Identification of Telephone Conversations. 2017. 3325–3328. Available online: https://hal.archives-ouvertes.fr/hal-02107632 (accessed on 30 December 2020). [CrossRef] [Green Version]
- Pavllo, D.; Feichtenhofer, C.; Auli, M.; Grangier, D. Modeling human motion with quaternion-based neural networks. Int. J. Comput. Vis. 2020, 128, 855–872. [Google Scholar] [CrossRef] [Green Version]
- Comminiello, D.; Lella, M.; Scardapane, S.; Uncini, A. Quaternion convolutional neural networks for detection and localization of 3D sound events. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 8533–8537. [Google Scholar]
- Zhu, X.; Xu, Y.; Xu, H.; Chen, C. Quaternion Convolutional Neural Networks. 2019. Available online: https://arxiv.org/abs/1903.00658 (accessed on 30 December 2020).
- Tay, Y.; Zhang, A.; Tuan, L.A.; Rao, J.; Zhang, S.; Wang, S.; Fu, J.; Hui, S.C. Lightweight and efficient neural natural language processing with quaternion networks. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 1494–1503. [Google Scholar]
- Parcollet, T.; Ravanelli, M.; Morchid, M.; Linarès, G.; De Mori, R. Speech recognition with quaternion neural networks. arXiv 2018, arXiv:1811.09678. [Google Scholar]
- Parcollet, T.; Morchid, M.; Linares, G.; De Mori, R. Quaternion convolutional neural networks for theme identification of telephone conversations. In Proceedings of the 2018 IEEE Spoken Language Technology Workshop, SLT 2018, Athens, Greece, 18–21 December 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 685–691. [Google Scholar] [CrossRef]
- Tran, T.; You, D.; Lee, K. Quaternion-based self-attentive long short-term user preference encoding for recommendation. In Proceedings of the International Conference on Information and Knowledge Management, Galway, Ireland, 19–23 October 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1455–1464. [Google Scholar] [CrossRef]
- Chen, B.; Gao, Y.; Xu, L.; Hong, X.; Zheng, Y.; Shi, Y.-Q. Color image splicing localization algorithm by quaternion fully convolutional networks and superpixel-enhanced pairwise conditional random field. MBE 2019, 16, 6907–6922. [Google Scholar] [CrossRef]
- Jin, L.; Zhou, Y.; Liu, H.; Song, E. Deformable quaternion gabor convolutional neural network for color facial expression recognition. In Proceedings of the International Conference on Image Processing, ICIP, Abu Dhabi, United Arab Emirates, 25–28 October 2020; IEEE Computer Society: Washington, DC, USA, 2020; pp. 1696–1700. [Google Scholar] [CrossRef]
- Qiu, X.; Parcollet, T.; Ravanelli, M.; Lane, N.; Morchid, M. Quaternion neural networks for multi-channel distant speech recognition. In Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH, Shanghai, China, 14–18 September 2020; International Speech Communication Association: Baixas, France, 2020; pp. 329–333. [Google Scholar] [CrossRef]
- Kumar, D.; Kumar, N.; Mishra, S. QUARC: Quaternion multi-modal fusion architecture for hate speech classification. arXiv 2020. Available online: https://github.com/smlab-niser/quaternionFusion (accessed on 24 February 2021).
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the EMNLP 2014—2014 Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014. [Google Scholar] [CrossRef]
- Onyekpe, U.; Kanarachos, S.; Palade, V.; Christopoulos, S.-R.G. Vehicular localisation at high and low estimation rates during GNSS outages: A deep learning approach. In Deep Learning Applications, Volume 2. Advances in Intelligent Systems and Computing; Wani, M.A., Khoshgoftaar, T.M., Palade, V., Eds.; Springer: Singapore, 2020; Volume 1232, pp. 229–248. ISBN 978-981-15-6758-2. [Google Scholar]
- Vincenty, T. Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Surv. Rev. 1975, 23, 88–93. [Google Scholar] [CrossRef]
- Pietrzak, M. Vincenty · PyPI. Available online: https://pypi.org/project/vincenty/ (accessed on 12 April 2019).
- Onyekpe, U.; Palade, V.; Kanarachos, S.; Szkolnik, A. IO-VNBD: Inertial and odometry benchmark dataset for ground vehicle positioning. Data Br. 2021, 35, 106885. [Google Scholar] [CrossRef] [PubMed]
- Gal, Y.; Ghahramani, Z. A theoretically grounded application of dropout in recurrent neural networks. arXiv 2016, arXiv:1512.05287. [Google Scholar]


| Challenging Scenarios | IO-VNB Data Subset |
|---|---|
| Hard Brake (HB) | V-Vw16b |
| V-Vw17 | |
| V-Vta9 | |
| Sharp Cornering and Successive Left and Right Turns (SLR) | V-Vw6 |
| V-Vw7 | |
| V-Vw8 | |
| Wet Road (WR) | V-Vtb8 |
| V-Vtb11 | |
| V-Vtb13 |
| Number of Neurons | HB (m) | SLR (m) | WR (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Physical Model | GRU | QGRU | Physical Model | GRU | QGRU | Physical Model | GRU | QGRU | |
| 4 | 9.99 | 5.16 | 3.02 | 8.19 | 3.46 | 1.31 | 5.36 | 3.3 | 2.29 |
| 8 | 3.63 | 2.9 | 2.16 | 1.24 | 3.26 | 2.42 | |||
| 16 | 3.55 | 2.86 | 1.8 | 1.24 | 3.41 | 2.24 | |||
| 32 | 3.52 | 2.94 | 1.31 | 1.24 | 3.38 | 2.09 | |||
| 64 | 3.15 | 2.94 | 1.58 | 1.3 | 3.42 | 2.25 | |||
| 128 | 3.58 | 3.13 | 1.32 | 1.32 | 2.36 | 2.09 | |||
| 256 | 3.76 | 3.14 | 1.36 | 1.44 | 2.48 | 2.35 | |||
| Number of Neurons | Number of Trainable Parameters | |
|---|---|---|
| GRU | QGRU | |
| 4 | 101 | 377 |
| 8 | 297 | 1137 |
| 16 | 977 | 3809 |
| 32 | 3489 | 13,761 |
| 64 | 13,121 | 52,097 |
| 128 | 50,817 | 202,497 |
| 256 | 199,937 | 798,209 |
| Number of Neurons | Classification Accuracy (%) | |
|---|---|---|
| GRU | QGRU | |
| 4 | 87.51 | 91.72 |
| 8 | 91.18 | 92.57 |
| 16 | 92.6 | 93.62 |
| 32 | 93.62 | 93.15 |
| 64 | 94.3 | 95.28 |
| 128 | 95.01 | 95.12 |
| 256 | 95.16 | 95.23 |
| Number of Neurons | Number of Trainable Parameters | |
|---|---|---|
| GRU | QGRU | |
| 4 | 203 | 815 |
| 8 | 495 | 2007 |
| 16 | 1367 | 5543 |
| 32 | 4263 | 17,223 |
| 64 | 14,663 | 59,015 |
| 128 | 53,895 | 216,327 |
| 256 | 206,087 | 825,063 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onyekpe, U.; Palade, V.; Kanarachos, S.; Christopoulos, S.-R.G. A Quaternion Gated Recurrent Unit Neural Network for Sensor Fusion. Information 2021, 12, 117. https://doi.org/10.3390/info12030117
Onyekpe U, Palade V, Kanarachos S, Christopoulos S-RG. A Quaternion Gated Recurrent Unit Neural Network for Sensor Fusion. Information. 2021; 12(3):117. https://doi.org/10.3390/info12030117
Chicago/Turabian StyleOnyekpe, Uche, Vasile Palade, Stratis Kanarachos, and Stavros-Richard G. Christopoulos. 2021. "A Quaternion Gated Recurrent Unit Neural Network for Sensor Fusion" Information 12, no. 3: 117. https://doi.org/10.3390/info12030117
APA StyleOnyekpe, U., Palade, V., Kanarachos, S., & Christopoulos, S.-R. G. (2021). A Quaternion Gated Recurrent Unit Neural Network for Sensor Fusion. Information, 12(3), 117. https://doi.org/10.3390/info12030117








