Adaptive Machine Learning for Robust Diagnostics and Control of Time-Varying Particle Accelerator Components and Beams
Abstract
:1. Introduction
Adaptive Machine Learning
2. Unknown Time-Varying Systems and Adaptive Feedback Control
3. Machine Learning for Time-Varying Systems
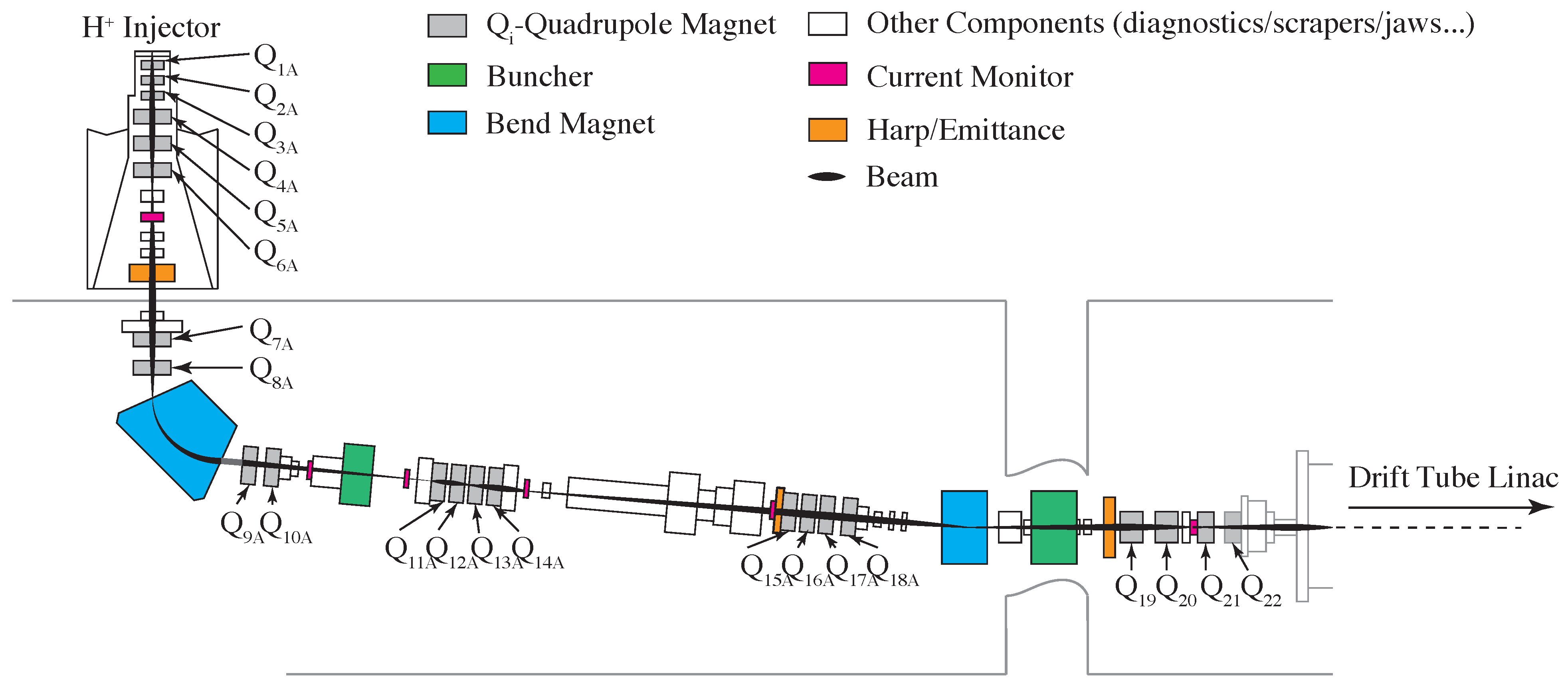
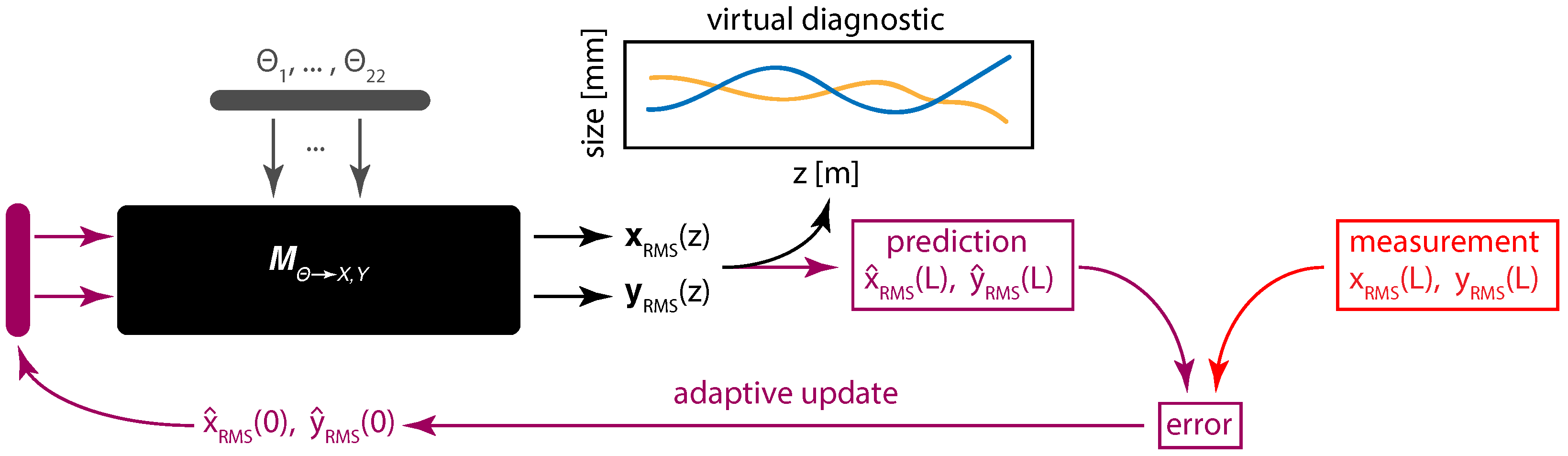
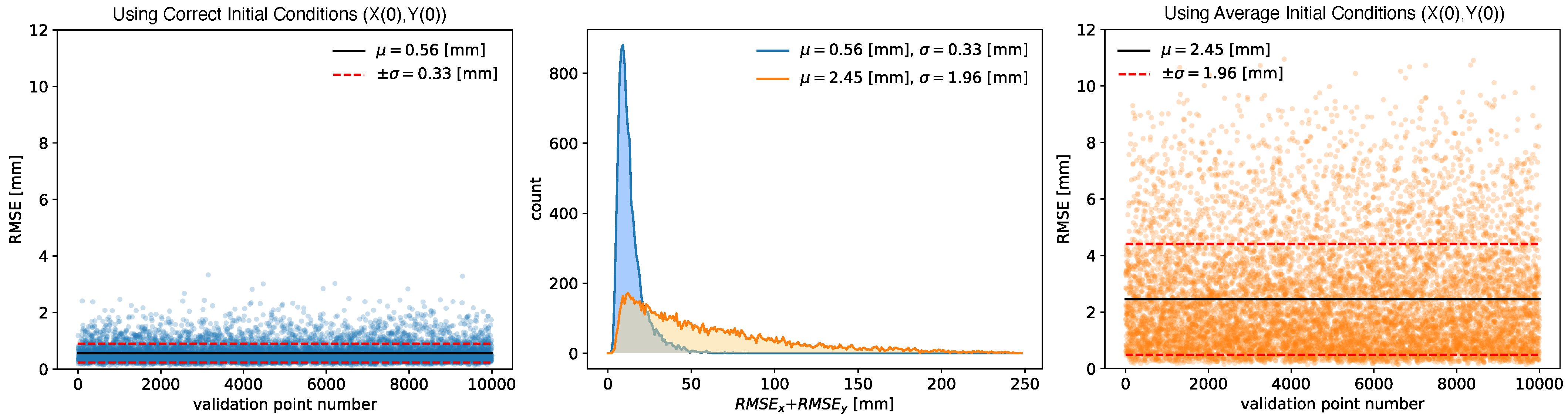
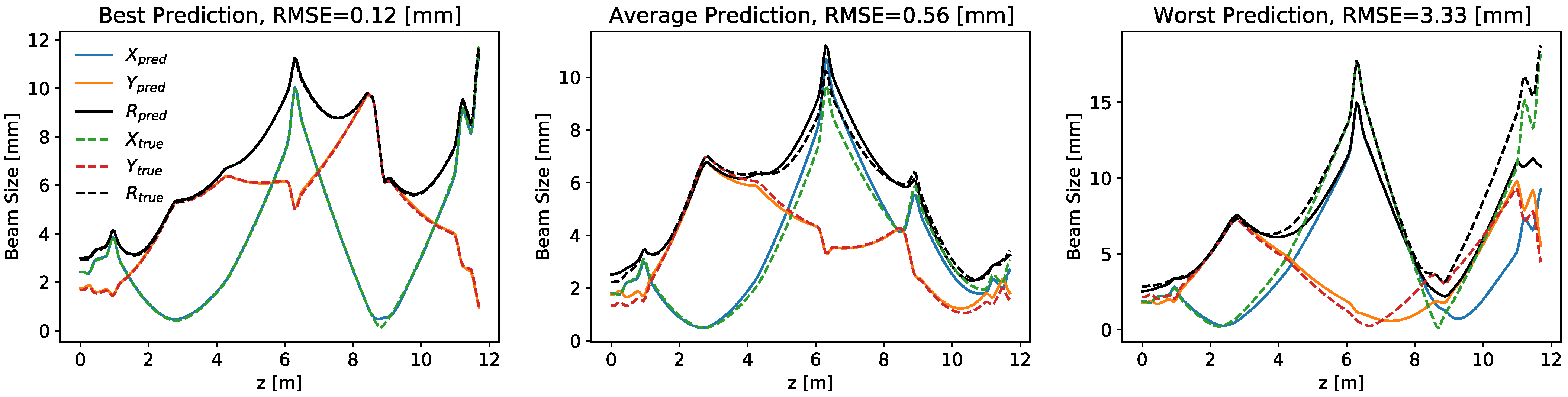
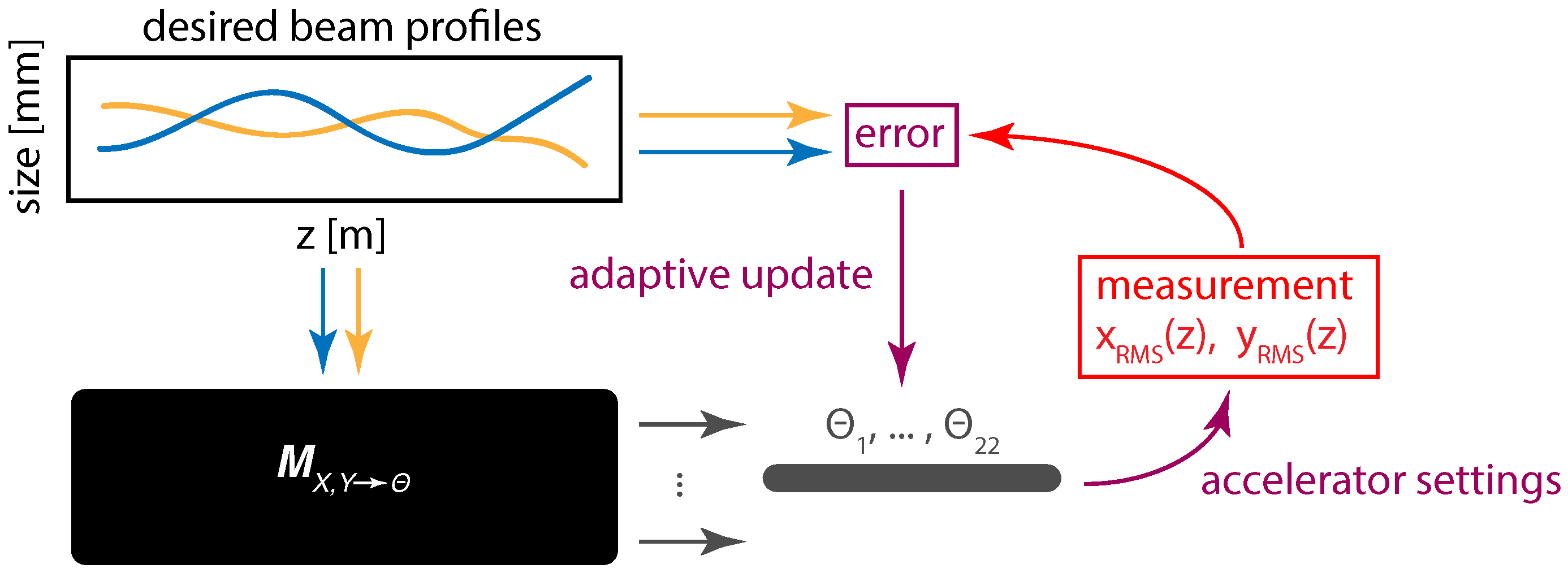
4. Controls and Diagnostics for a 22 Dimensional System
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Kleene, S.C. Representation of Events in Nerve Nets and Finite Automata; Technical Report; Rand Project Air Force: Santa Monica, CA, USA, 1951. [Google Scholar]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Li, Y.; Cheng, W.; Yu, L.H.; Rainer, R. Genetic algorithm enhanced by machine learning in dynamic aperture optimization. Phys. Rev. Accel. Beams 2018, 21, 054601. [Google Scholar] [CrossRef] [Green Version]
- Edelen, A.; Neveu, N.; Frey, M.; Huber, Y.; Mayes, C.; Adelmann, A. Machine learning for orders of magnitude speedup in multiobjective optimization of particle accelerator systems. Phys. Rev. Accel. Beams 2020, 23, 044601. [Google Scholar] [CrossRef] [Green Version]
- Kranjčević, M.; Riemann, B.; Adelmann, A.; Streun, A. Multiobjective optimization of the dynamic aperture using surrogate models based on artificial neural networks. Phys. Rev. Accel. Beams 2021, 24, 014601. [Google Scholar] [CrossRef]
- Emma, C.; Edelen, A.; Hogan, M.; O’Shea, B.; White, G.; Yakimenko, V. Machine learning-based longitudinal phase space prediction of particle accelerators. Phys. Rev. Accel. Beams 2018, 21, 112802. [Google Scholar] [CrossRef] [Green Version]
- Hanuka, A.; Emma, C.; Maxwell, T.; Fisher, A.S.; Jacobson, B.; Hogan, M.; Huang, Z. Accurate and confident prediction of electron beam longitudinal properties using spectral virtual diagnostics. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Chen, Y.; Brinker, F.; Decking, W.; Tomin, S.; Schlarb, H. Deep Learning-Based Autoencoder for Data-Driven Modeling of an RF Photoinjector. arXiv 2021, arXiv:2101.10437. [Google Scholar]
- McIntire, M.; Cope, T.; Ermon, S.; Ratner, D. Bayesian optimization of FEL performance at LCLS. In Proceedings of the 7th International Particle Accelerator Conference, Busan, Korea, 8–13 May 2016. [Google Scholar]
- Li, Y.; Rainer, R.; Cheng, W. Bayesian approach for linear optics correction. Phys. Rev. Accel. Beams 2019, 22, 012804. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Li, Y.; Balcewicz, M.; Neufcourt, L.; Cheng, W. Reconstruction of Storage Ring’s Linear Optics with Bayesian Inference. arXiv 2019, arXiv:1902.11157. [Google Scholar]
- Duris, J.; Kennedy, D.; Hanuka, A.; Shtalenkova, J.; Edelen, A.; Baxevanis, P.; Egger, A.; Cope, T.; McIntire, M.; Ermon, S.; et al. Bayesian optimization of a free-electron laser. Phys. Rev. Lett. 2020, 124, 124801. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Hao, Y.; Cheng, W.; Rainer, R. Analysis of beam position monitor requirements with Bayesian Gaussian regression. arXiv 2019, arXiv:1904.05683. [Google Scholar]
- Shalloo, R.; Dann, S.; Gruse, J.N.; Underwood, C.; Antoine, A.; Arran, C.; Backhouse, M.; Baird, C.; Balcazar, M.; Bourgeois, N.; et al. Automation and control of laser wakefield accelerators using Bayesian optimization. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
- Fol, E.; de Portugal, J.C.; Franchetti, G.; Tomás, R. Optics corrections using machine learning in the LHC. In Proceedings of the 2019 International Particle Accelerator Conference, Melbourne, Australia, 19–24 May 2019. [Google Scholar]
- Fol, E.; de Portugal, J.C.; Tomás, R. Unsupervised Machine Learning for Detection of Faulty Beam Position Monitors. In Proceedings of the 10th International Particle Accelerator Conference (IPAC’19), Melbourne, Australia, 19–24 May 2019; Volume 2668. [Google Scholar]
- Arpaia, P.; Azzopardi, G.; Blanc, F.; Bregliozzi, G.; Buffat, X.; Coyle, L.; Fol, E.; Giordano, F.; Giovannozzi, M.; Pieloni, T.; et al. Machine learning for beam dynamics studies at the CERN Large Hadron Collider. Nucl. Instruments Methods Phys. Res. Sect. A 2021, 985, 164652. [Google Scholar] [CrossRef]
- Adelmann, A. On nonintrusive uncertainty quantification and surrogate model construction in particle accelerator modeling. SIAM/ASA J. Uncertain. Quantif. 2019, 7, 383–416. [Google Scholar] [CrossRef]
- Hirlaender, S.; Bruchon, N. Model-free and Bayesian Ensembling Model-based Deep Reinforcement Learning for Particle Accelerator Control Demonstrated on the FERMI FEL. arXiv 2020, arXiv:2012.09737. [Google Scholar]
- Kain, V.; Hirlander, S.; Goddard, B.; Velotti, F.M.; Della Porta, G.Z.; Bruchon, N.; Valentino, G. Sample-efficient reinforcement learning for CERN accelerator control. Phys. Rev. Accel. Beams 2020, 23, 124801. [Google Scholar] [CrossRef]
- Bruchon, N.; Fenu, G.; Gaio, G.; Lonza, M.; O’Shea, F.H.; Pellegrino, F.A.; Salvato, E. Basic reinforcement learning techniques to control the intensity of a seeded free-electron laser. Electronics 2020, 9, 781. [Google Scholar] [CrossRef]
- Bruchon, N.; Fenu, G.; Gaio, G.; Lonza, M.; Pellegrino, F.A.; Salvato, E. Toward the application of reinforcement learning to the intensity control of a seeded free-electron laser. In Proceedings of the 2019 23rd International Conference on Mechatronics Technology (ICMT), Salerno, Italy, 23–26 October 2019; pp. 1–6. [Google Scholar]
- O’Shea, F.; Bruchon, N.; Gaio, G. Policy gradient methods for free-electron laser and terahertz source optimization and stabilization at the FERMI free-electron laser at Elettra. Phys. Rev. Accel. Beams 2020, 23, 122802. [Google Scholar] [CrossRef]
- Scheinker, A.; Krstić, M. Model-Free Stabilization by Extremum Seeking; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Dalesio, L.R.; Kozubal, A.; Kraimer, M. EPICS architecture. In Technical Report; Los Alamos National Lab.: Los Alamos, NM, USA, 1991. [Google Scholar]
- Agapov, I.; Geloni, G.; Tomin, S.; Zagorodnov, I. OCELOT: A software framework for synchrotron light source and FEL studies. Nucl. Instruments Methods Phys. Res. Sect. A 2014, 768, 151–156. [Google Scholar] [CrossRef]
- Scheinker, A.; Bohler, D.; Tomin, S.; Kammering, R.; Zagorodnov, I.; Schlarb, H.; Scholz, M.; Beutner, B.; Decking, W. Model-independent tuning for maximizing free electron laser pulse energy. Phys. Rev. Accel. Beams 2019, 22, 082802. [Google Scholar] [CrossRef] [Green Version]
- Scheinker, A.; Hirlaender, S.; Velotti, F.M.; Gessner, S.; Della Porta, G.Z.; Kain, V.; Goddard, B.; Ramjiawan, R. Online multi-objective particle accelerator optimization of the AWAKE electron beam line for simultaneous emittance and orbit control. AIP Adv. 2020, 10, 055320. [Google Scholar] [CrossRef]
- Scheinker, A.; Gessner, S. Adaptive method for electron bunch profile prediction. Phys. Rev. Spec. Top. Accel. Beams 2015, 18, 102801. [Google Scholar] [CrossRef] [Green Version]
- Scheinker, A.; Edelen, A.; Bohler, D.; Emma, C.; Lutman, A. Demonstration of model-independent control of the longitudinal phase space of electron beams in the linac-coherent light source with femtosecond resolution. Phys. Rev. Lett. 2018, 121, 044801. [Google Scholar] [CrossRef] [Green Version]
- Scheinker, A.; Cropp, F.; Paiagua, S.; Filippetto, D. Adaptive deep learning for time-varying systems with hidden parameters: Predicting changing input beam distributions of compact particle accelerators. arXiv 2021, arXiv:2102.10510. [Google Scholar]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 3. [Google Scholar]
- Wu, M. A note on stability of linear time-varying systems. IEEE Trans. Autom. Control 1974, 19, 162. [Google Scholar] [CrossRef]
- Wu, M.Y. On stability of linear time-varying systems. Int. J. Syst. Sci. 1984, 15, 137–150. [Google Scholar] [CrossRef]
- Mudgett, D.; Morse, A. Adaptive stabilization of linear systems with unknown high-frequency gains. IEEE Trans. Autom. Control 1985, 30, 549–554. [Google Scholar] [CrossRef]
- Nussbaum, R.D. Some remarks on a conjecture in parameter adaptive control. Syst. Control Lett. 1983, 3, 243–246. [Google Scholar] [CrossRef]
- Scheinker, A. Extremum Seeking for Stabilization. Ph.D. Thesis, University of California San Diego, San Diego, CA, USA, 2012. [Google Scholar]
- Scheinker, A.; Krstić, M. Minimum-seeking for CLFs: Universal semiglobally stabilizing feedback under unknown control directions. IEEE Trans. Autom. Control 2012, 58, 1107–1122. [Google Scholar] [CrossRef]
- Scheinker, A.; Scheinker, D. Bounded extremum seeking with discontinuous dithers. Automatica 2016, 69, 250–257. [Google Scholar] [CrossRef]
- Scheinker, A.; Scheinker, D. Constrained extremum seeking stabilization of systems not affine in control. Int. J. Robust Nonlinear Control 2018, 28, 568–581. [Google Scholar] [CrossRef]
- Scheinker, A.; Scheinker, D. Extremum seeking for optimal control problems with unknown time-varying systems and unknown objective functions. Int. J. Adapt. Control. Signal Process. 2020. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming and Lagrange multipliers. Proc. Natl. Acad. Sci. USA 1956, 42, 767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirk, D.E. Optimal Control Theory: An Introduction; Courier Corporation: Chelmsford, MA, USA, 2004. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kapchinskij, I.; Vladimirskij, V. Limitations of proton beam current in a strong focusing linear accelerator associated with the beam space charge. In Proceedings of the 2nd International Conference on High Energy Accelerators and Instrumentation, Geneva, Switzerland, 14–19 September 1959. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scheinker, A. Adaptive Machine Learning for Robust Diagnostics and Control of Time-Varying Particle Accelerator Components and Beams. Information 2021, 12, 161. https://doi.org/10.3390/info12040161
Scheinker A. Adaptive Machine Learning for Robust Diagnostics and Control of Time-Varying Particle Accelerator Components and Beams. Information. 2021; 12(4):161. https://doi.org/10.3390/info12040161
Chicago/Turabian StyleScheinker, Alexander. 2021. "Adaptive Machine Learning for Robust Diagnostics and Control of Time-Varying Particle Accelerator Components and Beams" Information 12, no. 4: 161. https://doi.org/10.3390/info12040161
APA StyleScheinker, A. (2021). Adaptive Machine Learning for Robust Diagnostics and Control of Time-Varying Particle Accelerator Components and Beams. Information, 12(4), 161. https://doi.org/10.3390/info12040161





