Vectorization of Floor Plans Based on EdgeGAN

Abstract

A 2D floor plan (FP) often contains structural, decorative, and functional elements and annotations. Vectorization of floor plans (VFP) is an object detection task that involves the localization and recognition of different structural primitives in 2D FPs. The detection results can be used to generate 3D models directly. The conventional pipeline of VFP often consists of a series of carefully designed complex algorithms with insufficient generalization ability and suffer from low computing speed. Considering the VFP is not suitable for deep learning-based object detection frameworks, this paper proposed a new VFP framework to solve this problem based on a generative adversarial network (GAN). First, a private dataset called ZSCVFP is established. Unlike current public datasets that only own not more than 5000 black and white samples, ZSCVFP contains 10,800 colorful samples disturbed by decorative textures in different styles. Second, a new edge-extracting GAN (EdgeGAN) is designed for the new task by formulating the VFP task as an image translation task innovatively that involves the projection of the original 2D FPs into a primitive space. The output of EdgeGAN is a primitive feature map, each channel of which only contains one category of the detected primitives in the form of lines. A self-supervising term is introduced to the generative loss of EdgeGAN to ensure the quality of generated images. EdgeGAN is faster than the conventional and object-detection-framework-based pipeline with minimal performance loss. Lastly, two inspection modules that are also suitable for conventional pipelines are proposed to check the connectivity and consistency of PFM based on the subspace connective graph (SCG). The first module contains four criteria that correspond to the sufficient conditions of a fully connected graph. The second module that classifies the category of all subspaces via one single graph neural network (GNN) should be consistent with the text annotations in the original FP (if available). The reason is that GNN treats the adjacent matrix of SCG as weights directly. Thus, GNN can utilize the global layout information and achieve higher accuracy than other common classifying methods. Experimental results are given to illustrate the efficiency of the proposed EdgeGAN and inspection approaches.

1. Introduction

A 2D floor plan (FP) often contains structural, decorative, and functional elements and annotations. Figure 1 depicts that the vectorization of FP (VFP) aims to detect different structural primitives in the FP and assemble them into one 2D floor vector graph (FVG) that can be stretched into a 3D model. Manual methods often require meticulous measurements; thus, VFP has attracted remarkable attention for the past 20 years [1]. VFP is always a challenge because of the diversity of drawing styles and standards.

The conventional pipeline of VFP [2] (Figure 2) relies on a sequence of low-level image processing heuristics. Many researchers have devoted themselves to designing complicated algorithms to parse the local geometric constructions and retrieve structural elements based on drawing features and pixel information. Lu et al. proposed a self-incremental axis-net-based hierarchical recognition model to recognize dimensions, coordinate systems, and structural components [3], and integrate architectural information dispersed in multiple drawings and tables under the guidance of semantics and prior domain knowledge [4]. In their later work [5], the concept of primitive recognition and integration was proposed for the first time. Zhu [6] proposed a shape-operation graph to recognize walls and parse the topology of the entire layout based on structural primitives. Jiang [7] focused on the recovery of distortion to obtain the exact size. Gimenez et al. [8] also discussed methods that can be used to recognize walls, openings, and spaces. Special segmentation and recognition methods for text annotations, which could obtain high-level semantic information about scale [9], measurement [10], type of subspace [11], were proposed. The text annotations can be recognized accurately with the development of optical character recognition [12], especially those that are based on deep learning (DL) [13].

Artificial neural networks have been applied in VFP with the development of DL. Dodge et al. [14] used a fully convolutional neural network (CNN) to detect structural elements and achieve a mean intersection-over-union score of 89.9\% on R-FP and 94.4\% on the public CVC-FP dataset. Chen et al. [15] applied CNNs in translating a rasterized image to a set of junctions that represented low-level geometric and semantic information (e.g., wall corners or door endpoints). Moreover, they formulated the integer programming to aggregate junctions into a set of simple primitives (e.g., wall lines, door lines, or icon boxes) to produce an FVG with consistent constraints between topology and geometry. DL-based object detection framework can only detect doors and windows because there is no suitable annotation to describe the complex geometrical characteristic of architectural primitives. Thus, they can only replace some modules of the conventional pipeline. Faster RCNN [16] and YOLO [17], as well as other anchor-based frameworks, propose numerous boxes and combined them based on intersection over union (IoU). In a PFM, walls are described in form of lines, and if we use inflated boxes as ground truth, sloping or curved walls cannot be localized accurately. Anchor-free frameworks, CenterNet [18], and CornerNet [19] for instance, cannot solve this problem either. Subspaces segmentation is a typical semantic segmentation task, which can be achieved by a Unet [20] or a generative adversarial network (GAN) [21] in an end-to-end manner. Due to the lack of a large-scale segmentation dataset, only one literature has exploited this method on a mixed dataset PYTH [22], most samples of which are not public. Therefore, this study develops a special edge extraction GAN (EdgeGAN) to detect architectural primitives, which is a compromise between the two approaches.

GAN, which is a new learning framework for a generative model, has drawn great attention since it was proposed by Goodfellow et al. [21] in 2014. GAN has sprouted many branches, including conditional GAN [23,24], Wasserstein GAN [25,26], pix2pix [27], and has been used successfully in image translation, style migration, denoising, superresolution and repair, image matting, semantic segmentation, and dataset expansion [28,29]. GAN is a general-purpose solution for translating an input image into a corresponding output image with the same setting, which is mapped pixels to pixels.

One important milestone of GAN for image translation is pix2pix introduced by Isola et al. [27], which is developed from conditional GAN [24]. The most usual architecture of the generator is the encoder–decoder or its improved version “U-Net” with skip connections between mirrored layers in the encoder and decoder stacks [20]. Wang et al. [30] expanded pix2pix to high-resolution image synthesis and semantic manipulation by introducing a new robust adversarial learning objective together with new multiscale generator and discriminator architectures. In another work of Wang et al. [31], a video-to-video translation framework with spatial–temporal adversarial objective achieved high-resolution, photorealistic, and temporally coherent video results on a diverse set of input formats including segmentation masks, sketches, and poses.

CycleGAN is another important milestone for the unpaired image-to-image translation [32]. Two independent works also proposed the same method inspired by different motivations, namely, as DuelGAN [33] or DiscoNet [34]. Pix2pix learns the forward mapping (i.e., $y=G(x)$), whereas CycleGAN learns two-cycle mappings (i.e., $x=F(y^{\prime })=F(G(x))$ and $y=G(x^{\prime })=G(F(y))$) with the input $x$ and output $y$ unpaired. Considering that pixel-level annotation for most tasks is impossible, CycleGAN has a wider range of applications while requiring the training of more samples.

In this work, a new VFP framework based is proposed based on pix2pix. The main contributions of this work are presented as follows:

(1)

A colorful and larger dataset called ZSCVFP is established. Unlike current public datasets, which only contain black and white FPs without decorative disturbance or style variation, such as CVC-FP [14] and CubiCasa5K [35], ZSCVFP’s FPs are drawn with decorative disturbance in different styles, thereby causing difficulty in the extraction of primitives. The ground truth annotations in the form of points and lines, together with the corresponding images, are provided. Furthermore, ZSCVFP has a total of 10,800 samples. This number is higher than the 121 and 5000 samples of CVC-FP and CubiCasa5K, respectively.

(2)

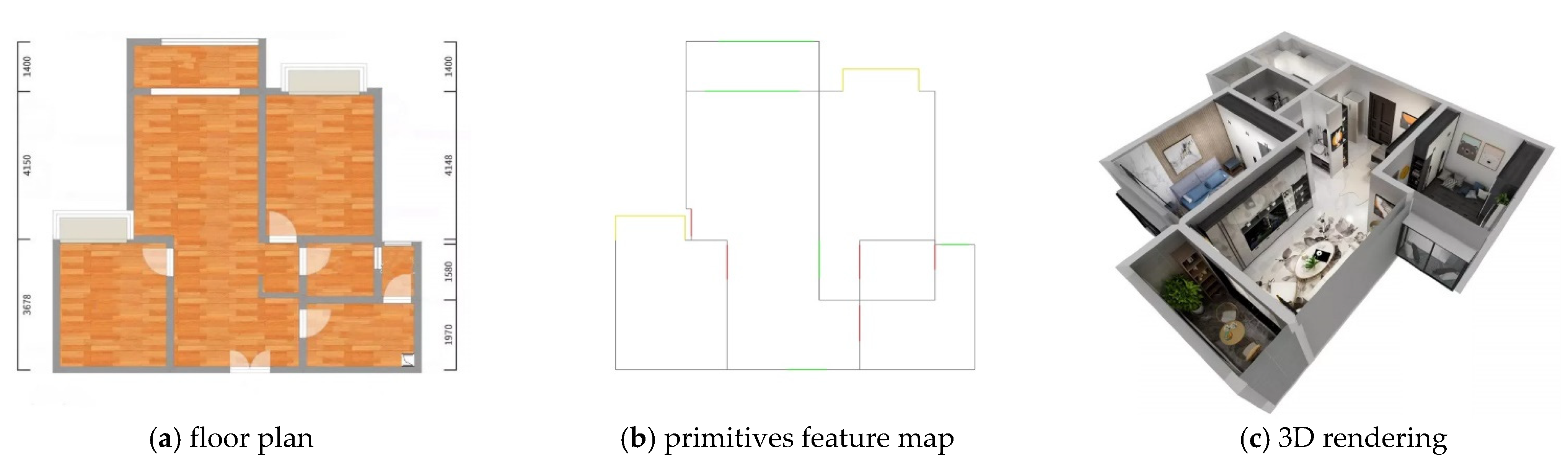
VFP is formulated as an image translation task innovatively, and EdgeGAN based on pix2pix is designed for the new task. EdgeGAN projects the FPs into the primitive space. Each channel of the primitive feature map (PFM) only contains some lines that represent one category of primitives. A self-supervising term is added to the generative loss of EdgeGAN to enhance the quality of PFM. Unlike conventional pipelines (even if some modules are replaced with deep-learning methods) that consist of a series of carefully designed algorithms, EdgeGAN obtains the FVG in an end-to-end manner. EdgeGAN is about 15 times as fast as the conventional pipeline. To the best knowledge of the authors, this study is the first to apply GAN in VFP.

(3)

Four criteria, which are sufficient conditions for a fully connected graph, are given to inspect the connectivity of subspaces segmented from the PFM. The connective inspection can provide auxiliary information for the designers to adjust the FVG.

(4)

The graph neural network (GNN) is used to predict the categories of subspaces segmented from the PFM. Given that GNN treats the adjacent matrix of the connective graph as weights directly, it can utilize global layout information and achieve higher accuracy than other common classifying methods.

This work is organized as follows. Section 2 establishes the ZSCVFP dataset and introduces the goal of the new VFP framework. Section 3 presents the main algorithms. Section 4 provides the experimental results. At last, Section 5 draws some conclusions.

2. Problem Description

In this section, the ZSCVFP dataset and the goal of the new VFP framework are introduced.

Framework Based on EdgeGAN

As mentioned, current public datasets are all black and white without decorative disturbance. However, the original FPs provided by customers in practical applications are complex and diverse. Thus, the new dataset ZSCVFP is established for this reason. ZSCVFP contains 8800 FPs in the training set and 2000 FPs in the test set. For a given FP $\mathit{X}\in {ℝ}^{w\times h\times 3}$ where $w$ and $h$ are the width and height, respectively, the pseudo-annotations of walls, windows, and doors are given in the form of a point set $\mathcal{P}=\left\{p_1,p_2,\cdots \right\}$ and three line sets ${ℒ}_{wall}=\left\{w_1,w_2,\cdots \right\}$, ${ℒ}_{window}=\left\{v_1,v_2,\cdots \right\}$, and ${ℒ}_{door}=\left\{d_1,d_2,\cdots \right\}$, respectively. The elements of ${ℒ}_{wall}$, ${ℒ}_{window}$, and ${ℒ}_{door}$ are paired points from $\mathcal{P}$. The corresponding PFM $\mathit{Z}\in {ℝ}^{w\times h\times 3}$ is also provided in the dataset, as shown in the center subfigure of Figure 1.

The walls’ annotations are obtained by a conventional pipeline that has been developed by ourselves in a previous work. The doors and windows are annotated manually with a tool (Figure 3). When the annotations are inconsistent, the windows and doors will be adjusted according to the walls to keep the geometrical constraints on the primitives. This adjustment will reduce the accuracy of annotations more or less.

In the new framework based on EdgeGAN, the generated PFM is denoted as $\mathit{Y}=G_1\left(\mathit{X}\right)\in {ℝ}^{w\times h\times n_c}$ where $n_c$ is the number of categories of primitives to be recognized. For the dataset ZSCVFP, $n_c=3$. Each channel of $\mathit{Y}$ is a binary image that corresponds to one primitive category. The final goal of the task, which is to extract $\mathcal{H}=\left(\mathcal{P},{\mathcal{L}}_{wall},{\mathcal{L}}_{window},{\mathcal{L}}_{door}\right)$ from $\mathit{Y}$, is very easy if the quality of $\mathit{Y}$ is good enough.

The set of text annotations detected in $\mathit{X}$ is denoted as $\mathcal{T}=\{t_1,t_2,\cdots \}$, and the set of subspaces extracted from $\mathit{Y}$ is denoted as $\mathcal{S}=\left\{s_1,s_2,\cdots ,s_{n-1},s_n\right\}$. For each subspace $s_i$, the feature vector consists of the number of windows, number of doors, ratio of area, etc. The feature matrix $\mathcal{S}$ is denoted as ${\mathit{X}}^{\mathcal{G}}\in {ℝ}^{n\times m}$, where $m$ is the length of the feature, $n$ is the number of subspaces. The probability matrix predicted by a GNN $G_2$ is denoted $\mathit{C}=G_2\left({\mathit{X}}^{\mathcal{G}}\right)\in {ℝ}^{n\times n}$, where $n_s$ is the number of classes.

The formal representation of the new task’s goal can be summarized as follows:

(1)

Design a $G_1$ to obtain the PFM that is robust with decorative disturbances in variant styles;

(2)

Search for efficient criteria to inspect whether $\mathcal{S}$ is fully connected;

(3)

Design a GNN $G_2$ to predict the category of subspaces.

3. Methods

In this section, the EdgeGAN is designed first. Then, the SCG of VFP is defined, and some connective criteria are given based on it. Lastly, a classifying GNN for subspaces is presented.

3.1. EdgeGAN

EdgeGAN learns a map from the input FPs $\mathit{X}$ to the output $\mathit{Z}$, and $\mathit{Y}$ is the ground truth. The architecture of EdgeGAN is depicted in Figure 4. Two convolution layers, six Resnet blocks, and two deconvolution layers are connected in series with skip connect, which is a typical realization of U-Net [20] that has been used widely [27].

Two special kernels are defined as

${\mathit{K}}_1=\left[\begin{array}{ccc}0& 0& 0\\ 1& 1& 1\\ 0& 0& 0\end{array}\right]$, and ${\mathit{K}}_2=\left[\begin{array}{ccc}0& 1& 0\\ 0& 1& 0\\ 0& 1& 0\end{array}\right]$.

The generative loss function of EdgeGAN is defined as

$$l_G=\frac{1}{N}{\displaystyle \sum _{i=1}^N\underset{G\_BCE\_loss}{\underbrace{-\log D\left(\mathit{X},\mathit{Z}\right)}}+\underset{G\_L1\_loss}{\underbrace{{\lambda }_1\left|\mathit{Y}-\mathit{Z}\right|}}+\underset{G\_filter\_loss}{\underbrace{{\lambda }_2\left|\mathit{Y}-F\left(\mathit{Y}\right)\right|}}},$$

(1)

and the discriminative loss function is defined as

$$l_D=\frac{1}{N}{\displaystyle \sum _{i=1}^N\underset{D\_fake\_loss}{\underbrace{-\log D\left(\mathit{X},\mathit{Z}\right)}}\underset{D\_real\_loss}{\underbrace{-\log [1-D\left(\mathit{X},\mathit{Y}\right)]}}},$$

(2)

where $N$ is the batch size and $F\left(\mathit{Y}\right)$ is a filter function defined as

$$F\left(\mathit{Y}\right)=clip\left(\mathrm{maxpooling}2\mathrm{D}\left(\mathit{Y},{\mathit{K}}_1\right)+\mathrm{maxpooling}2\mathrm{D}\left(\mathit{Y},{\mathit{K}}_2\right),0,1\right)$$

In the loss functions, $G\_BCE\_loss$, $D\_fake\_loss$, and $D\_real\_loss$ are all binary cross-entropy (BCE) loss, $G\_L1\_loss$ and $G\_filter\_loss$ are L1 loss, and ${\lambda }_1$ and ${\lambda }_2$ are the weights for them. Those 3 BCE terms, which constitute the standard GAN loss and are designed for the maximin optimization problem

$$\underset{G}{\min } \underset{D}{\max }\left\{E_{\mathit{Y}~P\left(\mathit{Y}\right)}\left[\log D\left(\mathit{Y}\right)\right]+E_{\mathit{X}~P\left(\mathit{X}\right)}\left[\log \left(1-D\left(G(\mathit{X})\right)\right)\right]\right\},$$

guide the generator $G$ to generate better PFM $\mathit{Z}$ and the discriminator to recognize the difference between the distribution of $\mathit{Z}$ and that of the ground truth $\mathit{Y}$. Additionally, $G\_L1\_loss$ provides pixel-level supervision information that is suitable for a pix2pix task. $G\_filter\_loss$ is a new term that composes a self-supervised loss about $\mathit{Y}$. In $F\left(\mathit{Y}\right)$, $\mathrm{maxpooling}2\mathrm{D}\left(\mathit{A},\mathit{K}\right)$ composes a max-pooling operation with a kernel $\mathit{K}$ on the input multichannel image $\mathit{A}$. With those two special kernels ${\mathit{K}}_1$ and ${\mathit{K}}_2$, the $\mathrm{maxpooling}2\mathrm{D}$ can extract the horizontal and vertical lines, respectively, as illustrated in Figure 5b,c. The horizontal and vertical maps are added then. As those elements of $\mathrm{maxpooling}2\mathrm{D}\left(\mathit{Y},{\mathit{K}}_1\right)+\mathrm{maxpooling}2\mathrm{D}\left(\mathit{Y},{\mathit{K}}_2\right)$ the intersections would be bigger $1$, we designed a clip function to truncate it. With the clip function $clip\left(\mathit{A},a,b\right)$, elements of $\mathit{A}$ smaller than $a$ become $a$, and elements larger than $b$ become $b$. The $clip$ operation makes the filtered PFM still be a probability map. The adding and clipping operations combine those lines to a new PFM, in which many isolate points have been filtered, as illustrated in Figure 5d.

With the self-supervised loss, the generator will learn to generate PFMs of higher quality. As ${\mathit{K}}_1$ and ${\mathit{K}}_2$ are designed for horizontal and vertical lines, it is not going to work for irregular walls.

In each training batch, the generator and discriminator are updated alternatively. ${\lambda }_2$ is set to 0 in the first several epochs to keep $G\_L1\_loss$ playing a leading role in the initial stage of training. When the PFM can be generated roughly, the self-supervising loss starts to come into play gradually.

3.2. Criteria for Connective Inspection

The set of subspaces extracted from a vector graph is denoted as $\mathcal{S}=\left\{s_1,s_2,\cdots ,s_{n-1},s_n\right\}$, where $s_i,i=1,2,\cdots ,n-1$ are the internal subspaces, and $s_n$ is the subspace outside the external contour, as shown in Figure 6 and Figure 7. As the regions annotated with “AC” in Figure 6 are the spaces for air conditioners out of the door, they are ignored in Figure 7 and Figure 8. The undirected graph of $\mathcal{S}$ can be written as $\mathcal{H}=\{\mathcal{S},\mathcal{D},\mathcal{W}\}$, where $\mathcal{D}=\left\{\right(i,j)\in \mathcal{S}\times \mathcal{S}:i~j\}$, and $\mathcal{W}=\left\{\right(i,j)\in \mathcal{S}\times \mathcal{S}:i~j\}$. $(i,j)\in \mathcal{D}$ and $(j,i)\in \mathcal{D}$ if subspace $i$ and $j$ are connected with a door; moreover, $(i,j)\in \mathcal{W}$ and $(j,i)\in \mathcal{W}$ if subspace $i$ and $j$ are connected with a window. Denote the adjacency matrix as $M^{\mathcal{H}}\in {ℝ}^{n\times n}$. The elements $m_{ij}^{\mathcal{H}}$, $0\le i,j\le n$, of $M^{\mathcal{H}}$ has the following properties:

(1)

$m_{ij}^{\mathcal{H}}=1$ if $(i,j)\in \mathcal{D}$; $m_{ij}^{\mathcal{H}}=0.5$ if $(i,j)\in \mathcal{W}$; otherwise $m_{ij}=0$;

(2)

$m_{ii}^{\mathcal{H}}=1$;

(3)

$m_{ij}^{\mathcal{H}}=m_{ji}^{\mathcal{H}}$, that is, $M^{\mathcal{H}}$ is symmetrical.

The subgraph without windows and its adjacency matrix are denoted as $\mathcal{G}=\{\mathcal{S},\mathcal{D}\}$ and $M^{\mathcal{G}}\in {ℝ}^{n\times n}$ respectively. The elements $m_{ij}^{\mathcal{G}}=1$ if $m_{ij}^{\mathcal{H}}=1$, otherwise $m_{ij}^{\mathcal{G}}=0$. The Laplacian matrix of $\mathcal{G}$ is defined as $L_{\mathcal{G}}=diag\left\{{\displaystyle {\sum }_{j=1,j\ne i}^n{m}_{ij}}\right\}-M_{\mathcal{G}}$, and its eigenvalues are denoted as ${\lambda }_1\left(L_{\mathcal{G}}\right)\le {\lambda }_2\left(L_{\mathcal{G}}\right)\le \cdots \le {\lambda }_n\left(L_{\mathcal{G}}\right)$. If ${\lambda }_2\left(L_{\mathcal{G}}\right)>0$, then $\mathcal{G}$ is a connected graph.

The degree of internal and external connectivity of each subspace are denoted as $C_i^{inner}={\displaystyle {\sum }_{j=1}^{n-1}{m}_{ij}}$ and $C_i^{external}=m_{in}$ respectively. The criteria for inspection of connectivity include the following:

(1)

There is a door on the external door at least, i.e., ${\displaystyle {\sum }_{i=1}^{n-1}{C}_i^{external}}\ge 1$;

(2)

The number of doors on the external doors is often less than 2, i.e., ${\displaystyle {\sum }_{i=1}^{n-1}{C}_i^{external}}\le 2$;

(3)

Each subspace except those with special architectural functionality (for example, the regions for air condition and pipe) has at least one door, that is, $C_i^{inner}\ge 1$ and $\underset{i=1,2,\cdots ,n-1}{\min }\left\{\underset{j=1,2,\cdots ,n-1}{\max }\left\{m_{ij}\right\}\right\}\ge 1$, where $i,j=1,2,\cdots ,n-1$;

(4)

$\mathcal{G}$ is a connected graph, that is, ${\lambda }_2\left(L_g\right)>0$.

All those four criteria are sufficient conditions for a fully connected graph. Furthermore, Criterion (4) is the sufficient condition of Criteria (1)–(3), but its computation is much complicated than other criteria.

3.3. Classifying of Subspaces Based on GNN

A GNN with $K$ layers is defined as

$${\mathit{H}}^{\left(k+1\right)}=\sigma \left({\mathit{M}}^{\mathcal{H}}{\mathit{H}}^{\left(k\right)}{\mathit{W}}^{\left(k\right)}\right),$$

where $k=1,2,\cdots ,K-1$ is the index of layer, ${\mathit{W}}^k\in {\mathbb{R}}^{d_{k-1}\times d_k}$ is the weight parameters to be learned, $d_k$ is the output dimension of the $k$th layer of the GNN, and $\sigma (\cdot )$ is the activation function.

The input of GNN is the feature matrix ${\mathit{X}}^g\in {\mathbb{R}}^{n\times m}$ of $\mathcal{G}$ and the output is the classifying probability matrix ${\mathit{C}}^g\in {\mathbb{N}}^{n\times n_s}$, where $m$ is the length of the feature, $n$ is the number of subspaces, and $n_s$ is the number of categories. The input dimension of the first layer is $d_0=n$, and the last output is ${\mathit{H}}^k={\mathit{C}}^{\mathcal{G}}$ with $d_K=n_s$.

The BCE loss function adopted to train the GNN is as follows:

$$l_{\mathcal{G}}=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N-\left[{\mathit{H}}^K\log {\overline{\mathit{C}}}^{\mathcal{G}}+\left(1-{\mathit{H}}^K\right)\log \left(1-{\overline{C}}^{\mathcal{G}}\right)\right]$$

(3)

where ${\overline{\mathit{C}}}^{\mathcal{G}}$ is the one-hot labeled category. Considering that the number of subspaces in each VFP varies, ${\mathit{M}}^{\mathcal{G}}$ is expanded to ${\overline{\mathit{M}}}^{\mathcal{G}}\in {\mathbb{R}}^{20\times 20}$ with ${\overline{\mathit{M}}}^{\mathcal{G}}=diag\{{\mathit{X}}^{\mathcal{G}},I_{(20-n)}\}$, and ${\mathit{X}}^{\mathcal{G}}$ is expanded to ${\overline{\mathit{X}}}^{\mathcal{G}}\in {\mathbb{R}}^{20\times 20}$ with ${\overline{\mathit{X}}}^{\mathcal{G}}=diag\{{\mathit{X}}^{\mathcal{G}},0_{(20-n)}\}$. The output dimension of the last layer becomes $d_K+1$ and the label vector ${\overline{\mathit{C}}}^{\mathcal{G}}=\left[\begin{array}{c}{\mathit{C}}^{\mathcal{G}}\\ d^k·1_{(20-n)\times 1}\end{array}\right]$. The labels of subspace are coded from 0 to $d_k-1$. Thus, the new virtual subspace is labeled with $d_k$.

4. Experimental Results and Discussion

In this section, three experiments are conducted to illustrate the proposed methods. First, EdgeGAN is compared with the DL-based pipeline on the ZSCCSVFP dataset. Second, the usage of connective criteria is demonstrated by presenting an example. Lastly, the GNN is compared with four common classifying methods to validate its advantage in terms of structural information.

4.1. EdgeGAN

In this experiment, all training sets are executed on the hardware platform “CPU Intel Core i9-9900K, 64 GB memory, and GPU NVIDIA RTX2080TI×2,” and the software is “Python 3.6, Pytorch 1.4.0 [36], Cuda 10.0, and Cudnn 7.4.2 [37].” The maximal training epoch is 220, and the batch size is 128. ${\lambda }_1$ is always set to 10, and ${\lambda }_2$ is set to 0 in the first 10 epochs and 100 in the subsequent epochs. The learning rate is set to 0.0002 at the first 20 epochs and decreased to 0 linearly in subsequent epochs. The training is recorded in Figure 8. $G\_filter\_loss$ is 0 in the first 10 epochs and decreases gradually. The $G\_L1\_loss$ is stable at approximately 1.38 since the 20th epoch. Thus, it is not a suitable measurement of accuracy. The corresponding evolutionary process of $\mathit{Y}$ is depicted in Figure 9.

The quality of generated images can be divided into three levels:

(1)

Level 1: The generated images are free from noisy points and have high-quality lines, and the recognition accuracy of primitives is close to the conventional pipeline. The proportion of level 1 is approximately 40%. These images can be used to obtain vector graphics with a few manual adjustments, similar to the conventional pipeline. Figure 10 compares the number of adjusting operations that are counted by a decoration designer on 100 FPs with level 1 results. Although the results of EdgeGAN satisfy the requirements of the application, its performance is still slightly weaker than that of the DL-based pipeline. The mean value of operations of the DL-based pipeline (16.50) is close to that of EdgeGAN (16.67). However, the standard deviation of EdgeGAN (8.34) is much larger than that of the DL-based pipeline (4.4628), which means that the latter is more stable. Moreover, 30 PFMs generated by the DL-based pipeline need less than eight operations, while only 21 PFMs by EdgeGAN, which means that the former has a higher rate of excellence. The results of EdgeGAN. Considering that the pseudo-ground truth annotations themselves are obtained on the basis of the conventional pipeline and suffer from inaccuracy, the results are reasonable. The performance of EdgeGAN can be improved if it is training on a larger and higher quality dataset.

(2)

Level 2: In addition to inaccurate primitives, some noisy points, broken lines, redundancy lines, or unaligned lines are presented in the generated images, as shown in the lines in the main body of Figure 11. The proportion of level 2 is approximately 55%. The self-supervising loss can relieve but cannot eliminate this phenomenon. Some postprocessing methods are necessary to address these problems. Solving this problem by using the EdgeGAN itself is direct but still challenging.

(3)

Level 3: Serious defects in quality or accuracy with a proportion of approximately 5% are observed in the sloping walls in Figure 11. The reason is that the number of samples with sloping walls is less than 100, which is much less than horizontal and vertical walls.

On one single RTX2080TI, the frame rate of EdgeGAN and its postprocessing is approximately 32 fps; and the frame of the DL-based pipeline on an Intel 9900 K CPU is approximately 2 fps. Although EdgeGAN can obtain PFM at a much higher speed, a gap still exists between the integral accuracy and quality of generated images and the requirements of applications.

4.2. Connectivity of Subspaces

The adjacent matrix of the vector graph in Figure 6 is as follows. Notably, subspace 1, 2, and 4 are ignored.

$${\mathit{M}}_{\mathcal{G}}=\left[\begin{array}{ccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 1& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 1\end{array}\right].$$

Thus, the Laplacian matrix is

$${\mathit{L}}_{\mathcal{G}}=\left[\begin{array}{ccccccccc}-1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& -1& -1& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& -1& -1\\ 0& 0& 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& 0& -1& 0& 0\end{array}\right].$$

The graph is not connected because ${\lambda }_2\left({\mathit{L}}_{\mathcal{G}}\right)>0$. ${\mathit{M}}_{\mathcal{G}}$ shows that the presence of five unconnected loops. Other criteria can also be calculated easily with ${\mathit{M}}_{\mathcal{G}}$.

4.3. Classifying of Subspaces Based on GNN

A new dataset that contains feature matrices annotated with subspace types is established to validate the advantage of GNN. The distributions of instances in the dataset are listed in

Table 1. Number of instances in the dataset.

	Training Set	Test Set
master bedroom	809	200
balcony	1242	315
bathroom	1143	287
study room	174	46
living room	809	200
second bedroom	2358	587
kitchen	805	200

. The features used here include window ratio, area ratio, number of doors, number of windows, and number of edges. Four widely used methods [38], namely, C4.5, iterative dichotomiser 3 (ID3), basic backpropagation (BP) neural network, and classification and regression tree (CART), are compared with GNN. The input of these four methods is the feature vector of one subspace, which means that they can only predict the type of one subspace independently. The input dimension of the BP network with one hidden layer is 5, the output dimension is 7, and the number of neurons in the hidden layer is 20. Part of the decision tree obtained by CART is shown in Figure 12.

Only GNN considers the connective graph and achieves higher accuracy than other methods. The results are listed in

Table 2. Accuracy of subspace decision.

Method	C4.5	ID3	BP	CART	GNN
Accuracy	74.82%	75.49%	79.13%	79.66%	84.35%

. The confusion matrices of CART and EdgeGAN are depicted in Figure 13 and Figure 14, respectively. The accuracies of the study room and the kitchen are enhanced dramatically.

5. Conclusions

EdgeGAN generates PFM in an end-to-end manner with a frame rate of 32 fps on an RTX2080TI GPU, which is much faster than the DL-based pipeline’s 2 fps since many modules of the pipeline can only run on a CPU. Although the accuracy of EdgeGAN is slightly lower than that of the DL-based pipeline, especially on sloping walls, its potential can be further exploited if given a larger and higher quality training set. Four connective criteria are proposed to inspect the connectivity of subspaces segmented from one FP. Those criteria are also suitable for postprocessing the results of traditional methods and object detection frameworks. GNN utilizes the connective information to predict the categories of subspaces and achieves 4.69% higher accuracy than other classification approaches. The category information of subspaces can be used to check with the depictive texts of FP.

In this study, since the PFM generation and subspace segmentation are fulfilled separately, the computing speed and performance can be improved further if they are realized in an end-to-end manner based on a one-stage framework. Thus, we will develop a one-stage multitask framework that finishes primitive detection, subspace segmentation, optical character recognition, and consistency inspection, simultaneously, in a future study. Furthermore, to improve the quality of PFM about irregular walls, some deep activate contour methods, such as deep snake [39] and deep level set loss [40], will also be exploited.