Interference Alignment Inspired Opportunistic Communications in Multi-Cluster MIMO Networks with Wireless Power Transfer
Abstract
1. Introduction
2. Related Work
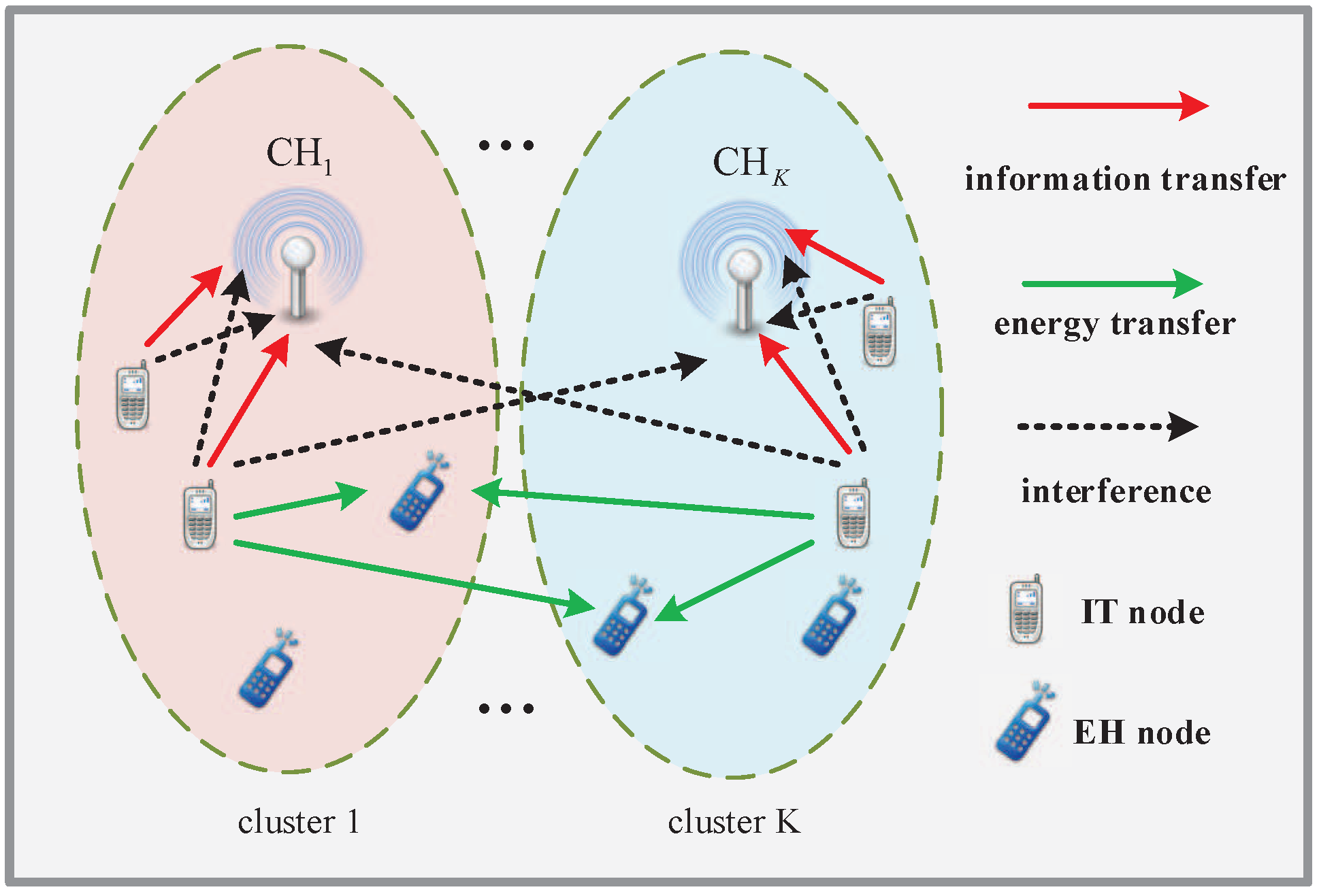
3. System Model
4. The Proposed IAOC Scheme
4.1. Scheduling Metric Design
4.2. Node Scheduling
4.3. Transmit Beamforming Vector Design
4.4. Receive Combining Vector Design
| Algorithm 1: The alternating optimization algorithm for IAOC |
|
4.5. Feedback Overhead and Computational Complexity
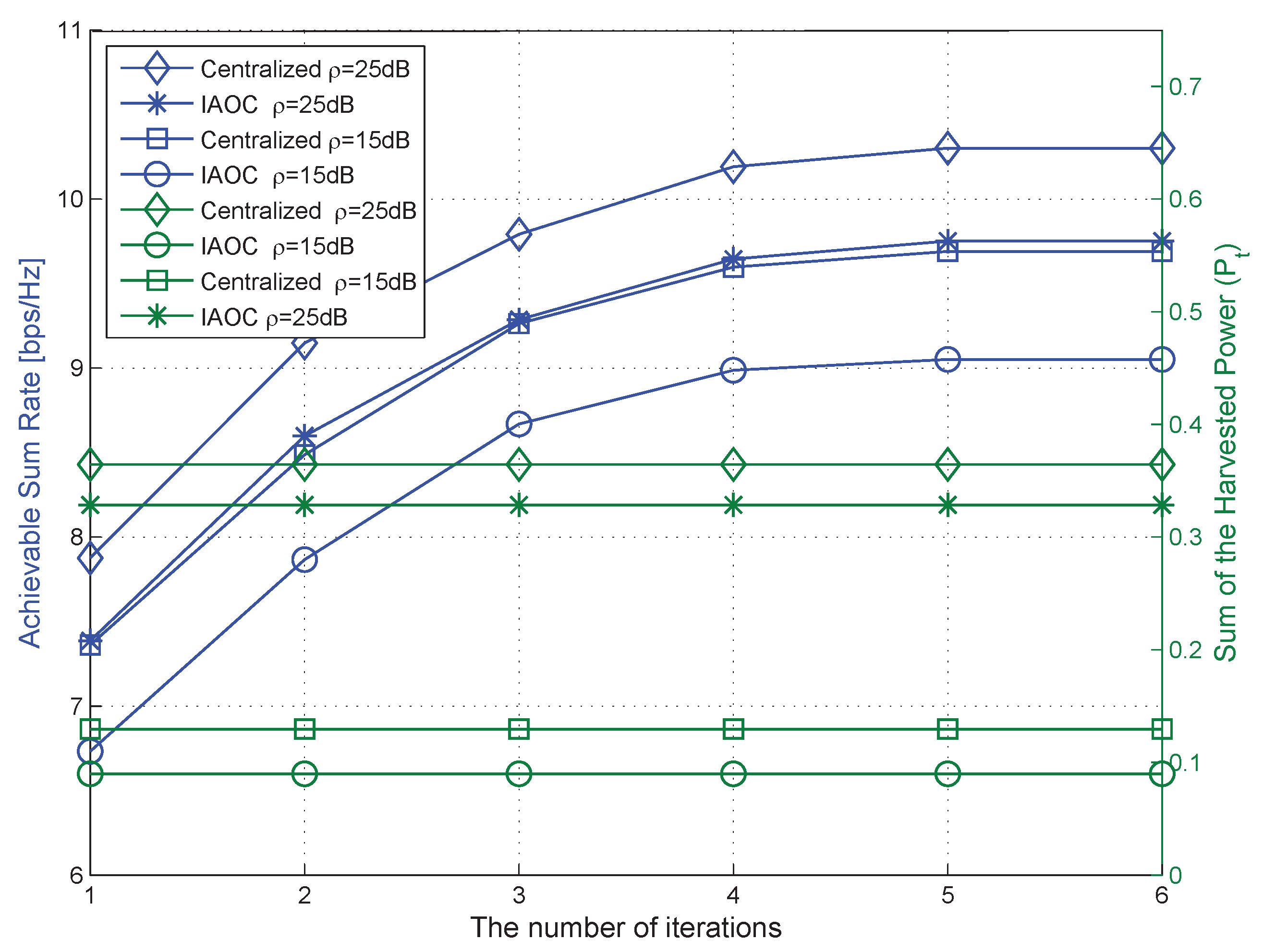
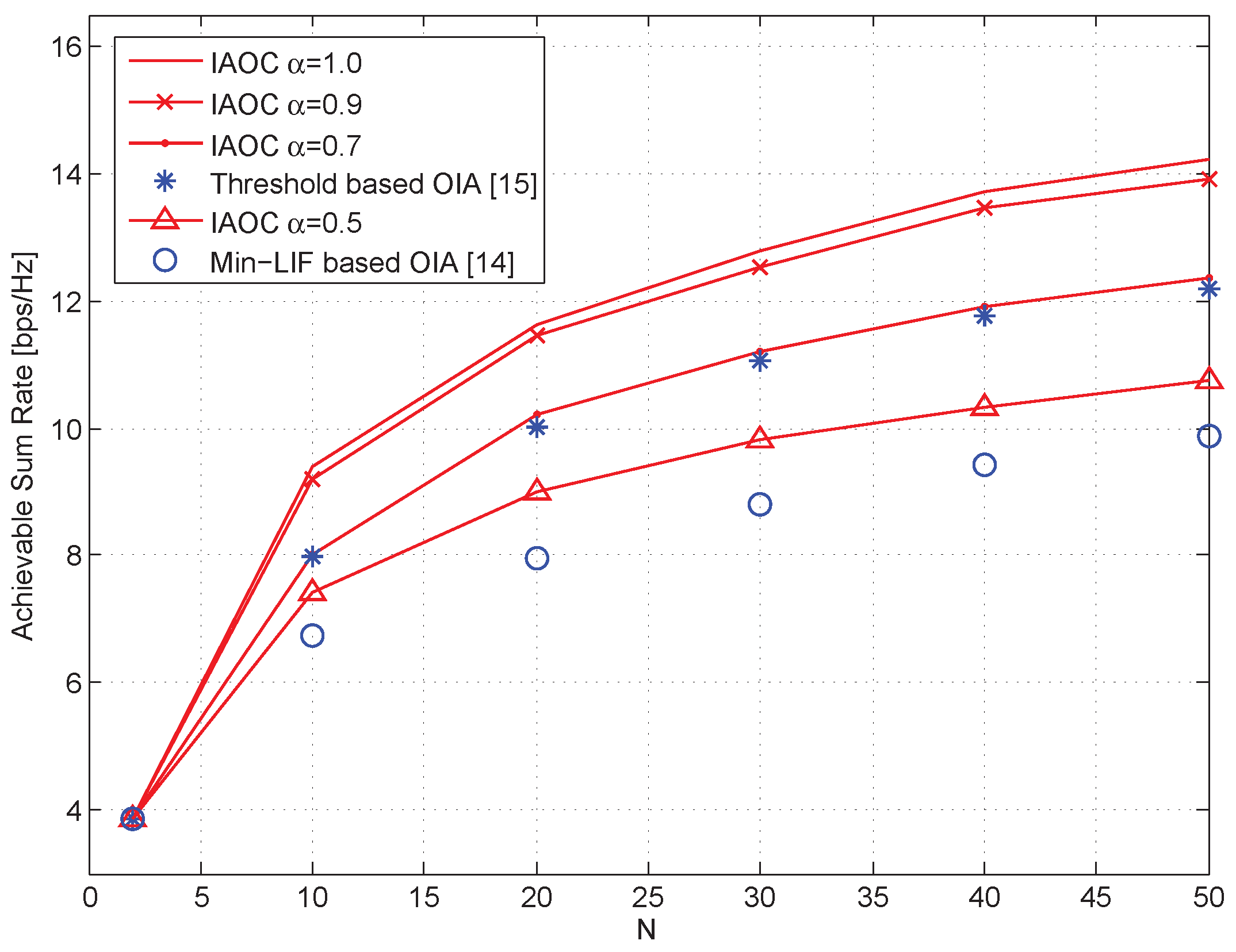
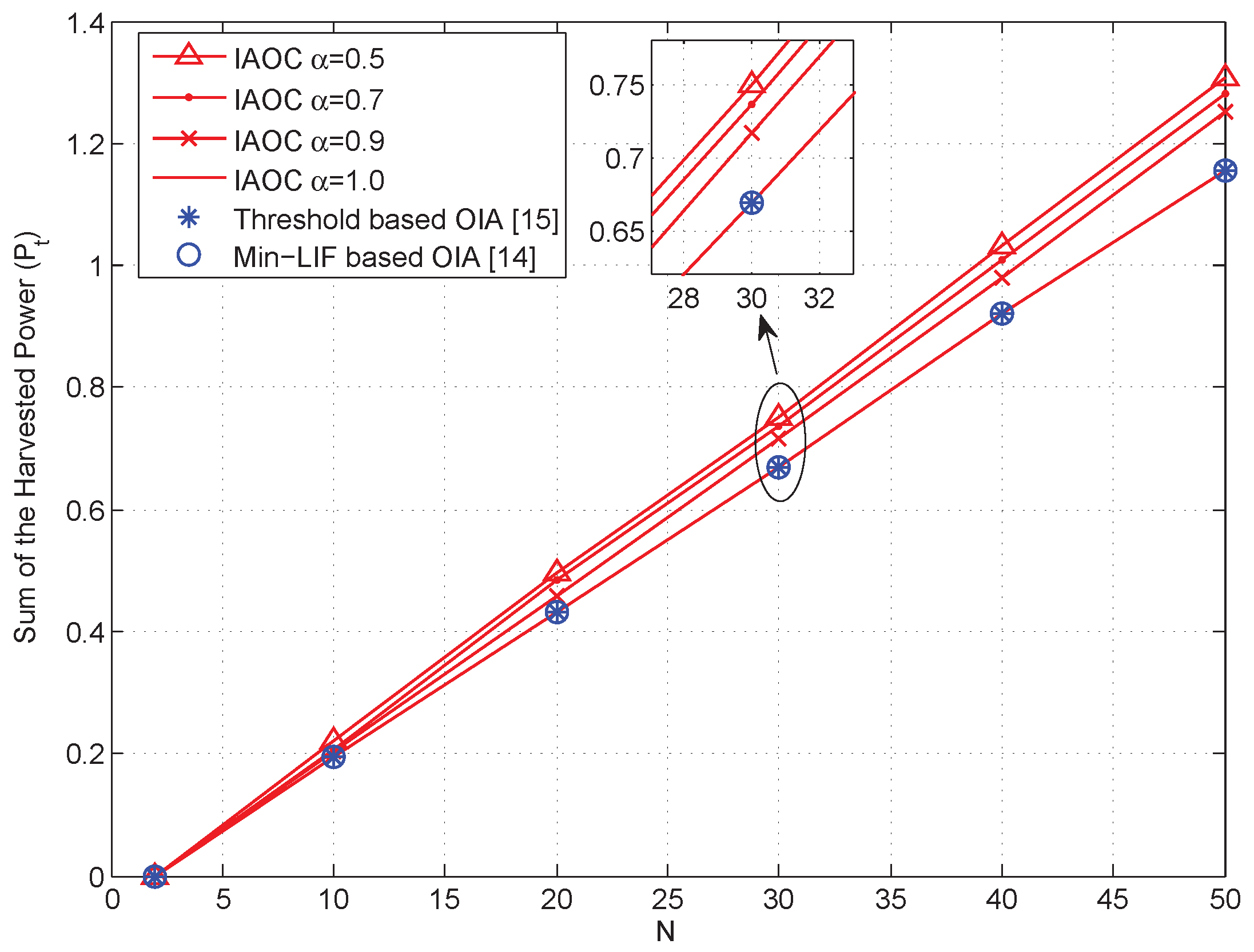
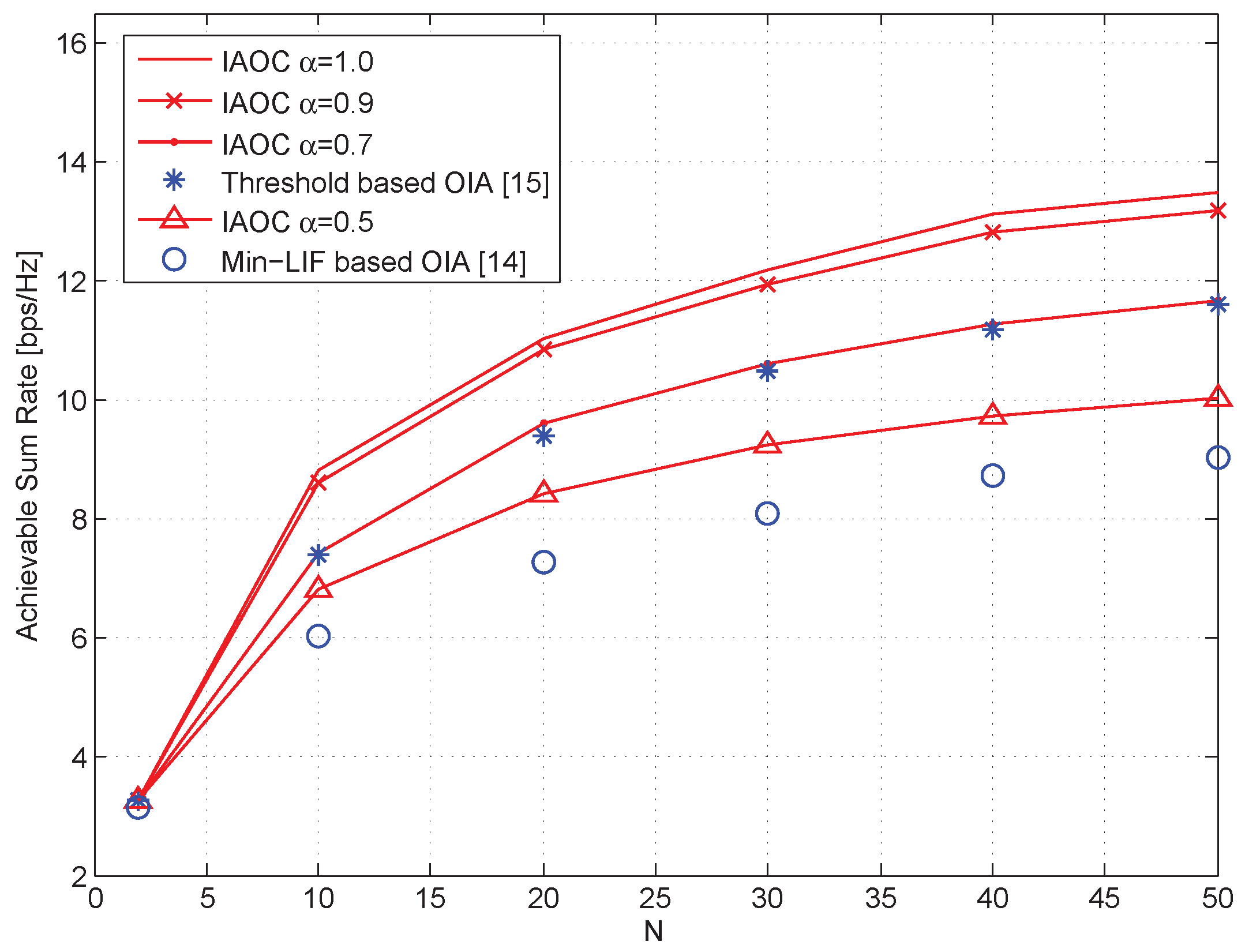
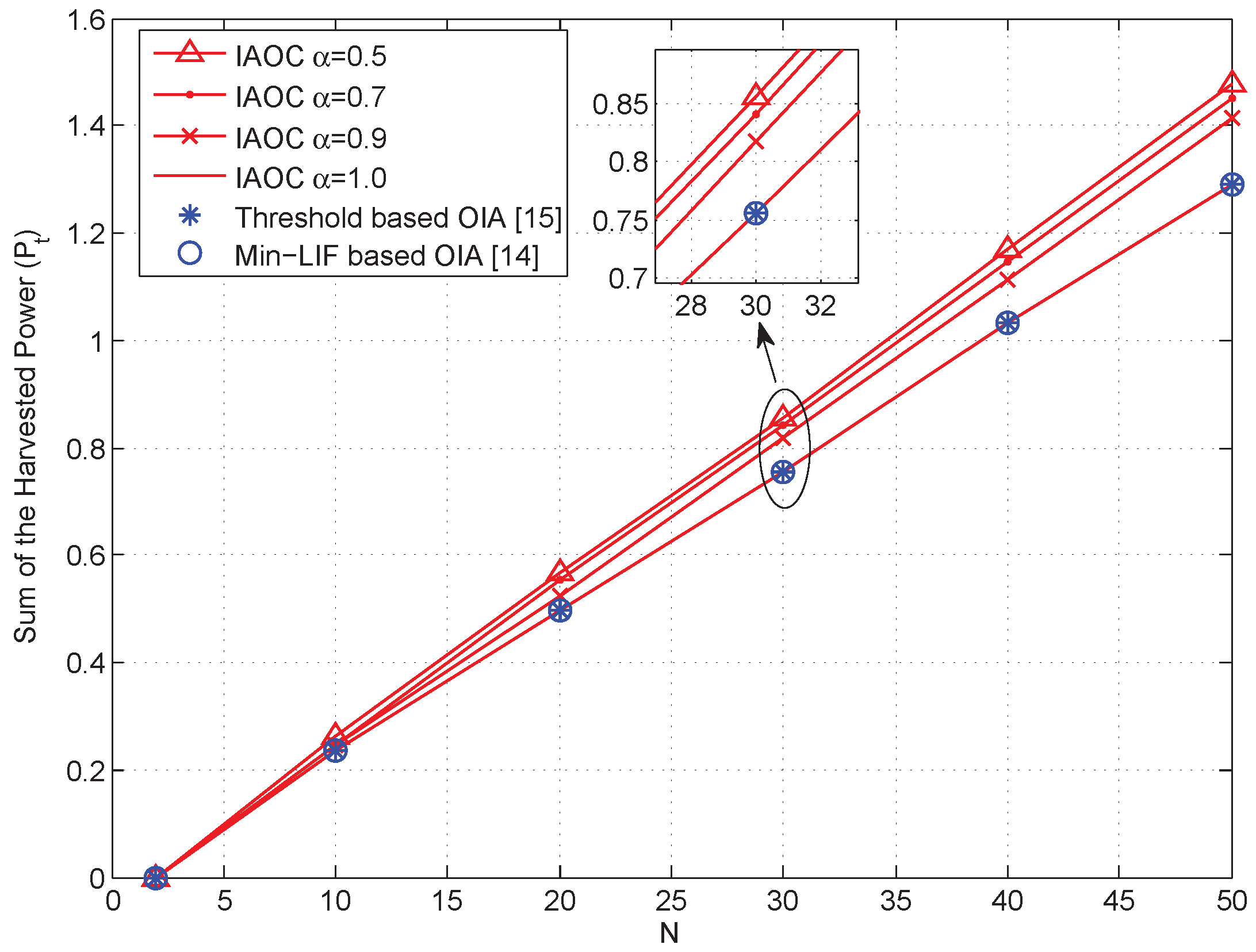
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, M.; Gao, L.; Huang, J. Communication, Computation, and Caching Resource Sharing for the Internet of Things. IEEE Commun. Mag. 2020, 58, 75–80. [Google Scholar] [CrossRef]
- Dastjerdi, A.V.; Buyya, R. Fog Computing: Helping the Internet of Things Realize Its Potential. Computer 2016, 49, 112–116. [Google Scholar] [CrossRef]
- Cadambe, V.; Jafar, S. Interference alignment and degrees of freedom of the K user interference channel. IEEE Trans. Inf. Theory 2008, 54, 3425–3441. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.N.; Jin, M.; Yan, Q.; Leung, V.C.M. Interference Alignment and Its Applications: A Survey, Research Issues, and Challenges. IEEE Commun. Surv. Tut. 2016, 18, 1779–1803. [Google Scholar] [CrossRef]
- Gou, T.; Jafar, S.A. Degrees of Freedom of the K-user M × N MIMO interference channel. IEEE Trans. Inf. Theory 2010, 56, 6040–6057. [Google Scholar] [CrossRef]
- Suh, C.; Tse, D. Interference Alignment for Cellular Networks. In Proceedings of the 2008 46th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 23–26 September 2008; pp. 1037–1044. [Google Scholar]
- Ahn, S.K.; Chae, S.H. Blind Integer-Forcing Interference Alignment for Downlink Cellular Networks. IEEE Commun. Lett. 2019, 23, 306–309. [Google Scholar] [CrossRef]
- Lv, W.; Wang, R.; Wu, J.; Xu, J.; Li, P.; Dou, J. Degrees of Freedom of the Circular Multirelay MIMO Interference Channel in IoT Networks. IEEE Internet Things J. 2018, 5, 1957–1966. [Google Scholar] [CrossRef]
- Wan, X.; Zhu, X.; Jiang, Y.; Liu, Y.; Zhao, J. An Interference Alignment and ICA-Based Semiblind Dual-User Downlink NOMA System for High-Reliability Low-Latency IoT. IEEE Internet Things J. 2020, 7, 10837–10851. [Google Scholar] [CrossRef]
- Castanheira, D.; Silva, A.; Gameiro, A. Set Optimization for Efficient Interference Alignment in Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2014, 13, 5648–5660. [Google Scholar] [CrossRef][Green Version]
- Sheng, J.; Tang, Z.; Wu, C.; AI, B.; Wang, Y. Game Theory-Based Multi-Objective Optimization Interference Alignment Algorithm for HSR 5G Heterogeneous Ultra-Dense Network. IEEE Trans. Veh. Tech. 2020, 69, 13371–13382. [Google Scholar] [CrossRef]
- Xu, F.; Tao, M.; Zheng, T. Cache-Aided Interference Management in Partially Connected Linear Networks. IEEE Trans. Commun. 2020, 68, 301–316. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, K.; Zhang, S.; Dobre, O.A. Subchannel Allocation Based on Clustered Interference Alignment for Differentiated Data Streams in Dense Small Cell Networks. IEEE Trans. Veh. Tech. 2020, 69, 14049–14054. [Google Scholar] [CrossRef]
- Yang, H.J.; Shin, W.Y.; Jung, B.C.; Paulraj, A. Opportunistic Interference Alignment for MIMO Interfering Multiple-Access Channels. IEEE Trans. Wirel. Commun. 2013, 12, 2180–2192. [Google Scholar] [CrossRef]
- Jung, B.C.; Kim, S.M.; Yang, H.J.; Shin, W.Y. On the Joint Design of Beamforming and User Scheduling in Multi-Cell MIMO Uplink Networks. In Proceedings of the 2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014; pp. 428–432. [Google Scholar]
- Cha, H.S.; Jeon, S.W.; Kim, D.K. Blind Interference Alignment for the K-User MISO BC Under Limited Symbol Extension. IEEE Trans. Signal Process. 2018, 66, 2861–2875. [Google Scholar] [CrossRef]
- Arti, M.K. A Novel Downlink Interference Alignment Method for Multi-User MIMO System With No CSIT: A Space-Time Coding Approach. IEEE Trans. Veh. Tech. 2020, 69, 10937–10948. [Google Scholar] [CrossRef]
- Johnny, M.; Vahid, A. Exploiting Coherence Time Variations for Opportunistic Blind Interference Alignment. IEEE Trans. Commun. 2020, 68, 6054–6069. [Google Scholar] [CrossRef]
- Ayach, O.E.; Heath, R.W. Interference Alignment with Analog Channel State Feedback. IEEE Trans. Wirel. Commun. 2012, 11, 626–636. [Google Scholar] [CrossRef]
- Chen, X.; Yuen, C. Performance Analysis and Optimization for Interference Alignment over MIMO Interference Channels with Limited Feedback. IEEE Trans. Signal Process. 2014, 62, 1785–1795. [Google Scholar] [CrossRef]
- Castanheira, D.; Silva, A.; Gameiro, A. Retrospective Interference Alignment for the K-User M × N MIMO Interference Channel. IEEE Trans. Wirel. Commun. 2016, 15, 8368–8379. [Google Scholar] [CrossRef]
- Shahjehan, W.; Shah, S.W.; Lloret, J.; Bosch, I. Joint Interference and Phase Alignment among Data Streams in Multicell MIMO Broadcasting. Appl. Sci. 2018, 8, 1237. [Google Scholar] [CrossRef]
- Lee, J.; Choi, W. On the Achievable DoF and User Scaling Law of Opportunistic Interference Alignment in 3-Transmitter MIMO Interference Channels. IEEE Trans. Wirel. Commun. 2013, 12, 2743–2753. [Google Scholar] [CrossRef]
- Leithon, J.; Yuen, C.; Suraweera, H.A.; Gao, H. A New Opportunistic Interference Alignment Scheme and Performance Comparison of MIMO Interference Alignment with Limited Feedback. In Proceedings of the 2012 IEEE Globecom Workshops, Anaheim, CA, USA, 3–7 December 2012; pp. 1123–1127. [Google Scholar]
- Yang, H.J.; Shin, W.Y.; Jung, B.C.; Suh, C.; Paulraj, A. Opportunistic Downlink Interference Alignment for Multi-Cell MIMO Networks. IEEE Trans. Wirel. Commun. 2017, 16, 1533–1548. [Google Scholar] [CrossRef]
- Suo, L.; Li, J.; Li, H.; Zhang, S.; Davidson, T.N. Achievable Sum Rate and Degrees of Freedom of Opportunistic Interference Alignment in MIMO Interfering Broadcast Channels. IEEE Trans. Commun. 2019, 67, 4062–4073. [Google Scholar] [CrossRef]
- Jung, B.C.; Shin, W.Y. Opportunistic Interference Alignment for Interference-Limited Cellular TDD Uplink. IEEE Commun. Lett. 2011, 15, 148–150. [Google Scholar] [CrossRef]
- Jung, B.C.; Park, D.; Shin, W.Y. Opportunistic Interference Mitigation Achieves Optimal Degrees-of-Freedom in Wireless Multi-Cell Uplink Networks. IEEE Trans. Commun. 2012, 60, 1935–1944. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Z.; Yu, F.R.; Zhao, N.; Yin, H.; Leung, V.C.M.; Zhang, Y. Deep-Reinforcement-Learning-Based Optimization for Cache-Enabled Opportunistic Interference Alignment Wireless Networks. IEEE Trans. Veh. Tech. 2017, 66, 10433–10445. [Google Scholar] [CrossRef]
- Benaya, A.M.; Elsabrouty, M.; Muta, O. Queue-Aware Opportunistic Interference Alignment in Downlink MU-MIMO Cellular Systems. IEEE Access 2018, 6, 50860–50874. [Google Scholar] [CrossRef]
- Ren, Y.; Lv, T.; Gao, H.; Li, Y. Secure Wireless Information and Power Transfer in Heterogeneous Networks. IEEE Access 2017, 5, 4967–4979. [Google Scholar] [CrossRef]
- Zhang, X.; Lv, T.; Ren, Y.; Lin, Z. Joint Content Push and Transmission in NOMA With SWIPT Caching Helper. IEEE Commun. Lett. 2020, 24, 922–925. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.R.; Leung, V.C.M. Simultaneous Wireless Information and Power Transfer in Interference Alignment Networks. IEEE Wirel. Commun. 2015, 22, 88–95. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.R.; Leung, V.C.M. Wireless Energy Harvesting in Interference Alignment Networks. IEEE Commun. Mag. 2015, 53, 72–78. [Google Scholar] [CrossRef]
- Koo, B.; Park, D. Interference Alignment and Wireless Energy Transfer via Antenna Selection. IEEE Commun. Lett. 2014, 18, 548–551. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.R.; Leung, V.C.M. Wireless Power Transfer Based on Angle Switching in Interference Alignment Wireless Networks. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 3776–3781. [Google Scholar]
- Xie, Z.; Chen, Y.; Gao, Y. Joint Iterative Interference Alignment and Energy Harvesting for Multi-User Networks. IEEE Wirel. Commun. Lett. 2015, 4, 597–600. [Google Scholar] [CrossRef]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: New York, NY, USA, 1990. [Google Scholar]
- Gao, H.; Leithon, J.; Yuen, C.; Suraweera, H.A. New Uplink Opportunistic Interference Alignment: An Active Alignment Approach. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 3066–3071. [Google Scholar]
- Hur, S.H.; Jung, B.C.; Rao, B.D. Sum rate enhancement by maximizing SGINR in an opportunistic interference alignment scheme. In Proceedings of the 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 6–9 November 2011; pp. 354–358. [Google Scholar]
- Lv, T.; Gao, H.; Cao, R.; Zhou, J. Co-Ordinated Secure Beamforming in K-User Interference Channel With Multiple Eavesdroppers. IEEE Wirel. Commun. Lett. 2016, 5, 212–215. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Zhang, X.; Makhanbet, M. Interference Alignment Inspired Opportunistic Communications in Multi-Cluster MIMO Networks with Wireless Power Transfer. Information 2021, 12, 335. https://doi.org/10.3390/info12080335
Ren Y, Zhang X, Makhanbet M. Interference Alignment Inspired Opportunistic Communications in Multi-Cluster MIMO Networks with Wireless Power Transfer. Information. 2021; 12(8):335. https://doi.org/10.3390/info12080335
Chicago/Turabian StyleRen, Yuan, Xuewei Zhang, and Meruyert Makhanbet. 2021. "Interference Alignment Inspired Opportunistic Communications in Multi-Cluster MIMO Networks with Wireless Power Transfer" Information 12, no. 8: 335. https://doi.org/10.3390/info12080335
APA StyleRen, Y., Zhang, X., & Makhanbet, M. (2021). Interference Alignment Inspired Opportunistic Communications in Multi-Cluster MIMO Networks with Wireless Power Transfer. Information, 12(8), 335. https://doi.org/10.3390/info12080335





