Multi-Attribute Group Decision-Making Based on Interval-Valued q-Rung Orthopair Fuzzy Power Generalized Maclaurin Symmetric Mean Operator and Its Application in Online Education Platform Performance Evaluation
Abstract
:1. Introduction
2. Basic Notions
2.1. The Interval-Valued q-Rung Orthopair Fuzzy Sets
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
- (1)
- if, then;
- (2)
- if, then
- if, then;
- if, then.
2.2. The Power Average and Generalized Maclaurin Systems Mean Operators
- (1)
- ;
- (2)
- ;
- (3)
- , if.
3. Novel Aggregation Operators for IVq-ROFNs
3.1. The Interval-Valued q-Rung Orthopair Fuzzy Power Average Operator
- (1)
- ;
- (2)
- ;
- (3)
- , if.
3.2. The Interval-Valued q-Rung Orthopair Fuzzy Power Weighted Average Operator
3.3. The Interval-Valued q-Rung Orthopair Fuzzy Power Generalized Maclaurin Symmetric Mean Operator
3.4. The Interval-Valued q-Rung Orthopair Fuzzy Power Weighted Generalized Maclaurin Symmetric Mean Operator
4. A New Multi-Attribute Group Decision-Making Method Based on Interval-Valued q-Rung Orthopair Fuzzy Numbers
5. An Application of the Proposed Method in Online Education Platform Performance Evaluation
5.1. Online Education Platforms Performance Evaluation Process
5.2. Parameter Analysis
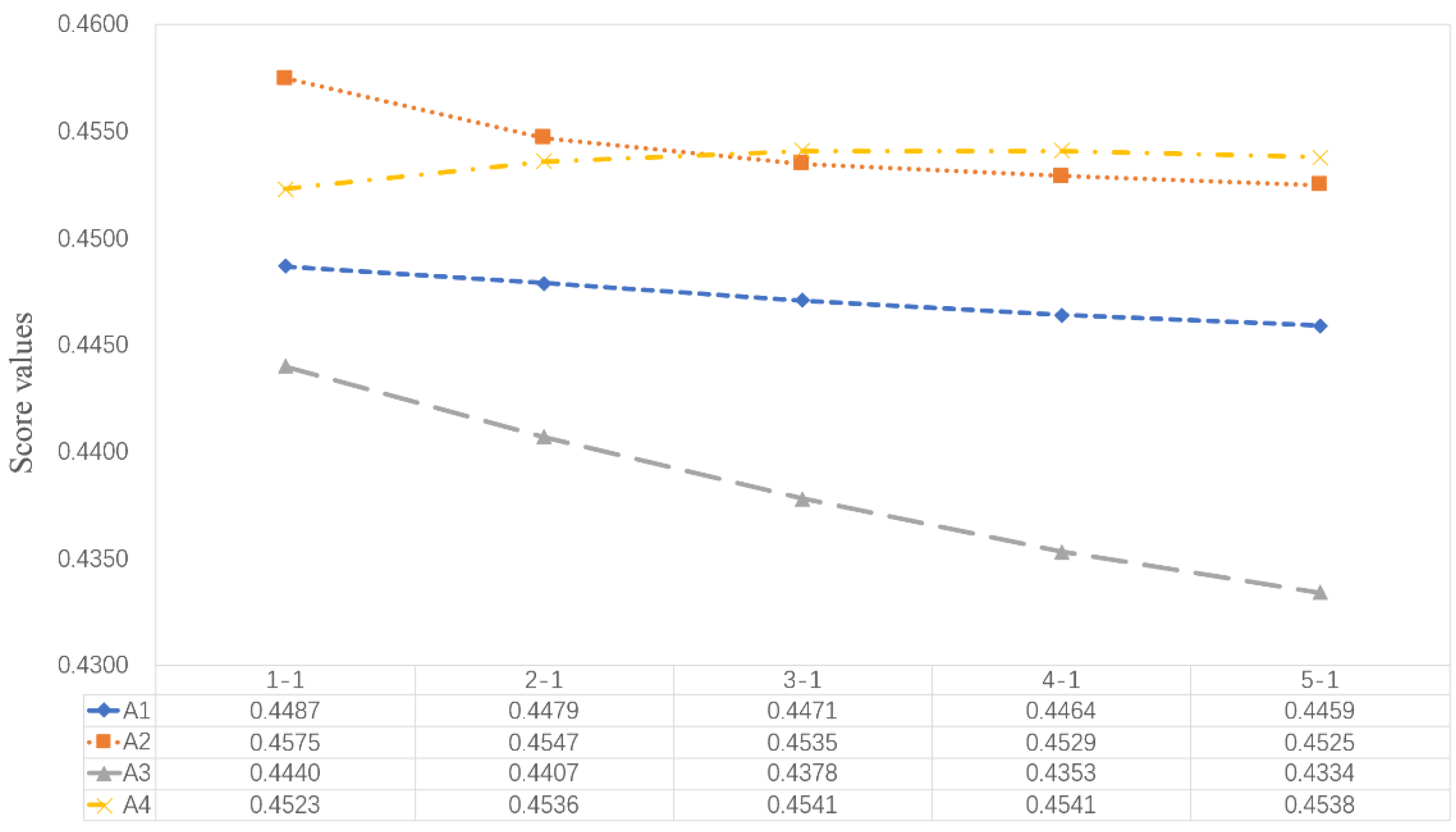
5.2.1. The Impact of q
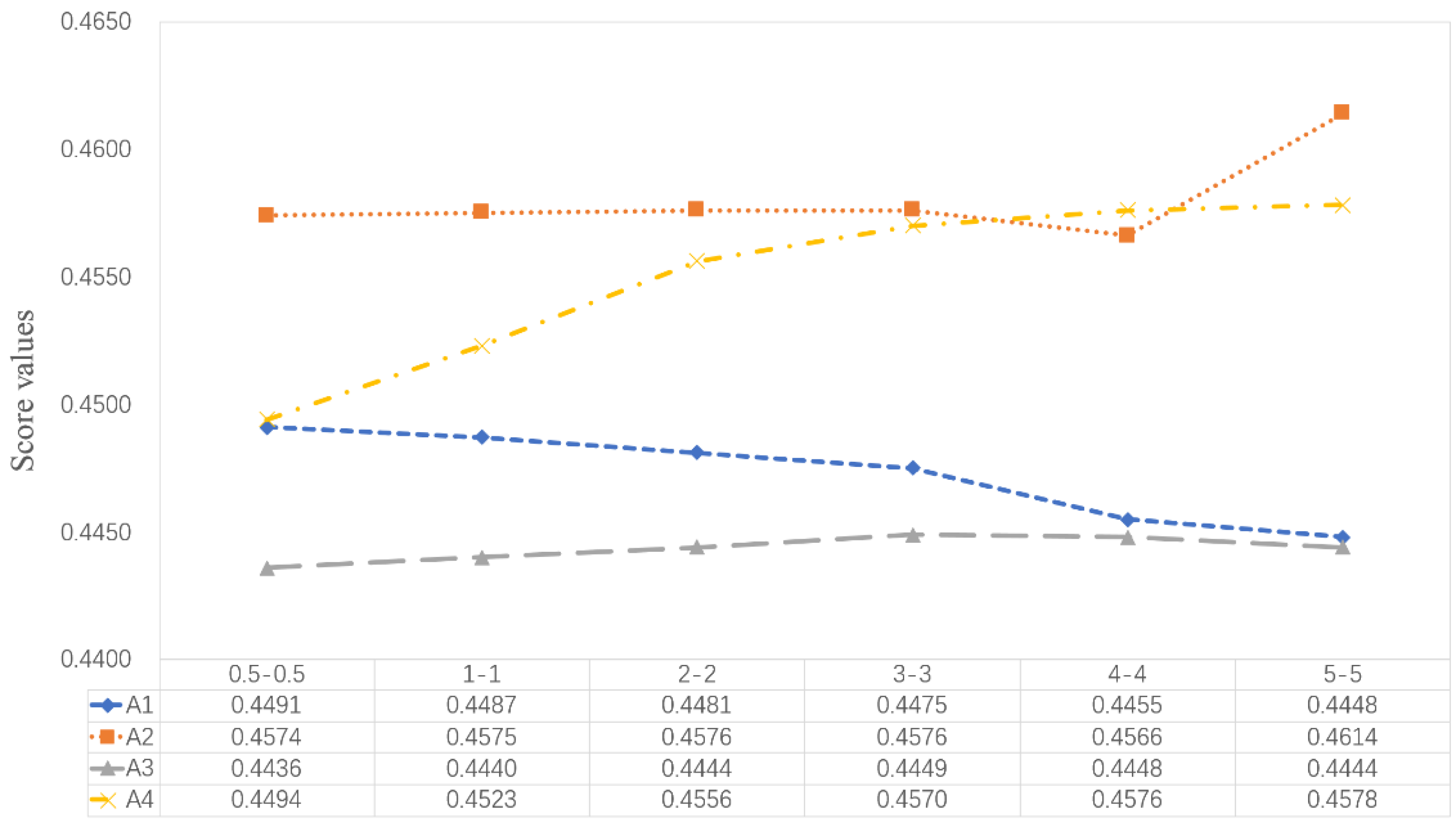
5.2.2. The Impact of
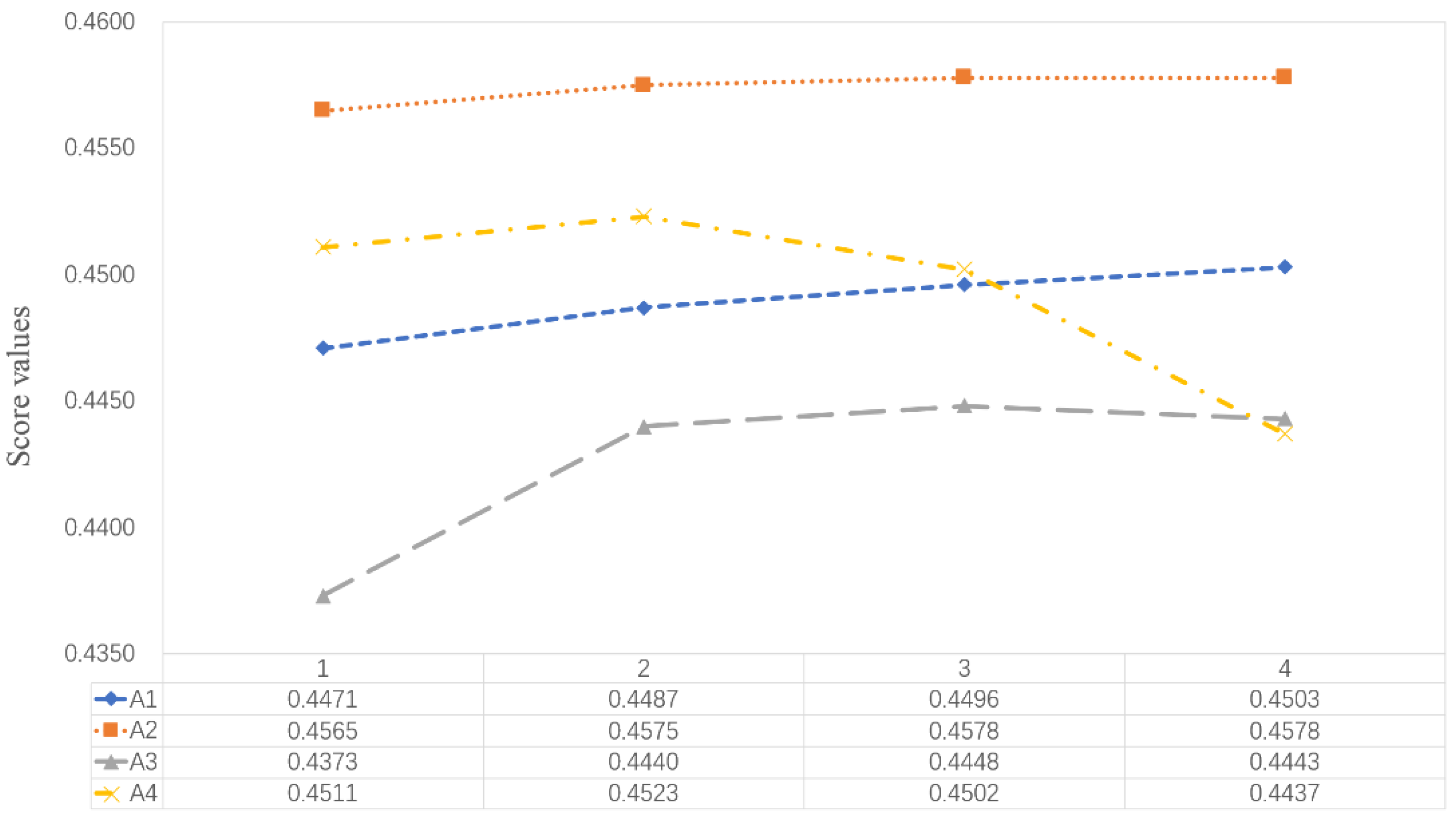
5.2.3. The Impact of k
5.3. Comparison Analysis
5.3.1. Compared with Power Bonferroni Mean Based Decision-Making Method
5.3.2. Compared with Power Heronian Mean Based Decision-Making Method
5.3.3. Compared with Power Maclaurin Symmetric Mean Based Decision-Making Methods
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cao, Y.C.; Li, H.M.; Su, L.M. Decision-making for project delivery system with related-indicators based on Pythagorean fuzzy weighted Muirhead mean operator. Information 2021, 11, 451. [Google Scholar] [CrossRef]
- Sahin, B.; Yip, T.L.; Tseng, P.-H.; Kabak, M.; Soylu, A. An application of a fuzzy TOPSIS multi-criteria decision analysis algorithm for dry bulk carrier selection. Information 2020, 11, 251. [Google Scholar] [CrossRef]
- Hu, X.; Yang, S.; Zhu, Y.-R. Multiple attribute decision making based on linguistic generalized weighted Heronian mean. Symmetry 2021, 13, 1191. [Google Scholar] [CrossRef]
- Riaz, M.; Farid, H.M.A.; Aslam, M.; Pamucar, D.; Bozanić, D. Novel approach for third-party reverse logistic provider selection process under linear Diophantine fuzzy prioritized aggregation operators. Symmetry 2021, 13, 1152. [Google Scholar] [CrossRef]
- Feng, X.; Shang, X.P.; Xu, Y.; Wang, J. A method to multi-attribute decision-making based on interval-valued q-rung dual hesitant linguistic Maclaurin symmetric mean operators. Complex. Intell. Syst. 2020, 6, 447–468. [Google Scholar] [CrossRef]
- Yager, R.R. The power average operator. IEEE Trans. Syst. Man, Cybern.-Part A Syst. Humans 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Xu, Z.X. Approaches to multiple attribute group decision making based on intuitionistic fuzzy power aggregation operators. Knowl. -Based Syst. 2011, 24, 749–760. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 169–186. [Google Scholar] [CrossRef]
- Wang, L.; Shen, Q.G.; Zhu, L. Dual hesitant fuzzy power aggregation operators based on Archimedean t-conorm and t-norm and their application to multiple attribute group decision making. Appl. Soft Comput. 2015, 38, 23–50. [Google Scholar] [CrossRef]
- Liu, P.D.; Teng, F. Multiple attribute decision making method based on normal neutrosophic generalized weighted power averaging operator. Int. J. Mach. Learn. Cybern. 2018, 9, 281–293. [Google Scholar] [CrossRef]
- Garg, H. Linguistic single-valued neutrosophic power aggregation operators and their applications to group decision-making problems. IEEE-CAA J. Autom. 2020, 7, 546–558. [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. Generalized intuitionistic fuzzy soft power aggregation operator based on t-norm and their application in multicriteria decision-making. Int. J. Intell. Syst. 2019, 34, 215–246. [Google Scholar] [CrossRef]
- Liu, P.D.; Qin, X.Y. Power average operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision making. J. Intell. Fuzzy Syst. 2017, 32, 1029–1043. [Google Scholar] [CrossRef]
- Xiong, S.H.; Chen, Z.S.; Chang, J.P.; Chin, K.S. On extended power average operators for decision-making: A case study in emergency response plan selection of civil aviation. Comput. Ind. Eng. 2019, 130, 258–271. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, J.Q.; Wang, T.L. A linguistic neutrosophic multi-criteria group decision-making approach with EDAS method. Arab J. Sci Eng. 2019, 44, 2737–2749. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Bolletino Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A guide for Practitioners. Studies In Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Xu, Z.S.; Yager, R.R. Intuitionistic fuzzy Bonferroni means. IEEE Trans. Syst. Man Cybern. Part. B Cybern. 2010, 41, 568–578. [Google Scholar]
- Yang, Y.; Chin, K.S.; Ding, H.; Lv, H.X.; Li, Y.L. Pythagorean fuzzy Bonferroni means based on T-norm and its dual T-conorm. Int. J. Intell. Syst. 2019, 34, 1303–1336. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S. Hesitant fuzzy Bonferroni means for multi-criteria decision making. J. Oper. Res. Soc. 2013, 64, 1831–1840. [Google Scholar] [CrossRef]
- Tu, H.N.; Wang, C.Y.; Zhou, X.Q.; Tao, S.D. Dual hesitant fuzzy aggregation operators based on Bonferroni means and their applications to multiple attribute decision making. Ann. Fuzzy Math. Infor. 2017, 14, 265–278. [Google Scholar]
- Liu, P.D.; Chen, S.M. Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans. Cybern. 2016, 47, 2514–2530. [Google Scholar] [CrossRef]
- Liu, P.D.; You, X.L. Some linguistic intuitionistic fuzzy Heronian mean operators based on Einstein T-norm and T-conorm and their application to decision-making. J. Intell. Fuzzy Syst. 2018, 35, 2433–2445. [Google Scholar] [CrossRef]
- Yu, D.J.; Li, D.F.; Merigo, J.M. Dual hesitant fuzzy group decision making method and its application to supplier selection. Int. J. Mach. Learn. Cyb. 2016, 7, 819–831. [Google Scholar] [CrossRef]
- Xu, Y.; Shang, X.P.; Wang, J.; Xu, W.H.; Huang, H.Q. Some q-rung dual hesitant fuzzy Heronian mean operators with their application to multiple attribute group decision-making. Symmetry 2018, 10, 472. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.L.; Ouyang, T.X.; Fu, X.l.; Peng, X.D. A decision-making algorithm for online shopping using deep-learning-based opinion pairs mining and q-rung orthopair fuzzy interaction Heronian mean operators. J. Intell. Fuzzy Syst. 2020, 35, 783–825. [Google Scholar] [CrossRef]
- Liu, P.D.; Li, Y. Some partitioned Heronian mean aggregation operators based on intuitionistic linguistic information and their application to decision-making. J. Intell. Fuzzy Syst. 2020, 38, 1–29. [Google Scholar] [CrossRef]
- Deng, X.M.; Wang, J.; Wei, G.W. Some 2-tuple linguistic Pythagorean Heronian mean operators and their application to multiple attribute decision-making. J. Exp. Theor. Artif. Intell. 2019, 31, 555–574. [Google Scholar] [CrossRef]
- Liu, P.D.; Ali, Z.; Mahmood, T. A method to multi-attribute group decision-making problem with complex q-rung orthopair linguistic information based on Heronian mean operators. Int. J. Comput. Int. Syst. 2019, 12, 1465–1496. [Google Scholar] [CrossRef] [Green Version]
- He, Y.D.; He, Z.; Wang, G.D.; Chen, H.Y. Hesitant fuzzy power Bonferroni means and their application to multiple at-tribute decision making. IEEE Trans. Fuzzy Syst. 2014, 23, 1655–1668. [Google Scholar] [CrossRef]
- Liu, P.D.; Liu, X. Multi-attribute group decision making methods based on linguistic intuitionistic fuzzy power Bonferroni mean operators. Complexity 2017, 2017, 3571459. [Google Scholar] [CrossRef]
- Liu, P.D.; Li, H.G. Interval-valued intuitionistic fuzzy power Bonferroni aggregation operators and their application to group decision making. Cogn. Comput. 2017, 9, 494–512. [Google Scholar] [CrossRef]
- Wang, L.; Li, N. Pythagorean fuzzy interaction power Bonferroni mean aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2020, 35, 150–183. [Google Scholar] [CrossRef]
- Liu, P.D. Multiple attribute group decision making method based on interval-valued intuitionistic fuzzy power Heronian aggregation operators. Comput. Ind. Eng. 2017, 108, 199–212. [Google Scholar] [CrossRef]
- Ju, D.W.; Ju, Y.B.; Wang, A.H. Multi-attribute group decision making based on power generalized Heronian mean operator under hesitant fuzzy linguistic environment. Soft Comput. 2019, 23, 3823–3842. [Google Scholar] [CrossRef]
- Liu, P.D.; Mahmood, T.; Khan, Q. Group decision making based on power Heronian aggregation operators under linguistic neutrosophic environment. Int. J. Fuzzy Syst. 2018, 20, 970–985. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Wei, G.W.; Wei, C.; Wu, J. Some power Heronian mean operators in multiple attribute decision-making based on q-rung orthopair hesitant fuzzy environment. J. Exp. Theor. Artif. Intell. 2019, 32, 909–937. [Google Scholar] [CrossRef]
- Liu, P.D.; Khan, Q.; Mahmood, T. Group decision making based on power Heronian aggregation operators under neutrosophic cubic environment. Soft Comput. 2020, 24, 1971–1997. [Google Scholar] [CrossRef]
- Jiang, S.Q.; He, W.; Qin, F.F.; Chen, Q.Q. Multiple attribute group decision-making based on power Heronian aggregation operators under interval-valued dual hesitant fuzzy environment. Math. Probl. Eng. 2020, 2020, 2080413. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Y.; Xu, W.H.; Wang, J.; Yang, G.M. A novel multiple attribute group decision-making approach based on interval-valued Pythagorean fuzzy linguistic sets. IEEE Access 2020, 8, 176797–176817. [Google Scholar] [CrossRef]
- Wang, J.Q.; Yang, Y.; Li, L. Multi-criteria decision-making method based on single-valued neutrosophic linguistic Maclaurin symmetric mean operators. Neural Comput. Appl. 2018, 30, 1529–1547. [Google Scholar] [CrossRef]
- Maclaurin, C. A second letter to Martin Folkes, Esq concerning the roots of equations, with demonstration of other rules of algebra. Philos. Trans. 1729, 36, 59–96. [Google Scholar]
- Qin, J.D. Generalized Pythagorean fuzzy Maclaurin symmetric means and its application to multiple attribute SIR group decision model. Int. J. Fuzzy Syst. 2018, 20, 943–957. [Google Scholar] [CrossRef]
- Liu, P.D.; Wang, Y.M. Multiple attribute decision making based on q-rung orthopair fuzzy generalized Maclaurin symmetric mean operators. Inform. Sci. 2020, 518, 181–210. [Google Scholar] [CrossRef]
- Liu, P.; Gao, H. Multicriteria decision making based on generalized Maclaurin symmetric means with multi-hesitant fuzzy linguistic information. Symmetry 2018, 10, 81. [Google Scholar] [CrossRef] [Green Version]
- Garg, H.; Arora, R. Generalized Maclaurin symmetric mean aggregation operators based on Archimedean t-norm of the intuitionistic fuzzy soft set information. Artif. Intell. Rev. 2020, 54, 3173–3213. [Google Scholar] [CrossRef]
- Liu, P.D.; Li, Y. Multi-attribute decision making method based on generalized Maclaurin symmetric mean aggregation operators for probabilistic linguistic information. Comput. Ind. Eng. 2019, 131, 282–294. [Google Scholar] [CrossRef]
- Ju, Y.B.; Luo, C.; Ma, J.; Gao, H.X.; Gonzalez, E.D.R.S.; Wang, A.H. Some interval-valued q-rung orthopair weighted averaging operators and their applications to multiple-attribute decision making. Int. J. Intell. Syst. 2019, 34, 2584–2606. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE T. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Xing, Y.P.; Zhang, R.T.; Zhou, Z.; Wang, J. Some q-rung orthopair fuzzy point weighted aggregation operators for multi-attribute decision making. Soft Comput. 2019, 23, 11627–11649. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.T.; Zhu, X.M.; Zhou, Z.; Shang, X.P.; Li, W.Z. Some q-rung orthopair fuzzy Muirhead means with their application to multi-attribute group decision making. J. Intell. Fuzzy Syst. 2019, 36, 1599–1614. [Google Scholar] [CrossRef]
- Khan, M.J.; Kumam, P.; Shutaywi, M. Knowledge measure for the q-rung orthopair fuzzy sets. Int. J. Intell. Syst. 2020, 36, 628–655. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.W.; Wang, R.; Alsaadi, F.E.; Wei, C.; Zhang, Y.; Wu, J. Some q-rung interval-valued orthopair fuzzy Maclaurin symmetric mean operators and their applications to multiple attribute group decision making. Int. J. Intell. Syst. 2019, 34, 2769–2806. [Google Scholar] [CrossRef]
- Gao, H.X.; Ju, Y.B.; Zhang, W.K.; Ju, D.W. Multi-attribute decision-making method based on interval-valued q-rung orthopair fuzzy Archimedean Muirhead mean operators. IEEE Access 2019, 7, 74300–74315. [Google Scholar] [CrossRef]
- Joshi, B.P.; Singh, A.; Bhatt, P.K.; Vaisla, K.S. Interval valued q-rung orthopair fuzzy sets and their properties. J. Intell. Fuzzy Syst. 2018, 35, 5225–5230. [Google Scholar] [CrossRef]
- Garg, H.; Ali, Z.; Mahmood, T. Algorithms for complex interval-valued q-rung orthopair fuzzy sets in decision making based on aggregation operators, AHP, and TOPSIS. Expert Syst. 2021, 38, 1–36. [Google Scholar] [CrossRef]
- Liu, Z.M.; Teng, F.; Liu, P.D.; Ge, Q. Interval-valued intuitionistic fuzzy power Maclaurin symmetric mean aggregation operators and their application to multiple attribute group decision-making. Int. J. Uncertain Quan. 2018, 8, 211–232. [Google Scholar] [CrossRef]
- Mu, Z.M.; Zeng, S.Z.; Wang, P.Y. Novel approach to multi-attribute group decision-making based on interval-valued Pythagorean fuzzy power Maclaurin symmetric mean operator. Comput. Ind. Eng. 2021, 155, 107049. [Google Scholar] [CrossRef]
- Ji, C.L.; Zhang, R.T.; Wang, J. Probabilistic dual-hesitant Pythagorean fuzzy sets and their application in multi-attribute group decision-making. Cogn. Comput. 2021, 13, 919–935. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.; Wang, J.; Shang, X. Some q-rung orthopair linguistic Heronian mean operators with their application to multi-attribute group decision making. Arch. Control Sci. 2018, 28, 551–583. [Google Scholar]
- Liu, Z.; Xu, H.; Yu, Y.; Li, J. Some q-rung orthopair uncertain linguistic aggregation operators and their application to multiple attribute group decision making. Int. J. Intell. Syst. 2019, 34, 2521–2555. [Google Scholar] [CrossRef]
- Liu, P.; Liu, W. Multiple-attribute group decision-making based on power Bonferroni operators of linguistic q-rung orthopair fuzzy numbers. Int. J. Intell. Syst. 2019, 34, 652–689. [Google Scholar] [CrossRef]



| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 |
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 |
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 |
| G1 | G2 | |
|---|---|---|
| A1 | ||
| A2 | ||
| A3 | ||
| A4 | ||
| G3 | G4 | |
| A1 | ||
| A2 | ||
| A3 | ||
| A4 |
| q | Ranking Orders | |
|---|---|---|
| q = 1 | 0.4530, , , | |
| q = 2 | , , , | |
| q = 3 | ,, , | |
| q = 4 | , , , | |
| q = 5 | , , , | |
| q = 6 | , , , | |
| q = 7 | , , , | |
| q = 8 | , ,, | |
| q = 9 | , , , | |
| q = 10 | , , , | |
| q = 20 | , , , | |
| q = 30 | , , , | |
| q = 40 | , , , |
| Ranking Orders | |||
|---|---|---|---|
| , , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| ,,, | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , , , |
| k | Ranking Orders | |
|---|---|---|
| k = 1 | 0.4471, , , | |
| k = 2 | , , , | |
| k = 3 | , , , | |
| k = 4 | , , , |
| Method | Score Values | Ranking Orders |
|---|---|---|
| Liu and Li’s [32] method ) | , , , | |
| Our proposed method , ) | , , , |
| Method | Score Values | Ranking Orders |
|---|---|---|
| Liu’s [34] method ) | , , , | |
| Our proposed method ; ) | , , , |
| Method | Ranking Orders | |
|---|---|---|
| Liu et al.’s [57] method ) | , , , | |
| Mu et al.’s [58] method ) | , , , | |
| Our proposed method ; ) | , , , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhou, Y. Multi-Attribute Group Decision-Making Based on Interval-Valued q-Rung Orthopair Fuzzy Power Generalized Maclaurin Symmetric Mean Operator and Its Application in Online Education Platform Performance Evaluation. Information 2021, 12, 372. https://doi.org/10.3390/info12090372
Wang J, Zhou Y. Multi-Attribute Group Decision-Making Based on Interval-Valued q-Rung Orthopair Fuzzy Power Generalized Maclaurin Symmetric Mean Operator and Its Application in Online Education Platform Performance Evaluation. Information. 2021; 12(9):372. https://doi.org/10.3390/info12090372
Chicago/Turabian StyleWang, Jun, and Yang Zhou. 2021. "Multi-Attribute Group Decision-Making Based on Interval-Valued q-Rung Orthopair Fuzzy Power Generalized Maclaurin Symmetric Mean Operator and Its Application in Online Education Platform Performance Evaluation" Information 12, no. 9: 372. https://doi.org/10.3390/info12090372
APA StyleWang, J., & Zhou, Y. (2021). Multi-Attribute Group Decision-Making Based on Interval-Valued q-Rung Orthopair Fuzzy Power Generalized Maclaurin Symmetric Mean Operator and Its Application in Online Education Platform Performance Evaluation. Information, 12(9), 372. https://doi.org/10.3390/info12090372





