Fuzzy Keyword Searchable Encryption Scheme Based on Blockchain

Abstract

Searchable encryption is a keyword-based ciphertext retrieval scheme, which can selectively retrieve encrypted documents on encrypted cloud data. Most existing searchable encryption schemes focus only on exact keyword searches and cannot return data of interest in fuzzy search. In addition, during the searchable encryption, the cloud server may return invalid results to the data user to save computing costs or for other reasons. At the same time, the user may refuse to pay the service fee after receiving the correct result. To solve the above problems, this paper proposes a fuzzy keyword searchable encryption scheme based on blockchain, which uses edit distance to generate fuzzy keyword sets and generates a secure index with verification tags for each fuzzy keyword set to verify the authenticity of the returned results. The penalty mechanism is introduced through the blockchain to realize the fairness of service payment between users and cloud servers. Security analysis shows that the scheme achieves non-adaptive semantic security. Performance analysis and functional comparison show that the scheme is effective and can meet the requirements of searching applications in the cloud environment.

1. Introduction

With the continuous expansion of Internet data, cloud storage has become a popular data storage mode. It has the feature of paying on demand, so cloud servers provide services to users who are willing to pay for them. Due to its flexible and efficient computing power, a large number of people prefer to store their data in the cloud to save local space and maintenance costs. To protect the privacy of high-sensitivity data, users need to encrypt the data before uploading. Although this method protects the privacy of sensitive data, it also causes inconvenience in retrieving encrypted documents.

In order to solve the inconvenience of ciphertext search, searchable encryption was first proposed in 2000 [1]. However, the traditional searchable encryption scheme is an honest and curious system that relies on cloud servers. That is, the server must return the correct result to the user without verification. However, in practice, the cloud server is a semi-honest and curious entity, so there may be malicious behavior, and the server may return a subset of search results or some irrelevant documents. In addition, users may refuse to pay the service fee by falsely claiming that they did not receive the correct results. This situation leads to unfair payment for services and mutual distrust between users and servers. Ideally, if the server does not return search results or returns incorrect results to the user, the user would like to be able to redeem the promised service fees, and the server would be financially penalized. Conversely, the server is guaranteed to receive a service fee when it returns the correct search results. Therefore, a reliable ciphertext retrieval scheme is urgently needed to solve the unfair payment of services between cloud servers and users, which can effectively prevent malicious operations and achieve fair payment. To solve the problem of unfair payment, we usually rely on trusted third parties, such as banks or other trusted institutions. When conflicts occur, they are resolved by trusted third parties. In order to avoid the collusive threat of third-party organizations and achieve fair service payment, blockchain technology has attracted much attention.

Blockchain has the characteristic of decentralization and is tamper-proof, which can be well combined with cloud technology. A smart contract on blockchain is a range of digitally defined commitments that can be written directly into code and executed automatically. Smart contracts allow trusted transactions without third parties that can be tracked and irreversible. As such, smart contracts are well suited to serve as verification nodes for searchable encryption systems to ensure that users get the right results. In such systems, smart contracts compel each party to perform actions in accordance with the contract. That is, users must pay the corresponding service fee after getting the correct search results, and as long as the cloud server returns the correct results, the corresponding service fee can be obtained. If the participants act in bad faith, they will be punished accordingly. Therefore, blockchain can solve the problem of unfairness between users and cloud servers in searchable encryption systems.

The blockchain-based searchable encryption scheme not only realizes ciphertext search but also solves the fairness problem between the user and the cloud. However, a scheme that can realize fair payment and support fuzzy keyword query is still lacking. Simply put, the search keyword is inconsistent with the preset keyword. For example, the default keyword is “Word”, but the user enters “Ward” for a search, which is very common in practice. When the above situation occurs, the cloud server will return a large amount of irrelevant data to the user, which will greatly reduce the availability of the system and make the user experience very poor. The fuzzy keyword searchable encryption algorithm can well solve the problem of keyword inconsistency and return the files required by users as much as possible, which greatly enhances the usability of the searchable encryption system based on blockchain. In addition, during data encryption, the system also needs to consider data updates, such as adding, deleting, and modifying data. Therefore, a searchable encryption scheme that supports fuzzy keyword search with verification of search results, fair payment, and dynamic data update is very important.

2. Related Work

In order to solve the retrieval problem on ciphertext, Song et al. [1] first proposed a symmetric searchable encryption (SSE) scheme, which realizes the search function based on ciphertext but needs to scan all documents, so the efficiency is low. To improve the search efficiency of the ciphertext, Goh et al. [2] established a secure index according to the keywords, and the cloud server returned ciphertext documents required by the user through the match between the trapdoor and index. Curtmola et al. [3] redefined the security of symmetric searchable encryption (SSE) and proposed two more secure SSE schemes. Guo et al. [4] used a Bloom filter to build the index tree and proposed a multi-keyword searchable encryption scheme, which not only supported the ranking of results but also realized the dynamic operation of data, which greatly improved the availability of the system. In reality, cloud servers are semi-honest, inquisitive entities that can be dishonest in their search. In order to prevent dishonest behavior of cloud servers, Chai et al. [5] proposed a verifiable SSE scheme. Jiang et al. [6] proposed a verifiable multi-keyword ranking search scheme, which constructed a special data structure QSet based on the inverted index structure to achieve efficient multi-keyword search. Zhang et al. [7] proposed an efficient and verifiable multi-keyword search encryption scheme. This scheme not only realizes the privacy of search mode and forward security of files but also realizes the integrity verification of outsourced data. Although the above scheme considers malicious behaviors of the cloud server, it does not consider malicious behaviors of the user, such as refusing the service fee after receiving correct results. Therefore, there is an unfair service payment problem between the cloud server and the user in the retrieval process.

In order to realize the fairness of ciphertext retrieval, Cai et al. [8] used smart contracts to record encrypted logs on the blockchain as unforgeable evidence and designed a fair protocol to detect and punish dishonest behaviors of cloud servers and users so as to realize the fairness of the system. Li et al. [9] stored encrypted data and secure indexes on the blockchain in order to avoid malicious attacks from the cloud and proposed two corresponding searchable encryption schemes according to the data size. Hu et al. [10] constructed a distributed searchable encryption scheme based on blockchain and encouraged participants to honestly implement contract rules by designing smart contracts to ensure that cloud servers and users get corresponding rewards. Zhang et al. [11] used digital signatures to construct secure indexes and proposed a searchable encryption scheme that supports two-way authentication, which can conduct a trusted keyword search without a third party and support result verification. In addition, the scheme implements server-side verifiability to prevent cloud servers from being attacked by malicious data owners. Chen et al. [12] proposed a blockchain-based EHR searchable encryption scheme. In this scenario, indexes are constructed and stored in the blockchain through complex logical expressions so that data users can use the expressions to search for indexes. Wang et al. [13] proposed a verifiable health record sharing scheme based on blockchain, which combined symmetric searchable encryption and attribute-based encryption technology to realize ciphertext search and support fine-grained access control. Li et al. [14] proposed a verifiable public-key searchable encryption scheme based on blockchain and outsourced the verification work to the TrueBit network, which greatly reduced the computational cost of miners. However, the above schemes only support an exact keyword search; that is, the correct results can be obtained only when the search keyword entered by the user is consistent with the predefined keyword. However, few schemes support both fuzzy keyword search and fair payment.

Exact keyword searchable encryption does not tolerate keyword inconsistency problems. In order to solve this problem, Li et al. [15] implemented fuzzy keyword retrieval on encrypted cloud data for the first time and constructed fuzzy keyword sets by using edit distance and wildcard technology. Wang et al. [16] constructed a new Trie-traverse search index based on the existing fuzzy keyword search scheme so that it has a constant search time. Ge et al. [17] proposed a verifiable fuzzy keyword searchable encryption scheme, which generates an index vector for each fuzzy keyword set to reduce computation cost and storage space. Jiang et al. [18] proposed a new verifiable fuzzy keyword search scheme, in which a confusion function is calculated for each fuzzy keyword set index to encrypt the true index. In addition, the cloud can decrypt the corresponding index directly by fuzzy keywords, which greatly simplifies the search process and improves search efficiency. None of the above fuzzy keyword search schemes can guarantee fairness between cloud servers and users. Yan et al. [19] proposed a fuzzy searchable encryption scheme based on blockchain. Although the scheme supports fuzzy keyword query and realizes fair payment, the efficiency of using an RSA accumulator to realize result verification is low, so it is not applicable in practical application. Therefore, an efficient and fair fuzzy keyword search scheme is urgently needed.

Based on the above analysis, the main contributions of this paper are as follows:

(1)

Fuzzy keyword search. In this paper, fuzzy keyword sets are constructed by editing distance, and security indexes are constructed for each fuzzy keyword set. The cloud server can return search results by searching for matches between trap doors and security indexes. When a keyword inconsistency problem occurs, our scheme will deduce some valid keywords from the input keyword as much as possible, and return the closest matching document.

(2)

Fair payment. In order to ensure the correctness of the results obtained by the data user, the data user generates an authentication tag for each fuzzy keyword set to verify the search results. At the same time, the smart contract is deployed to perform the validation operation and return the correct results to the user. In addition, smart contracts can automatically detect malicious behaviors of users or cloud servers and punish them accordingly to ensure the honest behavior of all participants so as to achieve fair payment.

(3)

Dynamic update. To improve system availability, our scheme supports the addition, modification, and deletion of cloud data. In addition, through security analysis and performance comparison analysis, it is proven that the scheme is secure and effective and can meet the requirements of ciphertext search applications in the cloud environment.

3. Preliminaries

3.1. Symmetric Searchable Encryption

The symmetric searchable encryption scheme includes five polynomial time algorithms $SSE=\left(Gen, Enc, Tropdoor, Search, Dec\right)$. Algorithm $Gen$ is responsible for generating key $SK$; algorithm $Enc$ is responsible for encrypting document $C$ and building index $I$; $Tropdoor$ is responsible for generating search traps. The algorithm $Search$ is responsible for the search operation and outputs the ciphertext document $C\left(W\right)$ containing the keyword $W$. Algorithm $Dec$ is responsible for decrypting the returned ciphertext document $C\left(W\right)$. Symmetric encryption schemes should be able to resist selective plaintext attacks. We choose the AES encryption algorithm that meets the above requirements to encrypt the document.

3.2. Pseudorandom Function and Message Authentication Function

The pseudorandom function (PRF) and the pseudorandom permutation function (PRP) are computable random functions that cannot be distinguished by any polynomial-time adversary. In our scheme, PRF-f is used to blind the index vectors, and PRP-π is used to blur the positions of keywords. The parameters of the above two functions are as follows:

$$\mathsf{\pi }:{\left\{0,1\right\}}^k\times {\left\{0,1\right\}}^l\to {\left\{0,1\right\}}^l$$

(1)

$$\mathrm{f}:{\left\{0,1\right\}}^k\times {\left\{0,1\right\}}^l\to {\left\{0,1\right\}}^N$$

(2)

where l is the maximum length of the keyword, k is the key, and N is the number of documents. Set:

$$\mathrm{MAC}:{\left\{0,1\right\}}^k\times {\left\{0,1\right\}}^{\ast }\to {\left\{0,1\right\}}^N$$

(3)

which is a verification tag generating function, which has the characteristics of irreversibility and message unforgeability. We use the MAC function to generate verification labels for the encrypted data to verify the correctness of the search results returned from the cloud server. In our scheme, we define $\mathrm{Tag}=\mathrm{MAC}\left(k_0,m\right)$, where $k_0$ is the key, and $m$ is the message.

3.3. Edit Distance

In our scheme, edit distance is used to evaluate the similarity between two keywords. Edit distance is the minimum number of operations required to convert keyword A to keyword B using character operations. There are generally three basic operations:

Substitution: convert one character in a word to another character.

Delete: remove a character from words.

Insert: insert a character into words.

For example, the following would be required to convert the keyword “word” to the keyword “wear”:

(1)

word → ward (o → a)

(2)

ward → war (delete d)

(3)

war → wear (insert e)

Assuming given keyword $w_{\mathrm{i}}$ and edit distance $d$, the fuzzy keyword set based on wildcards can be expressed as follows:

$$S{w}_{i,t}=\{w_{i,1},w_{i,2},···w_{i,t}\}$$

(4)

If we assume that $d$ = 1, the fuzzy keyword set of keyword “word” is as follows:

$$S_{word,1}=\{word,\ast ord,w\ast rd,wo\ast d,wor\ast ,word\ast ,wor\ast d,wo\ast rd,w\ast ord,\ast word\}$$

(5)

3.4. Inverted Index

In this paper, the index table is constructed based on the inverted index [20], as shown in

Table 1. Inverted index.

	F1	F2	F3	···	FN
w1	1	1	0	···	0
w2	0	1	1	···	0
w3	1	0	0	···	1
⋮	⋮	⋮	⋮		⋮
wn	0	0	1	···	1

. Denote the index vector of keyword $w_i$ by $v(w_i)$ and set $add{r}_i=w_i$. If the file $F_j\left(1\le j\le N\right)$ contains the keyword $w_i$, then let $v(w_i)[j]=1$; otherwise, let $v(w_i)[j]=0$.

3.5. Security Index

For any fuzzy keyword set $s_{w_{i,d}}$, the confusion function can be calculated as follows:

$$\mathsf{\Phi }\left(w_i\right)=g^{\prod w_{i,j}\in s_{w_{i,d}}{}^{{\mathsf{\pi }}_{k_2}\left(w_{i,j}\right)}}$$

(6)

To encrypt the real index, by using PRP-π to disrupt the real position of keywords, the index vector $v(w_i)$ is blinded with PRF-f to get the $\pi k_1\left(w_i\right)$ and security index:

$$Ev\left(w_i\right)\leftarrow f\left(\mathsf{\Phi }\left(w_i\right)\right)\oplus v\left(w_i\right)$$

(7)

For any fuzzy keyword $w_{i,t}\in s_{w_{i,d}}$, it is calculated as follows:

$$\phi \left(w_{i,t}\right)=g^{\prod w_{i,j}\in s_{w_{i,d}}-w_{i.t}{}^{{\mathsf{\pi }}_{k_2}\left(w_{i,j}\right)}}$$

(8)

For any fuzzy keyword $w_{i,a}$, $w_{i,b}\in s_{w_{i,d}}$, the same confusion function can be obtained by using ${\mathsf{\pi }}_{k_2}\left(w_{i,a}\right)$, ${\mathsf{\pi }}_{k_2}\left(w_{i,b}\right)$.

$$\begin{array}{l}\mathsf{\Phi }\left(w_i\right)=\mathsf{\phi }{\left(w_{i,a}\right)}^{{\mathsf{\pi }}_{k_2}\left(w_{i,a}\right)}=\mathsf{\phi }{\left(w_{i,b}\right)}^{{\mathsf{\pi }}_{k_2}\left(w_{i,b}\right)}\\ =g^{{\mathsf{\pi }}_{k_2}\left(w_{i,1}\right)·{\mathsf{\pi }}_{k_2}\left(w_{i,2}\right)···{\mathsf{\pi }}_{k_2}\left(w_{i,t}\right)}\\ =g^{\prod w_{i,j}\in s_{w_{i,d}}{}^{{\mathsf{\pi }}_{k_2}\left(w_{i,j}\right)}}\end{array}$$

(9)

Therefore, any fuzzy keyword $w_{i,t}\in s_{w_{i,d}}$ can be used to decrypt the security index and obtain the inverted index:

$$v\left(w_i\right)\leftarrow f\left(\mathsf{\Phi }\left(w_i\right)\right)\oplus Ev\left(w_i\right)=f\left(\mathsf{\phi }{\left(w_{i,t}\right)}^{{\mathsf{\pi }}_{k_2}\left(w_{i,t}\right)}\right)\oplus Ev\left(w_i\right)$$

(10)

4. Problem Formulation

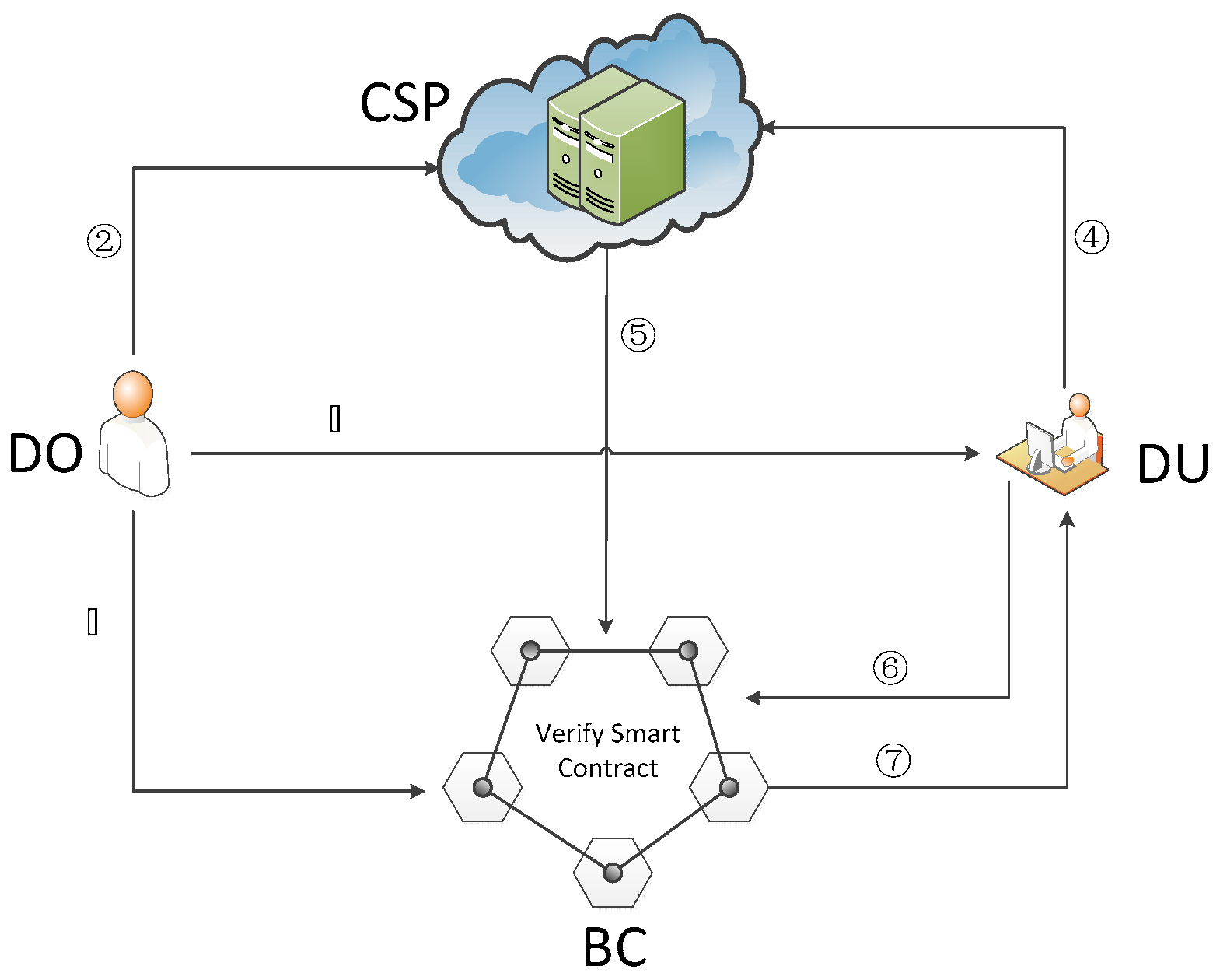
4.1. System Model

The model of the fuzzy keyword searchable encryption system based on blockchain is shown in Figure 1. It consists of four actors, namely the data owner (DO), the data user (DU), the cloud server (CSP), and the blockchain (BC). DO is primarily responsible for encrypting data and building indexes and uploading them to cloud servers. DU is mainly responsible for generating search traps and uploading them to the cloud server to complete the search. The CSP performs the search operation and sends the search results to the blockchain for verification. The BC performs the verification operation, and the smart contract motivates the CSP and DU to perform the contract operation honestly to get the correct result and the corresponding service fee.

4.2. Algorithm Definition

The blockchain-based fuzzy keyword searchable encryption scheme consists of the following seven probabilistic polynomial-time algorithms.

(1)

$KeyGen\left(k\right)$: The algorithm is executed by the DO, which inputs security parameter $k$ and outputs the key set $K=\left(sk,k_0,k_1,k_2\right)$.

(2)

$BuildIndex\left(K,F\right)$: The algorithm is executed by the DO, which inputs key set $K$ and the plaintext set $F=\left(F_1, F_2,\dots , F_N\right)$ and then outputs the security index $I$ and the encrypted document set $C=\left(C_1, C_2,\dots , C_N\right)$.

(3)

$Trapdoor\left(K,w\right)$: The algorithm is executed by the DU, which inputs security parameter $K$ and query keyword $w$ and then outputs the search trap door $Tw$.

(4)

$Search\left(Tw,I,C\right)$: The algorithm is executed by the CSP. The CSP inputs trap door $Tw$, security index $I$, and encrypted document set $C$ and then outputs encrypted document result $C\left(w\right)$ and verification tag pair $(\phi \left(w\right),Ta{g}_w)$.

(5)

$Verify(K,C\left(w\right),Tw,(\phi \left(w\right),Ta{g}_w))$: The algorithm is executed by a smart contract. The smart contract inputs security parameter $K$, the encrypted document set $C\left(w\right)$, search trap door $Tw$, and verification tag pair $(\phi \left(w\right),Ta{g}_w)$ and then outputs receive or reject.

(6)

$Dec\left(sk,C\left(w\right)\right)$: The algorithm is executed by the DU, which inputs key $sk$ and encrypted document set $C\left(w\right)$ and then outputs plaintext set $D\left(w\right)$.

(7)

$Updata(K,F_{n+1},F_j)$: The algorithm is executed by the DO. The DO inputs key set $K$, adds the new document $F_{n+1}$, modifies or deletes the document $F_j$, and then outputs the new encrypted document set $C^{\prime }$, security index $I^{\prime }$, and verification tag ${Tagw}^{\prime }$.

4.3. Specific Construction

The algorithm of the scheme is described as follows:

(1)

$KeyGen\left(k\right)$: The data owner inputs the security parameters $k$ and outputs the key set $K=\left(sk,k_0,k_1,k_2\right)$, where $sk\leftarrow SKE.Gen\left(1^k\right)$ is the key for encrypting and decrypting documents; $k_0,k_1,k_2\leftarrow {\{0,1\}}^k$, $k_0$ is the key of MAC, $k_1$ is the key of PRP-π, and $k_2$ is the key of PRF-f.

(2)

$BuildIndex\left(K, F\right)$: In order to improve the search efficiency of the system, we extend the inverted index and construct a linked list with three nodes as the index. The structure of the index is shown in Figure 2.

a. The data owner extracts the keywords from the documents that need to be uploaded to the cloud and builds the keyword set $W$. Next, the document set $F\left(w_i\right)$ is established according to the keyword $w_i\in W$.

b. After completing step a, build the index according to $F\left(w_i\right)$. Let $V\left(w_i\right)\left(1\le I \le n\right)$ denote the index vector of keyword $w_i$. If $w_i$ is in file $F_j$, the data owner will set $v(w_i)[j]=1$; otherwise, $v(w_i)[j]=0$.

c. The data owner constructs a fuzzy keyword $S_{w_{i,d}}$, where $d$ represents the edit distance, $w_i$ represents the included keywords, and $W_{i,t}(1\le i\le n,1\le t\le |S{w}_i{}_{,d}|)$ denotes the keywords in $S_{w_{i,d}}$.

d. The data owner calculates $C\left(w_i\right)\leftarrow SKE.En{c}_{sk}\left(F\left(w_i\right)\right)$ to encrypt all documents. Calculate ${\pi }_{k1}(w_i{}_{,t})(1\le i\le n,1\le t\le |S{w}_i{}_{,d}|)$ for each fuzzy key in $S{w}_i{}_{,d}$ and store it in the first node. The data owner computes $Ev\left(w_i\right)\leftarrow f\left(\mathsf{\Phi }\left(w_i\right)\right)\oplus v\left(w_i\right)$ and stores $Ev\left(w_i\right)$ in the second node. Finally, the authentication tag pair $\left(\phi \left(w_{i,t}\right),Tag{w}_{i,t}\right)$ is calculated for all fuzzy keywords in $S{w}_i{}_{,d}$, where:

$$\phi \left(w_{i,t}\right)=g^{\prod w_{i,j}\in s_{w_{i,d}-w_{i,t}}{}^{{\mathsf{\pi }}_{k_2}\left(w_{i,j}\right)}}$$

(11)

$$Tag{w}_{i,t}=MAC({\pi }_{k1}\left(w_i\right),{\pi }_{k1}(w_i{}_{,t}),Ev\left(w_i\right),C\left(w_i\right),\phi \left(w_{i,t}\right))$$

(12)

e. Finally, the data owner stores the linked lists in a hash table as a secure index $I$.

(3)

$Trapdoor\left(K,w\right)$: When data users want to search for files that contain the keyword $w^{\prime }$, they first calculate trap ${Tw}^{\prime }=\{(\pi k_1({w^{\prime }}_1),\pi k_2({w^{\prime }}_1)),(\pi k_1({w^{\prime }}_2),\pi k_2({w^{\prime }}_2)),\dots ,(\pi k_1({w^{\prime }}_t),\pi k_2({w^{\prime }}_t))\}$ and send it to the cloud server.

(4)

$Search\left(Tw,I,C\right)$: When the cloud server receives the trapdoor, it looks for all $\pi k_1\left({w^{\prime }}_i\right)$ in ${Tw}^{\prime }=\{(\pi k_1({w^{\prime }}_1),\pi k_2({w^{\prime }}_1),(\pi k_1({w^{\prime }}_2),\pi k_2({w^{\prime }}_2)),\dots ,(\pi k_1({w^{\prime }}_t),\pi k_2({w^{\prime }}_t))\}$. If the $\pi k_1\left(w_{i,a}\right)$ exists in the index ${{Iw}^{\prime }}_i=\{(\pi k_1(w_{i,1}),\phi (w_{i,1})),(\pi k_1(w_{i,2}),\phi (w_{i,2})),\dots ,(\pi k_1(w_{i,t}),\phi (w_{i,t}))\}$, make $\pi k_1\left(w_{i,a}\right)=\pi k_1({w^{\prime }}_i)$. Then, find the corresponding index file $C_j$ and corresponding proof $\left(\phi \left(w_{i,a}\right),Tag w_{i.a}\right)$ and calculate $\mathsf{\Phi }\left(w_i\right)=\mathsf{\phi }\left(w_{i,a}\right){ }^{{\mathsf{\pi }}_{k2} \left({\mathrm{w}}_{i,a}\right)}$ to decrypt the security index $Ev\left(w_i\right)$, which is used to obtain the inverted index $v\left(w_i\right)\leftarrow f(\mathsf{\Phi }\left(w_i\right))\oplus Ev\left(w_i\right)$. If $v\left(w_i\right)\left[j\right]=1$, the cloud server adds $C_j$ to $C\left(w^{\prime }\right)$; otherwise, do not add it. Finally, the cloud service submits $C\left(w^{\prime }\right)$, $(\phi (w_{i,t}),Tag w_{i,a})$, $\pi k_1\left({w^{\prime }}_i\right)$ together with the margin to the blockchain to complete the verification.

(5)

$Verify(K,{Tag}_{i,t},C(w^{\prime }),{\pi }_{k1}(w_{i,1}),T_{w^{\prime }}\phi (w_{i,t}))$: Users invoke smart contracts by submitting service fees and a search trapdoor to the blockchain. The blockchain extracts $v(w^{\prime })$ from $C(w^{\prime })$. If $C\left(w^{\prime }\right)$ is in $C_j$, the jth bit in $v(w^{\prime })$ is 1; otherwise, it is 0. Then, the blockchain computes $Ev\left(w_i\right)\leftarrow f\left(\mathsf{\Phi }\left(w_i\right)\right)\oplus v\left(w_i\right)$, where $\mathsf{\Phi }\left(w^{\prime }\right)=\mathsf{\phi }\left(w_{i,t} \right){ }^{{\mathsf{\pi }}_{k2} \left({\mathrm{w}}_{i,t}\right)}$. Then, check if $Tag{w}_{i,t}$ is equal to $MAC({\pi }_{k1}(w_i),{\pi }_{k1}(w_{i,t}),Ev(w_i),C(w_i),\phi (w_{i,t}))$. If so, the blockchain sends the result to the data user and submits the deposit and service fee to the cloud server; otherwise, it rejects the result. In addition, the deposit of the cloud server is deducted as a penalty, and the service fee is returned to the user.

(6)

$Dec\left(sk,C\left(w\right)\right)$: The data user decrypts $C(w^{\prime })$ by computing $F(w^{\prime })\leftarrow SKE.De{c}_{sk}(C(w^{\prime }))$.

(7)

$Updata(K,F_{n+1},F_j)$: DO can add document $F_{n+1}$, delete document $F_j$ or dynamically modify document $F_j$, output the updated encrypted document $C^{\prime }$, security index $I^{\prime }$, and verification tag ${Tagw}^{\prime }$, and upload them to the cloud again.

Case 1:

Adding. The DO adds a document$F_{n+1}$and then encrypts the document$F_{n+1}$using the$C\left(w_i\right)\leftarrow SKE.En{c}_{sk}\left(F\left(w_i\right)\right)$algorithm and calls$BuildIndex\left(K,F\right)$algorithm to update the security index$I^{\prime }$. Finally, the data user sends the encrypted document$C^{\prime }$and the security index$C^{\prime }$to the CSP.

Case 2:

Deleting. The DO tends to delete the document$F_j$. First of all, DO gets encrypted document$C_j$and security index$I^{\prime }$by calculating$C\left(w_i\right)\leftarrow SKE.En{c}_{sk}\left(F\left(w_i\right)\right)$and$BuildIndex\left(K,F\right)$and then sends$I^{\prime }$and$C_j$to the CSP. After receiving a delete request from DO, the CSP removes$C_j$from the encrypted document set$C$.

Case 3:

Modifying. The DO wants to replace$F_j$with${F_j}^{\prime }$. The DO encrypts${F_j}^{\prime }$to get the corresponding ciphertext${C_j}^{\prime }$and generates a new security index$I^{\prime }$. After receiving a modification request from DO, the CSP replaces$C_j$with${C_j}^{\prime }$in the encrypted document set$C$.

5. Scheme Analysis

5.1. Security Analysis

In this paper, we demonstrate the security of the system by designing real games and simulation games. Real games are played by a challenger and an adversary A, while simulation games are played by a simulator Sim and an adversary A.

Real Games $\left(Gam{e}_{real}\right)$:

(1)

Adversary A selects an arbitrary set of document sets and keyword sets $\left(F,W\right)$ and sends them to the challenger.

(2)

The challenger uses the key generation algorithm to obtain the key set K and, on this basis, uses the encryption algorithm and index generation algorithm to obtain $\left(I,C\right)$ and then sends $\left(I,C\right)$ to adversary A.

(3)

Adversary A selects a keyword $w$ and sends it to the challenger.

(4)

Challenger sends trapdoor $Tw$ to adversary A.

(5)

Adversary A outputs $b\in \left\{0,1\right\}$.

Simulation Game $\left(Gam{e}_{sim}\right)$:

(1)

Adversary A chooses the same set $\left(F,W\right)$ as in the real games and sends it to the simulator Sim.

(2)

Simulator Sim calculates $\left(I^{\prime },C^{\prime }\right)$ and sends it to adversary A.

(3)

Adversary A selects a keyword $w$ and sends it to simulator Sim.

(4)

Simulator Sim calculates the trapdoor $T^{\prime }w$ and sends it to adversary A.

(5)

Adversary A outputs $b\in \left\{0,1\right\}$.

If there exists any probabilistic polynomial-time (PPT) simulator Sim and PPT adversary A, such that |Pr(A outputs b = 1 in $Gam{e}_{real}$)−Pr(A outputs b = 1 in $Gam{e}_{sim}$)| is negligible, it can be verified that the symmetric searchable encryption scheme satisfies security.

5.2. Fairness Analysis

The fairness of the proposed scheme is guaranteed by the smart contract, which can automatically perform the predefined verification operations and handle the payment process of both parties.

Due to the irreversible and tamper-proof characteristics of blockchain, smart contracts cannot be modified once deployed. In our deployed validation contract, only if the cloud server returns the correct search results to the user, it can get the corresponding service fee. At the same time, users need to pay a deposit as a service fee during the search before getting the results. In addition, if the blockchain detects that the result returned by the cloud server is invalid, the verification contract returns the deposit originally temporarily stored to the user. Therefore, due to the strict reward and punishment mechanism of the blockchain, both cloud servers and users will honestly follow the contract rules to satisfy their own needs.

In our scheme, we combine blockchain technology with searchable encryption technology to make the system realize fair payment as well as ciphertext search.

5.3. Performance Analysis

In this paper, we compared our scheme with the schemes proposed in the literature [13,17,19] in terms of function, as shown in

Table 2. Function comparison.

Scheme	Fair Payment	Keyword Type	Verification Side	Update Dynamically	Wildcard Technology
Scheme [13]	√	Exact keyword	Smart contract	×	×
Scheme [17]	×	Fuzzy keyword	User node	×	×
Scheme [19]	√	Fuzzy keyword	Smart contract	√	×
Our scheme	√	Fuzzy keyword	Smart contract	√	√

. Both schemes [13,19] achieve result verification and fair payment through smart contracts, but scheme [13] does not support fuzzy keyword search. Although scheme [17] also realizes result verification, its verification operation is performed by the user, which undoubtedly increases the computational burden of the user. Both schemes [17,19] support fuzzy keyword search, but they do not use wildcard technology when building fuzzy keyword sets, which leads to large index space and low efficiency.

In terms of functions, our proposed scheme has more complete functions and higher system availability, so it is more suitable for cloud storage applications.

The effectiveness of the proposed scheme is compared with other schemes in the four aspects of index generation time cost, trapdoor generation time cost, search time cost, and verification time cost, as shown in

Table 3. Performance comparison.

Scheme	Index Generation	Trapdoor Generation	Search	Verification
Scheme [13]	O(n)	O(1)	O(1)	|w’|2
Scheme [17]	O(n)	O(1)	O(m)	1XOR + 1F
Scheme [19]	O(n)	O(1)	O(m)	1E + 2H|w’|
Our scheme	O(n)	O(1)	O(1)	1XOR + 1F

. Among them, N indicates the number of documents, n indicates the number of exact keywords, M indicates the maximum number of fuzzy keywords, |W’| indicates the number of documents containing search keywords, XOR indicates the exclusive or operation, E indicates the exponential operation, F indicates the pseudo-random function, and H indicates the hash operation.

In the index generation stage, both schemes [17,19] and this scheme use edit distance to construct a fuzzy keyword set. However, this scheme uses wildcard technology to greatly reduce the number of fuzzy keywords in the fuzzy keyword set, so the efficiency of this scheme is better than that of the scheme [17,19].

In the search phase, this scheme uses the hash table structure instead of the linked list structure used by schemes [17,19] to construct the index, so the time complexity of this scheme in the search phase is O(1). In addition, this paper uses the confusion function to encrypt and confuse the real index, so that the cloud can directly decrypt the index by fuzzy keywords. In this scheme, the cloud can find the corresponding encrypted index by searching πk₁(w) and then obtain the corresponding proof to decrypt the secure index. Instead of using fuzzy keywords to match the exact keywords, the corresponding index can be obtained, which greatly simplifies the search process and improves the search efficiency.

In the verification phase, scheme [19] needs to calculate one exponential operation and two hash operations for each document containing keywords, while scheme [17] and this scheme only need simple XOR operation and hash operation. Therefore, in terms of time cost, this scheme is comparable to scheme [17] but is far less than scheme [19]. In addition, the verification operation in this paper is performed by the smart contract instead of the user, so the user’s computation overhead is reduced.

6. Conclusions

In this paper, we propose a fuzzy keyword searchable encryption scheme based on blockchain. Firstly, the fuzzy keyword set is constructed for each exact keyword, then the index vector is generated for the fuzzy keyword set, and the secure index is constructed by using a three-node hash table. In addition, an obfuscation function is calculated for each fuzzy keyword set index to encrypt and obfuscate the real index so that the cloud can directly decrypt the corresponding index through the fuzzy keyword, instead of finding the exact keyword first and then using the returned keyword to construct the decryption scheme again to obtain the index, which simplifies the search process and greatly improves the search efficiency. Finally, in order to resist the malicious attack of the cloud server, a verification tag is generated for each fuzzy keyword set, and the verification is completed by the smart contract to achieve the verifiability of the returned results and the fairness of the transaction. Through security analysis and performance comparison, the security and effectiveness of our scheme are proven.