Atmospheric Propagation Modelling for Terrestrial Radio Frequency Communication Links in a Tropical Wet and Dry Savanna Climate
Abstract
1. Introduction
- ▪
- We propose a prognostic-based empirical attenuation model for terrestrial radio frequency communication links in tropical wet and dry savanna climates based on experimental data.
- ▪
- We present a classification of rain rate values based on rainfall depth levels obtained from experimental measurements.
- ▪
- We determine the propagation loss due to attenuation from atmospheric variables obtained from experimental measurements.
2. Theoretical Framework
2.1. Propagation through Free Space
2.2. Propagation through the Rain
2.3. Propagation through Cloud
2.4. Propagation through Gases
2.5. Total Attenuation Propagation Loss
2.6. The Computational Complexity of the Proposed Framework
3. Materials and Methods
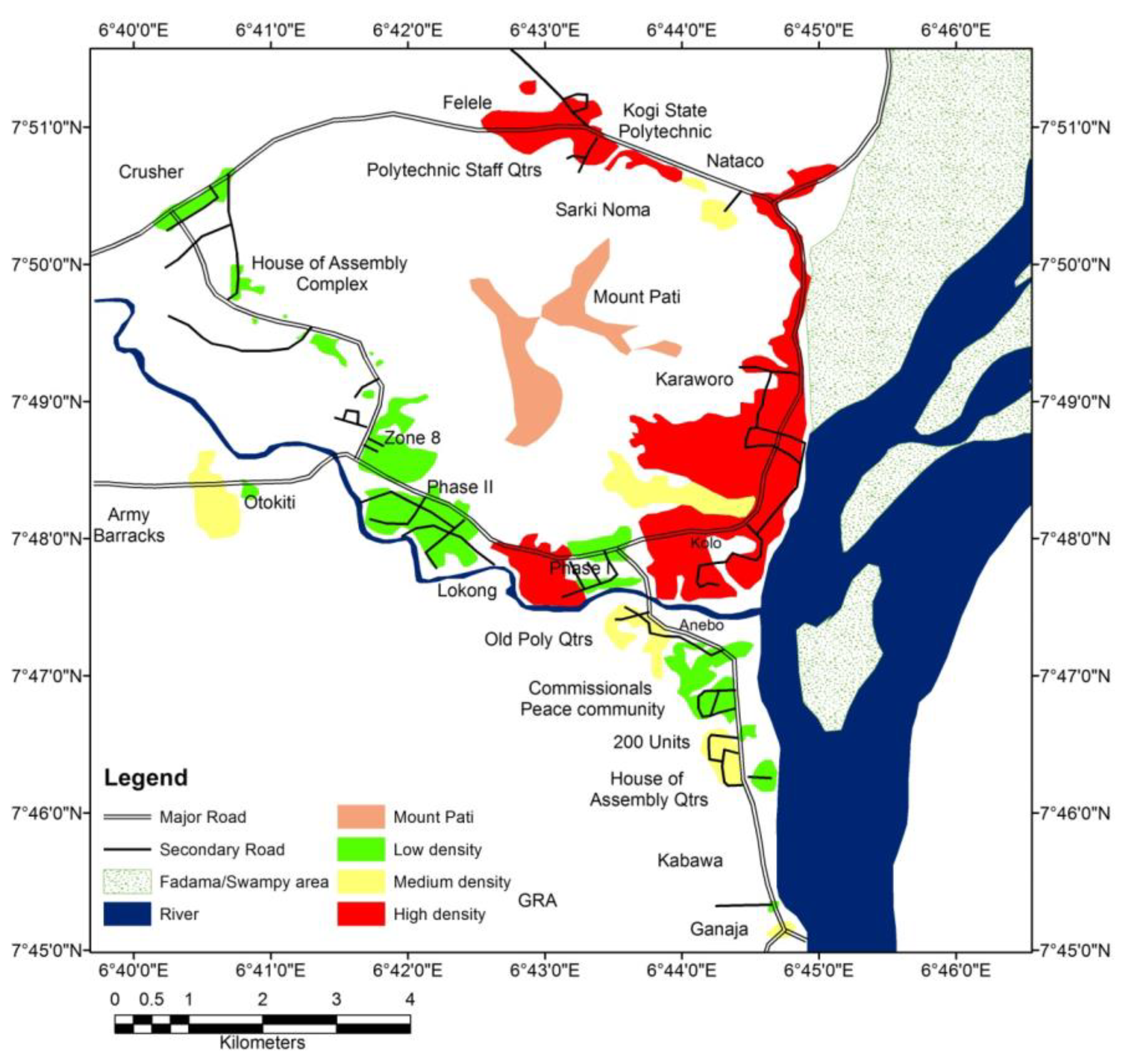
3.1. Description of Study Location
3.2. Method of Data Collection
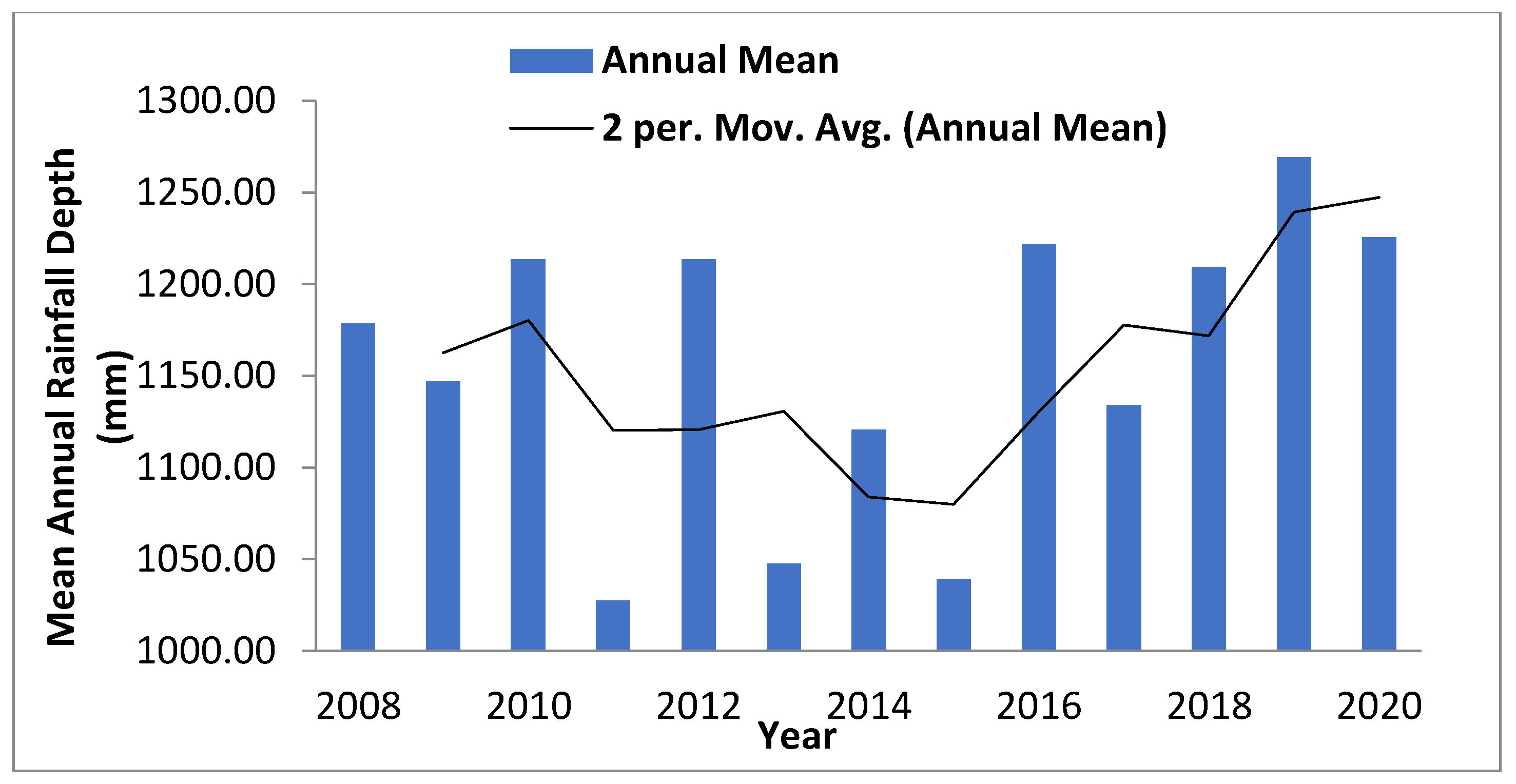
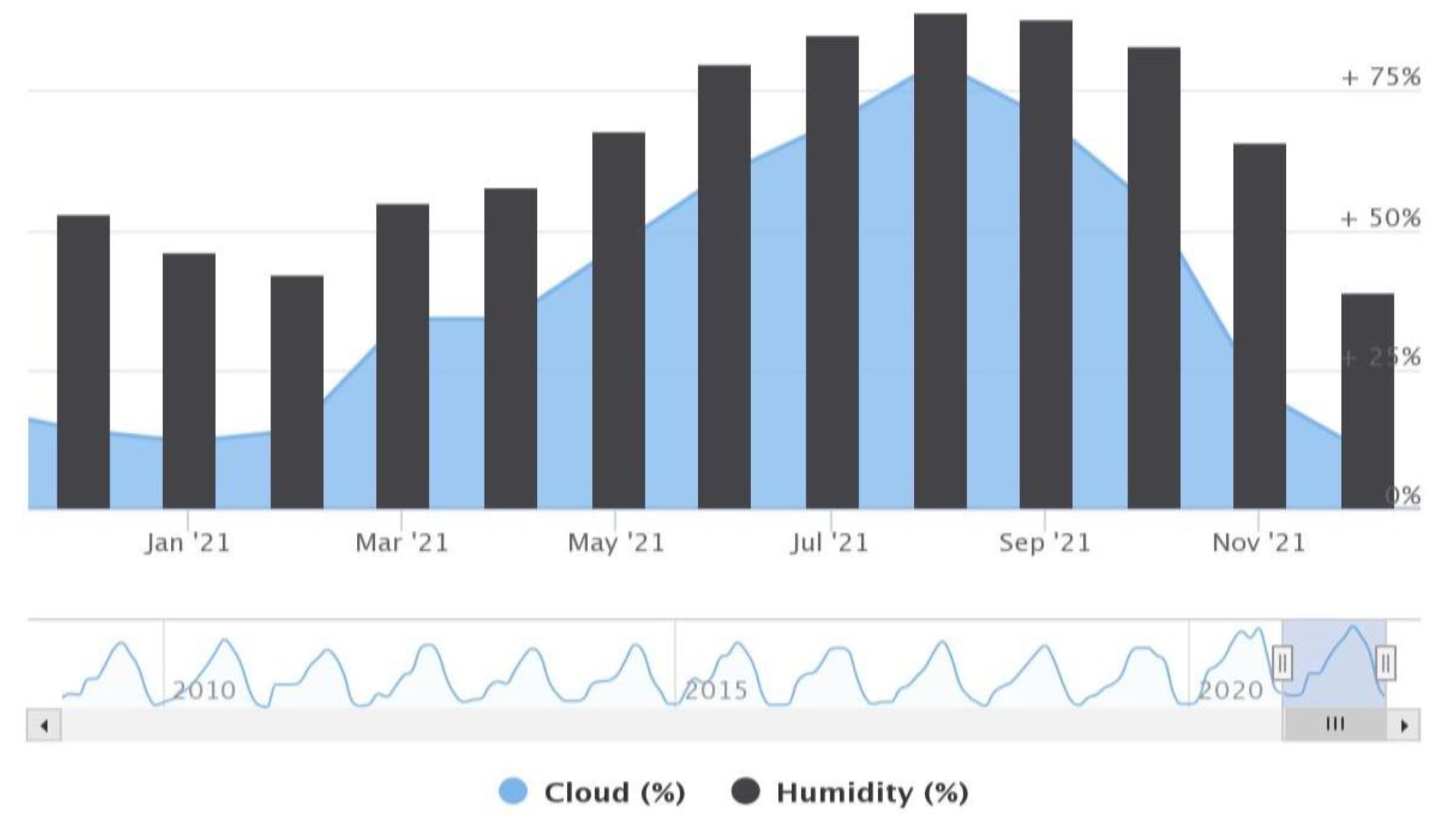
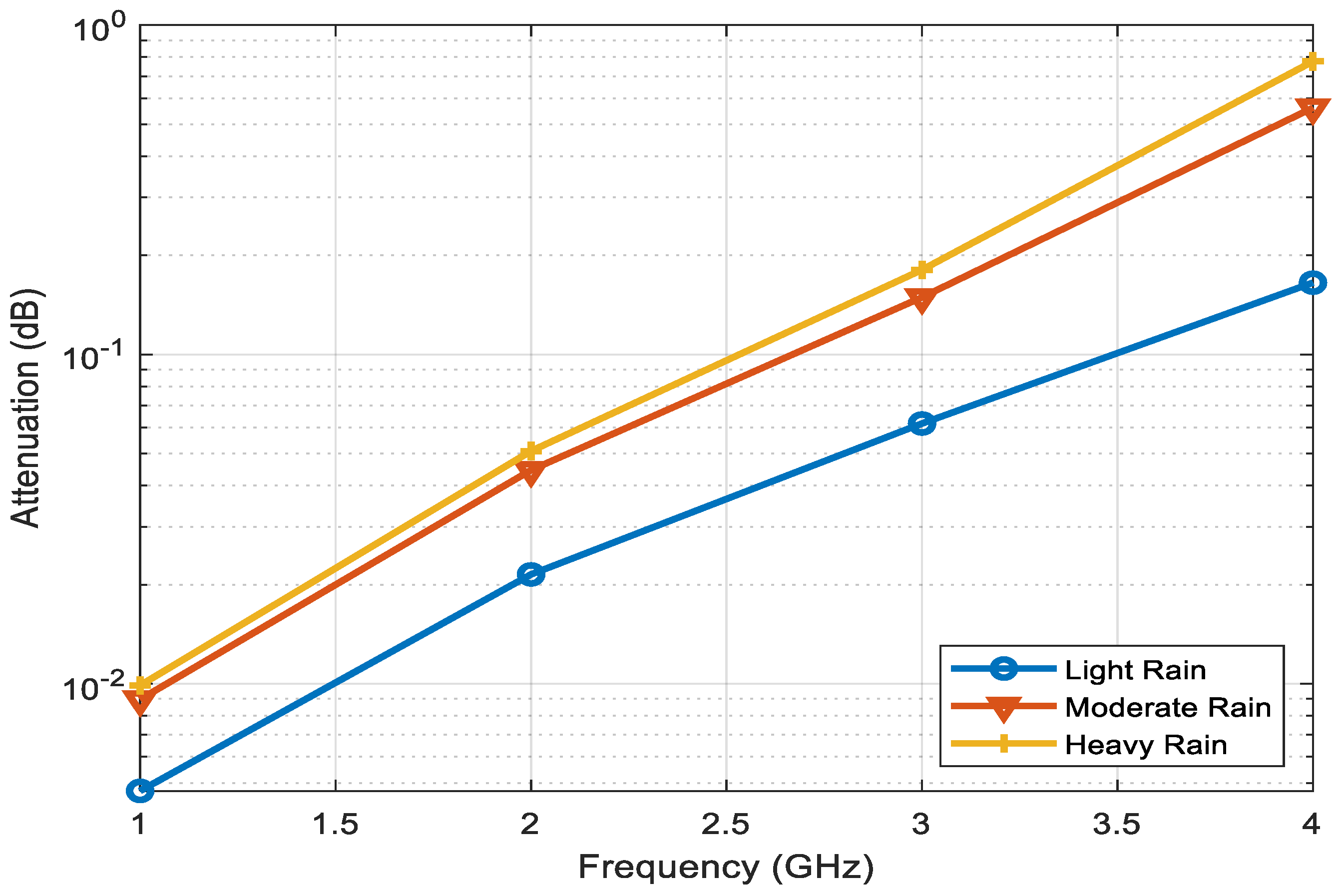
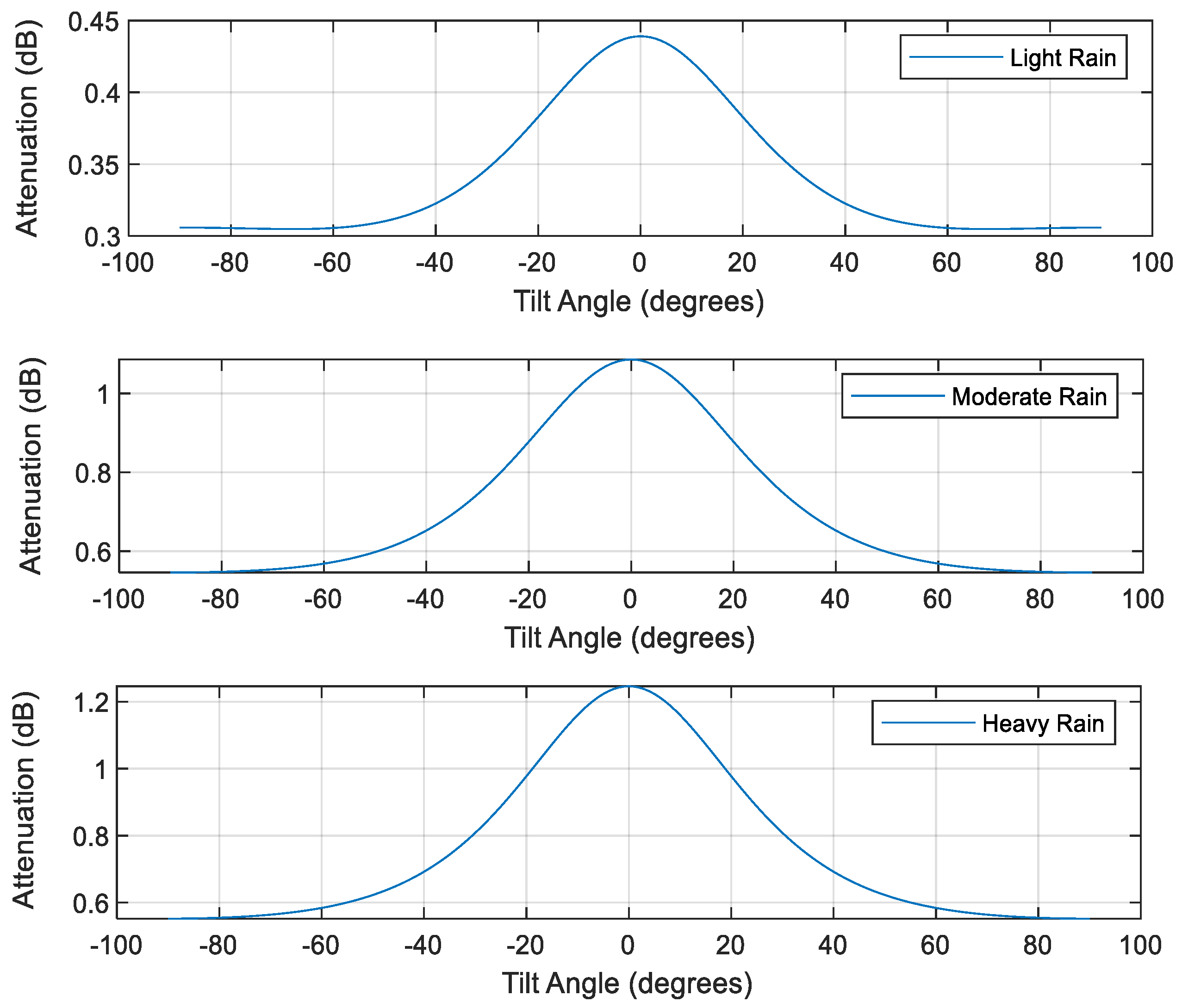
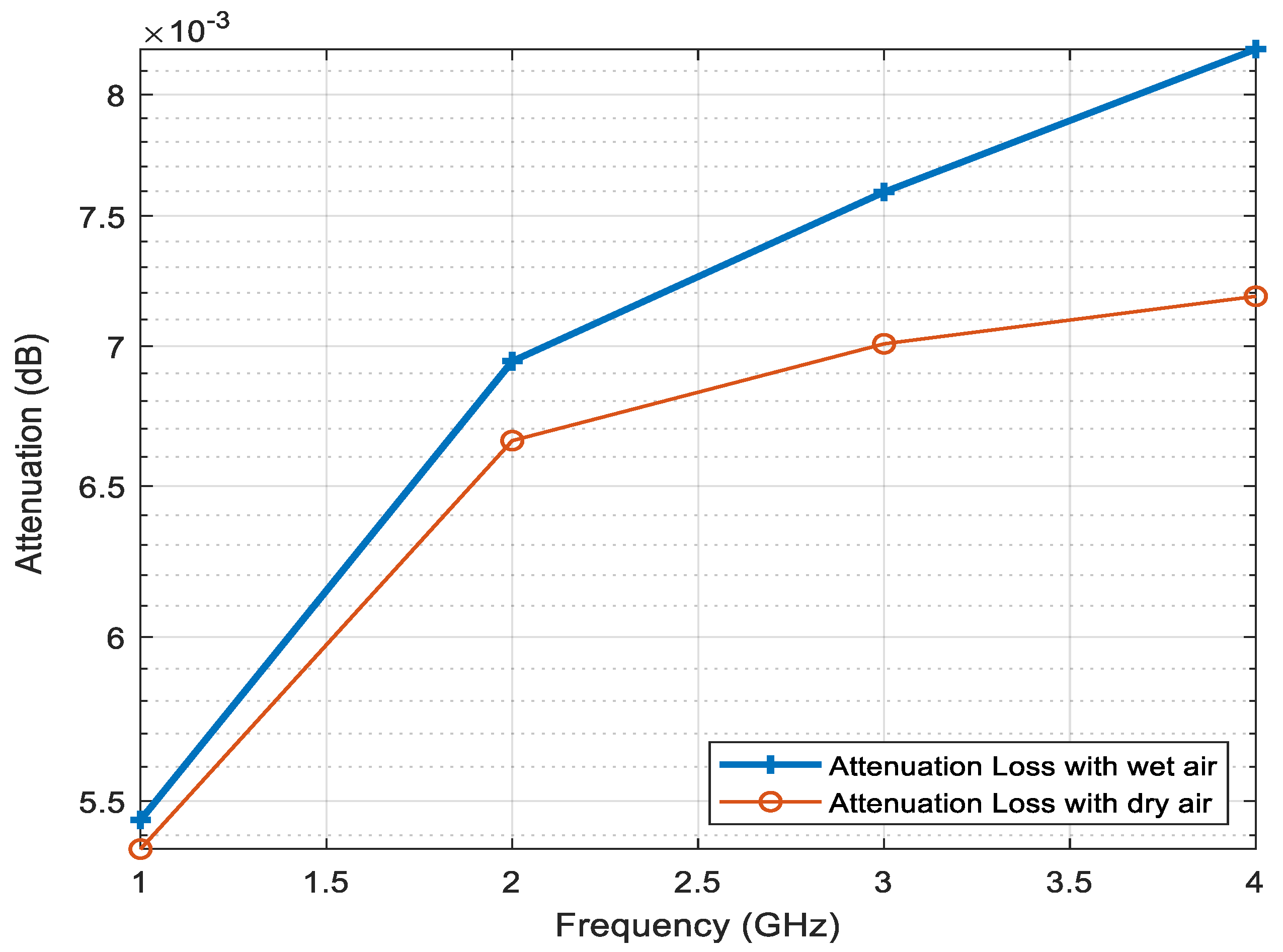
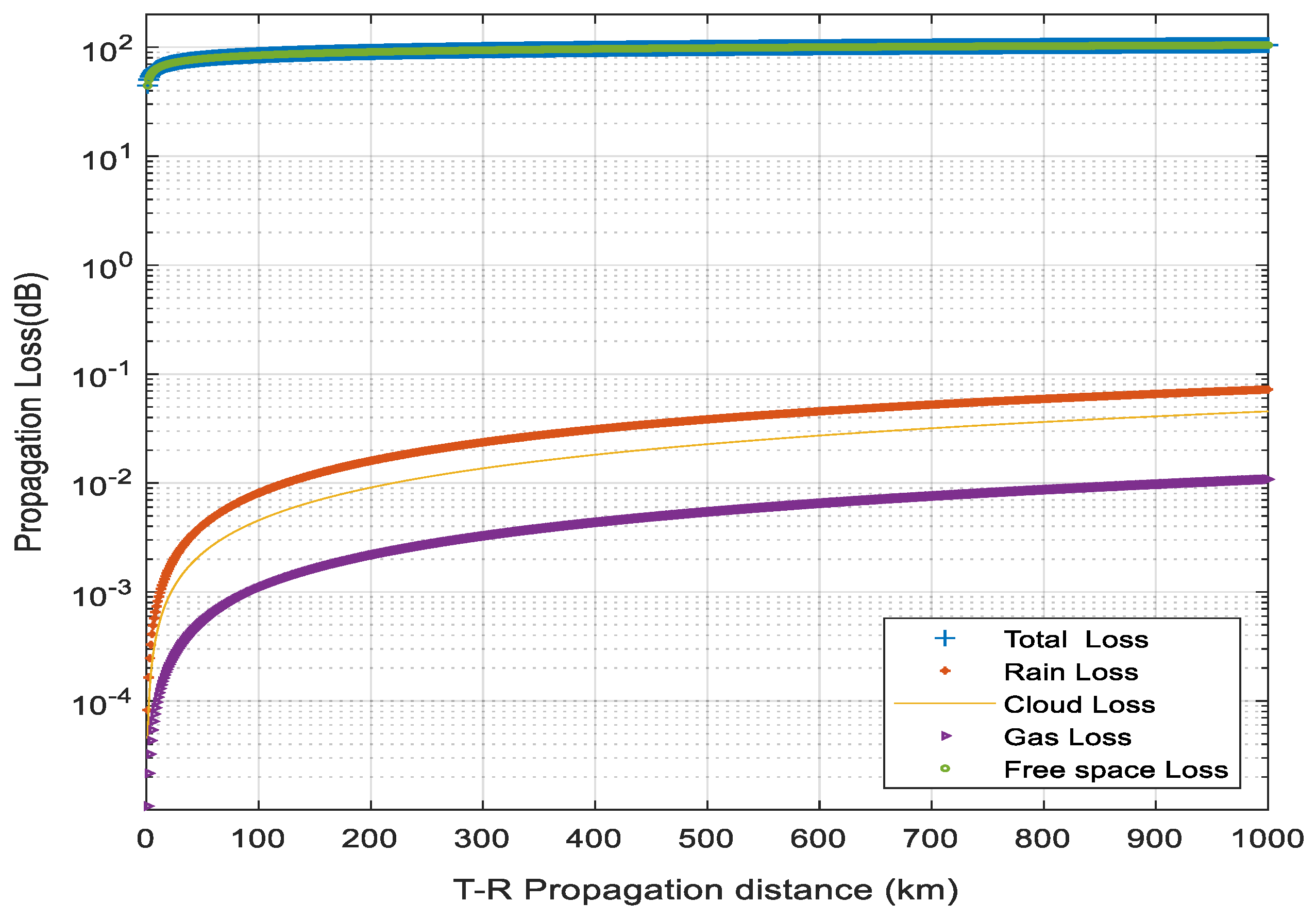
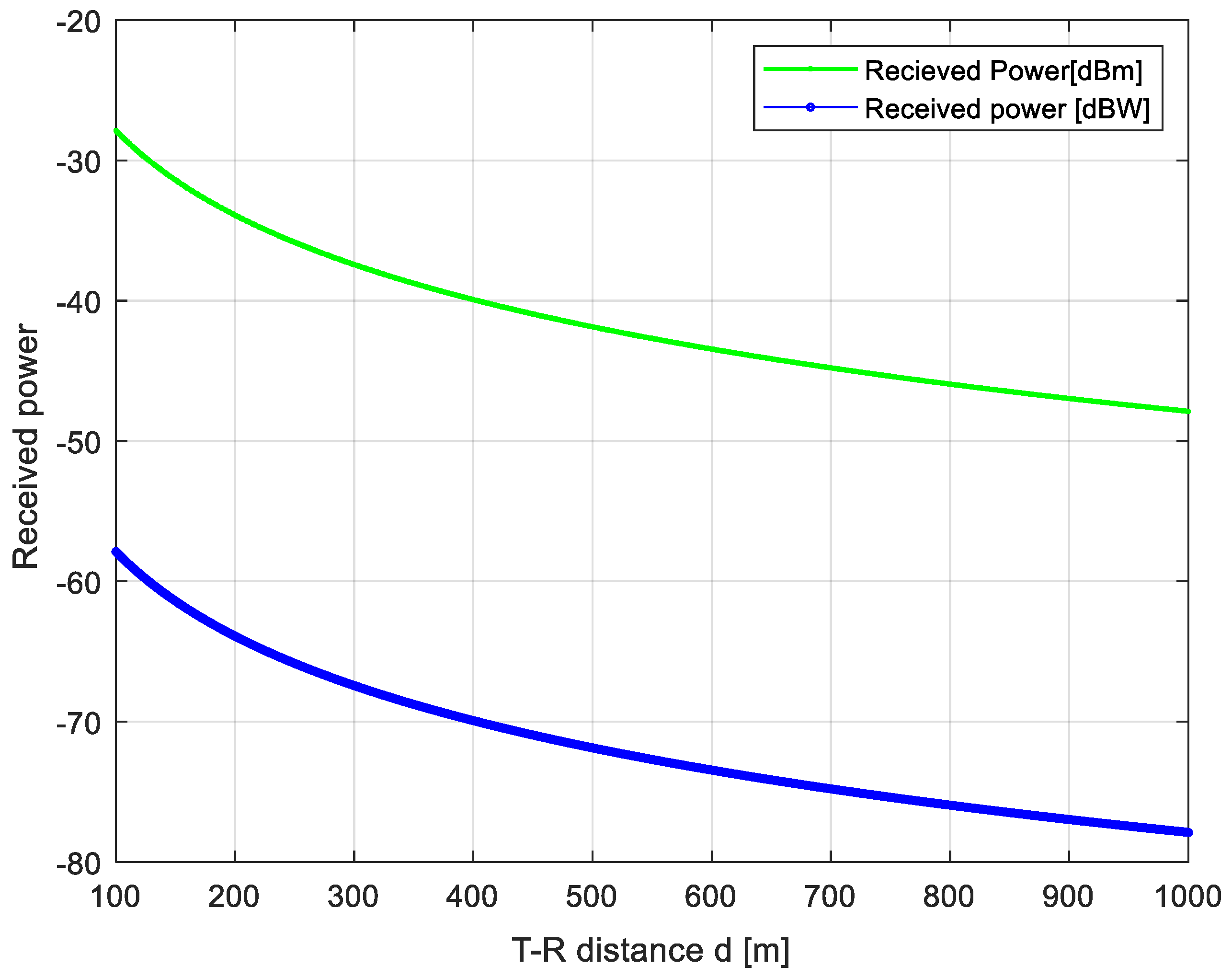
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Furqan, M.; Goswami, B. Satellite Communication Networks. In Handbook of Real-Time Computing; Tian, Y.-C., Levy, D.C., Eds.; Springer: Singapore, 2020; pp. 1–22. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, C.; Kuang, L.; Jin, J.; He, Y.; Han, Z. Spatial Spectrum Sharing for Satellite and Terrestrial Communication Networks. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1075–1089. [Google Scholar] [CrossRef]
- Schirru, L.; Ledda, F.; Lodi, M.B.; Fanti, A.; Mannaro, K.; Ortu, M.; Mazzarella, G. Electromagnetic Field Levels in Built-up Areas with an Irregular Grid of Buildings: Modeling and Integrated Software. Electronics 2020, 9, 765. [Google Scholar] [CrossRef]
- Yang, F.; Duan, X.; Guo, Q.; Lu, S.; Hsu, K. The spatiotemporal variations and propagation of droughts in Plateau Mountains of China. Sci. Total Environ. 2022, 805, 150257. [Google Scholar] [CrossRef] [PubMed]
- Isabona, J.; Imoize, A.L. Terrain-based adaption of propagation model loss parameters using non-linear square regression. J. Eng. Appl. Sci. 2021, 68, 1–19. [Google Scholar] [CrossRef]
- Ojuh, D.O.; Isabona, J. Field Electromagnetic Strength Variability Measurement and Adaptive Prognostic Approximation with Weighed Least Regression Approach in the Ultra-high Radio Frequency Band. Int. J. Intell. Syst. Appl. 2021, 13, 14–23. [Google Scholar] [CrossRef]
- Isabona, J. Wavelet Generalized Regression Neural Network Approach for Robust Field Strength Prediction. Wirel. Pers. Commun. 2020, 114, 3635–3653. [Google Scholar] [CrossRef]
- Ebhota, V.C.; Isabona, J.; Srivastava, V.M. Environment-Adaptation Based Hybrid Neural Network Predictor for Signal Propagation Loss Prediction in Cluttered and Open Urban Microcells. Wirel. Pers. Commun. 2018, 104, 935–948. [Google Scholar] [CrossRef]
- Moupfouma, F. Rain induced attenuation prediction model for terrestrial and satellite-Earth microwave links. Ann. Telecommun. 1987, 42, 539–550. [Google Scholar] [CrossRef]
- Afahakan, I.; Udofia, K.; Umoren, M. Analysis of Rain Rate and Rain Attenuation for Earth-Space Communication Links over Uyo-Akwa Ibom State. Niger. J. Technol. 2015, 35, 137. [Google Scholar] [CrossRef]
- Hassan, N.U.L.; Huang, C.; Yuen, C.; Ahmad, A.; Zhang, Y. Dense small satellite networks for modern terrestrial communication systems: Benefits, infrastructure, and technologies. IEEE Wirel. Commun. 2020, 27, 96–103. [Google Scholar] [CrossRef]
- Barclay, L. Propagation of Radiowaves; IET: London, UK, 2003; Volume 502. [Google Scholar]
- Ekpenyong, M.; Umoren, E.; Isabona, J. A Rain Attenuation Model for Predicting Fading Effect on Wireless Communication Systems in the Tropics. Niger. J. Sp. Res. 2009, 6, 21–32. [Google Scholar]
- Linga, P.; Iddi, H.; Kissaka, M. Contour Mapping for Rain Rate and Rain Attenuation in Microwave and Millimetre Wave Earth-Satellite Link Design in Tropical Tanzania. Tanzania J. Sci. 2020, 46, 886–902. [Google Scholar]
- Abdulrahman, A.Y.; Rahman, T.B.A.; Rahim, S.K.B.A.; Islam, R.U. A new rain attenuation conversion technique for tropical regions. Prog. Electromagn. Res. B 2010, 26, 53–67. [Google Scholar] [CrossRef][Green Version]
- Rimven, G.R.; Paulson, K.S.; Bellerby, T. Estimating One-Minute Rain Rate Distributions in the Tropics from TRMM Satellite Data (October 2017). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3660–3667. [Google Scholar] [CrossRef]
- Han, H.; Zhao, J.; Niyato, D.; Di Renzo, M.; Pham, Q.-V. Intelligent Reflecting Surface Aided Network: Power Control for Physical-Layer Broadcasting. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards Smart and Reconfigurable Environment: Intelligent Reflecting Surface Aided Wireless Network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef]
- Imoize, A.; Adedeji, O.; Tandiya, N.; Shetty, S. 6G Enabled Smart Infrastructure for Sustainable Society: Opportunities, Challenges, and Research Roadmap. Sensors 2021, 21, 1709. [Google Scholar] [CrossRef]
- Diamanti, M.; Charatsaris, P.; Tsiropoulou, E.E.; Papavassiliou, S. The Prospect of Reconfigurable Intelligent Surfaces in Integrated Access and Backhaul Networks. IEEE Trans. Green Commun. Netw. 2021. [Google Scholar] [CrossRef]
- Zhou, S.; Xu, W.; Wang, K.; Di Renzo, M.; Alouini, M.-S. Spectral and Energy Efficiency of IRS-Assisted MISO Communication with Hardware Impairments. IEEE Wirel. Commun. Lett. 2020, 9, 1366–1369. [Google Scholar] [CrossRef]
- Taha, A.; Alrabeiah, M.; Alkhateeb, A. Enabling Large Intelligent Surfaces with Compressive Sensing and Deep Learning. IEEE Access 2021, 9, 44304–44321. [Google Scholar] [CrossRef]
- Qin, Z.; Ye, H.; Li, G.Y.; Juang, B.-H.F. Deep Learning in Physical Layer Communications. IEEE Wirel. Commun. 2019, 26, 93–99. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, M.; Wong, K.-K.; Poor, H.V.; Cui, S. Federated Learning for 6G: Applications, Challenges, and Opportunities. Engineering 2021, 8, 33–41. [Google Scholar] [CrossRef]
- Kestwal, M.C.; Joshi, S.; Garia, L.S. Prediction of Rain Attenuation and Impact of Rain in Wave Propagation at Microwave Frequency for Tropical Region (Uttarakhand, India). Int. J. Microw. Sci. Technol. 2014, 2014, 1–6. [Google Scholar] [CrossRef]
- Linga, P.H.; Iddi, H.U.; Kissaka, M. Rain attenuation distribution for satellite microwave links application in Tanzania. Indones. J. Electr. Eng. Comput. Sci. 2020, 17, 982–987. [Google Scholar] [CrossRef][Green Version]
- Marzuki, D.K.H.; Harysandi, D.K.; Oktaviani, R.; Meylani, L.; Vonnisa, M.; Harmadi, H.; Hashiguchi, H.; Shimomai, T.; Luini, L.; Nugroho, S.; et al. ITU-R P. 837-6 and ITU-R P. 837-7 performance to estimate indonesian rainfall. TELKOMNIKA (Telecommun. Comput. Electron. Control.) 2020, 18, 2292–2303. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Das, R.; Guha, R.; Barman, S.D.; Bhattacharya, A.B. Variability of millimetrewave rain attenuation and rain rate prediction: A survey. Indian J. Radio Space Phys. 2007, 36, 325–344. [Google Scholar]
- Maitra, A.; Chakraborty, S. Cloud Liquid Water Content and Cloud Attenuation Studies with Radiosonde Data at a Tropical Location. J. Infrared Millim. Terahertz Waves 2009, 30, 367–373. [Google Scholar] [CrossRef]
- Adhikari, A.; Bhattacharya, A.; Maitra, A. Rain-Induced Scintillations and Attenuation of Ku-Band Satellite Signals at a Tropical Location. IEEE Geosci. Remote Sens. Lett. 2012, 9, 700–704. [Google Scholar] [CrossRef]
- Huang, J.; Gong, S.; Cai, B. The frequency scaling ratio factor of rain attenuation in Ka waveband along earth-space path in China. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Inner Mongolia, China, 15–17 July 2011; pp. 7831–7833. [Google Scholar]
- Ahuna, M.N.; Afullo, T.; Alonge, A. 30-Second and One-Minute Rainfall Rate Modelling and Conversion for Millimetric Wave Propagation in South Africa. SAIEE Afr. Res. J. 2016, 107, 17–29. [Google Scholar] [CrossRef]
- Owolawi, P.A.; Malinga, S.J.; Afullo, T.J.O. Estimation of terrestrial rain attenuation at microwave and millimeter wave signals in South Africa using the ITU-R model. In Proceedings of the Progress in Electromagnetic Research Symposium, PIERS, Kuala Lumpur, Malaysia, 27–30 March 2012.
- Ojo, J.; Owolawi, P. Development of one-minute rain-rate and rain-attenuation contour maps for satellite propagation system planning in a subtropical country: South Africa. Adv. Space Res. 2014, 54, 1487–1501. [Google Scholar] [CrossRef]
- Sumbiri, D.; Afullo, T.J.O.; Alonge, A. Rain attenuation prediction for terrestrial links at microwave and millimeter bands over Rwanda. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shangai, China, 8–11 August 2016; pp. 4233–4236. [Google Scholar]
- Sumbiri, D.; Afullo, T.J.; Alonge, A.A. Rainfall Zoning and Rain Attenuation Mapping for Microwave and Millimetric Applications in Central Africa. Int. J. Commun. Antenna Propag. (IRECAP) 2016, 6, 198. [Google Scholar] [CrossRef]
- Shrestha, S.; Choi, D.-Y. Rain Attenuation Study over an 18 GHz Terrestrial Microwave Link in South Korea. Int. J. Antennas Propag. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Rose, T.; Czekala, H. RPG-RATPRO Radiometer Operating Manual (Version 7.70); Technical Report; Radiometer Physics GmbH: Meckenheim, Germany, 2009. [Google Scholar]
- Grábner, M.; Kvicera, V.; Kostelecky, J. Application of Water Vapour Profiling for Gaseous Attenuation Estimation–Radiometer versus Radiosonde Results. Radio Science. 2009. Available online: https://agupubs.onlinelibrary.wiley.com/doi/10.1029/2020RS007093 (accessed on 10 February 2022).
- Ben-Daoud, A.; Ben-Daoud, M.; Moroșanu, G.A.; Rabet, S.M. The use of low impact development technologies in the attenuation of flood flows in an urban area: Settat city (Morocco) as a case. Environ. Chall. 2021, 6, 100403. [Google Scholar] [CrossRef]
- Christofilakis, V.; Tatsis, G.; Chronopoulos, S.K.; Sakkas, A.; Skrivanos, A.G.; Peppas, K.P.; Nistazakis, H.E.; Baldoumas, G.; Kostarakis, P. Earth-to-Earth Microwave Rain Attenuation Measurements: A Survey On the Recent Literature. Symmetry 2020, 12, 1440. [Google Scholar] [CrossRef]
- Christofilakis, V.; Tatsis, G.; Lolis, C.J.; Chronopoulos, S.K.; Kostarakis, P.; Bartzokas, A.; Nistazakis, H.E. A rain estimation model based on microwave signal attenuation measurements in the city of Ioannina, Greece. Meteorol. Appl. 2020, 27, 1932. [Google Scholar] [CrossRef]
- Papatsoris, K.; Polimeris, A.D.; Lazou, A.A. Development of rain attenuation and rain rate maps for satellite communications system design in Greece. In Proceedings of the 2008 IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–8 July 2008; pp. 1–4. [Google Scholar]
- Salami, G.; Faruk, N.; Surajudeen-Bakinde, N.; Ngobigha, F. Challenges and Trends in 5G Deployment: A Nigerian Case Study. In Proceedings of the 2019 2nd International Conference of the IEEE Nigeria Computer Chapter (NigeriaComputConf), Zaria, Nigeria, 14–17 October 2019; pp. 1–6. [Google Scholar]
- Fanti, A.; Schirru, L.; Casu, S.; Lodi, M.B.; Riccio, G.; Mazzarella, G. Improvement and Testing of Models for Field Level Evaluation in Urban Environment. IEEE Trans. Antennas Propag. 2020, 68, 4038–4047. [Google Scholar] [CrossRef]
- Ajose, S.; Imoize, A.L. Propagation measurements and modelling at 1800 MHz in Lagos Nigeria. Int. J. Wirel. Mob. Comput. 2013, 6, 165. [Google Scholar] [CrossRef]
- Ibhaze, A.E.; Imoize, A.L.; Ajose, S.O.; John, S.N.; Ndujiuba, C.U.; Idachaba, F.E. An Empirical Propagation Model for Path Loss Prediction at 2100MHz in a Dense Urban Environment. Indian J. Sci. Technol. 2017, 10, 1–9. [Google Scholar] [CrossRef]
- Imoize, A.L.; Ajose, O.S.; Ibhaze, A.; Akingbogun, O.O.; Denwigwe, I.H. Experimental Determination of Penetration Loss into Multi-Storey Buildings at 900 and 1800 MHz. Indones. J. Electr. Eng. Informatics (IJEEI) 2019, 7, 494–507. [Google Scholar] [CrossRef]
- Imoize, A.L.; Ibhaze, A.E.; Nwosu, P.O.; Ajose, S.O. Determination of Best-fit Propagation Models for Pathloss Prediction of a 4G LTE Network in Suburban and Urban Areas of Lagos, Nigeria. West Indian J. Eng. 2019, 41, 13–21. [Google Scholar]
- Ojo, S.; Imoize, A.; Alienyi, D. Radial basis function neural network path loss prediction model for LTE networks in multitransmitter signal propagation environments. Int. J. Commun. Syst. 2021, 34, 1–26. [Google Scholar] [CrossRef]
- Ojuh, O.; Isabona, J. Radio Frequency EMF Exposure due to Gsm Mobile Phones Base Stations: Measurements and Analysis in Nigerian Environment. Niger. J. Technol. 2015, 34, 809. [Google Scholar] [CrossRef][Green Version]
- Imoize, A.L.; Ogunfuwa, T.E. Propagation measurements of a 4G LTE network in Lagoon environment. Niger. J. Technol. Dev. 2019, 16, 1–9. [Google Scholar] [CrossRef]
- Mandeep, J.S.; Hui, O.W.; Abdullah, M.; Tariqul, M.; Ismail, M.; Suparta, W.; Yatim, B.; Menon, P.S.; Abdullah, H. Modified ITU-R rain attenuation model for equatorial climate. In Proceedings of the 2011 IEEE International Conference on Space Science and Communication (IconSpace), Penang, Malaysia, 12–13 July 2011; pp. 89–92. [Google Scholar]
- Series, R.P. Propagation data and prediction methods required for the design of terrestrial line-of-sight systems. Recomm. ITU-R 2015, 7, 512–530. [Google Scholar]
- Diba, F.D.; Afullo, T.J.; Alonge, A. Rainfall Rate and Attenuation Performance Analysis at Microwave and Millimeter Bands for the Design of Terrestrial Line-of-Sight Radio Links in Ethiopia. SAIEE Afr. Res. J. 2016, 107, 177–186. [Google Scholar] [CrossRef]
- Ananya, S.T.; Islam, S.; Mahmud, A.R.; Podder, P.K.; Uddin, J. Atmospheric Propagation Impairment Effects for Wireless Communications. Int. J. Wirel. Mob. Netw. 2020, 12, 45–61. [Google Scholar] [CrossRef]
- Gataullin, Y.; Kozlowski, R. Implementation of rain and gaseous attenuation models for 26–30 GHz Ka-Band Communication. In Proceedings of the 6th IASTED International Conference Antennas, Radar, and Wave Propagation (ARP 2009), Banff, AL, USA, 6–8 July 2009. [Google Scholar]
- Chen, J.; Kanj, I.A.; Xia, G. Improved upper bounds for vertex cover. Theor. Comput. Sci. 2010, 411, 3736–3756. [Google Scholar] [CrossRef]
- Adeoye, N.O. Spatio-temporal analysis of land use/cover change of Lokoja-a confluence town. J. Geogr. Geol. 2012, 4, 40. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isabona, J.; Imoize, A.L.; Ojo, S.; Lee, C.-C.; Li, C.-T. Atmospheric Propagation Modelling for Terrestrial Radio Frequency Communication Links in a Tropical Wet and Dry Savanna Climate. Information 2022, 13, 141. https://doi.org/10.3390/info13030141
Isabona J, Imoize AL, Ojo S, Lee C-C, Li C-T. Atmospheric Propagation Modelling for Terrestrial Radio Frequency Communication Links in a Tropical Wet and Dry Savanna Climate. Information. 2022; 13(3):141. https://doi.org/10.3390/info13030141
Chicago/Turabian StyleIsabona, Joseph, Agbotiname Lucky Imoize, Stephen Ojo, Cheng-Chi Lee, and Chun-Ta Li. 2022. "Atmospheric Propagation Modelling for Terrestrial Radio Frequency Communication Links in a Tropical Wet and Dry Savanna Climate" Information 13, no. 3: 141. https://doi.org/10.3390/info13030141
APA StyleIsabona, J., Imoize, A. L., Ojo, S., Lee, C.-C., & Li, C.-T. (2022). Atmospheric Propagation Modelling for Terrestrial Radio Frequency Communication Links in a Tropical Wet and Dry Savanna Climate. Information, 13(3), 141. https://doi.org/10.3390/info13030141









