Enhancing Inference on Physiological and Kinematic Periodic Signals via Phase-Based Interpretability and Multi-Task Learning
Abstract
:1. Introduction
- Infusing phase information to the input and as a regularizer to improve model performance.
- Adding a unit for inducing interpretability for periodic physiological and sensory data.
- Exploring the trade-off between performance and interpretability for better understanding the underlying system.
- Generating synthetic sensory data by leveraging the interpretable unit.
2. Materials and Methods
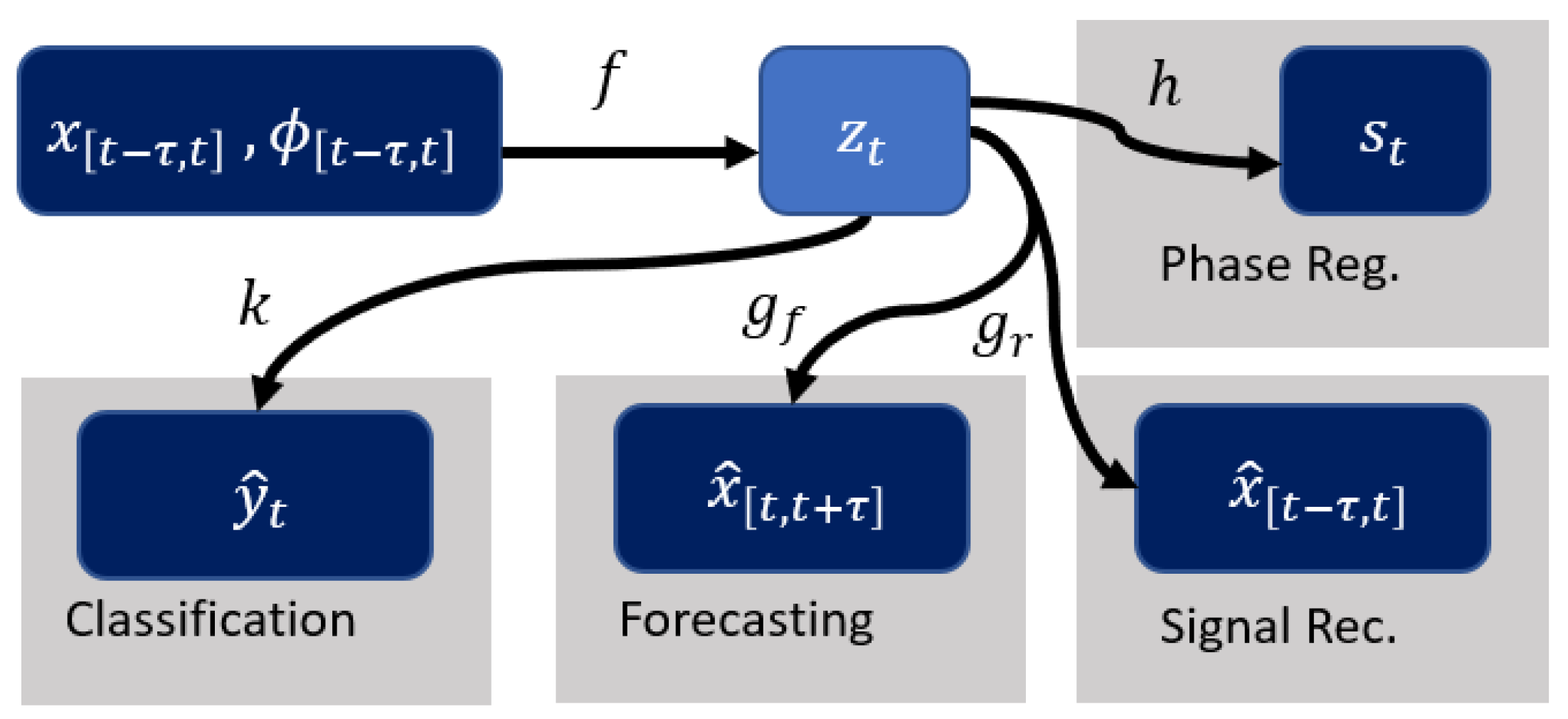
2.1. Mathematical Formulation
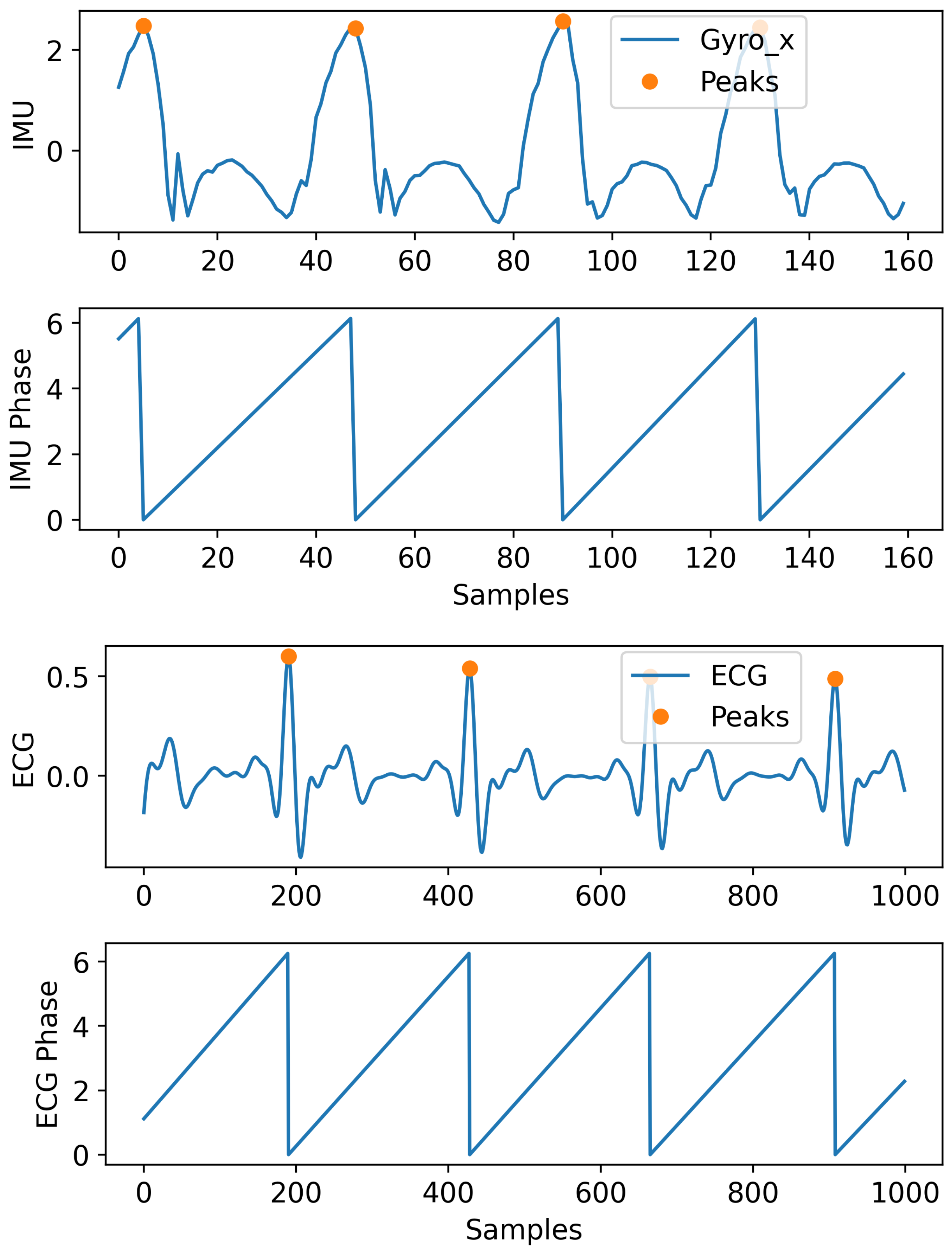
2.2. Phase Computation and Encoding
2.3. Signal Encoder and Decoder Architecture
2.4. Phase Regularization
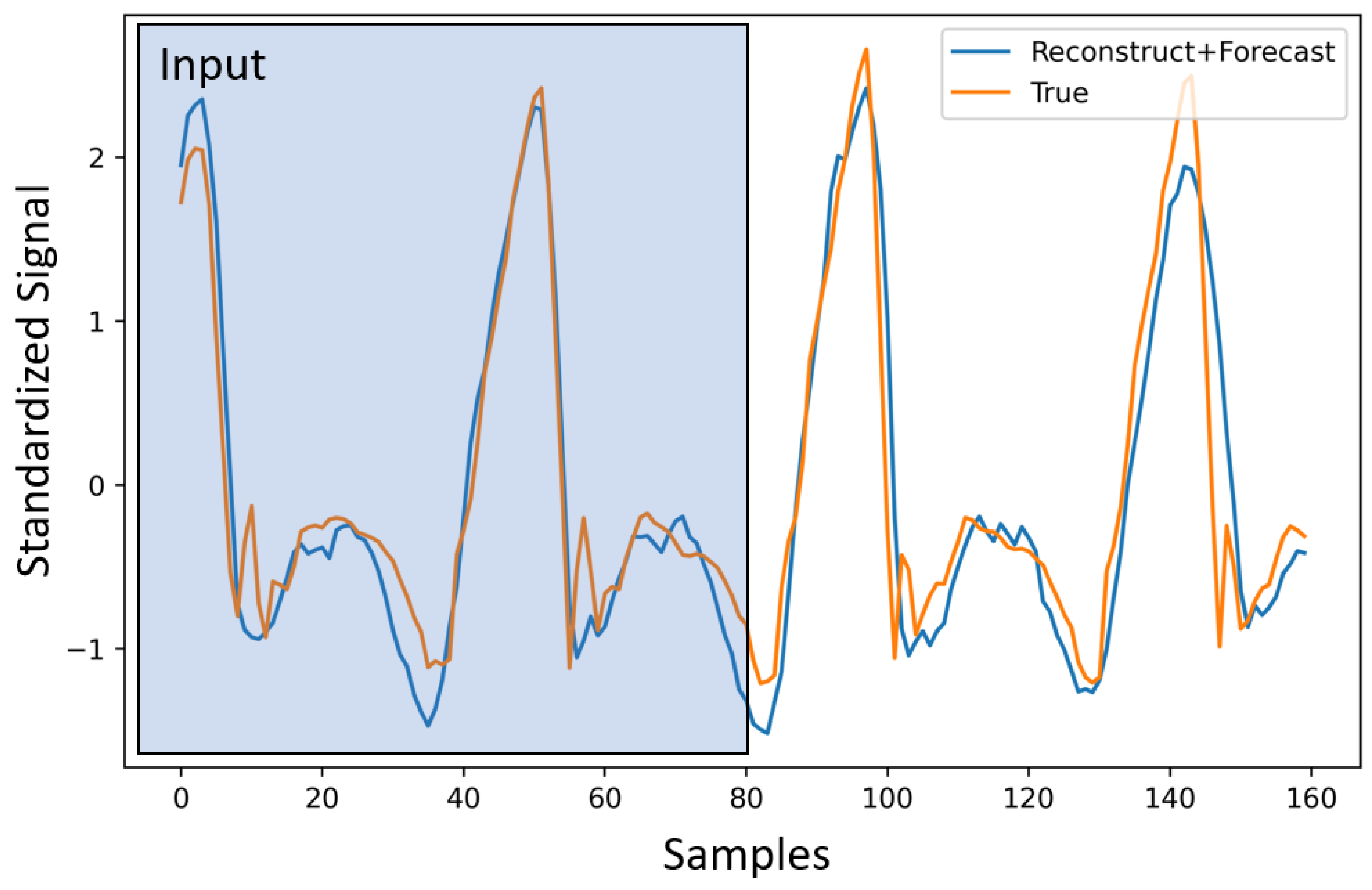
2.5. Forecasting Task
2.6. Classification Task
2.7. Weighting Loss Terms
3. Results
3.1. IMU Dataset and Preprocessing for Gait Task
3.2. Model and Training for Gait Task
3.3. Impact of Encoding and h on Gait Task
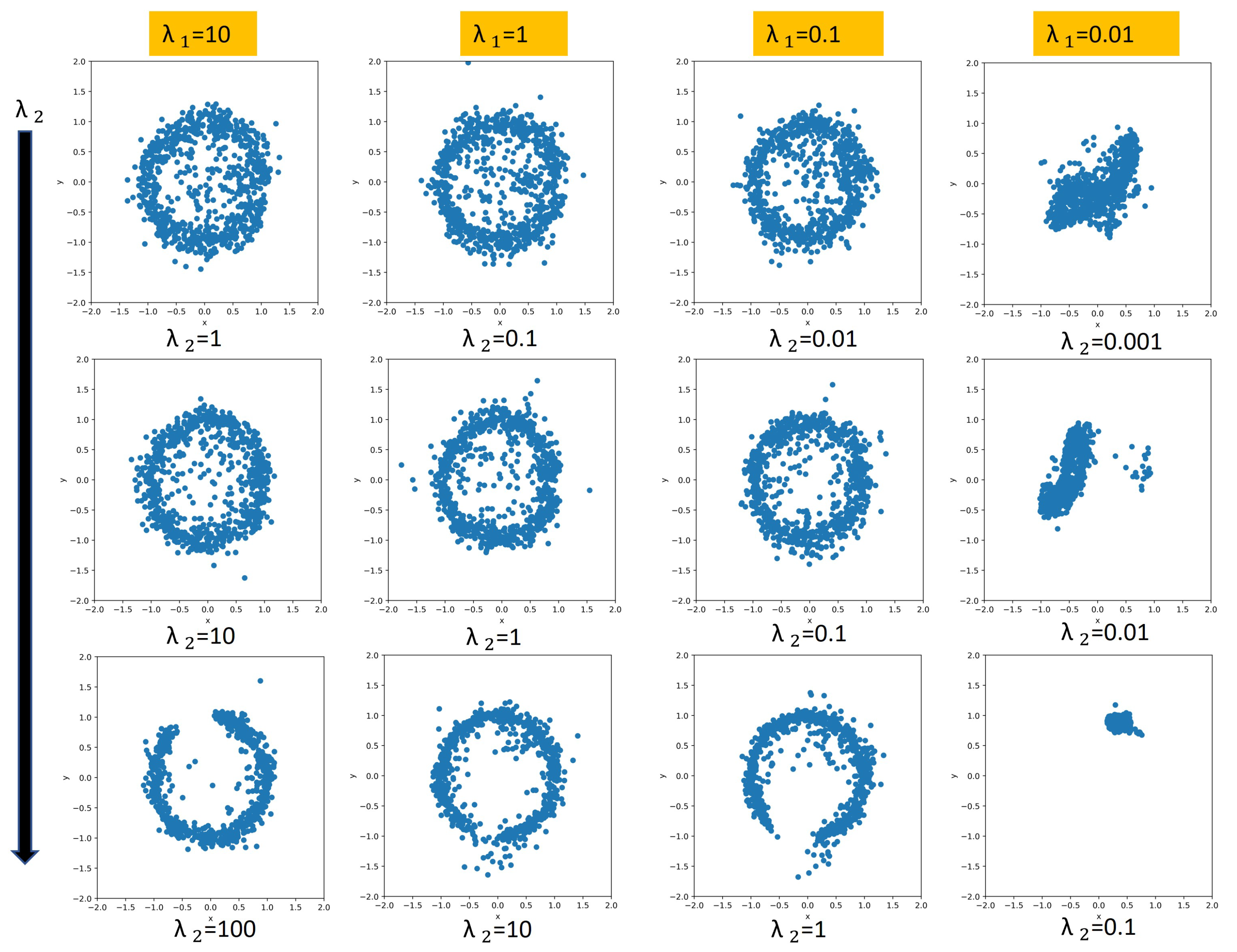
3.4. Relationship between and for Gait Task
3.5. Multi-Task Learning for Gait Task
3.6. Gait Signal Generation
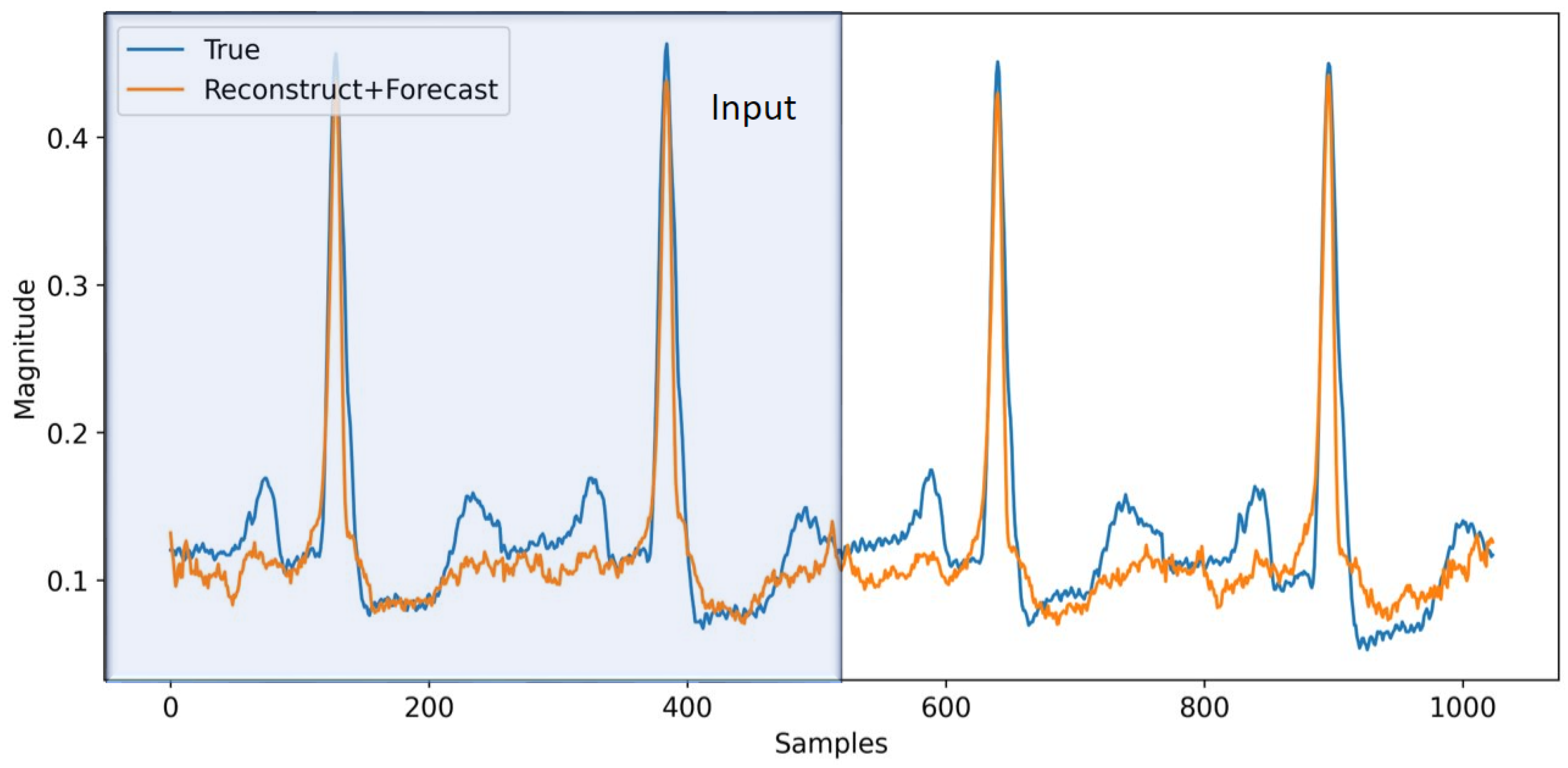
3.7. ECG Forecasting
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Metric Definition
Appendix A.2. Model Architecture
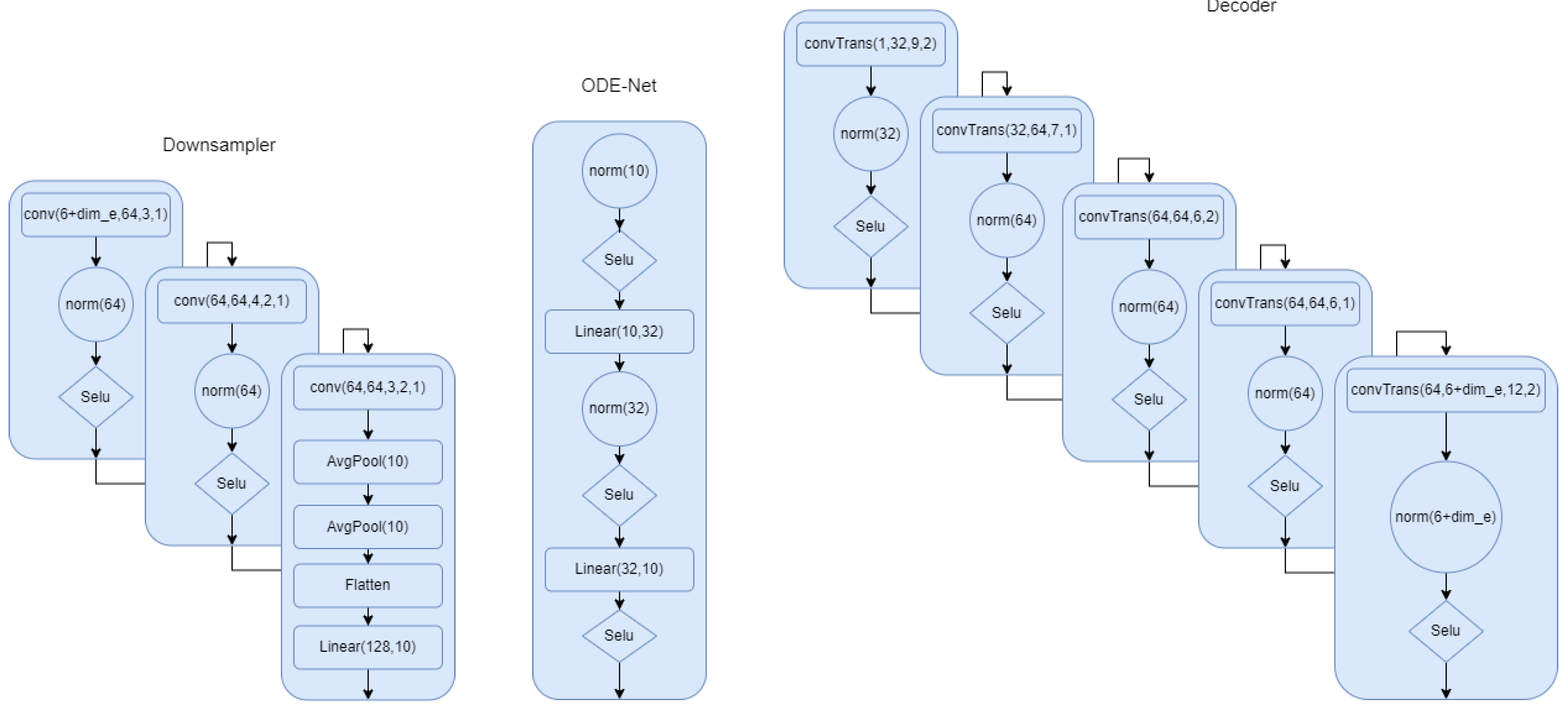
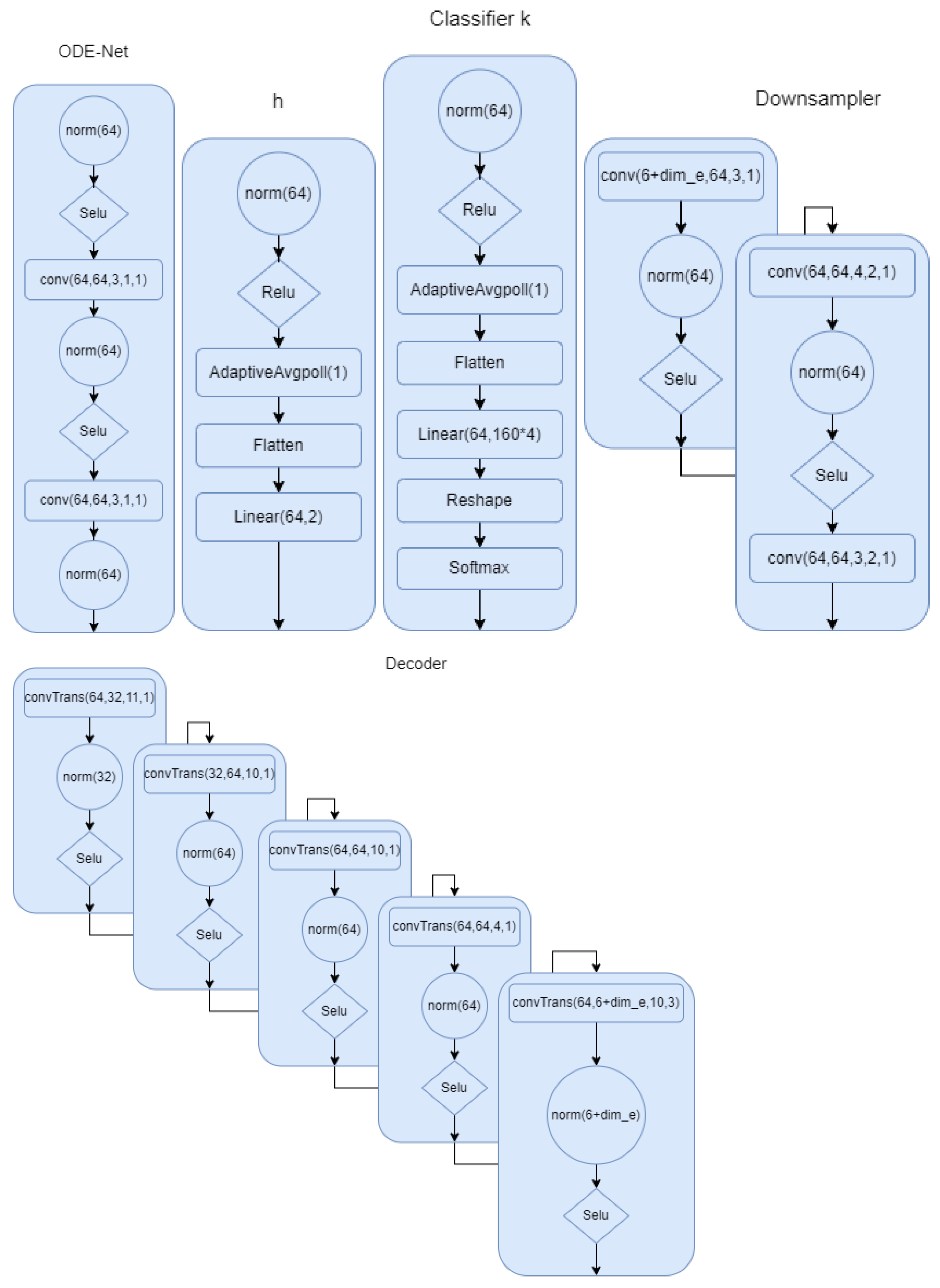
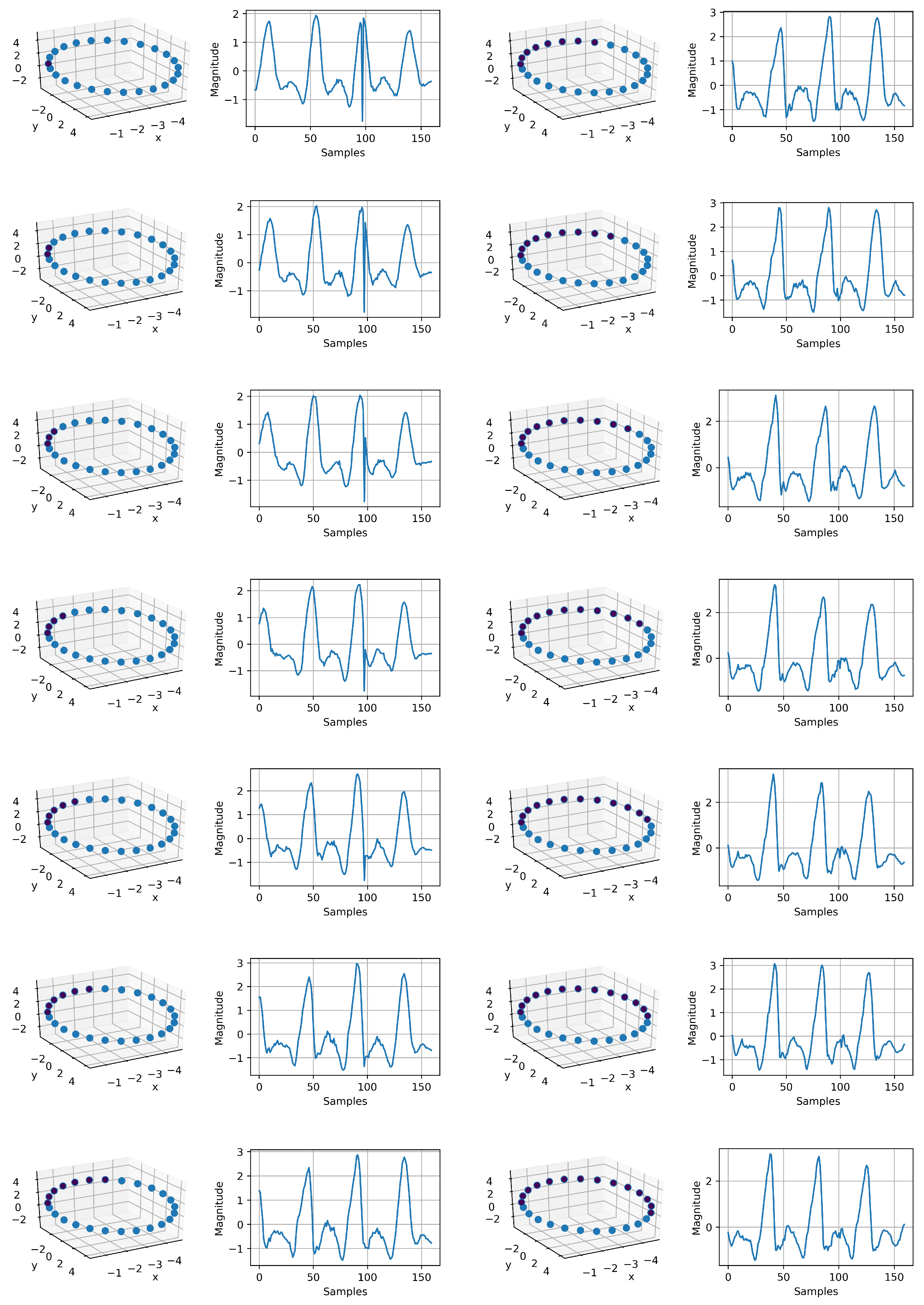
Appendix A.3. IMU Generation
References
- Dama, F.; Sinoquet, C. Analysis and modeling to forecast in time series: A systematic review. arXiv 2021, arXiv:2104.00164. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Rajan, D.; Thiagarajan, J.; Spanias, A. Attend and diagnose: Clinical time series analysis using attention models. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Harutyunyan, H.; Khachatrian, H.; Kale, D.C.; Steeg, G.V.; Galstyan, A. Multitask learning and benchmarking with clinical time series data. Sci. Data 2019, 6, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jadon, S.; Milczek, J.K.; Patankar, A. Challenges and approaches to time-series forecasting in data center telemetry: A Survey. arXiv 2021, arXiv:2101.04224. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM fully convolutional networks for time series classification. IEEE Access 2018, 6, 1662–1669. [Google Scholar] [CrossRef]
- Nakano, K.; Chakraborty, B. Effect of Data Representation for Time Series Classification—A Comparative Study and a New Proposal. Mach. Learn. Knowl. Extr. 2019, 1, 1100–1120. [Google Scholar] [CrossRef] [Green Version]
- Elsayed, N.; Maida, A.; Bayoumi, M.A. Gated Recurrent Neural Networks Empirical Utilization for Time Series Classification. In Proceedings of the 2019 International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Atlanta, GA, USA, 14–17 July 2019; pp. 1207–1210. [Google Scholar]
- Thomsen, J.; Sletfjerding, M.B.; Stella, S.; Paul, B.; Jensen, S.B.; Malle, M.G.; Montoya, G.; Petersen, T.C.; Hatzakis, N.S. DeepFRET: Rapid and automated single molecule FRET data classification using deep learning. bioRxiv 2020. [Google Scholar] [CrossRef] [PubMed]
- Shih, S.Y.; Sun, F.K.; Lee, H.y. Temporal pattern attention for multivariate time series forecasting. Mach. Learn. 2019, 108, 1421–1441. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence, Virtual Conference, 2–9 February 2021. [Google Scholar]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural Ordinary Differential Equations. Adv. Neural Inf. Process. Syst. 2018, 31, 6571–6583. [Google Scholar]
- Chen, R.T.Q.; Amos, B.; Nickel, M. Learning Neural Event Functions for Ordinary Differential Equations. arXiv 2021, arXiv:2011.03902. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “ Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Chen, C.; Li, O.; Tao, C.; Barnett, A.J.; Su, J.; Rudin, C. This looks like that: Deep learning for interpretable image recognition. arXiv 2018, arXiv:1806.10574. [Google Scholar]
- Sun, X.; Yang, D.; Li, X.; Zhang, T.; Meng, Y.; Han, Q.; Wang, G.; Hovy, E.; Li, J. Interpreting Deep Learning Models in Natural Language Processing: A Review. arXiv 2021, arXiv:2110.10470. [Google Scholar]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Zhong, B.; da Silva, R.L.; Tran, M.; Huang, H.; Lobaton, E. Efficient Environmental Context Prediction for Lower Limb Prostheses. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3980–3994. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as points. arXiv 2019, arXiv:1904.07850. [Google Scholar]
- Cramér, H.; Wold, H. Some theorems on distribution functions. J. Lond. Math. Soc. 1936, 1, 290–294. [Google Scholar] [CrossRef]
- Moody, G.B. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://tsaug.readthedocs.io/en/stable/quickstart.html (accessed on 22 June 2022).
- Available online: https://github.com/ARoS-NCSU/PhysSignals-InterpretableInference (accessed on 22 June 2022).
- Loshchilov, I.; Hutter, F. Fixing Weight Decay Regularization in Adam. arXiv 2018, arXiv:1711.05101. Available online: https://openreview.net/forum?id=rk6qdGgCZ (accessed on 22 June 2022).
- Hinton, G. Coursera Neural Networks for Machine Learning Lecture 6. 2018. Available online: http://www.cs.toronto.edu/~hinton/coursera/lecture6/lec6.pdf (accessed on 22 June 2022).


| Model | h | None | One-Hot | Gauss. |
|---|---|---|---|---|
| Forecast 1 s | M1 | 0.7884 | 0.5584 | 0.5241 |
| Forecast 2 s | M1 | 0.8211 | 0.5824 | 0.5464 |
| Forecast 1 s | M2 | 0.6212 | 0.4322 | 0.4147 |
| Forecast 2 s | M2 | 0.6998 | 0.4837 | 0.4616 |
| Type | Fcst. | C1 | C2 | C3 | C4 |
|---|---|---|---|---|---|
| One-hot | 1 s | 0.434 | 0.539 | 0.427 | 0.411 |
| 2 s | 0.482 | 0.589 | 0.468 | 0.467 | |
| Gaussian | 1 s | 0.413 | 0.520 | 0.412 | 0.402 |
| 2 s | 0.458 | 0.571 | 0.443 | 0.453 |
| f1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| √ | × | √ | × | × | 0.4843 | 0.3671 | 0.5782 | 1.4954 | 0.3166 | - |
| √ | √ | × | √ | × | - | 0.2611 | - | - | - | 0.58 |
| √ | √ | × | × | √ | - | 0.2712 | - | - | - | 0.48 |
| √ | √ | × | √ | √ | - | 0.2765 | - | - | - | 0.68 |
| √ | √ | √ | × | × | 0.4850 | 0.3730 | 0.5757 | 1.4973 | 0.3177 | - |
| √ | √ | √ | × | √ | 0.4817 | 0.3699 | 0.5720 | 1.4943 | 0.3142 | 0.48 |
| √ | √ | √ | √ | × | 0.4846 | 0.3738 | 0.5744 | 1.4954 | 0.3162 | 0.54 |
| √ | √ | √ | √ | √ | 0.4814 | 0.3648 | 0.5748 | 1.4917 | 0.3159 | 0.76 |
| f1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| √ | × | √ | × | × | 0.2023 | 0.1943 | 0.2099 | 1.6703 | 0.1033 | - |
| √ | √ | × | √ | × | - | 0.1440 | - | - | - | 0.33 |
| √ | √ | × | × | √ | - | 0.1528 | - | - | - | 0.28 |
| √ | √ | × | √ | √ | - | 0.1559 | - | - | - | 0.45 |
| √ | √ | √ | × | × | 0.1911 | 0.1821 | 0.1997 | 1.6643 | 0.0941 | - |
| √ | √ | √ | × | √ | 0.1855 | 0.1721 | 0.1981 | 1.6594 | 0.0927 | 0.27 |
| √ | √ | √ | √ | × | 0.1972 | 0.1898 | 0.2044 | 1.6664 | 0.1040 | 0.37 |
| √ | √ | √ | √ | √ | 0.1932 | 0.1860 | 0.2002 | 1.6640 | 0.0977 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soleimani, R.; Lobaton, E. Enhancing Inference on Physiological and Kinematic Periodic Signals via Phase-Based Interpretability and Multi-Task Learning. Information 2022, 13, 326. https://doi.org/10.3390/info13070326
Soleimani R, Lobaton E. Enhancing Inference on Physiological and Kinematic Periodic Signals via Phase-Based Interpretability and Multi-Task Learning. Information. 2022; 13(7):326. https://doi.org/10.3390/info13070326
Chicago/Turabian StyleSoleimani, Reza, and Edgar Lobaton. 2022. "Enhancing Inference on Physiological and Kinematic Periodic Signals via Phase-Based Interpretability and Multi-Task Learning" Information 13, no. 7: 326. https://doi.org/10.3390/info13070326
APA StyleSoleimani, R., & Lobaton, E. (2022). Enhancing Inference on Physiological and Kinematic Periodic Signals via Phase-Based Interpretability and Multi-Task Learning. Information, 13(7), 326. https://doi.org/10.3390/info13070326







