Design of a Fuzzy Logic Controller for the Double Pendulum Inverted on a Cart
Abstract
:1. Introduction
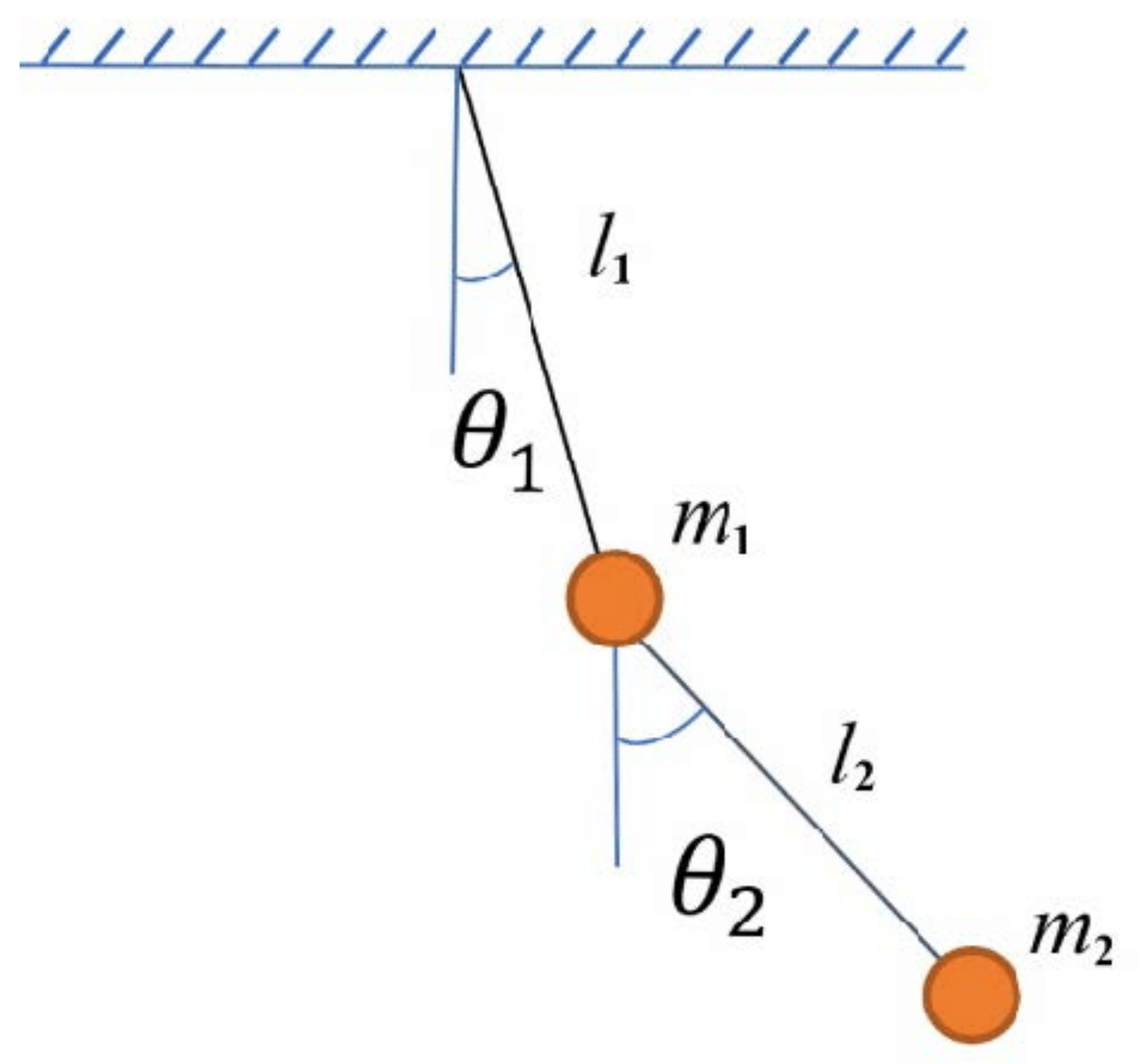
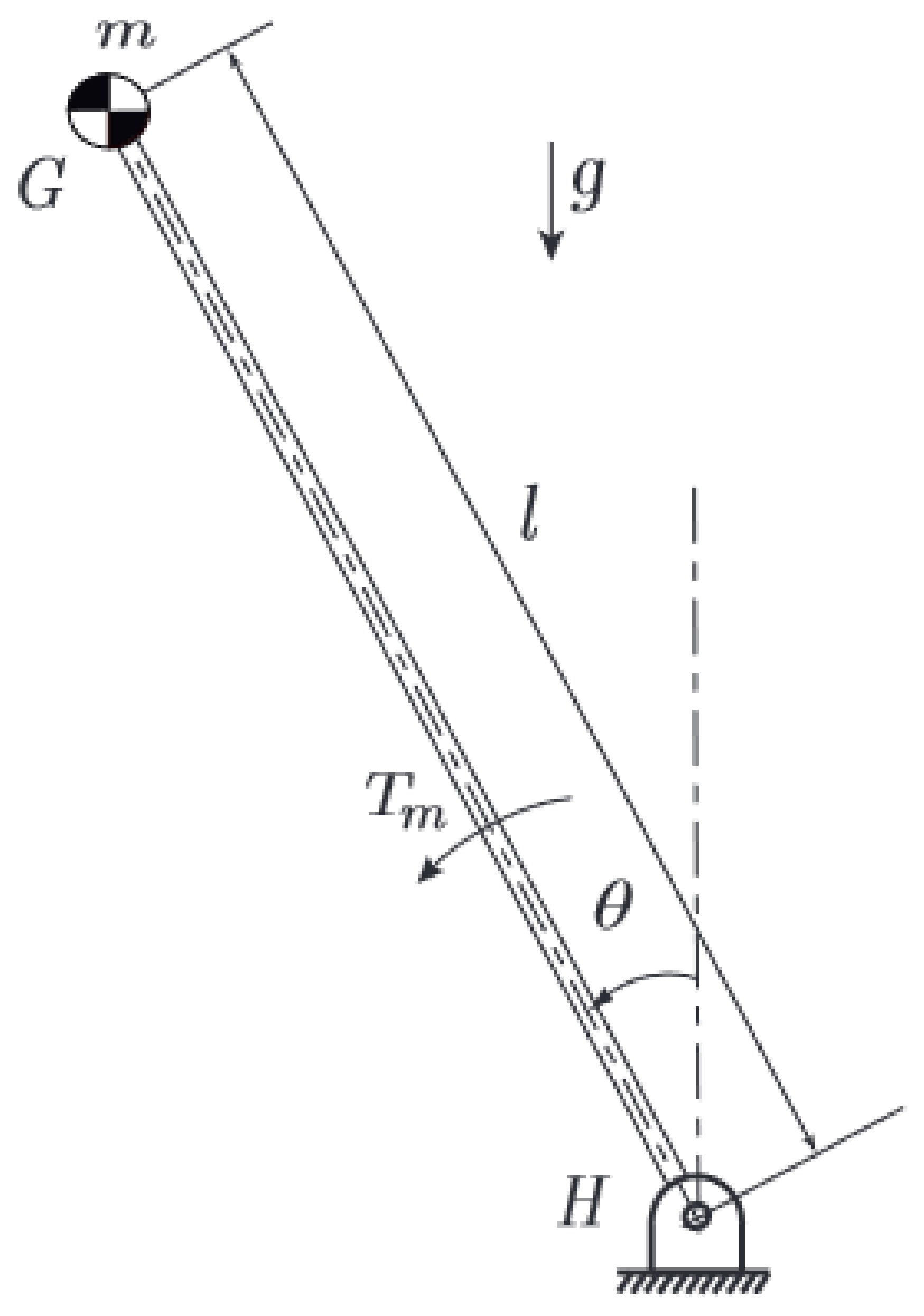
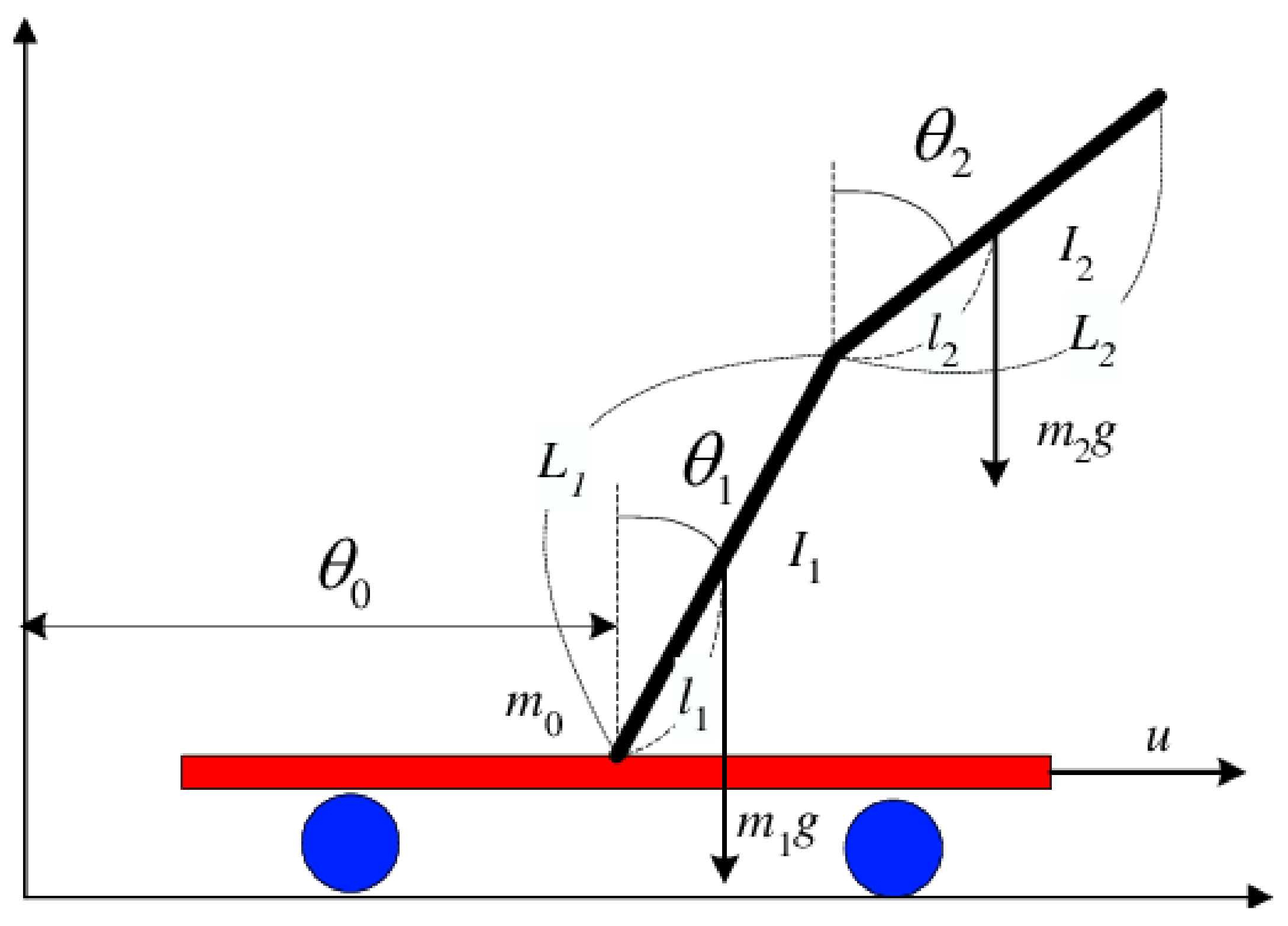
2. Double-Inverted Pendulum
2.1. Dip Elements
2.2. Double-Inverted Pendulum Dynamics
2.3. The Lagrange Method
2.4. Euler–Lagrange Equations
2.5. State Space Equations of the Double-Inverted Pendulum
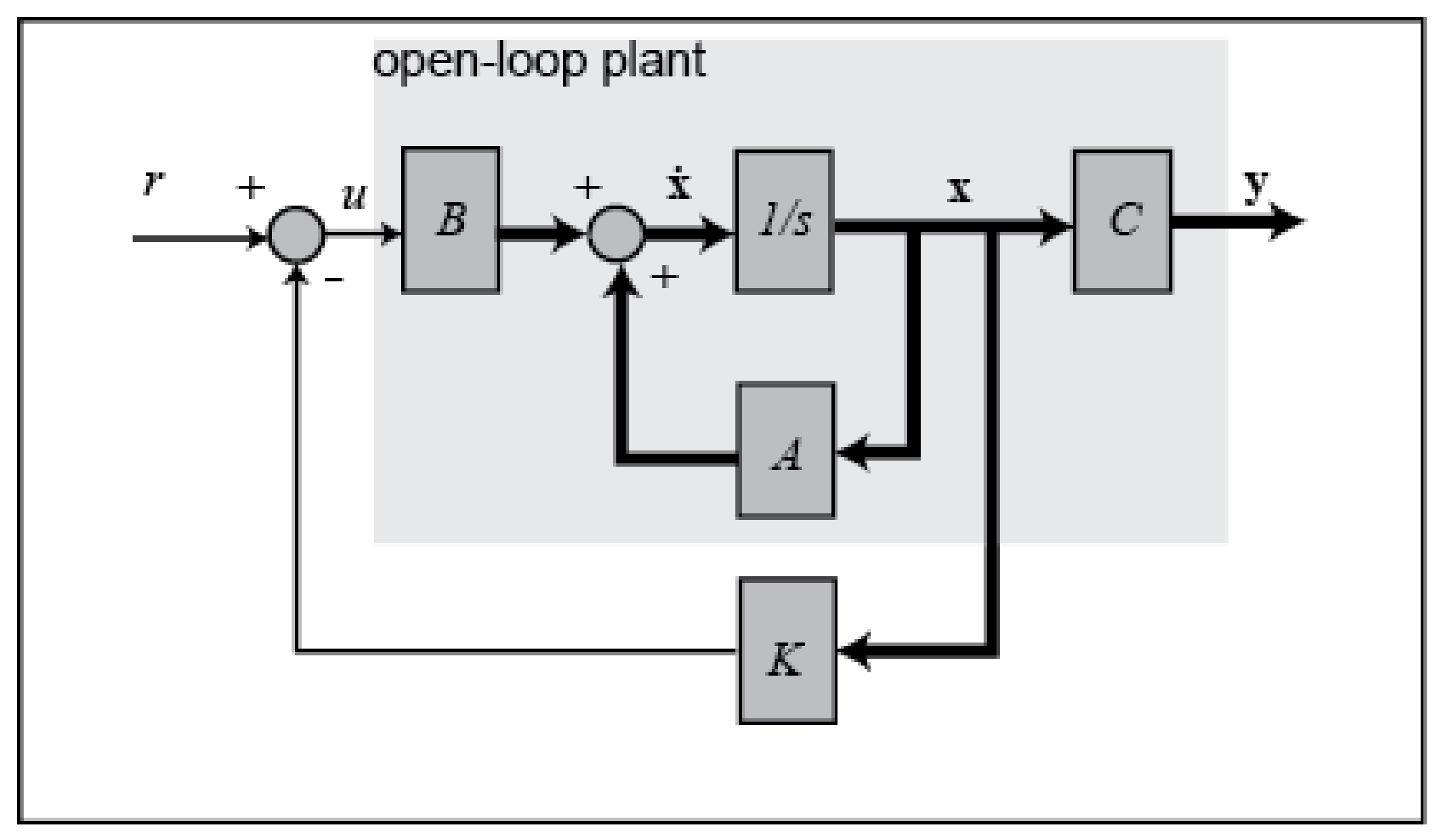
3. Linear Quadratic Regulation Control
- —Movement of the cart along the x axis
- —Angle of the first pendulum
- —Angle of the second pendulum
- —Velocity of the cart
- —Angular velocity of the first pendulum
- —Angular velocity of the second pendulum
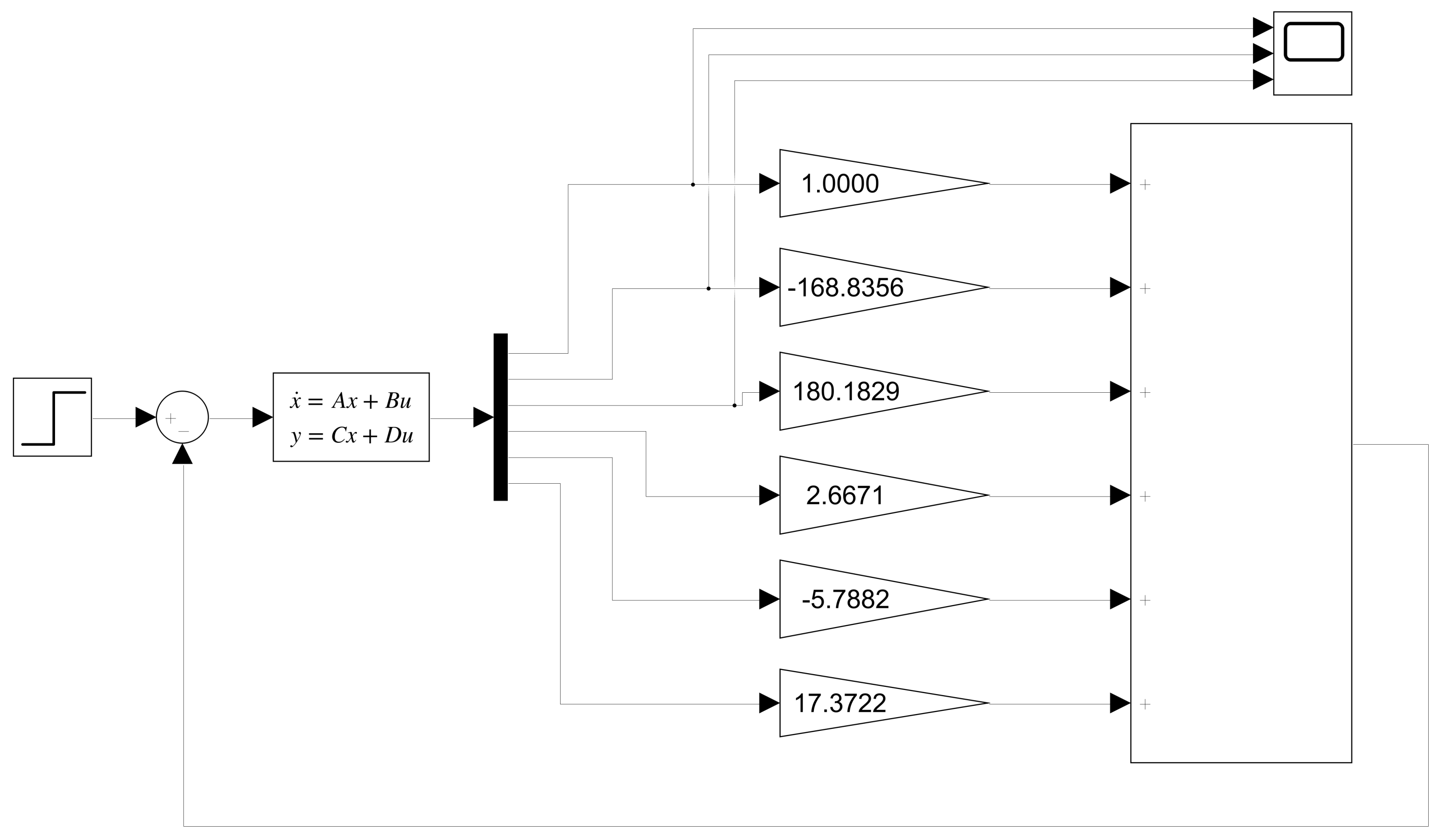
3.1. LQR Customization
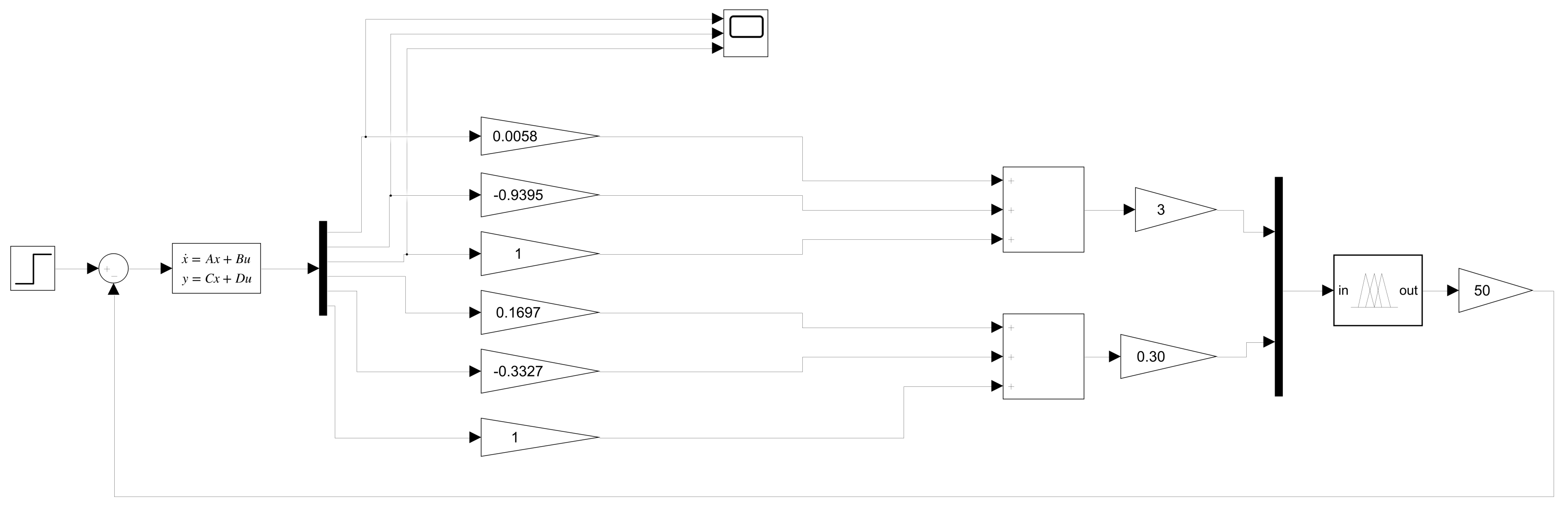
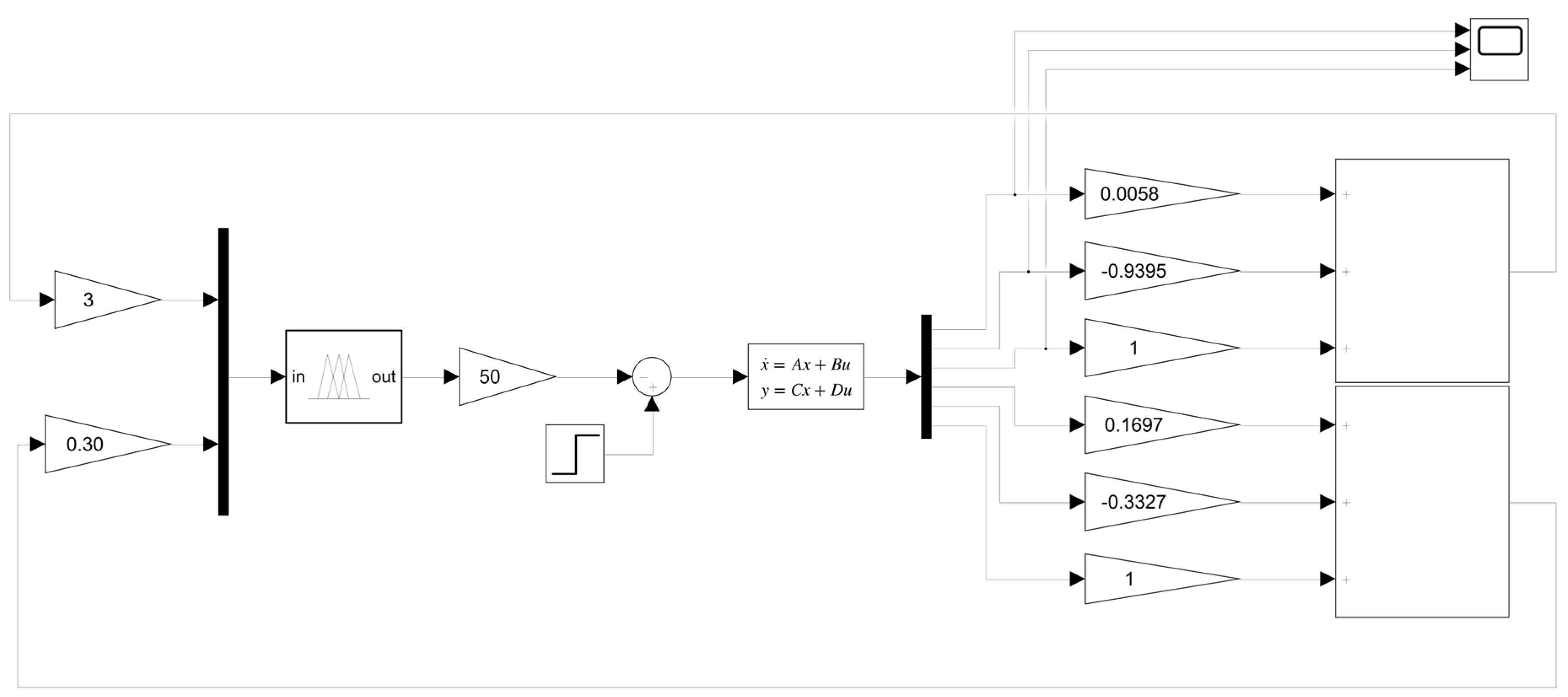
3.2. Simulink Model for LQR
4. Fuzzy Control
4.1. Fuzzy Logic Controllers
- IF input is A THEN output is B
- IF input1 is A AND input2 is B THEN output is C
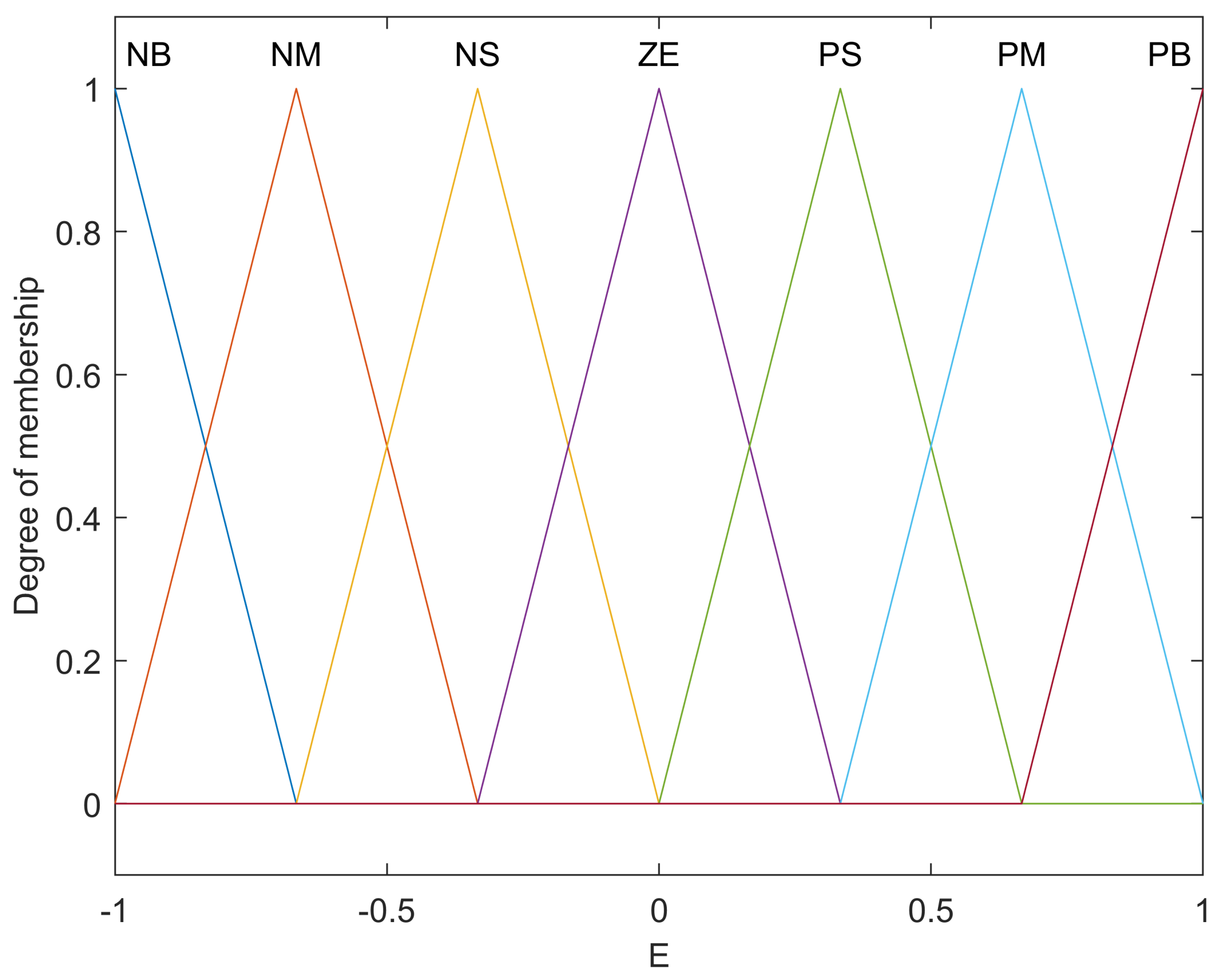
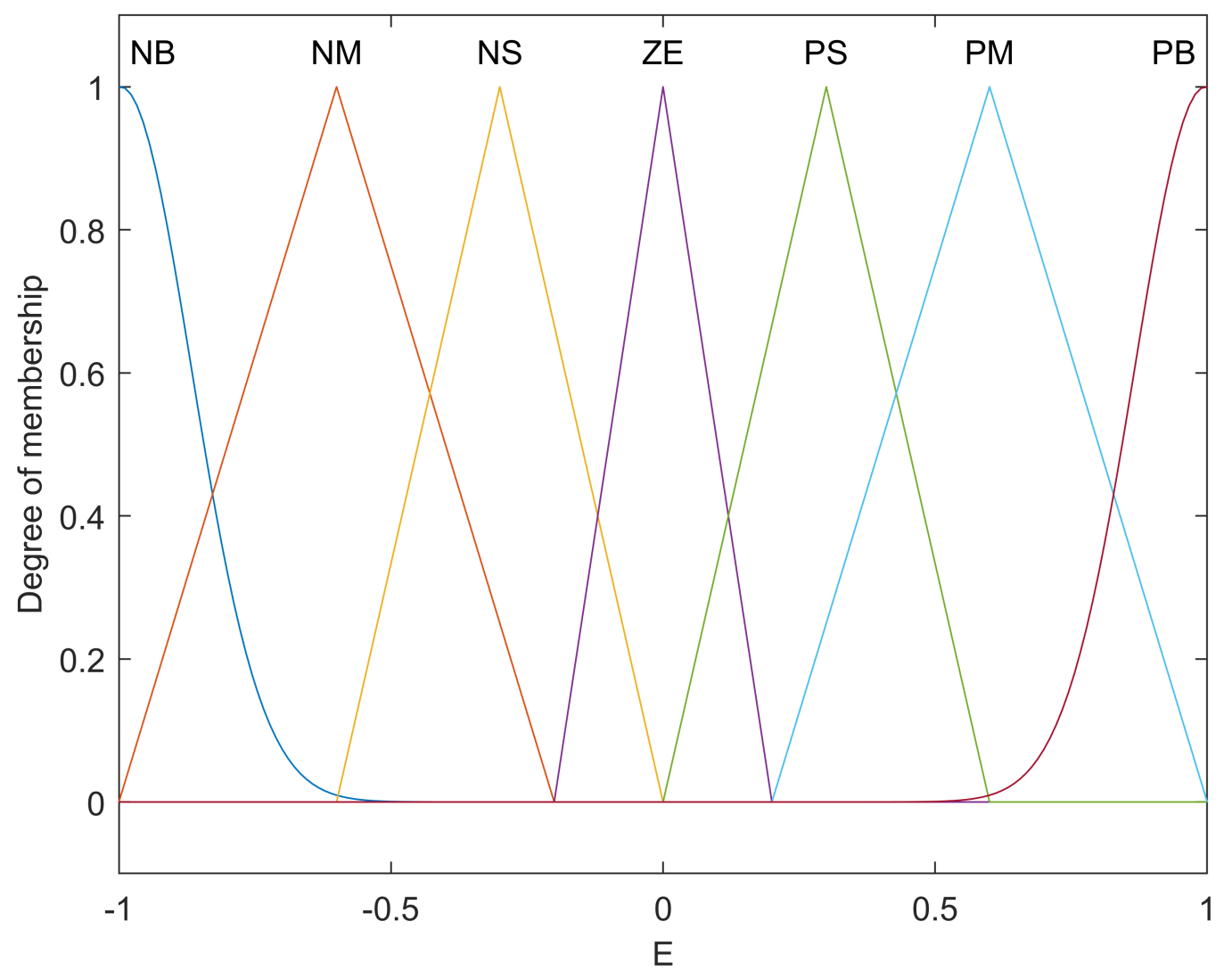
4.2. Fuzzy Logic Controller for the DIP
- the error e
- the derivative of the error ec
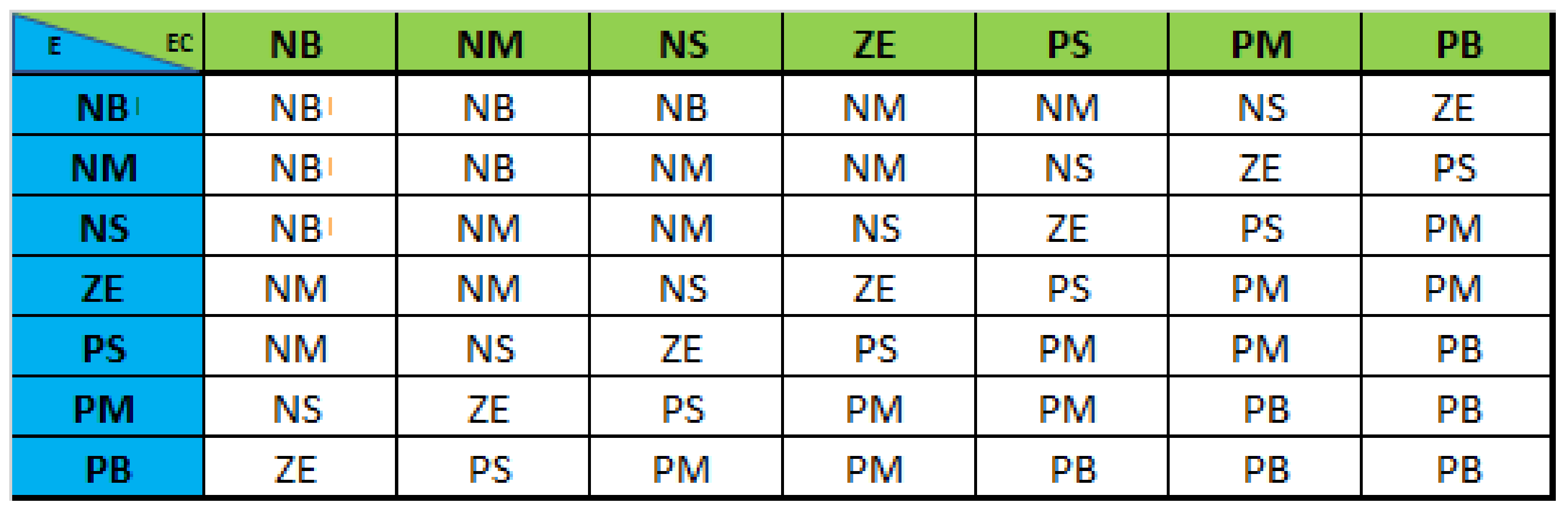
- IF E is NB AND EC is NB THEN U is NB
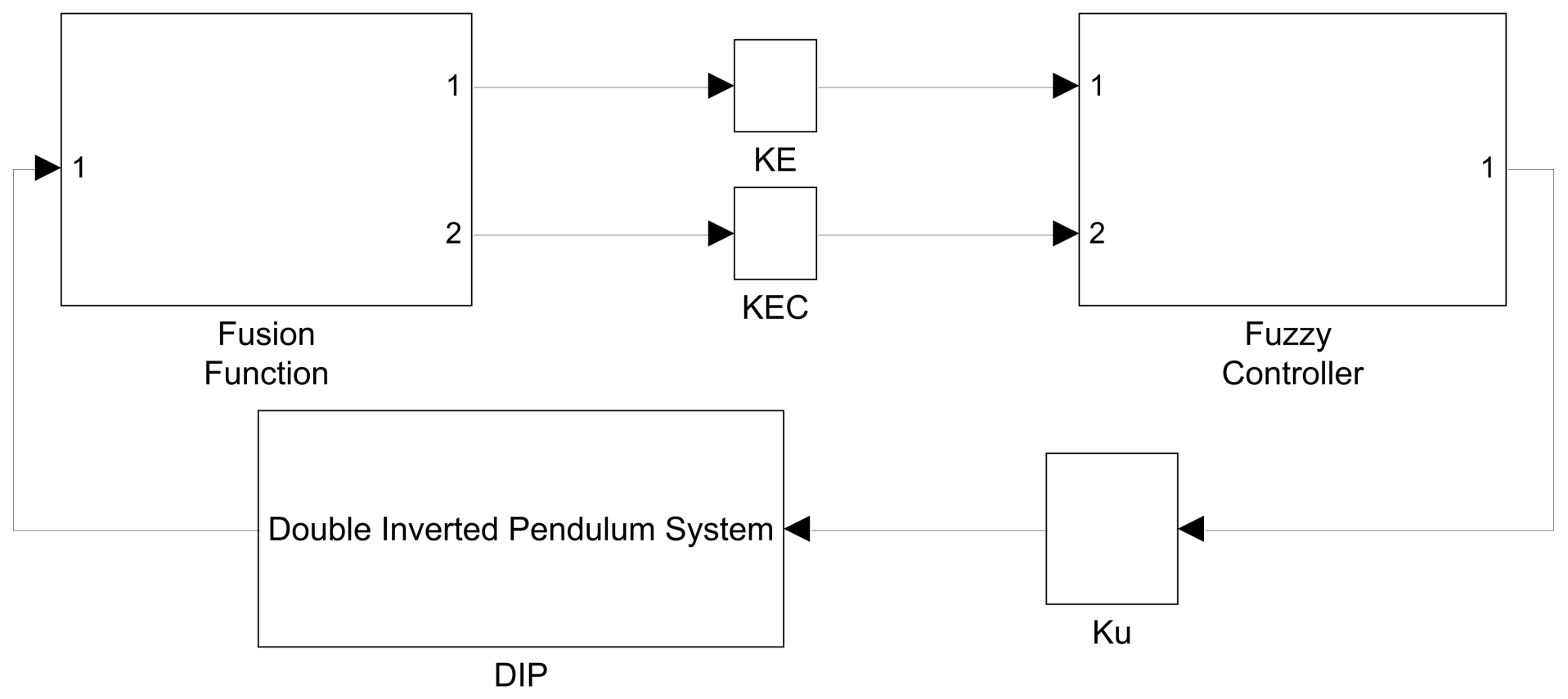
4.3. Creating the Fusion Function
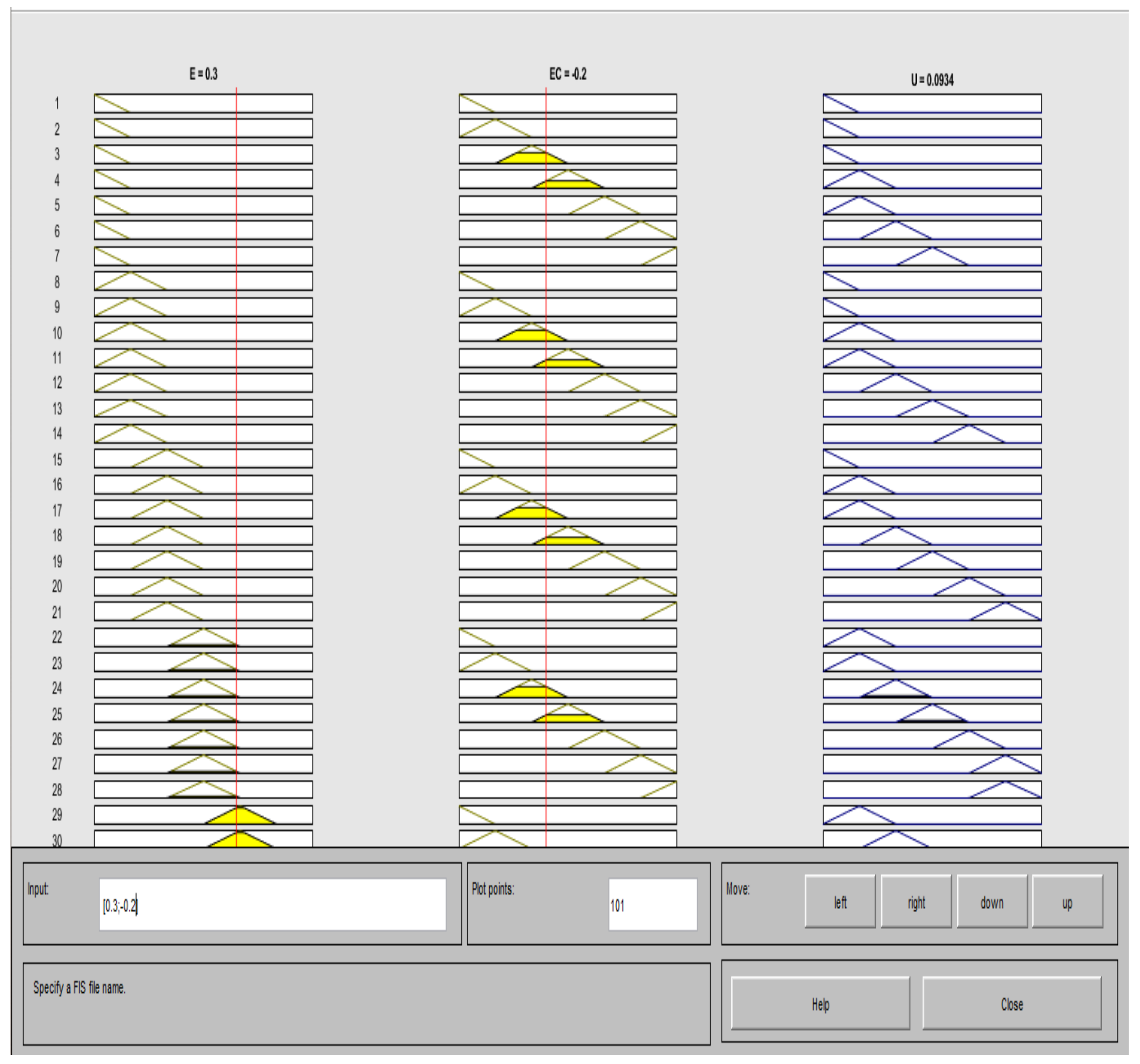
4.4. Design of the FLC in Simulink
4.5. Adjusting the FLC
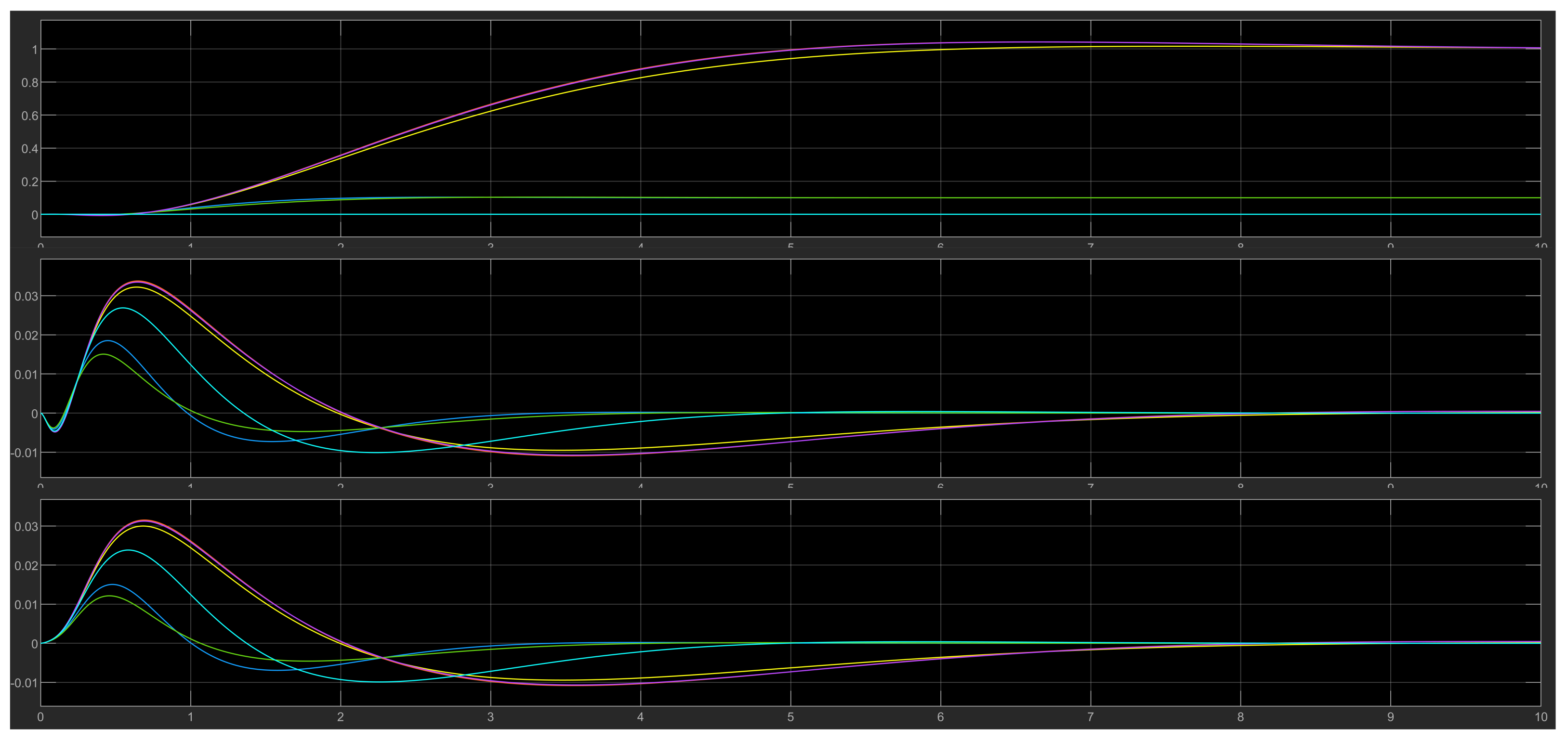
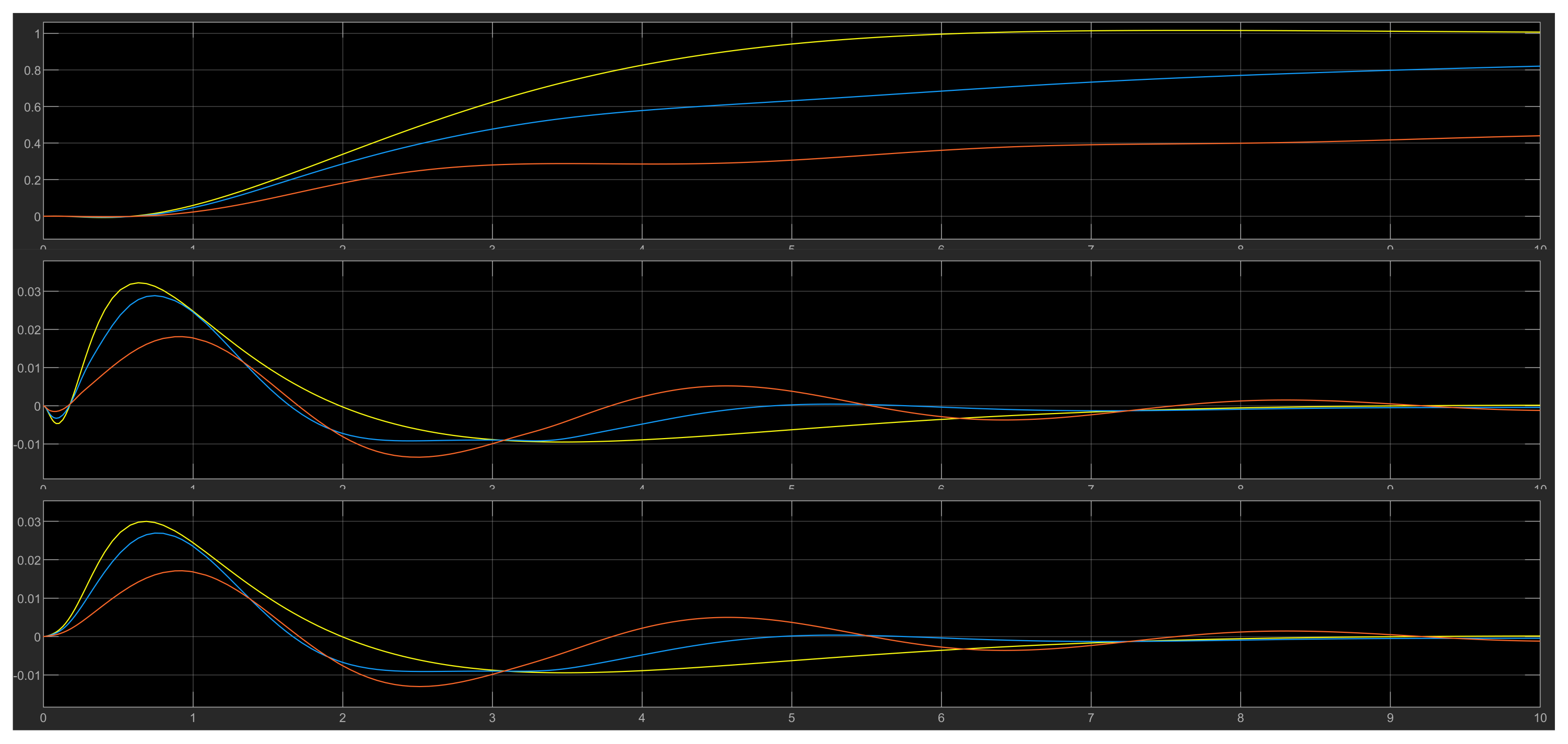
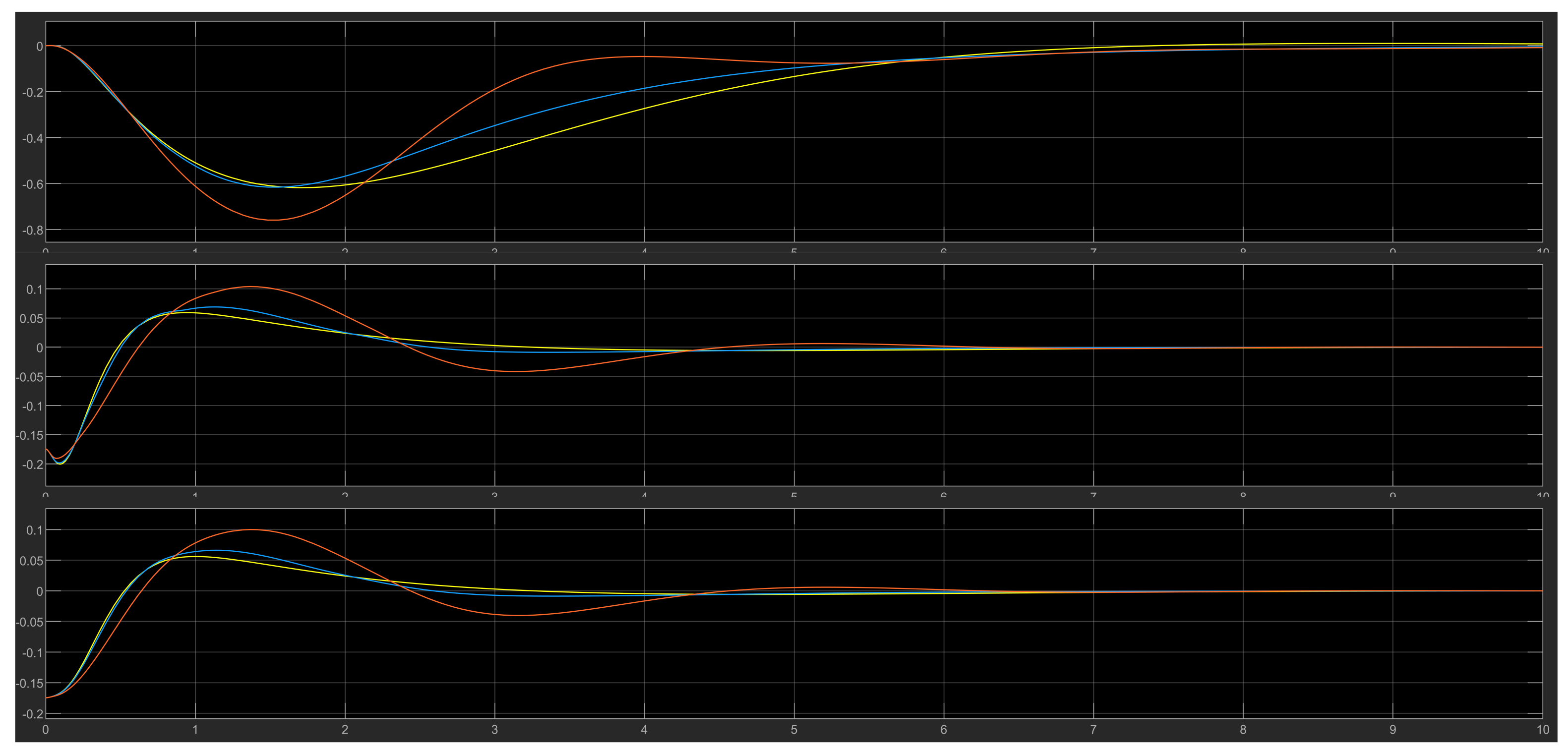
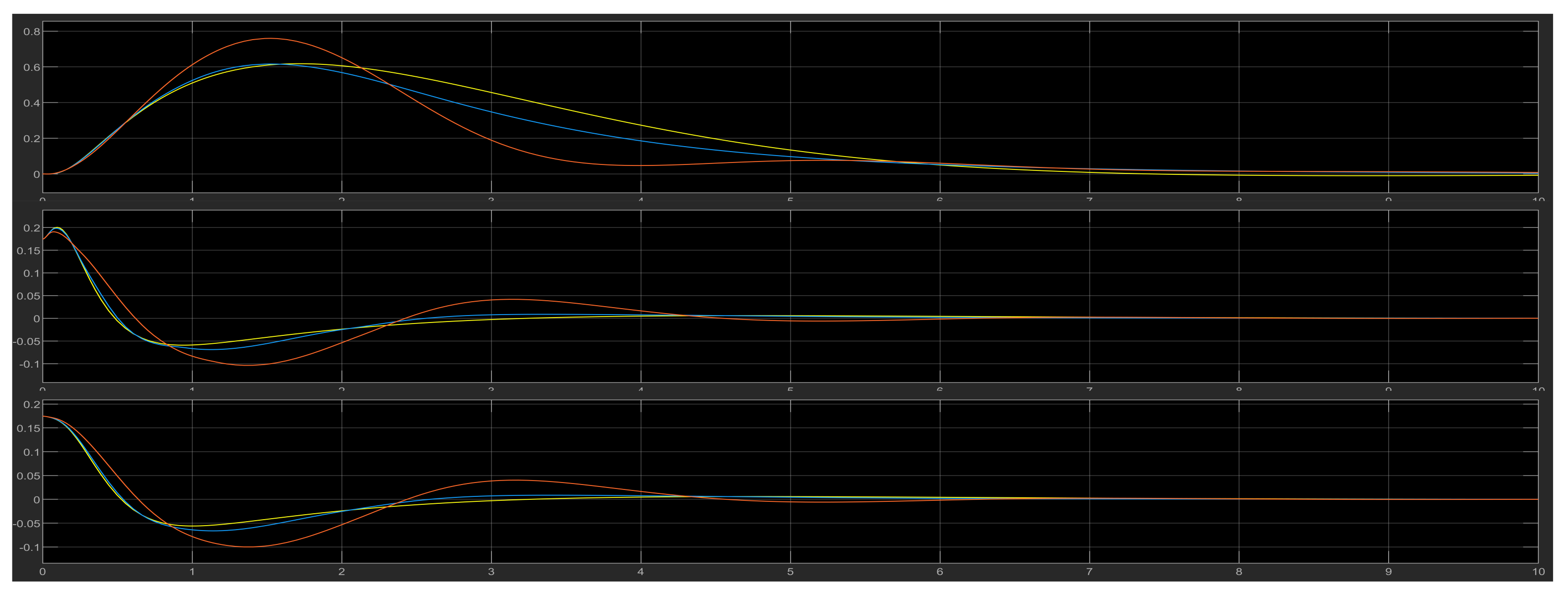
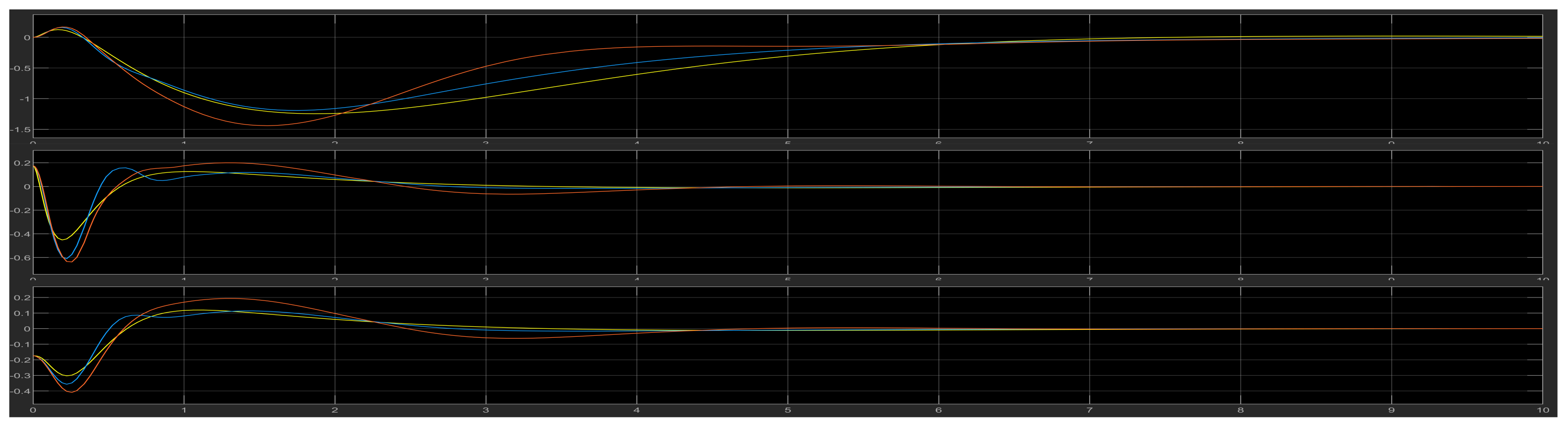
4.6. Test Results for Various Initial Values of the DIP
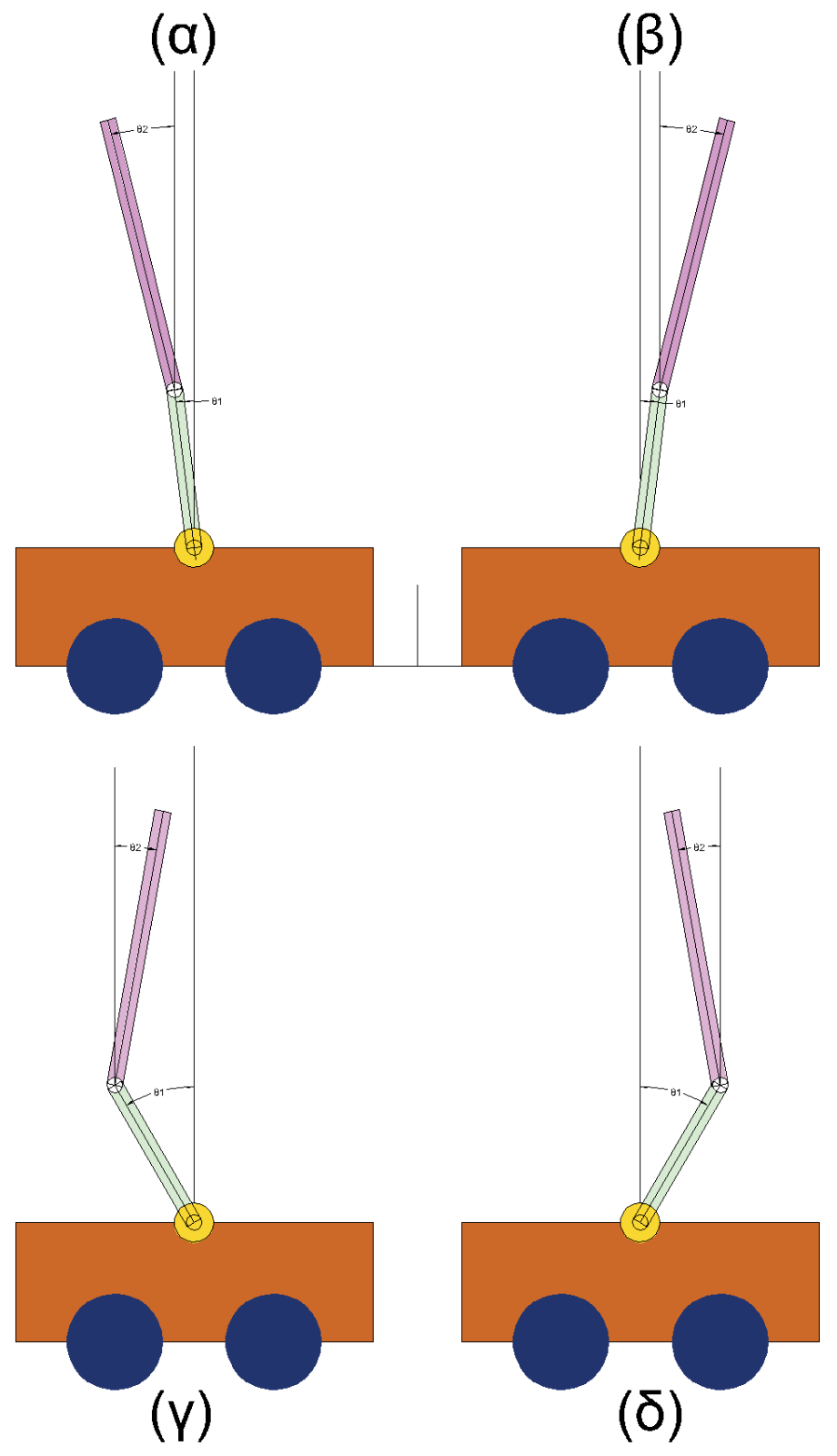
- Both pendulums start at a negative angle, Figure 21 ()
- Both pendulums start at a positive angle, Figure 21 ()
- The first pendulum starts at a negative angle and the second pendulum starts at a positive angle, Figure 21 ()
- The first pendulum starts at a positive angle and the second pendulum starts at a negative angle, Figure 21 ()
4.6.1. Case 1
4.6.2. Case 2
4.6.3. Case 3
4.6.4. Case 4
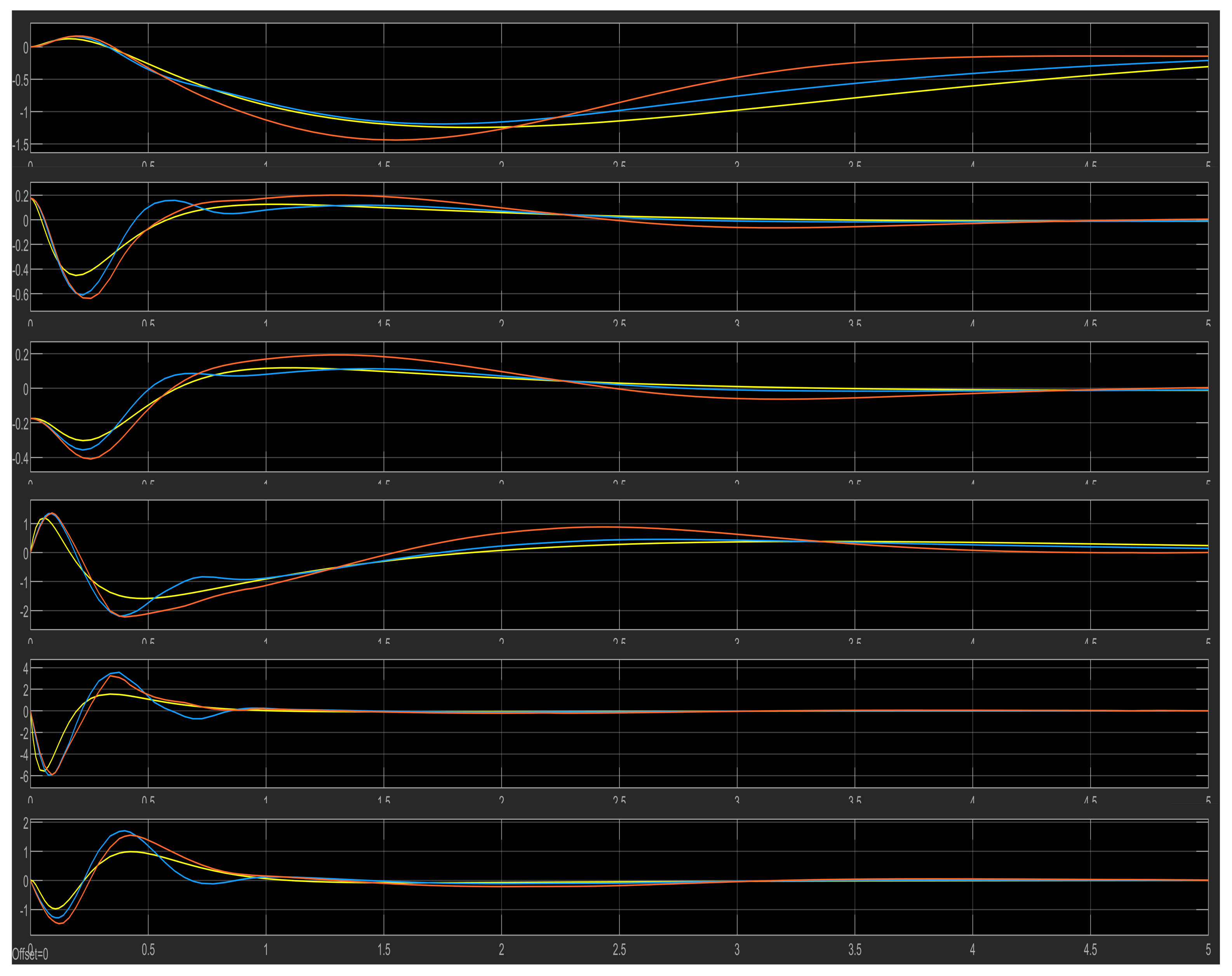
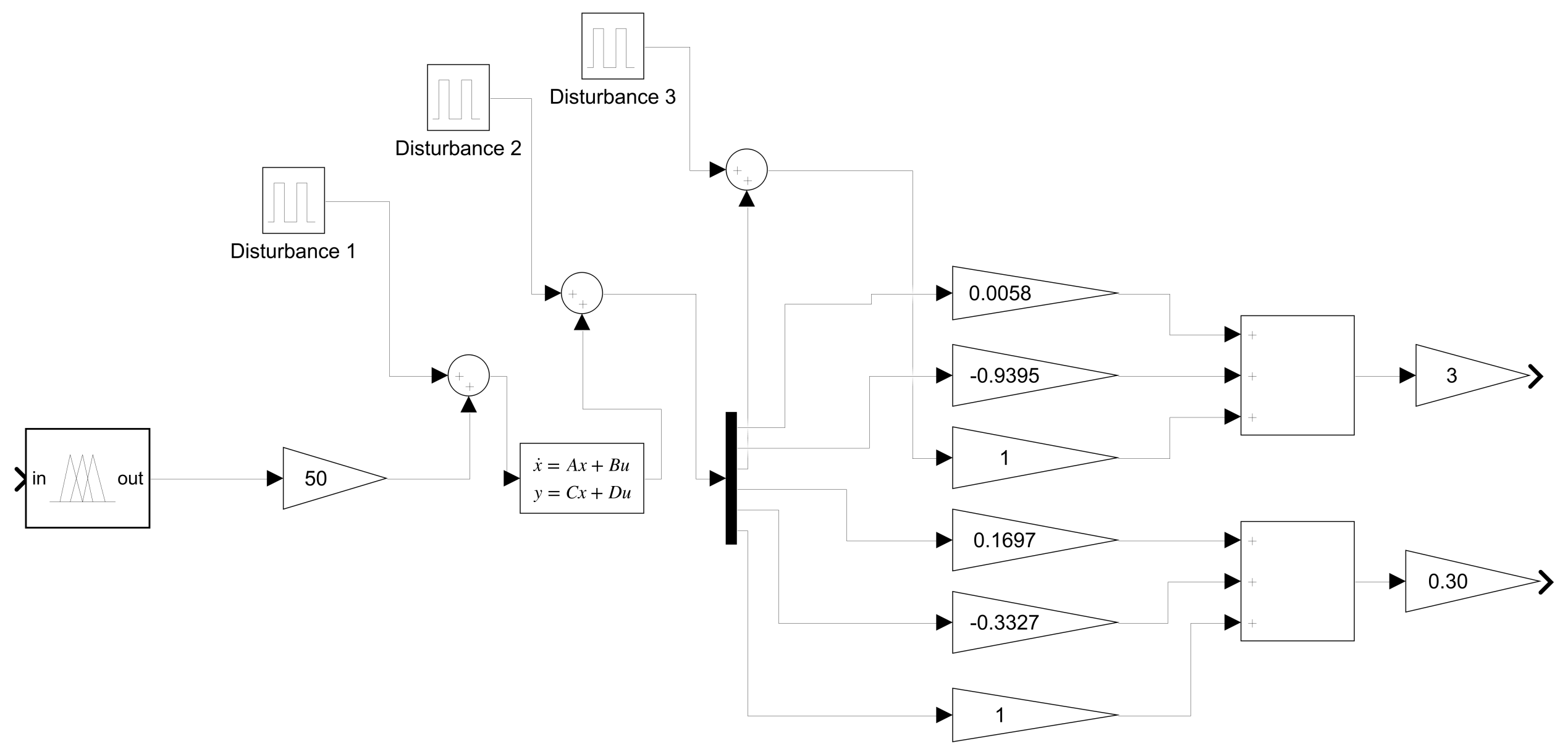
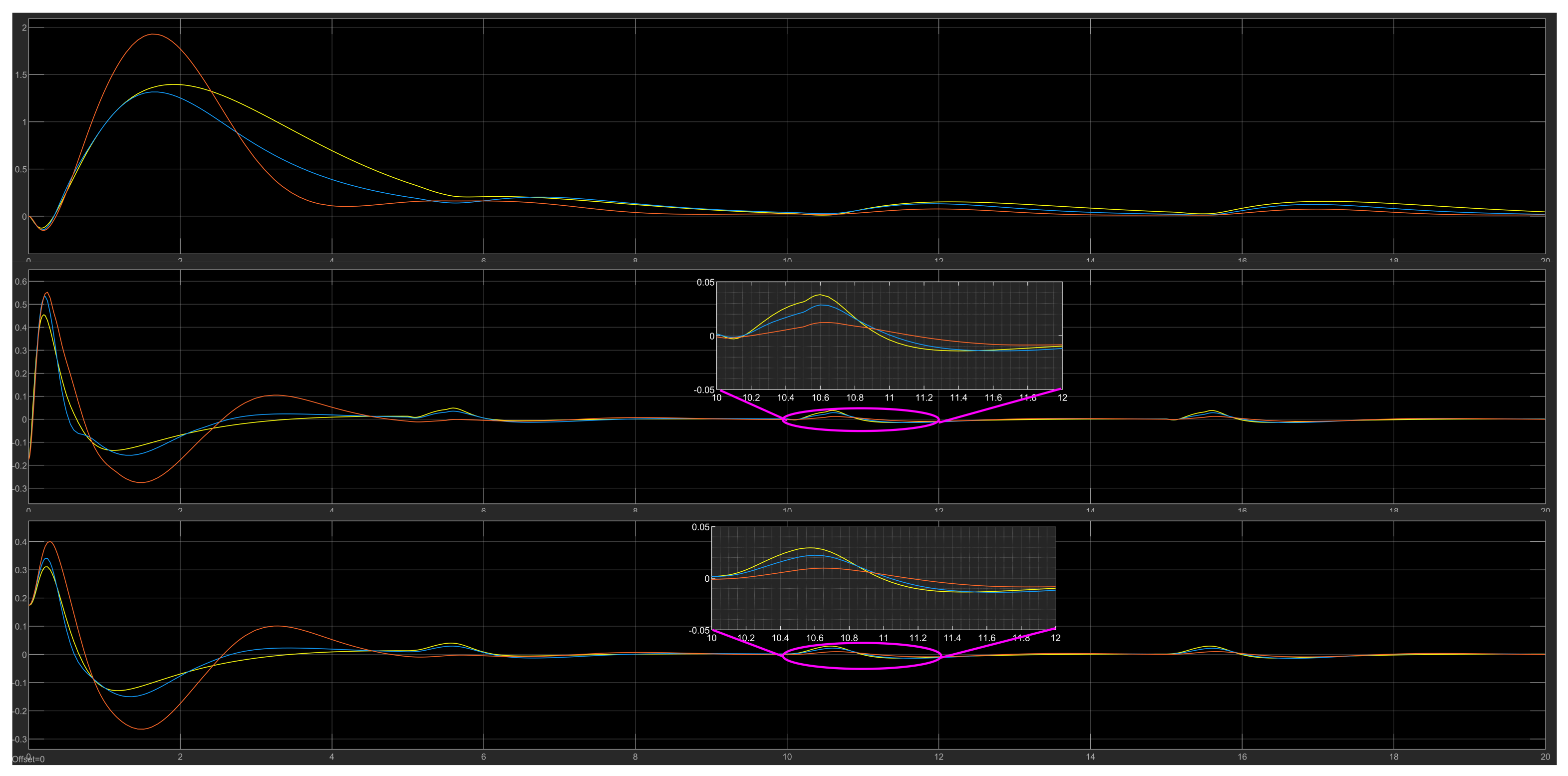
4.7. Disturbance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dorf, R.C.; Bishop, R.H. Modern Control Systems; Pearson: London, UK, 2011. [Google Scholar]
- Craig, J. Introduction to Robotics: Mechanics and Control; Pearson: London, UK, 2018. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 28–44. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy algorithms. Inf. Control 1968, 12, 94–102. [Google Scholar] [CrossRef]
- King, R.E. Computational Intelligence in Control Engineering; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Kosko, B.; Toms, M. Fuzzy Thinking: The New Science of Fuzzy Logic; Hyperion: New York, NY, USA, 1993. [Google Scholar]
- Theodorou, Y. Introduction to Fuzzy Logic (Book in Greek), 1st ed.; Editions TZIOLA: Thessaloniki, Greece, 2010. [Google Scholar]
- Hazem, Z.B.; Fotuhi, M.J.; Bingül, Z. Development of a Fuzzy-LQR and Fuzzy-LQG stability control for a double link rotary inverted pendulum. J. Frankl. Inst. 2020, 357, 10529–10556. [Google Scholar] [CrossRef]
- Hazem, Z.B.; Fotuhi, M.J.; Bingül, Z. A study of anti-swing fuzzy LQR control of a double serial link rotary pendulum. IETE J. Res. 2021, 1–12. [Google Scholar] [CrossRef]
- Fotuhi, M.J.; Hazem, Z.B.; Bingül, Z. Modelling and torque control of an non-linear friction inverted pendulum driven with a rotary series elastic actuator. In Proceedings of the 2019 3rd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 11–13 October 2019; pp. 1–6. [Google Scholar]
- Luhao, W.; Zhanshi, S. LQR-Fuzzy control for double-inverted pendulum. In Proceedings of the 2010 International Conference on Digital Manufacturing & Automation, Changcha, China, 18–20 December 2010; Volume 1, pp. 900–903. [Google Scholar]
- Kudinov, Y.; Pashchenko, F.; Kelina, A.; Vasutin, D.; Duvanov, E.; Pashchenko, A. Analysis of Control System Models with Conventional LQR and Fuzzy LQR Controller. Procedia Comput. Sci. 2019, 150, 737–742. [Google Scholar] [CrossRef]
- Hazem, Z.B.; Fotuhi, M.J.; Bingül, Z. Anti-swing radial basis neuro-fuzzy linear quadratic regulator control of double link rotary pendulum. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 531–545. [Google Scholar] [CrossRef]
- The Pendulum. My Attempt at Building a Diverse Company from the Start. Available online: https://medium.com/assist/the-pendulum-my-attempt-at-building-a-diverse-company-from-the-start-bd9e50523a3d (accessed on 1 May 2022).
- Izadgoshasb, I.; Lim, Y.Y.; Tang, L.; Padilla, R.V.; Tang, Z.S.; Sedighi, M. Improving efficiency of piezoelectric based energy harvesting from human motions using double pendulum system. Energy Convers. Manag. 2019, 184, 559–570. [Google Scholar] [CrossRef]
- Bhounsule, P. A Controller Design Framework for Bipedal Robots: Trajectory Optimization and Event-Based Stabilization. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2012. [Google Scholar]
- Bogdanov, A. Optimal Control of a Double-Inverted Pendulum on a Cart; Tech. Rep. CSE-04-006; Oregon Health and Science University, OGI School of Science and Engineering: Beaverton, OR, USA, 2004. [Google Scholar]
- Brull, T. Course: Systems and Control Theory; Lecture Notes: Equations of Motion for an Inverted Double Pendulum on a Cart (in Generalized Coordinates); Institute of Mathematics: Berlin, Germany; Available online: https://www3.math.tu-berlin.de/Vorlesungen/SoSe12/Kontrolltheorie/matlab/inverted_pendulum.pdf (accessed on 2 July 2022).
- Jaiwat, P.; Ohtsuka, T. Real-time swing-up of double-inverted pendulum by nonlinear model predictive control. In Proceedings of the 5th International Symposium on Advanced Control of Industrial Processes, Hiroshima, Japan, 28–30 May 2014; pp. 290–295. [Google Scholar]
- Demirci, M. Design of feedback controllers for linear system with applications to control of a double-inverted pendulum. Int. J. Comput. Cogn. 2004, 2, 65–84. [Google Scholar]
- Morin, D. Introduction to Classical Mechanics: With Problems and Solutions; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Available online: https://gitfront.io/r/marasgeon/d401cb516187aa5b83beaeab04b15d3885621b56/MATLAB-code/tree/SEEDA/ (accessed on 2 July 2022).
- Inverted Pendulum: System Modeling. Available online: https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=ControlStateSpace (accessed on 1 May 2022).
- Van Leekwijck, W.; Kerre, E.E. Defuzzification: Criteria and classification. Fuzzy Sets Syst. 1999, 108, 159–178. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y. Reduced-dimensional fuzzy controller design based on fusion function and application in double-inverted pendulum. In Proceedings of the 2010 The 2nd International Conference on Industrial Mechatronics and Automation, Wuhan, China, 30–31 May 2010; Volume 2, pp. 337–340. [Google Scholar]
- Wang, L.; Zheng, S.; Wang, X.; Fan, L. Fuzzy control of a double-inverted pendulum based on information fusion. In Proceedings of the 2010 International Conference on Intelligent Control and Information Processing, Dalian, China, 13–15 August 2010; pp. 327–331. [Google Scholar]
- Lee, C.C. Fuzzy logic in control systems: Fuzzy logic controller. I. IEEE Trans. Syst. Man Cybern. 1990, 20, 404–418. [Google Scholar] [CrossRef]
- Sugeno, M. An introductory survey of fuzzy control. Inf. Sci. 1985, 36, 59–83. [Google Scholar] [CrossRef]
- Braae, M.; Rutherford, D. Fuzzy relations in a control setting. Kybernetes 1978, 7, 185–188. [Google Scholar] [CrossRef]
- Larkin, L.I. A fuzzy logic controller for aircraft flight control. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984; pp. 894–897. [Google Scholar]
- Li, Q.R.; Tao, W.H.; Sun, N.; Zhang, C.Y.; Yao, L.H. Stabilization control of double-inverted pendulum system. In Proceedings of the 2008 3rd International Conference on Innovative Computing Information and Control, Dalian, China, 18–20 June 2008; p. 417. [Google Scholar]
- Hazem, Z.B.; Fotuhi, M.J.; Bingül, Z. A comparative study of the friction models with adaptive coefficients for a rotary triple inverted pendulum. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 1–6. [Google Scholar]
- Elkinany, B.; Alfidi, M.; Chaibi, R.; Chalh, Z. TS fuzzy system controller for stabilizing the double-inverted pendulum. Adv. Fuzzy Syst. 2020, 2020, 8835511. [Google Scholar]
- Chen, W.; Theodomile, N. Simulation of a triple inverted pendulum based on fuzzy control. World J. Eng. Technol. 2016, 4, 267. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, C.; Ding, Y.; Zhang, Q. LQR optimal control of triple inverted pendulum based on fuzzy quotient space theory. In Proceedings of the 2012 IEEE International Conference on Granular Computing, Hangzhou, China, 11–13 August 2012; pp. 633–638. [Google Scholar]








| Variable | Value |
|---|---|
| 1 Kg | |
| 0.3 Kg | |
| 0.6 Kg | |
| 0.2 m | |
| 0.4 m | |
| g | 9.81 m s |
| Values at time 4.9 s | |||
|---|---|---|---|
| Cart | 1st Pendulum | 2nd Pendulum | |
| LQR | −1.048 | −0.02574 | −0.02547 |
| FLC | −0.620 | −0.02513 | −0.02504 |
| FLC modified | −0.167 | −0.01635 | −0.01716 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maraslidis, G.S.; Kottas, T.L.; Tsipouras, M.G.; Fragulis, G.F. Design of a Fuzzy Logic Controller for the Double Pendulum Inverted on a Cart. Information 2022, 13, 379. https://doi.org/10.3390/info13080379
Maraslidis GS, Kottas TL, Tsipouras MG, Fragulis GF. Design of a Fuzzy Logic Controller for the Double Pendulum Inverted on a Cart. Information. 2022; 13(8):379. https://doi.org/10.3390/info13080379
Chicago/Turabian StyleMaraslidis, George S., Theodore L. Kottas, Markos G. Tsipouras, and George F. Fragulis. 2022. "Design of a Fuzzy Logic Controller for the Double Pendulum Inverted on a Cart" Information 13, no. 8: 379. https://doi.org/10.3390/info13080379
APA StyleMaraslidis, G. S., Kottas, T. L., Tsipouras, M. G., & Fragulis, G. F. (2022). Design of a Fuzzy Logic Controller for the Double Pendulum Inverted on a Cart. Information, 13(8), 379. https://doi.org/10.3390/info13080379









