Pedestrian Detection and Tracking System Based on Deep-SORT, YOLOv5, and New Data Association Metrics
Abstract
:1. Introduction
2. Related Work
2.1. Object Tracking
2.2. Tracking by Detection
2.3. Joint Tracking
2.4. Tracking Applied in Pedestrian Detection Systems
3. Methodology
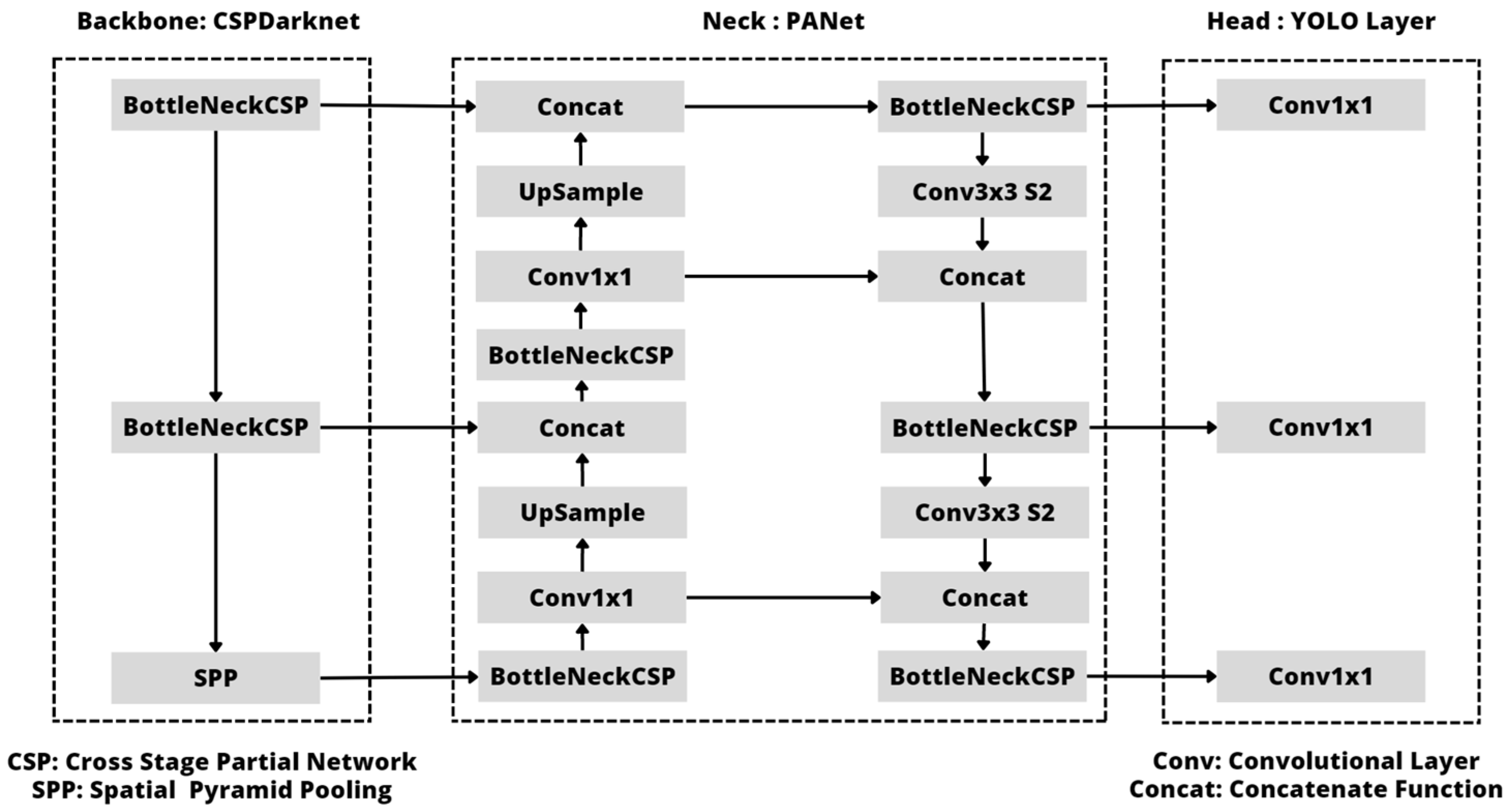
3.1. YOLOv5
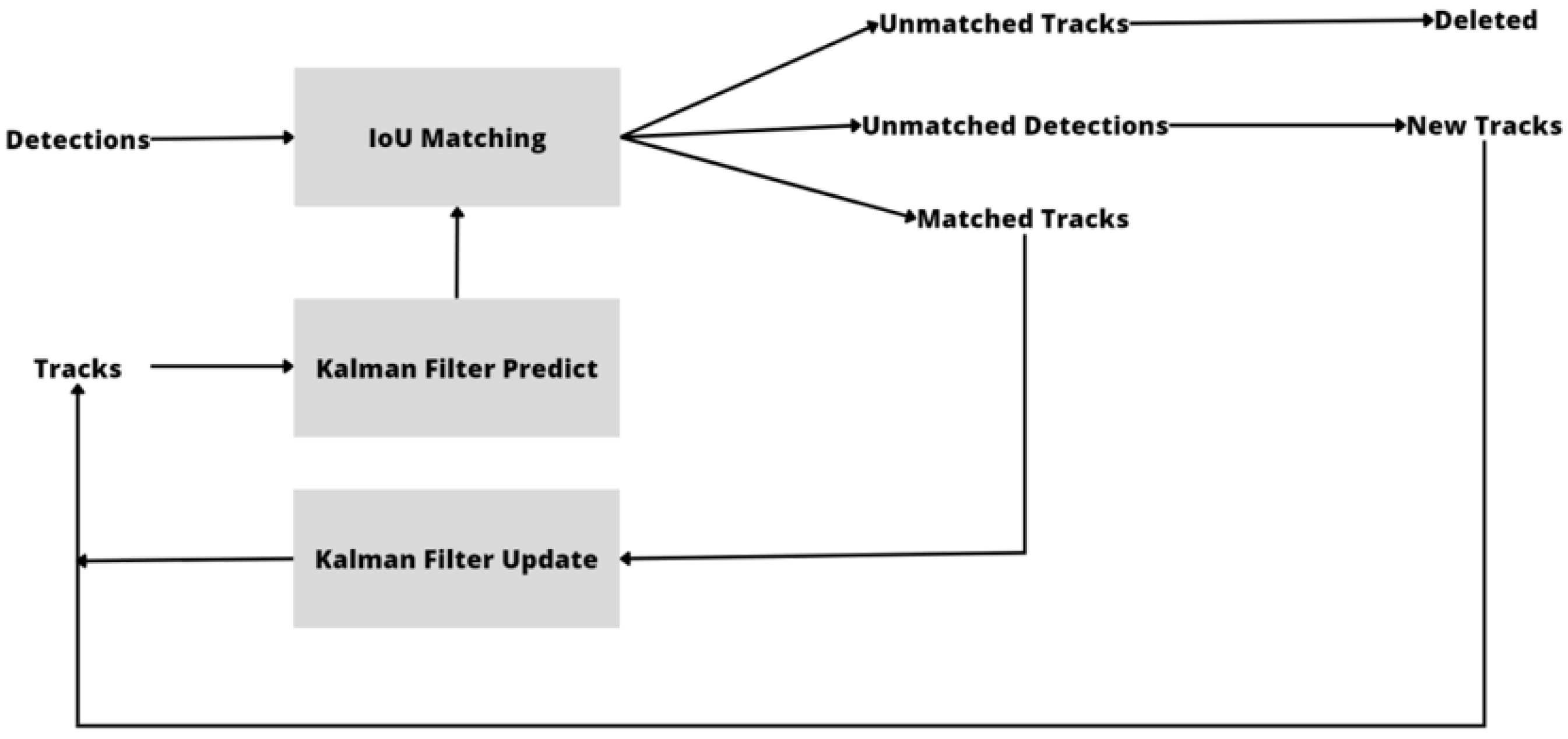
3.2. SORT
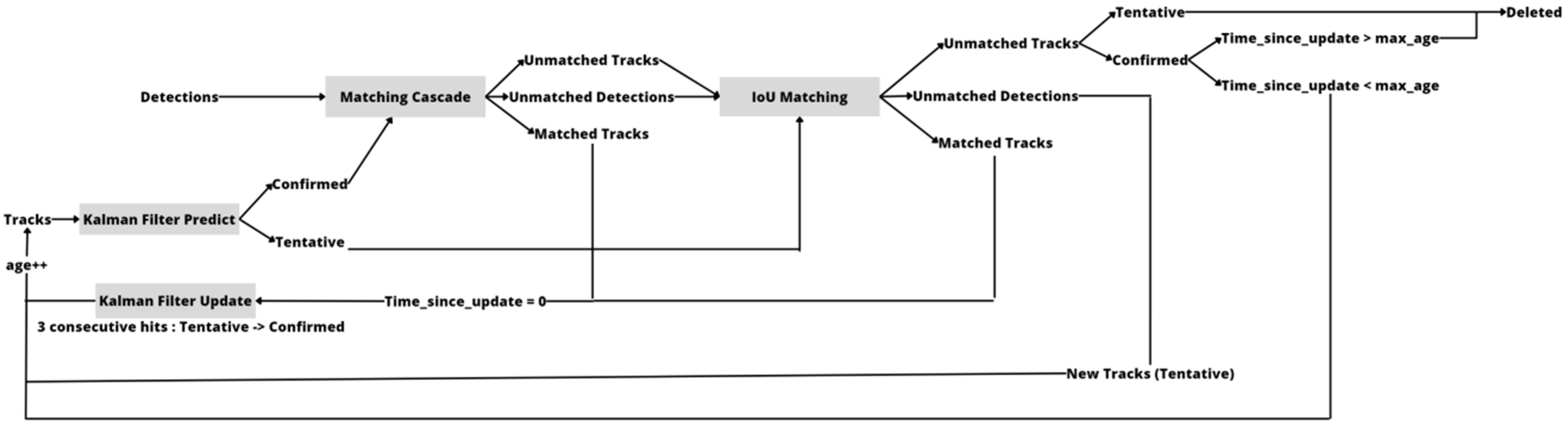
3.3. Deep-SORT
3.4. Data Association
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Razzok, M.; Badri, A.; Ruichek, Y.; Sahel, A. Street crossing pedestrian detection system a comparative study of descriptor and classification methods. In Colloque sur les Objets et systèmes Connectés; Higher School of Technology of Casablanca (ESTC): Casablanca, Morocco; University Institute of Technology of Aix-Marseille: Marseille, France, 2019. [Google Scholar]
- Razzok, M.; Badri, A.; Mourabit, I.E.L.; Ruichek, Y.; Sahel, A. A new pedestrian recognition system based on edge detection and different census transform features under weather conditions. IAES Int. J. Artif. Intell. 2022, 11, 582–592. [Google Scholar] [CrossRef]
- Razzok, M.; Badri, A.; Mourabit, I.E.L.; Ruichek, Y.; Sahel, A. Pedestrian Detection System Based on Deep Learning. IJAAS Int. J. Adv. Appl. Sci. 2022, 11, 194–198. [Google Scholar] [CrossRef]
- Zhou, H.; Wu, T.; Sun, K.; Zhang, C. Towards high accuracy pedestrian detection on edge gpus. Sensors 2022, 22, 5980. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Zhu, C.; Yin, X.-C. Occluded Pedestrian Detection via Distribution-Based Mutual-Supervised Feature Learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10514–10529. [Google Scholar] [CrossRef]
- Devi, S.; Thopalli, K.; Malarvezhi, P.; Thiagarajan, J.J. Improving Single-Stage Object Detectors for Nighttime Pedestrian Detection. Int. J. Pattern Recognit. Artif. Intell. 2022, 36, 2250034. [Google Scholar] [CrossRef]
- Velázquez, J.A.A.; Huertas, M.R.; Eleuterio, R.A.; Gutiérrez, E.E.G.; Del Razo López, F.; Lara, E.R. Pedestrian Localization in a Video Sequence Using Motion Detection and Active Shape Models. Appl. Sci. 2022, 12, 5371. [Google Scholar] [CrossRef]
- Chen, X.; Jia, Y.; Tong, X.; Li, Z. Research on Pedestrian Detection and DeepSort Tracking in Front of Intelligent Vehicle Based on Deep Learning. Sustainability 2022, 14, 9281. [Google Scholar] [CrossRef]
- He, L.; Wu, F.; Du, X.; Zhang, G. Cascade-SORT: A robust fruit counting approach using multiple features cascade matching. Comput. Electron. Agric. 2022, 200, 107223. [Google Scholar] [CrossRef]
- Tsai, C.-Y.; Su, Y.-K. MobileNet-JDE: A lightweight multi-object tracking model for embedded systems. Multimed. Tools Appl. 2022, 81, 9915–9937. [Google Scholar] [CrossRef]
- Sun, Y.; Yan, Y.; Zhao, J.; Cai, C. Research on Vision-based pedestrian detection and tracking algorithm. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 1021–1027. [Google Scholar] [CrossRef]
- Shahbazi, M.; Bayat, M.H.; Tarvirdizadeh, B. A motion model based on recurrent neural networks for visual object tracking. Image Vis. Comput. 2022, 126, 104533. [Google Scholar] [CrossRef]
- Gad, A.; Basmaji, T.; Yaghi, M.; Alheeh, H.; Alkhedher, M.; Ghazal, M. Multiple Object Tracking in Robotic Applications: Trends and Challenges. Appl. Sci. 2022, 12, 9408. [Google Scholar] [CrossRef]
- Brasó, G.; Cetintas, O.; Leal-Taixé, L. Multi-Object Tracking and Segmentation Via Neural Message Passing. Int. J. Comput. Vis. 2022, 130, 3035–3053. [Google Scholar] [CrossRef]
- Chen, J.; Wang, F.; Li, C.; Zhang, Y.; Ai, Y.; Zhang, W. Online Multiple Object Tracking Using a Novel Discriminative Module for Autonomous Driving. Electronics 2021, 10, 2479. [Google Scholar] [CrossRef]
- Xue, Y.; Ju, Z. Multiple pedestrian tracking under first-person perspective using deep neural network and social force optimization. Optik 2021, 240, 166981. [Google Scholar] [CrossRef]
- Li, B.; Fu, C.; Ding, F.; Ye, J.; Lin, F. All-day object tracking for unmanned aerial vehicle. IEEE Trans. Mob. Comput. 2022. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Z.; Wu, J.; Tian, Y.; Tang, H.; Guo, X. Real-Time Vehicle Detection Based on Improved YOLO v5. Sustainability 2022, 14, 12274. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Roy, A.M.; Bose, R.; Bhaduri, J. A fast accurate fine-grain object detection model based on YOLOv4 deep neural network. Neural Comput. Applic. 2022, 34, 3895–3921. [Google Scholar] [CrossRef]
- Roy, A.M.; Bhaduri, J.; Kumar, T.; Raj, K. WilDect-YOLO: An efficient and robust computer vision-based accurate object localization model for automated endangered wildlife detection. Ecol. Inform. 2023, 75, 101919. [Google Scholar] [CrossRef]
- Welch, G.F. Kalman filter. In Computer Vision: A Reference Guide; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–3. [Google Scholar]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple online and realtime tracking. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP 2016), Phoenix, AZ, USA, 25–28 September 2016; pp. 3464–3468. [Google Scholar] [CrossRef] [Green Version]
- Wojke, N.; Bewley, A.; Paulus, D. Simple online and realtime tracking with a deep association metric. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3645–3649. [Google Scholar] [CrossRef] [Green Version]
- Konstantinova, P.; Udvarev, A.; Semerdjiev, T. A Study of a Target Tracking Algorithm Using Global Nearest Neighbor Approach. In Proceedings of the 4th International Conference Conference on Computer Systems and Technologies: E-Learning, Rousse, Bulgaria, 19–20 June 2003; pp. 290–295. [Google Scholar] [CrossRef]
- Kirubarajan, T.; Bar-Shalom, Y. Probabilistic data association techniques for target tracking in clutter. Proc. IEEE 2004, 92, 536–557. [Google Scholar] [CrossRef]
- Gu, S.; Zheng, Y.; Tomasi, C. Efficient Visual Object Tracking with Online Nearest Neighbor Classifier. Comput. Vis. ACCV 2010, 2011, 271–282. [Google Scholar] [CrossRef]
- Jiang, Z.; Huynh, D.Q. Multiple Pedestrian Tracking from Monocular Videos in an Interacting Multiple Model Framework. IEEE Trans. Image Process. 2018, 27, 1361–1375. [Google Scholar] [CrossRef] [PubMed]
- Rezatofighi, S.H.; Milan, A.; Zhang, Z.; Shi, Q.; Dick, A.; Reid, I. Joint Probabilistic Data Association Revisited. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3047–3055. [Google Scholar] [CrossRef]
- Kim, C.; Li, F.; Ciptadi, A.; Rehg, J.M. Multiple Hypothesis Tracking Revisited. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4696–4704. [Google Scholar] [CrossRef]
- Carvalho, G.d.S. Kalman Filter-Based Object Tracking Techniques for Indoor Robotic Applications. Ph.D. Thesis, Universidade de Coimbra, Coimbra, Portugal, 2021. [Google Scholar]
- Milan, A.; Leal-Taixé, L.; Reid, I.; Roth, S.; Schindler, K. MOT16: A benchmark for multi-object tracking. arXiv 2016, arXiv:1603.00831. [Google Scholar] [CrossRef]
- Yadav, S.; Payandeh, S. Understanding Tracking Methodology of Kernelized Correlation Filter. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 1330–1336. [Google Scholar] [CrossRef]
- Ramalakshmi, V.; Alex, M.G. Visual object tracking using discriminative correlation filter. In Proceedings of the 2016 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 21–22 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, S.; Yao, H.; Sun, X.; Lu, X. Sparse coding based visual tracking: Review and experimental comparison. Pattern Recognit. 2013, 46, 1772–1788. [Google Scholar] [CrossRef]
- Koller-Meier, E.B.; Ade, F. Tracking multiple objects using the Condensation algorithm. Robot. Auton. Syst. 2001, 34, 93–105. [Google Scholar] [CrossRef]
- Held, D.; Thrun, S.; Savarese, S. Learning to Track at 100 FPS with Deep Regression Networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 749–765. [Google Scholar] [CrossRef] [Green Version]
- Kocur, V.; Ftacnik, M. Multi-Class Multi-Movement Vehicle Counting Based on CenterTrack. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 19–25 June 2021. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Wang, X.; Zeng, W.; Liu, W. FairMOT: On the Fairness of Detection and Re-identification in Multiple Object Tracking. Int. J. Comput. Vis. 2021, 129, 3069–3087. [Google Scholar] [CrossRef]
- Reid, D. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control. 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Nevatia, R. Global data association for multi-object tracking using network flows. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar] [CrossRef]
- Babenko, B.; Yang, M.-H.; Belongie, S. Visual tracking with online Multiple Instance Learning. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar] [CrossRef]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-Learning-Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1409–1422. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Wang, G.; Chan, K.L.; Wang, L. Tracklet Association with Online Target-Specific Metric Learning. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, H.; Liu, N.; Kim, M.; Zhang, W.; Yang, M.-H. Online Multi-Object Tracking with Dual Matching Attention Networks. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2018; pp. 379–396. [Google Scholar] [CrossRef] [Green Version]
- Gordon, N.J.; Maskell, S.; Kirubarajan, T. Efficient particle filters for joint tracking and classification. In Proceedings of the Signal and Data Processing of Small Targets 2002, Orlando, FL, USA, 7 August 2002. [Google Scholar] [CrossRef]
- Vercauteren, T.; Guo, D.; Wang, X. Joint multiple target tracking and classification in collaborative sensor networks. In Proceedings of the International Symposium on Information Theory, 2004, ISIT, Chicago, IL, USA, 27 June–2 July 2004. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Thangali, A.; Sclaroff, S.; Betke, M. Coupling detection and data association for multiple object tracking. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Kitani, K.; Weng, X. Joint Object Detection and Multi-Object Tracking with Graph Neural Networks. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar] [CrossRef]
- Gavrila, D.M.; Munder, S. Multi-cue Pedestrian Detection and Tracking from a Moving Vehicle. Int. J. Comput. Vis. 2006, 73, 41–59. [Google Scholar] [CrossRef] [Green Version]
- Breitenstein, M.D.; Reichlin, F.; Leibe, B.; Koller-Meier, E.; Van Gool, L. Online Multiperson Tracking-by-Detection from a Single, Uncalibrated Camera. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1820–1833. [Google Scholar] [CrossRef]
- Basso, F.; Munaro, M.; Michieletto, S.; Pagello, E.; Menegatti, E. Fast and Robust Multi-people Tracking from RGB-D Data for a Mobile Robot. Intell. Auton. Syst. 2013, 12, 265–276. [Google Scholar] [CrossRef]
- Thoreau, M.; Kottege, N. Deep Similarity Metric Learning for Real-Time Pedestrian Tracking. arXiv 2018, arXiv:1806.07592. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Gu, C. Online multi-object tracking with pedestrian re-identification and occlusion processing. Vis Comput. 2021, 37, 1089–1099. [Google Scholar] [CrossRef]
- Dutta, J.; Pal, S. A note on Hungarian method for solving assignment problem. J. Inf. Optim. Sci. 2015, 36, 451–459. [Google Scholar] [CrossRef]
- Korepanova, A.A.; Oliseenko, V.D.; Abramov, M.V. Applicability of similarity coefficients in social circle matching. In Proceedings of the 2020 XXIII International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 27–29 May 2020; pp. 41–43. [Google Scholar] [CrossRef]
- Vijaymeena, M.; Kavitha, K. A survey on similarity measures in text mining. Mach. Learn. Appl. Int. J. 2016, 3, 19–28. [Google Scholar] [CrossRef]
- Gragera, A.; Suppakitpaisarn, V. Semimetric Properties of Sørensen-Dice and Tversky Indexes. WALCOM Algorithms Comput. 2016, 9627, 339–350. [Google Scholar] [CrossRef]
- Pereira, R.; Carvalho, G.; Garrote, L.; Nunes, U.J. Sort and Deep-SORT Based Multi-Object Tracking for Mobile Robotics: Evaluation with New Data Association Metrics. Appl. Sci. 2022, 12, 1319. [Google Scholar] [CrossRef]
- Ristani, E.; Solera, F.; Zou, R.; Cucchiara, R.; Tomasi, C. Performance measures and a data set for multi-target, multi-camera tracking. Eur. Conf. Comput. Vis. 2016, 9914, 17–35. [Google Scholar] [CrossRef] [Green Version]
- Bernardin, K.; Stiefelhagen, R. Evaluating multiple object tracking performance: The clear mot metrics. EURASIP J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef] [Green Version]
| Cost Matrix | Evaluation Metrics | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IDF1↑ | IDP↑ | IDR↑ | Rcll↑ | Prcn↑ | FAR↓ | GT | MT↑ | PT | ML↓ | FP↓ | FN↓ | IDs↓ | FM↓ | MOTA↑ | MOTP↑ | MOTAL↑ | |
| IOU | 43.675 | 69.827 | 31.775 | 39.162 | 86.060 | 2.174 | 202 | 27 | 79 | 96 | 5010 | 48,048 | 247 | 730 | 32.506 | 79.756 | 32.815 |
| Sorensen | 43.727 | 69.877 | 31.819 | 39.172 | 86.025 | 2.181 | 202 | 27 | 81 | 94 | 5026 | 48,040 | 243 | 726 | 32.501 | 79.726 | 32.805 |
| Cosinei | 43.702 | 69.837 | 31.802 | 39.163 | 86.003 | 2.185 | 202 | 27 | 81 | 94 | 5034 | 48,047 | 242 | 721 | 32.483 | 79.728 | 32.786 |
| Overlap | 43.429 | 69.381 | 31.607 | 39.152 | 85.944 | 2.195 | 202 | 27 | 81 | 94 | 5057 | 48,056 | 250 | 724 | 32.432 | 79.738 | 32.746 |
| Overlapr | 43.659 | 69.793 | 31.765 | 39.168 | 86.059 | 2.175 | 202 | 27 | 80 | 95 | 5011 | 48,043 | 246 | 731 | 32.512 | 79.739 | 32.820 |
| Euclidean | 41.732 | 66.779 | 30.349 | 38.690 | 85.131 | 2.316 | 202 | 27 | 82 | 93 | 5337 | 48,421 | 368 | 762 | 31.466 | 79.849 | 31.929 |
| Manhattan | 42.038 | 67.254 | 30.575 | 38.668 | 85.057 | 2.329 | 202 | 27 | 81 | 94 | 5365 | 48,438 | 359 | 753 | 31.421 | 79.840 | 31.872 |
| Chebyshev | 42.429 | 67.754 | 30.885 | 38.815 | 85.150 | 2.320 | 202 | 27 | 82 | 93 | 5346 | 48,322 | 343 | 750 | 31.612 | 79.824 | 32.043 |
| Cosine | 40.278 | 64.542 | 29.273 | 38.380 | 84.620 | 2.391 | 202 | 27 | 79 | 96 | 5509 | 48,666 | 375 | 744 | 30.929 | 79.961 | 31.401 |
| R | 39.588 | 63.431 | 28.773 | 37.573 | 82.830 | 2.670 | 202 | 24 | 80 | 98 | 6151 | 49,303 | 523 | 873 | 29.122 | 79.824 | 29.781 |
| R1 | 39.974 | 64.111 | 29.040 | 37.701 | 83.231 | 2.604 | 202 | 25 | 81 | 96 | 5999 | 49,202 | 486 | 851 | 29.490 | 79.862 | 30.102 |
| R2 | 36.918 | 59.397 | 26.782 | 35.950 | 79.728 | 3.133 | 202 | 22 | 80 | 100 | 7219 | 50,585 | 665 | 956 | 25.967 | 79.994 | 26.805 |
| Cost Matrix | Evaluation Metrics | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IDF1↑ | IDP↑ | IDR↑ | Rcll↑ | Prcn↑ | FAR↓ | GT | MT↑ | PT | ML↓ | FP↓ | FN↓ | IDs↓ | FM↓ | MOTA↑ | MOTP↑ | MOTAL↑ | |
| C1 | 43.610 | 69.715 | 31.729 | 39.163 | 86.048 | 2.177 | 202 | 27 | 80 | 95 | 5015 | 48,047 | 249 | 732 | 32.498 | 79.732 | 32.810 |
| C2 | 43.663 | 69.798 | 31.767 | 39.171 | 86.065 | 2.174 | 202 | 27 | 80 | 95 | 5009 | 48,041 | 246 | 731 | 32.517 | 79.736 | 32.826 |
| C3 | 43.748 | 69.928 | 31.831 | 39.185 | 86.083 | 2.171 | 202 | 27 | 80 | 95 | 5003 | 48,030 | 253 | 731 | 32.530 | 79.729 | 32.847 |
| C4 | 43.675 | 69.830 | 31.774 | 39.208 | 86.167 | 2.158 | 202 | 27 | 79 | 96 | 4971 | 48,012 | 258 | 728 | 32.587 | 79.750 | 32.910 |
| C5 | 43.685 | 69.861 | 31.778 | 39.190 | 86.157 | 2.158 | 202 | 27 | 79 | 96 | 4973 | 48,026 | 266 | 730 | 32.556 | 79.755 | 32.890 |
| C6 | 43.389 | 69.351 | 31.570 | 39.171 | 86.048 | 2.177 | 202 | 27 | 80 | 95 | 5016 | 48,041 | 249 | 730 | 32.504 | 79.741 | 32.817 |
| C7 | 43.793 | 69.990 | 31.866 | 39.170 | 86.031 | 2.180 | 202 | 27 | 81 | 94 | 5023 | 48,042 | 243 | 727 | 32.502 | 79.727 | 32.807 |
| C8 | 43.727 | 69.877 | 31.819 | 39.172 | 86.025 | 2.181 | 202 | 27 | 81 | 94 | 5026 | 48,040 | 243 | 726 | 32.501 | 79.726 | 32.805 |
| C9 | 41.995 | 67.131 | 30.554 | 38.837 | 85.328 | 2.289 | 202 | 26 | 83 | 93 | 5274 | 48,305 | 320 | 731 | 31.754 | 79.722 | 32.156 |
| C10 | 41.363 | 66.262 | 30.066 | 38.171 | 84.124 | 2.469 | 202 | 25 | 82 | 95 | 5689 | 48,831 | 428 | 784 | 30.425 | 79.862 | 30.964 |
| C11 | 42.498 | 67.872 | 30.933 | 38.842 | 85.225 | 2.308 | 202 | 27 | 82 | 93 | 5318 | 48,301 | 334 | 753 | 31.685 | 79.795 | 32.105 |
| C12 | 43.727 | 69.875 | 31.819 | 39.172 | 86.022 | 2.182 | 202 | 27 | 81 | 94 | 5027 | 48,040 | 243 | 726 | 32.499 | 79.726 | 32.804 |
| C13 | 43.611 | 69.702 | 31.733 | 39.170 | 86.036 | 2.179 | 202 | 27 | 80 | 95 | 5021 | 48,042 | 247 | 732 | 32.499 | 79.730 | 32.809 |
| C14 | 43.702 | 69.837 | 31.802 | 39.163 | 86.003 | 2.185 | 202 | 27 | 81 | 94 | 5034 | 48,047 | 242 | 721 | 32.483 | 79.728 | 32.786 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razzok, M.; Badri, A.; El Mourabit, I.; Ruichek, Y.; Sahel, A. Pedestrian Detection and Tracking System Based on Deep-SORT, YOLOv5, and New Data Association Metrics. Information 2023, 14, 218. https://doi.org/10.3390/info14040218
Razzok M, Badri A, El Mourabit I, Ruichek Y, Sahel A. Pedestrian Detection and Tracking System Based on Deep-SORT, YOLOv5, and New Data Association Metrics. Information. 2023; 14(4):218. https://doi.org/10.3390/info14040218
Chicago/Turabian StyleRazzok, Mohammed, Abdelmajid Badri, Ilham El Mourabit, Yassine Ruichek, and Aïcha Sahel. 2023. "Pedestrian Detection and Tracking System Based on Deep-SORT, YOLOv5, and New Data Association Metrics" Information 14, no. 4: 218. https://doi.org/10.3390/info14040218
APA StyleRazzok, M., Badri, A., El Mourabit, I., Ruichek, Y., & Sahel, A. (2023). Pedestrian Detection and Tracking System Based on Deep-SORT, YOLOv5, and New Data Association Metrics. Information, 14(4), 218. https://doi.org/10.3390/info14040218






