The Psychometric Function for Focusing Attention on Pitch
Abstract
1. Introduction
Previous Studies: Energy Detection
2. Methods
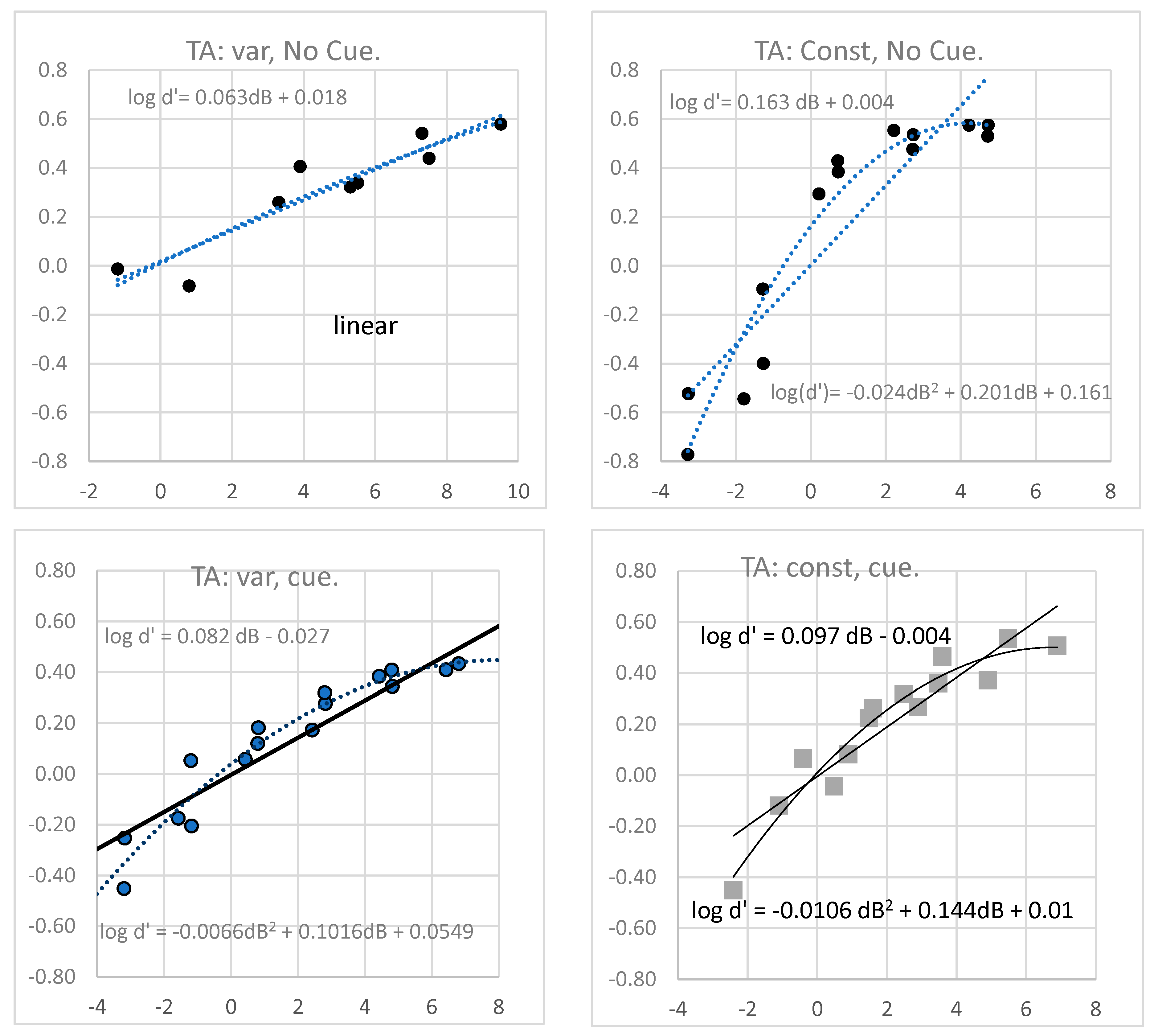
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Green, D.M. Detection of auditory sinusoids of uncertain frequency. J. Acoust. Soc. Am. 1961, 33, 897–903. [Google Scholar] [CrossRef]
- Gilliom, J.D.; Mills, W.M. Information extraction from contralateral cues in the detection of signals of uncertain frequency. J. Acoust. Soc. Am. 1976, 59, 1428–1433. [Google Scholar] [CrossRef] [PubMed]
- Green, T.J.; McKeown, J.D. Capture of attention in selective frequency listening. J. Exp. Psychol. Hum. Percept. Perform. 2001, 27, 1197–1210. [Google Scholar] [CrossRef]
- Schlauch, R.S.; Hafter, E.R. Listening bandwidths and frequency uncertainty in pure-tone signal detection. J. Acoust. Soc. Am. 1991, 90, 1332–1339. [Google Scholar] [CrossRef]
- Swets, J.A. Central factors in auditory frequency selectivity. Psychol. Bull. 1963, 60, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Hübner, R.; Hafter, E.R. Cuing mechanisms in auditory signal detection. Percept. Psychophys. 1995, 57, 197–202. [Google Scholar] [CrossRef]
- Grossberg, S. Conscious Mind, Resonant Brain; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Dresp-Langley, B. The Grossberg Code: Universal Neural Network Signatures of Perceptual Experience. Information 2023, 14, 82. [Google Scholar] [CrossRef]
- Scharf, B. Critical bands. In Foundations of Modem Auditory Theory; Tobias, J.V., Ed.; Academic Press: New York, NY, USA, 1970; Volume 1, pp. 157–202. [Google Scholar]
- Swets, J.; Sewall, S.T. Stimulus vs Response uncertainty in recognition. J. Acoust. Soc. Am. 1961, 33, 1586–1592. [Google Scholar] [CrossRef]
- Angeloni, C.; Geffen, M.N. Contextual modulation of sound processing in the auditory cortex. Curr. Opin. Neurobiol. 2018, 49, 8–15. [Google Scholar] [CrossRef]
- Greenberg, G.Z.; Larkin, W.D. Frequency-response characteristics of auditory observers detecting signals of a single frequency in noise: The probe-signal method. J. Acoust. Soc. Am. 1968, 44, 1513–1523. [Google Scholar] [CrossRef]
- Botte, M.-C. Auditory attentional bandwidth: Effect of level and frequency range. J. Acoust. Soc. Am. 1995, 98, 2475–2485. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Scharf, B.; Buus, S. Effective attenuation of signals in noise under focused attention. J. Acoust. Soc. Am. 1994, 89, 2837–2842. [Google Scholar] [CrossRef] [PubMed]
- Reeves, A. The Auditory Attention Band: Data and model. In Human Information Processing: Vision, Memory, and Attention; Charles Chubb, C., Ed.; APA Books: Washington, DC, USA, 2013. [Google Scholar]
- Scharf, B.; Quigley, S.; Aoki, C.; Peachey, N.; Reeves, A. Focused auditory attention and frequency selectivity. Percept. Psychophys. 1987, 42, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Wright, B.A.; Dai, H. Detection of unexpected tones with short and long durations. J. Acoust. Soc. Am. 1994, 95, 931–938. [Google Scholar] [CrossRef]
- Scharf, B.; Magnan, J.; Chays, A. On the role of the olivocochlear bundle in hearing: 16 case studies. Hear. Res. 1997, 103, 101–122. [Google Scholar] [CrossRef]
- Lesicko, A.M.H.; Geffen, M.N. Diverse functions of the auditory cortico-collicular pathway. Hear. Res. 2022, 425, 108488. [Google Scholar] [CrossRef]
- Romero, G.E.; Russell, L.O. Central circuitry and function of the cochlear efferent systems. Hear. Res. 2004, 425, 108516. [Google Scholar] [CrossRef]
- Tan, M.N.; Robertson, D.; Hammond, G.R. Separate contributions of enhanced and suppressed sensitivity to the auditory attentional filter. Hear. Res. 2008, 241, 18–25. [Google Scholar] [CrossRef]
- Lu, Z.-L.; Dosher, B.A. External noise distinguishes attention mechanisms. Vis. Res. 1998, 38, 1183–1198. [Google Scholar] [CrossRef]
- Treisman, A. Monitoring and storage of irrelevant messages in selective attention. J. Verbal Learn. Verbal Behav. 2004, 3, 449–459. [Google Scholar] [CrossRef]
- Richards, V.M.; Neff, D.L. Cuing effects for informational masking. J. Acoust. Soc. Am. 2004, 115, 289–300. [Google Scholar] [CrossRef] [PubMed]
- Scharf, B.; Reeves, A.; Suciu, J. The time required to focus on a cued signal frequency. J. Acoust. Soc. Am. 2007, 121, 2149–2157. [Google Scholar] [CrossRef] [PubMed]
- Reeves, A.; Seluakumaran, K.; Scharf, B. Contralateral Proximal Interference. J. Acoust. Soc. Am. 2021, 149, 3352–3365. [Google Scholar] [CrossRef]
- Zwicker, E. Dependence of post-masking on masker duration and its relation to temporal effects in loudness. J. Acoust. Soc. Am. 1984, 75, 219–223. [Google Scholar] [CrossRef] [PubMed]
- Reeves, A.; Scharf, B. Auditory frequency focusing is very rapid. J. Acoust. Soc. Am. 2010, 128, 795–803. [Google Scholar] [CrossRef] [PubMed]
- Kontsevich, L.L.; Chen, C.C.; Tyler, C.W. Separating the effects of response nonlinearity and internal noise psychometrically. Vis. Res. 2002, 42, 1771–1784. [Google Scholar] [CrossRef]
- Buus, S.; Schorer, E.; Florentine, M.; Zwicker, E. Decision rules in detection of simple and complex tones. J. Acoust. Soc. Am. 1986, 80, 1646–1657. [Google Scholar] [CrossRef] [PubMed]
- Dai, H. Signal-frequency uncertainty in spectral-shape discrimination: Psychometric functions. J. Acoust. Soc. Am. 1994, 96, 1388–1396. [Google Scholar] [CrossRef]
- Green, D.M.; Swets, J.A. Signal Detection Theory and Psychophysics; Peninsular Publishing Inc.: Los Altos, CA, USA, 1988. [Google Scholar]
- Green, D.M.; Birdsall, T.G.; Tanner, W.P. Signal Detection as a Function of Signal Intensity and Duration. J. Acoust. Soc. Am. 1957, 29, 523–531. [Google Scholar] [CrossRef]
- Scharf, B.; Reeves, A.; Giovanetti, H. Role of attention in overshoot: Frequency certainty versus uncertainty. J. Acoust. Soc. Am. 2008, 123, 1555–1561. [Google Scholar] [CrossRef]
- Baer, T.; Moore, B.C.J.; Glasberg, B.R. Detection and intensity discrimination of Gaussian-shaped tone pulses as a function of duration. J. Acoust. Soc. Am. 1999, 106, 1907–1916. [Google Scholar] [CrossRef] [PubMed]
- Barascud, N.; Pearce, M.T.; Griffiths, T.D.; Friston, K.J.; Chait, M. Brain responses in humans reveal ideal observer-like sensitivity to complex acoustic patterns. Proc. Natl. Acad. Sci. USA 2016, 113, E616–E625. [Google Scholar] [CrossRef] [PubMed]
- Dauer, T.; Nerness, B.; Fujioka, T. Predictability of higher-order temporal structure of musical stimuli is associated with auditory evoked response. Int. J. Psychophysiol. 2020, 153, 53–56. [Google Scholar] [CrossRef] [PubMed]




| Amp | dB | Pccon | Pcvar | Pcon | Pvar | d’con | d’var | log d’con | log d’var |
|---|---|---|---|---|---|---|---|---|---|
| 1.12 | 1 | 0.54 | 0.55 | 0.541 | 0.551 | 0.145 | 0.181 | −0.839 | −0.741 |
| 1.26 | 2 | 0.55 | 0.58 | 0.551 | 0.582 | 0.181 | 0.291 | −0.741 | −0.535 |
| 1.41 | 3 | 0.64 | 0.66 | 0.643 | 0.663 | 0.518 | 0.596 | −0.286 | −0.225 |
| 1.58 | 4 | 0.66 | 0.68 | 0.663 | 0.684 | 0.596 | 0.676 | −0.225 | −0.170 |
| 1.78 | 5 | 0.78 | 0.76 | 0.786 | 0.765 | 1.120 | 1.023 | 0.049 | 0.010 |
| 2.00 | 6 | 0.87 | 0.82 | 0.878 | 0.827 | 1.644 | 1.330 | 0.216 | 0.124 |
| 2.24 | 7 | 0.91 | 0.91 | 0.918 | 0.918 | 1.972 | 1.972 | 0.295 | 0.295 |
| 2.51 | 8 | 0.97 | 0.93 | 0.980 | 0.939 | 2.893 | 2.184 | 0.461 | 0.339 |
| 2.82 | 9 | 0.98 | 0.97 | 0.990 | 0.980 | 3.279 | 2.893 | 0.516 | 0.461 |
| 3.16 | 10 | 0.98 | 0.95 | ||||||
| 3.55 | 11 | 0.98 | 0.98 | linear | slope | 0.177 | 0.146 |
| Hz | 632 | 767 | 917 | 1082 | 1266 | 1481 | 1720 | 1994 | 2318 | 2693 | 3140 |
| NA | 36.2 | 36.3 | 36.3 | 36.3 | 36.1 | 36.0 | 36.8 | 37.6 | 38.4 | 39.2 | 40.3 |
| TA | 31.6 | 32.4 | 33.5 | 33.2 | 33.4 | 35.5 | 36.7 | 36.1 | 37.5 | 37.3 | 38.9 |
| MA | 36.2 | 36.6 | 36.9 | 37.2 | 37.6 | 38.0 | 38.3 | 38.6 | 38.9 | 39.2 | 39.5 |
| Listener | Cue var | Cue const | No Cue var | No Cue const | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fr.group | dB SPL | log(d) | dB SL | dB SPL | log(d) | dB SL | dB SPL | log(d) | dB SL | dB SPL | log(d’) | dB SL |
| TA Low | 38.90 | 0.34 | 4.82 | 39.0 | 0.51 | 6.89 | 38.00 | 0.41 | 3.90 | 35.00 | 0.58 | 4.21 |
| 34.08 | 36.90 | 0.28 | 2.82 | 37.0 | 0.37 | 4.89 | 34.90 | −0.08 | 0.80 | 33.00 | 0.55 | 2.21 |
| 32.11 | 34.90 | 0.18 | 0.82 | 35.0 | 0.27 | 2.89 | 32.90 | −0.01 | −1.20 | 31.00 | 0.29 | 0.21 |
| 34.10 | 32.90 | −0.21 | −1.18 | 33.0 | 0.08 | 0.89 | 29.90 | −0.72 | −3.20 | 29.00 | −0.54 | −1.79 |
| 30.79 | 30.90 | −0.25 | −3.18 | 31.0 | −0.12 | −1.11 | ||||||
| TA Med | 43.80 | 0.43 | 6.80 | 42.0 | 0.54 | 5.47 | 39.80 | 0.54 | 7.31 | 39.00 | 0.53 | 4.72 |
| 36.99 | 41.80 | 0.41 | 4.80 | 40.0 | 0.36 | 3.47 | 37.80 | 0.32 | 5.31 | 37.00 | 0.48 | 2.72 |
| 36.53 | 39.80 | 0.32 | 2.80 | 39.0 | 0.32 | 2.47 | 35.80 | 0.26 | 3.31 | 35.00 | 0.43 | 0.72 |
| 32.49 | 37.80 | 0.12 | 0.80 | 38.0 | 0.22 | 1.47 | 33.80 | −0.52 | 1.31 | 33.00 | −0.09 | −1.28 |
| 34.28 | 35.80 | 0.05 | −1.20 | 37.0 | −0.04 | 0.47 | 31.00 | −0.77 | −3.28 | |||
| 33.80 | −0.45 | −3.20 | ||||||||||
| TA High | 47.96 | 0.46 | 8.43 | 45.0 | 0.47 | 3.59 | 43.96 | 0.58 | 9.51 | 45.00 | 0.58 | 4.73 |
| 39.53 | 45.96 | 0.41 | 6.43 | 43.0 | 0.26 | 1.59 | 41.96 | 0.44 | 7.51 | 43.00 | 0.54 | 2.73 |
| 41.41 | 43.96 | 0.38 | 4.43 | 41.0 | 0.07 | −0.41 | 39.96 | 0.34 | 5.51 | 41.00 | 0.38 | 0.73 |
| 34.45 | 41.96 | 0.17 | 2.43 | 39.0 | −0.45 | −2.41 | 37.96 | 0.19 | 3.51 | 39.00 | −0.40 | −1.27 |
| 40.27 | 39.96 | 0.06 | 0.43 | 37.0 | −1.02 | −4.41 | 37.00 | −0.52 | −3.27 | |||
| 37.96 | −0.18 | −1.57 | ||||||||||
| NA Low | 42.28 | 0.41 | 4.56 | 44.0 | 0.55 | 6.02 | 38.28 | 0.54 | 2.01 | 37.00 | 0.38 | 2.39 |
| 37.72 | 40.28 | 0.31 | 2.56 | 42.0 | 0.50 | 4.02 | 36.28 | 0.24 | 0.01 | 35.00 | 0.23 | 0.39 |
| 37.98 | 38.28 | 0.11 | 0.56 | 40.0 | 0.24 | 2.02 | 34.28 | −0.77 | −1.99 | 33.00 | −0.33 | −1.61 |
| 36.27 | 36.28 | −0.44 | −1.44 | 38.0 | 0.05 | 0.02 | 32.28 | −1.50 | −3.99 | 31.00 | −0.77 | −3.61 |
| 34.61 | 34.28 | −0.12 | −3.44 | 36.0 | −0.28 | −1.98 | ||||||
| 32.28 | −0.50 | −5.44 | ||||||||||
| NA Med | 42.29 | 0.38 | 3.42 | 42.0 | 0.32 | 5.53 | 38.29 | 0.39 | 1.78 | 39.00 | 0.41 | 3.54 |
| 38.86 | 40.29 | 0.18 | 1.42 | 41.0 | 0.20 | 4.53 | 36.29 | 0.20 | −0.22 | 37.00 | 0.33 | 1.54 |
| 36.47 | 38.29 | 0.03 | −0.58 | 39.0 | 0.20 | 2.53 | 34.29 | −0.78 | −2.22 | 35.00 | −0.19 | −0.46 |
| 36.50 | 36.29 | −0.24 | −2.58 | 37.0 | 0.05 | 0.53 | 32.29 | −1.22 | −4.22 | 33.00 | −0.27 | −2.46 |
| 35.46 | 34.29 | −0.88 | −4.58 | 35.0 | −0.12 | −1.47 | ||||||
| 32.29 | −0.58 | −6.58 | ||||||||||
| NA High | 44.84 | 0.42 | 4.65 | 44.0 | 0.34 | 3.14 | 40.84 | 0.44 | 1.54 | 39.00 | 0.33 | 1.30 |
| 40.19 | 42.84 | 0.31 | 2.65 | 42.0 | 0.07 | 1.14 | 38.84 | 0.04 | −0.46 | 37.00 | −0.17 | −0.70 |
| 40.86 | 40.84 | 0.09 | 0.65 | 40.0 | 0.00 | −0.86 | 36.84 | −0.97 | −2.46 | 35.00 | −0.70 | −2.70 |
| 39.31 | 38.84 | −0.21 | −1.35 | 38.0 | −0.41 | −2.86 | 34.84 | −1.45 | −4.46 | 33.00 | −1.40 | −4.70 |
| 37.70 | 36.84 | −0.28 | −3.35 | 36.0 | −0.45 | −4.86 | ||||||
| MA Low | 38.57 | 0.44 | 3.47 | 41.0 | 0.44 | 8.23 | 40.57 | 0.55 | 7.06 | 39.00 | 0.55 | 7.00 |
| 35.09 | 36.57 | 0.41 | 1.47 | 39.0 | 0.39 | 6.23 | 38.57 | 0.38 | 5.06 | 37.00 | 0.52 | 5.00 |
| 32.77 | 34.57 | 0.15 | −0.53 | 37.0 | 0.32 | 4.23 | 36.57 | 0.38 | 3.06 | 35.00 | 0.47 | 3.00 |
| 33.50 | 32.57 | −0.59 | −2.53 | 35.0 | 0.22 | 2.23 | 34.57 | 0.01 | 1.06 | 33.00 | 0.32 | 1.00 |
| 32.00 | 30.57 | −0.90 | −4.53 | 33.0 | −0.08 | 0.23 | ||||||
| MA Med | 39.79 | 0.48 | 4.82 | 41.0 | 0.51 | 5.08 | 41.79 | 0.53 | 4.84 | 39.00 | 0.58 | 3.55 |
| 34.97 | 37.79 | 0.39 | 2.82 | 39.0 | 0.44 | 3.08 | 39.79 | 0.44 | 2.84 | 37.00 | 0.46 | 1.55 |
| 35.92 | 35.79 | 0.15 | 0.82 | 37.0 | 0.24 | 1.08 | 37.79 | 0.36 | 0.84 | 35.00 | 0.22 | −0.45 |
| 36.95 | 33.79 | −0.26 | −1.18 | 35.0 | −0.02 | −0.92 | 35.79 | −0.34 | −1.16 | 33.00 | −0.78 | −2.45 |
| 35.45 | 31.79 | −0.30 | −3.18 | 33.0 | −0.50 | −2.92 | ||||||
| MA High | 41.03 | 0.42 | 3.83 | 41.0 | 0.38 | 3.05 | 43.03 | 0.47 | 5.93 | 43.00 | 0.60 | 5.88 |
| 37.20 | 39.03 | 0.20 | 1.83 | 39.0 | 0.23 | 1.05 | 41.03 | 0.37 | 3.93 | 41.00 | 0.51 | 3.88 |
| 37.95 | 37.03 | −0.03 | −0.17 | 37.0 | −0.11 | −0.95 | 39.03 | 0.14 | 1.93 | 39.00 | 0.25 | 1.88 |
| 37.10 | 35.03 | −0.30 | −2.17 | 35.0 | −0.54 | −2.95 | 37.03 | −0.41 | −0.07 | 37.00 | 0.07 | −0.12 |
| 37.12 | 33.03 | −0.39 | −4.17 | 33.0 | −0.65 | −4.95 | 35.00 | −0.34 | −2.12 | |||
| Listener | Condition | Means over Frequencies | Shift | Shift | ||
|---|---|---|---|---|---|---|
| slope | inter cpt | r2 lin | r2 lin | r2 quad | ||
| TA | var No Cue | 0.073 | −2.46 | 0.88 | 0.86 | 0.87 |
| const NoC | 0.165 | −5.77 | 0.82 | 0.83 | 0.92 | |
| var Cue | 0.084 | −3.08 | 0.89 | 0.86 | 0.98 | |
| const Cue | 0.110 | −4.13 | 0.94 | 0.85 | 0.94 | |
| NA | var No Cue | 0.340 | −12.76 | 0.90 | 0.91 | 0.99 |
| const NoC | 0.195 | −7.05 | 0.95 | 0.89 | 0.93 | |
| var Cue | 0.102 | −3.96 | 0.87 | 0.85 | 0.85 | |
| const Cue | 0.089 | −3.43 | 0.94 | 0.89 | 0.90 | |
| MA | var No Cue | 0.099 | −3.57 | 0.85 | 0.69 | 0.81 |
| const NoC | 0.125 | −4.35 | 0.88 | 0.71 | 0.92 | |
| var Cue | 0.134 | −4.76 | 0.94 | 0.87 | 0.89 | |
| const Cue | 0.109 | −3.94 | 0.91 | 0.83 | 0.94 | |
| Mean | var No Cue | 0.171 | −6.26 | 0.88 | 0.82 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reeves, A. The Psychometric Function for Focusing Attention on Pitch. Information 2023, 14, 279. https://doi.org/10.3390/info14050279
Reeves A. The Psychometric Function for Focusing Attention on Pitch. Information. 2023; 14(5):279. https://doi.org/10.3390/info14050279
Chicago/Turabian StyleReeves, Adam. 2023. "The Psychometric Function for Focusing Attention on Pitch" Information 14, no. 5: 279. https://doi.org/10.3390/info14050279
APA StyleReeves, A. (2023). The Psychometric Function for Focusing Attention on Pitch. Information, 14(5), 279. https://doi.org/10.3390/info14050279







