Multiple Explainable Approaches to Predict the Risk of Stroke Using Artificial Intelligence
Abstract
:1. Introduction
- The most crucial attributes have been decided upon using four feature selection techniques: Pearson’s correlation, Mutual information, Particle swarm optimization and Harris Hawks algorithm. Comparison of the feature selection methods have been made in this study.
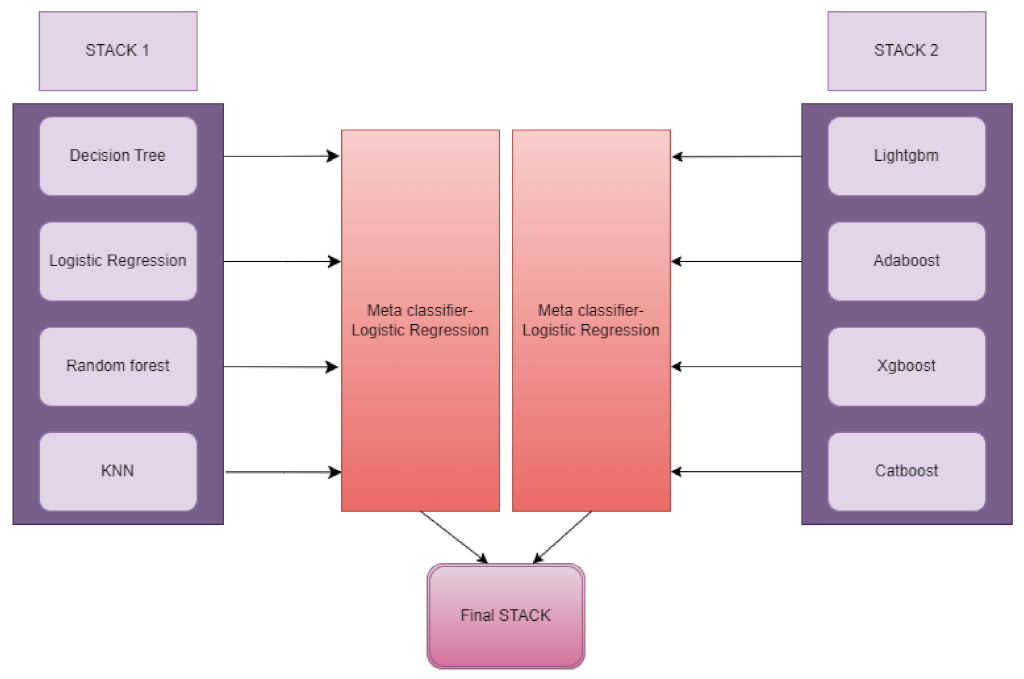
- A novel customised “ensemble-stacking” architecture was designed and used to improve the performance utilizing baseline classifiers.
- This is a unique study that used five XAI techniques, such as LIME, SHAP, ELI5, Anchor and Qlattice, on the dataset to demystify stroke predictions.
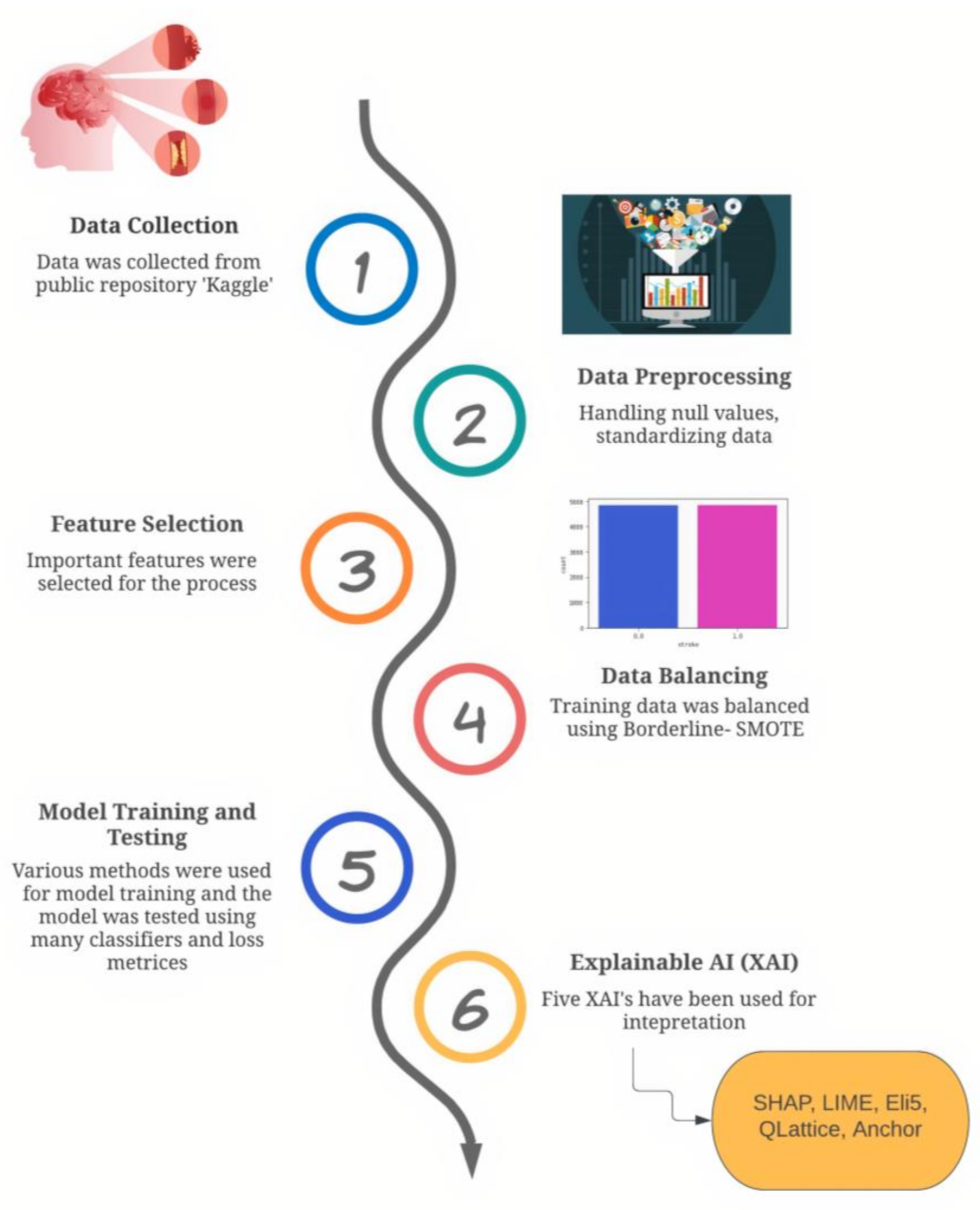
2. Materials and Methods
2.1. Data Description
2.2. Data Preprocessing
2.3. Feature Selection
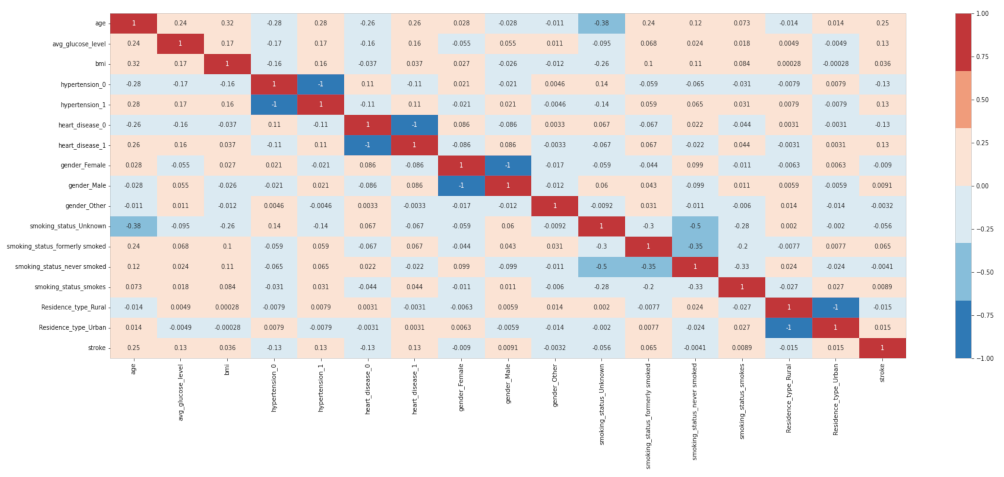
2.3.1. Pearson’s Correlation
2.3.2. Mutual Information (MI)
2.3.3. Particle Swarm Optimization
2.3.4. Harris Hawks Algorithm
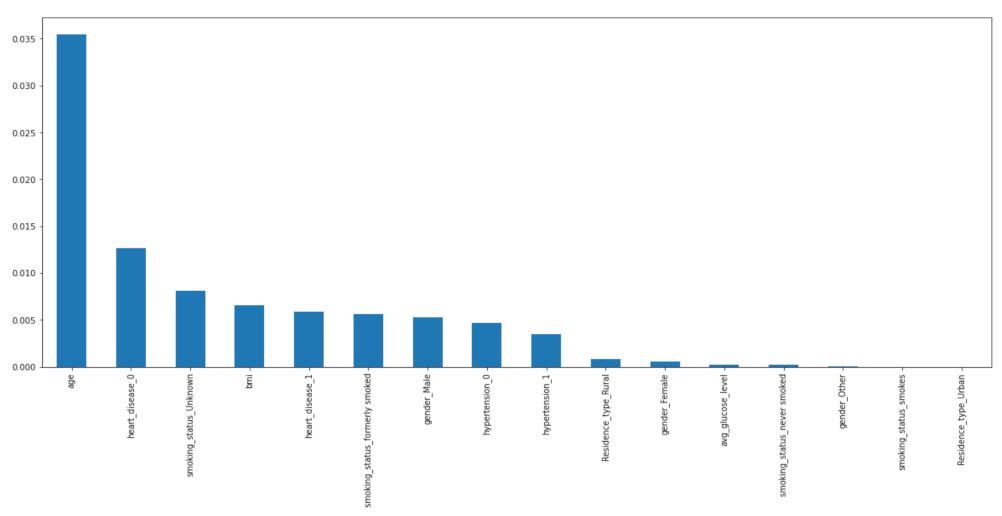
2.3.5. Important Features
2.4. Machine Learning Terminologies
- SHAP (SHapley Additive exPlanations): It uses a model-neutral approach for analysing the output of any machine learning model by figuring out how much each feature contributed to the final prediction.
- LIME (Local Interpretable Model-agnostic Explanations): It is a technique for generating local interpretations of black-box models by approximating them with interpretable models trained on subsets of the data.
- ELI5 (Explain Like I’m 5): It is a Python library that provides simple explanations of machine learning models using a variety of techniques, including feature importance, decision trees, and permutation feature importance.
- Qlattice: It is a visualization tool for exploring machine learning models that allows users to interactively explore the model’s decision-making process by visualizing the feature contributions to the final prediction.
- Anchor: It is uses rules and conditions to explain the model output. It uses the evaluation metrics precision and coverage to identify the importance of that particular condition.
3. Results
3.1. Performance Metrics
- Accuracy: The accuracy is its capacity to distinguish between patients experiencing a stroke and those who do not correctly. The proportion of true positive and true negative outcomes in all analysed cases should be determined in order to determine the prediction’s accuracy. The mathematical formula is:
- Precision: It is a statistic that determines the proportion of patients who actually suffered a stroke compared to all other patients. This implies that it also considers patients who have received a false-positive stroke diagnosis. The equation is as follows:
- Recall: It is a measure of performance that is described as the ratio of patients who had a stroke accurately to all the patients who had been affected. This statistic puts a focus on false-negative situations. When there are few false-negative cases, the recall is extraordinarily high. It is calculated using the following formula:
- F1 score: A evaluation metric that combines a model’s precision and recall scores. It is calculated using the following formula:
- AUC: The true positive rate versus the false-positive rate for various test scenarios is plotted on the receiver operating characteristic (ROC) curve. It shows how effectively the models distinguish between the binary classifications. The AUC is the region beneath this curve. AUC values that are high show that the classifier is working effectively.
3.2. Model Evaluation
3.3. Explainable Artificial Intelligence (XAI)
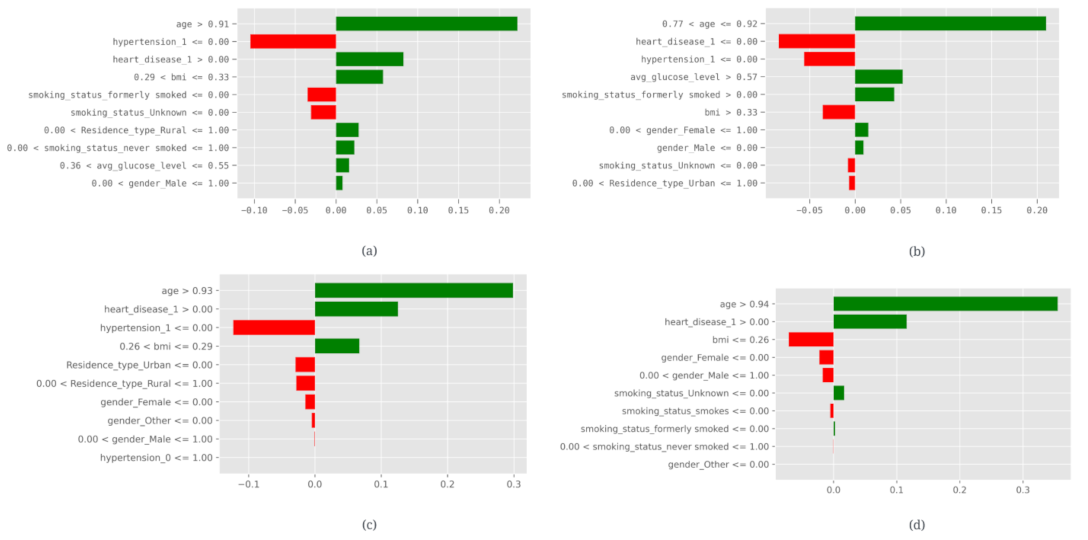
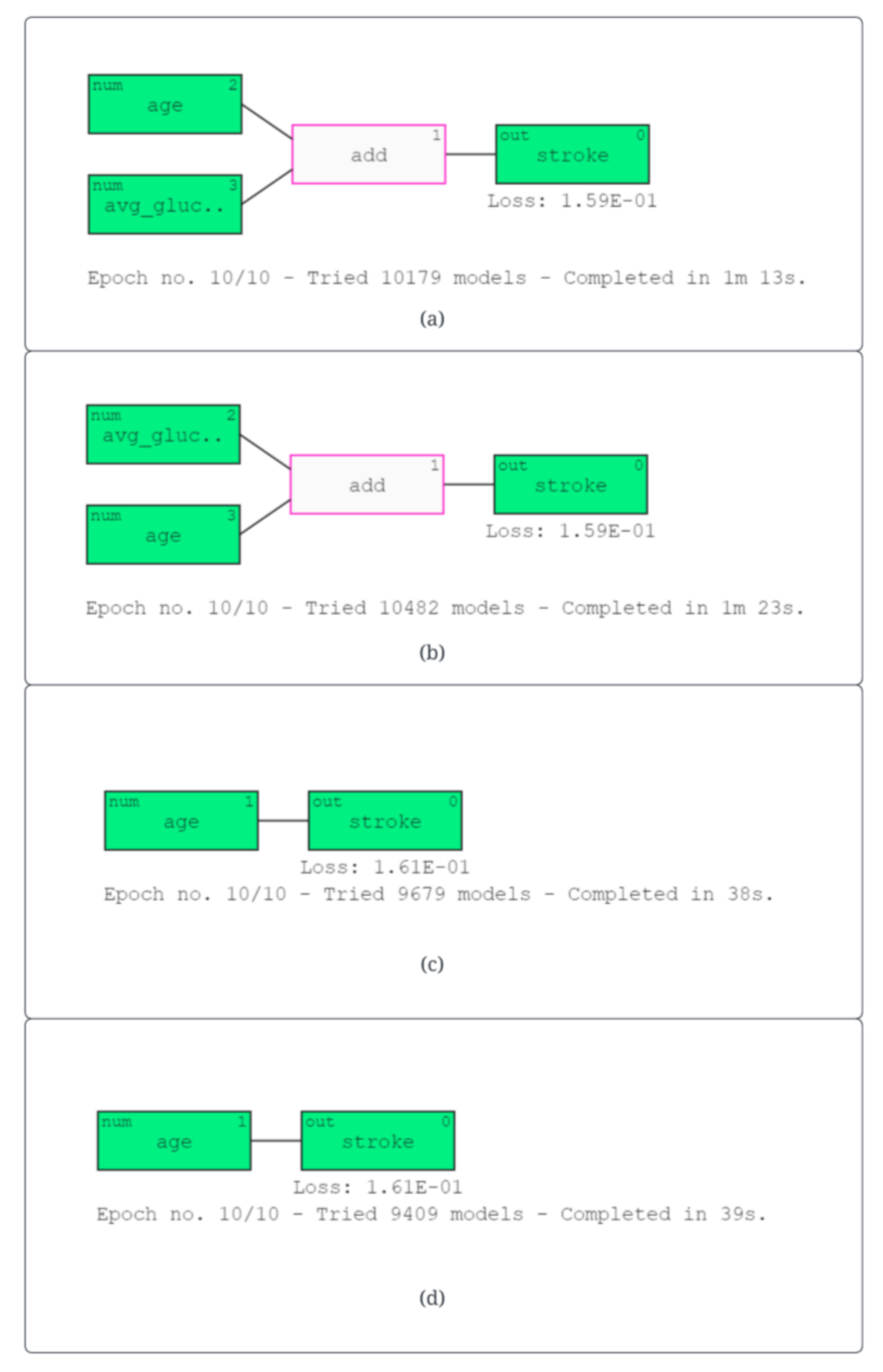
| (a) logreg (5.2 age + 1.2 avgglucoselevel − 7.0) | (5) |
| (b) logreg (5.4 age + 1.2 avgglucoselevel − 7.1) | (6) |
| (c) logreg (5.6 age−6.8) | (7) |
| (d) logreg (5.7 age−6.9) | (8) |
4. Discussion
5. Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Sun, W.; Wang, Y.; Wang, X.; Liu, Y.; Zhao, S.; Long, D.; Chen, L.; Yu, L. Clinical course and mortality of stroke patients with coronavirus disease 2019 in Wuhan, China. Stroke 2020, 51, 2674–2682. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Ryu, J.; Kim, D.H. Automated epileptic seizure waveform detection method based on the feature of the mean slope of wavelet coefficient counts using a hidden Markov model and EEG signals. ETRI J. 2020, 42, 217–229. [Google Scholar] [CrossRef]
- McIntosh, J. Stroke: Causes, Symptoms, Diagnosis, and Treatment, 2020. Available online: https://www.medicalnewstoday.com/articles/7624 (accessed on 7 April 2023).
- Tanaka, M.; Szabó, Á.; Vécsei, L. Preclinical modeling in depression and anxiety: Current challenges and future research directions. Adv. Clin. Exp. Med. 2023, 32, 505–509. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, S.; Di Fazio, C.; Vicario, C.M.; Avenanti, A. Neuropharmacological modulation of N-methyl-D-aspartate, noradrenaline and endocannabinoid receptors in fear extinction learning: Synaptic transmission and plasticity. Int. J. Mol. Sci. 2023, 24, 5926. [Google Scholar] [CrossRef]
- Rajkumar, R.P. Biomarkers of Neurodegeneration in Post-Traumatic Stress Disorder: An Integrative Review. Biomedicines 2023, 11, 1465. [Google Scholar] [CrossRef]
- Medicine, N. Before Stroke Warning Signs. Northwestern Medicine. Available online: https://www.nm.org/conditions-and-care-areas/neurosciences/comprehensive-stroke-centers/before-stroke/warning-signs (accessed on 7 April 2023).
- Battaglia, S.; Nazzi, C.; Thayer, J.F. Fear-induced bradycardia in mental disorders: Foundations, current advances, future perspectives. Neurosci. Biobehav. Rev. 2023, 149, 105163. [Google Scholar] [CrossRef]
- Polyák, H.; Galla, Z.; Nánási, N.; Cseh, E.K.; Rajda, C.; Veres, G.; Spekker, E.; Szabó, Á.; Klivényi, P.; Tanaka, M.; et al. The tryptophan-kynurenine metabolic system is suppressed in cuprizone-induced model of demyelination simulating progressive multiple sclerosis. Biomedicines 2023, 11, 945. [Google Scholar] [CrossRef]
- Dang, J.; Tao, Q.; Niu, X.; Zhang, M.; Gao, X.; Yang, Z.; Yu, M.; Wang, W.; Han, S.; Cheng, J.; et al. Meta-Analysis of Structural and Functional Brain Abnormalities in Cocaine Addiction. Front. Psychiatry 2022, 13, 927075. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Nambiar, A.R.; Dutta, D. A study of machine learning in healthcare. In Proceedings of the 2017 IEEE 41st Annual Computer Software and Applications Conference (COMPSAC), IEEE, Turin, Italy, 4–8 July 2017; Volume 2, pp. 236–241. [Google Scholar] [CrossRef]
- Srinivas, S.; Ravindran, A.R. Optimizing outpatient appointment system using machine learning algorithms and scheduling rules: A prescriptive analytics framework. Expert Syst. Appl. 2018, 102, 245–261. [Google Scholar] [CrossRef]
- Mohanta, B.; Das, P.; Patnaik, S. Healthcare 5.0: A paradigm shift in digital healthcare system using artificial intelligence, IOT and 5G communication. In Proceedings of the 2019 International Conference on Applied Machine Learning (ICAML), IEEE, Bhubaneswar, India, 25–26 May 2019; pp. 191–196. [Google Scholar] [CrossRef]
- Saraswat, D.; Bhattacharya, P.; Verma, A.; Prasad, V.K.; Tanwar, S.; Sharma, G.; Bokoro, P.N.; Sharma, R. Explainable AI for healthcare 5.0: Opportunities and challenges. IEEE Access 2022, 10, 84486–84517. [Google Scholar] [CrossRef]
- Pawar, U.; O’Shea, D.; Rea, S.; O’Reilly, R. Incorporating Explainable Artificial Intelligence (XAI) to aid the Understanding of Machine Learning in the Healthcare Domain. AICS 2020, 169–180. [Google Scholar] [CrossRef]
- Vij, A.; Nanjundan, P. Comparing strategies for post-hoc explanations in machine learning models. In Mobile Computing and Sustainable Informatics, Proceedings of the ICMCSI 2021, Lalitpur, Nepal, 29–30 January 2021; Springer: Singapore, 2021; pp. 585–592. [Google Scholar] [CrossRef]
- Govindarajan, P.; Soundarapandian, R.K.; Gandomi, A.H.; Patan, R.; Jayaraman, P.; Manikandan, R. Classification of stroke disease using machine learning algorithms. Neural Comput. Appl. 2020, 32, 817–828. [Google Scholar] [CrossRef]
- Tazin, T.; Alam, M.N.; Dola, N.N.; Bari, M.S.; Bourouis, S.; Monirujjaman Khan, M. Stroke disease detection and prediction using robust learning approaches. J. Healthc. Eng. 2021, 2021, 7633381. [Google Scholar] [CrossRef] [PubMed]
- Emon, M.U.; Keya, M.S.; Meghla, T.I.; Rahman, M.M.; Al Mamun, M.S.; Kaiser, M.S. Performance analysis of machine learning approaches in stroke prediction. In Proceedings of the 2020 4th International Conference on Electronics, Communication and Aerospace Technology (ICECA), IEEE, Coimbatore, India, 5–7 November 2020; pp. 1464–1469. [Google Scholar] [CrossRef]
- Sailasya, G.; Kumari, G.L. Analyzing the performance of stroke prediction using ML classification algorithms. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 0120662. [Google Scholar] [CrossRef]
- Shoily, T.I.; Islam, T.; Jannat, S.; Tanna, S.A.; Alif, T.M.; Ema, R.R. Detection of stroke disease using machine learning algorithms. In Proceedings of the 2019 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), IEEE, Kanpur, India, 6–8 July 2019; pp. 1–6. [Google Scholar] [CrossRef]
- FEDESORIANO. “Stroke Prediction Dataset”, Kaggle. 2020. Available online: https://www.kaggle.com/datasets/fedesoriano/stroke-prediction-dataset (accessed on 30 May 2023).
- Tanasa, D.; Trousse, B. Advanced data preprocessing for intersites web usage mining. IEEE Intell. Syst. 2004, 19, 59–65. [Google Scholar] [CrossRef]
- Khanna, V.V.; Chadaga, K.; Sampathila, N.; Prabhu, S.; Bhandage, V.; Hegde, G.K. A Distinctive Explainable Machine Learning Framework for Detection of Polycystic Ovary Syndrome. Appl. Syst. Innov. 2023, 6, 32. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Advances in Intelligent Computing, Proceedings of the International Conference on Intelligent Computing, ICIC 2005, Hefei, China, 23–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; Part I; pp. 878–887. [Google Scholar] [CrossRef]
- Ahlgren, P.; Jarneving, B.; Rousseau, R. Requirements for a cocitation similarity measure, with special reference to Pearson’s correlation coefficient. J. Am. Soc. Inf. Sci. Technol. 2003, 54, 550–560. [Google Scholar] [CrossRef]
- Pradhan, A.; Prabhu, S.; Chadaga, K.; Sengupta, S.; Nath, G. Supervised learning models for the preliminary detection of COVID-19 in patients using demographic and epidemiological parameters. Information 2022, 13, 330. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, IEEE, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), IEEE, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Unler, A.; Murat, A. A discrete particle swarm optimization method for feature selection in binary classification problems. Eur. J. Oper. Res. 2010, 206, 528–539. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, G.; Chen, H.; Dong, H.; Zhu, X.; Wang, S. An improved particle swarm optimization for feature selection. J. Bionic Eng. 2011, 8, 191–200. [Google Scholar] [CrossRef]
- Mohemmed, A.W.; Zhang, M.; Johnston, M. Particle swarm optimization based adaboost for face detection. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, IEEE, Trondheim, Norway, 18–21 May 2009; pp. 2494–2501. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Yin, Q.; Cao, B.; Li, X.; Wang, B.; Zhang, Q.; Wei, X. An intelligent optimization algorithm for constructing a DNA storage code: NOL-HHO. Int. J. Mol. Sci. 2020, 21, 2191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qu, C.; He, W.; Peng, X.; Peng, X. Harris hawks optimization with information exchange. Appl. Math. Model. 2020, 84, 52–75. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, R.; Wang, X.; Chen, H.; Li, C. Boosted binary Harris hawks optimizer and feature selection. Eng. Comput. 2021, 37, 3741–3770. [Google Scholar] [CrossRef]
- Kamboj, V.K.; Nandi, A.; Bhadoria, A.; Sehgal, S. An intensify Harris hawks optimizer for numerical and engineering optimization problems. Appl. Soft. Comput. 2020, 89, 106018. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Selim, A.; Ashmawy, M.G.; Kamel, S. Developing and applying chaotic harris hawks optimization technique for extracting parameters of several proton exchange membrane fuel cell stacks. IEEE Access 2019, 8, 1146–1159. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, S.; Wang, M.; Heidari, A.A.; Zhao, X. Parameters identification of photovoltaic cells and modules using diversification-enriched Harris hawks optimization with chaotic drifts. J. Clean. Prod. 2020, 244, 118778. [Google Scholar] [CrossRef]
- Moayedi, H.; Gör, M.; Lyu, Z.; Bui, D.T. Herding Behaviors of grasshopper and Harris hawk for hybridizing the neural network in predicting the soil compression coefficient. Measurement 2020, 152, 107389. [Google Scholar] [CrossRef]
- Wei, Y.; Lv, H.; Chen, M.; Wang, M.; Heidari, A.A.; Chen, H.; Li, C. Predicting entrepreneurial intention of students: An extreme learning machine with Gaussian barebone Harris hawks optimizer. IEEE Access 2020, 8, 76841–76855. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Parameters extraction of three-diode photovoltaic model using computation and Harris Hawks optimization. Energy 2020, 195, 117040. [Google Scholar] [CrossRef]
- Stacking in Machine Learning—Javatpoint. Available online: https://www.javatpoint.com/stacking-in-machine-learning#:~:text=Stacking%20is%20one%20of%20the (accessed on 25 April 2023).
- Korica, P.; Gayar, N.E.; Pang, W. Explainable artificial intelligence in healthcare: Opportunities, gaps and challenges and a novel way to look at the problem space. In Intelligent Data Engineering and Automated Learning–IDEAL 2021, Proceedings of the 22nd International Conference, IDEAL 2021, Manchester, UK, 25–27 November 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 333–342. [Google Scholar] [CrossRef]
- Chadaga, K.; Prabhu, S.; Sampathila, N.; Chadaga, R. A machine learning and explainable artificial intelligence approach for predicting the efficacy of hematopoietic stem cell transplant in pediatric patients. Healthc. Anal. 2023, 3, 100170. [Google Scholar] [CrossRef]
- Raihan, M.J.; Khan, M.A.; Kee, S.H.; Nahid, A.A. Detection of the chronic kidney disease using XGBoost classifier and explaining the influence of the attributes on the model using SHAP. Sci. Rep. 2023, 13, 6263. [Google Scholar] [CrossRef]
- Bhandari, M.; Yogarajah, P.; Kavitha, M.S.; Condell, J. Exploring the Capabilities of a Lightweight CNN Model in Accurately Identifying Renal Abnormalities: Cysts, Stones, and Tumors, Using LIME and SHAP. Appl. Sci. 2023, 13, 3125. [Google Scholar] [CrossRef]
- Chadaga, K.; Prabhu, S.; Bhat, V.; Sampathila, N.; Umakanth, S.; Chadaga, R. A Decision Support System for Diagnosis of COVID-19 from Non-COVID-19 Influenza-like Illness Using Explainable Artificial Intelligence. Bioengineering 2023, 10, 439. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Hussain, I.; Rahman, M.M.; Park, S.J.; Hossain, M.A. Explainable Artificial Intelligence Model for Stroke Prediction Using EEG Signal. Sensors 2022, 22, 9859. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, S.; Chu, C.H.; Grad, R.; Karanofsky, M.; Arsenault, M.; Ronquillo, C.E.; Vedel, I.; McGilton, K.; Wilchesky, M. Explainable machine learning model to predict COVID-19 severity among older adults in the province of Quebec. Ann. Fam. Med. 2023, 21, 3619. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]
- Mokhtari, K.E.; Higdon, B.P.; Başar, A. Interpreting financial time series with SHAP values. In Proceedings of the 29th Annual International Conference on Computer Science and Software Engineering, Markham, ON, Canada, 4–6 November 2019; pp. 166–172. [Google Scholar]
- Zafar, M.R.; Khan, N. Deterministic local interpretable model-agnostic explanations for stable explainability. Mach. Learn. Knowl. Extr. 2021, 3, 525–541. [Google Scholar] [CrossRef]
- Kumarakulasinghe, N.B.; Blomberg, T.; Liu, J.; Leao, A.S.; Papapetrou, P. Evaluating local interpretable model-agnostic explanations on clinical machine learning classification models. In Proceedings of the 2020 IEEE 33rd International Symposium on Computer-Based Medical Systems (CBMS), IEEE, Rochester, MN, USA, 28–30 July 2020; pp. 7–12. [Google Scholar] [CrossRef]
- Riyantoko, P.A.; Diyasa, I.G. “FQAM” Feyn-QLattice Automation Modelling: Python Module of Machine Learning for Data Classification in Water Potability. In Proceedings of the 2021 International Conference on Informatics, Multimedia, Cyber and Information System (ICIMCIS), IEEE, Virtual, 28–29 October 2021; pp. 135–141. [Google Scholar] [CrossRef]
- Purwono, P.; Ma’arif, A.; Negara, I.M.; Rahmaniar, W.; Rahmawan, J. Linkage Detection of Features that Cause Stroke using Feyn Qlattice Machine Learning Model. J. Ilm. Tek. Elektro Komput. Inform. 2021, 7, 423. [Google Scholar] [CrossRef]
- Kawakura, S.; Hirafuji, M.; Ninomiya, S.; Shibasaki, R. Adaptations of Explainable Artificial Intelligence (XAI) to Agricultural Data Models with ELI5, PDPbox, and Skater using Diverse Agricultural Worker Data. Eur. J. Artif. Intell. Mach. Learn. 2022, 1, 27–34. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-precision model-agnostic explanations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orlean, LA, USA, 2–3 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Gallagher, R.J.; Reing, K.; Kale, D.; Ver Steeg, G. Anchored correlation explanation: Topic modeling with minimal domain knowledge. Trans. Assoc. Comput. Linguist. 2017, 5, 529–542. [Google Scholar] [CrossRef] [Green Version]
- Abedi, V.; Khan, A.; Chaudhary, D.; Misra, D.; Avula, V.; Mathrawala, D.; Kraus, C.; Marshall, K.A.; Chaudhary, N.; Li, X.; et al. Using artificial intelligence for improving stroke diagnosis in emergency departments: A practical framework. Ther. Adv. Neurol. Disord. 2020, 13, 1756286420938962. [Google Scholar] [CrossRef] [PubMed]
- Sharma, C.; Sharma, S.; Kumar, M.; Sodhi, A. Early Stroke Prediction Using Machine Learning. In Proceedings of the 2022 International Conference on Decision Aid Sciences and Applications (DASA), IEEE, Chiangrai, Thailand, 23–25 March 2022; pp. 890–894. [Google Scholar] [CrossRef]
- Al-Zubaidi, H.; Dweik, M.; Al-Mousa, A. Stroke prediction using machine learning classification methods. In Proceedings of the 2022 International Arab Conference on Information Technology (ACIT), IEEE, Abu Dhabi, United Arab Emirates, 22–24 November 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Gupta, S.; Raheja, S. Stroke Prediction using Machine Learning Methods. In Proceedings of the 2022 12th International Conference on Cloud Computing, Data Science & Engineering (Confluence), IEEE, Virtual, 27–28 January 2022; pp. 553–558. [Google Scholar] [CrossRef]







| Attribute Number | Attribute Name Mentioned in the Data File | Attribute Name | Description of the Attribute |
|---|---|---|---|
| 1 | id | Id | Unique identifier number for each patient |
| 2 | gender | Gender | Female, Male, Other |
| 3 | age | Age (years) | Patient’s age |
| 4 | hypertension | Hypertension (0/1) | If patient has hypertension (1) or no hypertension (0) |
| 5 | heart_disease | Heart disease (0/1) | If patient has any heart disease (1) or no heart disease (0) |
| 6 | ever_married | Yes-married No-not married | Patient’s marital status |
| 7 | work_type | Work type | If the patient is a child or has a government job, if they have never worked, if they work in a private organization, or if they are self-employed |
| 8 | Residence_type | Residence type | If the patient lives in urban residential area or rural residential area |
| 9 | avg_glucose_level | Average glucose level | Average glucose level present in the blood |
| 10 | bmi | BMI | Body mass index of the patient |
| 11 | smoking_status | Smoking status | If the patient formerly smoked, if they have never smoked, if they smoke or Unknown (information is unavailable) |
| 12 | stroke | 0-no stroke 1-had stroke | If the patient had stroke (1) or did not have stoke (0) |
| Methods Used | Features |
|---|---|
| Mutual Information | ‘age’, ‘heart_disease_0’, ‘smoking_status_Unknown’, ‘bmi’, ‘heart_disease_1’, ‘smoking_status_formerly smoked’, ‘gender_Male’, ‘hypertension_0’, ‘hypertension_1’, ‘Residence_type_Rural’. |
| Pearson’s Correlation | ‘age’, ‘heart_disease_1’, ‘heart_disease_0’, ‘avg_glucose_level’, ‘hypertension_1’, ‘hypertension_0’, ‘smoking_status_formerly smoked’, ‘smoking_status_Unknown’, ‘bmi’, ‘Residence_type_Rural’. |
| Particle swarm optimization | ‘age’, ‘heart_disease_0’, ‘heart_disease_1’, ‘hypertension_0’, ‘hypertension_1’, ‘gender_Male’, ‘gender_Female’, ‘gender_Other’, ‘bmi’, ‘Residence_type_Rural’, ‘Residence_type_Urban’. |
| Harris Hawks algorithm | ‘age’, ‘heart_disease_0’, ‘heart_disease_1’, ‘gender_Male’, ‘gender_Female’, ‘gender_Other’, ‘bmi’, ‘smoking_status_Unknown’, ‘smoking_status_formerly smoked’, ‘smoking_status_never smoked’, ‘smoking_status_smokes’. |
| Pearson’s Correlation | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Accuracy | Precision | Recall | F1-Score | AUC | Log Loss | Hamming Loss | Jaccord Score | MCC |
| Random Forest | 0.92 | 0.90 | 0.95 | 0.93 | 0.98 | 2.628 | 0.076 | 0.863 | 0.849 |
| Logistic Regression | 0.83 | 0.80 | 0.88 | 0.84 | 0.90 | 5.753 | 0.166 | 0.728 | 0.669 |
| Decision Tree | 0.89 | 0.89 | 0.90 | 0.89 | 0.93 | 3.746 | 0.108 | 0.806 | 0.783 |
| KNN | 0.92 | 0.89 | 0.95 | 0.92 | 0.92 | 2.752 | 0.079 | 0.857 | 0.842 |
| SVM- Linear kernal | 0.83 | 0.80 | 0.90 | 0.84 | 0.90 | 5.789 | 0.167 | 0.729 | 0.670 |
| SVM- Sigmoidal kernal | 0.59 | 0.59 | 0.59 | 0.59 | 0.71 | 14.170 | 0.410 | 0.420 | 0.179 |
| Stack 1 | 0.92 | 0.90 | 0.96 | 0.92 | 0.98 | 2.716 | 0.078 | 0.859 | 0.844 |
| AdaBoost | 0.90 | 0.89 | 0.92 | 0.90 | 0.97 | 3.445 | 0.099 | 0.822 | 0.800 |
| CatBoost | 0.85 | 0.81 | 0.92 | 0.86 | 0.93 | 5.274 | 0.152 | 0.751 | 0.700 |
| LGBM | 0.95 | 0.96 | 0.94 | 0.95 | 0.99 | 1.775 | 0.051 | 0.901 | 0.897 |
| XGB | 0.95 | 0.95 | 0.95 | 0.95 | 0.99 | 1.846 | 0.053 | 0.899 | 0.893 |
| Stack 2 | 0.95 | 0.95 | 0.95 | 0.95 | 0.99 | 1.722 | 0.049 | 0.905 | 0.900 |
| Final Stack | 0.94 | 0.91 | 0.96 | 0.94 | 0.99 | 2.219 | 0.064 | 0.883 | 0.872 |
| Mutual information | |||||||||
| Model | Accuracy | Precision | Recall | F1-Score | AUC | Log Loss | Hamming Loss | Jaccord score | MCC |
| Random Forest | 0.94 | 0.92 | 0.96 | 0.94 | 0.98 | 2.130 | 0.061 | 0.887 | 0.877 |
| Logistic Regression | 0.83 | 0.80 | 0.89 | 0.84 | 0.89 | 5.735 | 0.166 | 0.729 | 0.671 |
| Decision Tree | 0.88 | 0.88 | 0.89 | 0.89 | 0.92 | 3.995 | 0.115 | 0.795 | 0.768 |
| KNN | 0.94 | 0.91 | 0.97 | 0.94 | 0.94 | 2.095 | 0.060 | 0.890 | 0.880 |
| SVM- Linear kernal | 0.83 | 0.80 | 0.89 | 0.84 | 0.89 | 5.948 | 0.172 | 0.721 | 0.659 |
| SVM- Sigmoidal kernal | 0.59 | 0.60 | 0.56 | 0.58 | 0.67 | 14.259 | 0.412 | 0.407 | 0.174 |
| Stack 1 | 0.94 | 0.91 | 0.97 | 0.94 | 0.99 | 2.077 | 0.060 | 0.890 | 0.881 |
| AdaBoost | 0.90 | 0.89 | 0.92 | 0.90 | 0.97 | 3.374 | 0.097 | 0.825 | 0.804 |
| CatBoost | 0.84 | 0.80 | 0.91 | 0.85 | 0.93 | 5.522 | 0.159 | 0.740 | 0.685 |
| LGBM | 0.96 | 0.96 | 0.95 | 0.96 | 0.99 | 1.527 | 0.044 | 0.915 | 0.911 |
| XGB | 0.95 | 0.95 | 0.95 | 0.95 | 0.99 | 1.687 | 0.048 | 0.907 | 0.902 |
| Stack 2 | 0.96 | 0.96 | 0.96 | 0.96 | 0.99 | 1.402 | 0.040 | 0.922 | 0.918 |
| Final Stack | 0.95 | 0.93 | 0.97 | 0.95 | 0.99 | 1.740 | 0.050 | 0.906 | 0.900 |
| Random Forest | 0.94 | 0.92 | 0.97 | 0.94 | 0.98 | 2.059 | 0.059 | 0.890 | 0.881 |
| Logistic Regression | 0.83 | 0.81 | 0.87 | 0.84 | 0.91 | 5.771 | 0.167 | 0.725 | 0.667 |
| Decision Tree | 0.91 | 0.91 | 0.91 | 0.91 | 0.95 | 3.125 | 0.090 | 0.834 | 0.819 |
| KNN | 0.92 | 0.88 | 0.97 | 0.92 | 0.95 | 2.823 | 0.081 | 0.856 | 0.840 |
| SVM- Linear kernal | 0.83 | 0.81 | 0.87 | 0.84 | 0.91 | 5.913 | 0.171 | 0.718 | 0.659 |
| SVM- Sigmoidal kernal | 0.56 | 0.57 | 0.56 | 0.56 | 0.7 | 15.147 | 0.438 | 0.391 | 0.122 |
| Stack 1 | 0.94 | 0.93 | 0.95 | 0.94 | 0.98 | 2.166 | 0.062 | 0.884 | 0.874 |
| AdaBoost | 0.90 | 0.88 | 0.94 | 0.91 | 0.97 | 3.338 | 0.096 | 0.830 | 0.808 |
| CatBoost | 0.87 | 0.83 | 0.94 | 0.88 | 0.94 | 4.510 | 0.130 | 0.783 | 0.745 |
| LGBM | 0.95 | 0.95 | 0.95 | 0.95 | 0.99 | 1.811 | 0.052 | 0.900 | 0.895 |
| XGB | 0.95 | 0.94 | 0.96 | 0.95 | 0.99 | 1.740 | 0.050 | 0.905 | 0.899 |
| Stack 2 | 0.95 | 0.95 | 0.95 | 0.95 | 0.99 | 1.775 | 0.051 | 0.903 | 0.897 |
| Final Stack | 0.94 | 0.93 | 0.95 | 0.94 | 0.99 | 2.059 | 0.059 | 0.889 | 0.880 |
| Particle swarm optimization | |||||||||
| Model | Accuracy | Precision | Recall | F1-Score | AUC | Log Loss | Hamming Loss | Jaccord score | MCC |
| Random Forest | 0.93 | 0.91 | 0.95 | 0.93 | 0.98 | 2.539 | 0.073 | 0.866 | 0.853 |
| Logistic Regression | 0.83 | 0.80 | 0.88 | 0.84 | 0.89 | 5.806 | 0.168 | 0.725 | 0.666 |
| Decision Tree | 0.91 | 0.92 | 0.90 | 0.91 | 0.94 | 3.107 | 0.089 | 0.834 | 0.820 |
| KNN | 0.91 | 0.88 | 0.96 | 0.92 | 0.94 | 3.001 | 0.086 | 0.847 | 0.829 |
| SVM- Linear kernal | 0.82 | 0.80 | 0.86 | 0.83 | 0.89 | 6.162 | 0.178 | 0.709 | 0.645 |
| SVM- Sigmoidal kernal | 0.57 | 0.58 | 0.55 | 0.57 | 0.66 | 14.703 | 0.425 | 0.393 | 0.149 |
| Stack 1 | 0.93 | 0.94 | 0.93 | 0.93 | 0.98 | 2.273 | 0.065 | 0.877 | 0.868 |
| AdaBoost | 0.89 | 0.86 | 0.93 | 0.89 | 0.96 | 3.817 | 0.110 | 0.809 | 0.781 |
| CatBoost | 0.86 | 0.83 | 0.92 | 0.87 | 0.93 | 4.723 | 0.136 | 0.773 | 0.731 |
| LGBM | 0.95 | 0.96 | 0.94 | 0.95 | 0.99 | 1.740 | 0.050 | 0.904 | 0.899 |
| XGB | 0.95 | 0.94 | 0.96 | 0.95 | 0.99 | 1.846 | 0.053 | 0.900 | 0.893 |
| Stack 2 | 0.95 | 0.96 | 0.94 | 0.95 | 0.99 | 1.651 | 0.047 | 0.908 | 0.904 |
| Final Stack | 0.94 | 0.94 | 0.94 | 0.94 | 0.99 | 2.201 | 0.063 | 0.881 | 0.872 |
| Sl.no. | Algorithm | Mutual Information Hyperparameters | Pearson’s Correlation Hyperparameters | Particle Swarm optimization | Harris Hawks Algorithm |
|---|---|---|---|---|---|
| 1. | Random Forest (RF) | {“bootstrap” is True, “n_estimators” is 1000, “max_depth” is 90, “max_features” is 2, “min_samples_split” is 8, and “min_samples_leaf” is 3} | {“bootstrap” is True, “n_estimators” is 1000, “max_depth” is 100, “max_features” is 2, “min_samples_split” is 8, and “min_samples_leaf” is 3} | {“bootstrap” is True, “n_estimators” is 300, “max_depth” is 80, “max_features” is 3, “min_samples_split” is 8, and “min_samples_leaf” is 3} | {“bootstrap” is True, “n_estimators” is 1000, “max_depth” is 110, “max_features” is 3, “min_samples_split” is 8, and “min_samples_leaf” is 3} |
| 2. | Logistic Regression (LR) | {‘Penalty’: l2 and ‘C’:1} | {‘Penalty’: l2 and ‘C’:1} | {‘Penalty’: l2 and ‘C’:1} | {‘Penalty’: l2 and ‘C’:1} |
| 3. | Decision tree (DT) | {‘criteria’: ‘entropy’,’splitter’: ‘best’,’max_depth’: 70, ‘max_features’: ‘log2’ 10 for “min_samples_split,” 1 for “min_samples_leaf.”} | {‘criteria’: ‘entropy’,’splitter’: ‘best’,’max_depth’: 20, ‘max_features’: ‘log2’ 10 for “min_samples_split,” 1 for “min_samples_leaf.”} | {‘criteria’: ‘gini’,’splitter’: ‘best’,’max_depth’: 20, ‘max_features’: ‘sqrt’ 10 for “min_samples_split,” 1 for “min_samples_leaf.”} | {‘criteria’: ‘entropy’,’splitter’: ‘best’,’max_depth’: 20, ‘max_features’: ‘log2’ 10 for “min_samples_split,” 1 for “min_samples_leaf.”} |
| 4. | K Nearest Neighbours (KNN) | {“n_neighbors” = 1} | {“n_neighbors” = 1} | {“n_neighbors” = 3} | {“n_neighbors” = 3} |
| 5. | SVM—Linear kernal | (Kernel: “linear,” Probability: “True”) | (Kernel: “linear,” Probability: “True”) | (Kernel: “linear,” Probability: “True”) | (Kernel: “linear,” Probability: “True”) |
| 6. | SVM—Sigmoidal kernal | (Kernel: “Sigmoid,” Probability: True) | (Kernel: “Sigmoid,” Probability: True) | (Kernel: “Sigmoid,” Probability: True) | (Kernel: “Sigmoid,” Probability: True) |
| 7. | AdaBoost | {‘Learning_rate’ = 1.0, ‘n_estimators’ = 1000} | {‘Learning_rate’ = 1.0, ‘n_estimators’ = 1000} | {‘Learning_rate’ = 1.0, ‘n_estimators’ = 1000} | {‘Learning_rate’ = 1.0, ‘n_estimators’ = 1000} |
| 8. | CatBoost | {‘border_count’: 32, The learning rate is 0.03 “depth”: 3, “l2_leaf_reg”: 5, ‘iterations’: 250} | {‘border_count’: 32, The learning rate is 0.03 depth: 3, and leaf registration: 1. ‘iterations’: 250} | {‘border_count’: 32, The learning rate is 0.03 “depth”: 3, “l2_leaf_reg”: 10, ‘iterations’: 250} | {‘border_count’: 32, The learning rate is 0.03 “depth”: 3, “l2_leaf_reg”: 5, ‘iterations’: 250} |
| 9. | LGBM | {‘lambda_l1’: 0, ‘reg_alpha’: 0.1, ‘lambda_l2’: 0, ‘num_leaves’: 127, ‘min_data_in_leaf’: 30} | {‘lambda_l1’: 0, ‘reg_alpha’: 0.1, ‘lambda_l2’: 0, ‘num_leaves’: 127, ‘min_data_in_leaf’: 30} | {‘lambda_l1’: 0, ‘reg_alpha’: 0.1, ‘lambda_l2’: 0, ‘num_leaves’: 127, ‘min_data_in_leaf’: 30} | {‘lambda_l1’: 0, ‘reg_alpha’: 0.1, ‘lambda_l2’: 0, ‘num_leaves’: 127, ‘min_data_in_leaf’: 30} |
| 10. | XGB | {“colsample_bytree” = 0.4, “min_child_weight” = 1, “gamma” = 0.1, and “max depth” = 8, Learning rate: 0.15} | {“colsample_bytree” = 0.4, “min_child_weight” = 1, “gamma” = 0.1, and “max depth” = 8, Learning rate: 0.15} | {“colsample_bytree” = 0.4, “min_child_weight” = 1, “gamma” = 0.2, and “max depth” = 8, Learning rate: 0.15} | {“colsample_bytree” = 0.4, “min_child_weight” = 1, “gamma” = 0.2, and “max depth” = 8, Learning rate: 0.15} |
| 11. | Stack 1 | {average_probas: False, meta_classifier: logistic regression, use_probas: True} | {average_probas: False, meta_classifier: logistic regression, use_probas: True} | {average_probas: False, meta_classifier: logistic regression, use_probas: True} | {average_probas: False, meta_classifier: logistic regression, use_probas: True} |
| 12. | Stack 2 | {average_probas: False, max_iter: 9000, use_probas: True, meta-classifier: logistic regression} | {average_probas: False, max_iter: 9000, use_probas: True, meta-classifier: logistic regression} | {average_probas: False, max_iter: 9000, use_probas: True, meta-classifier: logistic regression} | {average_probas: False, max_iter: 9000, use_probas: True, meta-classifier: logistic regression} |
| 13. | Final Stack | {max_iter = 9000, average_probas: False, meta_classifier = logistic regression, use_probas: True} | {max_iter = 9000, average_probas: False, meta_classifier = logistic regression, use_probas: True} | {max_iter = 9000, average_probas: False, meta_classifier = logistic regression, use_probas: True} | {max_iter = 9000, average_probas: False, meta_classifier = logistic regression, use_probas: True} |
| Mutual information | ||||
|---|---|---|---|---|
| Instance | Patient Prediction | Anchor Condition | Precision | Coverage |
| 1 | Non—stroke | age <= 0.77 AND smoking_status_never smoked > 0.00 | 0.89 | 0.17 |
| 2 | Non—stroke | age <= 0.77 AND Residence_type_Rural <= 0.00 | 0.86 | 0.25 |
| 3 | Non—stroke | 0.77 < age <= 0.91 AND avg_glucose_level > 0.55 | 0.77 | 0.18 |
| 4 | Non—stroke | age <= 0.91 AND 0.26 < bmi <= 0.29 | 0.72 | 0.34 |
| 5 | Non—stroke | age <= 0.77 AND bmi <= 0.26 | 0.93 | 0.16 |
| 6 | Stroke | age > 0.52 AND heart_disease_1 > 0.00 | 0.83 | 0.14 |
| 7 | Stroke | 0.77 < age <= 0.91 AND smoking_status_formerly smoked > 0.00 | 0.69 | 0.16 |
| 8 | Stroke | age > 0.77 AND heart_disease_1 > 0.00 | 0.73 | 0.11 |
| 9 | Stroke | age > 0.52 AND hypertension_1 > 0.00 | 0.77 | 0.20 |
| 10 | Stroke | age > 0.91 AND heart_disease_1 > 0.00 | 0.83 | 0.11 |
| Pearson’s correlation | ||||
| Instance | Patient Prediction | Anchor Condition | Precision | Coverage |
| 1 | Non—stroke | age <= 0.77 AND 0.30 < avg_glucose_level <= 0.57 | 0.87 | 0.42 |
| 2 | Non—stroke | age <= 0.77 AND smoking_status_Unknown > 0.35 | 0.90 | 0.15 |
| 3 | Non—stroke | age <= 0.77 AND avg_glucose_level <= 0.57 | 0.88 | 0.43 |
| 4 | Non—stroke | age > 0.77 AND avg_glucose_level > 0.57 | 0.78 | 0.18 |
| 5 | Non—stroke | age <= 0.77 AND bmi <= 0.26 | 0.97 | 0.15 |
| 6 | Stroke | 0.77 < age <= 0.92 AND 0.37 < avg_glucose_level <= 0.57 | 0.72 | 0.29 |
| 7 | Stroke | age > 0.52 AND avg_glucose_level > 0.37 | 0.67 | 0.42 |
| 8 | Stroke | age > 0.77 AND avg_glucose_level > 0.57 | 0.80 | 0.18 |
| 9 | Stroke | age > 0.92 AND heart_disease_1 > 0.00 | 0.76 | 0.06 |
| 10 | Stroke | age > 0.92 AND smoking_status_Unknown <= 0.00 | 0.68 | 0.20 |
| Particle swarm optimization | ||||
| Instance | Patient Prediction | Anchor Condition | Precision | Coverage |
| 1 | Non—stroke | age <= 0.77 ANDheart_disease_1 <= 0.00 | 0.88 | 0.48 |
| 2 | Non—stroke | age <= 0.77 ANDbmi <= 0.33 | 0.87 | 0.34 |
| 3 | Non—stroke | age <= 0.77 ANDbmi <= 0.33 | 0.91 | 0.35 |
| 4 | Non—stroke | age <= 0.77 ANDheart_disease_1 <= 0.00 | 0.87 | 0.48 |
| 5 | Non—stroke | age <= 0.93 ANDbmi <= 0.29 | 0.73 | 0.35 |
| 6 | Stroke | age > 0.77 AND0.26 < bmi <= 0.33 | 0.65 | 0.41 |
| 7 | Stroke | age > 0.93 ANDhypertension_1 > 0.00 | 0.81 | 0.16 |
| 8 | Stroke | 0.77 < age <= 0.93 AND0.26 < bmi <= 0.29 | 0.64 | 0.40 |
| 9 | Stroke | age > 0.52 ANDbmi > 0.26 | 0.61 | 0.62 |
| 10 | Stroke | age > 0.77 AND0.26 < bmi <= 0.29 | 0.65 | 0.41 |
| Harris Hawks algorithm | ||||
| Instance | Patient Prediction | Anchor Condition | Precision | Coverage |
| 1 | Non—stroke | age <= 0.77 ANDsmoking_status_formerly smoked <= 0.00 | 0.89 | 0.41 |
| 2 | Non—stroke | age <= 0.77 ANDbmi > 0.33 | 0.89 | 0.15 |
| 3 | Non—stroke | age > 0.52 ANDsmoking_status_Unknown <= 0.00 | 0.60 | 0.60 |
| 4 | Non—stroke | 0.77 < age <= 0.94 AND0.26 < bmi <= 0.29 | 0.63 | 0.40 |
| 5 | Non—stroke | age <= 0.94 AND0.00 < smoking_status_never smoked <= 1.00 | 0.82 | 0.23 |
| 6 | Stroke | age > 0.94 ANDheart_disease_1 > 0.00 | 0.75 | 0.12 |
| 7 | Stroke | 0.77 < age <= 0.94 ANDheart_disease_1 > 0.00 | 0.76 | 0.11 |
| 8 | Stroke | age <= 0.77 ANDbmi <= 0.26 | 1.00 | 0.15 |
| 9 | Stroke | age > 0.94 AND0.00 < smoking_status_never smoked <= 1.00 | 0.73 | 0.14 |
| 10 | Stroke | age > 0.77 ANDsmoking_status_Unknown <= 0.00 | 0.62 | 0.41 |
| Sl. No. | Model | Classifiers | Accuracy | Explainable AI Techniques |
|---|---|---|---|---|
| 1. | [62] | Random forest, Decision tree and Naive bayes algorithms | 98.94% | No |
| 2. | [63] | SVM, Random forest, Decision tree, Logistic regression and voting classifier | 94.7% | No |
| 3. | [64] | Logistic regression, naive bayes, KNN, decision trees, adaboost, xgboost, and random forests | 97% | No |
| 4. | Our proposed model | Decision trees, random forests, logistic regression, SVM (Linear, sigmoidal), KNN, AdaBoost, CatBoost, LGBM, XGBoost and stacking models | 96% | LIME, Qlattice, SHAP, ELI5, Anchor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
S, S.; Chadaga, K.; Sampathila, N.; Prabhu, S.; Chadaga, R.; S, S.K. Multiple Explainable Approaches to Predict the Risk of Stroke Using Artificial Intelligence. Information 2023, 14, 435. https://doi.org/10.3390/info14080435
S S, Chadaga K, Sampathila N, Prabhu S, Chadaga R, S SK. Multiple Explainable Approaches to Predict the Risk of Stroke Using Artificial Intelligence. Information. 2023; 14(8):435. https://doi.org/10.3390/info14080435
Chicago/Turabian StyleS, Susmita, Krishnaraj Chadaga, Niranjana Sampathila, Srikanth Prabhu, Rajagopala Chadaga, and Swathi Katta S. 2023. "Multiple Explainable Approaches to Predict the Risk of Stroke Using Artificial Intelligence" Information 14, no. 8: 435. https://doi.org/10.3390/info14080435
APA StyleS, S., Chadaga, K., Sampathila, N., Prabhu, S., Chadaga, R., & S, S. K. (2023). Multiple Explainable Approaches to Predict the Risk of Stroke Using Artificial Intelligence. Information, 14(8), 435. https://doi.org/10.3390/info14080435









