Gaussian Kernel Approximations Require Only Bit-Shifts

Abstract

An approach to approximate the 2D Gaussian filter for all possible kernel sizes based on the binary optimization technique is introduced. The approximate filter coefficients are designed as negative powers of two, allowing hardware implementation with remarkable savings in the chip area. The proposed approximate filters were evaluated and compared with competing methods using both similarity analysis and edge detection applications. The proposed method and the competing works for masks of size $3\times 3$, $5\times 5$, and $7\times 7$ were implemented in a Xilinx Artix-7 FPGA. The proposed method showed up to a 60.0% reduction in DSP usage and a 75.0% increase in the maximum operating frequency when compared with state-of-art methods for the $7\times 7$ kernel size case and a 48.8% reduction in the dynamic power normalized by the maximum operating frequency.

1. Introduction

As the building block of many computer vision algorithms [1,2], the 2D Gaussian filter is a fundamental tool in image processing. It is widely employed for noise removal and edge detection [3] in the Sobel detector and the Canny algorithm [4,5]. Gaussian filters are also relevant for image classification [6], texture recognition [7,8,9], 3D model retrieval [10], satellite and aerial imaging and medical imaging [11,12,13], and in super-resolution problems [14,15], such as in the context of surveillance [16]. Further recent applications can be seen in the context of biomedical image processing for health monitoring and clinical diagnoses [17]; magnetic resonance imagery [18]; identification of geological faults [19]; shape-from-focus and depth estimation [20]; and image reconstruction [21].

However, 2D spatial filtering is prone to exhibit a significant multiplicative complexity, often realized in floating-point representation in software implementations [1,4]. Because of the ever-increasing demand for high resolution images and videos, the computational complexity increase is substantial [22,23]. At the same time, economizing power and resource consumption is of utmost importance in many scenarios such as consumer electronics [24,25], augmeted reality and robotics [26], space exploration [27], and biomedical device technology [28].

In [29], low-complexity approximate Gaussian kernels were proposed for fixed-point architectures. In the same vein, Garg and Sharma [30] proposed another low-complexity approximation for 2D Gaussian filters. In [31], Cabello et al. [31] derived a low-complexity approximate 2D Gaussian filter with a root mean square error (MSE) below 5%. Systems implemented in hardware employing approximate low-complexity 2D Gaussian filtering would have the benefit of the power savings, resource consumption reduction, and improved hardware metrics resulting from the application of the proposed method [22,23,24,25,26,27,28]. Generally, approximation methods consist of mapping the exact coefficients into fixed-point representation at different precision levels. Such approaches pave the way for hardware implementation requiring no multipliers. Nevertheless, a large number of additions and bit-shifting operations—implied by the fixed-point representation—are still required.

In view of the above context, this work has multiple goals. In particular, we aim to

• Provide a method for obtaining 2D Gaussian filter approximations for any odd integer kernel size, based on binary integer programming methods;
• Derive a mathematical formalism capable of suitably approximating each Gaussian kernel filter coefficient to a single negative power of two, which requires only one bit-shifting operation to be implemented in hardware;
• Demonstrate the suitability of the approximate kernels in the context of image filtering;
• Analyze the complexity and performance of the proposed method according to its hardware realization compared to competing methods archived in the literature.

In Section 2, we review the mathematical background related to the Gaussian kernel, propose the design criteria for the sought approximate kernels, and introduce the mathematical formalism of an optimization problem that captures the adopted criteria. Section 3 provides the numerical results of the application of the proposed methods to particular filter sizes. Additionally, a computational complexity analysis of the obtained approximations was derived; and an experimental analysis in the context of fundamental image processing filtering operations was also performed. Section 4 furnishes the implementation details of the VLSI realization of the derived approximate filters along with performance analyses in terms of hardware consumption and time-related measurements. Section 5 provides a general discussion on the methods and results contained in this work. The conclusions are in Section 6.

2. Approximate Gaussian Kernel

2.1. Definitions and Design Criteria

The exact 2D Gaussian filter consists of an $N\times N$ matrix, whose elements are given by the sampled zero-mean 2D Gaussian distribution with variance ${\sigma }^2$:

$$\begin{array}{c}\hfill g[m,n]={\displaystyle \frac{1}{S}}·{\displaystyle \frac{1}{2\pi {\sigma }^2}}·exp\left\{{\displaystyle \frac{-(m^2+n^2)}{2{\sigma }^2}}\right\},-{\displaystyle \frac{N-1}{2}}\le m,n\le {\displaystyle \frac{N-1}{2}},\end{array}$$

(1)

where $N>1$ and odd; quantities m and n are, respectively, the vertical and horizontal coordinate values of the kernel relative to the matrix central element; and S is a normalizing constant to ensure that the kernel coefficients sum to one, so that pixel intensity is preserved and bias is prevented [3]. In this work, we consider filters with unitary variance (${\sigma }^2=1$), which comprise a commonly employed class of Gaussian filters [29,30].

In general, a good approximation for digital filters [32,33] should be capable of (i) demanding low computational complexity and (ii) retaining the meaningful mathematical properties of the exact filter [34]. For this, we adopt the following design requirements for the sought 2D Gaussian filter approximation:

Req. 1.

The approximate filter coefficients must be trivial multiplicands [35];

Req. 2.

The arithmetic operation counts (number of bit-shifting operations and additions) for the approximate filter coefficient representation must be minimal;

Req. 3.

The distance between the exact and approximate filters must be minimized according to an energy-based measure;

Req. 4.

The resulting filter must possess unitary gain to preserve the average intensity of processed data [29];

Req. 5.

The symmetry of the exact Gaussian kernel must be transferred to its approximate counterpart.

Reqs. 1 and 2 are satisfied when the entries of the approximate filter are negative powers of two, which are trivial multiplicands and require no extra additions in the associate binary representation. Since $0<g[m,n]<1$, the approximate filter coefficients must satisfy $\widehat{g}[m,n]\in \{2^{-1},2^{-2},\dots ,2^{-K}\}$, where K is the number of bits allocated to the fractional part of the binary representation.

2.2. Optimization Framework

The design requirements discussed above must have a mathematical structure. We aim to transform the problem of finding good 2D Gaussian filter approximations into the problem of obtaining negative powers of two that optimally approximate the exact coefficients. To that end, we introduce an optimization problem that employs an $N\times N\times K$ indicator function $x[m,n,k]$, $m,n=-(N-1)/2,\dots ,-1,0,1,\dots ,(N-1)/2$, $k=1,2,\dots ,K$, specifying the particular negative power of two to be assigned for each approximate coefficient $\widehat{g}[m,n]$. Thus, we have

$$\begin{array}{c}\hfill x[m,n,k]=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\widehat{g}[m,n]=2^{-k},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(2)

To ensure that only one negative power of two is assigned to $\widehat{g}[m,n]$, the following condition must hold true:

$$\begin{array}{c}\hfill \sum _{k=1}^{K}x[m,n,k]=1,\forall m,n.\end{array}$$

(3)

Notice that the exact filter coefficients satisfy the following identity:

$$\begin{array}{c}\hfill \sum _{k=1}^{K}g[m,n]·x[m,n,k]=g[m,n]·\sum _{k=1}^{K}x[m,n,k]=g[m,n]·\left(1\right)=g[m,n].\end{array}$$

(4)

In turn, the approximate filter can also be related to the indicator function $x[m,n,k]$, according to the following format:

$$\begin{array}{c}\hfill \widehat{g}[m,n]=\sum _{k=1}^K{2}^{-k}·x[m,n,k],-{\displaystyle \frac{N-1}{2}}\le m,n\le {\displaystyle \frac{N-1}{2}}.\end{array}$$

(5)

To satisfy Req. 3, we adopt the mean square error (MSE) as the metric to be minimized, as suggested in [3]. Thus, the MSE between the exact and approximate filters can be written as

$$\begin{array}{cc}\hfill MSE(\widehat{g},g)& ={\displaystyle \frac{1}{N^2}}\sum _{m=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}\sum _{n=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}{\left(\widehat{g}[m,n]-g[m,n]\right)}^2.\hfill \end{array}$$

(6)

By invoking (4) and (5), the inner quadratic term of the above double summation can be elaborated as follows:

$$\begin{array}{cc}[\sum _{k=1}^K{2}^{-k}·x[m,n,k]\hfill & -\sum _{k=1}^{K}g[m,n]·x[m,n,k]{]}^2\hfill \end{array}$$

(7)

$$\begin{array}{cc}& ={\left[\sum _{k=1}^K(2^{-k}-g[m,n])·x[m,n,k]\right]}^2\hfill \end{array}$$

(8)

$$\begin{array}{cc}& =\underset{S_1}{\underbrace{\sum _{k=1}^K{d}^2(m,n,k)}}+\underset{S_2}{\underbrace{\sum _{k=1}^K\sum _{\begin{array}{c}j=1\\ j\ne k\end{array}}^{K}d(m,n,j)·d(m,n,k)}},\hfill \end{array}$$

(9)

where $d(m,n,k)=(2^{-k}-g[m,n])·x[m,n,k]$.

Let us examine the two summations at the right-hand side of (7), $S_1$ and $S_2$, respectively. For the single summation $S_1$, it is true that $x^2[m,n,k]=x[m,n,k]$, because $x[·,·,·]$ is an indicator function (cf. (2)). Therefore, we have

$$\begin{array}{cc}\hfill S_1\triangleq \sum _{k=1}^K{d}^2(m,n,k)& =\sum _{k=1}^K{(2^{-k}-g[m,n])}^2·x^2[m,n,k]\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & =\sum _{k=1}^K{(2^{-k}-g[m,n])}^2·x[m,n,k].\hfill \end{array}$$

(11)

As for the double summation $S_2$, we remark that $x[m,n,j]·x[m,n,k]=0$, for $j\ne k$, which is a direct consequence of (2) and (3). Thus, it follows that

$$\begin{array}{cc}\hfill S_2& \triangleq \sum _{k=1}^K\sum _{\begin{array}{c}j=1\\ j\ne k\end{array}}^{K}d(m,n,j)·d(m,n,k)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & =\sum _{k=1}^K\sum _{\begin{array}{c}j=1\\ j\ne k\end{array}}^K(2^{-j}-g[m,n])·x[m,n,j]·(2^{-k}-g[m,n])·x[m,n,k]\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & =0.\hfill \end{array}$$

(14)

By making the appropriate substitutions, applying the result back into (7), and disregarding the outer multiplicative constant in (6), we obtain the following minimization problem:

$$\begin{array}{c}\hfill min\sum _{m=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}\sum _{n=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}\sum _{k=1}^K{\left(2^{-k}-g[m,n]\right)}^2·x[m,n,k].\end{array}$$

(15)

Moreover, the quantities $x[m,n,k]$ must be subject to the constraints mathematically described below.

• Due to Req. 4, we have

  $$\begin{array}{c}\hfill \sum _{m=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}\sum _{n=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}\widehat{g}[m,n]=1.\end{array}$$

  (16)
  Therefore, the above equation can be re-cast in suitable terms for the optimization problem as the following constraint:

  $$\begin{array}{c}\hfill \sum _{m=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}\sum _{n=-{\displaystyle \frac{N-1}{2}}}^{{\displaystyle \frac{N-1}{2}}}\sum _{k=1}^K{2}^{-k}·x[m,n,k]=1.\end{array}$$

  (17)
• Req. 5 imposes the natural symmetry structure of the original exact 2D Gaussian filter to the approximate candidate solutions. Therefore, the sought optimal solution must satisfy the following condition. If

  $$\begin{array}{c}\hfill g[m_1,n_1]=g[m_2,n_2],\end{array}$$

  (18)

  then

  $$\begin{array}{c}\hfill x[m_1,n_1,k]=x[m_2,n_2,k],\end{array}$$

  (19)

  for $-{\displaystyle \frac{N-1}{2}}\le m_1,n_1,m_2,n_2\le {\displaystyle \frac{N-1}{2}}$ and $k=1,2,\dots ,K$.

In view of the considerations above, we obtain that the originally quadratic problem of minimizing the MSE in (6) was recast as an integer linear programming matching problem with $N^2·K$ variables. The problem in (15) with the above listed constraints is suitably structured to take advantage of contemporary linear programming packages dedicated to binary optimization, such as the GNU Linear Programming Kit (GLPK) [36], which employs the Hungarian algorithm [37].

3. Results and Analyses

In this section, we provide particular solutions to the discussed optimization problem, which are submitted to mathematical and empirical analyses. For the mathematical analysis, we performed a computational complexity evaluation where the arithmetic complexity costs were quantified. For the empirical analysis, we considered image processing experiments—blurring and edge detection—where standard images were submitted to the proposed approximate 2D Gaussian filters. In both analyses, we supplied comprehensive comparisons with exact and competing methods.

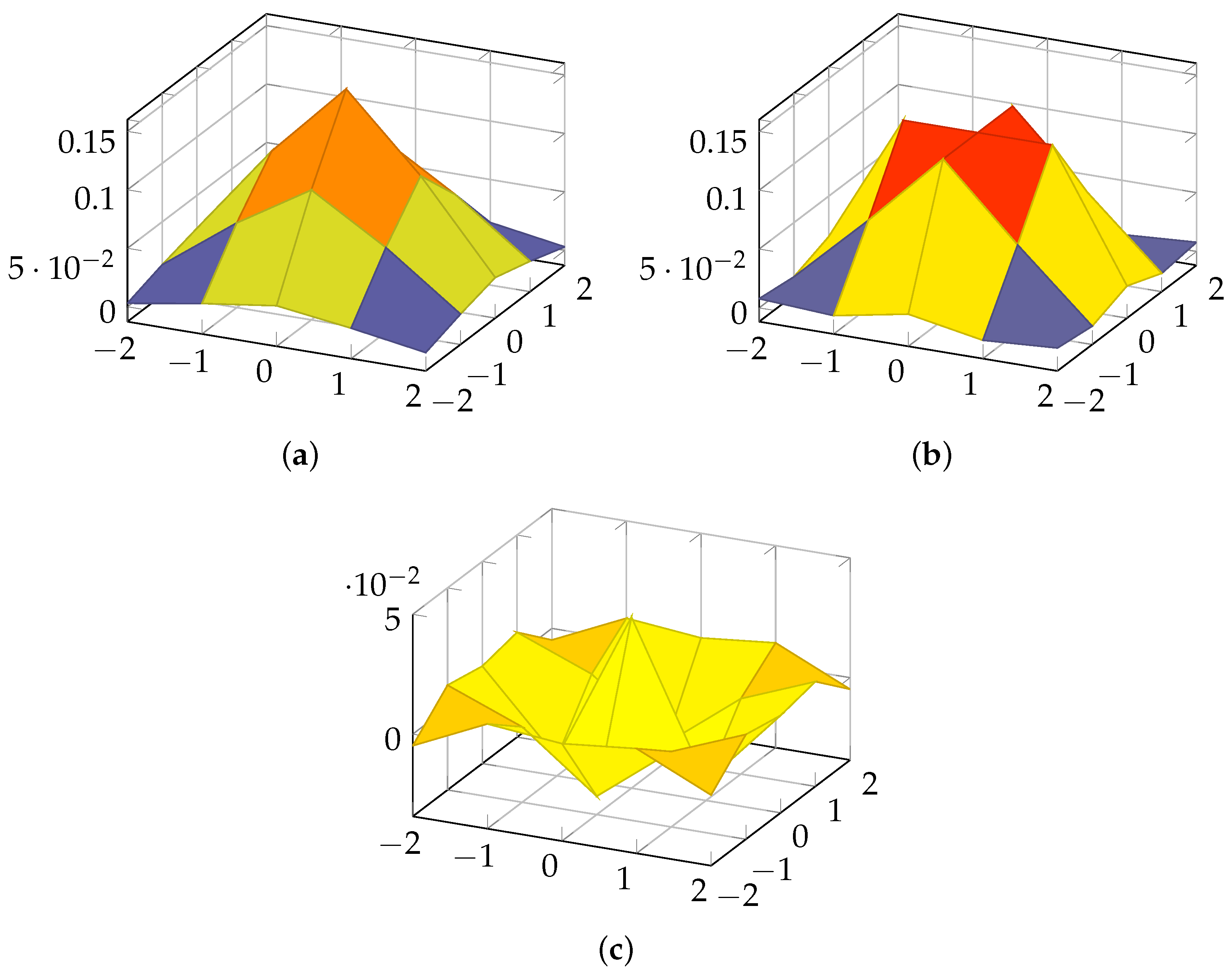
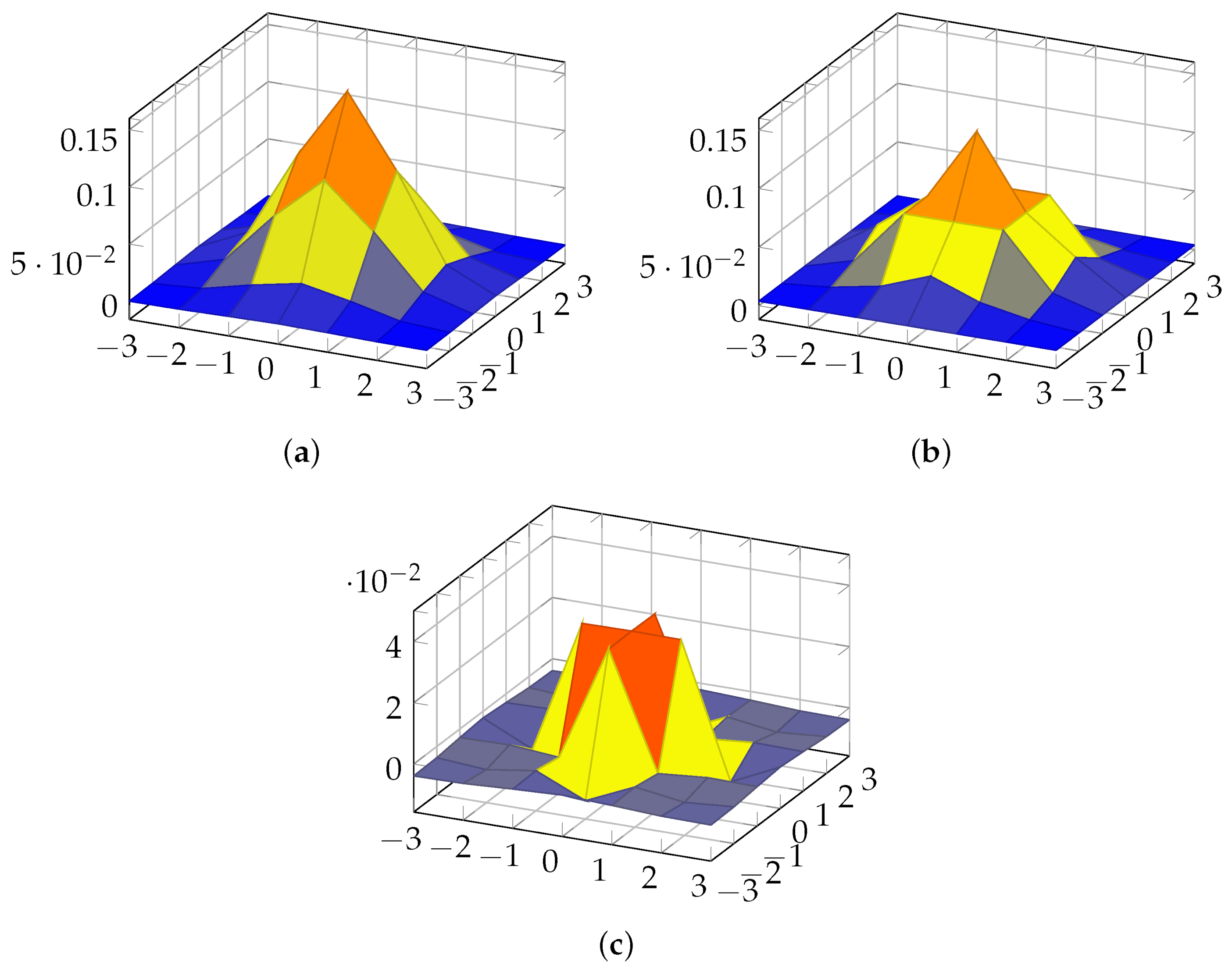
3.1. Particular Solutions

The mathematical optimization framework described in the previous section is general enough to permit the derivation of approximate filters for any variation in the design parameters, namely the number of fractional bits K and the filter size N. Thus, depending on the specific conditions required by the application context at hand, a different approximation might be obtained. In order to advance our analysis, in this paper, we selected popular values for the filter size: $N\in \{3,5,7\}$ [38,39,40,41,42].

As for the values of K, we selected 6, 8, and 15 bits. These values were adopted to allow fair comparisons with the competing designs in the literature. Another reason to select relatively small values of K, such as 6, is due to the fact that the approximation structures are more likely to benefit computing architectures with modest computational power and hardware resources. In the following, we fixed $K=8$ and varied $N\in \{3,5,7\}$. For $N=3$, we have

$$\begin{array}{c}\hfill 2^{-2}·\left[\begin{array}{ccc}{2}^{-2}& 2^{-1}& 2^{-2}\\ 2^{-1}& 1& 2^{-1}\\ 2^{-2}& 2^{-1}& 2^{-2}\end{array}\right].\end{array}$$

(20)

For instance, the $5\times 5$ approximation is given by

$$\begin{array}{c}\hfill 2^{-3}·\left[\begin{array}{ccccc}{2}^{-4}& 2^{-5}& 2^{-3}& 2^{-5}& 2^{-4}\\ 2^{-5}& 2^{-1}& 1& 2^{-1}& 2^{-5}\\ 2^{-3}& 1& 1& 1& 2^{-3}\\ 2^{-5}& 2^{-1}& 1& 2^{-1}& 2^{-5}\\ 2^{-4}& 2^{-5}& 2^{-3}& 2^{-5}& 2^{-4}\end{array}\right].\end{array}$$

(21)

Finally, for the $7\times 7$ kernel, the implied approximation is

$$\begin{array}{c}\hfill 2^{-3}·\left[\begin{array}{ccccccc}{2}^{-5}& 2^{-5}& 2^{-5}& 2^{-5}& 2^{-5}& 2^{-5}& 2^{-5}\\ 2^{-5}& 2^{-4}& 2^{-3}& 2^{-2}& 2^{-3}& 2^{-4}& 2^{-5}\\ 2^{-5}& 2^{-3}& 2^{-1}& 2^{-1}& 2^{-1}& 2^{-3}& 2^{-5}\\ 2^{-5}& 2^{-2}& 2^{-1}& 1& 2^{-1}& 2^{-2}& 2^{-5}\\ 2^{-5}& 2^{-3}& 2^{-1}& 2^{-1}& 2^{-1}& 2^{-3}& 2^{-5}\\ 2^{-5}& 2^{-4}& 2^{-3}& 2^{-2}& 2^{-3}& 2^{-4}& 2^{-5}\\ 2^{-5}& 2^{-5}& 2^{-5}& 2^{-5}& 2^{-5}& 2^{-5}& 2^{-5}\end{array}\right].\end{array}$$

(22)

The above approximate Gaussian kernels are displayed as 3D surfaces in Figure 1, Figure 2 and Figure 3. The exact Gaussian kernels are also shown for comparison.

3.2. Computational Complexity Analysis

These approximate filters were assessed in terms of the computational cost. For this, we evaluated the arithmetic complexity resulting from the application of the Gaussian kernel. The arithmetic complexity consists of counting the number of fundamental arithmetical operations required to perform a given mathematical operation [35]. The counting is chiefly independent of technological particularities and takes into consideration the employed number representation and general architecture-related aspects of computing [43]. We measured two arithmetic complexity figures: the number of multiplications (# of Multiplications) and the number of additions (# of Additions). In usual computer architectures, the cost of evaluating a multiplication is much higher than the cost of an addition operation [35], and bit-shifting operations can be virtually cost-free in comparison to multiplication or addition operations.

The assessed arithmetic complexities are displayed in

Table 1. Evaluation of arithmetic complexity.

N	Wordlength	Method	# of Multiplications	# of Additions
3	6	Exact	9	8
		Khorbotly–Hassan [29]	0	18
		Garg–Sharma [30]	0	13
		Cabello et al. [31]	0	31
		Proposed	0	8
5	8	Exact	25	24
		Khorbotly–Hassan [29]	0	66
		Garg–Sharma [30]	0	41
		Cabello et al. [31]	0	76
		Proposed	0	24
7	15	Exact	49	48
		Khorbotly–Hassan [29]	0	180
		Garg–Sharma [30]	0	77
		Cabello et al. [31]	0	103
		Proposed	0	48

and compared with the complexities of the exact filter and the competing approximations [29,30,31]. The null multiplication counts imply that the multiplications are being computed approximately by means of a sequence of bit-shifting operations, which are more efficient compared to executing the full multiplication algorithm.

Because we aim at the implementation of low-complexity 2D Gaussian filters, we used the minimal wordlength to represent the Gaussian filter coefficients, according to the number representations outlined by Garg–Sharma [30] and by Khorbotly–Hassan [29], corresponding to 6-, 8-, and 15-bit representations for the $3\times 3$, $5\times 5$, and $7\times 7$, respectively (using the Khorbotly–Hassan [29] notation, we used $(6,-8)$, $(8,-10)$, and $(15,-17)$, for masks sizes $3\times 3$, $5\times 5$, and $7\times 7$, respectively).

3.3. Image Processing Experimental Analysis

We employed the proposed approximate filters in three computational experiments based on two popular image processing contexts: (i) image blurring and (ii) edge detection. The two described blurring experiments demonstrate the usage of the discussed methods for smoothing (lowpass) spatial filtering; whereas the one edge detection experiment illustrates sharpening (highpass) spatial filtering.

For the blurring experiment, we performed relative and absolute measurements. The first blurring experiment was a relative measurement procedure. It aimed to capture the performance of the proposed method and its competitors relative to the exact method. In other words, individual approximate filtered output images were compared with the corresponding filtered output images from the exact filter. The outputs were compared with the outputs.

For the second blurring experiment, we had an absolute measurement procedure. This experiment aimed at assessing the overall system performance. The goal was to quantify the absolute performance of all methods, including the exact one, comparing the filtered output images with the unfiltered input image. The outputs were compared with the inputs.

In terms of the edge detection experiment, we show evidence of the effectiveness of the approximate methods as a preprocessing computational stage for the Sobel algorithm [3].

3.3.1. Blurring Experiment: Relative Measurements

For the image blurring experiment, forty-four 8-bit images from a public image database [44] with different sizes, including 256 × 256, 512 × 512, and 1024 × 1024, were employed. We applied the exact and approximate 2D Gaussian filters to the images in grey-level format and compared the filtered outputs from the proposed and competing methods against the filtered output from the exact filter. This approach quantified the accuracy deviation of the approximate methods relative to the exact method.

The measurements were performed according to two image quality assessment metrics: peak signal-to-noise ratio (PSNR) [45] and structural similarity index measure (SSIM) [46]. The values of both metrics were averaged over all images to reduce the variance effects [47].

Table 2. Error analysis for the relative measurement blurring experiment. Average PSNR and SSIM measurements from the filtered output images relative to the exact output images.

N	Wordlength	Method	PSNR	SSIM
3	6	Khorbotly–Hassan [29]	65.0584	0.9997
		Garg–Sharma [30]	57.3749	0.9994
		Cabello et al. [31]	53.3941	0.9984
		Proposed	51.9224	0.9984
5	8	Khorbotly–Hassan [29]	66.0763	0.9999
		Garg–Sharma [30]	41.8214	0.9984
		Cabello et al. [31]	50.7928	0.9985
		Proposed	51.8503	0.9981
7	15	Khorbotly–Hassan [29]	85.2323	0.9999
		Garg–Sharma [30]	57.3294	0.9991
		Cabello et al. [31]	43.4979	0.9984
		Proposed	50.4509	0.9977

presents the results.

3.3.2. Blurring Experiment: Absolute Measurements

To better visualize the performance of the proposed approximations, we considered a zoomed $32\times 32$ patch extracted from the $512\times 512$ image texmos3.s512 (‘USC texture mosaic #3’) from [44]. This image block was submitted to the exact 2D Gaussian filter and to the proposed approximate filters. The resulting images are shown in Figure 4.

The PSNR and SSIM measurements were evaluated considering all the filtered output images compared with the unfiltered input image.

Table 3. Error analysis for the absolute measurement blurring experiment. The PSNR and SSIM measurements from the approximate and exact output images shown in Figure 4 relative to the original unfiltered image.

N	Method	PSNR	SSIM
3	Exact	25.9539	0.99997
	Khorbotly–Hassan [29]	25.9678	0.99997
	Garg–Sharma [30]	25.7377	0.99996
	Cabello et al. [31]	25.9373	0.99997
	Proposed	26.6959	0.99997
5	Exact	25.0316	0.99996
	Khorbotly–Hassan [29]	25.0022	0.99996
	Garg–Sharma [30]	24.7035	0.99995
	Cabello et al. [31]	24.9931	0.99996
	Proposed	25.1014	0.99996
7	Exact	24.9563	0.99996
	Khorbotly–Hassan [29]	24.9565	0.99996
	Garg–Sharma [30]	24.8965	0.99996
	Cabello et al. [31]	24.8295	0.99995
	Proposed	23.6457	0.99994

summarizes the results.

3.3.3. Edge Detection Experiment

The proposed $5\times 5$ 2D filter was also considered as a preprocessing step for edge detection using the Sobel algorithm [4]. We considered the image 4.1.03 (‘Female’) from [44] corrupted by additive white Gaussian noise with variance equal to 1% of the pixel representation range. Figure 5 depicts the results.

Without preprocessing, the intensity of the detected edges was similar to background noise. On the other hand, filtering provided better differentiation. The Sobel algorithm equipped with the selected approximate filter was able to generate edges with comparable qualitative performance.

4. VLSI Architectures

4.1. FPGA Realization

The proposed 2D filters of size $3\times 3$, $5\times 5$, and $7\times 7$ were implemented on a field programmable gate array (FPGA). The device used for the hardware implementation was the Xilinx Artix-7 XC7A35T-1CPG236C (Xilinx, San Jose, CA, USA). The methods by Khorbotly–Hassan [29] and Garg–Sharma [30] were set with identical sizes and physically realized.

The design of an $N\times N$ mask, $N\in \{3,5,7\}$, considers a row-wise serial rearrangement of the input image, where the pixels are flattened into a 1D array of length $N^2$. Because symmetric mask coefficients have the same value, the corresponding pixels can be summed before being scaled by the corresponding quantities approximating those coefficients. The intermediary quantities are added in pairs forming a trellis, which pipelines each intermediary value in a systolic manner. Each stage of the pipeline that involves a summation increases the wordlength by one bit; at the end of the processing, the final quantity is scaled down and represented as an 8-bit binary number.

The proposed designs were tested in the FPGA by connecting it to a controller state machine and connected to an universal asynchronous receiver–transmitter (UART) block. The UART core interfaced with the controller state machine using the ARM Advanced Microcontroller Bus Architecture Advanced eXtensible Interface 4 (AMBA AXI-4) (Xilinx, San Jose, CA, USA) protocol.

The personal computer (PC) communicated with the controller through the UART by sending a batch of pixels corresponding to the pixels that would overlap with the kernel mask through a raster scanner manner. The batch of pixels was then passed to the design and processed. Then, the controller state machine sent the mask output back to the personal computer, which stored it. This operation was performed over the whole image and then saved to a text file containing all the processed pixels’ values. The file with the data obtained through the FPGA processing was then compared with the output of processing the original images with a software model of the proposed mask implemented in Python. The above procedure was repeated for the competing methods to ensure the correct implementation. For a qualitative assessment, Figure 6 shows the result of the image processing using the proposed kernel and the competing methods in the FPGA. The use of the proposed kernel did not impact the image quality degradation (cf. Table 2).

4.2. Performance Measurements

The FPGA implementations were evaluated according to the following metrics: the number of occupied slices, the number of look-up tables (LUT), the flip-flop (FF) count, the number of digital signal processing multipliers (DSP), the critical path delay ($T_{\mathrm{cpd}}$), the maximum operating frequency $F_{\max }=T_{\mathrm{cpd}}^{-1}$, and the dynamic power ($D_p$) normalized by $F_{\max }$. The measured results are shown in

Table 4. FPGA measures of the implemented architectures for masks of size $3\times 3$ using 6-bit coefficients.

Metric	Method
	Proposed	Khorbotly–Hassan [29]	Garg–Sharma [30]	Cabello et al. [31]
# Slices	34	32	39	33
# LUT	84	83	106	86
# FF	102	84	107	84
# DSP	0	2	0	2
$T_{\mathrm{cpd}}$ (ns)	3.938	4.220	3.763	5.362
$F_{\max }$ (MHz)	253.936	236.966	265.745	186.496
$D_p$ (mW MHz−1)	0.012	0.013	0.012	0.021

,

Table 5. FPGA measures of the implemented architectures for masks of size $5\times 5$ using 8-bit coefficients.

Metric	Method
	Proposed	Khorbotly–Hassan [29]	Garg–Sharma [30]	Cabello et al. [31]
# Slices	92	82	90	80
# LUT	222	221	237	224
# FF	305	293	303	295
# DSP	0	2	1	2
$T_{\mathrm{cpd}}$ (ns)	4.208	5.801	5.405	5.888
$F_{\max }$ (MHz)	237.643	172.384	185.014	169.837
$D_p$ (mW MHz−1)	0.021	0.041	0.032	0.047

and

Table 6. FPGA measures of the implemented architectures for masks of size $7\times 7$ using 15-bit coefficients.

Metric	Method
	Proposed	Khorbotly–Hassan [29]	Garg–Sharma [30]	Cabello et al. [31]
# Slices	172	166	157	152
# LUT	446	451	444	383
# FF	584	534	536	547
# DSP	4	16	10	5
$T_{\mathrm{cpd}}$ (ns)	4.486	6.189	5.717	5.642
$F_{\max }$ (MHz)	222.916	161.577	174.917	177.242
$D_p$ (mW MHz−1)	0.031	0.105	0.052	0.051

for kernel sizes $3\times 3$, $5\times 5$, and $7\times 7$, respectively.

For the sake of further comparison, we included the case where the competing methods were implemented using 8-bit coefficients in

Table 7. FPGA measures of the implemented architectures for masks of size $3\times 3$ using 8-bit coefficients.

Metric	Method
	Proposed	Khorbotly–Hassan [29]	Garg–Sharma [30]	Cabello et al. [31]
# Slices	34	33	32	33
# LUT	84	85	83	86
# FF	102	84	84	84
# DSP	0	3	2	2
$T_{\mathrm{cpd}}$ (ns)	3.938	5.682	4.220	5.362
$F_{\max }$ (MHz)	253.936	175.994	236.967	186.496
$D_p$ (mW MHz−1)	0.012	0.023	0.013	0.021

.

5. Discussion

In this section, we offer a discussion on the mathematical, experimental, and technological contributions detailed in this paper.

5.1. Mathematical Formalism and Design Criteria

The proposed method ensures that the filter gain is equal to one, due to the normalization constraint of the optimization problem, as shown in (16) and (17). Therefore, all our proposed solutions satisfy the normalization condition by construction. This is one of contributions of our work, because the competing methods do not always satisfy the normalization condition. In [29], the kernel coefficients are not required to maintain strict unity sum. The Gaussian kernel coefficients proposed in [30] also do not sum to one. Similarly, in [31], Cabello et al. do not necessarily furnish normalized kernels. In those works, the kernels sum to a close-to-one value, which might or might not result in (i) perceptual changes in the brightness level of the output filtered images, (ii) filtering bias, and (iii) small changes related to the inter-pixel covariances.

In [30,31], the kernel symmetry could be maintained as a consequence of the direct element-wise approximation employed in those works. In contrast, the proposed method adds a layer of sophistication because it does not approximate the kernel coefficients individually. We take into consideration the entire filter matrix and the interplay between the coefficients is captured by the adopted optimization problem to ensure a minimal approximation error. Thus, to ensure the rotational invariance symmetry of the obtained Gaussian kernels, a specific constraint was included in the optimization problem, as shown in (16) and (17).

In the proposed approach, the approximate kernel coefficients are required to be non-null, because the approximate filter coefficients are approximated to a negative power of two. Accordingly, the value zero could only be achieved at large negative powers capable of incurring a loss of significance. Thus, by design and on purpose, zero was not included in the current study. Another reason to avoid zero entries is to prevent the degeneration of the approximate Gaussian kernel of size N into the approximation of size $N-1$ (i.e., the larger kernel is equal to the smaller kernel but padded with surrounding zeros). Yet another reason to restrict zeros was to permit a fair comparison with the considered competing methods, whose kernels are populated with non-null values.

The next step in this research includes an extension of the current methodology to allow not only zeros but also a control variable on the complexity of non-null entries. In the current method, we restricted the entries to be a single power of two. However, in principle, we could tailor the method to additively accommodate extra powers of two to ensure that the total complexity does not exceed a prescribed upper bound in the most effective manner (minimum error). To the best of our knowledge, the current literature does not provide such a method.

5.2. Complexity Analysis and Image Experiments

As a consequence of approximating the filter coefficients to powers of two, no multiplication is required, and the obtained additive complexity is substantially smaller compared with the competing methods [29,30]. The additive complexity could be lower because we restricted the approximations to a single power of two as opposed to an additive combination of powers of two, as shown in [30], for instance. Such mathematical properties greatly benefit the hardware realization, because the powers of two correspond to rewiring (no actual computation cost) in an application-specific integrated circuit (ASIC).

As shown in Table 1, the equivalent $5\times 5$ proposed filter requires $62.5\%$ and $41.5\%$ fewer arithmetic operations than the designs in [29] and [30], respectively. Similar gains are observed for the $3\times 3$ and $7\times 7$ kernels, where the proposed approximation could outperform the method in [30] with $38.5\%$ and $37.5\%$ fewer arithmetic operations, respectively.

Overall, Figure 4, Figure 5 and Figure 6 emphasize the visual similarity among the results provided by the proposed approximate filter when compared with the exact 2D Gaussian filter and with the competing methods. The key point in favor of our work is that the proposed approximations could generate virtually indistinguishable results, in some cases even better ones (cf. Table 2), at a much smaller computational cost (cf. Table 1).

By inspecting the numerical results from Table 2 and Table 3, one notices that the proposed method offered quantitatively similar results to the methods described in [29,30,31] at a lower computational cost, as shown in Table 1. For instance, in the relative measurement blurring experiment, notice that all approximate kernels inflict a PSNR degradation. However, the proposed approximate filters consistently achieved high values of PSNR and SSIM—above 50 dB and $0.99$, respectively (Table 2). Such measurements can be considerably beyond the quality level required in typical image processing tasks [3]. In the absolute measurement blurring experiment, the results show the effectiveness of the approximations, as the measurements were largely consubstantial (Table 3).

As a consequence of the reported similar image quality measurements, the main criterion for comparison of the methods becomes the computational cost, which is favorable to the proposed methods as shown in Table 1 and also in the hardware realization assessment discussed in the next subsection.

5.3. Hardware Realization

The proposed 2D Gaussian filters show reductions in hardware resources compared with the Khorbotly–Hassan [29], Garg–Sharma [30], and Cabello et al. [31] designs. From Table 6, we notice that the $7\times 7$ proposed kernel requires fewer than half of the DSP blocks required by the corresponding mask following the method in [30], one-quarter of the number required by the method in [29], and slightly less than the number required by the method in [31]. The number of slices, FFs, and LUTs in the proposed mask are slightly higher than the competing methods. Indeed, the DSP blocks themselves possess a significantly larger gate count and also require a larger area in the FPGA chip when compared with simple FFs and LUTs [48] (pp. 13–14). One can notice that the measured $F_{\max }$ is 37.96%, 27.44%, and 25.76% higher than the measurements from the Khorbotly–Hassan [29], Garg–Sharma [30], and Cabello et al. [31] masks, respectively. The normalized dynamic power $D_p$ is also considerably reduced, at 70.47%, 40.38%, and 39.21% smaller than the figures from the methods in [29,30], and [31], respectively, when $7\times 7$ masks are considered.

Considering the reported figures in Table 5, the number of slices, FFs, and LUTs for the $5\times 5$ proposed methods are very close to the numbers of the corresponding competing methods. However, the proposed $5\times 5$ kernel design does not require DSP blocks, which allows it to reach a higher maximum operating frequency $F_{\max }$, 37.85%, 28.44%, and 39.92% higher than the measurements from the designs in [29,30], and [31], respectively. The normalized dynamic power is also reduced when compared with the competing methods.

As shown in Table 4, the $3\times 3$ proposed masks does not show significant improvements when compared with the 6-bit coefficient competitors. This is because of the small mask size and the very low magnitude of its coefficients, which render hardware architectures that require few gates. In such a case, the maximum operating frequency of the proposed mask outperforms the Khorbotly–Hassan method but does not overcome the performance of the Garg–Sharma mask for the 6-bit coefficient case. Additionally, from the results shown in Table 7, one can notice that the proposed design outperforms both competitors in terms of resources (fewer DSP blocks) and the resulting maximum operating frequency and normalized dynamic power.

Final Remarks and Recommendations

As final remarks, we emphasize that our method can be applied, with little modification, to other classes of 2D digital filters. To that end, it suffices that the relevant error metric and the sought structure be suitably translated into an objective function and a set of constraints matching the optimization framework advanced in this paper.

The main advantage of our proposed method is the low computation complexity of the resulting filters, which implies low-complexity hardware. On the other hand, the potential disadvantage is the possible performance degradation that any approximate method might effect.

We emphasized the word “possible” because, although degradation is often present in approximate methods, it is plausible that no degradation might take place as measured by the overall system’s figures of merit. Indeed, if the application context presents a system error floor capable of absorbing the implied numerical losses effected by the approximate computation stage, then the approximation errors will not be detectable.

An example of such a case where an approximation might not degrade the system performance is found in the approximation of the transform stage of JPEG-like compression [49]. Indeed, if taken in isolation, an approximation might underperform compared to its exact counterpart; however, when it is part of a complex system with unclear interactions among nonlinear sub-systems (e.g., quantization, decimation, source coding, etc.), the overall system performance might not be impacted (might even be enhanced), as shown in [50].

In the image processing experiments described in Section 3.3, the output images have consistently shown good results as corroborated by the favorable PSNR and SSIM measurements. It is quite reasonable to infer that the reported quality figures relative to the exact case are exceeding acceptance levels in many applications, especially in those contexts that involve human vision. Thus, a comprehensive analysis of the balance between the computational costs, accuracy, and performance ultimately rests on the technology user with a specific context and known loss functions for decision making.

6. Conclusions

In this paper, a method for obtaining approximate 2D Gaussian filters is proposed. The proposed approximate methods present a significant reduction in computational cost. This fact suggests that the proposed filters enable the use of algorithms such as image blurring and edge detection in contexts of limited computing resources and low-energy devices. The hardware usage results also indicate that the proposed filter is the most power efficient compared with the competing methods, as it has the lowest computational cost, while presenting practically acceptable qualitative and quantitative performance.