A Study of Futures Price Forecasting with a Focus on the Role of Different Economic Markets
Abstract
1. Introduction
- (1)
- Through Granger causality tests, it was identified that factors such as Chinese soybean futures and US corn futures have Granger causality relationships with Chinese corn futures prices. Accordingly, this study combines factors such as Chinese soybean prices and US corn prices separately with the historical prices of Chinese corn futures and incorporates them as input variables into the SCINet network model. Through this approach, a novel framework for predicting corn futures prices is proposed. Compared with traditional methods that use only single corn futures prices as inputs, the proposed framework provides a more comprehensive consideration of the multiple factors influencing corn futures price fluctuations, thereby significantly improving prediction accuracy.
- (2)
- Through Granger causality tests on Chinese corn, soybean, and US corn futures prices, this study analyses the interdependent relationships among these factors. This not only enhances the predictive performance of the model but also advances interdisciplinary research at the intersection of economics, agriculture, and deep learning. The findings successfully apply the theory to the practical prediction of Chinese agricultural futures prices, while also providing valuable insights for other researchers studying markets such as futures and stocks.
- (3)
- This study employs the SCINet deep learning model, which is relatively uncommon in financial time series research, and differs from most previous studies on futures price prediction in terms of forecasting horizons. Most prior research focuses on predicting the price for the following day, whereas the model presented here is capable of directly providing multi-step forecasts, that is, forecasts for multiple days. Compared to the rolling multi-step prediction method used in previous studies, the model in this paper effectively reduces the adverse impact of error accumulation, leading to improved prediction accuracy. Moreover, in contrast to single-day forecasts, the five-day and ten-day predictions in this study offer greater utility for helping investors make decisions in advance. Empirical results demonstrate that the SCINet model outperforms others in the comparative experiments.
2. Literature Review
2.1. Futures Price Forecasting Models
2.2. Model Input Feature Processing and Selection
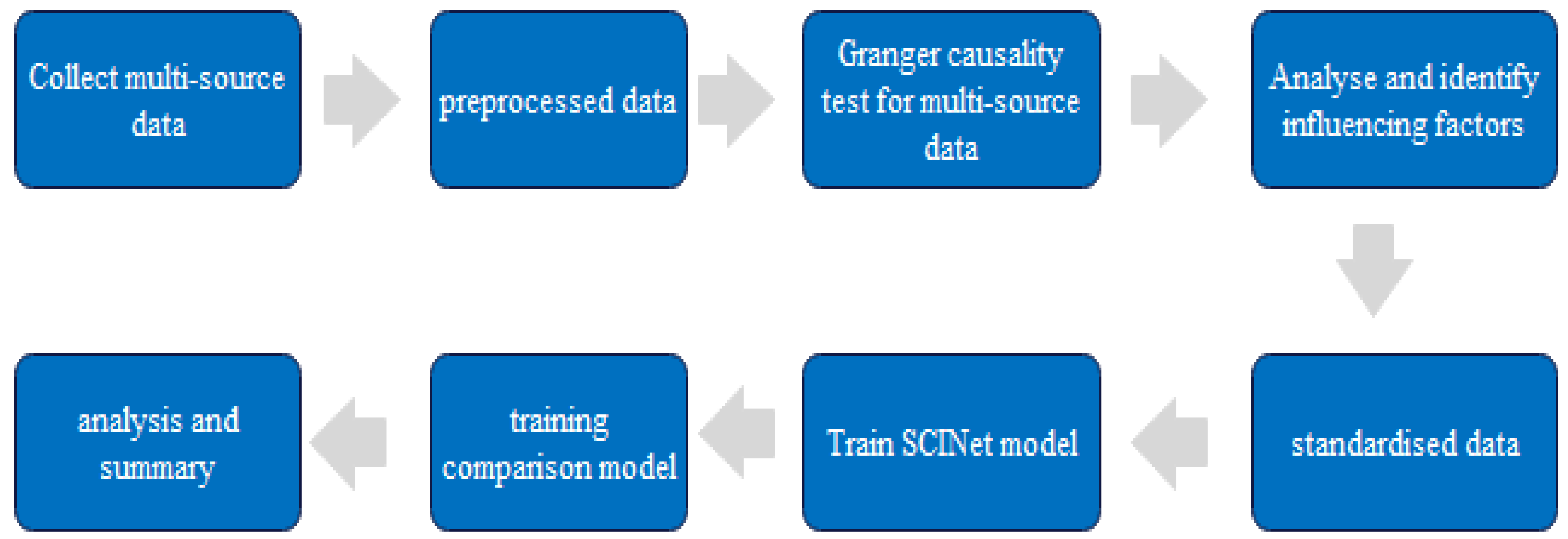
3. Materials and Methods
3.1. Granger Causality Test
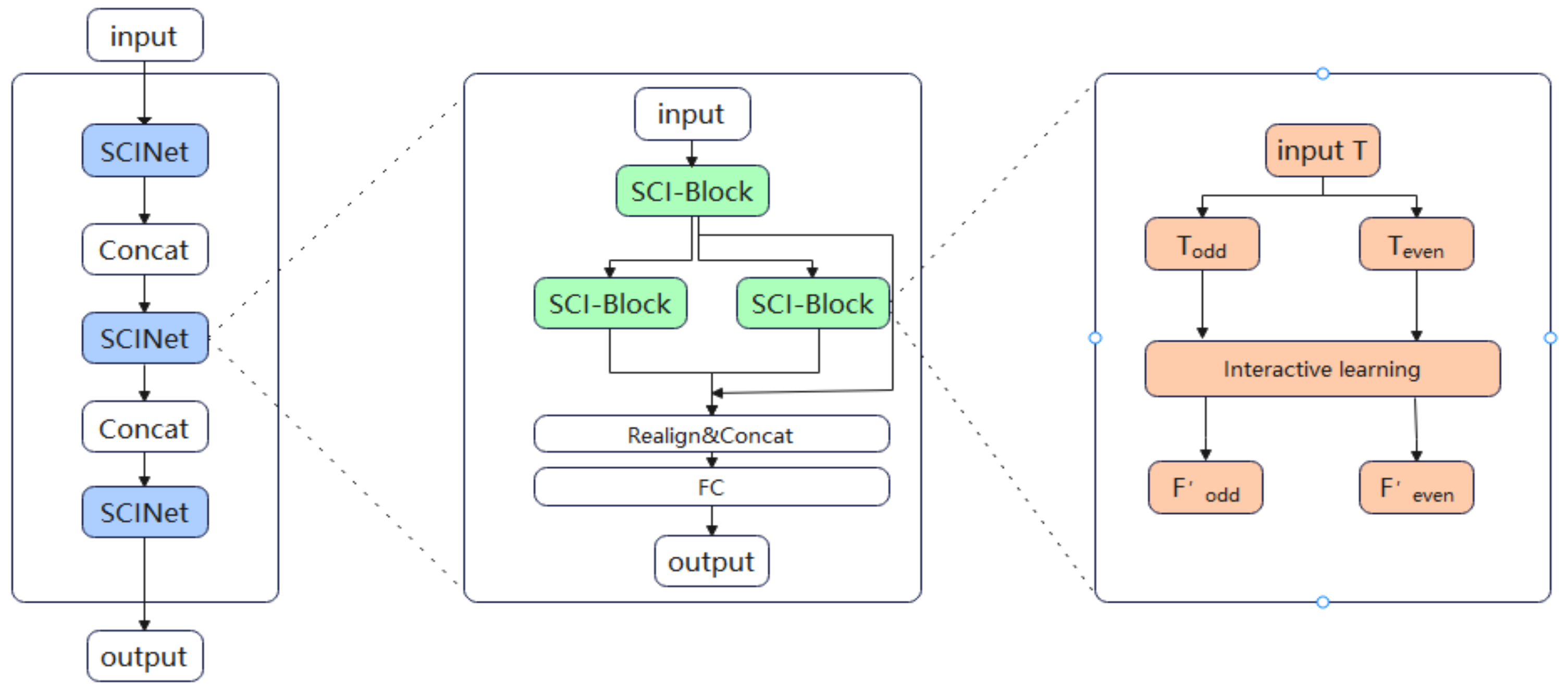
3.2. SCINet Model
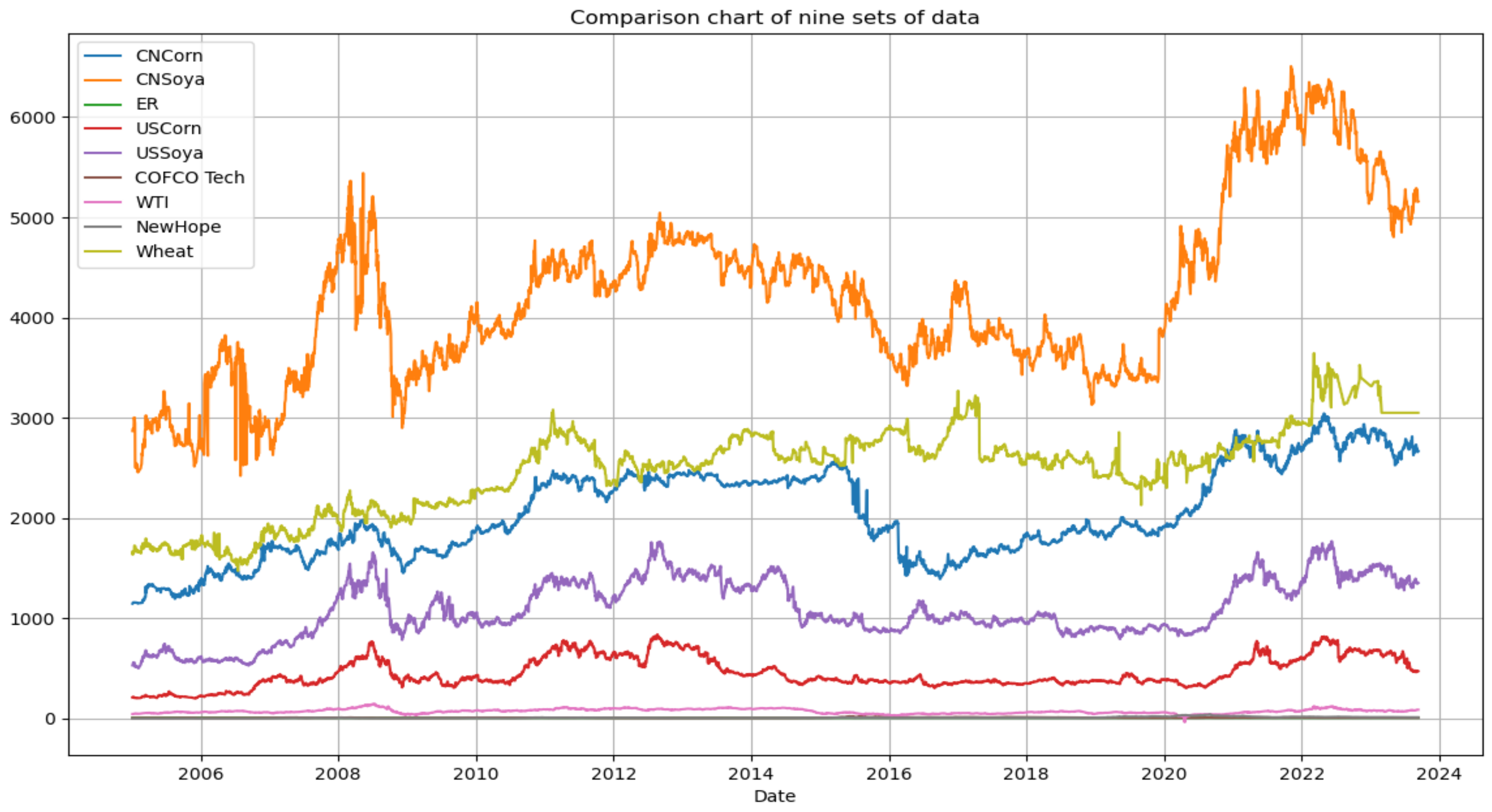
3.3. Data Description
3.4. Performance Evaluation Criteria
4. Empirical Results
4.1. Granger Test Results and Analysis
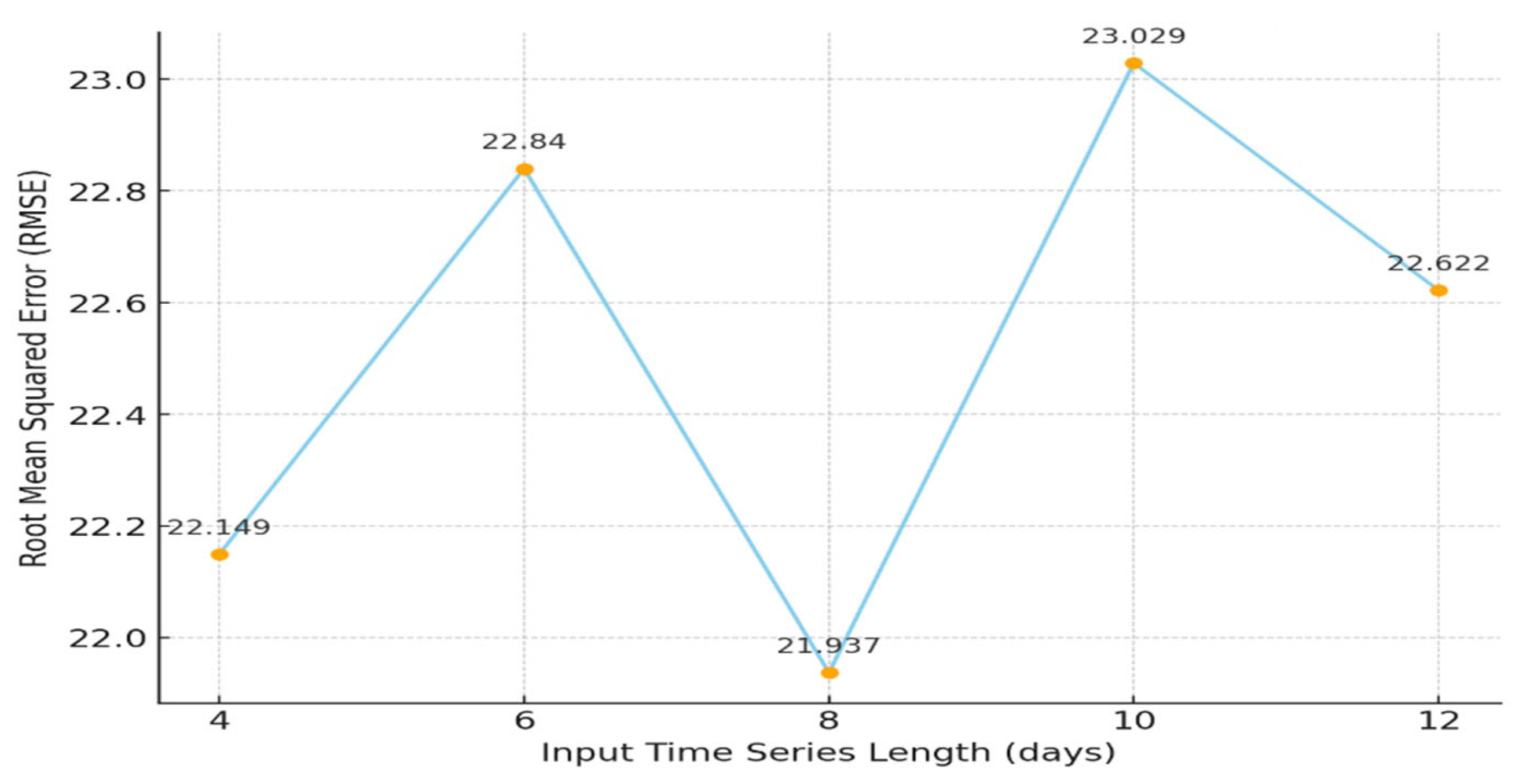
4.2. Analysis of Single-Step Prediction Results
4.3. Analysis of Multi-Step Forecast Results
4.3.1. 5-Day Forecast Result Analysis
4.3.2. 10-Day Forecast Result Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Erenstein, O.; Jaleta, M.; Sonder, K.; Mottaleb, K.; Prasanna, B.M. Global Maize Production, Consumption and Trade: Trends and R&D Implications. Food Secur. 2022, 14, 1295–1319. [Google Scholar]
- Fu, H.M.; Zhang, H.Q.; Yao, X.L.; Zhou, L.; Pan, G.X. Can Corn Stove Bioethanol Production Substantially Contribute to China’s Carbon Neutrality Ambition? Resour. Conserv. Recycl. Adv. 2022, 15, 200111. [Google Scholar] [CrossRef]
- Yin, T.; Wang, Y. Nonlinear Analysis and Prediction of Soybean Futures. Agric. Econ. 2021, 67, 200–207. [Google Scholar] [CrossRef]
- Liu, W.; Wang, C.; Li, Y.; Liu, Y.; Huang, K. Ensemble Forecasting for Product Futures Prices Using Variational Mode Decomposition and Artificial Neural Networks. Chaos Solitons Fractals 2021, 146, 110822. [Google Scholar] [CrossRef]
- Ohyver, M.; Pudjihastuti, H. Arima Model for Forecasting the Price of Medium Quality Rice to Anticipate Price Fluctuations. Proc. Procedia Comput. Sci. 2018, 135, 707–711. [Google Scholar]
- Li, J.; Wang, J. Forcasting of Energy Futures Market and Synchronization Based on Stochastic Gated Recurrent Unit Model. Energy 2020, 213, 118787. [Google Scholar] [CrossRef]
- Jiang, F.; He, J.; Zeng, Z. Pigeon-Inspired Optimization and Extreme Learning Machine via Wavelet Packet Analysis for Predicting Bulk Commodity Futures Prices. Sci. China Inf. Sci. 2019, 62, 070204:1–070204:19. [Google Scholar] [CrossRef]
- Heaton, J.B.; Polson, N.G.; Witte, J.H. Deep Learning in Finance. arXiv 2016, arXiv:1602.06561. [Google Scholar]
- Gupta, N.; Nigam, S. Crude Oil Price Prediction Using Artificial Neural Network. Proc. Procedia Comput. Sci. 2020, 170, 642–647. [Google Scholar]
- Du, Y.; Chen, K.; Chen, S.; Yin, K. Prediction of Carbon Emissions Trading Price in Fujian Province: Based on BP Neural Network Model. Front. Energy Res. 2022, 10, 939602. [Google Scholar] [CrossRef]
- Jiang, B.; Gong, H.; Qin, H.; Zhu, M. Attention-LSTM Architecture Combined with Bayesian Hyperparameter Optimization for Indoor Temperature Prediction. Build. Environ. 2022, 224, 109536. [Google Scholar] [CrossRef]
- Sareen, K.; Panigrahi, B.K.; Shikhola, T.; Sharma, R. An Imputation and Decomposition Algorithms Based Integrated Approach with Bidirectional LSTM Neural Network for Wind Speed Prediction. Energy 2023, 278, 127799. [Google Scholar] [CrossRef]
- Yang, B.; Sun, S.; Li, J.; Lin, X.; Tian, Y. Traffic Flow Prediction Using LSTM with Feature Enhancement. Neurocomputing 2019, 332, 320–327. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, J.; Wu, Z. China’s Commercial Bank Stock Price Prediction Using a Novel K-Means-LSTM Hybrid Approach. Expert Syst. Appl. 2022, 202, 117370. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Wang, M.; Lim, M.K.; Ghadimi, P. Predictive Analytics of the Copper Spot Price by Utilizing Complex Network and Artificial Neural Network Techniques. Resour. Policy 2019, 63, 101414. [Google Scholar] [CrossRef]
- Wang, D.; Luo, H.; Grunder, O.; Lin, Y.; Guo, H. Multi-Step Ahead Electricity Price Forecasting Using a Hybrid Model Based on Two-Layer Decomposition Technique and BP Neural Network Optimized by Firefly Algorithm. Appl. Energy 2017, 190, 390–407. [Google Scholar] [CrossRef]
- Kocak, E.; Bilgili, F.; Bulut, U.; Kuskaya, S. Is Ethanol Production Responsible for the Increase in Corn Prices? Renew. Energy 2022, 199, 689–696. [Google Scholar] [CrossRef]
- Suh, D.H.; Moss, C.B. Decompositions of Corn Price Effects: Implications for Feed Grain Demand and Livestock Supply. Agric. Econ. 2017, 48, 491–500. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y. Corn Cash Price Forecasting with Neural Networks. Comput. Electron. Agric. 2021, 184, 106120. [Google Scholar] [CrossRef]
- Demirer, R.; Kutan, A.M.; Shen, F. The Effect of Ethanol Listing on Corn Prices: Evidence from Spot and Futures Markets. Energy Econ. 2012, 34, 1400–1406. [Google Scholar] [CrossRef]
- Kristiansen, T. A Time Series Spot Price Forecast Model for the Nord Pool Market. Int. J. Electr. Power Energy Syst. 2014, 61, 20–26. [Google Scholar] [CrossRef]
- Guo, L.; Huang, X.; Li, Y.; Li, H. Forecasting Crude Oil Futures Price Using Machine Learning Methods: Evidence from China. Energy Econ. 2023, 127, 107089. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. Scinet: Time Series Modeling and Forecasting with Sample Convolution and Interaction. Adv. Neural Inf. Process. Syst. 2022, 35, 5816–5828. [Google Scholar] [CrossRef]
- Deng, C.; Huang, Y.; Hasan, N.; Bao, Y. Multi-Step-Ahead Stock Price Index Forecasting Using Long Short-Term Memory Model with Multivariate Empirical Mode Decomposition. Inf. Sci. 2022, 607, 297–321. [Google Scholar] [CrossRef]
- Contreras, J.; Espínola, R.; Nogales, F.J.; Conejo, A.J. ARIMA Models to Predict Next-Day Electricity Prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhuang, X.H. Application of ARIMA Model in Short-Term Prediction of International Crude Oil Price. Adv. Mater. Res. 2013, 798, 979–982. [Google Scholar]
- Lanza, A.; Manera, M.; Giovannini, M. Modeling and Forecasting Cointegrated Relationships among Heavy Oil and Product Prices. Energy Econ. 2005, 27, 831–848. [Google Scholar] [CrossRef]
- Yi, A.; Yang, M.; Li, Y. Macroeconomic Uncertainty and Crude Oil Futures Volatility–Evidence from China Crude Oil Futures Market. Front. Environ. Sci. 2021, 9, 636903. [Google Scholar] [CrossRef]
- Zou, H.F.; Xia, G.P.; Yang, F.T.; Wang, H.Y. An Investigation and Comparison of Artificial Neural Network and Time Series Models for Chinese Food Grain Price Forecasting. Neurocomputing 2007, 70, 2913–2923. [Google Scholar] [CrossRef]
- Sánchez Lasheras, F.; de Cos Juez, F.J.; Suárez Sánchez, A.; Krzemień, A.; Riesgo Fernández, P. Forecasting the COMEX Copper Spot Price by Means of Neural Networks and ARIMA Models. Resour. Policy 2015, 45, 37–43. [Google Scholar] [CrossRef]
- Hoseinzade, E.; Haratizadeh, S. CNNpred: CNN-Based Stock Market Prediction Using a Diverse Set of Variables. Expert Syst. Appl. 2019, 129, 273–285. [Google Scholar] [CrossRef]
- Cen, Z.; Wang, J. Crude Oil Price Prediction Model with Long Short Term Memory Deep Learning Based on Prior Knowledge Data Transfer. Energy 2019, 169, 160–171. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Li, D.; Li, Y.; Wang, C.; Chen, M.; Wu, Q. Forecasting Carbon Prices Based on Real-Time Decomposition and Causal Temporal Convolutional Networks. Appl. Energy 2023, 331, 120452. [Google Scholar] [CrossRef]
- Duan, P.; Goh, Y.M.; Zhou, J. The Impact of COVID-19 Pandemic on Construction Safety in China and the U.S.: A Comparative Study. Saf. Sci. 2023, 161, 106076. [Google Scholar] [CrossRef]
- Song, L.; Wang, H. Improved CEEMDAN-Based Aero-Engine Gas-Path Parameter Forecasting Using SCINet. J. Mech. Sci. Technol. 2023, 37, 1485–1500. [Google Scholar] [CrossRef]
- Ding, J.; Deng, F.; Liu, Q.; Wang, J. Regional Forecasting of Significant Wave Height and Mean Wave Period Using EOF-EEMD-SCINet Hybrid Model. Appl. Ocean Res. 2023, 136, 103582. [Google Scholar] [CrossRef]
- Guo, K.; Liu, F.; Sun, X.; Zhang, D.; Ji, Q. Predicting Natural Gas Futures’ Volatility Using Climate Risks. Financ. Res. Lett. 2023, 55, 103915. [Google Scholar] [CrossRef]
- Deng, S.; Huang, X.; Qin, Z.; Fu, Z.; Yang, T. A Novel Hybrid Method for Direction Forecasting and Trading of Apple Futures. Appl. Soft Comput. 2021, 110, 107734. [Google Scholar] [CrossRef]
- Lu, Y.; Teng, Y.; Zhang, Q.; Dai, J. Prediction Model for the Chemical Futures Price Using Improved Genetic Algorithm Based Long Short-Term Memory. Processes 2023, 11, 238. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, K.; Zhang, X.; Tan, B.; Lu, Q. Forecasting Crude Oil Futures Prices Using BiLSTM-Attention-CNN Model with Wavelet Transform. Appl. Soft Comput. 2022, 130, 109723. [Google Scholar] [CrossRef]
- Cavalcante, R.C.; Brasileiro, R.C.; Souza, V.L.F.; Nobrega, J.P.; Oliveira, A.L.I. Computational Intelligence and Financial Markets: A Survey and Future Directions. Expert Syst. Appl. 2016, 55, 194–211. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, F.; Liu, S.; Wu, Y.; Wang, L. A Hybrid VMD–BiGRU Model for Rubber Futures Time Series Forecasting. Appl. Soft Comput. J. 2019, 84, 105739. [Google Scholar] [CrossRef]
- Zhu, B.; Han, D.; Wang, P.; Wu, Z.; Zhang, T.; Wei, Y.M. Forecasting Carbon Price Using Empirical Mode Decomposition and Evolutionary Least Squares Support Vector Regression. Appl. Energy 2017, 191, 521–530. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wei, Y.; Zhu, Q. A New Hybrid VMD-ICSS-BiGRU Approach for Gold Futures Price Forecasting and Algorithmic Trading. IEEE Trans. Comput. Soc. Syst. 2021, 8, 1357–1368. [Google Scholar] [CrossRef]
- Hua, R.; Liu, Q.; Tse, Y.; Yu, Q. The Impact of Natural Disaster Risk on the Return of Agricultural Futures. J. Asian Econ. 2023, 87, 101632. [Google Scholar] [CrossRef]
- Liang, J.; Jia, G. China Futures Price Forecasting Based on Online Search and Information Transfer. Data Sci. Manag. 2022, 5, 187–198. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Liu, M.; Zhu, X.; Wei, L. A Novel Text-Based Framework for Forecasting Agricultural Futures Using Massive Online News Headlines. Int. J. Forecast. 2022, 38, 35–50. [Google Scholar] [CrossRef]
- Dahl, R.E.; Oglend, A.; Yahya, M. Dynamics of Volatility Spillover in Commodity Markets: Linking Crude Oil to Agriculture. J. Commod. Mark. 2020, 20, 100111. [Google Scholar] [CrossRef]
- Ahumada, H.; Cornejo, M. Forecasting Food Prices: The Case of Corn, Soybeans and Wheat. Int. J. Forecast. 2016, 32, 838–848. [Google Scholar] [CrossRef]
- Hanif, W.; Mensi, W.; Vo, X.V.; BenSaïda, A.; Hernandez, J.A.; Kang, S.H. Dependence and Risk Management of Portfolios of Metals and Agricultural Commodity Futures. Resour. Policy 2023, 82, 103567. [Google Scholar] [CrossRef]
- Lu, M.; Chang, B.H.; Salman, A.; Razzaq, M.G.A.; Uddin, M.A. Time Varying Connectedness between Foreign Exchange Markets and Crude Oil Futures Prices. Resour. Policy 2023, 86, 104128. [Google Scholar] [CrossRef]
- Čermák, M.; Ligocká, M. Could Exist a Causality Between the Most Traded Commodities and Futures Commodity Prices in the Agricultural Market? Agris On-Line Pap. Econ. Inform. 2022, 14, 11–25. [Google Scholar] [CrossRef]
- Xu, X. Causality, Price Discovery, and Price Forecasts: Evidence from U.S. Corn Cash and Futures Markets. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2015. [Google Scholar]
- Xu, X. Linear and Nonlinear Causality between Corn Cash and Futures Prices. J. Agric. Food Ind. Organ. 2018, 16, 20160006. [Google Scholar] [CrossRef]
- Xu, X. Causal Structure among US Corn Futures and Regional Cash Prices in the Time and Frequency Domain. J. Appl. Stat. 2018, 45, 2455–2480. [Google Scholar] [CrossRef]
- Liang, Y.; Li, S.; Yan, C.; Li, M.; Jiang, C. Explaining the Black-Box Model: A Survey of Local Interpretation Methods for Deep Neural Networks. Neurocomputing 2021, 419, 168–182. [Google Scholar] [CrossRef]
- Xu, X.; Thurman, W.N. Using Local Information to Improve Short-Run Corn Cash Price Forecasts. In Proceedings of the NCCC-134 Conference on Applied Commodity Price Analysis, Forecasting, and Market Risk Management, St. Louis, MO, USA, 20–21 April 2015. [Google Scholar] [CrossRef]
- Xu, X. Cointegration and Price Discovery in US Corn Cash and Futures Markets. Empir. Econ. 2018, 55, 1889–1923. [Google Scholar] [CrossRef]
- Xu, X. Price Dynamics in Corn Cash and Futures Markets: Cointegration, Causality, and Forecasting through a Rolling Window Approach. Financ. Mark. Portf. Manag. 2019, 33, 155–181. [Google Scholar] [CrossRef]
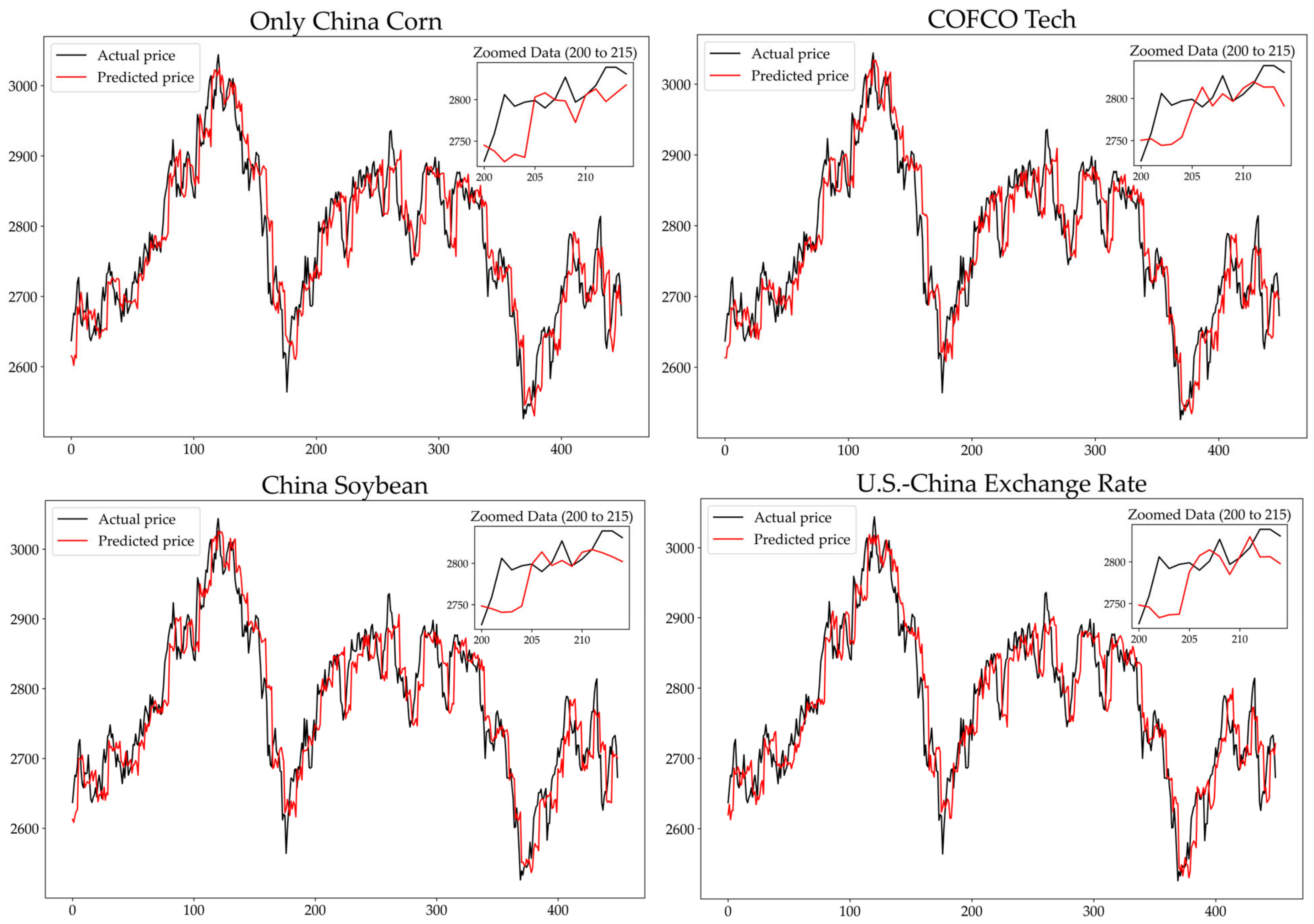
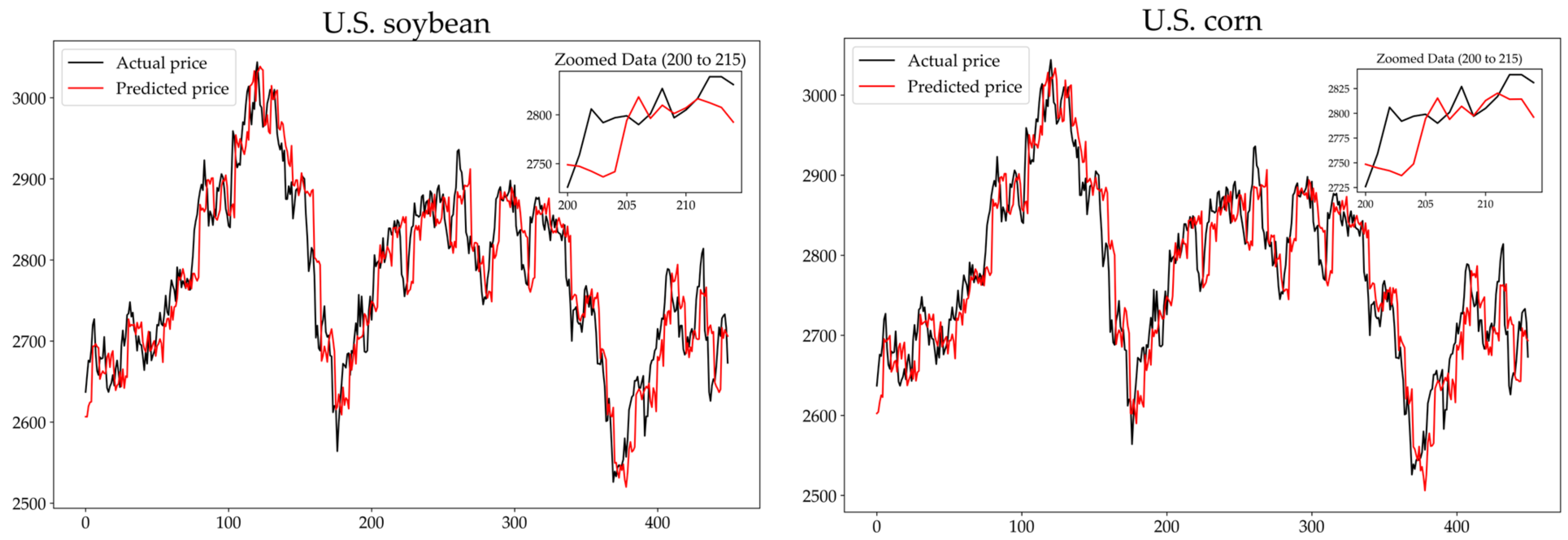


| Null Hypothesis: | F-Statistic | Prob. |
|---|---|---|
| CNSOYA does not Granger Cause CNCORN | 4.22524 | 5 × 10−5 |
| CNCORN does not Granger Cause CNSOYA | 1.85103 | 0.0633 |
| COFCO_TECH does not Granger Cause CNCORN | 4.84958 | 6 × 10−6 |
| CNCORN does not Granger Cause COFCO_TECH | 3.14646 | 0.0015 |
| ER does not Granger Cause CNCORN | 1.25277 | 0.0037 |
| CNCORN does not Granger Cause ER | 0.46051 | 0.7039 |
| NEWHOPE does not Granger Cause CNCORN | 2.41437 | 0.0134 |
| CNCORN does not Granger Cause NEWHOPE | 0.64827 | 0.7375 |
| USCORN does not Granger Cause CNCORN | 13.3787 | 3 × 10−19 |
| CNCORN does not Granger Cause USCORN | 1.68446 | 0.0968 |
| USSOYA does not Granger Cause CNCORN | 10.2018 | 3 × 10−14 |
| CNCORN does not Granger Cause USSOYA | 1.50508 | 0.1498 |
| WHEAT does not Granger Cause CNCORN | 1.14643 | 0.3283 |
| CNCORN does not Granger Cause WHEAT | 1.10281 | 0.3577 |
| WTI does not Granger Cause CNCORN | 1.37031 | 0.2042 |
| CNCORN does not Granger Cause WTI | 0.58285 | 0.7929 |
| Model | MAE | MAPE | RMSE |
|---|---|---|---|
| TCN | 29.851 | 1.070 | 34.594 |
| GRU | 18.121 | 0.655 | 24.059 |
| LSTM | 17.810 | 0.643 | 23.162 |
| SCINet | 16.643 | 0.601 | 21.937 |
| Input Features | MAE | MAPE | RMSE |
|---|---|---|---|
| Chinese corn futures | 16.643 | 0.601 | 21.937 |
| COFCO Technology | 15.837 | 0.579 | 21.220 |
| US soybean futures | 16.523 | 0.591 | 21.821 |
| Exchange rate | 15.862 | 0.572 | 21.122 |
| US corn futures | 16.637 | 0.601 | 21.966 |
| Chinese soybean futures | 15.791 | 0.570 | 21.181 |
| All influencing factors | 17.127 | 0.618 | 22.460 |
| Input Features | MAE | MAPE | RMSE |
|---|---|---|---|
| Chinese corn futures | / | ||
| COFCO Technology | 4.84% | 3.66% | 3.27% |
| US soybean futures | 0.72% | 1.66% | 0.53% |
| Exchange rate | 4.69% | 4.82% | 3.71% |
| US corn futures | 0.04% | 0.00% | 0.13% |
| Chinese soybean futures | 5.12% | 5.15% | 3.45% |
| All influencing factors | −2.90% | −2.82% | −2.38% |
| Model | MAE | MAPE | RMSE |
|---|---|---|---|
| TCN | 46.809 | 1.686 | 58.247 |
| GRU | 43.187 | 1.554 | 52.293 |
| LSTM | 36.028 | 1.595 | 45.186 |
| SCINet | 32.847 | 1.186 | 42.101 |
| Input Features | MAE | MAPE | RMSE |
|---|---|---|---|
| Chinese corn futures | 32.847 | 1.186 | 42.101 |
| COFCO Technology | 31.916 | 1.151 | 40.838 |
| US soybean futures | 32.297 | 1.166 | 41.157 |
| Exchange rate | 31.799 | 1.148 | 40.855 |
| US corn futures | 32.724 | 1.183 | 41.630 |
| Chinese soybean futures | 31.618 | 1.141 | 40.420 |
| Input Features | MAE | MAPE | RMSE |
|---|---|---|---|
| Chinese corn futures | / | ||
| COFCO Technology | 2.83% | 2.95% | 3.00% |
| US soybean futures | 1.67% | 1.69% | 2.24% |
| Exchange rate | 3.19% | 3.20% | 2.86% |
| US corn futures | 0.374% | 0.253% | 1.12% |
| Chinese soybean futures | 3.74% | 3.79% | 3.40% |
| Model | MAE | MAPE | RMSE |
|---|---|---|---|
| TCN | 70.128 | 2.532 | 85.750 |
| GRU | 65.015 | 2.347 | 78.946 |
| LSTM | 59.657 | 2.093 | 74.215 |
| SCINet | 45.190 | 1.634 | 55.404 |
| Input Features | MAE | MAPE | RMSE |
|---|---|---|---|
| Chinese corn futures | 45.190 | 1.634 | 55.404 |
| COFCO Technology | 43.630 | 1.577 | 54.758 |
| US soybean futures | 44.912 | 1.624 | 56.166 |
| Exchange rate | 44.590 | 1.611 | 55.296 |
| US corn futures | 45.572 | 1.650 | 56.939 |
| Chinese soybean futures | 43.881 | 1.586 | 54.787 |
| Input Features | MAE | MAPE | RMSE |
|---|---|---|---|
| Chinese corn futures | / | ||
| COFCO Technology | 3.91% | 3.49% | 1.16% |
| US soybean futures | 1.08% | 0.61% | −1.37% |
| Exchange rate | 1.79% | 1.41% | 0.20% |
| US corn futures | −0.37% | −0.98% | −2.77% |
| Chinese soybean futures | 3.36% | 2.94% | 1.11% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, Q.; Hu, Y.; Liu, H. A Study of Futures Price Forecasting with a Focus on the Role of Different Economic Markets. Information 2024, 15, 817. https://doi.org/10.3390/info15120817
Wang Y, Liu Q, Hu Y, Liu H. A Study of Futures Price Forecasting with a Focus on the Role of Different Economic Markets. Information. 2024; 15(12):817. https://doi.org/10.3390/info15120817
Chicago/Turabian StyleWang, Yongxiang, Qingyang Liu, Yanrong Hu, and Hongjiu Liu. 2024. "A Study of Futures Price Forecasting with a Focus on the Role of Different Economic Markets" Information 15, no. 12: 817. https://doi.org/10.3390/info15120817
APA StyleWang, Y., Liu, Q., Hu, Y., & Liu, H. (2024). A Study of Futures Price Forecasting with a Focus on the Role of Different Economic Markets. Information, 15(12), 817. https://doi.org/10.3390/info15120817





