An Improved Multi-Objective Artificial Bee Colony Optimization Algorithm with Regulation Operators
Abstract
:1. Introduction
2. Literature Review
3. Multi-Objective Artificial Bee Colony (RMOABC) Algorithm with Regulation Operators
3.1. Design of the RMOABC Algorithm
3.1.1. External Archive (EA)
3.1.2. Adaptive Grid
3.1.3. Regulation Operator
3.2. Main Algorithm
| Algorithm 1. RMOABC Algorithm |
| FoodNumber: Number of foods sources |
| Trial: Stagnation number of a solution |
| Limit: Maximum number of trial for abandoning a food source |
| MFE: Maximum number of fitness evaluations |
| OBJNum: Number of objectives |
| Begin |
| Initialization |
| For iter = 0 to MFE |
| SendEmployedBees(); |
| SendOnlookerBees(); |
| SendScoutBees(); |
| UpdateExternalArchive(); |
| UpdateGrid(); |
| TrunkExternalArchive(); |
| End For |
| Return ExternalArchive |
| End |
| Function SendEmployedBees () |
| Begin |
| For i = 0 to FoodNumber−1 |
| Select a parameter p randomly |
| Select neighbor k from the solution randomly for producing a mutant solution |
| Generate a new candidate solution in the range of the parameter |
| Calculate the fitness according to the objective functions |
| If the new solution dominates the old one |
| Update the solution |
| End If |
| If the solution was not improved |
| Increase its Trial by 1 |
| End If |
| End For |
| End |
| Function SendOnlookerBees () |
| Begin |
| Calculate the probabilities of each solution |
| While (t < FoodNumber) |
| Select a parameter p randomly |
| Select neighbor k from the solution randomly for producing a mutant solution |
| Generate a new candidate solution in the range of the parameter |
| Calculate the fitness according to the objective functions |
| If the new solution dominates the old one |
| Update the solution |
| End If |
| If the solution was not improved |
| Increase its Trial by 1 |
| End If |
| End While |
| End |
| Function SendScoutBees () |
| Begin |
| For i = 0 to FoodNumber−1 |
| If Trial(i) exceeds limit |
| Re-initiate the ith solution |
| Set Trial(i) = 0 |
| End If |
| End For |
| End |
| Function UpdateExternalArchive () |
| Begin |
| Define boolean isDominated[swarm.length] |
| For i = 0 to FoodNumber−1 |
| For j = 0 to FoodNumber−1 and isDominated[i] is not true |
| If i is not equal j and isDominated[j] is not true |
| Verify the dominance of solution i and solution j |
| If solution j dominates solution i |
| Set isDominated[i] = true |
| End If |
| If solution i dominates solution j |
| Set isDominated[j] = true |
| End If |
| End If |
| End For |
| End For |
| For i = 0 to FoodNumber−1 |
| If isDominated[i] is false |
| Add the solution to the ExternalArchive |
| End If |
| End For |
| End |
| Function UpdateGrid () |
| Begin |
| Set maxValues [] = the max Fitness values of each objective of solutions in ExternArchive |
| Set minValues [] = the min Fitness Values of each objective of solutions in ExternArchive |
| For i = 0 to OBJNum−1 |
| Initialize the grid’s ranges to the maxValues[i]−minValues[i] |
| End For |
| For i = 0 to (length of hypercubes)−1 |
| Update the fitness limitation of hypercubes[i] based on the ranges |
| End For |
| For i = 0 to (length of hypercubes)−1 |
| Verify whether the solution[i] of the ExternArchive is in the limitation of the fitness |
| End For |
| For i = 0 to (length of hypercubes)−1 |
| Calculate the fitness diversity of the solution in archive |
| End For |
| End |
| Function TrunkExternalArchive() |
| Begin |
| While ExternalArchive is full |
| Select a solution from the ExternalArchive by the Adaptive Grid mechanism |
| Remove the bee with the selected solution in the ExternalArchive |
| End While |
| End |
4. Experimental Analyses
4.1. Multi-Objective Optimization Algorithms
4.1.1. Non-dominated Sorted Genetic Algorithm-II (NSGA-II)
| Algorithm 2. NSGA-II Algorithm |
| Begin |
| Initialize Npop random solutions |
| Evaluate initial solutions by their objective function values |
| Assign ranks to the solutions based on the ranking procedure (non-dominated sorting) |
| Calculate crowding distance |
| While (Stopping Criteria is not satisfied) |
| Create and fill the mating pool using binary tournament selection |
| Apply crossover and mutation operators to the mating pool |
| Evaluate objective function values of the new solutions |
| Merge the old population and the newly created solutions |
| Assign ranks according to the ranking procedure |
| Calculate crowding distance |
| Sort the population and select better solutions |
| End While |
| Output the non-dominated solutions |
| End |
4.1.2. Multiobjective Evolutionary Algorithm Based on Decomposition (MOEA/D)
| Algorithm 3. MOEA/D Algorithm |
| Input: |
| • multiobjective optimization problem (MOP); |
| • a stopping criterion; |
| • N: The number of the subproblems considered in MOEA/D; |
| • a uniform spread of N weight vectors: ; |
| • T: The number of the weight vectors in the neighborhood of each weight vector. |
| Output: an external population (EP), which is used to store nondominated solutions found during the search. |
| Begin |
| Initialization(); |
| While (Stopping Criteria is not satisfied) |
| Update(); |
| End While |
| Stop and output EP. |
| End |
| Function Initialization() |
| Begin |
| Set EP = . |
| Compute the Euclidean distances between any two weight vectors and then work out the T closest weight vectors to each weight vector. For each i = 1, …, N, set , where are the T closest weight vectors to . |
| Generate an initial population randomly or by a problem-specific method. Set . |
| Initialize by a problem-specific method. |
| End |
| Function Update() |
| Begin |
| For i = 1 to N, |
| Reproduction: Randomly select two indexes k, l from B(i), and then generate a new solution y from xk and xl by using genetic operators. |
| Improvement: Apply a problem-specific repair/ improvement heuristic on y to produce . |
| Update of z: For each , if , then set . |
| Update of Neighboring Solutions: For each index , if , then set and . |
| Update of EP: |
| Remove from EP all the vectors dominated by . Add to EP if no vectors in EP dominate . |
| End For |
| End |
4.2. Experiments Preparations
4.2.1. Parameter Settings
4.2.2. Benchmark Functions
4.2.3. Evaluation Indicators of Multi-Objective Optimization Algorithms
4.3. Experimental Results Analysis
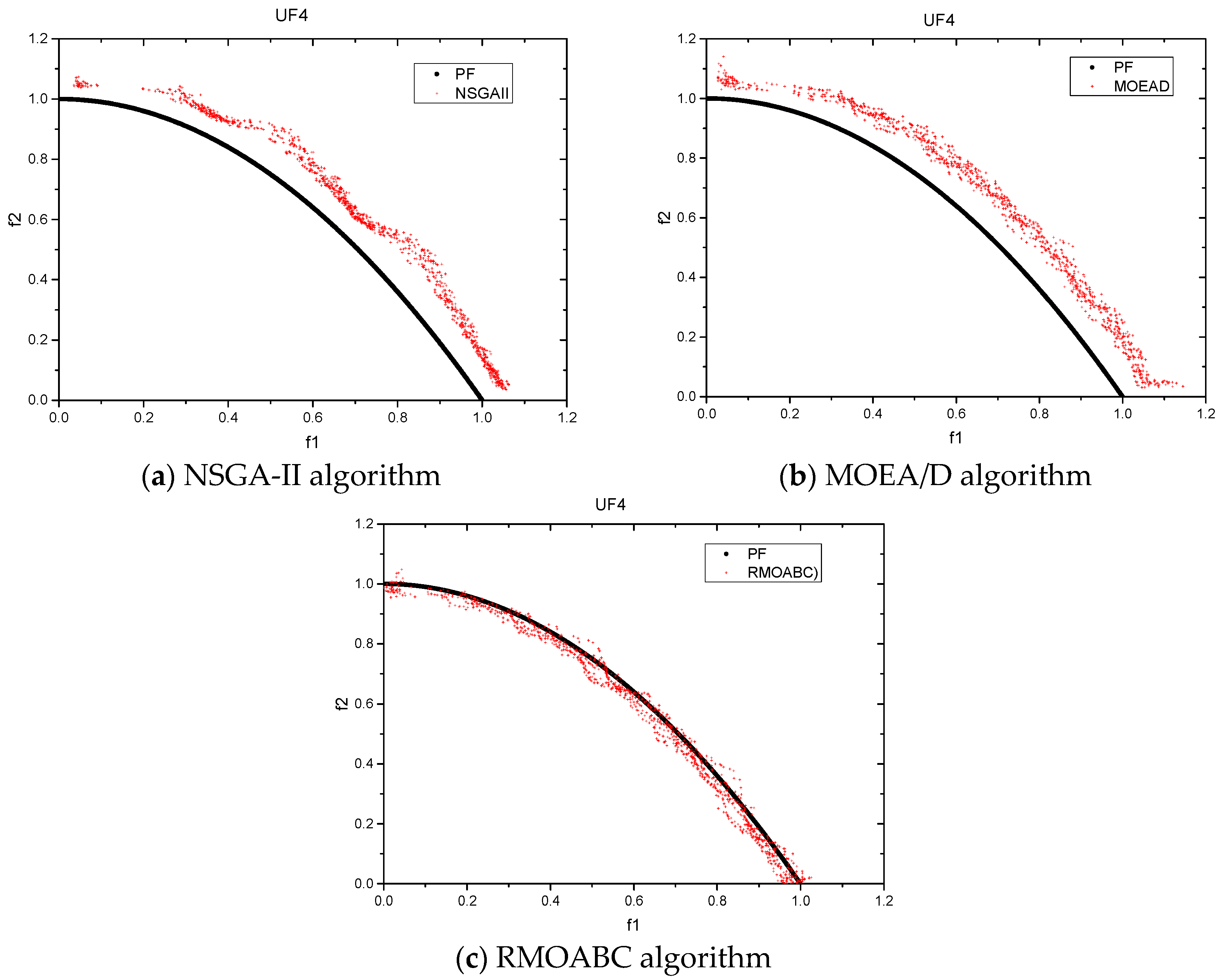
4.3.1. Pareto Front vs. Non-Dominated Solution
4.3.2. Statistics Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deb, K. Multi-Objective Optimization using Evolutionary Algorithms; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Li, Z.J.; Zhang, H.; Yao, C.; Kan, G.Y. Application of coupling global optimization of single-objective algorithm with multi-objective algorithm to calibration of Xinanjiang model parameters. J. Hydroelectr. Eng. 2013, 32, 6–12. [Google Scholar]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A survey on the applications of artificial bee colony in signal, image, and video processing. Signal Image Video Process. 2015, 9, 967–990. [Google Scholar] [CrossRef]
- Pareto, V. The Rise and Fall of the Elites; Bedminster Press: Totowa, NJ, USA, 1968. [Google Scholar]
- Coello, C.A.C. A comprehensive survey of evolutionary-based multiobjective optimization techniques. Knowl. Inf. Syst. 1999, 1, 129–156. [Google Scholar] [CrossRef]
- Raquel, C.R.; Naval, P.C., Jr. An effective use of crowding distance in multiobjective particle swarm optimization. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2005), Washington, DC, USA, 26 June 2005; pp. 257–264.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multi-objective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Reyes-Sierra, M.; Coello, C.A.C. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Tsou, C.S.; Chang, S.C.; Lai, P.W. Using crowding distance to improve multi-objective PSO with local search. In Swarm Intelligence: Focus on Ant and Particle Swarm Optimization; Chan, F.T.S., Tiwari, M.K., Eds.; Itech Education and Publishing: Vienna, Austria, 2007. [Google Scholar]
- Leong, W.F.; Yen, G.G. PSO-based multiobjective optimization with dynamic population size and adaptive local archives. IEEE Trans. Syst. Man Cybern. 2008, 38, 5. [Google Scholar]
- MOEA framework. Available online: http://moeaframework.org/ (accessed on 31 January 2017).
- Guliashki, V.; Toshev, H.; Korsemov, C. Survey of evolutionary algorithms used in multiobjective optimization. J. Probl. Eng. Cybern. Robot. 2009, 60, 42–54. [Google Scholar]
- Zhou, A.; Qu, B.Y.; Li, H.; Zhao, S.Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state-of-the-art. J. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Shivaie, M.; Sepasian, M.S.; Sheikheleslami, M.K. Multi-objective transmission expansion planning using fuzzy-genetic algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2011, 35, 141–159. [Google Scholar]
- Hedayatzadeh, R.; Hasanizadeh, B.; Akbari, R.; Ziarati, K. A multi-objective artificial bee colony for optimizing multi-objective problems. In Proceedings of the 3th International Conference on Advanced Computer Theory and Engineering, ICACTE, Chengdu, China, 20–22 August 2010; pp. 271–281.
- Akbari, R.; Hedayatzadeh, R.; Ziarati, K.; Hasanizadeh, B. A multi-objective artificial bee colony algorithm. J. Swarm Evol. Comput. 2012, 2, 39–52. [Google Scholar] [CrossRef]
- Zou, W.P.; Zhu, Y.L.; Chen, H.N.; Zhang, B.W. Solving multiobjective optimization problems using artificial bee colony algorithm. Discret. Dyn. Nat. Soc. 2011, 2011. [Google Scholar] [CrossRef]
- Omkar, S.N.; Senthilnath, J.; Khandelwal, R.; Naik, G.N.; Gopalakrishnan, S. Artificial bee colony (ABC) for multi-objective design optimization of composite structures. Appl. Soft Comput. 2011, 11, 489–499. [Google Scholar] [CrossRef]
- Akbari, R.; Ziarati, K. Multi-objective bee swarm optimization. Int. J. Innov. Comput. Inf. Control 2012, 8, 715–726. [Google Scholar]
- Zhang, H.; Zhu, Y.; Zou, W.; Yan, X. A hybrid multi-objective artificial bee colony algorithm for burdening optimization of copper strip production. Appl. Math. Model. 2012, 36, 2578–2591. [Google Scholar] [CrossRef]
- da Silva Maximiano, M.; Vega-Rodríguez, M.A.; Gómez-Pulido, J.A.; Sánchez-Pérez, J.M. A new multiobjective artificial bee colony algorithm to solve a real-world frequency assignment problem. Neural Comput. Appl. 2013, 22, 1447–1459. [Google Scholar] [CrossRef]
- Mohammadi, S.A.R.; Feizi Derakhshi, M.R.; Akbari, R. An Adaptive Multi-Objective Artificial Bee Colony with Crowding Distance Mechanism. Trans. Electr. Eng. 2013, 37, 79–92. [Google Scholar]
- Akay, B. Synchronous and Asynchronous Pareto-Based Multi-Objective Artificial Bee Colony Algorithms. J. Glob. Optim. 2013, 57, 415–445. [Google Scholar] [CrossRef]
- Luo, J.P.; Liu, Q.; Yang, Y.; Li, X.; Chen, M.R.; Cao, W.M. An artificial bee colony algorithm for multi-objective optimization. Appl. Soft Comput. 2017, 50, 235–251. [Google Scholar] [CrossRef]
- Kishor, A.; Singh, P.K.; Prakash, J. NSABC: Non-dominated sorting based multi-objective artificial bee colony algorithm and its application in data clustering. Neurocomput. 2016, 216, 514–533. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.R. A dynamic multi-colony artificial bee colony algorithm for multi-objective optimization. Appl. Soft Comput. 2015, 35, 766–785. [Google Scholar] [CrossRef]
- Nseef, S.K.; Abdullah, S.; Turky, A.; Kendall, G. An adaptive multi-population artificial bee colony algorithm for dynamic optimisation problems. Knowl.-Based Syst. 2016, 104, 14–23. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Huo, J.Y.; Zhang, Y.Z.; Zhao, H.X. An improved artificial bee colony algorithm for numerical functions. Int. J. Reason.-based Intell. Syst. 2015, 7, 200–208. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Gregorio, T.P.; Maximino, S.L. Handling Multiple Objectives with Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Bastos-Filho, J.A.C.; Figueiredo, E.M.N.; Martins-Filho, J.F.; Chaves, D.A.R.; Cani, M.E.V.S.; Pontes, M.J. Design of distributed optical-fiber raman amplifiers using multi-objective particle swarm optimization. J. Microw. Optoelectr. Electromagn. Appl. 2011, 10, 323–336. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Approximating the non-dominated front using the Pareto archived evolution strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.P.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [PubMed]
- Pasandideh, S.H.R.; Niaki, S.T.A.; Sharafzadeh, S. Optimizing a bi-objective multi-product EPQ model with defective items, rework and limited orders: NSGA-II and MOPSO algorithms. J. Manuf. Syst. 2013, 32, 764–770. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, S.; Zhao, A.; Suganthan, P.N.; Liu, W.; Tiwariz, S. Multiobjective Optimization Test Instances for the CEC 2009 Special Session and Competition; Technical report; University of Essex, The School of Computer Science and Electronic Engineering: Essex, UK, 2009. [Google Scholar]
- Shafii, M.F.; Smedt, D.E. Multi-objective calibration of a distributed hydrological model (WetSpa) using a genetic algorithm. Hydrol. Earth Syst. Sci. 2009, 13, 2137–2149. [Google Scholar] [CrossRef]








| Algorithm | Parameter | Value | Remark |
|---|---|---|---|
| NSGA-II | population size | 100 | |
| crossover probability | 0.8 | uniform crossover | |
| mutation probability | 0.02 | ||
| MOEA/D | population size | 300 | , m is the number of objectives |
| external archive capacity | 100 | ||
| T | 20 | ||
| H | 299 | ||
| crossover rate | 1.00 | ||
| mutation rate | 1/D | ||
| RMOABC | population size | 100 | |
| external archive capacity | 100 | ||
| adaptive grid number | 25 | ||
| Limit | 0.25 × NP × D |
| Algorithm | GD (Generational Distance) | SP (Spacing) | Times (in seconds) | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| NSGA-II | 1.9679×10−3 | 3.4112×10−4 | 6.2474×10−3 | 6.9286×10−4 | 4.3574 | 0.3224 |
| MOEA/D | 1.3843×10−2 | 5.3614×10−3 | 2.4305×10−2 | 8.5273×10−3 | 2.1108 | 0.1783 |
| RMOABC | 5.4088×10−4 | 2.4279×10−4 | 3.6033×10−3 | 7.1357×10−4 | 0.5388 | 0.0730 |
| Algorithm | GD (Generational Distance) | SP (Spacing) | Times (in seconds) | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| NSGA-II | 3.4387×10−3 | 1.0882×10−3 | 7.6290×10−3 | 1.8900×10−3 | 2.8958 | 0.5234 |
| MOEA/D | 2.5757×10−2 | 1.0759×10−2 | 2.2454×10−2 | 2.1028×10−2 | 0.8309 | 0.2213 |
| RMOABC | 2.9472×10−4 | 1.4764×10−4 | 3.3057×10−3 | 8.9793×10−4 | 0.5211 | 0.0468 |
| Algorithm | GD (Generational Distance) | SP (Spacing) | Times (in seconds) | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| NSGA-II | 1.0607×10−3 | 1.7559×10−4 | 7.0315×10−3 | 6.2416×10−4 | 1.7959 | 0.0693 |
| MOEA/D | 7.9187×10−3 | 2.7141×10−3 | 4.0872×10−2 | 1.4372×10−2 | 0.7610 | 0.1002 |
| RMOABC | 7.7966×10−4 | 1.2618×10−4 | 9.2795×10−3 | 2.9382×10−3 | 0.2342 | 0.0229 |
| Algorithm | GD (Generational Distance) | SP (Spacing) | Times (in seconds) | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| NSGA-II | 0.0449 | 0.0112 | 0.1770 | 0.0133 | 1.1736 | 0.0696 |
| MOEA/D | 0.0061 | 0.0105 | 0.0425 | 0.0726 | 1.9405 | 0.4917 |
| RMOABC | 0.0061 | 0.0051 | 0.1646 | 0.0167 | 0.4177 | 0.0164 |
| Algorithm | GD (Generational Distance) | SP (Spacing) | Times (in seconds) | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| NSGA-II | 0.0092 | 0.0035 | 0.0307 | 0.0259 | 20.5788 | 1.3663 |
| MOEA/D | 0.0043 | 0.0009 | 0.0192 | 0.0216 | 5.6236 | 0.3085 |
| RMOABC | 0.0030 | 0.0009 | 0.0082 | 0.0004 | 1.4772 | 0.1590 |
| Algorithm | GD (Generational Distance) | SP (Spacing) | Times (in seconds) | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| NSGA-II | 0.4161 | 0.1755 | 0.1898 | 0.1278 | 5.1115 | 1.0229 |
| MOEA/D | 0.2973 | 0.2028 | 0.1427 | 0.1178 | 4.4406 | 0.6877 |
| RMOABC | 0.1353 | 0.0880 | 0.1033 | 0.3172 | 1.24645 | 0.0476 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, J.; Liu, L. An Improved Multi-Objective Artificial Bee Colony Optimization Algorithm with Regulation Operators. Information 2017, 8, 18. https://doi.org/10.3390/info8010018
Huo J, Liu L. An Improved Multi-Objective Artificial Bee Colony Optimization Algorithm with Regulation Operators. Information. 2017; 8(1):18. https://doi.org/10.3390/info8010018
Chicago/Turabian StyleHuo, Jiuyuan, and Liqun Liu. 2017. "An Improved Multi-Objective Artificial Bee Colony Optimization Algorithm with Regulation Operators" Information 8, no. 1: 18. https://doi.org/10.3390/info8010018
APA StyleHuo, J., & Liu, L. (2017). An Improved Multi-Objective Artificial Bee Colony Optimization Algorithm with Regulation Operators. Information, 8(1), 18. https://doi.org/10.3390/info8010018






