Abstract
Designers and artists often require reference images at authoring time. The emergence of computer technology has provided new conditions and possibilities for artistic creation and research. It has also expanded the forms of artistic expression and attracted many artists, designers and computer experts to explore different artistic directions and collaborate with one another. In this paper, we present an efficient k-means-based method to segment the colors of an original picture to analyze the composition ratio of the color information and calculate individual color areas that are associated with their sizes. This information is transformed into regular geometries to reconstruct the colors of the picture to generate abstract images. Furthermore, we designed an application system using the proposed method and generated many works; some artists and designers have used it as an auxiliary tool for art and design creation. The experimental results of datasets demonstrate the effectiveness of our method and can give us inspiration for our work.
1. Introduction
The emergence of computer technology has provided new conditions and possibilities for artistic creation and research, and it has attracted many artists, designers and computer experts to explore different artistic directions and collaborate with one another. The use of computer technology is becoming increasingly convenient and common in artistic creation. With the development of computer image technology, particularly the development of neural network and machine intelligence technology in recent years, an increasing number of artists and designers have begun using computers as image-processing tools or as a supplementary method for artistic creation and the application of artistic design. The use of software to popularize artistic creations is also common.
Creating a painting is a subjective work that emphasizes individuality and feature. It is a complex process and relies on many subtle factors. One method for creating traditional paintings is manual. However, in the field of contemporary art, computer technology has greatly expanded the possibilities of artistic expression, for example, Manfred Mohr, Ronald Davis [1,2] and so on. The main objective of this paper is to describe our attempt to generate abstract paintings using computer technology, and the algorithm that we developed can also be used to help artists and designers provide references and auxiliary tools for creative projects.
In our work, to analyze the composition ratio of color information, a k-means-based method is presented to segment the colors of the original pictures. To generate abstract images, we calculate individual color areas to reconstruct the colors of the picture and transform them into regular geometries (e.g., circles). Furthermore, we created several pieces of artwork and designed an application system using the proposed method. The experimental results reveal that the method that we proposed can be used as an efficient auxiliary tool for art and design creation.
2. Related Works
Generally, computer painting involves using computer image and graphics software such as Photoshop to draw pictures or computer technology to simulate artistic visual effects such as those in oil paintings, pencil drawings, sketches, and prints. Computer image generation is a process where an image is produced using only a computer program without the explicit influence of humans during the creation process. This process is also known as a computer painting or algorithm painting, e.g., a fractal geometry produced by a fractal-pattern generation algorithm [3,4,5,6]. Although this type of fractal graph expression was not initially used for artistic expression, later produced many excellent pieces of art related to the fractal [7,8].
American scientist Ben F. Laposky is considered the first person to have produced algorithmic paintings. In 1952, Laposky created his work Electronic Abstractions using an early computer and an electronic cathode tube oscilloscope [9]. Since then, more artists and computer experts have collaborated to explore different artistic directions. In her work Transformation, one of the pioneers of computer art, Vera Molnar, used the principles of geometry by changing the proportions of circles, rectangles and triangles to obtain different aesthetic effects [10]. Zajec Edward has suggested that computers should be used to explore new possibilities of artistic creation from the point of intersection with art, such as the artistic effect of a reconstructed image after the original image is decomposed into band structure and geometry [11]. In the last few decades, with the development of computer graphics, designers and artists have gradually begun using computers to create graphics and process images. Deep Dream is an influential visual tool that Google recently created and was designed as an artificial neural network model based on simulating neurons in the human brain. The model is trained by receiving a large amount of data; it determines the rules from the data and uses these rules to evaluate and predict images that it has never observed. Using this process, the model appears to have its own “consciousness” and can create paintings by itself [12]. In 2015, Gatys et al. proposed an understanding of how people should create and perceive artistic images from the perspective of a deep neural network algorithm [13], mainly, the transfer of artistic style characteristics. Using computers for artistic creation and removing the limitations of traditional art forms have created new possibilities for art creation and stimulated the imagination and creativity of artists. It has enabled the development of new art forms and has provided a new space for technology development [14,15,16]. Meanwhile, there are some reports of mathematical methods to analyze art [17,18].
Abstract painting is one of the important forms of painting. It essentially simplifies the performance of the object and has its own meaning and value [19]. Some highly priced works in important auctions in recent years are abstract paintings, which include works of Pollock and Cy Twombly. Abstract painting is a concept that is relative to the concrete; its main use of points, lines, face, color, texture and other pure painting language expresses the emotions or ideas of the creators (see Figure 1). These features of abstract painting provide the theoretical support and possibility of intelligent creation using computers.

Figure 1.
Works by Kandinsky, which can be downloaded from an open-source website http://image.baidu.com/.
In primitive times, human beings began to think abstractly, summarize the external world and understand the essence of the law, which included some impressionistic, exaggerated expressions. The ancient Greeks paid attention to abstract and rational thinking in the field of painting, order, scale, and number, etc., hidden behind the form. The most important feature of vision is to select what one is interested in and ignore secondary information, which is an abstract process [20]. As the representative figure of abstract painting, Mondriaan believed that he could see the potential body of a landscape and that the painter’s task is to draw the structure and harmony in it. Kandinsky, who is another famous artist and representative figure of abstract painting, conducted many theoretical research projects on abstract painting and completed many works [21]. The famous artist of impressionism, Paul Gauguin, also believed that art is abstract. Some scholars have conducted simulation research on the abstract painting style characteristics of famous artists [22,23,24].
3. Our Work
This paper mainly focuses on abstract paintings and selects color as the primary performance element. Color is one of the main elements of visual aesthetics, which itself has an independent aesthetic value. The essence of color application is the proportion of color composition [25]. It is generally thought that a picture with a good looking color is often in line with visual rules that are common among people. This interpretation is supported by mathematical relationships, although we are accustomed to judging such elements using experience and intuition instead of formulas [26,27]. In practice, the application of color matching stems from practicing with different colors, and the aesthetic sense is sometimes cultivated under the guidance of existing color theories.
The focus of this study is to select a picture according to people’s aesthetic needs as a creative material to create images using computer technology. After the computer finishes the color segmentation of a picture, we analyze the mathematical relationships behind the color composition ratios of the picture and reconstruct a new abstract image in accordance with the colors in the picture and their composition ratios. The results can be used as computer artwork or an auxiliary tool and means of creation for artists and designers. This approach can be used for web design, graphic design, and other commercial design applications. In the specific application of artistic design work, the users can select one of their favorite pictures as a reference, analyze its color composition, and use the set of colors in a design project. This technique may produce pleasing visual effects to the individual, and many artists often use this method when painting. In contrast with the current art style of learning, we use the reference image of the color structure, reconstructing a new abstract painting.
In this paper, to analyze the composition ratio of color information, an efficient K-means-based method is presented to segment the colors of the original pictures. To generate abstract images, we calculate individual color areas associated with their sizes to reconstruct the colors of the picture and propose a new method to make them into regular geometries (such as circles). The experimental results for several real-world data sets demonstrate the effectiveness of our method. Furthermore, we create several pieces of artwork and design an application system using the proposed method. Computer technology can be used to make artistic creation more efficient, accurate and rapid, as well as expand the imagination and increase creative inspiration.
The remainder of this paper is organized as follows. In Section 2 and Section 3, the preliminary results are presented. The proposed computer-generated abstract paintings method is introduced in Section 4, and the experimental results from several real-world data sets demonstrate the effectiveness of our method. Finally, our conclusions are presented in Section 5.
4. Creating Abstract Paintings Using Algorithms
Our method to create abstract paintings is summarized in Algorithm 1 and introduced in detail in the following section.
| Algorithm 1 Creating Abstract Paintings method |
| Input: Original color images (I) Output: Abstract paintings Step 1: Segmenting the Colors of Original Pictures Step 2: The Statistics of Color Ratio Information Step 3: Drawing Abstract Paintings |
4.1. Selecting the Original Images and Segmenting the Colors
To generate abstract paintings, the first step is to select pictures depending on the creator’s requirements. Pictures with a pleasing appearance or color scheme always have certain color composition ratios, i.e., their color composition ratios conform to particular mathematical relationships and satisfy visual aesthetic preferences [28,29,30]. The pictures in the experiments in this paper are predominantly photos of flowers; some are from Baidu pictures, and some were taken by the authors.
Color segmentation means segmenting the color composition of the selected pictures according to their color richness. The proposed segmentation method can produce different colored patches with their original position information and retained area information. Then, the images are segmented into Lab color space images. In the Lab space, L is the luminance; thus, patches with different brightness values can be clearly separated [31]. The dimensions are , and each unit has three elements in the Lab space. M is the width of the original picture, and N is the height of the original picture. The entire segmentation method is summarized in Algorithm 2.
| Algorithm 2 Segmentation Method |
| Input: Image information () and the number of color clusters k Output: Label Step 1: Convert into a three-channel column vector V, where and Step 2: Use the k-means-based method for segmenting V and obtain the class center C Step 3: For each data point in the dataset V, i.e, , calculate its category by Equation (4) Step 4: For each class, recalculate the class centroid by Equation (5) Step 5: Repeat Step 3 to Step 4 until convergence |
The algorithm steps are as follows:
- The image information is contained in a matrix , and we convert I into a three-channel column vector V. When clustering data sets, each element of the vector consists of three color elements in the Lab space, i.e., a three-dimensional column vector,where .
- We determine the number of color clusters k, i.e., the number of color classes (in this paper, ).
- We use the K-means method and initially select k pieces of from dataset V as the starting cluster centers. The basic idea of K-means is that the mutual distances between the initial cluster centers should be as large as possible [32]:
- (a)
- We randomly select a point from dataset V as the center .
- (b)
- For each point i in dataset V, we calculate the distance between it and the nearest cluster center (pre-selected),and then obtain the summation of , i.e.,
- (c)
- Then, we take a random value between 0 and to calculate the next ’center’ using a weighting factor. This algorithm is implemented as follows: take random values Random and random . If , then the point becomes the next “center“; otherwise, select again.
- (d)
- Then, we repeat steps (b) and (c) until k cluster centers are selected, which ensures that the point (at a farther distance) can be selected as the cluster center.
- For each data point i in dataset V, we calculate its category, which belongs towhere , . represents point i and the nearest center within the k clusters, and the value of is between 1 and k.
- For each class, we recalculate the class centroid,where , i.e., the number of elements in the data set.
- Repeat steps 4 to 5 until convergence. We define the distortion function to ensure convergence as follows:

Figure 2.
An original picture.

Figure 3.
Color Segmentation of Original Picture.
4.2. The Statistics of Color Ratio Information
After the second step, we divide the Lab space into k pieces of color space to calculate the largest color space-to-area ratio, and we use this color as the background color in the next step of creating the pictures. We count the number of occurrences of color in the Lab space because the image is composed of pixels. Here, we use the ratio of the number of pixels of a particular color to describe the area ratio of the corresponding color in the entire original picture. The original image information is represented by the matrix , is the color of a certain point , is the area of color category n, and is the area ratio of color category n in the entire picture. Initially, , and . When , . The analysis chart in Figure 4 shows the configuration of the proportion of the major color classes in the picture.
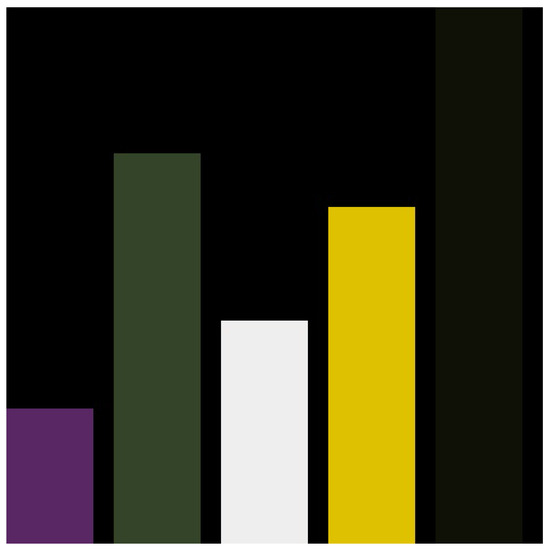
Figure 4.
Analysis chart of color composition of the original picture.
4.3. Drawing Abstract Paintings
After the main color patches in a picture are divided, we can calculate the representative colors of different patches. We calculate individual color areas and make them into regular geometries whose areas are associated with their sizes. We mainly use a circle as the regular geometric shape in this paper. Finally, we randomly use these shapes to form abstract images, where we set the background color of the image to the color with the largest proportion. The algorithm steps are as follows:
- Initialize ; there is a value visit equal to 0, and the dimension of visit is . indicates that the pixel has been visited. If , the pixel has not been visited. We re-count the number and size of separate patches in the original image and sort them in z and .
- Set a threshold p; and if , we record into the variable ; if , we record into the variable . Thus, we can filter out notably small patches. p is an integer value based on the effect of the generated abstract image; hence, different pictures can have different values.
- The largest color patch obtained using the K-means algorithm is set as the background color.
- The circles are drawn based on the size of the independent color patches and finally sorted in descending order. The radius of a circle is , and the center of a circle is :where is the width of the original picture, i.e., M; is the width of the original picture, N; and is a random number. Using a random number indicates that different abstract images can be generated based on the same original image. The fill color in the round circle is the color after clustering (except for the background color). Figure 5a is an abstract painting generated by our method.
 Figure 5. (a) Generated abstract painting; (b) A new abstract painting from the same original picture.
Figure 5. (a) Generated abstract painting; (b) A new abstract painting from the same original picture.
To draw a new picture from the same source image, the position of the color patches can be arbitrarily changed, and a new picture (Figure 5b) with different visual effects can be randomly formed. Thus, the creators can select pictures from all generated results according to their aesthetic preferences.
4.4. Adding Visual Elements and Enriching Picture Composition
When we generate abstract paintings according to the color composition of a source image, the positions of patches in the picture are generated at random. Therefore, the generated results of the same original picture are different every time. Some images have aesthetically pleasing configurations, and some may display less appealing visual effects, which include unattractive configurations caused by the odd positioning of dark and light patches. Hence, creators can select among a series of pictures according to their own aesthetic preferences.
Based on our work prior to this study, we selected to convert all color compositions of the original pictures into circles. We created pictures with circles in their background colors. To enrich the visual form of a picture, we can draw lines inside the areas of certain color patches if the area is smaller than a given color ratio. The composition of a different dot (which is actually a circle with a very small area), a line, and a plane (which is actually a circle with a notably large area) can be morphologically changed to produce different visual effects (Figure 6d). The steps as follows:

Figure 6.
(a) An original picture; (b) Drawing background color; (c) Drawing lines; (d) A complete picture generated through algorithm painting.
- Following Section 4.3, based on Figure 6b, we drew lines using the color information recorded by the object, whose lengths and positions were random. Then, a new image was generated, as shown in Figure 6c.
4.5. Experimental Data and Application
To make a change in shape, we can also change the previous circle to a square, using the same methods and steps as before. The center of a circle can be made into the center of a rectangle, and the height-width of the rectangle can be randomly generated depending on its area. Then, the rectangle can be placed at any location in the picture. Finally, we can obtain new rectangles and their frames using the rectangle function to produce an abstract painting (Figure 7).

Figure 7.
(a,c) An original picture; (b,d) Creation.
In this paper, we designed an application system (Figure 8) that uses a source image to construct an abstract painting. The main color composition and patches appear on the interface. Finally, a part of an abstract picture composed of these colors is formed (Figure 9, Figure 10 and Figure 11). If the user selects to re-create the same original picture, the colors will be randomly reconstructed, and all results are automatically saved. Then, the creator can select their preferred picture from the results.

Figure 8.
The user interface of application system for computer painting.

Figure 9.
(a) Creation; (b) Original picture; (c) Creation.

Figure 10.
(a) Original picture; (b) Creation.

Figure 11.
(a) Original picture; (b) Creation.
5. Conclusions and Future Work
According to a user’s aesthetic preferences, he or she can use computer technology to analyze the color composition of selected pictures to create abstract paintings by re-creating the content of existing pictures. We found this approach to creating abstract paintings notably interesting and useful. The experimental results can be used as a work of art and an auxiliary tool for art and design creation. Future studies will add other forms and combine more painting elements, traditional aesthetic rules, neural networks, and machine intelligence technology to create meaningful computer abstract paintings.
Acknowledgments
This work was supported by the National Science Fund for Distinguished Young Scholars of China (Grant No. 61625204) and the National Science Foundation of China (Grant No. 61375065 and No. 61602066). It was also partially supported by the State Key Program of National Science Foundation of China (Grant No. 61432012 and No. 61432014).
Author Contributions
The individual contributions can be summarized as follows. Mao Li and Jiancheng Lv conceived and designed the experiments; Mao Li performed the experiments; Mao Li and Jing Yin analyzed the data; Mao Li and Xiaojie Li wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Widewalls—Manfred Mohr. Available online: http://www.widewalls.ch/?se=Manfred+Mohr&t=0 (accessed on 13 June 2017).
- Widewalls—Ronald Davis. Available online: http://www.widewalls.ch/?se=Ronald+Davis%2C&t=0 (accessed on 13 June 2017).
- Fisher, Y.; McGuire, M.; Voss, R.F.; Barnsley, M.F.; Devaney, R.L.; Mandelbrot, B.B. The Science of Fractal Images; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wolfram, S.; Gad-el Hak, M. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2003. [Google Scholar]
- Mandelbrot, B.B.; Pignoni, R. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1983. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Taylor, R.P.; Micolich, A.P.; Jonas, D. Fractal analysis of Pollock’s drip paintings. Nature 1999, 399, 422. [Google Scholar] [CrossRef]
- Taylor, R.P.; Micolich, A.P.; Jonas, D. The Construction of Jackson Pollock’s Fractal Drip Paintings. Leonardo 2006, 35, 203–207. [Google Scholar] [CrossRef]
- Laposky, B.F. Oscillons: Electronic abstractions. Leonardo 1969, 2, 345–354. [Google Scholar] [CrossRef]
- Molnar, V. Toward aesthetic guidelines for paintings with the aid of a computer. Leonardo 1975, 8, 185–189. [Google Scholar] [CrossRef]
- Dietrich, F. Visual intelligence: The first decade of computer art (1965–1975). Leonardo 1986, 19, 159–169. [Google Scholar] [CrossRef]
- Deep Dream Web interface. Available online: http://psychic-vr-lab.com/deepdream/ (accessed on 5 December 2017).
- Gatys, L.A.; Ecker, A.S.; Bethge, M. A neural algorithm of artistic style. arXiv, 2015; arXiv:1508.06576. [Google Scholar]
- Franke, H.W. Computers and visual art. Leonardo 1971, 4, 331–338. [Google Scholar] [CrossRef]
- Judelman, G. Aesthetics and inspiration for visualization design: Bridging the gap between art and science. In Proceedings of the Eighth International Conference on Information Visualisation, London, UK, 16–16 July 2004; pp. 245–250. [Google Scholar]
- Marcos, A.F. Digital art: When artistic and cultural muse merges with computer technology. IEEE Comput. Graph. Appl. 2007, 27, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Mekler, G.; Martínez, R.A.; del Río, M.B.; Mansilla, R.; Miramontes, P.; Cocho, G. Universality of rank-ordering distributions in the arts and sciences. PLoS ONE 2009, 4, e4791. [Google Scholar] [CrossRef] [PubMed]
- Aragón, J.L.; Naumis, G.G.; Bai, M.; Torres, M.; Maini, P.K. Turbulent luminance in impassioned van Gogh paintings. J. Math. Imaging Vis. 2008, 30, 275–283. [Google Scholar] [CrossRef]
- Kandinsky, W.; Rebay, H. Point and Line to Plane; Courier Corporation: North Chelmsford, MA, USA, 1947. [Google Scholar]
- Nickas, B. Painting Abstraction: New Elements in Abstract Painting; Phaidon Press: London, UK, 2009. [Google Scholar]
- Quan, L. Abstract painting ancestor Kandinsky. Art Panorama 2011, 1, 103. [Google Scholar]
- Tao, W.; Liu, Y.; Zhang, K. Automatically generating abstract paintings in Malevich Style. In Proceedings of the 2014 IEEE/ACIS 13th International Conference on Computer and Information Science (ICIS), Taiyuan, China, 4–6 June 2014; pp. 201–205. [Google Scholar]
- Xiong, L.; Zhang, K. Generation of Miro’s surrealism. In Proceedings of the 9th International Symposium on Visual Information Communication and Interaction, Dallas, TX, USA, 24–26 September 2016; pp. 130–137. [Google Scholar]
- Zhang, K.; Yu, J. Generation of Kandinsky art. Leonardo 2016, 49, 48–54. [Google Scholar] [CrossRef]
- Edward, B. Thinking Like Artists; Northern Literature and Art Publishing House: Harbin, China, 2006. [Google Scholar]
- Holtzschue, L. Understanding Color: An Introduction for Designers; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ilam, K. Design Geometry-Research on the Proportion and Composition; Intellectual Press: Beijing, China, 2003; p. 104. [Google Scholar]
- Tokumaru, M.; Muranaka, N.; Imanishi, S. Color design support system considering color harmony. In Proceedings of the 2002 IEEE International Conference on Fuzzy Systems, Honolulu, HI, USA, 12–17 May 2002; pp. 378–383. [Google Scholar]
- Cohen-Or, D.; Sorkine, O.; Gal, R.; Leyvand, T.; Xu, Y.Q. Color harmonization. ACM Trans. Graph. 2006, 25, 624–630. [Google Scholar] [CrossRef]
- Kojima, R. Ryohei Kojima’s Design World; Guangxi Fine Arts Publishing House: Nanning, China, 2000; p. 188. [Google Scholar]
- Hammond, D.L. Validation of LAB color mode as a nondestructive method to differentiate black ballpoint pen inks. J. Forensic Sci. 2007, 52, 967–973. [Google Scholar] [CrossRef] [PubMed]
- Arthur, D.; Vassilvitskii, S. K-Means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).