Abstract
This paper aims to propose an innovative approach to group decision making (GDM) with interval-valued intuitionistic fuzzy (IVIF) preference relations (IVIFPRs). First, an IVIFPR is proposed based on the additive consistency of an interval-valued fuzzy preference relation (IVFPR). Then, two mathematical or adjusted programming models are established to extract two special consistent IVFPRs. In order to derive the priority weight of an IVIFPR, after taking the two special IVFPRs into consideration, a linear optimization model is constructed by minimizing the deviations between individual judgments and between the width degrees of the interval priority weights. For GDM with IVIFPRs, the decision makers’ weights are generated by combining the adjusted subjective weights with the objective weights. Subsequently, using an IVIF-weighted averaging operator, the collective IVIFPR is obtained and utilized to derive the IVIF priority weights. Finally, a practical example of a supplier selection is analyzed to demonstrate the application of the proposed method.
1. Introduction
In group decision making (GDM), decision makers (DMs) are usually required to provide their judgment on various alternatives using preference relations. The three types of preference relations in which the elements are described by crisp numerical numbers are multiplicative preference relations (MPRs) [1], reciprocal preference relations (RPRs) [2], and linguistic fuzzy preference relations (LFPRs) [3]. However, due to the practical uncertainty and vagueness of decision problems, DMs may find it difficult to provide pairwise comparison judgments with crisp numerical numbers for the alternatives. The intuitionistic fuzzy set (IFS) proposed by Atanassov [4] is a powerful tool to handle this problem, which is characterized by a membership and nonmembership degree. Later, Atanassov and Gargov [5] used the IFS to propose an interval-valued intuitionistic fuzzy set (IVIFS). Consequently, the interval-valued fuzzy preference relation (IVFPR) [6,7,8,9] and the interval-valued intuitionistic fuzzy (IVIF) preference relations (IVIFPR) [10,11,12,13,14] appeared in succession.
In order to obtain reasonable ranking orders, most of the existing research has focused on analyzing the consistency of the preference relations. For example, Xu and Chen [15] first proposed the consistent interval-valued intuitionistic judgment matrix. Subsequently, Xu and Cai [12,16] put forward some definitions on multiplicative and additive consistency in incomplete IVIFPRs and determined the missing elements in an IVIFPR while only knowing its off-diagonal elements. Inspired by the multiplicative transitivity of an IVIFPR, Liao et al. [10] introduced a multiplicative consistency concept to an IVIFPR, which was applied to adjust or repair an inconsistent IVIFPR using some iterative algorithms. The above research studies are direct extensions of the consistency of fuzzy preference relations (FPRs). Wan et al. [17] pointed out that the definitions in References [10,12,16] only independently considered the four endpoints of the preferred and nonpreferred IVIFPRs, which it is unreasonable to utilize to investigate the consistency of IVIFPRs directly. To address this issue, following the IFPR consistency concept in Liao and Xu [18], Wan et al. [17] presented a convex combination-based multiplicative consistency concept for IVIFPRs, which considered an IVIFPR to be consistent depending on whether or not the associated induced IFPR was consistent. With the same idea, Wan et al. [19,20] put forward a new concept of additive consistency of an IVIFPR by extracting two special IVIFPRs or IFPRs from an IVIFPR. Chu et al. [21] put forward a new definition of the additive consistency of an IVIFPR by dividing it into four preference relations. Meng et al. [22] introduced a new multiplicative consistency concept for IVIFPRs. Compared to that on multiplicatively consistent IVIFPRs, research on additively consistent IVIFPRs is very scarce and not yet well-rounded. Therefore, this paper continues to study additively consistent IVIFPRs and their application for GDM.
With regard to GDM problems, Xu and Chen [15] first proposed score and accuracy matrices to rank IVIFs and presented an approach to address GDM with IVIFPRs. Then, Xu and Yager [23] put forward a similarity measurement of IVIFs and analyzed the group consensus between the judgments of the DMs. Wu and Chiclana [24] introduced a new attitudinal expected score function for IVIFs and developed a nondominance-based prioritization method for IFPR and IVIFPR. Liao et al. [10] proposed a convergent iterative approach to solve GDM with IVIFPRs. Other studies [19,20,21,22,25,26,27,28] developed various approaches to address GDM problems with IVIFPRs. These investigations, as mentioned, can offer ideas and methods to address GDM with IVIFPRs. However, there are still some deficiencies, as stated below:
- (1)
- Prior research [10,12,16] has focused on multiplicatively consistent IVIFPRs and has failed to consider the IVIF judgment directly, which may not fully seize the primitive judgment information. Studies [17,19,21] have focused on additively consistent IVIFPRs while ignoring the consistency of the associated preference matrices, which may result in illogical conclusions. Consistency is an important indicator to measure the level of quality for preference information provided by DMs. Therefore, it is necessary to discuss the function of additively consistent IVIFPRs in the decision-making process.
- (2)
- The existing studies [15,23,24] have merely considered the case of a single DM (or expert) and neglected the GDM situation during the decision-making process. In general, an individual expert cannot provide a perfect suggestion for complex problems. In this case, it is necessary to employ more than one DM to make such a decision. Furthermore, for GDM problems, the DMs’ subjective weights and objective weights should all be considered in order to avoid subjective bias and objective rigidity. However, most studies (References [10,12,16,17,19,20,21]) cannot achieve this requirement. Therefore, it is vital to find a reasonable solution to determine the weights of the DMs for GDM with IVIFPRs.
In order to eliminate the above shortcomings, this paper focuses on discussing additively consistent IVIFPRs and their application to GDM problems. First, inspired by the works of Wan et al. [20] and Bustince [29], a new definition of additively consistent IVIFPRs is proposed based on the additive transitivity of an IVFPR. Then, two mathematical models are established to extract two special, consistent IVFPRs. In terms of deriving the priority weights of the alternatives, a linear optimization model is constructed by minimizing the deviations between the individual judgments as well as the width degrees of the interval priority weights. For GDM, a novel method is proposed to determine the weights of the DMs, by considering both the adjusted subjective weight and the objective weight. Finally, an innovative approach for GDM with IVIFPRs is proposed.
The rest of this paper is organized as follows. In Section 2, some basic related definitions and concepts on preference relations are reviewed and the concept of an additively consistent IVIFPR is introduced. In Section 3, two linear or adjusted optimization models are constructed to extract two special IVFPRs from an IVIFPR. Then, a linear programming method is proposed to derive the IVIF priority weights. In Section 4, an extended method for GDM with IVIFPRs is put forward. In Section 5, one practice example is illustrated to demonstrate the application of the proposed approach. In Section 6, brief concluding remarks are presented.
2. Preliminaries
In this section, some concepts associated with preference relations are reviewed.
2.1. Associated Concepts
Definition 1
([30]). An IVFPR on the alternative set is presented by an interval-valued fuzzy judgment matrix , where denotes that the preference degree for alternative over falls between and . Moreover, and fulfill the following conditions:
Definition 2
([6]). An IVFPR with is additively consistent if:
As and , for all , Equation (1) can be converted into the following:
Theorem 1
([31]). An IVFPR with is additively consistent if:
or equivalently:
Equations (2)–(4) are equivalent; that is to say, any one of Equations (2)–(4) can be seen as the condition of additive consistency for an IVFPR . Moreover, the elements in Equation (4) only confine the upper triangular part of . Thus, using Equation (4) can simplify the computation.
Definition 3
([6]). An interval priority weight vector with for is said to be normalized if it satisfies the following:
Definition 4
([6]). An IVFPR with is additively consistent if there is a normalized interval priority weight vector with that satisfies:
where reflects the importance of alternative and satisfies the conditions in Equation (5).
2.2. Additive Consistency of an IVIFPR
Definition 5
([15]). Let be a nonempty alternative set. An IVIFPR on the set X is denoted by with , where and are the ranges for the preference and no-preference degrees, respectively, for alternative over . Furthermore, is represented as the interval for the degree of hesitancy in the preference of alternative over . Moreover, and fulfill the conditions as follows:
The pair is called an interval-valued intuitionistic fuzzy value (IVIFV) [32], where and .
Xu and Chen [15] proposed the concepts of the score and accuracy functions, which provide one of the feasible methods to rank IVIFV.
Definition 6
([15]). For an IVIFV , the score function is:
and accuracy function is:
For any two IVIFVs, and .
- If , then the IFIFV is larger than the IFIFV , represented by .
- If , then:
- If , then the IVIFV is larger than the IVIFV , represented by .
- If , then the IVIFV is smaller than the IVIFV , represented by .
- If , then the IVIFV and are equal, represented by .
Bustince [29] pointed out that an IVIFV can be transformed into an IVFV using a proper operator . The operator of an IVIF is defined as:
where the parameter . is an interval-value fuzzy value (IVFV).
Using Equation (9), an IVIFV is transformed into the interval , where reflects the DM’s risk attitude. When , one has , which can be considered the highest preferred degree of IVIFV . When , one has , which can be considered the lowest preferred degree of IVIFV . Therefore, the preference degree of an IVIFV can be rewritten as .
Similarly, for an IVIFPR with , by Equation (9), let:
Therefore, the preference degree of the IVIFPR is denoted by where , and .
Using Equation (10), one can obtain the following matrix , where:
As per Definition 1, it can be easily confirmed that such a matrix is an IVFPR. Because and , the matrix can be viewed as an extracted IVFPR from the IVIFPR .
In order to avoid incoherent results, the consistency of preference relations should be checked. In what follows, according to the extracted IVFPR, a definition of the additive consistency of an IVIFPR is introduced.
Definition 7.
An IVIFPRwithis additively consistent if the IVFPRwithextracted using Equation (11) is additively consistent.
Theorem 2.
An IVIFPRwith is additively consistent if the following condition is satisfied:
where
The proof of Theorem 2 follows from Definition 7 and Equation (4).
3. Determination of the Priority Weights from an IVIFPR
In this section, some mathematical or adjusted programming models are established to extract two special IVFPRs from an IVIFPR. Then, a new linear optimization method is proposed to derive the priority weights using the two extracted IVFPRs.
3.1. Extracting Two Special Cases of IVFPRs from an IVIFPR
With the constant complexity calculation on IVIFV, it is very difficult to directly derive the priority weights from an IVIFPR. To simplify the solution procedure for IVIFPRs, due to Definition 7, it is natural and logical that the extracted consistent IVFPR can take part in deriving the priority weights of the alternatives. Next, we look at how to extract a consistent IVFPR from an IVIFPR.
As per Equation (10), it is sufficient to use only the upper diagonal elements of a given IVIFPR to extract the consistent IVFPR.
According to Equation (11), given an IVIFPR with , when different values of are chosen, numerous matrices with can be extracted from an IVIFPR . In this mapping, reflects the DM’s risk attitude. The larger the value of , the higher the DM’s risk. The smaller the value of , the lower the DM’s risk. When , denoting the absolute risk-taking case for each pairwise comparison of alternatives, one has , which can be interpreted as the largest preferred degree for the pair of alternatives . When , denoting the absolute risk-averse case for each pairwise comparison of alternatives, one has , which can be interpreted as the lowest preferred degree for the pair of alternatives .
Therefore, assume that the interval denotes the preferred degree to the pair of alternatives ; the preferred degree should be between and . That is to say, the preferred degree should meet the condition . Consequently, according to Definition 3.6 in Wang et al. [11], and . Noticing that , and , one has .
According to Definition 7, the consistency of an IVIFPR depends on whether the extracted IVFPR is consistent. Thus, the primary task is to find a suitable value of , which makes the extracted IVFPR consistent to a great extent. However, when there are infinite possible values of , more than one consistent IVFPR can be extracted. In this situation, two special cases are taken into consideration—the absolute risk-taking and the absolute risk-averse cases.
In order to extract the absolute risk-taking IVFPR from an IVIFPR , a mathematical programming model is constructed in the following manner:
Solving the model in Equation (13) using an optimization computer package (e.g., Lingo and MATLAB), we can obtain the optimal solution . Then, as per Equation (11), the absolute risk-taking IVFPR denoted by with can be extracted from the IVIFPR . It is obvious that the extracted IVFPR is consistent.
Analogously, solving the following model in Equation (14), the absolute risk-averse IVFPR denoted by with can be extracted from the IVIFPR . It is obvious that the extracted IVFPR is consistent.
If the nonempty feasible solutions of Equations (13) and (14) can be obtained, then the consistent IVFPRs R′ and R″ can be extracted using Equation (11) in the absolute risk-taking and the absolute risk-averse cases, respectively. Nevertheless, one cannot ensure that the models in Equations (13) and (14) will always have nonempty feasible solutions. If there are empty feasible solutions of Equations (13) and (14), no consistent IVFPRs can be obtained from the initial IVIFPR. To fix this limitation, some relaxed variables , and are introduced into the IVIFV, then each IVIFV in the IVIFPR is transformed into , where , thus converting Equation (11) into:
Therefore, if there are empty feasible solutions of Equations (13) and (14), the adjusted programming models of Equations (16) and (17) are constructed as:
Solving Equations (16) and (17), the optimal solutions can be obtained. Then, through Equation (15), the absolute risk-taking-consistent IVFPR with and the absolute risk-averse-consistent IVFPR with are obtained.
3.2. Deriving the Priority Weights from the Extracted IVFPRs
After discussing the additive consistency of the IVIFPR, the next work should focus on deriving the priority weights of the alternatives. As mentioned above, the matrices and , as two special IVFPRs extracted from the IVIFPR, are both used to derive the priority weights of alternatives. In this subsection, one suitable method is put forward to implement this.
According to Definition 4, an IVFPR with is additively consistent if there is a normalized interval fuzzy priority weight vector with that satisfies Equation (6). In practice, because of the complexity and indeterminacy of the decision-making problems, Equation (6) cannot always hold. Therefore, deviations between and can be introduced as and , respectively. Smaller values of and indicate that the IVFPR is more additively consistent. Moreover, the width degree of the interval fuzzy priority weight vector is denoted by . Entani and Inuiguchi [33] pointed out that the interval priority weight vector is closest to the given IVFPR when the width degree is minimized. That is to say, the narrower the interval priority weights, the clearer the evaluations for the alternatives.
Consequently, in order to find the smallest deviations and and width degree , the following optimization model is constructed to derive the normalized interval priority weights:
As , , , and , one can obtain and .
Therefore, Equation (18) can be simplified by considering only the upper diagonal elements as follow:
Let:
Then:
Then, Equation (19) can be rewritten as a linear programming model:
By solving Equation (20), the interval priority weights can be obtained from the IVFPR . However, there are numerous values of and associated with the extracted IVIFPR . As mentioned above, two special cases of extracted IVFPRs and should participate in deriving the priority weights of alternatives. When , solving Equation (20) yields the optimal solutions , denoted by . When solving Equation (20) yields the optimal solutions , denoted by .
Due to the interval valued priority vector, and refer to the initial IVIFPR. An IVIFPR should give an IVIF weight estimate [34]. Hence, assume that with for is an IVIF priority weight vector, where and can be interpreted as the ranges of the degrees of the membership and the nonmembership for the IVIFPR, respectively. Therefore, the interval valued priority vectors and can be fused to build the normalized one as follows:
with:
where , which can guarantee that the IVIFPR priority weight satisfies . Consequently, the IVIFPR priority weights are obtained from Equation (21).
4. An Innovative Approach for GDM with IVIFPRs
This section concerns addressing GDM problems with IVIFPRs. An extended method is developed to determine DMs’ weights and an innovative approach for GDM with IVIFPRs is proposed.
4.1. Description of GDM Problems with IVIFPRs
Let indicate the set of n non-inferior alternatives and be a group of experts/decision makers with a corresponding weight vector . Suppose that DM provides his/her individual IVIFPR with . Naturally, the priority weight vector of alternatives is an IVIF, and is denoted by , satisfying that and .
In a real GDP process, DMs usually come from various regions and may differ in knowledge structure, working experience, expression, and personal preferences. Thus, there are usually inconsistent opinions between DMs for the same GDM problem. In such a situation, in order to obtain the collective IVIFPR from all the individual IVIFPRs, it is necessary to find a reasonable solution to solve this issue. Bearing the above idea in mind, using the IVIF-weighted averaging operator in Xu and Yager [23], the collective IVIFPR with is obtained, where:
where is the weight of DM .
The DMs’ weight vector plays an important role in obtaining the collective IVIFPR . Section 4.2 aims to determine the DMs’ weights.
4.2. A Method for Determining the DMs’ Weights
Determining the DMs’ weights is a key issue when solving judgment information in GDM problems. Generally, the DM’s weights are composed of both subjective and objective weights. Liu and Li [35] pointed out that deriving the integrated DM’s weights requires three main steps: (i) Adjust given subjective weights; (ii) determine objective weights; and (iii) derive the integrated DM’s weights by combining the adjusted subjective weights with the determined objective weights.
4.2.1. Adjust Given Subjective Weights
Subjective weights are assigned in advance by known information, such as a DM’s reputation, status, occupation, familiarity with the current issue at hand, and so on. By definition, there are biases in subjective weights. Thus, it is unreasonable to assign subjective weights in advance. For instance, when some DMs with high weight have a low group consensus, that is, their judgment information severely deviates from other DMs or the group’s collective opinion, too much attention may be given to their preference, thus generating an irrational and inaccurate final solution. Therefore, the given subjective weights need to be adjusted. Pang and Liang [36] introduced three key evaluation indices—consistency, closeness, and uniformity—to evaluate the decision-making effect of each DM in GDM. In what follows, the consistency index defined in Pang and Liang [36] is extended to adjust given subjective weights.
In the aforementioned GDM problems, for alternatives , , and , if , then we say that comparing with , dominates in the IVIFPR provided by DM . We denoted this by . Then, the dominance relation can be expressed as:
The dominant class of concerning in can be represented as follows:
Therefore, the family set of the dominant classes given by DM for the alternative set X can be obtained as below:
As a result, the consensus index between DMs and can be defined according to the IVIFPRs and .
Definition 8.
In a given GDM problem with IVIFPRs, there are m DMs D = (d1, d2, …, dm) and n alternatives. The consensus index between DMsandis defined as:
where, andmeans the number of elements in the set.
It is easy to confirm that the consensus index fulfills the following properties:
(i) ; (ii) ; (iii) .
Equation (26) denotes the consensus index which can be applied to measure the similarity between DMs and by their individual IVIFPRs. Obviously, the larger the value of , the higher the similarity between DMs and . Thus, let be the support degree of DM supported by other DMs, which can be defined as follows:
Similar to Liu and li [35], Equation (27) is also interpreted as the overall relative importance index of the th DM, supported by the other DMs’ judgment information. That is to say, the larger the value of , the more importance should be assigned to DM . Thus, it can be used to adjust the given subjective weights. Let be the adjusted subjective weights, calculated as follows:
where is the given subjective weight and indicates the average support degree by other DMs.
4.2.2. Determine the DMs’ Objective Weights
In general, objective weights are obtained according to the quality of judgment information provided by each DM. In practical GDM, an individual DM’s opinion should be in accordance with the group’s opinion as much as possible. The group’s opinion usually represents the group’s ideal decision, to facilitate the description, which is presumed to be provided by the ideal DM . Similar to Yue [37], it is reasonable to think that the group’s ideal decision is the average of all individual experts’ decisions. Thus, the group’s ideal decision is denoted by with , where:
Then, by Definition 8, the consensus index between DM and the ideal DM is defined as:
Clearly, the higher the value of , the more important the DM ’s opinion in GDM. In this way, the DM should be assigned a higher weight. Therefore, the objective weight denoted by of the DM can be obtained by normalizing the consensus index :
4.2.3. Derive the Integrated DMs’ Weights
Combining the adjusted subjective weight with the objective weight , an integrated DM’s weight can be derived by the following formula:
where is a control parameter, which can be changed in the specific GDM problem.
4.3. Approach for Group Decision Making with IVIFPRs
Summarizing the aforementioned analysis, an innovative approach is put forward for solving GDM problems with IVIFPRs. The concrete steps are summarized below and graphically depicted in Figure 1.
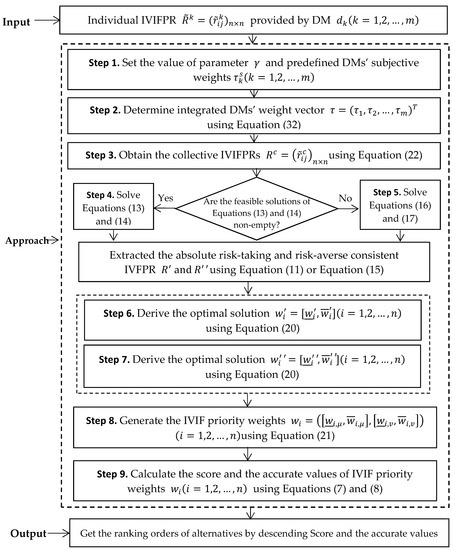
Figure 1.
Decision-making process for group decision-making (GDM) problems.
- Step 1.
- Set the value of parameter and predefine the subjective weights of DMs .
- Step 2.
- Determine the integrated DMs’ weight vector through Equation (32).
- Step 3.
- Using Equation (22), calculate the collective IVIFPRs by the integrated DMs’ weight vector .
- Step 4.
- Obtain the absolute risk-taking-consistent IVFPR and the absolute risk-averse-consistent IVFPR . If there are nonempty feasible solutions of Equations (13) and (14), can be obtained. Then, the absolute risk-taking-consistent IVFPR and the absolute risk-averse-consistent IVFPR can be extracted using Equation (11) and then skip to step 6. Otherwise, go to step 5.
- Step 5.
- Construct the adjusted programming models of Equations (16) and (17) to obtain the values of , then the absolute risk-taking-consistent IVFPR and the absolute risk-averse-consistent IVFPR can be extracted using Equation (15). Then, go to step 6.
- Step 6.
- Using the absolute risk-taking-consistent IVFPR , solving Equation (20) yields the optimal solutions .
- Step 7.
- Using the absolute risk-averse-consistent IVFPR , solving Equation (20) yields the optimal solutions .
- Step 8.
- Through Equation (21), the IVIF priority weights are derived.
- Step 9.
- Using Equations (7) and (8), calculate the score and accurate values of IVIF priority weights and obtain the ranking orders.
4.4. Advantages of the Proposed Approach
In this paper, a feasible approach for GDM with IVIFPRs is proposed. In comparison to existing works, some advantages can be summarized in the following:
- (1)
- The studies in References [17,19,21] neglected the consistency of associated IFPRs (IVFPRs or FPRs) from the original IVIFPR, which may cause distortion of the decision-making results. In this paper, according to the conditions of the additively consistent IVFPR, two special IVFPRs (the absolute risk-taking-consistent IVFPR and the absolute risk-averse-consistent IVFPR) can be extracted from the original IVIFPR using Equations (14) and (15). In particular, if there are empty feasible solutions of Equations (14) and (15), two adjusted programming models, Equations (16) and (17) are constructed. Such adjustment can ensure that the two extractive IVFPRs are additively consistent and can also facilitate the subsequent discussion.
- (2)
- Due to the complicated calculation on IVIFPRs, there are huge difficulties in deriving the priority weights of alternatives. In general, for GDM with IVIFPRs, when the input information is IVIF, the output information is supposed to be IVIF. In this paper, a workable method has been put forward to derive the priority weight vector with respect to IVIFVs from the IVIFPR. Based on the extraction above, a linear optimization model, Equation (20), is constructed to derive interval priority weights corresponding to the absolute risk-taking-consistent IVFPR and the absolute risk-averse-consistent IVFPR. This optimization model considers the deviations between individual judgment as well as the width degrees of interval priority weights, whereas the methods in existing literature [19,38] merely minimized the deviations between individual judgment, neglecting the width degrees. Since the IVIFV can demonstrate more uncertain information, then, according to the two interval priority weights and Equation (21), an IVIF priority weight is obtained and can avoid information loss to some extent.
- (3)
- Generally, DMs’ weights are composed of subjective and objective weights. In existing literature on GDM with IVIFPRs, the DMs’ weights are given in advance [10,12,16], determined by complex optimal models [17,19,21], or determined by a distance-based method [20,22]. Further, these studies mostly considered the subjective weight or the objective weight. In this paper, an extended approach for group decision making has been put forward, which considers both the subjective and objective weights. Owing to the existent biases of subjective weights, an approach for adjusting the subjective weight is proposed in Equation (28) and the objective weight is obtained through Equation (31). Then, the weights with respect to all DMs are determined by Equation (32). To some extent, the subjective and objective weights are sufficiently considered in the proposed model, which can reflect the DM’s overall competence and also be rational and effective.
5. Practical Example for GDM with IVIFPRs
In this section, a supplier selection example is provided to show the application of the proposed method. Then, comparative analyses are executed to illustrate the merits of the proposed method.
5.1. A Practical Example of Supplier Selection
With the development of today’s global market and fierce competition and challenges, supply chain management (SCM) has received extensive attention by many scholars. In this scenario, strengthening the cooperation with suppliers, especially strategic suppliers, plays an important role in SCM. Therefore, it is a critical tool to select a suitable supplier that meets the requirements of an enterprise’s development and exhibits the broader development perspective. Consider a company facing the supplier selection problem. After filtering and pre-evaluation, there are four potential alternatives for further selection. Additionally, three experts or DMs with different professional knowledge constitute an evaluation committee. They compare any two alternatives and provide individual IVIFPRs as follows:
In what follows, the proposed method in this paper is employed to solve this example.
- Step 1.
- Set the value of parameter and the predefined objective weights of DMs are .
- Step 2.
- Determine the integrated DMs’ weight vector .
- (i)
- Through Equation (28), the adjusted subjective weights of DMs are calculated as:
- (ii)
- Through Equation (31), the objective weights of DMs are generated as follows:
- (iii)
- Through Equation (32), the integrated DMs’ weights are calculated as follows:
- Step 3.
- Utilizing Equation (22), the collective IVIFPR is calculated as:
- Step 4.
- When constructing the two programming models of Equations (13) and (14), both the feasible solutions of are empty. Hence, we go to step 5.
- Step 5.
- Establishing the two adjusted programming models of Equations (16) and (17), we derive the respective values of . Then, through Equation (15), the absolute risk-taking-consistent IVFPR and the absolute risk-averse-consistent IVFPR are obtained:
- Step 6.
- Using the absolute risk-taking-consistent IVFPR , a fuzzy programming model is constructed by Equation (20) and solved using Lingo 11 software. The optimal solutions are derived as , , , .
- Step 7.
- Using the absolute risk-averse-consistent IVFPR , a linear programming model is constructed by Equation (20) and solved using Lingo 11 software. The optimal solutions are derived as , , , .
- Step 8.
- Through Equation (21), the IVIFPR priority weights are derived as follows:
- Step 9.
- According to Definition 6, the score functions of the IVIFV belong to interval [−1,1], and its associating weight should be a non-negative number. Therefore, the score function defined in Definition 6 should be modified to facilitate this situation without changing any of the following basic properties:
Through Equation (33), the score function and accuracy degrees of of are obtained as , , , , , , , and . Thus, as the scores function and accuracy degrees descend, the ranking order of alternatives is , and is the best alternative.
Additionally, for different values of the parameter in Equation (32), the results in the corresponding calculation are shown in Table 1 and described in Figure 2 and Figure 3. Table 1 and Figure 3 show that the best alternative is except when the parameter (i.e., the ranking order is and the best alternative is ). When , the ranking orders derived from the DMs’ absolutely subjective weights are . When , the ranking orders derived from the DMs’ absolutely objective weights are . When and , the ranking order is . When , the ranking order is . The above conclusions indicate that taking different values of the parameter is necessary. Moreover, from Figure 2 for different values of the parameter , it is observed that the DMs’ weights are changed from subjective to objective. Consequently, the above results demonstrate that the method proposed in this paper is an applicative and effective tool to solve GDM problems with IVIFPRs in practice.

Table 1.
Ranking orders of alternatives for different values of the parameter .
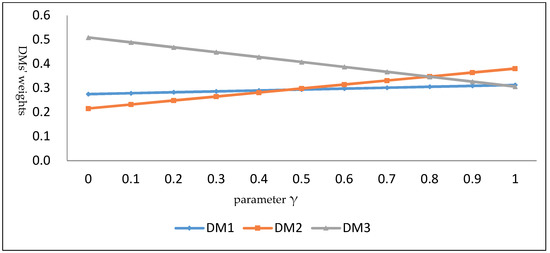
Figure 2.
Decision makers’ (DMs’) weights for different values of the parameter γ.
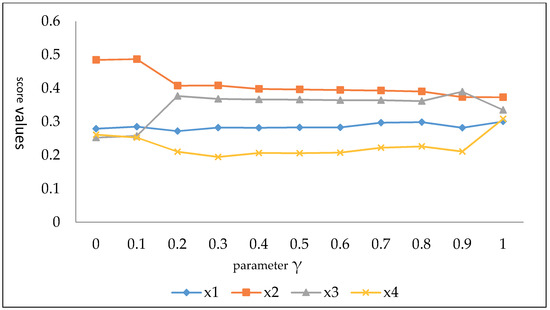
Figure 3.
Ranking orders of alternatives for different values of the parameter γ.
5.2. Comparative Analyses
This subsection aims to reveal the advantages of the proposed method by conducting comparative analyses with Wan’s method [19] and Chu’s method [21].
Wan and Chu [19,21] focused on GDM with the additive consistency of IVIFPRs. Using Wan’s method [19] to address the example in Section 5.1 for different values of the parameter , which is a control parameter that trades off majority versus minority principles defined in Wan’s method [19], the corresponding results are presented in Table 2. Similarly, using Chu’s method [21], the ranking order of alternatives is ; the best alternative is also .

Table 2.
Computation results with different values of the parameter by Wan’s method [19].
Table 2 shows that the ranking orders are always when choosing different values of the parameter by Wan’s method [19], and the best alternative is , which is the same conclusion as Chu’s method [21], as well as the proposed method. However, comparing with Wan and Chu [19,21], there are still some merits, as described in the following:
- (1)
- Wan’s Method [19] extracted two special IVFPRs (the lowest preferred and the highest preferred) from the original IVIFPR, and Chu’s method [21] divided the original IVIFPR into two parts—the membership degree part and nonmembership degree part—which contain two fuzzy preference matrices—the lower and the upper, respectively. There is no guarantee that the extracted two special IVFPRs in Wan’s Method [19] and the divided four fuzzy preference matrices in Chu’s Method [21] are consistent. As we know, consistency, as a pioneer of proper judgment, would influence the rationality of the decision results. In this paper, in order to extract two special cases of IVFPRs (the absolute risk-taking and the absolute risk-averse), we establish two mathematically optimal models by the additive transitivity condition of the IVFPR. What is more, the parameter defined in this paper is flexible. When parameter is fixed, for instance, and , the conclusions about the two special extracted IVFPRs of this paper are the same as those in Wan’s method [19], that is to say, Wan’s method [19] is a special case of the proposed method. Therefore, the extracted method by Equations (13) and (14), or (15) and (16) in this paper, is flexible and reasonable.
- (2)
- Regarding the determination of the priority weights, both Wan’s method [19] and Chu’s method [21] merely considered the deviations between individual judgment using associated matrices. This paper constructs a linear optimization model by minimizing the deviations between individual judgments as well as the width degrees of interval priority weights. Narrowing the width degrees can clarify the evaluations for the alternatives. Therefore, the constructed model is more rational and convincing.
- (3)
- When determining the integrated DMs’ weights, Wan’s and Chu’s methods [19,21] only considered the DMs’ objective weights, ignoring the DMs’ subjective weights. However, in this paper, given that there are biases in a priori subjective weights, we first adjust the subjective ones according to the definition of the consensus index, and then derive the objective weights. Finally, both weights are incorporated into the integrated DM’s weights by taking the control parameter into consideration, which can provide various choices for DMs in handling GDM problems.
6. Conclusions
This paper discusses additively consistent IVIFPRs and proposes an innovative approach for GDM problems with IVIFPRs. The main contributions of this paper are as follow:
- (1)
- The additive consistency concept of an IVIFPR has been defined according to the additive transitivity of an IVFPR.
- (2)
- Some mathematically optimal models are constructed to extract two special consistent IVFPRs (the absolute risk-taking-consistent IVFPR and the absolute risk-averse-consistent IVFPR) from the original IVIFPR.
- (3)
- In terms of deriving the priority weights of an IVIFPR, taking two special extracted IVFPRs into consideration, a linear optimization model is established by minimizing the deviations between individual judgment and the width degrees of interval priority weights.
- (4)
- In the GDM method, considering both the adjusted subjective weights and the objective weights, an integrated method is proposed to determine the DMs’ weights.
As incomplete IVIFPRs are ignored in the current approach, in future research, we will develop the proposed method to solve GDM problems with incomplete IVIFPRs. Moreover, there are other features in GDM problems, such as the social influence of DMs, such as that modeled by Capuano, N. et al. [39] and Pérez, L.G. et al. [40]. In this situation, the interactions between DMs should be taken into consideration. Although consideration of these interactions makes decision making more complicated, it provides a more reasonable approach to describing the decision-making environment.
Funding
This research was funded by the National Nature Science Foundation of China: (No. 71403055 and 71872047), the Humane and Social Science Fund Project of the Education Ministry (No. 15YJA630062), and Fujian Provincial Social Science Planning Project of China (No. FJ2018MGCZ010).
Acknowledgments
The author would like to thank the anonymous reviewers for their constructive comments, which greatly helped to improve this paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Tanino, T. Fuzzy Preference Orderings in Group Decision-Making. Fuzzy Sets Syst. 1984, 12, 117–131. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy-Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval Valued Intuitionistic Fuzzy-Sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Wang, Z.J.; Li, K.W. Goal programming approaches to deriving interval weights based on interval fuzzy preference relations. Inf. Sci. 2012, 193, 180–198. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F.; Liao, H. Isomorphic Multiplicative Transitivity for Intuitionistic and Interval-Valued Fuzzy Preference Relations and Its Application in Deriving Their Priority Vectors. IEEE Trans. Fuzzy Syst. 2018, 26, 193–202. [Google Scholar] [CrossRef]
- Wan, S.; Wang, F.; Dong, J. A group decision making method with interval valued fuzzy preference relation based on the geometric consistency. Inf. Fusion 2017, 40, 87–100. [Google Scholar] [CrossRef]
- Liu, F.; Aiwu, G.; Lukovac, V.; Vukic, M. A multicriteria model for the selection of the transport service provider: A single valued neutrosophic DEMATEL multicriteria model. Decis. Mak. 2018, 1, 121–130. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S.; Xia, M.M. Multiplicative consistency of interval-valued intuitionistic fuzzy preference relation. J. Intell. Fuzzy Syst. 2014, 27, 2969–2985. [Google Scholar]
- Wang, Z.J.; Li, K.W.; Wang, W.Z. An approach to multiattribute decision making with interval-valued intuitionistic fuzzy assessments and incomplete weights. Inf. Sci. 2009, 179, 3026–3040. [Google Scholar] [CrossRef]
- Xu, Z.; Cai, X. Group Decision Making with Incomplete Interval-Valued Intuitionistic Preference Relations. Group Decis. Negotiat. 2015, 24, 193–215. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. Soft computing based on maximizing consensus and fuzzy TOPSIS approach to interval-valued intuitionistic fuzzy group decision making. Appl. Soft Comput. J. 2015, 26, 42–56. [Google Scholar] [CrossRef]
- De Miguel, L.; Bustince, H.; Fernandez, J.; Indurain, E.; Kolesarova, A.; Mesiar, R. Construction of admissible linear orders for interval-valued Atanassov intuitionistic fuzzy sets with an application to decision making. Inf. Fusion 2016, 27, 189–197. [Google Scholar] [CrossRef]
- Ze-Shui, X.; Chen, J. Approach to Group Decision Making Based on Interval-Valued Intuitionistic Judgment Matrices. Syst. Eng. Theory Pract. 2007, 27, 126–133. [Google Scholar]
- Xu, Z.S.; Cai, X.Q. Incomplete interval-valued intuitionistic fuzzy preference relations. Int. J. Gen. Syst. 2009, 38, 871–886. [Google Scholar] [CrossRef]
- Wan, S.P.; Xu, G.L.; Dong, J.Y. A novel method for group decision making with interval-valued Atanassov intuitionistic fuzzy preference relations. Inf. Sci. 2016, 372, 53–71. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z. Priorities of Intuitionistic Fuzzy Preference Relation Based on Multiplicative Consistency. IEEE Trans. Fuzzy Syst. 2014, 22, 1669–1681. [Google Scholar] [CrossRef]
- Wan, S.P.; Wang, F.; Dong, J.Y. Additive consistent interval-valued Atanassov intuitionistic fuzzy preference relation and likelihood comparison algorithm based group decision making. Eur. J. Oper. Res. 2017, 263, 571–582. [Google Scholar] [CrossRef]
- Wan, S.P.; Wang, F.; Dong, J.Y. A Three-Phase Method for Group Decision Making With Interval-Valued Intuitionistic Fuzzy Preference Relations. IEEE Trans. Fuzzy Syst. 2018, 26, 998–1010. [Google Scholar] [CrossRef]
- Chu, J.; Liu, X.; Wang, L.; Wang, Y. A Group Decision Making Approach Based on Newly Defined Additively Consistent Interval-Valued Intuitionistic Preference Relations. Int. J. Fuzzy Syst. 2017, 20, 1027–1046. [Google Scholar] [CrossRef]
- Meng, F.Y.; Tang, J.; Wang, P.; Chen, X.H. A programming-based algorithm for interval-valued intuitionistic fuzzy group decision making. Knowl.-Based Syst. 2018, 144, 122–143. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Intuitionistic and interval-valued intutionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group. Fuzzy Optim. Decis. Mak. 2009, 8, 123–139. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F. Non-Dominance and Attitudinal Prioritisation Methods for Intuitionistic and Interval-Valued Intuitionistic Fuzzy Preference Relations; Pergamon Press, Inc.: Oxford, UK, 2012; pp. 13409–13416. [Google Scholar]
- Wan, S.P.; Wang, F.; Xu, G.L.; Dong, J.Y.; Tang, J. An intuitionistic fuzzy programming method for group decision making with interval-valued fuzzy preference relations. Fuzzy Optim. Decis. Mak. 2017, 16, 269–295. [Google Scholar] [CrossRef]
- Qiu, J.D.; Li, L. A new approach for multiple attribute group decision making with interval-valued intuitionistic fuzzy information. Appl. Soft Comput. 2017, 61, 111–121. [Google Scholar] [CrossRef]
- Mukhametzyanov, I.; Pamucar, D. A sensitivity analysis in MCDM problems: A statistical approach. Decis. Mak. Appl. Manag. Eng. 2018, 1. [Google Scholar] [CrossRef]
- Roy, J.; Adhikary, K.; Kar, S.; Pamucar, D. A rough strength relational DEMATEL model for analysing the key success factors of hospital service quality. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–142. [Google Scholar] [CrossRef]
- Bustince, H. Conjuntos Intuicionistas e Intervalo Valorados Difusos: Propiedades y Construccion, Relaciones Intuicionistas Fuzzy. Ph.D. Thesis, Public University of Navarre, Navarra, Spain, 1994. [Google Scholar]
- Xu, Z. On Compatibility of Interval Fuzzy Preference Relations. Fuzzy Optim. Decis. Mak. 2004, 3, 217–225. [Google Scholar] [CrossRef]
- Wang, Z.J. A note on “Incomplete interval fuzzy preference relations and their applications”. Comput. Ind. Eng. 2014, 77, 65–69. [Google Scholar] [CrossRef]
- Yager, R.R. Induced aggregation operators. Fuzzy Sets Syst. 2003, 137, 59–69. [Google Scholar] [CrossRef]
- Entani, T.; Inuiguchi, M. Pairwise comparison based interval analysis for group decision aiding with multiple criteria. Fuzzy Sets Syst. 2015, 274, 79–96. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M.S. A goal programming method for obtaining interval weights from an interval comparison matrix. Eur. J. Oper. Res. 2007, 177, 458–471. [Google Scholar] [CrossRef]
- Liu, W.; Li, L. An Approach to Determining the Integrated Weights of Decision Makers Based on Interval Number Group Decision Matrices; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 2015; pp. 92–98. [Google Scholar]
- Pang, J.; Liang, J. Evaluation of the results of multi-attribute group decision-making with linguistic information. Omega 2012, 40, 294–301. [Google Scholar] [CrossRef]
- Yue, Z.L. Deriving decision maker’s weights based on distance measure for interval-valued intuitionistic fuzzy group decision making. Expert Syst. Appl. 2011, 38, 11665–11670. [Google Scholar] [CrossRef]
- Zhang, H. A goal programming model of obtaining the priority weights from an interval preference relation. Inf. Sci. 2016, 354, 197–210. [Google Scholar] [CrossRef]
- Capuano, N.; Chiclana, F.; Fujita, H.; Herrera-Viedma, E.; Loia, V. Fuzzy Group Decision Making with Incomplete Information Guided by Social Influence. IEEE Trans. Fuzzy Syst. 2018, 26, 1704–1718. [Google Scholar] [CrossRef]
- Pérez, L.G.; Mata, F.; Chiclana, F.; Kou, G.; Herrera-Viedma, E. Modelling influence in group decision making. Soft Comput. 2016, 20, 1653–1665. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).