Improved Joint Probabilistic Data Association (JPDA) Filter Using Motion Feature for Multiple Maneuvering Targets in Uncertain Tracking Situations

Abstract

To track multiple maneuvering targets in cluttered environments with uncertain measurement noises and uncertain target dynamic models, an improved joint probabilistic data association-fuzzy recursive least squares filter (IJPDA-FRLSF) is proposed. In the proposed filter, two uncertain models of measurements and observed angles are first established. Next, these two models are further employed to construct an additive fusion strategy, which is then utilized to calculate generalized joint association probabilities of measurements belonging to different targets. Moreover, the obtained probabilities are applied to replace the joint association probabilities calculated by the standard joint probabilistic data association (JPDA) method. Considering the advantage of the fuzzy recursive least squares filter (FRLSF) on tracking a single maneuvering target, which can relax the restrictive assumption of measurement noise covariances and target dynamic models, FRLSF is still used to update the state of each target track. Thus, the proposed filter can not only provide the advantage of FRLSF but can also adjust the weights of measurements and observed angles in the generalized joint association probabilities adaptively according to their uncertainty. The performance of the proposed filter is evaluated in two experiments with simulation data and real data. It is found to be better than the performance of other three filters in terms of the tracking accuracy and the average run time.

1. Introduction

The multiple maneuvering target tracking (MMTT) becomes a critical problem of multiple target tracking in cluttered environments because of various uncertainties in the tracking process [1,2,3,4] such as uncertain measurement noises and uncertain target dynamic models. In practical tracking situation, the noise covariances of measurements are unknown, and they are uncertain. Similarly, the real target dynamic models are unknown or only assumed, and they are also uncertain. The main procedure of MMTT consists of data association and state estimation. Data association denotes distinguishing the real sources of measurements from targets or clutters, namely that the real source may be the real target, the false target or the clutter generated by the observed environment. It mainly concerns the problems related to clutter, noises and errors in the tracking process [5]. Currently, the existing data association methods include the standard nearest neighbor (NN) method [6], the probabilistic data association (PDA) method [7,8] and the joint probabilistic data association (JPDA) method [8,9,10]. In particular, the JPDA method is a well-known and effective data association method for multiple target tracking. It employs an association gate to prune away impossible hypotheses and then calculates the probability of a possible hypothesis on each target. However, it only uses the current measurements belonging to the target and does not utilize the historical measurements and the related motion information to calculate the association probabilities. Hence, it is still a suboptimal Bayesian algorithm [10].

Following data association, state estimation is used to estimate the target states according to the associated measurements. Under the hypothesis that both measurement noise covariances and target dynamic models are known, the traditional maneuvering target tracking methods can achieve perfect tracking performance [11]. Unfortunately, this hypothesis is difficult to satisfy in practical applications because of various uncertainties in the tracking process [2,3]. To solve the uncertain target dynamic model problem in target tracking, one strategy is to describe the unknown dynamic model of a target trajectory as several typical dynamic models with known parameters or their combination. The interacting multiple model (IMM) method is a representative algorithm to solve this problem, and its modified versions are continually developed in many practical applications [12]. However, once the IMM and its modified versions employ the assumed mismatched dynamic models, their tracking performance becomes undesirable [13]. The other strategy is to assume the unknown parameters of the target dynamic model as the random variables with a certain probability distribution function [14]. Unfortunately, because the actual target dynamic models and the tracking environments change over time, it is difficult to obtain the prior information of the unknown parameters in practical applications. In addition, the particle filter is also broadly applied in maneuvering target tracking [15]. For nonlinear non-Gaussian motion models, an interacting multiple model particle filter (IMM-PF) was proposed in [16,17]. However, since the computational complexity of the IMM-PF is increased in proportion to the number of particles in target tracking, it is still difficult for IMM-PF to satisfy the requirements of a real-time tracking system.

According to the above analysis, one must combine data association and state estimation for MMTT. The interacting multiple model-joint probabilistic data association filter (IMM-JPDAF) is a typical tracking method in MMTT and many of its modified versions have been proposed for different application scenarios [18]. However, most the MMTT methods are based on the statistical framework of the statistics theory under the assumption that the known measurement noise covariance and target dynamic models are known. In fact, the related prior information of measurement noises and target dynamic models are difficult to obtain in practical applications. This presents a great difficulty in implementing MMTT. Moreover, each node in a sensor network must process a growing number of data because of the large surveillance scale and a great number of sensors. In this big data situation riddled with imprecision and uncertainty, the traditional MMTT methods have higher computational complexity and processing requirements of the computation complexities while the MMTT methods based on the statistical theory become increasingly complicated. Considering that the fuzzy theory possesses the unique advantage in processing inaccurate and uncertain information, it has been widely applied in target tracking [19,20,21,22,23]. The fuzzy recursive least squares filter method (FRLSF) proposed in [22] utilizes measurement residuals and heading changes as two input variables of the designed fuzzy system, and this system is further employed to adjust the fading factor and realize single maneuvering target tracking. The improvement of FRLSF combined with the PDA algorithm is utilized in cluttered environments [24], thus providing an effective method to solve the MMTT problem.

The incorporation of the motion features on a moving target into a MMTT method is a good strategy to improve the accuracy of data association [22]. In particular, the observed angle is an important motion feature on maneuvering targets and is often employed in maneuvering target tracking [24,25]. Therefore, it can be introduced into the calculation of association probabilities to improve the association accuracy. Based on these facts, we have presented at a conference the generalized joint probabilistic data association-FRLSF (GJPDA-FRLSF) for communication [25]. This filter attempts to incorporate multiple motion features into the calculation of association probabilities and is able to achieve better tracking accuracy. However, it is difficult to illustrate how and why they can improve the performance of association results. By modifying GJPDA-FRLSF, we further propose the improved JPDA-FRLSF (IJPDA-FRLSF) for MMTT. The GJPDA-FRLSF method only employs the observed angles and measurements to calculate the association probabilities and adopts simulation data to analyze the effectiveness of the weights of the observed angles and measurements in the association results by the additive fusion strategy. For clarity, this paper extends and updates the previous work [25]. In addition, a real-data experiment is added to illustrate the feasibility of the proposed IJPDA-FRLSF. In IJPDA-FRLSF, two uncertain models of measurements and observed angles are estimated. Next, an adaptive additive fusion strategy is developed to calculate the generalized joint association probabilities for reconstructing the joint association probabilities of measurements belonging to different targets in JPDA. Hence, IJPDA-FRLSF can adjust the weights of measurements and observed angles in the association results according to their uncertainty. In addition, considering the advantage of the FRLSF method mentioned above, it is employed to update the state of each target trajectory.

The rest of this paper is organized as follows. In Section 2, two uncertain models of measurements and observed angles are established, and an uncertain fusion strategy is constructed to calculate the generalized joint association probability. Section 3 presents a simplified form of FRLSF. IJPDA-FRLSF is proposed for MMTT in Section 4. Section 5 presents the experimental results and the performance comparisons with the existing algorithms. Finally, the conclusions are provided in Section 6.

2. Uncertain Models and Fusion of Measurements and Observed Angles

In practical applications, the performance of a MMTT method greatly depends on the quality of uncertain measurements from each sensor. Hence, one must measure the uncertainty of measurements first. Considering that observed angles are extracted from uncertain measurements, they also possess uncertainty to some extent, which is defined in the following subsection. As a result, one must measure the uncertainties of measurements and observed angles and then combine them to calculate the associated probabilities.

2.1. Uncertain Models of Measurements and Observed Angles

To provide a quantitative description of the uncertainties of measurements and observed angles at all times in a cluttered environment, such as shown in Figure 1 (only the measurements and the clutters in the given associated gate are shown here), we make the following definitions:

Definition 1. 

The uncertain measure ${\omega }_k$ of measurements is defined by

$${\omega }_k=H(p_k^t)/{\sigma }_k$$

(1)

Here,$p_k^t$is the simple expression of$p({\mathit{z}}_{k,i}|{\mathit{x}}_k^t)$,${\mathit{z}}_{k,i}$and$p({\mathit{z}}_{k,i}|{\mathit{x}}_k^t)$denote the$i$th measurement and its statistical probability belonging to the state${\mathit{x}}_k^t$of the target$t$. ${\sigma }_k$ and $H(p_k^t)$ denote the standard deviation and the statistical entropy of measurements, respectively, calculated by

$${\sigma }_k={\displaystyle \sum _{i=1}^{m_k}{\left[{({\mathit{z}}_{k,i}-{\widehat{\mathit{z}}}_{k|k-1}^t)}^{\mathrm{T}}({\mathit{z}}_{k,i}-{\widehat{\mathit{z}}}_{k|k-1}^t)\right]}^{1/2}}/m_k{g}_z$$

(2)

$$H(p_k^t)=-{\displaystyle \sum _{i=1}^{m_k}p({\mathit{z}}_{k,i}|{\mathit{x}}_k^t)\ln p({\mathit{z}}_{k,i}|{\mathit{x}}_k^t)}$$

(3)

where ${\widehat{\mathit{z}}}_{k|k-1}^t$ and $m_k$ denotes the predicted measurement and the number of measurements, respectively while $g_z$ is the given association gate. In Equation (1), ${\sigma }_k$ describes the clustering feature of measurements at time $k$, and $H(p_k^t)$ describes the distribution of statistical probabilities assigned to the measurements. For easy calculation in the following section, one can normalize the uncertain measure ${\omega }_k$ by ${\omega }_k^{\prime }={\omega }_k/{\omega }_{\max }$, where ${\omega }_{\max }$ is the maximum value for all observed times.

Definition 2. 

The uncertain measure${\tilde{\omega }}_k$of the observed angles is defined by

$${\tilde{\omega }}_k=\tilde{H}(u_k^t)/{\tilde{\sigma }}_k$$

(4)

Here,$u_k^t$is the simple expression of$u({\varphi }_{k,i}|{\mathit{x}}_k^t)$,$u({\varphi }_{k,i}|{\mathit{x}}_k^t)$is the corresponding fuzzy membership degree belonging to the state${\mathit{x}}_k^t$of the target$t$. ${\tilde{\sigma }}_k$and$\tilde{H}(u_k^t)$denote the standard deviation and the fuzzy entropy of observed angles calculated by

$${\tilde{\sigma }}_k={\displaystyle \sum _{i=1}^{n_k}{\left[({\varphi }_{k,i}-{\widehat{\varphi }}_{k|k-1}^t)({\varphi }_{k,i}-{\widehat{\varphi }}_{k|k-1}^t)\right]}^{1/2}}/n_k{g}_{\theta }$$

(5)

$$\tilde{H}(u_k^t)=-{\displaystyle \sum _{i=1}^{n_k}u({\varphi }_{k,i}|{\mathit{x}}_k^t)\ln u({\varphi }_{k,i}|{\mathit{x}}_k^t)}$$

(6)

where${\varphi }_{k,i}$denotes the$i$th observed angle, and${\widehat{\varphi }}_{k|k-1}^t$denotes the course angle for the target$t$, as shown in Figure 2, which can be calculated by Equations (7) and (8). In addition, $n_k$is the number of observed angles, and$g_{\varphi }$ is the given association gate.

$${\varphi }_{k,i}=\arctan \left[(y_{k,i}-{\widehat{y}}_{k-1}^t)/(x_{k,i}-{\widehat{x}}_{k-1}^t)\right]$$

(7)

$${\widehat{\varphi }}_{k|k-1}^t=\arctan \left[({\widehat{y}}_{k|k-1}^t-{\widehat{y}}_{k-1}^t)/({\widehat{x}}_{k|k-1}^t-{\widehat{x}}_{k-1}^t)\right]$$

(8)

where $x_{k,i}$, ${\widehat{x}}_{k|k-1}^t$ and ${\widehat{x}}_{k-1}^t$ are the components of measurement ${\mathit{z}}_{k,i}$, predicted state ${\widehat{\mathit{x}}}_{k|k-1}^t$ and state estimate ${\widehat{\mathit{x}}}_{k-1}^t$ in the x-axis direction, respectively, and $y_{k,i}$, ${\widehat{y}}_{k|k-1}^t$ and ${\widehat{y}}_{k-1}^t$ are their corresponding components in the y-axis direction. From Equation (4), ${\tilde{\sigma }}_k$ describes the clustering feature of the observed angles, $\tilde{H}(u_k^t)$ describes the distribution of the fuzzy membership degrees assigned to the observed angles. For easy calculation in the following section, one can normalize uncertain measure ${\tilde{\omega }}_k$ by ${\tilde{\omega }}_k^{\prime }={\tilde{\omega }}_k/{\tilde{\omega }}_{\max }$, where ${\tilde{\omega }}_{\max }$ is the maximum value for all observed times.

2.2. Analyzing the Influence of Clutters on Measurements and Observed Angles

To analyze the influence of clutter on two uncertain models established in Section 2.1, we consider an example of a target moving with constant velocity in cluttered environments with five different clutter densities as shown in Figure 1. Figure 3 and Figure 4 show the corresponding variation curves of the uncertain measures of measurements and observed angles calculated by Equations (1) and (4), respectively.

As shown in Figure 3, both the non-normalizing and normalizing uncertain measure values increase with an increasing clutter density according to their corresponding variation curves, although the increasing rate of the latter becomes relatively weaker because of normalization. Moreover, the uncertain measure value can vary with the clutter density at different times. Similarly to the uncertain measure of measurements, the non-normalizing and the normalizing uncertain measure values of observed angles both present the same change trend of the clutter density. Hence, we can utilize the uncertain measures of measurements and observed angles to describe their uncertainty accurately.

2.3. Uncertain Fusion of Measurements and Observed Angles

In multiple-sensor multiple-target tracking, information fusion is usually applied to improve the tracking performance by fusing multisource information [1]. To improve the association accuracy, one can incorporate multisource information to calculate the association probabilities of the measurements belonging to different targets. Two fusion strategies including multiplicative fusion and additive fusion are often utilized to integrate multisource information as follows [26]:

$$p({\mathit{s}}_k^1,\cdots ,{\mathit{s}}_k^l|{\mathit{x}}_k^t)=\underset{i=1}{\overset{l}{\mathsf{\Pi }}}p({\mathit{s}}_k^i|{\mathit{x}}_k^t)$$

(9)

$$p({\mathit{s}}_k^1,\dots ,{\mathit{s}}_k^l|{\mathit{x}}_k^t)={\displaystyle \sum _{i=1}^l{w}_{k,i}p({\mathit{s}}_k^i|{\mathit{x}}_k^t)}$$

(10)

where $w_{k,i}$ is the weight of the information ${\mathit{s}}_k^i$, $p({\mathit{s}}_k^i|{\mathit{x}}_k^t)$ denotes the probability of the information ${\mathit{s}}_k^i$ belonging to the state ${\mathit{x}}_k^t$ of the target $t$, and $l$ denotes the order of the type of information.

Normally, the multiplicative fusion requires different information to be conditionally independent; however, most of the motion information in the tracking process is correlated in practical applications [27]. Hence, one can utilize additive fusion to process measurements and observed angles in a uniform frame for the calculation the probability ${\rho }_{k,i}^t$:

$$\rho ({\mathit{z}}_{k,i},{\varphi }_{k,i}|{\mathit{x}}_k^t)=\left[w_{k,1}p({\mathit{z}}_{k,i}|{\mathit{x}}_k^t)+w_{k,2}u({\varphi }_{k,i}|{\mathit{x}}_k^t)\right]/c_{\rho }$$

(11)

Here, $w_{k,1}={({\omega }_k^{\prime })}^{-1}$; $w_{k,2}={({\tilde{\omega }}_k^{\prime })}^{-1}$; ${\rho }_{k,i}^t$ is also called as the generalized joint association probability; $c_{\rho }$ is a normalizing constant. According to Equation (11), one can adjust the weights of the statistical probability and the fuzzy membership degree adaptively in the generalized joint association probability according to their uncertainty.

3. Fuzzy Recursive Least Squares Filter (FRLSF)

Assuming that there is a single target $t$ in the surveillance field, its dynamic model and measurement model are defined as follows:

$${\mathit{x}}_{k+1}^t={\Phi }_k^t{\mathit{x}}_k^t+{\mathit{w}}_k^t$$

(12)

$${\mathit{z}}_{k,t}=H_k^t{\mathit{x}}_k^t+{\mathit{v}}_k^t$$

(13)

where ${\mathit{x}}_k^t$ denotes an n-dimensional state vector of the target $t$, ${\mathit{z}}_{k,t}$ denotes an m-dimensional measurement vector, ${\Phi }_k^t$ is an $n\times n$ state transition matrix, and $H_k^t$ is an $m\times n$ measurement transition matrix. The process noise ${\mathit{w}}_k^t$ is assumed to be a Gaussian noise with zero mean and covariance $Q_k^t$, and the measurement noise ${\mathit{v}}_k^t$ is assumed to be a Gaussian noise with zero mean and covariance $R_k^t$.

$$E\left({\mathit{w}}_k^t{({\mathit{w}}_j^t)}^{\mathrm{T}}\right)=Q_k^t{\delta }_{kj}$$

(14)

$$E\left({\mathit{v}}_k^t{({\mathit{v}}_j^t)}^{\mathrm{T}}\right)=R_k^t{\delta }_{kj}$$

(15)

where ${\delta }_{kj}$ denotes the Kronecker delta function.

To track a single maneuvering target in situations with unknown measurement noise covariances, the FRLSF method proposed in [24] employs a fuzzy reference to adjust the fading factor of the recursive least squares filter (RLSF). It achieves good tracking performance if no clutter is present in surveillance. Next, the filter is further extended for cluttered environments, and its simplified form is deduced in [24]. The main equations of the FRLSF are given as follows:

$${\widehat{\mathit{x}}}_k^t={\widehat{\mathit{x}}}_{k-1}^t+K_k^t{V}_k^t$$

(16)

$$P_k^t={({\tilde{\lambda }}_k^t)}^{-1}{P}_{k-1}^t-K_k^t{S}_k^t{(K_k^t)}^{\mathrm{T}}$$

(17)

where $P_k^t$ is an $n\times n$ filter covariance matrix; $V_k^t$, $S_k^t$, $K_k^t$ and ${\tilde{\lambda }}_k^t\in (0,1]$ are the n-dimensional predicted innovation, the $n\times n$ innovation covariance matrix, the $n\times n$ gain matrix, and the fuzzy fading factor. They can be respectively calculated using the following equations

$$V_k^t={\widehat{\mathit{z}}}_{k,t}-H_k^t{\Phi }_k^t{\widehat{\mathit{x}}}_{k-1}^t$$

(18)

$$S_k^t={({\tilde{\lambda }}_k^t)}^{-1}{H}_k{P}_{k-1}^t{(H_k^t)}^{\mathrm{T}}+I$$

(19)

$$K_k^t=P_{k-1}^t{(H_k^t)}^{\mathrm{T}}{(S_k^t)}^{-1}$$

(20)

$${\tilde{\lambda }}_k^t=\frac{{\displaystyle \sum _{l=1}^L{\overline{\lambda }}_r^l\underset{v_{k,t}\in {\tilde{A}}_i^l,{\theta }_{k,t}\in {\tilde{B}}_j^l}{\sup }\min \left(u_{{\tilde{A}}_i^l}(v_{k,t}),u_{{\tilde{B}}_j^l}({\vartheta }_{k,t})\right)}}{{\displaystyle \sum _{l=1}^L\underset{v_{k,t}\in {\tilde{A}}_i^l,{\theta }_{k,t}\in {\tilde{B}}_j^l}{\sup }\min \left(u_{{\tilde{A}}_i^l}(v_{k,t}),u_{{\tilde{B}}_j^l}({\vartheta }_{k,t})\right)}}$$

(21)

where ${\widehat{\mathit{z}}}_{k,t}$ is the fused measurement on the target $t$ as described in reference [24], $I$ is an $n\times n$ unit matrix and $L$ is the number of the designed fuzzy rules. ${\tilde{A}}_i^l$ and ${\tilde{B}}_i^l$ denote the corresponding fuzzy sets for the measurement residual $v_{k,t}$ and heading change ${\vartheta }_{k,t}$, respectively. ${\overline{\lambda }}_r^l$ is the corresponding value when the membership function of ${\tilde{\lambda }}_k^t$ obtains the maximum value at each fuzzy set defined on; $u_{{\tilde{A}}_i^l}$ and $u_{{\tilde{B}}_j^l}$ denote their corresponding membership degrees. ${\vartheta }_{k,t}$, $v_{k,t}$ and ${\widehat{\mathit{z}}}_{k,t}$ are calculated from equations

$${\vartheta }_{k,t}=|{\varphi }_{k,t}-{\widehat{\varphi }}_{k|k-1}^t|/{\vartheta }_{\max }$$

(22)

$$v_{k,t}={\left[{(V_k^t)}^{\mathrm{T}}{V}_k^t\right]}^{1/2}/v_{\max }$$

(23)

$${\widehat{\mathit{z}}}_{k,t}={\displaystyle \sum _{i=0}^{m_k}{\beta }_{k,i}^t{\mathit{z}}_{k,i}}$$

(24)

$${\mathit{z}}_{k,0}=H_k^t{\Phi }_k^t{\widehat{\mathit{x}}}_k^t$$

(25)

where ${\vartheta }_{\max }$ and $v_{\max }$ are the corresponding empirical maximum value of the measurement residuals and the heading changes, respectively. ${\mathit{z}}_{k,i}$ is the $i$th measurement associated with the target $t$ (in particular, ${\mathit{z}}_{k,0}$ is called the zero measurement, and it denotes that there exist no measurements belonging to the target $t$). ${\beta }_{k,i}$ is the association probability of measurement ${\mathit{z}}_{k,i}$ belonging to the target $t$ calculated by the standard probabilistic data association algorithm [7].

The estimation of the initial states of each trajectory is an important prerequisite to keep the stability of the tracking performance of the designed filter, and its solution strategy will be studied in later in this paper. Here, we mainly focus on the performance of the designed filter after the two initial sampling points. To better illustrate its tracking performance, we assume that the target move with a constant velocity at the two initial sampling points. Hence, similarly to RLSF, the initial states of FRLSF can be approximately estimated with measurements ${\mathit{z}}_1$ and ${\mathit{z}}_2$ by

$${\widehat{\mathit{x}}}_2=P_2\left[H_1^{\mathrm{T}},H_2^{\mathrm{T}}\right]{\left[{\mathit{z}}_1^{\mathrm{T}},{\mathit{z}}_2^{\mathrm{T}}\right]}^{\mathrm{T}}$$

(26)

$$P_2={\left([H_1^{\mathrm{T}},H_2^{\mathrm{T}}]{[H_1^{\mathrm{T}},H_2^{\mathrm{T}}]}^{\mathrm{T}}\right)}^{-1}$$

(27)

which is also demonstrated in [22,24]. Here, $H_1$ and $H_2$ are $m\times m$ measurement transition matrices, and $P_2$ is an $n\times n$ filter covariance matrix.

From Equations (16) and (17), FRLSF employs the fuzzy fading factor ${\tilde{\lambda }}_k$ to adaptively adjust the weight of the predicted innovation $V_k^t$ in the state estimate ${\widehat{\mathit{x}}}_k^t$ of the target $t$ through the designed fuzzy inference rules

$$R^l:\mathrm{IF} v_{k,t}\in {\tilde{A}}_i^l \mathrm{AND} {\vartheta }_{k,t}\in {\tilde{B}}_j^l, \mathrm{THEN} {\tilde{\lambda }}_k^l\in {\tilde{C}}_r^l$$

where $I$ is an $m\times m$ unit matrix while ${\tilde{C}}_r^l$ and $u_{{\tilde{C}}_r^l}$ are assumed to be the fuzzy set and the membership function for ${\tilde{\lambda }}_k^t$, respectively. Here, $u_{{\tilde{A}}_i^l}$, $u_{{\tilde{B}}_j^l}$ and $u_{{\tilde{C}}_r^l}$ adopt a triangular function given by Equation (28), as shown Figure 5.

$$u(x)=1-\frac{|x-{\sigma }_r^l|}{c_r^l}$$

(28)

where $x$ denotes a fuzzy variance, and $[c_i^l-{\sigma }_i^l,c_i^l+{\sigma }_i^l]$ is the corresponding interval of the $i$th fuzzy set ${\tilde{X}}_i^l$.

4. Improved Joint Probabilistic Data Association-Fuzzy Recursive Least Squares Filter (IJPDA-FRLSF)

Based on the above analysis, we can employ generalized joint association probabilities to reconstruct joint association probability in the standard JPDA algorithm based on Equation (11) in Section 2, utilize FRLSF in Section 3 to estimate the target states, and finally propose the IJPDA-FRLSF method for MMTT in cluttered environments with unknown measurement noise covariances and unknown target dynamic models. The main procedures of the proposed filter are described as follows.

4.1. Calculating the Generalized Joint Association Probability

Let us assume that the validated measurement set at time k is $Z_k=\{{\mathit{z}}_{k,i}{\}}_{i=1}^{m_k}$ where m_k is a number of these measurements, and $Z_k=\{Z_l{\}}_{l=1}^k$ denotes the cumulative set of validated measurements up to time k. According to Equation (11), the generalized joint association probability is composed of the statistical probability and the fuzzy membership degree. Next, we further derive the expression of the generalized joint association probability in the JPDA frame as follows.

The statistical probability $p_{k,i}^t$ and the fuzzy membership degree $u_{k,i}^t$ in Equation (11) correspond to the joint association probability and the fuzzy association degree, respectively

$$p({\mathit{z}}_{k,i}|{\mathit{x}}_k^t)={\beta }_{k,i}^t$$

(29)

$$u({\varphi }_{k,i}|{\mathit{x}}_k^t)=e^{-{({\varphi }_{k,i}-{\widehat{\varphi }}_{k|k-1}^t)}^2/2{\varphi }_{\max }}/c_u$$

(30)

Here, ${\beta }_{k,i}^t$ is the joint association probability of measurement ${\mathit{z}}_{k,i}$ belonging to the target $t$ determined by the difference between ${\mathit{z}}_{k,i}$ and ${\widehat{\mathit{x}}}_{k|k-1}^t$ (its detailed derivation can be found in [8] and is only briefly summarized below). $u_{k,i}^t$ is the fuzzy association membership degree of the observed angles ${\varphi }_{k,i}$ associated with the target $t$; ${\widehat{\varphi }}_{k|k-1}^t$ denotes the corresponding course angle, ${\theta }_{\max }$ is the maximum value for all observed angles at each time; and $c_u$ is a normalizing constant. According to the standard JPDA method, the joint association probability can be expressed as follows

$${\beta }_{k,i}^t={\displaystyle \sum _{{\theta }_k}p(e_k|Z^k){\widehat{\omega }}_i^t(e_k)}$$

(31)

$${\beta }_{k,0}^t=1-{\displaystyle \sum _{i=1}^{m_k}{\beta }_{k,i}^t}$$

(32)

$$p(e_k|{\mathit{Z}}^k)=\frac{1}{c}\frac{\Phi !}{V^{\Phi }}{\displaystyle \prod _{i=1}^{m_k}{N}_{t_i}{({\mathit{z}}_{k,i})}^{{\tau }_i}}{\displaystyle \prod _{i=1}^N{(P_D^t)}^{{\delta }_t}{(1-P_D^t)}^{1-{\delta }_t}}$$

(33)

where ${\widehat{\omega }}_i^t(e_k)$ indicates a binary variable indicating whether the joint event $e_k$ contains the association of the track $t$ with the measurement $i$, ${\beta }_{k,0}^t$ is the probability that there exist no validated measurements belonging to the target, $N_{t_i}({\mathit{z}}_{k,i})$ is the probability density of the predicted measurements belonging to the target $t_i$, ${\tau }_i$ is the number of targets associated with the measurement $i$, ${\delta }_t$ is a target indicator indicating whether there is a measurement belonging to a the target $t$ (${\delta }_t=1$) or not (${\delta }_t=0$), $\Phi$ is the number of clutters, $P_D^t$ is the detection probability for the target $t$, $V$ is the volume of the extension gates of the target, and $c$ is the normalizing constant.

Based on the presented definitions, the generalized joint association probability ${\rho }_{k,i}^t$ in Equation (11) can be modified as follows

$$\rho ({\mathit{z}}_{k,i},{\theta }_{k,i}|{\mathit{x}}_k^t)=(w_{k,1}{\beta }_{k,i}^t+w_{k,2}{u}_{k,i}^t)/c_{\rho }$$

(34)

As for Equation (34), the generalized joint association probability can utilize the uncertainties of measurements and observed angles to adjust their weights in the association results.

4.2. The propsed IJPDA-FRLSF

Based on Section 3 and Section 4.1, the main equations of the proposed filter can be described as follows:

• Step 1. Initialize state ${\widehat{\mathit{x}}}_2^t$ and filter covariance $P_2^t$ of target $t$ for $t=1,2,\cdots ,n_k$ using Equations (26) and (27), and start the recursive formulas at time $k=3$.
• Step 2. Compute predicted innovation $V_{k,i}^t$ on measurement ${\mathit{z}}_{k,i}$ using Equation (18).
• Step 3. Compute innovation covariance $S_k^t$ using Equation (19).
• Step 4. Compute gain matrix $K_k^t$ using Equation (20).
• Step 5. Reconstruct the generalized joint association probability ${\rho }_{k,i}^t$ using Equation (34).
• Step 6. Compute the fuzzy fading factor ${\tilde{\lambda }}_k^t$ using Equation (21).
• Step 7. Update the target state ${\widehat{\mathit{x}}}_k^t$ and filter covariance $P_k^t$ by FRLSF using Equations (35) and (36)

  $${\widehat{\mathit{x}}}_k^t={\widehat{\mathit{x}}}_{k-1}^t+K_k^t{V}_k^t$$

  (35)

  $$P_k^t={({\tilde{\lambda }}_k^t)}^{-1}{P}_{k-1}-(1-{\rho }_{k,0}^t)K_k^t{S}_k^t{(K_k^t)}^{\mathrm{T}}+{\displaystyle \sum _{i=0}^{m_k}{\rho }_{k,i}^t\left[{\widehat{\mathit{x}}}_{k,i}^t{({\widehat{\mathit{x}}}_{k,i}^t)}^{\mathrm{T}}-{\widehat{\mathit{x}}}_k^t{({\widehat{\mathit{x}}}_k^t)}^{\mathrm{T}}\right]}$$

  (36)

  where ${\widehat{\mathit{x}}}_{k,i}^t$ is the local state estimate by FRLSF.
• Step 8. Repeat the steps 2–7 for the next iterations.

5. Experimental Results and Analysis

Two experiments using simulation data and real data have been conducted to evaluate the performance of the proposed IJPDA-FRLSF in comparison with the intuitionistic fuzzy-joint probabilistic data association filter (IF-JPDAF) [21], the interacting multiple model-joint probabilistic data association filter (IMM-JPDAF) [28] and the improved joint probabilistic data association-recursive least squares filter (IJPDA-RLSF) in terms of the tracking accuracy and average run time. The experiments were conducted on a computer with a computer with a dual-core CPU of Intel Core(TM) 2.93 GHz, 8-GB RAM. The programs for the four methods were implemented in MATLAB version 2014a and executed for 50 Monte Carlo runs. Here, the 50 Monte Carlo runs denote that the data set of the true trajectories is fixed and the set of measurements is generated 50 times in the following two experiments. Furthermore, the estimated error for each target denotes the average root-mean-square (RMS) position error for 50 Monte Carlo runs.

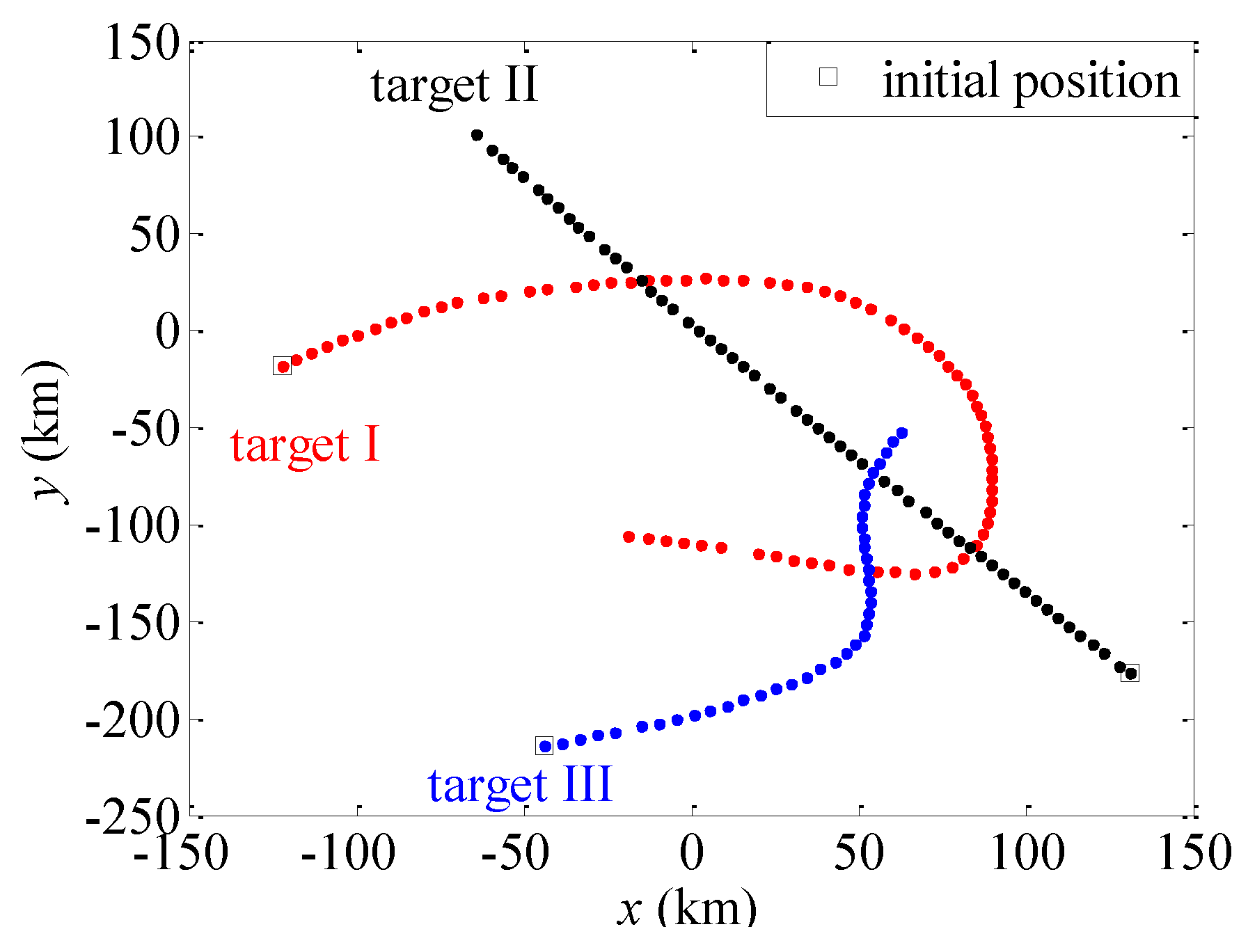
5.1. An Example of a Simulation Data Set: Two Crossing Targets

In the simulation scenario, there are two crossing targets moving in the air surveillance of a 2-D Cartesian xy-plane according to the given trajectories, as shown in Figure 6. Their initial states are given as ${\widehat{\mathit{x}}}_0^1=(0 \mathrm{m},180 \mathrm{m}/\mathrm{s},2000 \mathrm{m},-45 {\mathrm{m}/\mathrm{s})}^{\mathrm{T}}$ and ${\widehat{\mathit{x}}}_0^2=(0 {\mathrm{m},180 \mathrm{m}/\mathrm{s},100 \mathrm{m},45 \mathrm{m}/\mathrm{s})}^{\mathrm{T}}$. The motion processes of the two targets are further divided into five periods, as shown in

Table 1. Dynamic models of two crossing targets.

Target I		Target II
Periods	Time	Periods	Time
constant velocity (CV)	14 s	constant velocity (CV)	14 s
constant turn (CT)	1 s	constant turn (CT)	1 s
constant acceleration (CA)	14 s	constant acceleration (CA)	14 s
constant turn (CT)	1 s	constant turn (CT)	1 s
constant velocity (CV)	5 s	constant velocity (CV)	6 s

. Here, the turn model of a moving target is approximately described by

$${\mathit{x}}_k^t=\left[\begin{array}{cccc}1& \frac{\sin {\varpi }_k^{t}T}{{\varpi }_k^t}& 0& -\frac{1-\cos {\varpi }_k^{t}T}{{\varpi }_k}\\ 0& \cos {\varpi }_k^{t}T& 0& -\sin {\varpi }_k^{t}T\\ 0& \frac{1-\cos {\varpi }_k^{t}T}{{\varpi }_k}& 1& \frac{\sin {\varpi }_k^{t}T}{{\varpi }_k}\\ 0& \sin {\varpi }_k^{t}T& 0& \cos {\varpi }_k^{t}T\end{array}\right]{\mathit{x}}_{k-1}^t+G_k^t{\mathit{w}}_{1,k}^t$$

(37)

$$G_k^t={\left[\begin{array}{llll}{T}^2/2\hfill & T\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & T^2/2\hfill & T\hfill \end{array}\right]}^{\mathrm{T}}$$

(38)

$${\mathit{z}}_k^t=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right]{\mathit{x}}_k^t+{\mathit{w}}_{2,k}^t$$

(39)

where ${\mathit{x}}_k^t={(x_k^t,{\dot{x}}_k^t,y_k^t,{\dot{y}}_k^t)}^{\mathrm{T}}$ is the state vector of target $t$; $x_k^t$ and $y_k^t$ are the x and y coordinates of the target $t$, respectively, and ${\dot{x}}_k^t$ and ${\dot{y}}_k^t$ are the corresponding velocities in the x and y coordinates. ${\varpi }_k=\pm 0.0524\mathrm{rad}/\mathrm{s}$ is the turn rate and $T=1\mathrm{s}$ is the sampling interval. In the CA period, the acceleration velocity is $a_{\mathit{x}}=5{\mathrm{m}/\mathrm{s}}^2$. The detection probability of a true measurement $P_D$ is set to 1, and the gate probability $P_G$ is set to 0.99. For all the target dynamic models, the process noise ${\mathit{w}}_{1,k}^t$ is assumed to be a Gaussian noise with zero mean and covariance $Q_k^t=diag([{20}^2{\mathrm{m}}^2{\mathrm{s}}^{-4} {20}^2{\mathrm{m}}^2{\mathrm{s}}^{-4}])$, that is, ${\mathit{w}}_{1,k}^t~N(0,Q_k^t)$. The measurement noise ${\mathit{w}}_{2,k}^t$ is also assumed to be a Gaussian noise with zero mean and covariance $R_k^t=diag([{50}^2{\mathrm{m}}^2 {50}^2{\mathrm{m}}^2])$, that is, ${\mathit{w}}_{2,k}^t~N(0,R_k^t)$. In addition, the clutter model is assumed to have a uniform distribution while the number of false measurements (or clutters) is assumed to follow the Poisson distribution with the known parameter $\lambda =1$ (the number of false measurements per unit of volume (km²)).

Figure 6 shows the true crossing trajectories and their measurements, which correspond to the measurements of one of the 50 Monte Carlo cases. Considering that the performance of IMM-JPDAF is constrained by the target dynamic models assumed, it is further divided into three types to facilitate the comparison as follows: (i) two dynamic models (constant velocity (CV) and constant acceleration (CA)) with the mismatched measurement covariance $R_k^t=diag([{20}^2{\mathrm{m}}^2{\mathrm{s}}^{-4} {20}^2{\mathrm{m}}^2{\mathrm{s}}^{-4}])$; (ii) three dynamic models (CV, CA and constant turn (CT)) with a matched measurement noise covariance; (iii) three dynamic models (CV, CA and CT) with the mismatched measurement noise covariance $R_k^t=diag([{30}^2{\mathrm{m}}^2{\mathrm{s}}^{-4} 30^2{\mathrm{m}}^2{\mathrm{s}}^{-4}])$. These three versions of IMM-JPDAFs are denoted as IMM-JPDAF(II), IMM-JPDAF(IIIA) and IMM-JPDAF(IIIB), respectively. Figure 7 shows the tracking results of the four evaluated filters. Figure 8 and Figure 9 show the estimates of the fading factor $\tilde{\lambda }$ for Targets I and II. and Figure 10 and Figure 11 provide the average RMS position errors of all filters.

Figure 8 and Figure 9 belong to one of the Monte Carlo cases of the estimates of the fading factors. As for Figure 8 and Figure 9, the fading factor can reflect the changes of the maneuvering characteristics for the two targets correctly. The stronger the target maneuver, the smaller the fading factor. This is consistent with the target maneuvering motion. Hence, employing the fading factor to adjust the proposed filter is an effective strategy.

With respect to Figure 7, all estimated filters achieve the correct association results despite the two targets crossing, but they achieve different performance in tracking accuracy. Obviously, IF-JPDAF and IJPDA-RLSF perform well in the CV periods but perform poorly in the CA periods because they utilize the Kalman filter (KF) or RLSF, and these generally perform well for the CV model and are unsuitable for maneuvering motion. Because the tracking performances of these two filters are poor for maneuvering motion, we don’t further analyze their performance below. Similarly, the three versions of IMM-JPDAFs can also obtain a good tracking performance in the CV period.

As for Figure 10 and Figure 11, IMM-JPDAF(IIIA) is found to perform better on the whole than the other three estimated filters based on the whole motion process because it employs the matched measurement noise covariance and dynamic models. In addition, the performance of IJPDA-FRLSF is close to that of the IMM-JPDAF. Hence, when the measurement noise covariance and the target dynamic model are unknown or mismatched, the tracing performances of both IMM-JPDAF(II) and IMM-JPDAF(IIIB) are unsatisfactory in maneuvering situations. In this situation, the performance of IJPDA-FRLSF is better than the one of IMM-JPDA(II) and IMM-JPDAF(IIIB). One major reason for this case is that IJPDA-FRLSF utilizes FRLSF, which doesn’t require a known measurement noise covariance and dynamic models.

For a better illustration of the performances of the four evaluated filters,

Table 2. The average root-mean-square (RMS) position error for Target I (unit: m). Improved joint probabilistic data association-fuzzy recursive least squares filter (IJPDA-FRLSF), interacting multiple model-joint probabilistic data association filter (IMM-JPDAF).

Filter	CV	CT	CA	CT	CV
IJPDA-FRLSF	21.5	22.0	22.1	22.5	22.0
IMM-JPDAF(II)	14.8	13.3	32.0	37.3	37.0
IMM-JPDAF(IIIA)	17.5	16.9	26.2	35.3	25.0
IMM-JPDAF(IIIB)	22.7	23.5	35.3	47.2	38.5

and

Table 3. The average root-mean-square (RMS) position error for Target II (unit: m).

Filter	CV	CT	CA	CT	CV
IJPDA-FRLSF	22.1	21.9	22.1	22.6	21.8
IMM-JPDAF(II)	15.0	15.0	30.9	36.8	37.2
IMM-JPDAF(IIIA)	16.5	15.9	24.6	32.4	24.8
IMM-JPDAF(IIIB)	23.7	23.4	36.0	46.5	38.1

provide the average RMS position errors of five motion periods and the whole motion process (without the initial two samples) on targets I and II, respectively. Here, the five motion periods for target I in turn are: CV period (3–15 s), CT period (16 s), CA period (17–30 s), CT period (31 s), and CV period (32–36 s). Furthermore, the average RMS position errors of the five motion periods are beneficial for analyzing the performance of each filter for different dynamic models.

According to the total average RMS position error in Table 2 and Table 3, IMM-JPDAF(IIIA) performs better than IJPDA-RLSF, IMM-JPDAF(II) and IMM-JPDAF(IIIB) in the tracking accuracy. This finding is similar to the results obtained from Figure 10 and Figure 11. Although the IMM-JPDAF(IIIA) approach can obtain the highest accuracy when its assumed measurement noise covariance and target dynamic models are matched with the corresponding real values, this assumption is difficultly satisfactory in practice. In the situation with a mismatched measurement noise covariance and target dynamic models, the performance of the proposed filter is a close approximate of IMM-JPDAF(IIIA). Hence, the tracking accuracy of each filter as shown in Table 2 and Table 3 is consistent with the presented analysis using Figure 8 and Figure 9.

We further analyze the performance of each evaluated filter for different dynamic models. According to Table 2 and Table 3, IMM-JPDAF(II) performs better than IMM-JPADF(IIIA) and IMM-JPDAF(IIIB) in the first CV period because it employs less, but better-matched dynamic models. IMM-JPDAF(IIB) obtains the worst results because it utilizes mismatched dynamic models and a measurement noise covariance. This fact shows that employing the matched dynamic models and a measurement noise covariance directly affects the performance of the three versions of IMM-JPDAFs directly. In the second CV period, the order of the performance of IMM-JPDAs only has a little change because their performance is also influenced by the initial state estimates in this period, which are assumed to be equal as the first CV period. Hence, their performance in the second CV period is similar to the performance in the first CV period. Compared with IMM-JPDAF(II) and IMM-JPDAF(IIIA), IJPDA-FRLSF is suboptimal in the CV period. However, it doesn’t need to satisfy the strict assumption of the measurement noise covariance and dynamic models. Additionally, it is also hard to keep the assumption consistent with the real measurement noise covariance and dynamic models in practice.

Based on the average values calculated by the average RMS position errors of each filter in the four CT periods from Table 2 and Table 3, IJPDA-FRLSF performs best in all filters while IMM-JPDAF(IIIB) performs worst. Moreover, IMM-JPDAF(IIIA) is marginally better from IMM-JPDAF(II) because IMM-JPDAF(IIIA) employs the matched dynamic models as shown in the presented analysis. Thus, the order of the tracking performance from good to poor is: IJPDA-FRLSF, IMM-JPDAF(IIIA), IMM-JPDA F(II), and IMM-JPDAF(IIIB). Such order of the tracking performance of four evaluated filters is still valid in the CA period. As a result, IJPDA-FRLSF performs better in tracking accuracy than the other three versions of IMM-JPDAFs in the maneuvering periods (CT and CA).

With respect to the analysis presented above,

Table 4. The total performance evaluation for each filter.

Filter	CV	CT	CA	Total
IJPDA-FRLSF	mean	good	good	fair
IMM-JPDAF(II)	good	mean	mean	mean
IMM-JPDAF(IIIA)	fair	fair	fair	good
IMM-JPDAF(IIIB)	poor	poor	poor	poor

summarizes the complete performance evaluation of four evaluated filters. Using Table 4, it is easy to illustrate the tracking performance of each filter for different dynamic models. It also shows the total performance evaluation for each filter. In addition, the average run time of IJPDA-FRLSF, IJPDA-RLSF, IMM-JPDAF(II), IMM-JPDA(IIIA), IMM-JPDA(IIIB) and IF-JPDAF is 0.0083 s, 0.0130 s, 0.0214 s, 0.0248 s, 0.0235 s, and 0.1082 s, respectively. The average run time of IJPDA-FRLSF is less than that of the other three types of the IMM-JPDAF. Because IMM-JPDAF must execute the filtering procedure for all sub-models, its average run time becomes longer with the increasing number of sub-models. Then, both the IMM-JPDAF(IIIA) and the IMM-JPDAF(IIIB) methods consume more time than IMM-JPDAF(II). Moreover, because the execution of the fuzzy reference consumes a certain amount of time, IJPDA-FRLSF requires more time than IJPDA-RLSF. The average run time of IF-JPDAF is the longest of all filters because the fuzzy clustering for all measurements consume a lot of time.

In short, IJPDA-FRLSF can achieve satisfactory performance in tracking accuracy for MMTT. It has the advantage of efficiency and robustness compared with IMM-JPDAF, IF-JPDAF, and IJPDA-RLSF in situations with the unknown measurement noise covariance and the target dynamic models. The tracking performance of IMM-IJPDAF is influenced by the assumed measurement noise covariance and dynamic models. It can achieve a good tracking performance only if the assumed values are consistent with the real measurement noise covariance and dynamic models.

5.2. An Example of a Real Data Set: Three Crossing Targets

To further illustrate the feasibility of the proposed filter, a real data set is obtained from one of outfield experiments by using a single certain type of proximity radar, and the tracking targets are the three crossing civil aviation aircrafts. This data set is utilized to evaluate the performance. The real data set of three crossing targets is shown in Figure 12. It consists of 147, 113 and 80 periodic track dots. The parameters of the clutter model are the same as in Section 5.1. The radar performance parameters are given as follows: sampling interval $T=10 \mathrm{s}$. The process noise covariance $Q_k^t$ is set to $diag([{20}^2 {\mathrm{m}}^2{\mathrm{s}}^{-4} {20}^2 {\mathrm{m}}^2{\mathrm{s}}^{-4}])$, and the measurement noise covariance $R_k^t$ is equal to $diag([{150}^2{\mathrm{m}}^2 {150}^2{\mathrm{m}}^2])$. The initial positions of three targets are given by ${\mathit{z}}_0^1=[-122.15\mathrm{km},-18.26\mathrm{km}{]}^{\mathrm{T}}$, ${\mathit{z}}_0^2=[131.57\mathrm{km},-176.90\mathrm{km}{]}^{\mathrm{T}}$ and ${\mathit{z}}_0^3=[-44.06\mathrm{km},-214.29\mathrm{km}{]}^{\mathrm{T}}$.

Because the dynamic models of the three targets in the real scenario are unknown and complex, it is difficult to design their matched sub-models. For simplicity to illustrate the feasibility, the tracking results of IMM-JPDAF are unsatisfactory and even diverged so we only utilize the proposed filter for MMTT here. Figure 13, Figure 14 and Figure 15 show the average RMS position error of the proposed filter for the three targets on 50 Monte Carlo runs. According to the tracking results, the proposed filter can track MMT accurately in a real life situation with unknown measurement noise covariances and target dynamic models. Hence, we can conclude that the proposed filter is feasible in a real MMTT applications.

6. Conclusions

This paper presented an improved joint probabilistic data association-fuzzy recursive least squares filter (IJPDA-FRLSF) for multiple maneuvering target tracking (MMTT) in situations with unknown measurement noise covariances and unknown target dynamic models. In the proposed filter, two uncertain models of measurements and observed angles were established, and their related parameters were analyzed in temporal and spatial sense. Using these two uncertain models, an additive fusion strategy was constructed to calculate the generalized joint association probabilities of measurements belonging to different targets, which were utilized to replace the joint association probabilities of the standard joint probabilistic data association (JPDA) algorithm. The FRLSF method was utilized to update all tracks. The proposed filter can relax the restrictive assumptions of measurement noise covariances and target dynamic models. It benefits from FRLSF by not requiring a maneuver detector for a maneuvering target. Moreover, the filter can utilize multisource information to adjust the corresponding weights in the association results according to the uncertainties of measurements and observed angles.

The application of the improved JPDA algorithm and the FRLSF method has been found to be effective in solving the data association and the state estimation problem for MMTT. The experimental results on simulation data and real data illustrate that the proposed filter is effective and can be applied in situations with unknown measurement noise covariances and target dynamic models. The uncertain relationship between measurements and observed angles will be further studied in our future work on uncertain target tracking.