Logarithmic Similarity Measure between Interval-Valued Fuzzy Sets and Its Fault Diagnosis Method

Abstract

Fault diagnosis is an important task for the normal operation and maintenance of equipment. In many real situations, the diagnosis data cannot provide deterministic values and are usually imprecise or uncertain. Thus, interval-valued fuzzy sets (IVFSs) are very suitable for expressing imprecise or uncertain fault information in real problems. However, existing literature scarcely deals with fault diagnosis problems, such as gasoline engines and steam turbines with IVFSs. However, the similarity measure is one of the important tools in fault diagnoses. Therefore, this paper proposes a new similarity measure of IVFSs based on logarithmic function and its fault diagnosis method for the first time. By the logarithmic similarity measure between the fault knowledge and some diagnosis-testing samples with interval-valued fuzzy information and its relation indices, we can determine the fault type and ranking order of faults corresponding to the relation indices. Then, the misfire fault diagnosis of the gasoline engine and the vibrational fault diagnosis of a turbine are presented to demonstrate the simplicity and effectiveness of the proposed diagnosis method. The fault diagnosis results of gasoline engine and steam turbine show that the proposed diagnosis method not only gives the main fault types of the gasoline engine and steam turbine but also provides useful information for multi-fault analyses and predicting future fault trends. Hence, the logarithmic similarity measure and its fault diagnosis method are main contributions in this study and they provide a useful new way for the fault diagnosis with interval-valued fuzzy information.

1. Introduction

The technique of fault diagnoses has produced substantial economic benefits since various fault diagnosis methods have been developed and applied in engineering areas. In many real situations, the diagnosis data cannot provide deterministic values because the fault testing data obtained by experts are usually imprecise or uncertain due to a lack of data, time pressure, or the experts’ limited attention and knowledge. This kind of uncertainty in fault diagnosis problems can be handled by using the fuzzy set theory proposed by Zadeh [1]. Fuzzy sets are suitable for solving fault diagnosis problems with uncertain information. Hence, fuzzy approaches have been widely applied to fault diagnosis processes [2,3,4,5,6]. However, it may be difficult to exactly quantify the membership degree in the fuzzy set as an exact value in the interval [0, 1]. Usually, it is more suitable to represent its membership degree by an interval. Therefore, Zadeh [7] further extended fuzzy sets to interval-valued fuzzy sets (IVFSs). IVFSs are very suitable for expressing imprecise or uncertain fault information in real problems. After that, fuzzy sets were also extended to extension sets [8], intuitionistic fuzzy sets (IFSs) [9], vague sets (VSs) [10] and so on, and then they have been applied to various fault diagnoses. For instance, Wang [11] applied extension theory to the vibration fault diagnosis of generator sets. Then, Ye [12] applied extension theory to the misfire fault diagnosis of gasoline engines. Under VS environment, Ye et al. [13] presented the vibrational fault diagnosis method of steam turbine based on the similarity measure of VSs. Further, Ye [14] proposed a vibrational fault diagnosis method of steam turbine based on the fuzzy cross entropy measure of VSs. Based on the cosine of the included angle between two vectors, Lu and Ye [15] put forward a similarity measure with the weight of cosine similarity measures (CSMs) between VSs and applied it to the vibrational fault diagnosis of steam turbine. Furthermore, Shi and Ye [16] indicated some insufficiency of existing CSMs and further presented an improved CSM of VSs by considering the degree of hesitation and applied it to the vibrational fault diagnosis of the steam turbine. Because a neutrosophic number [17] is composed of its determinate and indeterminate parts and considered as a changeable interval number/uncertain interval number, Kong et al. [17] also put forward the misfire fault diagnosis method of gasoline engines by using the cosine function-based similarity measures of neutrosophic numbers. Ye [18] further proposed fault diagnosis methods of steam turbine based on the exponential similarity measure of neutrosophic numbers. As the extension of IFS, a single-valued neutrosophic set (SVNS) can be described independently by truth, indeterminacy, and falsity membership degrees. Thus, the cosine and tangent similarity measures of SVNSs [19,20] have been proposed and applied to the misfire fault diagnosis of the gasoline engine and the vibrational fault diagnosis of steam turbine under single-valued neutrosophic environment.

It is clear that the similarity measure is one of important tools in pattern recognition and fault diagnoses. However, existing literature scarcely deals with fault diagnosis problems, such as the gasoline engine and steam turbine, under interval-valued fuzzy environment. Furthermore, there is not any logarithmic similarity measure in existing research. Since IVFSs are more suitable for the expression of fault information in fault diagnosis problems, such as the misfire fault diagnosis of gasoline engine and the vibrational fault diagnosis of steam turbine with interval-valued fuzzy information [14,16,17]. Motivated by both logarithmic function and a distance measure, this paper proposes a new similarity measure of IVFSs by combining the logarithmic function with the distance measure (so-called logarithmic similarity measure) and its fault diagnosis method for both the misfire fault diagnosis of the gasoline engine and the vibrational fault diagnosis of the steam turbine under interval-valued fuzzy environment.

Since the logarithmic similarity measure and its fault diagnosis method are presented for the first time, they are the main contributions in this study. However, the proposed fault diagnosis method provides a new way for the fault diagnosis with interval-valued fuzzy information.

The remainder of this paper is structured as follows. Section 2 presents a new similarity measure of IVFSs based on logarithmic function and a distance measure, which is called the logarithmic similarity measure (LSM) of IVFSs, and investigates its properties. In Section 3, a fault diagnosis method is established based on the proposed LSM of IVFSs and used for the misfire fault diagnosis of the gasoline engine and the vibrational fault diagnosis of the steam turbine under interval-valued fuzzy environment to demonstrate the simplicity and effectiveness of the developed fault diagnosis method. Section 4 gives conclusions and a future research direction.

2. LSM between IVFSs

In this section, we propose the similarity measure of IVFSs based on the logarithmic function and distance measure.

In the real world, it is difficult for an expert to exactly quantify the membership degree of the fuzzy set as an exact number in the interval [0, 1]. Usually, it is more suitable to represent its membership degree by an interval. Thus, Zadeh [7] proposed the concept of an IVFS.

Definition 1 [7].

An IVFS A in the universe of discourse X is given by

$$A=\left\{\langle x,\left[{\mu }_A^L(x),{\mu }_A^U(x)\right]\rangle |x\in X\right\},$$

where ${\mu }_A^L(x)$: X → [0, 1] and ${\mu }_A^U(x)$: X → [0, 1] are called the lower limit of membership degree and the upper limit of membership degree of the element x to the set A, respectively, such that the condition $0\le {\mu }_A^L(x)$ ≤ ${\mu }_A^U(x)\le 1$. For convenience, a basic element in the IVFS A is denoted by $\tilde{a}=\left[{\mu }_A^L(x),{\mu }_A^U(x)\right]$ for short, which is called an interval-valued fuzzy element (IVFE).

Let two IVFSs be $A=\left\{\langle x_i,\left[{\mu }_A^L(x_i),{\mu }_A^U(x_i)\right]\rangle |x_i\in X\right\}$ and $B=\left\{\langle x_i,\left[{\mu }_B^L(x_i),{\mu }_B^U(x_i)\right]\rangle |x_i\in X\right\}$ in the universe of discourse X = {x₁, x₂, …, x_n}. Then, LSM between A and B can be defined as follows:

$$M(A,B)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\log }_2\left[2-\frac{\left(\left|{\mu }_A^L(x_i)-{\mu }_B^L(x_i)\right|+\left|{\mu }_A^U(x_i)-{\mu }_B^U(x_i)\right|\right)}{2}\right]}.$$

(1)

Obviously, LSM should satisfy the following properties (P1)–(P4):

(P1)

0 ≤ M(A, B) ≤ 1;

(P2)

M(A, B) = 1 if and only if A = B;

(P3)

M(A, B) = M(B, A);

(P4)

If C is an IVFS in X and A ⊆ B ⊆ C, then M(A, C) ≤ M(A, B) and M(A, C) ≤ M(B, C).

Proof. 

(P1)

Since the value of log₂(x) for x ∈ [1, 2] lies within [0, 1], the similarity measure value based on the logarithmic function also lies within [0, 1]. Hence, there is 0 ≤ M(A, B) ≤ 1.

(P2)

For any two IVFSs A and B, if A = B, this implies ${\mu }_A^L(x_i)$ = ${\mu }_B^L(x_i)$ and ${\mu }_A^U(x_i)$ = ${\mu }_B^U(x_i)$ for i = 1, 2, …, n and x_i ∈ X. Thus, there are $\left|{\mu }_A^L(x_i)-{\mu }_B^L(x_i)\right|=0$ and $\left|{\mu }_A^U(x_i)-{\mu }_B^U(x_i)\right|=0$. Hence M(A, B) = 1.

If M(A, B) = 1, this implies $\left|{\mu }_A^L(x_i)-{\mu }_B^L(x_i)\right|=0$ and $\left|{\mu }_A^U(x_i)-{\mu }_B^U(x_i)\right|=0$ for i = 1, 2, …, n and x_i ∈ X since log₂(2) = 1. Then, there are ${\mu }_A^L(x_i)$ = ${\mu }_B^L(x_i)$ and ${\mu }_A^U(x_i)$ = ${\mu }_B^U(x_i)$ for i = 1, 2, …, n and x_i ∈ X. Hence A = B.

(P3)

The proof is straightforward.

(P4)

If A ⊆ B ⊆ C, then this implies ${\mu }_A^L(x_i)$ ≤ ${\mu }_B^L(x_i)$ ≤ ${\mu }_C^L(x_i)$ and ${\mu }_A^U(x_i)$ ≤ ${\mu }_B^U(x_i)$ ≤ ${\mu }_C^U(x_i)$ for i = 1, 2, …, n and x_i ∈ X. Then, we have the following relations:

$$\begin{array}{c}\left|{\mu }_A^L(x_i)-{\mu }_B^L(x_i)\right|\le \left|{\mu }_A^L(x_i)-{\mu }_C^L(x_i)\right|,\\ \left|{\mu }_B^L(x_i)-{\mu }_C^L(x_i)\right|\le \left|{\mu }_A^L(x_i)-{\mu }_C^L(x_i)\right|,\end{array}$$

$$\begin{array}{c}\left|{\mu }_A^U(x_i)-{\mu }_B^U(x_i)\right|\le \left|{\mu }_A^U(x_i)-{\mu }_C^U(x_i)\right|\mathrm{and}\\ \left|{\mu }_B^U(x_i)-{\mu }_C^U(x_i)\right|\le \left|{\mu }_A^U(x_i)-{\mu }_C^U(x_i)\right|.\end{array}$$

Hence, M(A, C) ≤ M(A, B) and M(A, C) ≤ M(B, C) since the logarithmic measure function is a decreasing function with the increase of the distance $\left(\left|{\mu }_A^L(x_i)-{\mu }_B^L(x_i)\right|+\left|{\mu }_A^U(x_i)-{\mu }_B^U(x_i)\right|\right)/2$.

Therefore, the proofs of these properties are finished. ☐

Usually, one considers the importance of each element x_i for x_i ∈ X. Assume that the weight of an element x_i is w_i (i = 1, 2, …, n) with w_i ∈ [0, 1] and ${\displaystyle {\sum }_{i=1}^n{w}_i}=1$. Thus, we can introduce the following weighted LSM between IVFSs A and B:

$$M_w(A,B)={\displaystyle \sum _{i=1}^n{w}_i{\log }_2\left[2-\frac{\left(\left|{\mu }_A^L(x_i)-{\mu }_B^L(x_i)\right|+\left|{\mu }_A^U(x_i)-{\mu }_B^U(x_i)\right|\right)}{2}\right]}.$$

(2)

Especially when w_i = 1/n for i = 1, 2, …, n, Equation (2) is reduced to Equation (1).

Similarly, the weighted LSM also satisfies the following properties (P1)–(P4):

(P1)

0 ≤ M_w(A, B) ≤ 1;

(P2)

M_w(A, B) = 1 if and only if A = B;

(P3)

M_w(A, B) = M_w(B, A);

(P4)

If C is an IVFS in X and A ⊆ B ⊆ C, then M_w(A, C) ≤ M_w(A, B) and M_w(A, C) ≤ M_w(B, C).

By the above similar proofs, we can verify these properties (P1)–(P4), which are not repeated here.

3. Fault Diagnosis Method Based on the Proposed LSM and Its Applications

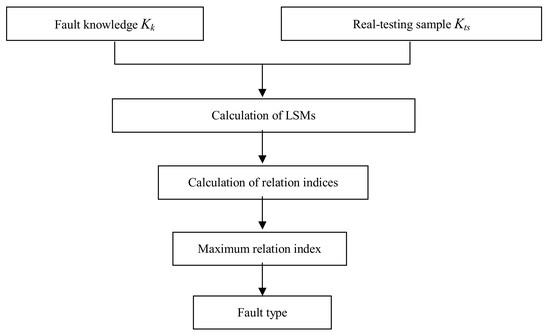
3.1. Fault Diagnosis Method

In this subsection, we develop a fault diagnosis method by using the proposed LSM of IVFSs.

For a fault diagnosis problem, assume that a set of m fault patterns (fault knowledge) is K = {K₁, K₂, …, K_m} and a set of n fault characteristics (attributes) is A = {A₁, A₂, …, A_n}. Then the fault information of a fault pattern K_k (k = 1, 2, …, m) with respect to a fault characteristic A_i (i = 1, 2, …, n) is represented by an IVFS K_k (k = 1, 2, …, m):

$$K_k=\left\{\langle A_i,\left[{\mu }_{K_k}^L(A_i),{\mu }_{K_k}^U(A_i)\right]\rangle |A_i\in A\right\}.$$

Then, the information of a testing sample is represented by an IVFS K_ts:

$$K_{ts}=\left\{\langle A_i,\left[{\mu }_{K_{ts}}^L(A_i),{\mu }_{K_{ts}}^U(A_i)\right]\rangle |A_i\in A\right\}.$$

The similarity measure value S_k (k = 1, 2, …, m) can be obtained by the following LSM between K_ts and K_k:

$$S_k=M_w(K_{ts},K_k)={\displaystyle \sum _{i=1}^n{w}_i{\log }_2\left[2-\frac{\left(\left|{\mu }_{K_{ts}}^L(A_i)-{\mu }_{K_k}^L(A_i)\right|+\left|{\mu }_{K_{ts}}^U(A_i)-{\mu }_{K_k}^U(A_i)\right|\right)}{2}\right]}$$

(3)

For easy fault diagnosis judgment, the LSM values of S_k (k = 1, 2, …, m) are normalized into the values of relation indices within the interval [−1, 1] by the following formula:

$${\eta }_k=\frac{2S_k-S_{\min }-S_{\max }}{S_{\max }-S_{\min }},k=1,2,\dots ,m,$$

(4)

where $S_{\max }=\underset{1\le k\le m}{\max }\{S_k\}$ and $S_{\min }=\underset{1\le k\le m}{\min }\{S_k\}$.

Thus, the relation indices can be ranked to determine the fault type or to predict a possible fault trend for the tested equipment. If the maximum value of the relation indices is ${\eta }_k=1$, then we can determine that the testing sample K_ts should belong to the fault pattern K_k.

The fault diagnosis process based on the LSM of IVFSs and relation indices are shown in Figure 1.

3.2. The Proposed Fault Diagnosis Method for Misfire Fault Diagnosis of Gasoline Engine

To demonstrate the application and effectiveness of the proposed fault diagnosis method, we introduce the misfire fault diagnosis of the gasoline engine as a practical example, which is discussed in [12,17].

Because burning quality of mixture gases descend in the combustion chamber of the gasoline engine, it can descend its power, increase its fuel consumption, and aggravate its pollution of exhaust emission. Therefore, we must find out bad burning status and eliminate the affected factors of low burning quality in the engine so as to keep better operating performance of the engine. Then, the components of the exhaust emission of engines mainly contains HC, NO_x, CO, CO₂, O₂, water vapor, etc., which can affect the burning quality of mixture gases in gasoline engines. The content of the components under different burning conditions can be changed in some range with the change of operating status or the occurrences of various mechanical and electronic faults in gasoline engines. Hence, one can identify the operating status of gasoline engines by analyzing the change of exhaust emission content.

Investigating the misfire fault diagnosis problem of the gasoline engine EQ6102, we can classify the misfire faults of the engine into three kinds of fault forms: no misfire (normal work), slight misfire, and severe misfire to indicate the operating status of the gasoline engine, where slight misfire indicates the decline in the performance of ignition capacitance or the ignition delay, or the spark plug misfire in a cylinder, and severe misfire implies the spark plug misfire in two cylinders of six cylinders. According to field-test data of the gasoline engine, we can obtain the fault knowledge corresponding to a set of the three kinds of fault forms K = {K₁, K₂, K₃} with respect to a set of five characteristics (five components) A = {A₁, A₂, A₃, A₄, A₅}, which is shown in

Table 1. Three kinds of fault forms for the engine EQ6102.

Kk (Fault Knowledge)	A1 (φHC × 10−2)	A2 (φCO2 × 10−1)	A3 (φNOx × 10)	A4 (φCO × 10−1)	A5 (φO2)
K1 (Normal work)	[0.03, 0.08]	[0.51, 0.95]	[0.03, 0.08]	[0.3, 0.5]	[0.062, 0.09]
K2 (Slight misfire)	[0.01, 0.046]	[0.426, 0.84]	[0.04, 0.12]	[0.29, 0.5]	[0.04, 0.11]
K3 (Severe misfire)	[0.2, 0.5]	[0.3, 0.7]	[0.1, 0. 3]	[0.1, 0.3]	[0.07, 0.15]

.

In Table 1, φ_HC × 10⁻², φ_CO2 × 10⁻¹, φ_NOx × 10, φ_CO × 10⁻¹ and φ_O2 in the characteristic set A = {A₁, A₂, A₃, A₄, A₅} indicate the exhaust emission concentration in HC, CO₂, NO_x, CO and O₂ expressed by volume percentage and the characteristic values of A_i are represented by IVFEs (interval values).

To verify the effectiveness of the proposed fault diagnosis method, we introduce the nine sets of real-testing samples (K_ts for s = 1, 2, …, 9) for the engine EQ6102 from Ye [12] and Kong et al. [17], which are shown in

Table 2. Tasting samples of exhaust emission for the engine EQ6102.

Real-Tasting Sample (Kts)	A1 (φHC × 10−2)	A2 (φCO2 × 10−1)	A3 (φNOx × 10)	A4 (φCO × 10−1)	A5 (φO2)	Actual Fault Form
Kt1	0.0455	0.47	0.033	0.48	0.0527	K2
Kt2	0.0572	0.75	0.062	0.42	0.0751	K1
Kt3	0.0261	0.65	0.086	0.453	0.0431	K2
Kt4	0.0312	0.62	0.051	0.287	0.1064	K2
Kt5	0.3761	0.45	0.139	0.179	0.1025	K3
Kt6	0.4220	0.52	0.188	0.194	0.0931	K3
Kt7	0.0189	0.81	0.091	0.459	0.0377	K2
Kt8	0.0555	0.86	0.057	0.39	0.0736	K1
Kt9	0.0551	0.85	0.050	0.386	0.0789	K1

.

Considering the importance of the five characteristics (five components), we introduce the weight vector w = (w₁, w₂, w₃, w₄, w₅)^T = (0.05, 0.35, 0.3, 0.2, 0.1)^T [7,12]. In Table 2, the characteristic values can be considered as the interval value of the equality of its lower limit and upper limit.

First, the LSM values between K_ts (s = 1, 2, …, 9) and K_k (k = 1, 2, 3) are calculated by use of Equation (3). For example, the calculating process of S_k = M_w(K_t1, K_k) for k = 1, 2, 3 is presented as follows:

$$\begin{array}{l}{S}_1=M_w(K_{t1},K_1)={\displaystyle \sum _{i=1}^5{w}_i{\log }_2\left[2-\left(\left|{\mu }_{K_{t1}}^L(A_i)-{\mu }_{K_1}^L(A_i)\right|+\left|{\mu }_{K_{t1}}^U(A_i)-{\mu }_{K_1}^U(A_i)\right|\right)/2\right]}\\ =0.05{\log }_2[2-\left(\left|0.0455-0.03\right|+\left|0.0455-0.08\right|\right)/2+0.35{\log }_2[2-\left(\left|0.47-0.51\right|+\left|0.47-0.95\right|\right)/2\\ +0.3{\log }_2[2-\left(\left|0.033-0.03\right|+\left|0.033-0.08\right|\right)/2+0.2{\log }_2[2-\left(\left|0.48-0.3\right|+\left|0.48-0.5\right|\right)/2\\ +0.1{\log }_2[2-\left(\left|0.0527-0.062\right|+\left|0.0527-0.09\right|\right)/2=0.9069,\end{array}$$

$$\begin{array}{l}{S}_2=M_w(K_{t1},K_2)={\displaystyle \sum _{i=1}^5{w}_i{\log }_2\left[2-\left(\left|{\mu }_{K_{t1}}^L(A_i)-{\mu }_{K_2}^L(A_i)\right|+\left|{\mu }_{K_{t1}}^U(A_i)-{\mu }_{K_2}^U(A_i)\right|\right)/2\right]}\\ =0.05{\log }_2[2-\left(\left|0.0455-0.01\right|+\left|0.0455-0.046\right|\right)/2+0.35{\log }_2[2-\left(\left|0.47-0.426\right|+\left|0.47-0.84\right|\right)/2\\ +0.3{\log }_2[2-\left(\left|0.033-0.04\right|+\left|0.033-0.12\right|\right)/2+0.2{\log }_2[2-\left(\left|0.48-0.29\right|+\left|0.48-0.5\right|\right)/2\\ +0.1{\log }_2[2-\left(\left|0.0527-0.04\right|+\left|0.0527-0.11\right|\right)/2=0.9158,\end{array}$$

$$\begin{array}{l}{S}_3=M_w(K_{t1},K_3)={\displaystyle \sum _{i=1}^5{w}_i{\log }_2\left[2-\left(\left|{\mu }_{K_{t1}}^L(A_i)-{\mu }_{K_3}^L(A_i)\right|+\left|{\mu }_{K_{t1}}^U(A_i)-{\mu }_{K_3}^U(A_i)\right|\right)/2\right]}\\ =0.05{\log }_2[2-\left(\left|0.0455-0.2\right|+\left|0.0455-0.5\right|\right)/2+0.35{\log }_2[2-\left(\left|0.47-0.3\right|+\left|0.47-0.7\right|\right)/2\\ +0.3{\log }_2[2-\left(\left|0.033-0.1\right|+\left|0.033-0.3\right|\right)/2+0.2{\log }_2[2-\left(\left|0.48-0.1\right|+\left|0.48-0.3\right|\right)/2\\ +0.1{\log }_2[2-\left(\left|0.0527-0.07\right|+\left|0.0527-0.15\right|\right)/2=0.8494.\end{array}$$

Using the similar calculation, we can obtain all the LSM values in

Table 3. LSM values between K_ts (s = 1, 2, …, 9) and K_k (k = 1, 2, 3) for the engine EQ6102.

Real-Tasting Sample (Kts)	LSM (Sk)
	K1	K2	K3
Kt1	0.9069	0.9158	0.8494
Kt2	0.9189	0.9169	0.8537
Kt3	0.9162	0.9173	0.8647
Kt4	0.9157	0.9169	0.8831
Kt5	0.8569	0.8826	0.9013
Kt6	0.8641	0.8719	0.9013
Kt7	0.9145	0.9172	0.8323
Kt8	0.9189	0.9113	0.8245
Kt9	0.9189	0.9142	0.8265

.

Then, the values of relation indices are calculated by Equation (4). For example, the calculating process of the relation indices η_k (k = 1, 2, 3) is presented below:

$${\eta }_1=\frac{2S_1-S_{\min }-S_{\max }}{S_{\max }-S_{\min }}=\frac{2\times 0.9069-0.8494-0.9158}{0.9158-0.8494}=0.7318,$$

$${\eta }_2=\frac{2S_2-S_{\min }-S_{\max }}{S_{\max }-S_{\min }}=\frac{2\times 0.9158-0.8494-0.9158}{0.9158-0.8494}=1.0000,$$

$${\eta }_3=\frac{2S_3-S_{\min }-S_{\max }}{S_{\max }-S_{\min }}=\frac{2\times 0.8494-0.8494-0.9158}{0.9158-0.8494}=-1.0000.$$

Using the similar calculation, the relation indices and diagnosis results of the proposed method are obtained and shown in

Table 4. Relation indices and fault diagnosis results of the engine EQ6102.

Real-Tasting Sample (Kts)	Relation Index (ηk)			Fault Diagnosis Result
	K1	K2	K3
Kt1	0.7318	1.0000	−1.0000	K2
Kt2	1.0000	0.9387	−1.0000	K1
Kt3	0.9581	1.0000	−1.0000	K2
Kt4	0.9332	1.0000	−1.0000	K2
Kt5	−1.0000	0.1573	1.0000	K3
Kt6	−1.0000	−0.5807	1.0000	K3
Kt7	0.9365	1.0000	−1.0000	K2
Kt8	1.0000	0.8390	−1.0000	K1
Kt9	1.0000	0.8972	−1.0000	K1

. From Table 2 and Table 4, we can see that fault diagnosis results are the same as actual fault types.

Furthermore, one can easily diagnose or predict fault forms of the engine EQ6102 from Table 4. For instance, for the real-tasting sample K_t2, the relation index regarding the fault form K₁ is equal to 1, which indicates the fault form K₁ (no misfire), and then one can predict that the engine has the slight misfire trend since the relation index regarding K₂ is 0.9387 and the fault form K₃ implies a very low possibility of severe misfire due to the negative relation index (−1). Similarly, one can also diagnose and predict fault forms corresponding to the relation indices for other testing samples in Table 4.

Obviously, the proposed fault diagnosis method can not only diagnose the main fault type of the engine, but it can also predict the future fault trend of the engine by the relation indices.

3.3. The Proposed Fault Diagnosis Method for Vibrational Fault Diagnosis of Steam Turbine

In this subsection, the proposed fault diagnosis method is applied to the vibrational fault diagnosis of the steam turbine to illustrate its effectiveness.

The vibration of huge steam turbine-generator sets suffer the influence of a lot of factors like the mechanical structure, load, vacuum degree, hot inflation of cylinder body and rotor, fluctuation of network load, temperature of lubricant oil, ground and so on. In generator sets, interactive effects in these factors show the vibration of the generator sets. In the vibration fault diagnosis of the generator sets, the relation between the cause and the fault symptom of the steam turbine has been established in [14,16]. Now, we investigate the vibrational fault diagnosis of steam turbine by use of the proposed fault diagnosis method to demonstrate its effectiveness.

Let us consider a set of 10 fault samples K = {K₁(Unbalance), K₂(Pneumatic force couple), K₃(Offset center), K₄(Oil-membrane oscillation), K₅(Radial impact friction of rotor), K₆(Symbiosis looseness), K₇(Damage of antithrust bearing), K₈(Surge), K₉(Looseness of bearing block), K₁₀(Non-uniform bearing stiffness)} as the fault knowledge and a set of nine frequency ranges for different frequency spectrum A = {A₁(0.01–0.39f), A₂(0.4–0.49f), A₃(0.5f), A₄(0.51–0.99f), A₅(f), A₆(2f), A₇(3–5f), A₈(Odd times of f), A₉(High frequency > 5f)} under operating frequency f as a characteristic set. Then, the fault information of the fault knowledge K_k (k = 1, 2, …, 10) with respect to the frequency range (characteristic) A_i (i = 1, 2, …, 9) can be expressed by the form of IVFSs and is shown in

Table 5. Fault knowledge of steam turbine.

Kk (Fault Knowledge)	Frequency Range (f: Operating Frequency)
	A1 (0.01–0.39f)	A2 (0.4–0.49f)	A3 (0.5f)	A4 (0.51–0.99f)	A5 (f)	A6 (2f)	A7 (3–5f)	A8 (Odd Times of f)	A9 (High Frequency > 5f)
K1 (Unbalance)	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.85, 1.00]	[0.04, 0.06]	[0.04, 0.07]	[0.00, 0.00]	[0.00, 0.00]
K2 (Pneumatic force couple)	[0.00, 0.00]	[0.28, 0.31]	[0.09, 0.12]	[0.55, 0.70]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.08, 0.13]
K3 (Offset center)	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.30, 0.58]	[0.40, 0.62]	[0.08, 0.13]	[0.00, 0.00]	[0.00, 0.00]
K4 (Oil-membrane oscillation)	[0.09, 0.11]	[0.78, 0.82]	[0.00, 0.00]	[0.08, 0.11]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]
K5 (Radial impact friction of rotor)	[0.09, 0.12]	[0.09, 0.11]	[0.08, 0.12]	[0.09, 0.12]	[0.18, 0.21]	[0.08, 0.13]	[0.08, 0.13]	[0.08, 0.12]	[0.08, 0.12]
K6 (Symbiosis looseness)	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.18, 0.22]	[0.12, 0.17]	[0.37, 0.45]	[0.00, 0.00]	[0.22, 0.28]
K7 (Damage of antithrust bearing)	[0.00, 0.00]	[0.00, 0.00]	[0.08, 0.12]	[0.86, 0.93]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]
K8 (Surge)	[0.00, 0.00]	[0.27, 0.32]	[0.08, 0.12]	[0.54, 0.62]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]
K9 (Looseness of bearing block)	[0.85, 0.93]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.08, 0.12]	[0.00, 0.00]
K10 (Non-uniform bearing stiffness)	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.00, 0.00]	[0.77, 0.83]	[0.19, 0.23]	[0.00, 0.00]	[0.00, 0.00]

[14,16]. For convenient comparison with [14,16], assume that the weight of each characteristic A_i is w_i = 1/9 for i = 1, 2, …, 9.

In the vibrational fault diagnosis of the steam turbine, two real-testing samples in [14,16] are introduced as IVFSs:

K_t1 = {(A₁, [0.0, 0.0]), (A₂, [0.00, 0.00]), (A₃, [0.1, 0.1]), (A₄, [0.9, 0.9]), (A₅, [0.0, 0.0]), (A₆, [0.0, 0.0]), (A₇, [0.0, 0.0]), (A₈, [0.0, 0.0]), (A₉, [0.0, 0.0])},

K_t2 = {(A₁, [0.39, 0.39]), (A₂, [0.07, 0.07]), (A₃, [0.00, 0.00]), (A₄, [0.06, 0.06]), (A₅, [0.00, 0.00]), (A₆, [0.13, 0.13]), (A₇, [0.00, 0.00]), (A₈, [0.00, 0.00]), (A₉, [0.35, 0.35])}.

For the fault diagnoses of the testing samples K_t1 and K_t2, the LSM values and relation indices between K_k (k = 1, 2, …, 10) and K_ts (s = 1, 2) are calculated by Equations (3) and (4) based on the above similar calculating processes; all of the LSM values and the relation indices and fault diagnosis results are shown in

Table 6. LSM values between K_k (k = 1, 2, …, 10) and K_ts (s = 1, 2).

Kts	LSM (Sk)
	K1	K2	K3	K4	K5	K6	K7	K8	K9	K10
Kt1	0.7879	0.9409	0.8003	0.8191	0.8501	0.8088	0.9956	0.9449	0.7933	0.7963
Kt2	0.8133	0.8525	0.8415	0.8577	0.9043	0.8907	0.8231	0.8480	0.8935	0.8406

and

Table 7. Relation indices and fault diagnosis results of steam turbine.

Kts	Relation Index (ηk)										Fault Diagnosis Result
	K1	K2	K3	K4	K5	K6	K7	K8	K9	K10
Kt1	−1	0.4732	−0.8807	−0.6993	−0.4007	−0.7986	1.0000	0.5117	−0.9476	−0.9193	K7
Kt2	−1	−0.1380	−0.3789	−0.0252	1.0000	0.7014	−0.7850	−0.2372	0.7612	−0.3993	K5

respectively.

For the first real-testing sample K_t1, we can see from Table 7 that the fault form of the turbine is K₇ due to the maximum relation index (1.0000), which indicates that the vibration fault of the turbine results firstly from the damage of antithrust bearing. Then, the fault form of surge contains high possibility because the relation index of the fault form K₈ are more than 0.5 and the fault form of pneumatic force couple contains some possibility due to the fault form K₂ with the positive relation index of 0.4732. Obviously, the fault forms K₅, K₄, K₆, K₃, K₁₀, and K₉ contain lower possibility due to the negative relation indices. Then, the fault form K₁ implies a very low possibility due to the minimum relation index (−1.0000). By actual checking, we discover that one of antithrust bearings is damage. Therefore, it causes the violent vibration of the turbine. Hereby, all the faults are ranked as K₇→K₈→K₂→K₅→K₄→K₆→K₃→K₁₀→K₉→K₁.

For the second real-testing sample K_t2, we can see from Table 7 that the vibration fault of the turbine is firstly resulted from the radial impact friction of rotor (K₅) and then the looseness of bearing block (K₉) and the symbiosis looseness (K₆) contain high possibility because their relation indices are more than 0.5. By actual checking, we discover the friction between the rotor and cylinder body in the turbine, and then the vibration values of four ground bolts of the bearing between the turbine and the gearbox are very different. We also discover that the gap between the nuts and the bearing block is oversized. Thus, the looseness of the bearing block also causes the violent vibration of the turbine. Hereby, all the faults are ranked as K₅→K₉→K₆→K₄→K₂→K₈→K₃→K₁₀→K₇→K₁.

Obviously, the proposed fault diagnosis method can not only diagnose the main fault type of the steam turbine but it can also predict the future fault trend of the steam turbine by the relation indices.

3.4. Comparative Analysis with the Related Methods

First, the proposed diagnosis method with the misfire fault diagnosis method of the gasoline engine EQ6102 based on the CSM of neutrosophic numbers was compared [17]. Based on the fault diagnosis method introduced in [17], the interval sets expressed as fault information are firstly transformed into the neutrosophic numbers, and then the CSM of neutrosophic numbers for the fault diagnosis of the gasoline engine. Then, all the diagnosis results and the actual fault results are shown in

Table 8. Various misfire fault diagnoses and actual misfire fault results of the gasoline engine EQ6102.

Real-Tasting Sample (Kts)	Fault Diagnosis Result in [17]	Fault Diagnosis Result of the New Diagnosis Method	Actual Fault Result
Kt1	K2	K2	K2
Kt2	K1	K1	K1
Kt3	K2	K2	K2
Kt4	K2	K2	K2
Kt5	K3	K3	K3
Kt6	K3	K3	K3
Kt7	K2	K2	K2
Kt8	K1	K1	K1
Kt9	K1	K1	K1

for convenient comparison.

Obviously, the new fault diagnosis method indicates the same fault diagnosis results as the ones in [17] and actual fault results for the gasoline engine from Table 8. Then, the new fault diagnosis method contains simpler calculation than the existing diagnosis method [17] because the latter has to transform interval numbers into neutrosophic numbers, while the former does not have this transformed process.

Second, the new diagnosis method and the diagnosis methods of the steam turbine based on the cross entropy and cosine similarity measures of VSs introduced in [14,16] were compared. Based on the fault diagnosis methods introduced in [14,16], the interval sets expressed as fault information are firstly transformed into VSs, and then the cross entropy and cosine similarity measures of VSs are used for the fault diagnosis of the steam turbine occur. For comparative convenience, all the diagnosis results and the actual fault results are shown in

Table 9. Various fault diagnosis results and actual fault results of the steam turbine.

Real-Tasting Sample (Kts)	Ranking Order of Fault Diagnoses in [14]	Ranking Order of Fault Diagnoses in [16]	Ranking Order of Fault Diagnoses Using the New Diagnosis Method	Fault Diagnosis Result	Actual Fault Result
Kt1	K7→K8→K2→K5→K3→ K4→K6→K10→K9→K1	K7→K2→K8→K5→K6→ K3→K4→K10→K9→K1	K7→K8→K2→K5→K4→ K6→K3→K10→K9→K1	K7	K7
Kt2	K5→K9→K6→K2→K4→ K8→K3→K10→K7→K1	K5→K6→K9→K8→K2→ K3→K4→K10→K7→K1	K5→K9→K6→K4→K2→ K8→K3→K10→K7→K1	K5	K5

.

In Table 9, the new fault diagnosis method indicates the same fault diagnosis results as the ones in [14,16] and the actual fault results for the steam turbine; there is little difference in their ranking orders based on different diagnosis methods. However, the new fault diagnosis method contains a simpler calculation than the existing methods [14,16] because the existing methods in [14,16] must transform interval sets into VSs, while the former does not require this transformed process.

The comparative analysis above demonstrates that the new fault diagnosis method in this paper is not only effective but also simpler than the existing diagnosis methods [14,16]. Therefore, it provides a useful new way to perform fault diagnosis under an interval-valued fuzzy environment.

4. Conclusions

This paper proposed a LSM between IVFSs and its fault diagnosis method. Furthermore, the proposed fault diagnosis method was applied to the misfire fault diagnosis of the gasoline engine and the vibrational fault diagnosis of the steam turbine under an interval-valued fuzzy environment. These fault diagnosis results demonstrated the effectiveness and rationality of the proposed diagnosis method. The proposed diagnosis method can not only diagnose the main fault type but it can also predict future fault trends according to the relation indices. The proposed fault diagnosis method is simpler than existing diagnosis methods based on the CSM and cross entropy measures. This method not only extends existing diagnosis methods but also provides a useful new way for fault diagnoses to be performed with interval-valued fuzzy information. Since the logarithmic similarity measure and its fault diagnosis method in this study are presented for the first time, the developed fault diagnosis technique will be extended to other fault diagnosis problems with single-valued neutrosophic information [19,20] in the future.