A Bloom Filter for High Dimensional Vectors
Abstract
:1. Introduction
- Improvements on the array. For most of the applications, Counting BF (CBF) [20] proves that 4-bit counter array is enough to defend FPPs brought by elements deletion. The Variable-Increment CBF (VI-CBF) [21] increases the counter at a variable step instead of 1 to further reduce the FPPs of the CBF. By combination with VI-CBF, fingerprint CBF (FP-CBF) adds fingerprints to the elements stored in the CBF to reduce the FPP of the VI-CBF. These two improvements on the FPP are at the cost of memory, VI-CBF needs more bits to store the variable steps and another one requires extra spaces to store the fingerprints. Improved associative deletion BF (IABF) [22], adopts multiple CBF to store multiple attributes, and a check CBF to keep the association information on these attributes of items in the given data set. By operation of these CBF, the IABF can support association attribute deletion. The Shifting Bloom filter (ShBF) [23] can quickly process membership, association, and multiplicity queries of sets, using a small amount of memory.
- Modifications on the structure. For a static set, it is possible to know the whole set in advance and design a perfect hash function to avoid hash collisions. However, for the set with uncertain cardinality, BF and CBF are unsuitable. Scalable BF (SBF) [24] and Dynamic BFs (DBF) [25] propose to represent a dynamic set instead of rehashing the dynamic set into a new filter as the set size changes. If the original DBF is full, the DBF adds a new CBF dynamically and merges it into the DBF. Let the DBF own sub-CBFs and a sub-CBF corresponds hash functions, time complexities of membership query (or deletion) for sub-CBF and DBF are and , respectively. However, in the DBF, there is no mechanism to control the overall FPP, although sub-CBF makes the upper bound of FPP converge, it does not support useful bit vector-based algebra operations between sub-CBFs and may cause unacceptable space waste; in addition, the DBF has to query all sub-CBFs one by one to discover the query. Partitioned BF (Par-BF) [26] partitions the whole required memory space into disjointed sub-CBF lists. Each sub-CBF list can index maximal elements. Each sub-CBF list can contain homogeneous CBFs at most. A thread is assigned into each sub-CBF list to do the matching, via parallel computing, the Par-BF gets query time optimization. PBF [27], PBF-BF and PBF-HT [28] extend the BF to represent and query elements with multi-dimensional text attributes. The PBF allocates dimensions into parallel BFs, but the integrity of an element is destroyed, which results in a high FPP. PBF-BF and PBF-HT also introduce parallel CBF (PBF) arrays to store dimensions, to keep these dimensions integrity, a check BF (PBF-BF) or a hash table (PBF-HT) is added. However, the space occupations increase linearly, not only with the rising cardinality, but also the dimensions, which lead to huge memory wastes and large query delays. All of them make parallel BFs not suitable for the big set in a high-dimensional space.
- Different hash functions. LshBF [29] schemes adopt local sensitive hash functions (LSH) instead of string hash functions to solve the Approximate Membership Query (AMQ). The LSH function follows a P-stable () distribution, only when p = 1 and 2, the probability density functions can be written, and they are a Cauchy distribution (p = 1) and Gaussian (normal) distribution (p = 2), respectively. The LSH function maps the neighbors in Euclidean spaces to nearby locations, and directly changes high-dimensional vectors into real numbers. To reduce the FPP, the LshBF-BF [30] adds a verification BF to further disperse points in the LshBF. Multi-Granularity LshBF-BF (MLBF) [31] develops multiple granularities search instead of one step in the LshBF-BF to further improve the search accuracy. However, MLBF is designed to only filter (query) objects with multiple logarithmic distance granularities. The integer-granularity locality-sensitive Bloom filter (ILBF) [32] filters objects with multiple integer distance granularities to shrink the distances and to reduce the FPP in MLBF. All these schemes are based on the LSH, according to the central limited theorem, after mapping, the LSH shrinks most of elements of the set around the mean, which results in a high FPP in member query, especially around the mean. For example, approximately 68.5% elements are projected to the locations between the negative and positive variance under Gaussian distribution. Through LSH mapping, the LshBFs transform high-dimensional vectors into real numbers, which avoids dimension disasters and brings computing and space overheads, but the aggregation of neighbors causes high FPPs. This, LshBFs are only suitable for AMQ not membership query.
- The modified hash functions can effectively discretize vectors with numerical high dimensions, uniformly and randomly. Based on the modified hash functions, HDBF extends the Bloom filters to represent and query numerical vectors in high-dimensional spaces.
- Compared with CBF, HDBF is more efficient in dealing with numerical dimensions, and can be a replacement for CBF in numerical high-dimensional spaces
- HDBF outperforms CBF in false positive probability, query delay, memory costs, and especially in numerical high-dimensional spaces.
- Different from parallel BFs (PBFs), HDBF will not bring dimension disaster. Moreover, it has memory and query overheads compared with PBFs.
2. Work Mechanism and Structure
2.1. Bloom Filter
| Algorithm 1 |
| unsigned int sax_hash(char *key) { 1. unsigned int h = 0; 2. while(*key) 3. h ^ = (h << 5) + (h >> 2) + (unsigned char)*key++; 4. return (h& 0x7FFFFFFF); } |
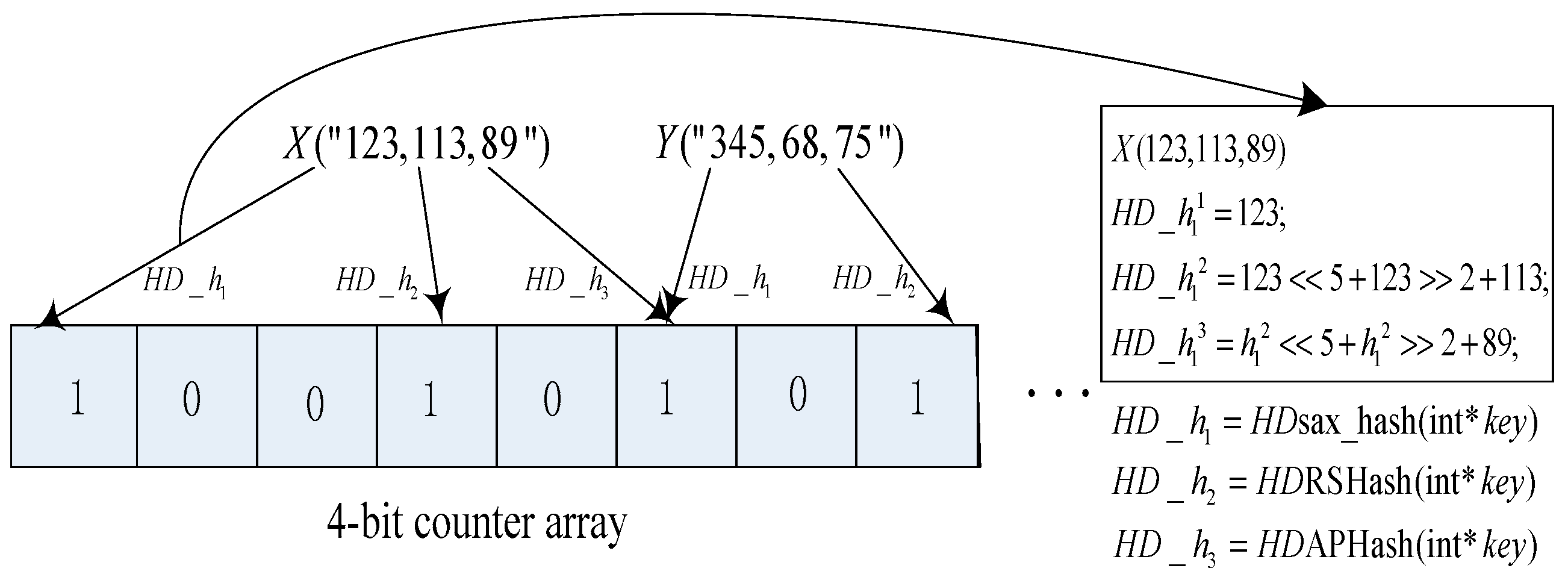
2.2. High Dimensional Bloom Filter (HDBF)
| Algorithm 2 |
| unsigned int HDsax_hash(int *key) { 1. unsigned int h=0; 2. while(*key) 3. h ^= (h<<5) + (h>>2) + (unsigned int)*key++; 4. return (h& 0x7FFFFFFF); } |
3. Performances
4. Experimental Section
4.1. Dataset and Settings
4.2. Distribution and Entropy
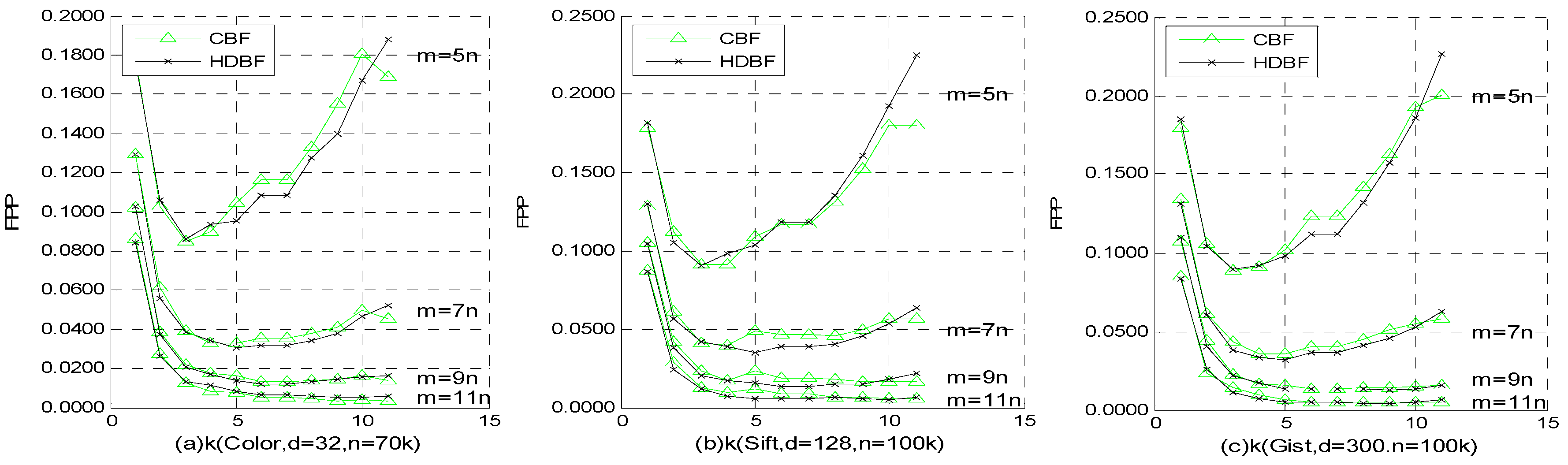
4.3. FPP
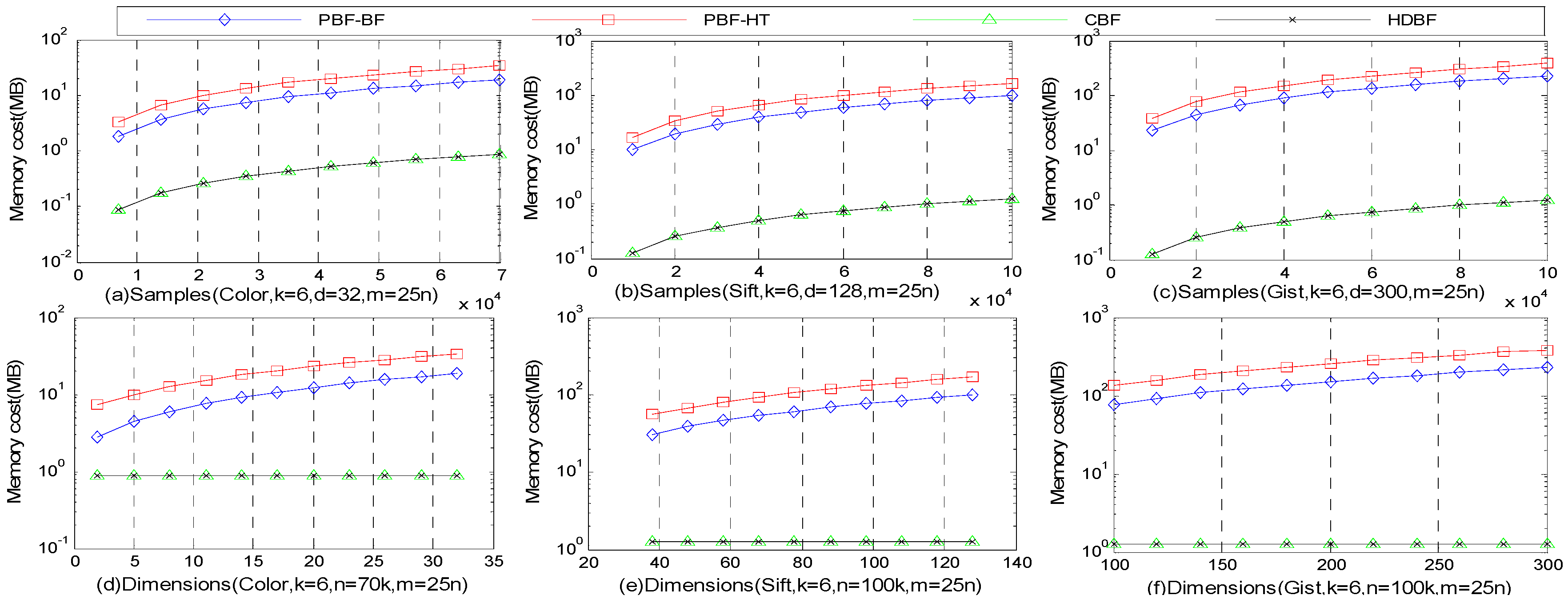
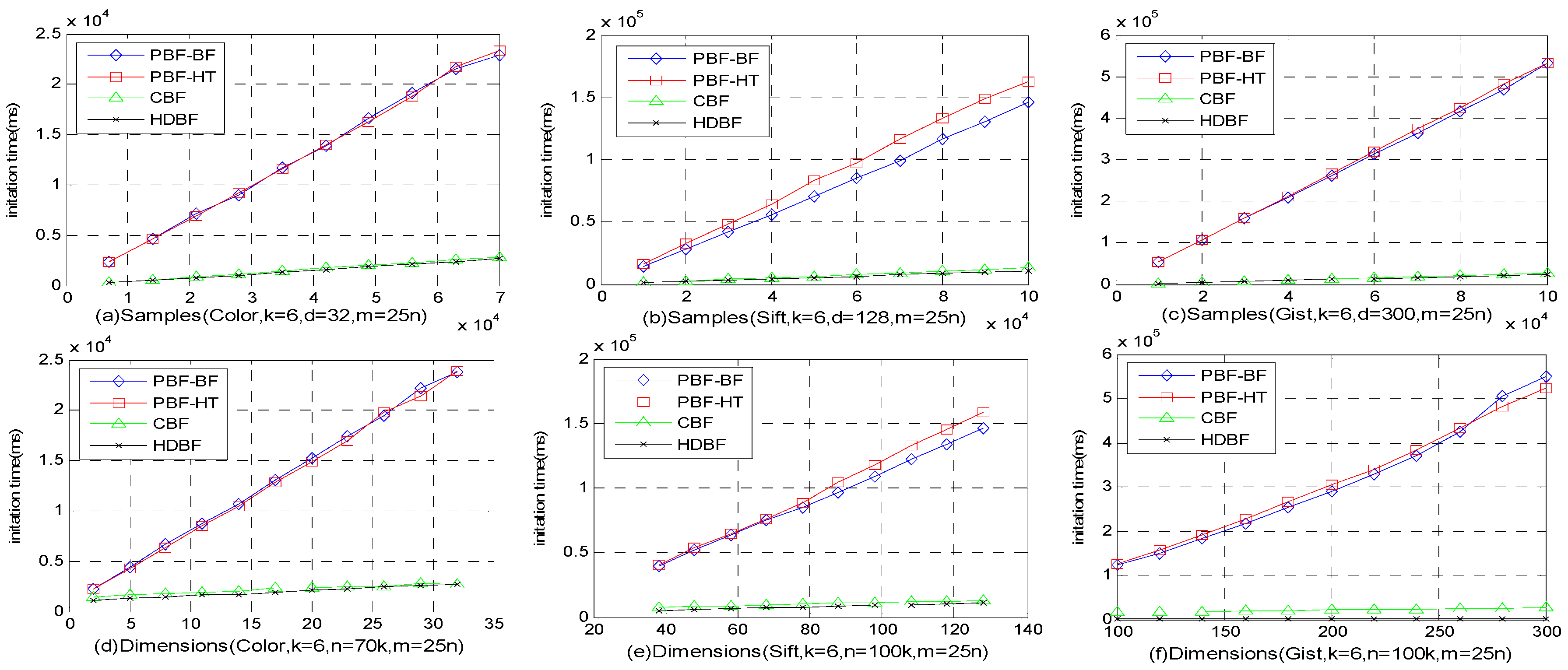
4.4. Memory Costs and Latency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hunt, W.; Mark, W.R.; Stoll, G. Fast kd-tree construction with an adaptive error-bounded heuristic. In Proceedings of the IEEE Symposium on Interactive Ray Tracing, Salt Lake City, UT, USA, 18–20 September 2006; pp. 81–88. [Google Scholar]
- Burkhardt, S.; Crauser, A.; Ferragina, P.; Lenhof, H.; Rivals, E.; Vingron, M. q-gram based database searching using a suffix array (QUASAR). In Proceedings of the Third Annual International Conference on Computational Molecular Biology, Lyon, France, 11–14 April 1999; ACM: New York, NY, USA, 1999; pp. 77–83. [Google Scholar]
- Burton, H.B. Space/Time Trade-Offs in Hash Coding with Allowable Errors. Commun. ACM 1970, 13, 422–426. [Google Scholar] [CrossRef]
- Broder, A.; Mitzenmacher, M. Network applications of bloom filters: A survey. Internet Math. 2004, 1, 485–509. [Google Scholar] [CrossRef]
- Tarkoma, S.; Rothenberg, C.E.; Lagerspetz, E. Theory and practice of bloom filters for distributed systems. IEEE Commun. Surv. Tutor. 2012, 14, 131–155. [Google Scholar] [CrossRef]
- Ju, H.M.; Lim, H. New Approach for Efficient IP Address Lookup Using a Bloom filter in Trie-Based Algorithms. IEEE Trans. Comput. 2016, 65. [Google Scholar] [CrossRef]
- Kwon, M.; Reviriego, P.; Pontarelli, S. A length-aware cuckoo filter for faster IP lookup. In Proceedings of the 2016 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), San Francisco, CA, USA, 10–14 April 2016. [Google Scholar]
- Nikolaevskiy, I.; Lukyanenko, A.; Polishchukc, T.; Polishchuk, V.; Gurtov, A. isBF: Scalable in-packet bloom filter based multicast. Comput. Commun. 2015, 70, 79–85. [Google Scholar] [CrossRef]
- Zengin, S.; Schmidt, E.G. A fast and accurate hardware string matching module with Bloom filters. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 305–317. [Google Scholar] [CrossRef]
- Lin, P.-C.; Lin, Y.-D.; Lai, Y.-C.; Zheng, Y.-J.; Lee, T.-H. Realizing a sub-linear time string-matching algorithm with a hardware accelerator using bloom filters. IEEE Trans. Very Large Scale Integr. Syst. 2009, 17, 1008–1020. [Google Scholar] [CrossRef]
- Alexander, H.; Khalil, I.; Cameron, C.; Tari, Z.; Zomaya, A. Cooperative Web Caching Using Dynamic Interest-Tagged filtered Bloom filters. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 2956–2969. [Google Scholar] [CrossRef]
- Antikainen, M.; Aura, T.; Särelä, M. Denial-of-service attacks in bloom-filter-based forwarding. Trans. Netw. IEEE/ACM 2014, 22, 1463–1476. [Google Scholar] [CrossRef]
- Parthasarathy, S.; Kundur, D. Bloom filter based intrusion detection for smart grid SCADA. In Proceedings of the IEEE Canadian Conference on Electrical & Computer Engineering (CCECE), Montreal, QC, Canada, 29 April–2 May 2012; pp. 1–6. [Google Scholar]
- Meghana, V.; Suresh, M.; Sandhya, S.; Aparna, R.; Gururaj, C. SoC implementation of network intrusion detection using counting bloom filter. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 20–21 May 2016; pp. 1846–1850. [Google Scholar]
- Aldwairi, M.; Al-Khamaiseh, K. Exhaust: Optimizing Wu-Manber pattern matching for intrusion detection using Bloom filters. In Proceedings of the IEEE Web Applications and Networking, Sousse, Tunisia, 21–23 March 2015; pp. 1–6. [Google Scholar]
- Bose, P.; Guo, H.; Kranakis, E.; Maheshwari, A.; Morin, P.; Morrison, J.; Smid, M.; Tang, Y. On the false-positive rate of Bloom filters. Inf. Process. Lett. 2008, 108, 210–213. [Google Scholar] [CrossRef] [Green Version]
- Christensen, K.; Roginsky, A.; Jimeno, M. A new analysis of the false positive rate of a Bloom filter. Inf. Process. Lett. 2010, 110, 944–949. [Google Scholar] [CrossRef]
- Rottenstreich, O.; Keslassy, I. The bloom paradox: When not to use a Bloom filter. IEEE/ACM Trans. Netw. 2015, 23, 703–716. [Google Scholar] [CrossRef]
- Lim, H.; Lee, J.; Yim, C. Complement Bloom filter for Identifying True Positiveness of a Bloom filter. IEEE Commun. Lett. 2015, 19. [Google Scholar] [CrossRef]
- Fan, L.; Cao, P.; Almeida, J. Summary cache: A scalable wide-area Web cache sharing protocol. Trans. Netw. IEEE/ACM 2000, 8, 281–293. [Google Scholar] [CrossRef]
- Rottenstreich, O.; Kanizo, Y.; Keslassy, I. The variable-increment counting Bloom filter. IEEE/ACM Trans. Netw. 2014, 22, 1092–1105. [Google Scholar] [CrossRef]
- Qian, J.; Zhu, Q.; Wang, Y. Bloom filter based associative deletion. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1986–1998. [Google Scholar] [CrossRef]
- Yang, T.; Liu, A.X.; Shahzad, M.; Zhong, Y.; Fu, Q.; Li, Z.; Xie, G.; Li, X. A shifting bloom filter framework for set queries. Proc. VLDB Endow. 2016, 9, 408–419. [Google Scholar] [CrossRef] [Green Version]
- Almeida, P.S.; Baquero, C.; Preguiça, N.; Hutchison, D. Scalable bloom filters. Inf. Process. Lett. 2007, 101, 255–261. [Google Scholar] [CrossRef] [Green Version]
- Guo, D.; Wu, J.; Chen, H.; Yuan, Y.; Luo, X. The Dynamic Bloom filters. IEEE Trans. Knowl. Data Eng. 2010, 22, 120–133. [Google Scholar] [CrossRef]
- Liu, Y.; Ge, X.; Du, D.H.C.; Huang, X. Par-BF: A Parallel Partitioned Bloom filter for Dynamic Data Sets. Int. J. High Perform. Comput. Appl. 2015, 30, 1–8. [Google Scholar] [CrossRef]
- Xiao, M.Z.; Dai, Y.F.; Li, X.M. Split bloom filter. Acta Electron. Sin. 2004, 32, 241–245. [Google Scholar]
- Xiao, B.; Hua, Y. Using Parallel Bloom filters for Multiattribute Representation on Network Services. IEEE Trans. Parallel Distrib. Syst. 2010, 21, 20–32. [Google Scholar] [CrossRef]
- Kirsch, A.; Mitzenmacher, M. Distance-sensitive bloom filters. In Proceedings of the 8th Workshop on Algorithm Engineering and Experiments/3rd Workshop on Analytic Algorithms and Combinatorics, Miami, FL, USA, 22–26 January 2006; pp. 41–50. [Google Scholar]
- Hua, Y.; Xiao, B.; Veeravalli, B.; Feng, D. Locality-Sensitive Bloom filter for Approximate Membership Query. IEEE Trans. Comput. 2012, 61, 817–830. [Google Scholar] [CrossRef]
- Qian, J.; Zhu, Q.; Chen, H. Multi-Granularity Locality-Sensitive Bloom filter. IEEE Trans. Comput. 2015, 64, 3500–3514. [Google Scholar] [CrossRef]
- Qian, J.; Zhu, Q.; Chen, H. Integer-Granularity Locality-Sensitive Bloom filter. IEEE Trans. Comput. 2016, 20, 2125–2128. [Google Scholar] [CrossRef]
- Wu, W.; Wu, S.; Zhang, L.; Zou, J.; Dong, L. LHash: A Light weight Hash Function. In Proceedings of the International Conference on Information Security and Cryptology, Guangzhou, China, 27 November 2013; pp. 291–308. [Google Scholar]
- Charles, D.X.; Lauter, K.E.; Goren, E.Z. Cryptographic Hash Functions from Expander Graphs. J. Cryptol. 2009, 22, 93–113. [Google Scholar] [CrossRef]
- Fagin, R.; Kumar, R.; Sivakumar, D. Efficient similarity search and classification via rank aggregation. In Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data, San Diego, CA, USA, 9–12 June 2003; pp. 301–312. [Google Scholar]
- Datasets for Approximate Nearest Neighbor Search. Available online: http://corpus-texmex.irisa.fr/ (accessed on 19 June 2018).






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shuai, C.; Yang, H.; Ouyang, X.; Gong, Z. A Bloom Filter for High Dimensional Vectors. Information 2018, 9, 159. https://doi.org/10.3390/info9070159
Shuai C, Yang H, Ouyang X, Gong Z. A Bloom Filter for High Dimensional Vectors. Information. 2018; 9(7):159. https://doi.org/10.3390/info9070159
Chicago/Turabian StyleShuai, Chunyan, Hengcheng Yang, Xin Ouyang, and Zeweiyi Gong. 2018. "A Bloom Filter for High Dimensional Vectors" Information 9, no. 7: 159. https://doi.org/10.3390/info9070159
APA StyleShuai, C., Yang, H., Ouyang, X., & Gong, Z. (2018). A Bloom Filter for High Dimensional Vectors. Information, 9(7), 159. https://doi.org/10.3390/info9070159



