Two-Dimensional Uniform and Non-Uniform Haar Wavelet Collocation Approach for a Class of Nonlinear PDEs
Abstract
:1. Introduction
2. Preliminaries
2.1. Uniform Haar Wavelet
2.2. Non-Uniform Haar Wavelet
3. Novel Approach and Convergence Analysis
3.1. Derivation: UHWCM
3.2. Convergence: UHWCM
3.3. Derivation: NUHWCM
3.4. Convergence: NUHWCM
4. Numerical Illustration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Molabahrami, A.; Khani, F. The Homotopy analysis method to solve the Burgers-Huxley Equation. Nonlinear Anal. Real World Appl. 2009, 10, 589–600. [Google Scholar] [CrossRef]
- Tomasiello, S. Numerical solutions of the Burgers-Huxley Equation by the IDQ method. Int. J. Comput. Math. 2010, 87, 129–140. [Google Scholar] [CrossRef]
- Saha Ray, S.; Gupta, A.K. Comparative analysis of variational iteration method and Haar wavelet method for the numerical solutions of Burgers–Huxley and Huxley equations. J. Math. Chem. 2014, 52, 1066–1080. [Google Scholar] [CrossRef]
- Javidi, M. A numerical solution of the Generalized Burgers-Huxley Equation by spectral collocation method. Appl. Math. Comput. 2006, 178, 338–344. [Google Scholar]
- Darvishi, M.; Kheybari, S.; Khani, F. Spectral collocation method and Darvishi’s preconditionings to solve the Generalized Burgers-Huxley Equation. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 2091–2103. [Google Scholar] [CrossRef]
- Javidi, M.; Golbabai, A. A new domain decomposition algorithm for generalized Burgers-Huxley Equation based on Chebyshev polynomials and preconditioning. Chaos Solitons Fractals 2009, 39, 849–857. [Google Scholar] [CrossRef]
- Haq, S.; Hussain, A.; Uddin, M. On the numerical solution of nonlinear Burgers’-type equations using meshless method of lines. Appl. Math. Comput. 2012, 218, 6280–6290. [Google Scholar] [CrossRef]
- Sari, M.; Gürarslan, G. Numerical Solutions of the Generalized Burgers-Huxley Equation by a Differential Quadrature Method. Math. Probl. Eng. 2009, 2009, 370765. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhu, Z.S.; Lu, Y.K. Solitary wave solutions of the generalised Burgers-Huxley Equation. J. Phys. Math. Gen. 1990, 23, 271–274. [Google Scholar] [CrossRef]
- Ismail, H.N.; Raslan, K.; Abd Rabboh, A.A. Adomian decomposition method for Burger’s–Huxley and Burger’s–Fisher equations. Appl. Math. Comput. 2004, 159, 291–301. [Google Scholar] [CrossRef]
- Hashim, I.; Noorani, M.; Said Al-Hadidi, M. Solving the generalized Burgers–Huxley equation using the Adomian decomposition method. Math. Comput. Model. 2006, 43, 1404–1411. [Google Scholar] [CrossRef]
- Batiha, B.; Noorani, M.; Hashim, I. Application of variational iteration method to the generalized Burgers–Huxley equation. Chaos Solitons Fractals 2008, 36, 660–663. [Google Scholar] [CrossRef]
- Çiçek, Y.; Tanoǧlu, G. Strang splitting method for Burgers-Huxley Equation. Appl. Math. Comput. 2016, 276, 454–467. [Google Scholar] [CrossRef]
- Mohanty, R.K.; Dai, W.; Liu, D. Operator compact method of accuracy two in time and four in space for the solution of time dependent Burgers-Huxley equation. Numer. Algorithms 2015, 70, 591–605. [Google Scholar] [CrossRef]
- Nourazar, S.S.; Soori, M.; Nazari-Golshan, A. On the Exact Solution of Burgers-Huxley Equation Using the Homotopy Perturbation Method. J. Appl. Math. Phys. 2015, 3, 285–294. [Google Scholar] [CrossRef]
- Mittal, R.; Tripathi, A. Numerical solutions of generalized Burgers–Fisher and generalized Burgers–Huxley equations using collocation of cubic B-splines. Int. J. Comput. Math. 2015, 92, 1053–1077. [Google Scholar] [CrossRef]
- Singh, B.K.; Arora, G.; Singh, M.K. A numerical scheme for the generalized Burgers–Huxley equation. J. Egypt. Math. Soc. 2016, 24, 629–637. [Google Scholar] [CrossRef]
- Mohanty, R.K.; Sharma, S. A new high-accuracy method based on off-step cubic polynomial approximations for the solution of coupled Burgers’ equations and Burgers–Huxley equation. Eng. Comput. 2020, 37, 3049–3066. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. A modified exponential method that preserves structural properties of the solutions of the Burgers–Huxley equation. Int. J. Comput. Math. 2018, 95, 3–19. [Google Scholar] [CrossRef]
- Batiha, B.; Noorani, M.; Hashim, I. Numerical simulation of the generalized Huxley equation by He’s variational iteration method. Appl. Math. Comput. 2007, 186, 1322–1325. [Google Scholar] [CrossRef]
- Hashemi, S.; Mohammadi Daniali, H.; Ganji, D. Numerical simulation of the generalized Huxley equation by He’s homotopy perturbation method. Appl. Math. Comput. 2007, 192, 157–161. [Google Scholar] [CrossRef]
- Hashim, I.; Noorani, M.; Batiha, B. A note on the Adomian decomposition method for the generalized Huxley equation. Appl. Math. Comput. 2006, 181, 1439–1445. [Google Scholar] [CrossRef]
- Moghimi, M.; Hejazi, F.S. Variational iteration method for solving generalized Burger–Fisher and Burger equations. Chaos Solitons Fractals 2007, 33, 1756–1761. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1993. [Google Scholar]
- Mickens, R.E. A best finite-difference scheme for the Fisher equation. Numer. Methods Partial. Differ. Equations 1994, 10, 581–585. [Google Scholar] [CrossRef]
- Mickens, R.E. Applications of Nonstandard Finite Difference Schemes; World Scientific: Singapore, 2000. [Google Scholar]
- Mickens, R. A nonstandard finite difference scheme for a Fisher PDE having nonlinear diffusion. Comput. Math. Appl. 2003, 45, 429–436. [Google Scholar] [CrossRef]
- Zibaei, S.; Zeinadini, M.; Namjoo, M. Numerical solutions of Burgers–Huxley equation by exact finite difference and NSFD schemes. J. Differ. Equ. Appl. 2016, 22, 1098–1113. [Google Scholar] [CrossRef]
- Verma, A.K.; Kayenat, S. An efficient Mickens’ type NSFD scheme for the Generalized Burgers-Huxley Equation. J. Differ. Equ. Appl. 2020, 26, 1213–1246. [Google Scholar] [CrossRef]
- Appadu, A.R.; İnan, B.; Tijani, Y.O. Comparative Study of Some Numerical Methods for the Burgers-Huxley Equation. Symmetry 2019, 11, 1333. [Google Scholar] [CrossRef]
- Verma, A.K.; Kayenat, S. On the stability of Micken’s type NSFD schemes for generalized Burgers Fisher equation. J. Differ. Equ. Appl. 2019, 25, 1706–1737. [Google Scholar] [CrossRef]
- Verma, A.; Rawani, M.K.; Agarwal, R.P. A Novel Approach to Compute the Numerical Solution of Variable Coefficient Fractional Burgers’ Equation with Delay. J. Appl. Comput. Mech. 2021, 7, 1550–1564. [Google Scholar]
- Majak, J.; Pohlak, M.; Eerme, M. Application of the Haar wavelet-based discretization technique to problems of orthotropic plates and shells. Mech. Compos. Mater. 2009, 45, 631–642. [Google Scholar] [CrossRef]
- Majak, J.; Pohlak, M.; Karjust, K.; Eerme, M.; Kurnitski, J.; Shvartsman, B. New higher order Haar wavelet method: Application to FGM structures. Compos. Struct. 2018, 201, 72–78. [Google Scholar] [CrossRef]
- Majak, J.; Shvartsman, B.; Ratas, M.; Bassir, D.; Pohlak, M.; Karjust, K.; Eerme, M. Higher-order Haar wavelet method for vibration analysis of nanobeams. Mater. Today Commun. 2020, 25, 101290. [Google Scholar] [CrossRef]
- Jiwari, R. A Haar wavelet quasilinearization approach for numerical simulation of Burgers’ equation. Comput. Phys. Commun. 2012, 183, 2413–2423. [Google Scholar] [CrossRef]
- Pandit, S.; Jiwari, R.; Bedi, K.; Koksal, M.E. Haar wavelets operational matrix based algorithm for computational modelling of hyperbolic type wave equations. Eng. Comput. 2017, 34, 2793–2814. [Google Scholar] [CrossRef]
- Jiwari, R.; Kumar, V.; Karan, R.; Alshomrani, A. Haar wavelet quasilinearization approach for MHD Falkner-Skan flow over permeable wall via Lie Group method. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, HFF–04–2016–0145. [Google Scholar] [CrossRef]
- Mittal, R.; Kaur, H.; Mishra, V. Haar wavelet-based numerical investigation of coupled viscous Burgers’ equation. Int. J. Comput. Math. 2015, 92, 1643–1659. [Google Scholar] [CrossRef]
- Mittal, R.C.; Pandit, S. Sensitivity analysis of shock wave Burgers’ equation via a novel algorithm based on scale-3 Haar wavelets. Int. J. Comput. Math. 2018, 95, 601–625. [Google Scholar] [CrossRef]
- Kaur, H.; Mishra, V.; Mittal, R.C. Numerical Solution of a Laminar Viscous Flow Boundary Layer Equation Using Uniform Haar Wavelet Quasi-linearization Method. World Acad. Sci. Eng. Technol. 2013, 79, 1682. [Google Scholar]
- Swati; Singh, K.; Verma, A.K.; Singh, M. Higher order Emden-Fowler type equations via uniform Haar Wavelet resolution technique. J. Comput. Appl. Math. 2020, 376, 112836. [Google Scholar] [CrossRef]
- Verma, A.K.; Tiwari, D. Higher resolution methods based on quasilinearization and Haar wavelets on Lane-Emden equations. Int. J. Wavelets Multiresolution Inf. Process. 2019, 17, 1950005. [Google Scholar] [CrossRef]
- Verma, A.K.; Tiwari, D. On some computational aspects of Hermite & Haar wavelets on a class of nonlinear singular BVPs. Appl. Anal. Discret. Math. 2021, 20. [Google Scholar] [CrossRef]
- Swati; Singh, M.; Singh, K. Uniform Haar wavelet technique with Newton’s method for a kind of derivative dependent SBVPs. J. Math. Chem. 2021, 59, 1610–1637. [Google Scholar] [CrossRef]
- Verma, A.K.; Kumar, N.; Tiwari, D. Haar wavelets collocation method for a system of nonlinear singular differential equations. Eng. Comput. 2020, 38, 659–698. [Google Scholar] [CrossRef]
- Dubeau, F.; Elmejdani, S.; Ksantini, R. Non-uniform Haar wavelets. Appl. Math. Comput. 2004, 159, 675–693. [Google Scholar] [CrossRef]
- Lepik, Ü. Solving integral and differential equations by the aid of non-uniform Haar wavelets. Appl. Math. Comput. 2008, 198, 326–332. [Google Scholar] [CrossRef]
- i Haq, F.; ul Islam, S.; Aziz, I. Numerical Solution of Singularly Perturbed Two-point BVPs Using Nonuniform Haar Wavelets. Int. J. Comput. Methods Eng. Sci. Mech. 2011, 12, 168–175. [Google Scholar] [CrossRef]
- Majak, J.; Shvartsman, B.; Pohlak, M.; Karjust, K.; Eerme, M.; Tungel, E. Solution of fractional order differential equation by the Haar Wavelet method. Numerical convergence analysis for most commonly used approach. AIP Conf. Proc. 2016, 1738, 480110. [Google Scholar]
- Oruç, Ö. A non-uniform Haar wavelet method for numerically solving two-dimensional convection-dominated equations and two-dimensional near singular elliptic equations. Comput. Math. Appl. 2019, 77, 1799–1820. [Google Scholar] [CrossRef]
- Saeed, U.; ur Rehman, M. Haar wavelet–quasilinearization technique for fractional nonlinear differential equations. Appl. Math. Comput. 2013, 220, 630–648. [Google Scholar] [CrossRef]
- Çelik, İ. Haar wavelet method for solving generalized Burgers–Huxley equation. Arab. J. Math. Sci. 2012, 18, 25–37. [Google Scholar] [CrossRef]
- Shukla, S.; Kumar, M. Error analysis and numerical solution of Burgers–Huxley equation using 3-scale Haar wavelets. Eng. Comput. 2020, 38, 3–11. [Google Scholar] [CrossRef]
- Verma, A.K.; Rawani, M.K.; Cattani, C. A numerical scheme for a class of generalized Burgers’ equation based on Haar wavelet nonstandard finite difference method. Appl. Numer. Math. 2021, 168, 41–54. [Google Scholar] [CrossRef]
- Ratas, M.; Salupere, A.; Majak, J. Solving nonlinear PDEs using the higher order Haar wavelet method on nonuniform and adaptive grids. Math. Model. Anal. 2021, 26, 147–169. [Google Scholar] [CrossRef]
- Lepik, Ü. Solving PDEs with the aid of two-dimensional Haar wavelets. Comput. Math. Appl. 2011, 61, 1873–1879. [Google Scholar] [CrossRef]
- Haq, S.; Ghafoor, A. An efficient numerical algorithm for multi-dimensional time dependent partial differential equations. Comput. Math. Appl. 2018, 75, 2723–2734. [Google Scholar] [CrossRef]
- Arbabi, S.; Nazari, A.; Darvishi, M.T. A two-dimensional Haar wavelets method for solving systems of PDEs. Appl. Math. Comput. 2017, 292, 33–46. [Google Scholar] [CrossRef]
- Oruç, Ö.; Esen, A.; Bulut, F. A Haar wavelet approximation for two-dimensional time fractional reaction–subdiffusion equation. Eng. Comput. 2019, 35, 75–86. [Google Scholar] [CrossRef]
- Çelik, İ. Haar wavelet approximation for magnetohydrodynamic flow equations. Appl. Math. Model. 2013, 37, 3894–3902. [Google Scholar] [CrossRef]
- Lepik, Ü.; Hein, H. Haar Wavelets with Applications; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Sari, M.; Gürarslan, G.; Dağ, I. A compact finite difference method for the solution of the generalized Burgers–Fisher equation. Numer. Methods Partial. Differ. Equ. 2010, 26, 125–134. [Google Scholar] [CrossRef]
- Ismail, H.N.; Rabboh, A.A. A restrictive Padé approximation for the solution of the generalized Fisher and Burger–Fisher equations. Appl. Math. Comput. 2004, 154, 203–210. [Google Scholar] [CrossRef]
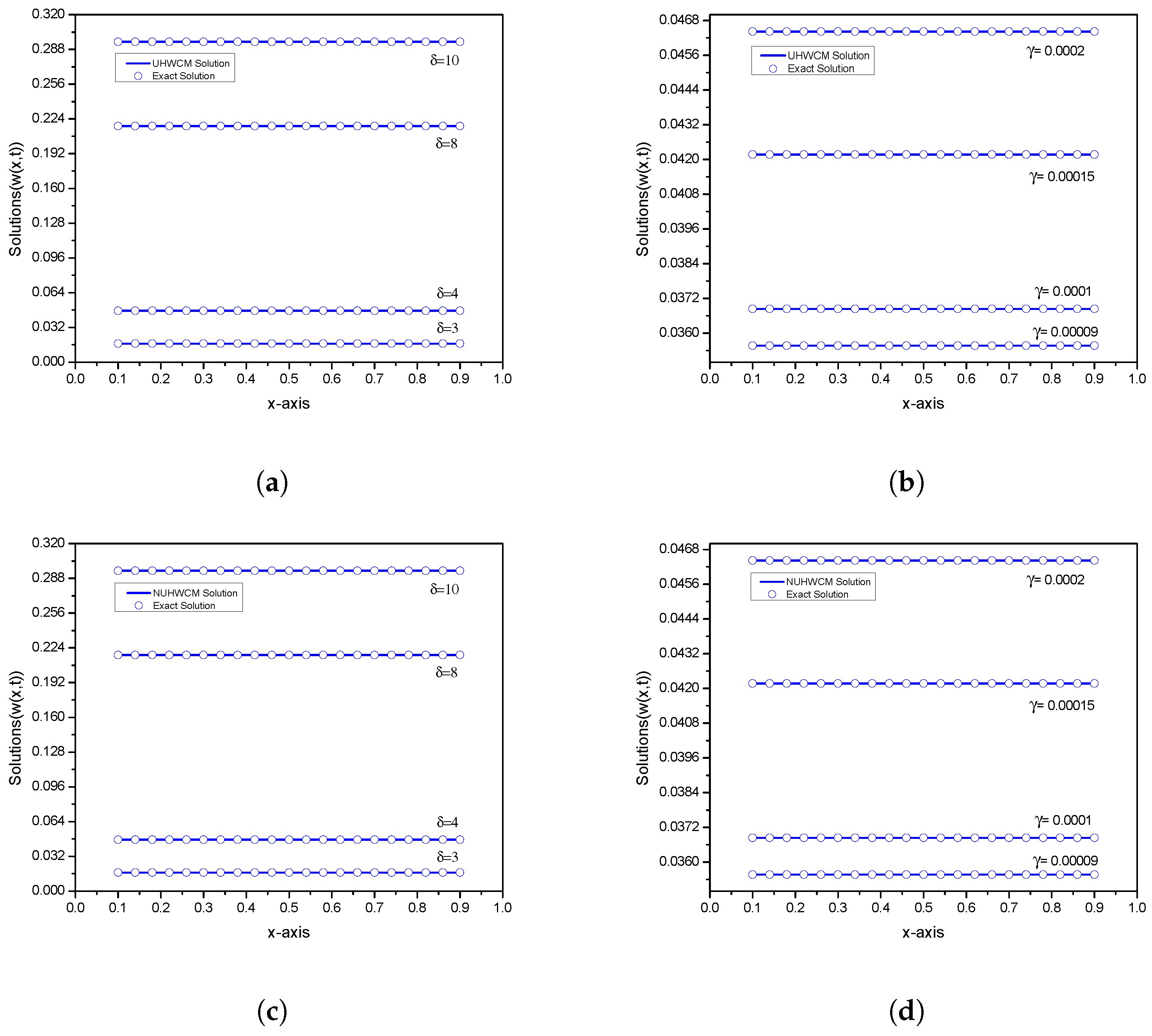
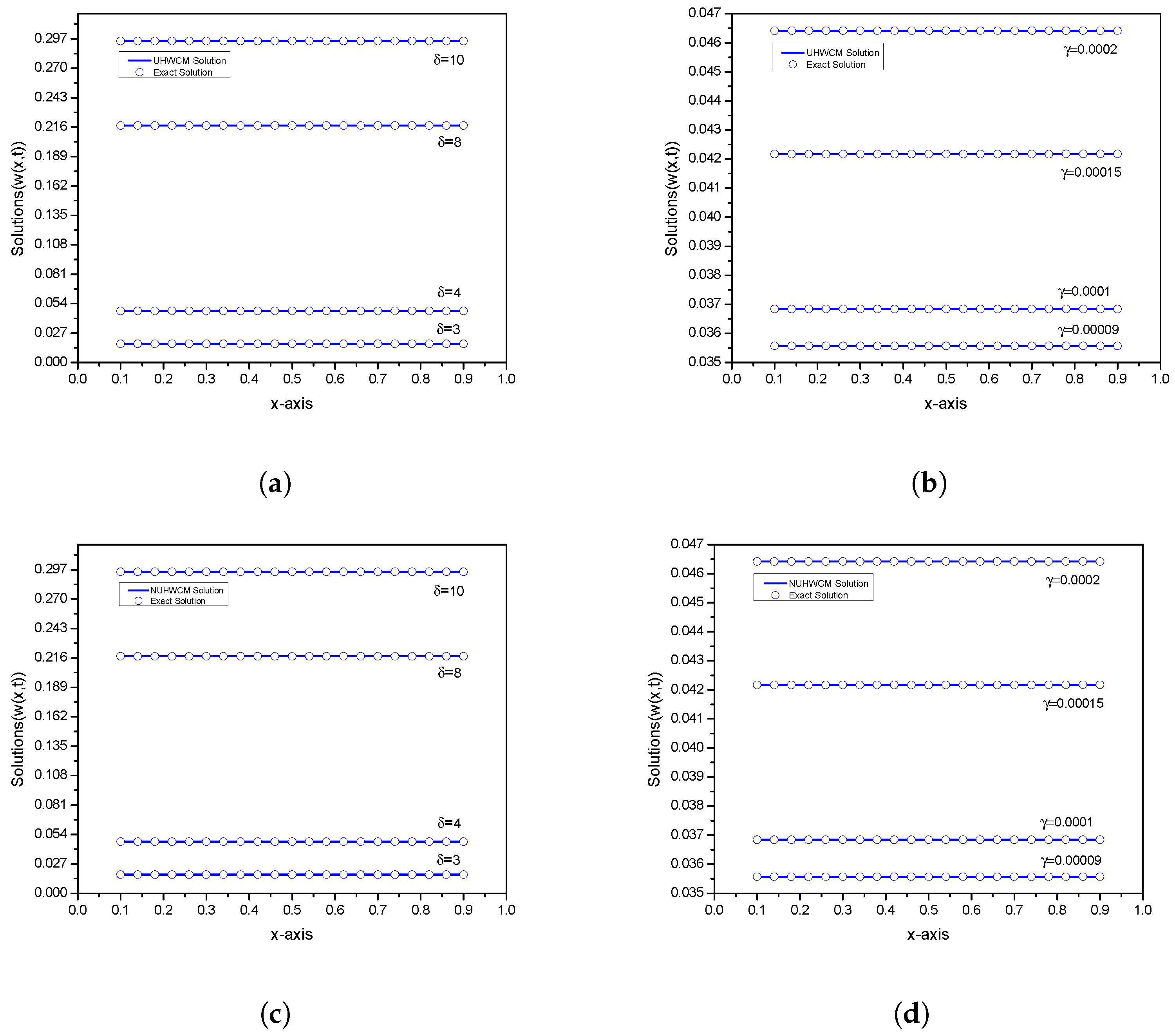
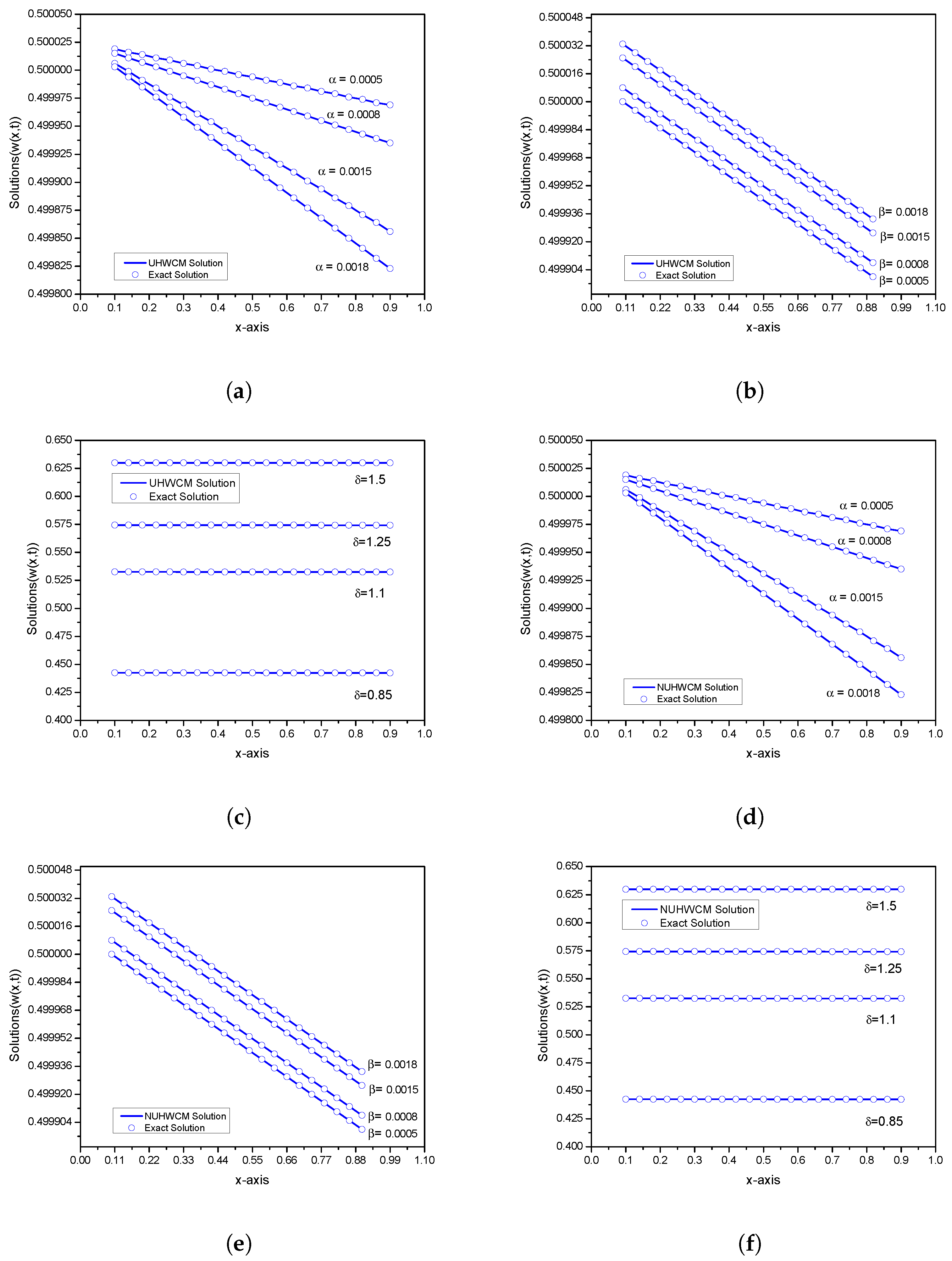

| x | t | Proposed Method | HWCFD [54] | VIM [12] | ADM [11] | ADM [10] | |||
|---|---|---|---|---|---|---|---|---|---|
| UHWCM | NUHWCM | ||||||||
| 0.1 | 0.05 | 4.02996 × 10 | 5.94152 × 10 | 3.99135 × 10 | 5.8416 × 10 | 5.09065400001 × 10 | 1.87405 × 10 | 1.87406 × 10 | 1.93715 × 10 |
| 0.1 | 0.1 | 8.05993 × 10 | 1.1883 × 10 | 7.9827 × 10 | 1.16832 × 10 | 3.94874100008 × 10 | 3.74813 × 10 | 3.74812 × 10 | 3.87434 × 10 |
| 0.1 | 1 | 1.59406 × 10 | 1.65469 × 10 | 1.59536 × 10 | 1.65483 × 10 | 1.66056969999 × 10 | 3.74812 × 10 | 3.74812 × 10 | 3.87501 × 10 |
| 0.5 | 0.05 | 1.02564 × 10 | 1.38108 × 10 | 1.01733 × 10 | 1.36407 × 10 | 9.99043449999 × 10 | 1.87405 × 10 | 1.87406 × 10 | 1.9373 × 10 |
| 0.5 | 0.1 | 2.05129 × 10 | 2.76215 × 10 | 2.03466 × 10 | 2.72815 × 10 | 1.06041257999 × 10 | 1.37481 × 10 | 3.74812 × 10 | 3.87464 × 10 |
| 0.5 | 1 | 4.75675 × 10 | 4.68696 × 10 | 4.75675 × 10 | 4.68694 × 10 | 2.16505682999 × 10 | 3.74813 × 10 | 3.74812 × 10 | 3.87531 × 10 |
| 0.9 | 0.05 | 4.03039 × 10 | 5.94204 × 10 | 3.99424 × 10 | 5.83573 × 10 | 2.04899342000 × 10 | 1.87405 × 10 | 1.87406 × 10 | 1.93745 × 10 |
| 0.9 | 0.1 | 8.06078 × 10 | 1.18841 × 10 | 7.98848 × 10 | 1.16715 × 10 | 2.16031254999 × 10 | 3.74813 × 10 | 3.74812 × 10 | 3.87494 × 10 |
| 0.9 | 1 | 1.5943 × 10 | 1.65492 × 10 | 1.59305 × 10 | 1.65496 × 10 | 4.16405665000 × 10 | 3.74813 × 10 × 10 | 3.74812 × 10 | 3.87561 × 10 |
| CPU Time (In Sec.) | 6.265 | 24.202 | 11.765 | 62.828 | |||||
| x | t | Proposed Method | HWCFD [54] | ADM [22] | ADM [10] | |||
|---|---|---|---|---|---|---|---|---|
| UHWCM | NUHWCM | |||||||
| 0.1 | 0.05 | 5.37357 × 10 | 7.92237 × 10 | 5.32208 × 10 | 7.78914 × 10 | 6.40665700005 × 10 | 2.49875 × 10 | 1.87465 × 10 |
| 0.1 | 0.1 | 1.07471 × 10 | 1.58447 × 10 | 1.06442 × 10 | 1.55783 × 10 | 8.69100700000 × 10 | 4.99750 × 10 | 3.74934 × 10 |
| 0.1 | 1 | 2.12557 × 10 | 2.20641 × 10 | 2.12731 × 10 | 2.20659 × 10 | 4.98093070000 × 10 | 4.99750 × 10 | 3.75002 × 10 |
| 0.5 | 0.05 | 1.36753 × 10 | 1.84144 × 10 | 1.35644 × 10 | 1.81877 × 10 | 1.57823008000 × 10 | 2.49875 × 10 | 1.87486 × 10 |
| 0.5 | 0.1 | 2.73505 × 10 | 3.68287 × 10 | 2.71288 × 10 | 3.63753 × 10 | 1.70102357000 × 10 | 4.99750 × 10 | 3.74977 × 10 |
| 0.5 | 1 | 6.34233 × 10 | 6.24928 × 10 | 6.34234 × 10 | 6.24925 × 10 | 3.91130589000 × 10 | 4.99750 × 10 | 3.75044 × 10 |
| 0.9 | 0.05 | 5.37357 × 10 | 7.92237 × 10 | 5.32537 × 10 | 7.78062 × 10 | 3.09239355999 × 10 | 2.49875 × 10 | 1.87508 × 10 |
| 0.9 | 0.1 | 1.07471 × 10 | 1.58447 × 10 | 1.06507 × 10 | 1.55612 × 10 | 3.31513703000 × 10 | 4.99750 × 10 | 3.75019 × 10 |
| 0.9 | 1 | 2.12557 × 10 | 2.20641 × 10 | 2.12391 × 10 | 2.20646 × 10 | 7.32451854999 × 10 | 4.99750 × 10 | 3.75086 × 10 |
| CPU Time (In Sec.) | 3.14 | 20.453 | 12.548 | 58.845 | ||||
| x | t | Proposed Method | NSFD [31] | CFDM [63] | RPA [64] | ADM [10] | |||
|---|---|---|---|---|---|---|---|---|---|
| UHWCM | NUHWCM | ||||||||
| 0.1 | 0.005 | 1.11022 × 10 | 1.11022 × 10 | 1.11022 × 10 | 1.11022 × 10 | 2.50063 × 10 | 4.38 × 10 | 9.75 × 10 | 9.68763 × 10 |
| 0.1 | 0.001 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 2.50063 × 10 | 1.01 × 10 | 1.75 × 10 | 1.93753 × 10 |
| 0.1 | 0.01 | 0 | 0 | 0 | 0 | 2.50064 × 10 | 7.53 × 10 | 1.90 × 10 | 1.93752 × 10 |
| 0.5 | 0.005 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 2.50063 × 10 | 5.21 × 10 | 9.75 × 10 | 9.68691 × 10 |
| 0.5 | 0.001 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 2.50063 × 10 | 1.01 × 10 | 1.75 × 10 | 1.93738 × 10 |
| 0.5 | 0.01 | 0 | 0 | 0 | 0 | 2.50065 × 10 | 1.04 × 10 | 1.90 × 10 | 1.93738 × 10 |
| 0.9 | 0.005 | 0 | 0 | 0 | 0 | 2.50063 × 10 | 4.38 × 10 | 9.75 × 10 | 9.68619 × 10 |
| 0.9 | 0.001 | 1.11022 × 10 | 1.11022 × 10 | 1.11022 × 10 | 1.11022 × 10 | 2.50063 × 10 | 1.01 × 10 | 1.75 × 10 | 1.93724 × 10 |
| 0.9 | 0.01 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 5.55112 × 10 | 2.50064 × 10 | 7.53 × 10 | 1.90 × 10 | 1.93724 × 10 |
| CPU Time (In Sec.) | 3.939 | 13.924 | 7.328 | 27.407 | |||||
| x | t | Proposed Method | NSFD [31] | RPA [64] | |||
|---|---|---|---|---|---|---|---|
| UHWCM | NUHWCM | ||||||
| 0.1 | 0.0005 | 8.94873 × 10 | 5.48376 × 10 | 9.06105 × 10 | 5.7152 × 10 | 2.90 × 10 | 0.000444925 |
| 0.1 | 0.0001 | 1.7942 × 10 | 1.10121 × 10 | 1.81667 × 10 | 1.1475 × 10 | 7.94 × 10 | 0.000446088 |
| 0.1 | 0.001 | 1.78417 × 10 | 1.10121 × 10 | 1.80664 × 10 | 1.13747 × 10 | 5.39 × 10 | 0.000444222 |
| 0.5 | 0.0005 | 2.51474 × 10 | 1.27795 × 10 | 2.58877 × 10 | 1.33266 × 10 | 3.27 × 10 | 0.001854465 |
| 0.5 | 0.0001 | 5.03903 × 10 | 2.56544 × 10 | 5.18708 × 10 | 2.67486 × 10 | 2.85 × 10 | 0.001860448 |
| 0.5 | 0.001 | 5.01757 × 10 | 2.54398 × 10 | 5.16562 × 10 | 2.6534 × 10 | 3.82 × 10 | 0.001847737 |
| 0.9 | 0.0005 | 6.75557 × 10 | 3.46276 × 10 | 6.89016 × 10 | 3.58104 × 10 | 2.18 × 10 | 0.00092005 |
| 0.9 | 0.0001 | 1.35346 × 10 | 6.94895 × 10 | 1.38038 × 10 | 7.18552 × 10 | 2.14 × 10 | 0.000931582 |
| 0.9 | 0.001 | 1.34818 × 10 | 6.89623 × 10 | 1.3751 × 10 | 7.13279 × 10 | 4.49 × 10 | 0.000904635 |
| CPU Time (In Sec.) | 3.766 | 8.984 | 9.234 | 26.906 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, N.; Verma, A.K.; Agarwal, R.P. Two-Dimensional Uniform and Non-Uniform Haar Wavelet Collocation Approach for a Class of Nonlinear PDEs. Computation 2023, 11, 189. https://doi.org/10.3390/computation11100189
Kumar N, Verma AK, Agarwal RP. Two-Dimensional Uniform and Non-Uniform Haar Wavelet Collocation Approach for a Class of Nonlinear PDEs. Computation. 2023; 11(10):189. https://doi.org/10.3390/computation11100189
Chicago/Turabian StyleKumar, Narendra, Amit K. Verma, and Ravi P. Agarwal. 2023. "Two-Dimensional Uniform and Non-Uniform Haar Wavelet Collocation Approach for a Class of Nonlinear PDEs" Computation 11, no. 10: 189. https://doi.org/10.3390/computation11100189
APA StyleKumar, N., Verma, A. K., & Agarwal, R. P. (2023). Two-Dimensional Uniform and Non-Uniform Haar Wavelet Collocation Approach for a Class of Nonlinear PDEs. Computation, 11(10), 189. https://doi.org/10.3390/computation11100189








