Finite Element Analysis of ACL Reconstruction-Compatible Knee Implant Design with Bone Graft Component
Abstract
:1. Introduction
2. Materials and Methods
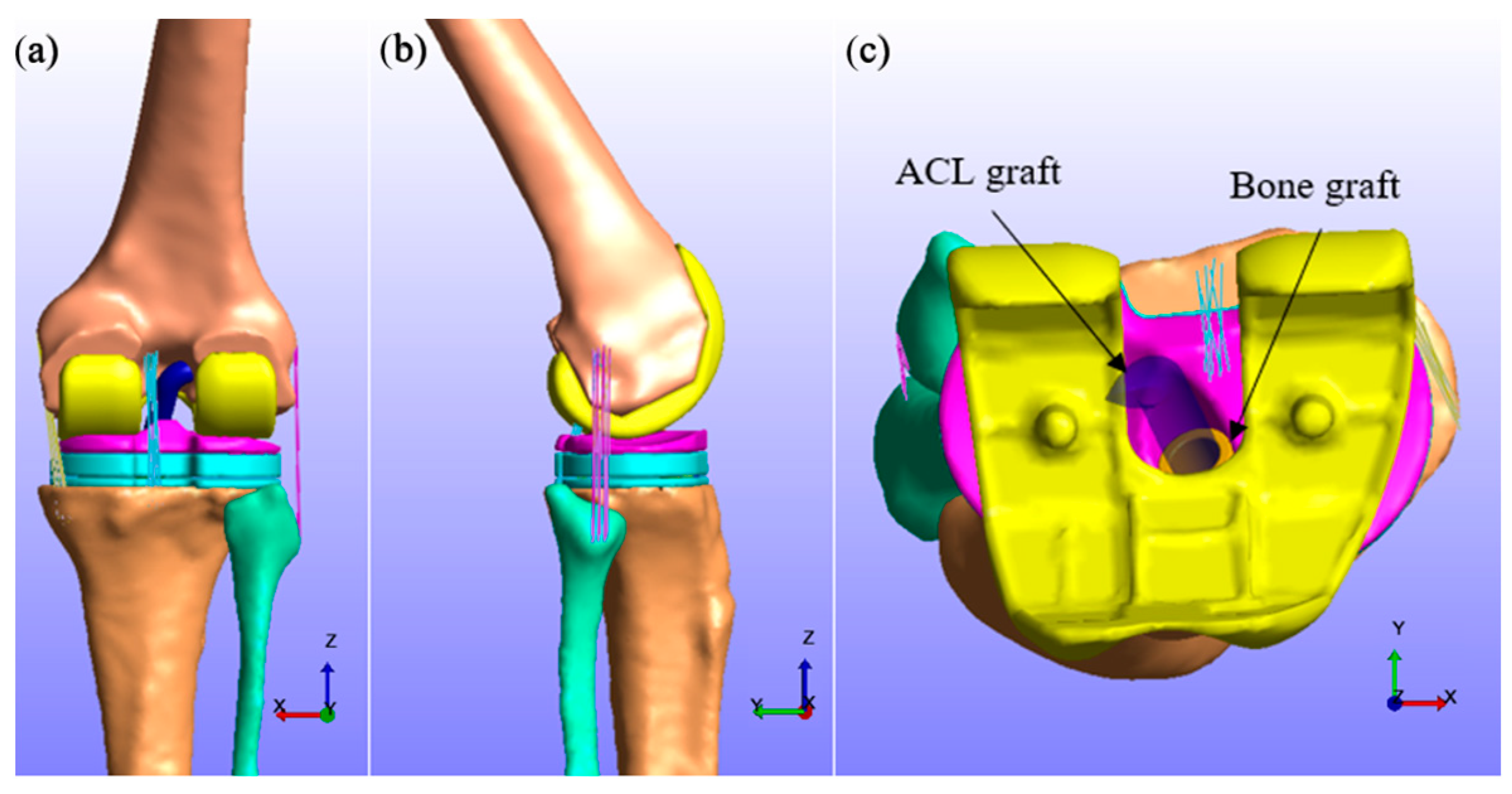
2.1. Preparation of Knee Implant and Ligament Graft Geometries
2.2. Finite Element Modelling in FEBio
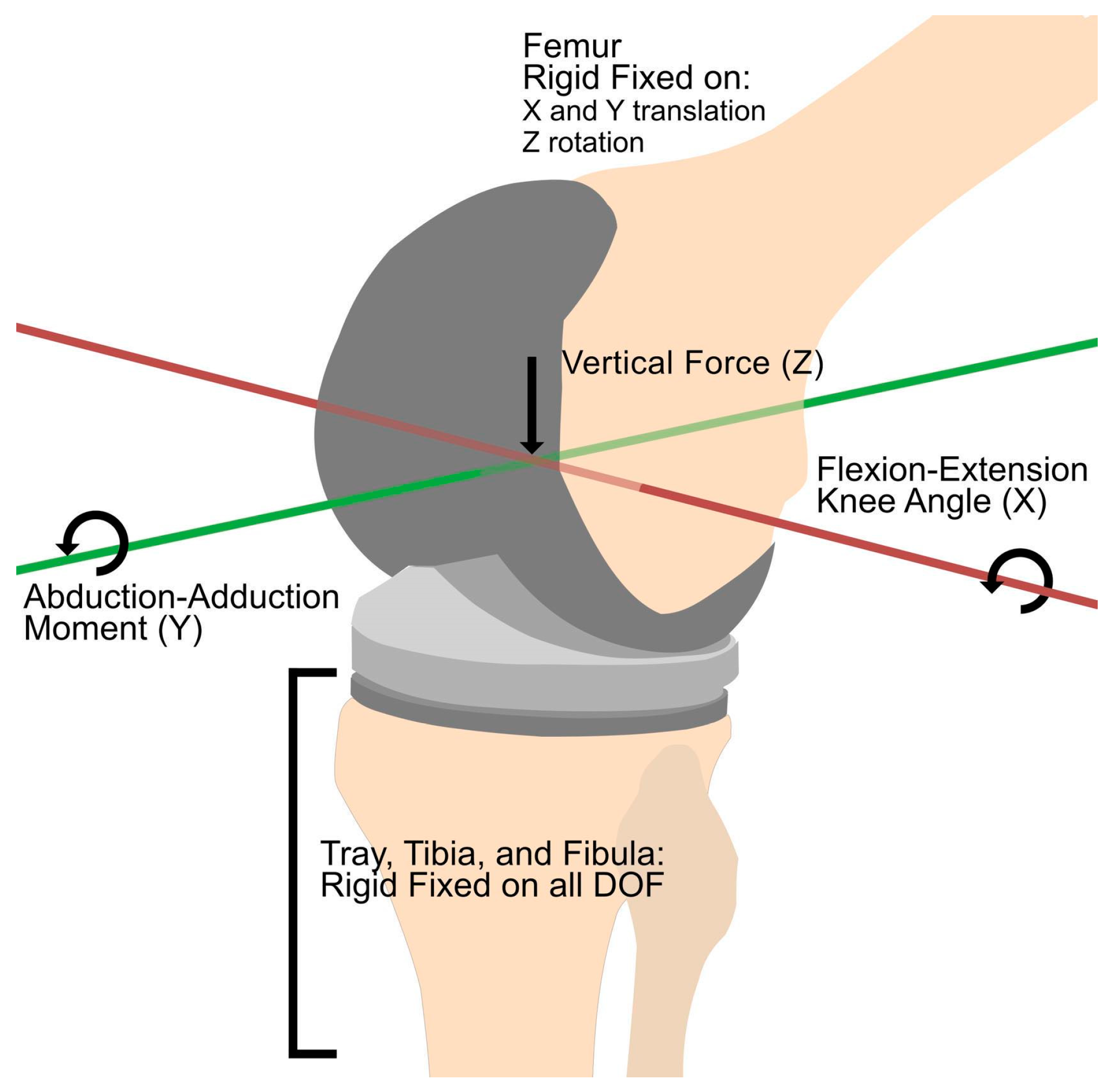
2.3. Defining Loads and Boundary Conditions
3. Results
3.1. Comparison of Contact Knee Loads
3.2. Measurement of ACL Graft Tension and Tibial Insert Contact Pressure
3.3. Comparison of Cortical and Cancellous Bone Graft
4. Discussion
4.1. Standardized Knee Loads and Actual Knee Loads
4.2. Bone Graft for ACL Graft Tunnel in Total Knee Replacement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anatomy, I.P. Anatomy and physiology, 5. The musculoskeletal system. Br. J. Healthc. Assist. 2018, 12, 6–9. [Google Scholar] [CrossRef]
- Bliven, K.C.H.; Anderson, B.E. Core Stability Training for Injury Prevention. Sport. Health 2013, 5, 514. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Yan, Y.; Ma, J.; Wei, P. Knee Joint Biomechanics in Physiological Conditions and How Pathologies Can Affect It: A Systematic Review. Appl. Bionics Biomech. 2020, 2020, 7451683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vad, V.B.; Adin, D.R.; Osteoarthritis, J.S.K. Knee Osteoarthritis. Crit. Rev. Phys. Rehabil. Med. 2022, 16, 211–231. [Google Scholar] [CrossRef]
- Grässel, S.; Muschter, D. Recent advances in the treatment of osteoarthritis. F1000Research 2020, 9, 325. [Google Scholar] [CrossRef]
- Hsu, H.; Siwiec, R.M. Knee Arthroplasty; StatPearls: St. Petersburg, FL, USA, 2022. Available online: https://www.ncbi.nlm.nih.gov/books/NBK507914/ (accessed on 18 April 2023).
- Dall’Oca, C.; Ricci, M.; Vecchini, E.; Giannini, N.; Lamberti, D.; Tromponi, C.; Magnan, B. Evolution of TKA design. Acta Bio Med. Atenei Parm. 2017, 88, 17. [Google Scholar]
- Marieswaran, M.; Jain, I.; Garg, B.; Sharma, V.; Kalyanasundaram, D. A review on biomechanics of anterior cruciate ligament and materials for reconstruction. Appl. Bionics Biomech. 2018, 2018, 4657824. [Google Scholar] [CrossRef] [Green Version]
- Raines, B.; Naclerio, E.; Sherman, S. Management of Anterior Cruciate Ligament Injury: What’s In and What’s Out? Indian J. Orthop. 2017, 51, 563–575. [Google Scholar] [CrossRef]
- Kiapour, A.M.; Murray, M.M. Basic science of anterior cruciate ligament injury and repair. Bone Jt. Res. 2014, 3, 20–31. [Google Scholar] [CrossRef]
- Tjoumakaris, F.P.; Herz-Brown, A.L.; Legath-Bowers, A.; Sennett, B.J.; Bernstein, J. Complications In Brief: Anterior Cruciate Ligament Reconstruction. Clin. Orthop. Relat. Res. 2012, 470, 630. [Google Scholar] [CrossRef] [Green Version]
- Smidt, K.P.; Bicknell, R. Prosthetics in Orthopedics; StatPearls: St. Petersburg, FL, USA, 2022. Available online: https://www.ncbi.nlm.nih.gov/books/NBK570628/ (accessed on 25 May 2022).
- Abdelbadie, A.; Toreih, A.A.; Radwan, M.A. ACL status in arthroplasty patients, why not to preserve? Sicot-J 2018, 4, 1. [Google Scholar] [CrossRef] [Green Version]
- Pritchett, J.W. Bicruciate Total Knee Replacement. In Personalized Hip and Knee Joint Replacement; Springer: Cham, Switzerland, 2020; pp. 265–275. [Google Scholar] [CrossRef]
- Archunan, M.W.; Petronis, S. Bone Grafts in Trauma and Orthopaedics. Cureus 2021, 13, e17705. [Google Scholar] [CrossRef]
- Roberts, T.T.; Rosenbaum, A.J. Bone grafts, bone substitutes and orthobiologics. Organogenesis 2012, 8, 114–124. [Google Scholar] [CrossRef] [Green Version]
- Haghani, R. Finite element modelling of adhesive bonds joining fibre-reinforced polymer (FRP) composites to steel. In Rehabilitation of Metallic Civil Infrastructure Using Fiber Reinforced Polymer (FRP) Composites Types Properties and Testing Methods; Woodhead Publishing: Sawston, UK, 2014; pp. 60–95. [Google Scholar] [CrossRef]
- Loi, I.; Stanev, D.; Moustakas, K. Total Knee Replacement: Subject-Specific Modeling, Finite Element Analysis, and Evaluation of Dynamic Activities. Front. Bioeng. Biotechnol. 2021, 9, 648356. [Google Scholar] [CrossRef]
- Fregly, B.J.; Besier, T.F.; Lloyd, D.G.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’Lima, D.D. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 2012, 30, 503–513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shino, K.; Mae, T.; Tachibana, Y. Anatomic ACL reconstruction: Rectangular tunnel/bone–patellar tendon–bone or triple-bundle/semitendinosus tendon grafting. J. Orthop. Sci. 2015, 20, 457–468. [Google Scholar] [CrossRef] [Green Version]
- Nema, S.K.; Balaji, G.; Akkilagunta, S.; Menon, J.; Poduval, M.; Patro, D. Radiologic assessment of femoral and tibial tunnel placement based on anatomic landmarks in arthroscopic single bundle anterior cruciate ligament reconstruction. Indian J. Orthop. 2017, 51, 286–291. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Chen, K.; Guo, L.; Cheng, L.; Wang, F.; Yang, L. Identifying the Functional Flexion-extension Axis of the Knee: An In-Vivo Kinematics Study. PLoS ONE 2015, 10, e0128877. [Google Scholar] [CrossRef] [Green Version]
- Fritsch, B.; Figueroa, F.; Semay, B. Graft Preparation Technique to Optimize Hamstring Graft Diameter for Anterior Cruciate Ligament Reconstruction. Arthrosc. Tech. 2017, 6, e2169–e2175. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.D.; Tran, Q.L. A cadaveric study on the anatomy of anterior cruciate ligament in Vietnamese adults. Asia-Pac. J. Sport. Med. Arthrosc. Rehabil. Technol. 2018, 14, 22–25. [Google Scholar] [CrossRef]
- Benos, L.; Stanev, D.; Spyrou, L.; Moustakas, K.; Tsaopoulos, D.E. A Review on Finite Element Modeling and Simulation of the Anterior Cruciate Ligament Reconstruction. Front. Bioeng. Biotechnol. 2020, 8, 967. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Zhang, D.Z.; Zhang, P.; Zhao, M.; Jafar, S. Mechanical properties of optimized diamond lattice structure for bone scaffolds fabricated via selective laser melting. Materials 2018, 11, 374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. Hyperelastic structures: A review on the mechanics and biomechanics. Int. J. Non-Linear Mech. 2023, 148, 104275. [Google Scholar] [CrossRef]
- Bergmann, G.; Bender, A.; Graichen, F.; Dymke, J.; Rohlmann, A.; Trepczynski, A.; Heller, M.O.; Kutzner, I. Standardized Loads Acting in Knee Implants. PLoS ONE 2014, 9, e86035. [Google Scholar] [CrossRef] [Green Version]
- Cassiolas, G.; Di Paolo, S.; Marchiori, G.; Grassi, A.; Della Villa, F.; Bragonzoni, L.; Visani, A.; Giavaresi, G.; Fini, M.; Zaffagnini, S.; et al. Knee Joint Contact Forces during High-Risk Dynamic Tasks: 90° Change of Direction and Deceleration Movements. Bioengineering 2023, 10, 179. [Google Scholar] [CrossRef]
- Jagodzinski, M.; Foerstemann, T.; Mall, G.; Krettek, C.; Bosch, U.; Paessler, H. Analysis of forces of ACL reconstructions at the tunnel entrance: Is tunnel enlargement a biomechanical problem? J. Biomech. 2005, 38, 23–31. [Google Scholar] [CrossRef]
- Aali, S.; Rezazadeh, F.; Badicu, G.; Grosz, W.R. Effect of Heel-First Strike Gait on Knee and Ankle Mechanics. Medicina 2021, 57, 657. [Google Scholar] [CrossRef]
- Pérez-González, A.; Iserte-Vilar, J.L.; González-Lluch, C. Interpreting finite element results for brittle materials in endodontic restorations. Biomed. Eng. Online 2011, 10, 44. [Google Scholar] [CrossRef] [Green Version]
- Christensen, R.M. A comparative evaluation of three isotropic, two property failure theories. J. Appl. Mech. 2006, 73, 852–859. [Google Scholar] [CrossRef]
- Gerhardt, L.-C.; Boccaccini, A.R. Review–Bioactive Glass and Glass-Ceramic Scaffolds for Bone Tissue Engineering. Materials 2010, 3, 3867–3910. [Google Scholar] [PubMed] [Green Version]
- Smotrova, E.; Li, S.; Tashkinov, M.; Shalimov, A.; Silberschmidt, V.V. Failure behaviour of human trabecular bone. Procedia Struct. Integr. 2021, 37, 257–262. [Google Scholar] [CrossRef]
- Sanyal, A.; Gupta, A.; Bayraktar, H.H.; Kwon, R.Y.; Keaveny, T.M. Shear strength behavior of human trabecular bone. J. Biomech. 2012, 45, 2513–2519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oftadeh, R.; Perez-Viloria, M.; Villa-Camacho, J.C.; Vaziri, A.; Nazarian, A. Biomechanics and Mechanobiology of Trabecular Bone: A Review. J. Biomech. Eng. 2015, 137, 010802. [Google Scholar] [CrossRef] [Green Version]
- Stewart, M. Engineering Principles. In Surface Production Operations; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–17. [Google Scholar] [CrossRef]
- Trivedi, S. Finite element analysis: A boon to dentistry. J. Oral Biol. Craniofacial Res. 2014, 4, 200–203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Apan, J.J.; Tayo, L.; Honra, J. Numerical Investigation of the Relationship between Anastomosis Angle and Hemodynamics in Ridged Spiral Flow Bypass Grafts. Appl. Sci. 2023, 13, 4046. [Google Scholar] [CrossRef]
- Colic, K.; Sedmak, A.; Grbovic, A.; Tatic, U.; Sedmak, S.; Djordjevic, B. Finite Element Modeling of Hip Implant Static Loading. Procedia Eng. 2016, 149, 257–262. [Google Scholar] [CrossRef] [Green Version]
- Kohli, A.; Mathad, M.; Hosamani, S.V.; Adagimath, M.K.; Kotturshettar, B.B. Finite element analysis of knee joint implant for varying bio material using ANSYS. Mater. Today Proc. 2022, 59, 941–950. [Google Scholar] [CrossRef]
- Maas, S.A.; Ellis, B.J.; Ateshian, G.A.; Weiss, J.A. FEBio: Finite Elements for Biomechanics. J. Biomech. Eng. 2012, 134, 011005. [Google Scholar] [CrossRef] [Green Version]
- DiFelice, G.S.; Villegas, C.; Taylor, S. Anterior Cruciate Ligament Preservation: Early Results of a Novel Arthroscopic Technique for Suture Anchor Primary Anterior Cruciate Ligament Repair. Arthrosc. J. Arthrosc. Relat. Surg. 2015, 31, 2162–2171. [Google Scholar] [CrossRef]
- Patrick, W.; Shady, E.M.; Christoph, T.; Ramin, K.; Xaver, F. Advanced Anterior Cruciate Ligament Repair and Reconstruction Techniques for Different Rupture Types. Arthrosc. Tech. 2020, 9, e969. [Google Scholar] [CrossRef] [PubMed]
- Voss, K.; Montavon, P.M. Fractures. In Feline Orthopedic Surgery and Musculoskeletal Disease; Elsevier: Amsterdam, The Netherlands, 2009; pp. 129–152. [Google Scholar] [CrossRef]




| Model Part | Properties | Mesh Elements |
|---|---|---|
| Femur, tibia, and fibula [18] | E = 13.4 GPa | 90,136 |
| ν = 0.24 | ||
| CoCrMo [18] | E = 210 GPa | 54,921 |
| ν = 0.3 | ||
| UHMWPE [18] | E = 1.2 GPa | 14,692 |
| ν = 0.46 | ||
| Ti6Al4V alloy [18] | E = 110 GPa | 37,146 |
| ν = 0.3 | ||
| Cortical bone [27] | E = 17 GPa | 28,103 |
| ν = 0.3 | ||
| Cancellous bone [27] | E = 0.4 GPa | 28,103 |
| ν = 0.46 | ||
| ACL graft [26] | c1 = 2.75 | 34,381 |
| c2 = 0.065 | ||
| c3 = 115.89 | ||
| c4 = 512.73 | ||
| λ = 1.042 |
| Data Source | Joint Angle | Reaction Force | ||
|---|---|---|---|---|
| 1st Peak | 2nd Peak | 1st Peak | 2nd Peak | |
| 6th GCC | 33° | 72° | 2688 N | 2118 N |
| Standardized knee loads [29] | 22° | 61° | 1657 N | 1946 N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carpena, F.L.F.; Tayo, L.L. Finite Element Analysis of ACL Reconstruction-Compatible Knee Implant Design with Bone Graft Component. Computation 2023, 11, 151. https://doi.org/10.3390/computation11080151
Carpena FLF, Tayo LL. Finite Element Analysis of ACL Reconstruction-Compatible Knee Implant Design with Bone Graft Component. Computation. 2023; 11(8):151. https://doi.org/10.3390/computation11080151
Chicago/Turabian StyleCarpena, Ferdinand Lauren F., and Lemmuel L. Tayo. 2023. "Finite Element Analysis of ACL Reconstruction-Compatible Knee Implant Design with Bone Graft Component" Computation 11, no. 8: 151. https://doi.org/10.3390/computation11080151
APA StyleCarpena, F. L. F., & Tayo, L. L. (2023). Finite Element Analysis of ACL Reconstruction-Compatible Knee Implant Design with Bone Graft Component. Computation, 11(8), 151. https://doi.org/10.3390/computation11080151





