Exploring Numba and CuPy for GPU-Accelerated Monte Carlo Radiation Transport
Abstract
:1. Introduction
2. Methodology
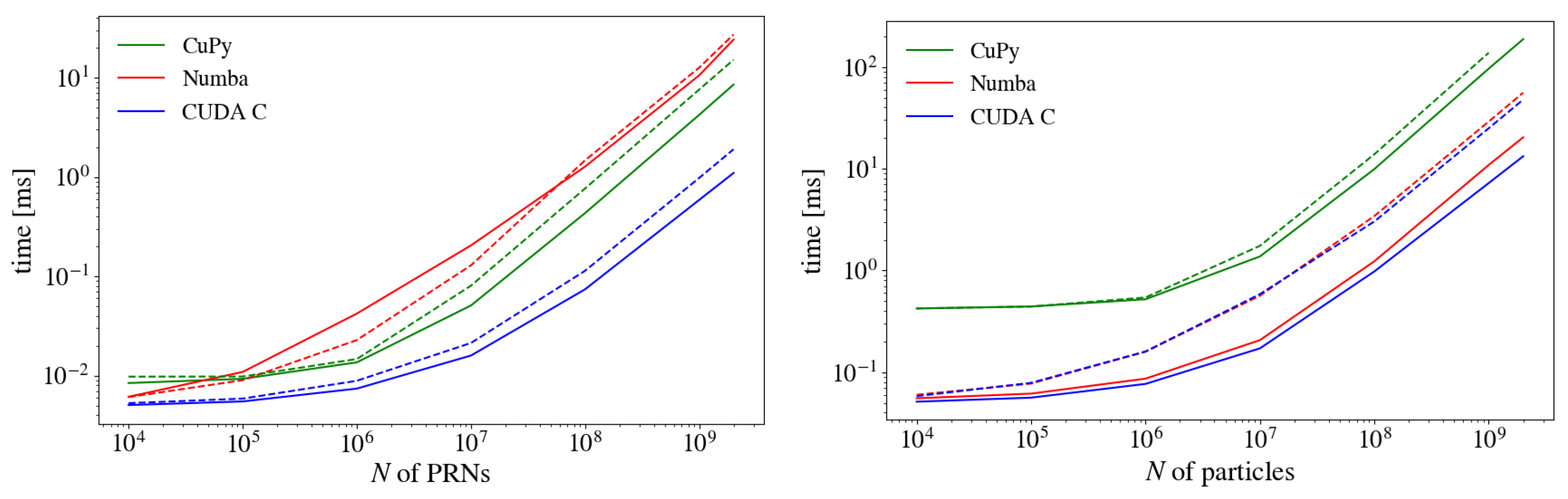
3. Results
3.1. Impact of Precision
3.2. Energy Consumption
3.3. Comparison of GPU Cards
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdelfattah, A.; Barra, V.; Beams, N.; Bleile, R.; Brown, J.; Camier, J.S.; Carson, R.; Chalmers, N.; Dobrev, V.; Dudouit, Y.; et al. GPU algorithms for efficient exascale discretizations. Parallel Comput. 2021, 108, 102841. [Google Scholar] [CrossRef]
- Pazner, W.; Kolev, T.; Camier, J.S. End-to-end GPU acceleration of low-order-refined preconditioning for high-order finite element discretizations. Int. J. High Perform. Comput. Appl. 2023, 37, 10943420231175462. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Y.; Liu, Z. A Survey on Convolutional Neural Network Accelerators: GPU, FPGA and ASIC. In Proceedings of the 2022 14th International Conference on Computer Research and Development (ICCRD), Shenzhen, China, 7–9 January 2022; pp. 100–107. [Google Scholar] [CrossRef]
- Pandey, M.; Fernandez, M.; Gentile, F.; Isayev, O.; Tropsha, A.; Stern, A.C.; Cherkasov, A. The transformational role of GPU computing and deep learning in drug discovery. Nat. Mach. Intell. 2022, 4, 211–221. [Google Scholar] [CrossRef]
- Matsuoka, S.; Domke, J.; Wahib, M.; Drozd, A.; Hoefler, T. Myths and legends in high-performance computing. Int. J. High Perform. Comput. Appl. 2023, 37, 245–259. [Google Scholar] [CrossRef]
- CUDA Best Practices. Available online: https://developer.nvidia.com/cuda-best-practices (accessed on 8 August 2023).
- AMD ROCm HIP Documentation. Available online: https://rocm.docs.amd.com/projects/HIP/en/latest/ (accessed on 10 December 2023).
- Martineau, M.; McIntosh-Smith, S.; Gaudin, W. Evaluating OpenMP 4.0’s Effectiveness as a Heterogeneous Parallel Programming Model. In Proceedings of the 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Chicago, IL, USA, 23–27 May 2016; pp. 338–347. [Google Scholar] [CrossRef]
- Wienke, S.; Springer, P.; Terboven, C.; an Mey, D. OpenACC—First Experiences with Real-World Applications. In Proceedings of the Euro-Par 2012 Parallel Processing, Rhodos, Greece, 27–31 August 2012; Kaklamanis, C., Papatheodorou, T., Spirakis, P.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 859–870. [Google Scholar]
- Stone, J.E.; Gohara, D.; Shi, G. OpenCL: A parallel programming standard for heterogeneous computing systems. Comput. Sci. Eng. 2010, 12, 66. [Google Scholar] [CrossRef] [PubMed]
- Reyes, R.; Lomüller, V. SYCL: Single-source C++ accelerator programming. In Proceedings of the International Conference on Parallel Computing, Edinburgh, UK, 1–4 September 2015. [Google Scholar]
- Zenker, E.; Worpitz, B.; Widera, R.; Huebl, A.; Juckeland, G.; Knupfer, A.; Nagel, W.E.; Bussmann, M. Alpaka–An Abstraction Library for Parallel Kernel Acceleration. In Proceedings of the 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Chicago, IL, USA, 23–27 May 2016; pp. 631–640. [Google Scholar] [CrossRef]
- Numba Developers. Numba Documentation. Numba. 2023. Available online: https://numba.pydata.org/ (accessed on 8 December 2023).
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A LLVM-Based Python JIT Compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, Austin, TX, USA, 15 November 2015; LLVM’15. [Google Scholar] [CrossRef]
- CuPy Developers. CuPy Documentation. 2023. Available online: https://docs.cupy.dev/en/stable/ (accessed on 30 January 2024).
- Okuta, R.; Unno, Y.; Nishino, D.; Hido, S.; Loomis, C. Cupy: A numpy-compatible library for nvidia gpu calculations. In Proceedings of the Workshop on Machine Learning Systems (LearningSys) in the Thirty-First Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; Volume 6. [Google Scholar]
- Nishino, R.; Loomis, S.H.C. Cupy: A numpy-compatible library for nvidia gpu calculations. In Proceedings of the 31st Confernce on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 151. [Google Scholar]
- Bauer, M.; Garland, M. Legate NumPy: Accelerated and Distributed Array Computing. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 17–19 November 2019. SC’19. [Google Scholar] [CrossRef]
- Trott, C.R.; Lebrun-Grandié, D.; Arndt, D.; Ciesko, J.; Dang, V.; Ellingwood, N.; Gayatri, R.; Harvey, E.; Hollman, D.S.; Ibanez, D.; et al. Kokkos 3: Programming Model Extensions for the Exascale Era. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 805–817. [Google Scholar] [CrossRef]
- Hornung, R.D.; Keasler, J.A. The RAJA Portability Layer: Overview and Status; Lawrence Livermore National Lab.(LLNL): Livermore, CA, USA, 2014. [Google Scholar]
- Fortenberry, A.; Tomov, S. Extending MAGMA Portability with OneAPI. In Proceedings of the 2022 Workshop on Accelerator Programming Using Directives (WACCPD), Dallas, TX, USA, 13–18 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 22–31. [Google Scholar]
- Lim, S.; Kang, P. Implementing scientific simulations on GPU-accelerated edge devices. In Proceedings of the 2020 International Conference on Information Networking (ICOIN), Barcelona, Spain, 7–10 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 756–760. [Google Scholar]
- Knight, J.C.; Nowotny, T. Larger GPU-accelerated brain simulations with procedural connectivity. Nat. Comput. Sci. 2021, 1, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Aydonat, U.; O’Connell, S.; Capalija, D.; Ling, A.C.; Chiu, G.R. An OpenCL™ Deep Learning Accelerator on Arria 10. In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2017; FPGA’17. pp. 55–64. [Google Scholar] [CrossRef]
- Kalaiselvi, T.; Sriramakrishnan, P.; Somasundaram, K. Survey of using GPU CUDA programming model in medical image analysis. Informatics Med. Unlocked 2017, 9, 133–144. [Google Scholar] [CrossRef]
- Kuan, L.; Neves, J.; Pratas, F.; Tomás, P.; Sousa, L. Accelerating Phylogenetic Inference on GPUs: An OpenACC and CUDA comparison. In Proceedings of the IWBBIO, Granada, Spain, 7–9 April 2014; pp. 589–600. [Google Scholar]
- Christgau, S.; Spazier, J.; Schnor, B.; Hammitzsch, M.; Babeyko, A.; Waechter, J. A comparison of CUDA and OpenACC: Accelerating the tsunami simulation easywave. In Proceedings of the ARCS 2014; 2014 Workshop Proceedings on Architecture of Computing Systems, Luebeck, Germany, 25–28 February 2014; VDE: Frankfurt am Main, Germany; Springer: Cham, Switzerland, 2014; pp. 1–5. [Google Scholar]
- Memeti, S.; Li, L.; Pllana, S.; Kołodziej, J.; Kessler, C. Benchmarking OpenCL, OpenACC, OpenMP, and CUDA: Programming productivity, performance, and energy consumption. In Proceedings of the 2017 Workshop on Adaptive Resource Management and Scheduling for Cloud Computing, Washington, DC, USA, 28 July 2017; pp. 1–6. [Google Scholar]
- Cloutier, B.; Muite, B.K.; Rigge, P. Performance of FORTRAN and C GPU extensions for a benchmark suite of Fourier pseudospectral algorithms. In Proceedings of the 2012 Symposium on Application Accelerators in High Performance Computing, Argonne, IL, USA, 10–11 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 145–148. [Google Scholar]
- Herdman, J.; Gaudin, W.; McIntosh-Smith, S.; Boulton, M.; Beckingsale, D.A.; Mallinson, A.; Jarvis, S.A. Accelerating hydrocodes with OpenACC, OpenCL and CUDA. In Proceedings of the 2012 SC Companion: High Performance Computing, Networking Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 465–471. [Google Scholar]
- Satake, S.I.; Yoshimori, H.; Suzuki, T. Optimizations of a GPU accelerated heat conduction equation by a programming of CUDA Fortran from an analysis of a PTX file. Comput. Phys. Commun. 2012, 183, 2376–2385. [Google Scholar] [CrossRef]
- Malik, M.; Li, T.; Sharif, U.; Shahid, R.; El-Ghazawi, T.; Newby, G. Productivity of GPUs under different programming paradigms. Concurr. Comput. Pract. Exp. 2012, 24, 179–191. [Google Scholar] [CrossRef]
- Karimi, K.; Dickson, N.G.; Hamze, F. A performance comparison of CUDA and OpenCL. arXiv 2010, arXiv:1005.2581. [Google Scholar]
- Fang, J.; Varbanescu, A.L.; Sips, H. A comprehensive performance comparison of CUDA and OpenCL. In Proceedings of the 2011 International Conference on Parallel Processing, Taipei, Taiwan, 13–16 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 216–225. [Google Scholar]
- Li, X.; Shih, P.C. An early performance comparison of CUDA and OpenACC. Matec Web Conf. 2018, 208, 05002. [Google Scholar] [CrossRef]
- Hoshino, T.; Maruyama, N.; Matsuoka, S.; Takaki, R. CUDA vs OpenACC: Performance case studies with kernel benchmarks and a memory-bound CFD application. In Proceedings of the 2013 13th IEEE/ACM International Symposium on Cluster, Cloud, and Grid Computing, Delft, The Netherlands, 13–16 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 136–143. [Google Scholar]
- Gimenes, T.L.; Pisani, F.; Borin, E. Evaluating the performance and cost of accelerating seismic processing with cuda, opencl, openacc, and openmp. In Proceedings of the 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Vancouver, BC, Canada, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 399–408. [Google Scholar]
- Guo, X.; Wu, J.; Wu, Z.; Huang, B. Parallel computation of aerial target reflection of background infrared radiation: Performance comparison of OpenMP, OpenACC, and CUDA implementations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1653–1662. [Google Scholar] [CrossRef]
- Oden, L. Lessons learned from comparing C-CUDA and Python-Numba for GPU-Computing. In Proceedings of the 2020 28th Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP), Västerås, Sweden, 11–13 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 216–223. [Google Scholar]
- Godoy, W.F.; Valero-Lara, P.; Dettling, T.E.; Trefftz, C.; Jorquera, I.; Sheehy, T.; Miller, R.G.; Gonzalez-Tallada, M.; Vetter, J.S.; Churavy, V. Evaluating performance and portability of high-level programming models: Julia, Python/Numba, and Kokkos on exascale nodes. arXiv 2023, arXiv:2303.06195. [Google Scholar]
- Di Domenico, D.; Lima, J.V.; Cavalheiro, G.G. NAS Parallel Benchmarks with Python: A performance and programming effort analysis focusing on GPUs. J. Supercomput. 2023, 79, 8890–8911. [Google Scholar] [CrossRef]
- Holm, H.H.; Brodtkorb, A.R.; Sætra, M.L. GPU computing with Python: Performance, energy efficiency and usability. Computation 2020, 8, 4. [Google Scholar] [CrossRef]
- Marowka, A. Python accelerators for high-performance computing. J. Supercomput. 2018, 74, 1449–1460. [Google Scholar] [CrossRef]
- Boytsov, A.; Kadochnikov, I.; Zuev, M.; Bulychev, A.; Zolotuhin, Y.; Getmanov, I. Comparison of python 3 single-GPU parallelization technologies on the example of a charged particles dynamics simulation problem. In Proceedings of the CEUR Workshop Proceedings, Dubna, Russia, 10–14 September 2018; pp. 518–522. [Google Scholar]
- Bhattacharya, M.; Calafiura, P.; Childers, T.; Dewing, M.; Dong, Z.; Gutsche, O.; Habib, S.; Ju, X.; Ju, X.; Kirby, M.; et al. Portability: A Necessary Approach for Future Scientific Software. In Proceedings of the Snowmass 2021, Seattle, WA, USA, 17–26 July 2022. [Google Scholar] [CrossRef]
- Ma, Z.X.; Jin, Y.Y.; Tang, S.Z.; Wang, H.J.; Xue, W.C.; Zhai, J.D.; Zheng, W.M. Unified Programming Models for Heterogeneous High-Performance Computers. J. Comput. Sci. Technol. 2023, 38, 211–218. [Google Scholar] [CrossRef]
- Thavappiragasam, M.; Elwasif, W.; Sedova, A. Portability for GPU-accelerated molecular docking applications for cloud and HPC: Can portable compiler directives provide performance across all platforms? In Proceedings of the 2022 22nd IEEE International Symposium on Cluster, Cloud and Internet Computing (CCGrid), Taormina, Italy, 16–19 May 2022; pp. 975–984. [Google Scholar] [CrossRef]
- Deakin, T.; Cownie, J.; Lin, W.C.; McIntosh-Smith, S. Heterogeneous Programming for the Homogeneous Majority. In Proceedings of the 2022 IEEE/ACM International Workshop on Performance, Portability and Productivity in HPC (P3HPC), Dallas, TX, USA, 13–18 November 2022; pp. 1–13. [Google Scholar] [CrossRef]
- Noebauer, U.M.; Sim, S.A. Monte Carlo radiative transfer. Living Rev. Comput. Astrophys. 2019, 5, 1. [Google Scholar] [CrossRef]
- Castor, J.I. Radiation Hydrodynamics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Alerstam, E.; Svensson, T.; Andersson-Engels, S. Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration. J. Biomed. Opt. 2008, 13, 060504. [Google Scholar] [CrossRef]
- Badal, A.; Badano, A. Monte Carlo simulation of X-ray imaging using a graphics processing unit. In Proceedings of the 2009 IEEE Nuclear Science Symposium Conference Record (NSS/MIC), Orlando, FL, USA, 24 October–1 November 2009; pp. 4081–4084. [Google Scholar] [CrossRef]
- Huang, B.; Mielikainen, J.; Oh, H.; Allen Huang, H.L. Development of a GPU-based high-performance radiative transfer model for the Infrared Atmospheric Sounding Interferometer (IASI). J. Comput. Phys. 2011, 230, 2207–2221. [Google Scholar] [CrossRef]
- Lippuner, J.; Elbakri, I.A. A GPU implementation of EGSnrc’s Monte Carlo photon transport for imaging applications. Phys. Med. Biol. 2011, 56, 7145. [Google Scholar] [CrossRef]
- Bergmann, R.M.; Vujić, J.L. Algorithmic choices in WARP—A framework for continuous energy Monte Carlo neutron transport in general 3D geometries on GPUs. Ann. Nucl. Energy 2015, 77, 176–193. [Google Scholar] [CrossRef]
- Zoller, C.; Hohmann, A.; Foschum, F.; Geiger, S.; Geiger, M.; Ertl, T.P.; Kienle, A. Parallelized Monte Carlo Software to Efficiently Simulate the Light Propagation in Arbitrarily Shaped Objects and Aligned Scattering Media. J. Biomed. Opt. 2018, 23, 065004. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Gu, X.; Graves, Y.J.; Folkerts, M.; Jiang, S.B. GPU-based fast Monte Carlo simulation for radiotherapy dose calculation. Phys. Med. Biol. 2011, 56, 7017. [Google Scholar] [CrossRef] [PubMed]
- Hissoiny, S.; Ozell, B.; Bouchard, H.; Després, P. GPUMCD: A new GPU-oriented Monte Carlo dose calculation platform. Med. Phys. 2011, 38, 754–764. [Google Scholar] [CrossRef]
- Shao, J.; Zhu, K.; Huang, Y. A fast GPU Monte Carlo implementation for radiative heat transfer in graded-index media. J. Quant. Spectrosc. Radiat. Transf. 2021, 269, 107680. [Google Scholar] [CrossRef]
- Young-Schultz, T.; Brown, S.; Lilge, L.; Betz, V. FullMonteCUDA: A fast, flexible, and accurate GPU-accelerated Monte Carlo simulator for light propagation in turbid media. Biomed. Opt. Express 2019, 10, 4711–4726. [Google Scholar] [CrossRef]
- Ma, B.; Gaens, M.; Caldeira, L.; Bert, J.; Lohmann, P.; Tellmann, L.; Lerche, C.; Scheins, J.; Rota Kops, E.; Xu, H.; et al. Scatter Correction Based on GPU-Accelerated Full Monte Carlo Simulation for Brain PET/MRI. IEEE Trans. Med. Imaging 2020, 39, 140–151. [Google Scholar] [CrossRef]
- Ma, D.; Yang, B.; Zhang, Q.; Liu, J.; Li, T. Evaluation of Single-Node Performance of Parallel Algorithms for Multigroup Monte Carlo Particle Transport Methods. Front. Energy Res. 2021, 9, 705823. [Google Scholar] [CrossRef]
- Shi, M.; Myronakis, M.; Jacobson, M.; Ferguson, D.; Williams, C.; Lehmann, M.; Baturin, P.; Huber, P.; Fueglistaller, R.; Lozano, I.V.; et al. GPU-accelerated Monte Carlo simulation of MV-CBCT. Phys. Med. Biol. 2020, 65, 235042. [Google Scholar] [CrossRef] [PubMed]
- Manssen, M.; Weigel, M.; Hartmann, A.K. Random number generators for massively parallel simulations on GPU. Eur. Phys. J. Spec. Top. 2012, 210, 53–71. [Google Scholar] [CrossRef]
- L’Écuyer, P.; Munger, D.; Oreshkin, B.; Simard, R. Random Numbers for Parallel Computers: Requirements and Methods, with Emphasis on Gpus; GERAD, HEC Montréal: Montréal, QC, Canada, 2015. [Google Scholar]
- Kim, Y.; Hwang, G. Efficient Parallel CUDA Random Number Generator on NVIDIA GPUs. J. Kiise 2015, 42, 1467–1473. [Google Scholar] [CrossRef]
- Bossler, K.; Valdez, G.D. Comparison of Kokkos and CUDA Programming Models for Key Kernels in the Monte Carlo Transport Algorithm. In Proceedings of the Nuclear Explosives Code Development Conference (NECDC) 2018, Los Alamos, NM, USA, 15–19 October 2018; Technical Report. Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2018. [Google Scholar]
- Hamilton, S.P.; Slattery, S.R.; Evans, T.M. Multigroup Monte Carlo on GPUs: Comparison of history- and event-based algorithms. Ann. Nucl. Energy 2018, 113, 506–518. [Google Scholar] [CrossRef]
- Choi, N.; Joo, H.G. Domain decomposition for GPU-Based continuous energy Monte Carlo power reactor calculation. Nucl. Eng. Technol. 2020, 52, 2667–2677. [Google Scholar] [CrossRef]
- Hamilton, S.P.; Evans, T.M.; Royston, K.E.; Biondo, E.D. Domain decomposition in the GPU-accelerated Shift Monte Carlo code. Ann. Nucl. Energy 2022, 166, 108687. [Google Scholar] [CrossRef]
- Bleile, R.; Brantley, P.; Richards, D.; Dawson, S.; McKinley, M.S.; O’Brien, M.; Childs, H. Thin-Threads: An Approach for History-Based Monte Carlo on GPUs. In Proceedings of the 2019 International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland, 15–19 July 2019; pp. 273–280. [Google Scholar] [CrossRef]
- Humphrey, A.; Sunderland, D.; Harman, T.; Berzins, M. Radiative Heat Transfer Calculation on 16384 GPUs Using a Reverse Monte Carlo Ray Tracing Approach with Adaptive Mesh Refinement. In Proceedings of the 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Chicago, IL, USA, 23–27 May 2016; pp. 1222–1231. [Google Scholar] [CrossRef]
- Silvestri, S.; Pecnik, R. A fast GPU Monte Carlo radiative heat transfer implementation for coupling with direct numerical simulation. J. Comput. Phys. X 2019, 3, 100032. [Google Scholar] [CrossRef]
- Heymann, F.; Siebenmorgen, R. GPU-based Monte Carlo Dust Radiative Transfer Scheme Applied to Active Galactic Nuclei. Astrophys. J. 2012, 751, 27. [Google Scholar] [CrossRef]
- Ramon, D.; Steinmetz, F.; Jolivet, D.; Compiègne, M.; Frouin, R. Modeling polarized radiative transfer in the ocean-atmosphere system with the GPU-accelerated SMART-G Monte Carlo code. J. Quant. Spectrosc. Radiat. Transf. 2019, 222-223, 89–107. [Google Scholar] [CrossRef]
- Lee, E.K.H.; Wardenier, J.P.; Prinoth, B.; Parmentier, V.; Grimm, S.L.; Baeyens, R.; Carone, L.; Christie, D.; Deitrick, R.; Kitzmann, D.; et al. 3D Radiative Transfer for Exoplanet Atmospheres. gCMCRT: A GPU-accelerated MCRT Code. Astrophys. J. 2022, 929, 180. [Google Scholar] [CrossRef]
- Peng, Z.; Shan, H.; Liu, T.; Pei, X.; Wang, G.; Xu, X.G. MCDNet—A Denoising Convolutional Neural Network to Accelerate Monte Carlo Radiation Transport Simulations: A Proof of Principle With Patient Dose From X-ray CT Imaging. IEEE Access 2019, 7, 76680–76689. [Google Scholar] [CrossRef]
- Ardakani, M.R.; Yu, L.; Kaeli, D.; Fang, Q. Framework for denoising Monte Carlo photon transport simulations using deep learning. J. Biomed. Opt. 2022, 27, 083019. [Google Scholar] [CrossRef]
- van Dijk, R.H.W.; Staut, N.; Wolfs, C.J.A.; Verhaegen, F. A novel multichannel deep learning model for fast denoising of Monte Carlo dose calculations: Preclinical applications. Phys. Med. Biol. 2022, 67, 164001. [Google Scholar] [CrossRef]
- Sarrut, D.; Etxebeste, A.; Muñoz, E.; Krah, N.; Létang, J.M. Artificial Intelligence for Monte Carlo Simulation in Medical Physics. Front. Phys. 2021, 9, 738112. [Google Scholar] [CrossRef]
- Xu, P.; Sun, M.Y.; Gao, Y.J.; Du, T.J.; Hu, J.M.; Zhang, J.J. Influence of data amount, data type and implementation packages in GPU coding. Array 2022, 16, 100261. [Google Scholar] [CrossRef]
- Almgren-Bell, J.; Awar, N.A.; Geethakrishnan, D.S.; Gligoric, M.; Biros, G. A Multi-GPU Python Solver for Low-Temperature Non-Equilibrium Plasmas. In Proceedings of the 2022 IEEE 34th International Symposium on Computer Architecture and High Performance Computing (SBAC-PAD), Bordeaux, France, 2–5 November 2022; pp. 140–149. [Google Scholar] [CrossRef]
- Radmanović, M.M. A Comparison of Computing Spectral Transforms of Logic Functions using Python Frameworks on GPU. In Proceedings of the 2022 57th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Ohrid, North Macedonia, 16–18 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, A.; Li, B.T. Multi-GPU thermal lattice Boltzmann simulations using OpenACC and MPI. Int. J. Heat Mass Transf. 2023, 201, 123649. [Google Scholar] [CrossRef]
- Dogaru, R.; Dogaru, I. A Python Framework for Fast Modelling and Simulation of Cellular Nonlinear Networks and other Finite-difference Time-domain Systems. In Proceedings of the 2021 23rd International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 26–28 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 221–226. [Google Scholar]
- Azizi, I. Parallelization in Python-An Expectation-Maximization Application. 2023. Available online: https://iliaazizi.com/projects/em_parallelized/ (accessed on 18 December 2023).
- Cohen, J.; Molemaker, M.J. A fast double precision CFD code using CUDA. J. Phys. Soc. Japan 1997, 66, 2237–2341. [Google Scholar]
- Dang, H.V.; Schmidt, B. CUDA-enabled Sparse Matrix–Vector Multiplication on GPUs using atomic operations. Parallel Comput. 2013, 39, 737–750. [Google Scholar] [CrossRef]
- cuRAND-NVIDIA’s CUDA Random Number Generation Library. Available online: https://developer.nvidia.com/curand (accessed on 24 July 2023).
- Collange, S.; Defour, D.; Tisserand, A. Power consumption of GPUs from a software perspective. In Proceedings of the Computational Science–ICCS 2009: 9th International Conference, Baton Rouge, LA, USA, 25–27 May 2009; Proceedings, Part I 9. Springer: Berlin/Heidelberg, Germany, 2009; pp. 914–923. [Google Scholar]
- Eklund, A.; Dufort, P.; Forsberg, D.; LaConte, S.M. Medical image processing on the GPU–Past, present and future. Med. Image Anal. 2013, 17, 1073–1094. [Google Scholar] [CrossRef]
- Després, P.; Jia, X. A review of GPU-based medical image reconstruction. Phys. Medica 2017, 42, 76–92. [Google Scholar] [CrossRef]
- Askar, T.; Shukirgaliyev, B.; Lukac, M.; Abdikamalov, E. Evaluation of pseudo-random number generation on GPU cards. Computation 2021, 9, 142. [Google Scholar] [CrossRef]


| GPU Card | CUDA Cores | Base Clock [MHz] | FP32 (Float) [TFLOPS] | FP64 (Double) [TFLOPS] | Bandwidth [GB/s] |
|---|---|---|---|---|---|
| A100 | 6912 | 765 | 19.49 | 9.746 | 1555 |
| V100 | 5120 | 1230 | 14.13 | 7.066 | 897 |
| RTX3080 | 8704 | 1440 | 29.77 | 0.465 | 760 |
| PRN Generation | 1D MCRT | ||||||
|---|---|---|---|---|---|---|---|
| Energy per PRN [Nanojoule] | Power [Watt] | Util [%] | Energy per Particle [Nanojoule] | Power [Watt] | Util [%] | ||
| CuPy | 2.82 | 206 | 100 | 22.1 | 221 | 100 | |
| Numba | 2.46 | 81 | 100 | 15.9 | 68 | 10 | |
| CUDA C | 1.17 | 76 | 100 | 4.34 | 125 | 46 | |
| PRN Generation [Watt] | 1D MCRT [Watt] | ||||||
|---|---|---|---|---|---|---|---|
| A100 | V100 | RTX3080 | A100 | V100 | RTX3080 | ||
| CuPy | 206 | 211 | 293 | 221 | 229 | 297 | |
| Numba | 81 | 145 | 174 | 68 | 85 | 133 | |
| CUDA C | 76 | 85 | 129 | 141 | 200 | 225 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askar, T.; Yergaliyev, A.; Shukirgaliyev, B.; Abdikamalov, E. Exploring Numba and CuPy for GPU-Accelerated Monte Carlo Radiation Transport. Computation 2024, 12, 61. https://doi.org/10.3390/computation12030061
Askar T, Yergaliyev A, Shukirgaliyev B, Abdikamalov E. Exploring Numba and CuPy for GPU-Accelerated Monte Carlo Radiation Transport. Computation. 2024; 12(3):61. https://doi.org/10.3390/computation12030061
Chicago/Turabian StyleAskar, Tair, Argyn Yergaliyev, Bekdaulet Shukirgaliyev, and Ernazar Abdikamalov. 2024. "Exploring Numba and CuPy for GPU-Accelerated Monte Carlo Radiation Transport" Computation 12, no. 3: 61. https://doi.org/10.3390/computation12030061
APA StyleAskar, T., Yergaliyev, A., Shukirgaliyev, B., & Abdikamalov, E. (2024). Exploring Numba and CuPy for GPU-Accelerated Monte Carlo Radiation Transport. Computation, 12(3), 61. https://doi.org/10.3390/computation12030061






