Multi-Directional Functionally Graded Sandwich Plates: Buckling and Free Vibration Analysis with Refined Plate Models under Various Boundary Conditions
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Preliminary Concepts and Definitions
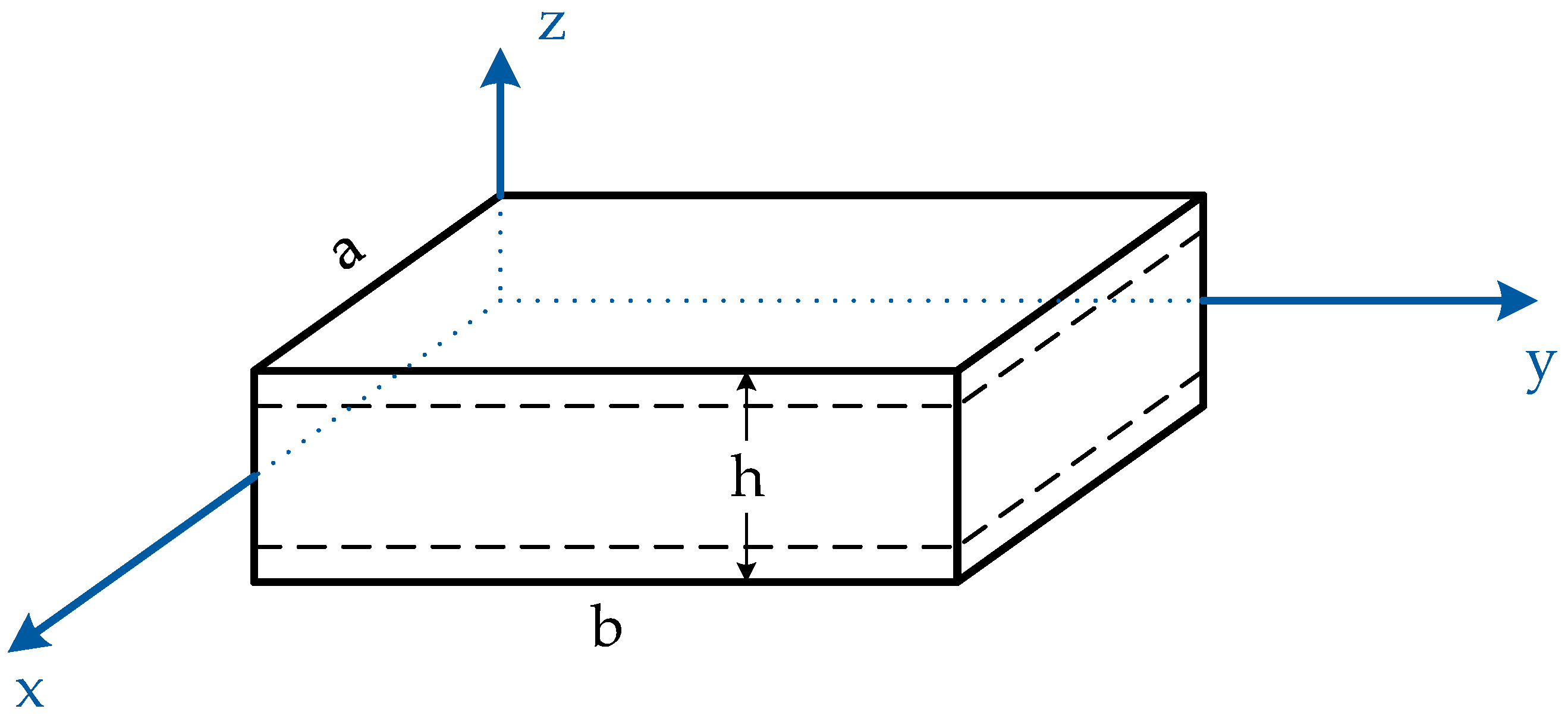
2.2. Modeling of FG Sandwich Plate
2.3. Displacement Field and Strains
2.4. Governing Equations
- Clamped (C):
- Simply supported (S):
3. Numerical Results and Discussion
- (1-0-1) FGM sandwich plate, consisting of two layers of equal thickness without a core, where h1 = h2 = 0.
- (1-2-1) FGM sandwich plate, with the core thickness equal to the sum of the face thicknesses: h2 = −h/4, h3 = h/4.
- (1-1-1) FGM sandwich plate, comprising three equal-thickness layers: h2 = −h/6, h3 = h/6.
- (2-2-1) FGM sandwich plate, featuring a core thickness twice that of the upper face and equal to the lower one, defined by h2 = −h/10, h3 = 3h/10.
- (1-1-2) FGM sandwich plate, with a core thickness equal to that of the lower face and with the thickness of the upper face twice that of the core: h2 = −h/4, h3 = 0.
- Ceramic (alumina, Al2O3): Young’s modulus Ec = 380 GPa, Poisson’s ratio vc = 0.3, density ρc = 3800 kg/m3;
- Metal (aluminum, Al): Young’s modulus Em = 70 GPa, Poisson’s ratio vm = 0.3, density ρm = 2702 kg/m3.
3.1. FG Sandwich Plates
3.1.1. Free Vibration Analysis of FG Sandwich Plates
3.1.2. Buckling Analysis of FG Sandwich Plates
3.2. Multi-Directional FG Sandwich Plates
3.2.1. Free Vibration Analysis of Multi-Directional FG Sandwich Plates
3.2.2. Buckling Analysis of Multi-Directional Sandwich Plates
4. Conclusions
- The boundary condition of FCFC invariably results in the highest frequency and buckling load values when compared to other tested conditions such as CCCC, CSCS, and SSSS. Noteworthy is the observation that the transverse grading parameter pz demonstrates a more significant effect than the longitudinal grading parameter px on these outcomes.
- In the context of sandwich plates with a hard core, an increment in the values of both px and pz is associated with a reduction in the plates’ natural frequency and buckling load. This situation is reversed for materials with a soft core, where an increase in px and pz corresponds to a decrease in their frequency and buckling load. This inverse relationship is due to the increased presence of ceramic constituents in the FG material, which are introduced as the grading parameters px and pz rise, thereby enhancing the natural frequency due to their higher stiffness relative to metals.
- Structural configurations that have a thicker core are shown to yield a higher stiffness. Specifically, for cores predominantly made of ceramic, enhancing the ceramic layer thickness effectively introduces additional stiffness akin to rigid plates, which elevates their natural frequencies. In contrast, for metal-based core configurations, an increase in metal core thickness imparts greater flexibility to the structure, leading to a decrease in its natural frequencies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saleh, B.; Jiang, J.; Ma, A.; Song, D.; Yang, D.; Xu, Q. Review on the Influence of Different Reinforcements on the Microstructure and Wear Behavior of Functionally Graded Aluminum Matrix Composites by Centrifugal Casting. Met. Mater. Int. 2020, 26, 933–960. [Google Scholar] [CrossRef]
- Ghatage, P.S.; Kar, V.R.; Sudhagar, P.E. On the numerical modelling and analysis of multi-directional functionally graded composite structures: A review. Compos. Struct. 2020, 236, 111837. [Google Scholar] [CrossRef]
- Kumar, S.; Mitra, A.; Roy, H. Large amplitude free vibration study of non-uniform plates with in-plane material inhomogeneity. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 232, 371–387. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, S.; Saran, V.; Harsha, S. Exact solution for free vibration analysis of linearly varying thickness FGM plate using Galerkin-Vlasov’s method. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 880–897. [Google Scholar] [CrossRef]
- Du, D.; Sun, W.; Yan, X.; Xu, K. Free vibration analysis of rotating thin-walled cylindrical shells with hard coating based on Rayleigh-Ritz method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 1170–1186. [Google Scholar] [CrossRef]
- Alipour, M.M.; Shariyat, M.; Shaban, M. A semi-analytical solution for free vibration of variable thickness two-directional-functionally graded plates on elastic foundations. Int. J. Mech. Mater. Des. 2010, 6, 293–304. [Google Scholar] [CrossRef]
- Nie, G.; Zhong, Z. Axisymmetric bending of two-directional functionally graded circular and annular plates. Acta Mech. Solida Sin. 2007, 20, 289–295. [Google Scholar] [CrossRef]
- Shariyat, M.; Jafari, R. Nonlinear low-velocity impact response analysis of a radially preloaded two-directional-functionally graded circular plate: A refined contact stiffness approach. Compos. Part B Eng. 2013, 45, 981–994. [Google Scholar] [CrossRef]
- Ahlawat, N.; Lal, R. Buckling and Vibrations of Multi-directional Functionally Graded Circular Plate Resting on Elastic Foundation. Procedia Eng. 2016, 144, 85–93. [Google Scholar] [CrossRef]
- Nguyen, D.K.; Nguyen, Q.H.; Tran, T.T.; Bui, V.T. Vibration of bi-dimensional functionally graded Timoshenko beams excited by a moving load. Acta Mech. 2017, 228, 141–155. [Google Scholar] [CrossRef]
- Van Do, T.; Nguyen, D.K.; Duc, N.D.; Doan, D.H.; Bui, T.Q. Analysis of bi-directional functionally graded plates by FEM and a new third-order shear deformation plate theory. Thin-Walled Struct. 2017, 119, 687–699. [Google Scholar] [CrossRef]
- Lieu, Q.X.; Lee, D.; Kang, J.; Lee, J. NURBS-based modeling and analysis for free vibration and buckling problems of in-plane bi-directional functionally graded plates. Mech. Adv. Mater. Struct. 2019, 26, 1064–1080. [Google Scholar] [CrossRef]
- Bhattacharyya, M.; Kapuria, S.; Kumar, A.N. On the Stress to Strain Transfer Ratio and Elastic Deflection Behavior for Al/SiC Functionally Graded Material. Mech. Adv. Mater. Struct. 2007, 14, 295–302. [Google Scholar] [CrossRef]
- Nakamura, T.; Wang, T.; Sampath, S. Determination of properties of graded materials by inverse analysis and instrumented indentation. Acta Mater. 2000, 48, 4293–4306. [Google Scholar] [CrossRef]
- Yas, M.H.; Moloudi, N. Three-dimensional free vibration analysis of multi-directional functionally graded piezoelectric annular plates on elastic foundations via state space based differential quadrature method. Appl. Math. Mech. 2015, 36, 439–464. [Google Scholar] [CrossRef]
- Nguyen-Ngoc, H.; Cuong-Le, T.; Nguyen, K.D.; Nguyen-Xuan, H.; Abdel-Wahab, M. Three-dimensional polyhedral finite element method for the analysis of multi-directional functionally graded solid shells. Compos. Struct. 2023, 305, 116538. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, G.; Ren, S.; Chen, W.; Han, W. Higher-order model with interlaminar stress continuity for multi-directional FG-GRC porous multilayer panels resting on elastic foundation. Eng. Struct. 2023, 286, 116074. [Google Scholar] [CrossRef]
- Ramteke, P.M.; Sharma, N.; Dwivedi, M.; Das, S.K.; Uttarwar, C.R.; Panda, S.K. Theoretical thermoelastic frequency prediction of multi (uni/bi) directional graded porous panels and experimental verification. Structures 2023, 54, 618–630. [Google Scholar] [CrossRef]
- Karamanli, A. Transient vibration analysis of strain gradient multi-directional functionally graded microplates under a moving concentrated load. Compos. Struct. 2023, 308, 116678. [Google Scholar] [CrossRef]
- Thai, S. Optimization of multi-directional functionally graded plates in thermal environment based on 3D isogeometric analysis and adaptive-hybrid evolutionary firefly algorithm. Thin-Walled Struct. 2023, 190, 111000. [Google Scholar] [CrossRef]
- Tang, Y.; Li, C.-L.; Yang, T. Application of the generalized differential quadrature method to study vibration and dynamic stability of tri-directional functionally graded beam under magneto-electro-elastic fields. Eng. Anal. Bound. Elem. 2023, 146, 808–823. [Google Scholar] [CrossRef]
- Daikh, A.A.; Belarbi, M.-O.; Vinh, P.V.; Li, L.; Houari, M.S.A.; Eltaher, M.A. Vibration analysis of tri-directionally coated plate via thickness-stretching and microstructure-dependent modeling. Mech. Res. Commun. 2024, 135, 104221. [Google Scholar] [CrossRef]
- Chami, G.M.B.; Kahil, A.; Hadji, L.; Madan, R.; Tounsi, A. Free vibration analysis of multi-directional porous functionally graded sandwich plates. Steel Compos. Struct. 2023, 46, 263–277. [Google Scholar] [CrossRef]
- Singh, A.; Kumari, P. Three-Dimensional free vibration analysis of composite FGM rectangular plates with in-plane heterogeneity: An EKM solution. Int. J. Mech. Sci. 2020, 180, 105711. [Google Scholar] [CrossRef]
- Singh, A.; Naskar, S.; Kumari, P.; Mukhopadhyay, T. Viscoelastic free vibration analysis of in-plane functionally graded orthotropic plates integrated with piezoelectric sensors: Time-dependent 3D analytical solutions. Mech. Syst. Signal Process. 2023, 184, 109636. [Google Scholar] [CrossRef]
- Vaishali; Mukhopadhyay, T.; Kumar, R.R.; Dey, S. Probing the multi-physical probabilistic dynamics of a novel functional class of hybrid composite shells. Compos. Struct. 2021, 262, 113294. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. A new hyperbolic-polynomial higher-order elasticity theory for mechanics of thick FGM beams with imperfection in the material composition. Compos. Struct. 2020, 249, 112486. [Google Scholar] [CrossRef]
- Mallick, A.; Gangi Setti, S.; Sahu, R.K. Centrifugally cast functionally graded materials: Fabrication and challenges for probable automotive cylinder liner application. Ceram. Int. 2023, 49, 8649–8682. [Google Scholar] [CrossRef]
- Verma, R.K.; Parganiha, D.; Chopkar, M. A review on fabrication and characteristics of functionally graded aluminum matrix composites fabricated by centrifugal casting method. SN Appl. Sci. 2021, 3, 227. [Google Scholar] [CrossRef]
- Abdalla, H.M.A.; Casagrande, D. An Intrinsic Material Tailoring Approach for Functionally Graded Axisymmetric Hollow Bodies Under Plane Elasticity. J. Elast. 2021, 144, 15–32. [Google Scholar] [CrossRef]
- Elkotb, H.H.; Mostafa, R.; Samad, A.A.A.; Enab, T.A. Manufacturing and Characterization of Functionally Graded Material Automotive Piston Using Centrifugal Casting Technique. Solid State Phenom. 2021, 318, 13–24. [Google Scholar]
- Madan, R.; Bhowmick, S. Fabrication and microstructural characterization of Al-SiC based functionally graded disk. Aircr. Eng. Aerosp. Technol. 2023, 95, 292–301. [Google Scholar] [CrossRef]
- Suresh, S.; Mortensen, A. Functionally graded metals and metal-ceramic composites: Part 2 Thermomechanical behaviour. Int. Mater. Rev. 1997, 42, 85–116. [Google Scholar] [CrossRef]
- Loh, G.H.; Pei, E.; Harrison, D.; Monzón, M.D. An overview of functionally graded additive manufacturing. Addit. Manuf. 2018, 23, 34–44. [Google Scholar] [CrossRef]
- Madan, R.; Bhowmick, S. Modeling of functionally graded materials to estimate effective thermo-mechanical properties. World J. Eng. 2022, 19, 291–301. [Google Scholar] [CrossRef]
- Rizov, V. Delamination Analysis of Multilayered Functionally Graded Beams which Exhibit Non-linear Creep Behavior. J. Appl. Comput. Mech. 2023, 9, 935–944. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Tadi Beni, Y.; Malikan, M. A comprehensive study on nonlinear hygro-thermo-mechanical analysis of thick functionally graded porous rotating disk based on two quasi-three-dimensional theories. Mech. Based Des. Struct. Mach. 2022, 50, 3596–3625. [Google Scholar] [CrossRef]
- Karami, B.; Ghayesh, M.H. Moving load excited dynamics of multi-layered imperfect microplates based on various micromechanical models. Int. J. Eng. Sci. 2024, 197, 104017. [Google Scholar] [CrossRef]
- Karami, B.; Ghayesh, M.H. Vibration characteristics of sandwich microshells with porous functionally graded face sheets. Int. J. Eng. Sci. 2023, 189, 103884. [Google Scholar] [CrossRef]
- Rezaei Farimani, M.; Mohadeszadeh, M. Thermo-elastic bending analysis of FGM rotating plate with axial grading and modified rule of mixture. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 299–307. [Google Scholar] [CrossRef]
- Delale, F.; Erdogan, F. The Crack Problem for a Nonhomogeneous Plane. J. Appl. Mech. 1983, 50, 609–614. [Google Scholar] [CrossRef]
- Sobhy, M. Buckling and free vibration of exponentially graded sandwich plates resting on elastic foundations under various boundary conditions. Compos. Struct. 2013, 99, 76–87. [Google Scholar] [CrossRef]
- Li, Q.; Iu, V.P.; Kou, K.P. Three-dimensional vibration analysis of functionally graded material sandwich plates. J. Sound Vib. 2008, 311, 498–515. [Google Scholar] [CrossRef]
- Zenkour, A.M. A comprehensive analysis of functionally graded sandwich plates: Part 2—Buckling and free vibration. Int. J. Solids Struct. 2005, 42, 5243–5258. [Google Scholar] [CrossRef]
- Thai, H.-T.; Nguyen, T.-K.; Vo, T.P.; Lee, J. Analysis of functionally graded sandwich plates using a new first-order shear deformation theory. Eur. J. Mech.—A/Solids 2014, 45, 211–225. [Google Scholar] [CrossRef]

| Boundary Conditions | x = 0 | y = 0 | x = a | y = b | Xm(x) | Yn(y) |
|---|---|---|---|---|---|---|
| SSSS | S | S | S | S | sin(λx) | sin(μx) |
| CSCS | C | S | C | S | sin2(λx) | sin(μx) |
| CCCC | C | C | C | C | sin2(λx) | sin2(μx) |
| FCFC | F | C | F | C | cos2(λx)·[sin2(λx) + 1] | sin2(μx) |
| pz | Theory | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|
| 0 | 3D [43] | 1.8268 | 1.8268 | 1.8268 | 1.8268 | 1.8268 |
| SSDT [44] | 1.8245 | 1.8245 | 1.8245 | 1.8245 | 1.8245 | |
| TSDT [44] | 1.8245 | 1.8245 | 1.8245 | 1.8245 | 1.8245 | |
| FSDT [44] | 1.8244 | 1.8244 | 1.8244 | 1.8244 | 1.8244 | |
| NFSDT [45] | 1.8244 | 1.8244 | 1.8244 | 1.8244 | 1.8244 | |
| Present 1 | 1.8245 | 1.8245 | 1.8245 | 1.8245 | 1.8245 | |
| Present 2 | 1.8245 | 1.8245 | 1.8245 | 1.8245 | 1.8245 | |
| 0.5 | 3D [43] | 1.4461 | 1.4861 | 1.5213 | 1.5493 | 1.5767 |
| SSDT [44] | 1.4444 | 1.4842 | 1.5193 | 1.5520 | 1.5745 | |
| TSDT [44] | 1.4442 | 1.4841 | 1.5192 | 1.5520 | 1.5727 | |
| FSDT [44] | 1.4417 | 1.4816 | 1.5170 | 1.5500 | 1.5727 | |
| NFSDT [45] | 1.4442 | 1.4841 | 1.5192 | 1.5471 | 1.5745 | |
| Present 1 | 1.4446 | 1.4844 | 1.5195 | 1.5474 | 1.5747 | |
| Present 2 | 1.4447 | 1.4845 | 1.5195 | 1.5474 | 1.5747 | |
| 1 | 3D [43] | 1.2447 | 1.3018 | 1.3552 | 1.3976 | 1.4414 |
| SSDT [44] | 1.2434 | 1.3002 | 1.3534 | 1.4079 | 1.4393 | |
| TSDT [44] | 1.2432 | 1.3001 | 1.3533 | 1.4079 | 1.4393 | |
| FSDT [44] | 1.2403 | 1.2973 | 1.3507 | 1.4056 | 1.4372 | |
| NFSDT [45] | 1.2429 | 1.3000 | 1.3533 | 1.3956 | 1.4393 | |
| Present 1 | 1.2437 | 1.3005 | 1.3537 | 1.3959 | 1.4396 | |
| Present 2 | 1.2438 | 1.3006 | 1.3537 | 1.3959 | 1.4396 | |
| 5 | 3D [43] | 0.9448 | 0.9810 | 1.0453 | 1.1098 | 1.1757 |
| SSDT [44] | 0.9463 | 0.9821 | 1.0448 | 1.1474 | 1.1740 | |
| TSDT [44] | 0.9460 | 0.9818 | 1.0447 | 1.1473 | 1.1740 | |
| FSDT [44] | 0.9426 | 0.9787 | 1.0418 | 1.1447 | 1.1716 | |
| NFSDT [45] | 0.9431 | 0.9796 | 1.0435 | 1.1077 | 1.1735 | |
| Present 1 | 0.9467 | 0.9824 | 1.0451 | 1.1094 | 1.1743 | |
| Present 2 | 0.9469 | 0.9826 | 1.0453 | 1.1095 | 1.1744 |
| nz | Theory | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|
| 0 | 3D [43] | 1.6771 | 1.6771 | 1.6771 | 1.6771 | 1.6771 |
| NFSDT [45] | 1.6697 | 1.6697 | 1.6697 | 1.6697 | 1.6697 | |
| Present 1 | 1.6701 | 1.6701 | 1.6701 | 1.6701 | 1.6701 | |
| 0.5 | 3D [43] | 1.3536 | 1.3905 | 1.4218 | 1.4454 | 1.4694 |
| NFSDT [45] | 1.3473 | 1.3841 | 1.4152 | 1.4386 | 1.4626 | |
| Present 1 | 1.3478 | 1.3844 | 1.4154 | 1.4388 | 1.4628 | |
| 1 | 3D [43] | 1.1749 | 1.2292 | 1.2777 | 1.3143 | 1.3534 |
| NFSDT [45] | 1.1691 | 1.2232 | 1.2714 | 1.3078 | 1.3467 | |
| Present 1 | 1.1703 | 1.2238 | 1.2717 | 1.3082 | 1.3471 | |
| 5 | 3D [43] | 0.8909 | 0.9336 | 0.9980 | 1.0561 | 1.1190 |
| NFSDT [45] | 0.8853 | 0.9286 | 0.9916 | 1.0488 | 1.1118 | |
| Present 1 | 0.89528 | 0.9365 | 0.9959 | 1.0533 | 1.1136 | |
| 10 | 3D [43] | 0.8683 | 0.8923 | 0.9498 | 1.0095 | 1.0729 |
| NFSDT [45] | 0.8599 | 0.8860 | 0.9428 | 1.0012 | 1.0648 | |
| Present 1 | 0.8725 | 0.8998 | 0.9508 | 1.0095 | 1.0679 |
| nz | Theory | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|
| 0 | 3D [43] | 0.8529 | 0.8529 | 0.8529 | 0.8529 | 0.8529 |
| NFSDT [45] | 0.8491 | 0.8491 | 0.8491 | 0.8491 | 0.8491 | |
| Present 1 | 0.8501 | 0.8501 | 0.8501 | 0.8501 | 0.8501 | |
| 0.5 | 3D [43] | 1.3789 | 1.3206 | 1.2805 | 1.2453 | 1.2258 |
| NFSDT [45] | 1.3686 | 1.3115 | 1.2729 | 1.2380 | 1.2185 | |
| Present 1 | 1.3829 | 1.3284 | 1.2859 | 1.2509 | 1.2255 | |
| 1 | 3D [43] | 1.5090 | 1.4333 | 1.3824 | 1.3420 | 1.3213 |
| NFSDT [45] | 1.4915 | 1.4156 | 1.3702 | 1.3302 | 1.3104 | |
| Present 1 | 1.5176 | 1.4557 | 1.4036 | 1.3625 | 1.3289 | |
| 5 | 3D [43] | 1.6587 | 1.5801 | 1.5028 | 1.4601 | 1.4267 |
| NFSDT [45] | 1.6305 | 1.5125 | 1.4589 | 1.4195 | 1.4026 | |
| Present 1 | 1.6585 | 1.6181 | 1.5665 | 1.5212 | 1.4748 | |
| 10 | 3D [43] | 1.6728 | 1.6091 | 1.5267 | 1.4831 | 1.4410 |
| NFSDT [45] | 1.6495 | 1.5196 | 1.4642 | 1.4266 | 1.4101 | |
| Present 1 | 1.6679 | 1.6394 | 1.5931 | 1.5484 | 1.5018 |
| nz | Theory | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|
| 0 | SSDT [44] | 13.0061 | 13.0061 | 13.0061 | 13.0061 | 13.0061 |
| TSDT [44] | 13.0050 | 13.0050 | 13.0050 | 13.0050 | 13.0050 | |
| FSDT [44] | 13.0045 | 13.0045 | 13.0045 | 13.0045 | 13.0045 | |
| NFSDT [45] | 13.0045 | 13.0045 | 13.0045 | 13.0045 | 13.0045 | |
| Present 1 | 13.0049 | 13.0049 | 13.0049 | 13.0049 | 13.0049 | |
| Present 2 | 13.0061 | 13.0061 | 13.0061 | 13.0061 | 13.0061 | |
| 0.5 | SSDT [44] | 7.3657 | 7.9420 | 8.4371 | 8.8104 | 9.2167 |
| TSDT [44] | 7.3644 | 7.9408 | 8.4365 | 8.8100 | 9.2168 | |
| FSDT [44] | 7.3373 | 7.9132 | 8.4103 | 8.7867 | 9.1952 | |
| NFSDT [45] | 7.3634 | 7.9403 | 8.4361 | 8.8095 | 9.2162 | |
| Present 1 | 7.3644 | 7.9408 | 8.4365 | 8.8099 | 9.2168 | |
| Present 2 | 7.3657 | 7.9419 | 8.4371 | 8.8104 | 9.2167 | |
| 1 | SSDT [44] | 5.1685 | 5.8412 | 6.4654 | 6.9498 | 7.5063 |
| TSDT [44] | 5.1671 | 5.8401 | 6.4647 | 6.9494 | 7.5066 | |
| FSDT [44] | 5.1424 | 5.8138 | 6.4389 | 6.9257 | 7.4837 | |
| NFSDT [45] | 5.1648 | 5.8387 | 6.4641 | 6.9485 | 7.5056 | |
| Present 1 | 5.1671 | 5.8401 | 6.4647 | 6.9494 | 7.5066 | |
| Present 2 | 5.1685 | 5.8412 | 6.4654 | 6.9498 | 7.5063 | |
| 5 | SSDT [44] | 2.6601 | 3.0441 | 3.5806 | 4.1129 | 4.7349 |
| TSDT [44] | 2.6582 | 3.0426 | 3.5796 | 4.1121 | 4.7347 | |
| FSDT [44] | 2.6384 | 3.0225 | 3.5596 | 4.0929 | 4.7148 | |
| NFSDT [45] | 2.6415 | 3.0282 | 3.5710 | 4.1024 | 4.7305 | |
| Present 1 | 2.6582 | 3.0426 | 3.5796 | 4.1121 | 4.7347 | |
| Present 2 | 2.6601 | 3.0441 | 3.5806 | 4.1129 | 4.7349 |
| nz | Theory | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|
| 0 | SSDT [44] | 6.5030 | 6.5030 | 6.5030 | 6.5030 | 6.5030 |
| TSDT [44] | 6.5025 | 6.5025 | 6.5025 | 6.5025 | 6.5025 | |
| FSDT [44] | 6.5022 | 6.5022 | 6.5022 | 6.5022 | 6.5022 | |
| NFSDT [45] | 6.5022 | 6.5022 | 6.5022 | 6.5022 | 6.5022 | |
| Present 1 | 6.5025 | 6.5025 | 6.5025 | 6.5025 | 6.5025 | |
| Present 2 | 6.5030 | 6.5030 | 6.5030 | 6.5030 | 6.5030 | |
| 0.5 | SSDT [44] | 3.6828 | 3.9710 | 4.2186 | 4.4052 | 4.6084 |
| TSDT [44] | 3.6822 | 3.9704 | 4.2182 | 4.4050 | 4.6084 | |
| FSDT [44] | 3.6687 | 3.9566 | 4.2052 | 4.3934 | 4.5976 | |
| NFSDT [45] | 3.6817 | 3.9702 | 4.2181 | 4.4047 | 4.6081 | |
| Present 1 | 3.6822 | 3.9704 | 4.2182 | 4.4049 | 4.6084 | |
| Present 2 | 3.6828 | 3.9709 | 4.2185 | 4.4052 | 4.6083 | |
| 1 | SSDT [44] | 2.5842 | 2.9206 | 3.2327 | 3.4749 | 3.7531 |
| TSDT [44] | 2.5836 | 2.9200 | 3.2324 | 3.4747 | 3.7533 | |
| FSDT [44] | 2.5712 | 2.9069 | 3.2195 | 3.4629 | 3.7418 | |
| NFSDT [45] | 2.5824 | 2.9193 | 3.2320 | 3.4742 | 3.7528 | |
| Present 1 | 2.5835 | 2.9200 | 3.2323 | 3.4747 | 3.7533 | |
| Present 2 | 2.5842 | 2.9206 | 3.2327 | 3.4749 | 3.7531 | |
| 5 | SSDT [44] | 1.3300 | 1.5220 | 1.7903 | 2.0564 | 2.3674 |
| TSDT [44] | 1.3291 | 1.5213 | 1.7898 | 2.0561 | 2.3673 | |
| FSDT [44] | 1.3192 | 1.5113 | 1.7798 | 2.0464 | 2.3574 | |
| NFSDT [45] | 1.3208 | 1.5141 | 1.7855 | 2.0512 | 2.3652 | |
| Present 1 | 1.3291 | 1.5213 | 1.7898 | 2.0560 | 2.3673 | |
| Present 2 | 1.3300 | 1.5220 | 1.7903 | 2.0564 | 2.3674 |
| Boundary Conditions | px | pz | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|---|
| SSSS | 0 | 0.5 | 1.4446 | 1.4844 | 1.5195 | 1.5474 | 1.5747 |
| 0 | 1 | 1.2437 | 1.3005 | 1.3537 | 1.3959 | 1.4396 | |
| 0 | 5 | 0.9467 | 0.9824 | 1.0451 | 1.1094 | 1.1743 | |
| 0.5 | 0.5 | 1.3965 | 1.4302 | 1.4635 | 1.4949 | 1.5216 | |
| 0.5 | 1 | 1.2113 | 1.2606 | 1.3109 | 1.3556 | 1.3983 | |
| 0.5 | 5 | 0.9451 | 0.9748 | 1.0338 | 1.0981 | 1.1613 | |
| 2 | 0.5 | 1.2835 | 1.3046 | 1.3353 | 1.3749 | 1.4024 | |
| 2 | 1 | 1.1378 | 1.1708 | 1.2156 | 1.2655 | 1.3076 | |
| 2 | 5 | 0.9414 | 0.9590 | 1.0103 | 1.0745 | 1.1341 | |
| CSCS | 0 | 0.5 | 2.1285 | 2.1868 | 2.2375 | 2.2772 | 2.3165 |
| 0 | 1 | 1.8379 | 1.9218 | 1.9992 | 2.0599 | 2.1231 | |
| 0 | 5 | 1.4017 | 1.4583 | 1.5511 | 1.6446 | 1.7399 | |
| 0.5 | 0.5 | 2.0571 | 2.1080 | 2.1569 | 2.2018 | 2.2407 | |
| 0.5 | 1 | 1.7894 | 1.8634 | 1.9373 | 2.0015 | 2.0638 | |
| 0.5 | 5 | 1.3983 | 1.4469 | 1.5345 | 1.6280 | 1.7208 | |
| 2 | 0.5 | 1.8894 | 1.9256 | 1.9718 | 2.0288 | 2.0697 | |
| 2 | 1 | 1.6788 | 1.7321 | 1.7988 | 1.8708 | 1.9329 | |
| 2 | 5 | 1.3899 | 1.4234 | 1.4999 | 1.5934 | 1.6813 | |
| CCCC | 0 | 0.5 | 2.6386 | 2.7106 | 2.7725 | 2.8205 | 2.8684 |
| 0 | 1 | 2.2834 | 2.3877 | 2.4827 | 2.5565 | 2.6338 | |
| 0 | 5 | 1.7439 | 1.8180 | 1.9334 | 2.0482 | 2.16583 | |
| 0.5 | 0.5 | 2.5497 | 2.6139 | 2.6744 | 2.7287 | 2.7767 | |
| 0.5 | 1 | 2.2225 | 2.3157 | 2.4069 | 2.4850 | 2.5616 | |
| 0.5 | 5 | 1.7387 | 1.8038 | 1.9129 | 2.0277 | 2.1425 | |
| 2 | 0.5 | 2.3406 | 2.3902 | 2.4486 | 2.5178 | 2.5689 | |
| 2 | 1 | 2.0835 | 2.1538 | 2.2371 | 2.3250 | 2.4021 | |
| 2 | 5 | 1.7257 | 1.7741 | 1.8701 | 1.9849 | 2.0939 | |
| FCFC | 0 | 0.5 | 2.7884 | 2.8643 | 2.9290 | 2.9788 | 3.0289 |
| 0 | 1 | 2.4168 | 2.5271 | 2.6268 | 2.7038 | 2.7847 | |
| 0 | 5 | 1.8478 | 1.9289 | 2.0510 | 2.1715 | 2.2954 | |
| 0.5 | 0.5 | 2.6941 | 2.7629 | 2.8266 | 2.8830 | 2.9335 | |
| 0.5 | 1 | 2.3519 | 2.4514 | 2.5474 | 2.6289 | 2.7094 | |
| 0.5 | 5 | 1.8415 | 1.9137 | 2.0294 | 2.1499 | 2.2709 | |
| 2 | 0.5 | 2.4724 | 2.5282 | 2.5906 | 2.6628 | 2.7171 | |
| 2 | 1 | 2.2035 | 2.2809 | 2.3695 | 2.4614 | 2.5428 | |
| 2 | 5 | 1.8257 | 1.8821 | 1.9843 | 2.1048 | 2.2199 |
| Boundary Conditions | px | pz | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|---|
| SSSS | 0 | 0.5 | 1.5758 | 1.5299 | 1.4876 | 1.4372 | 1.4173 |
| 0 | 1 | 1.7263 | 1.6846 | 1.6405 | 1.5798 | 1.5619 | |
| 0 | 5 | 1.8422 | 1.8421 | 1.8179 | 1.7541 | 1.7494 | |
| 0.5 | 0.5 | 1.6232 | 1.5879 | 1.5507 | 1.4986 | 1.4828 | |
| 0.5 | 1 | 1.7452 | 1.7137 | 1.6749 | 1.6146 | 1.6000 | |
| 0.5 | 5 | 1.8401 | 1.8441 | 1.8228 | 1.7601 | 1.7570 | |
| 2 | 0.5 | 1.7017 | 1.6887 | 1.6627 | 1.6085 | 1.6006 | |
| 2 | 1 | 1.7762 | 1.7652 | 1.7382 | 1.6791 | 1.6714 | |
| 2 | 5 | 1.8354 | 1.8476 | 1.8323 | 1.7718 | 1.7720 | |
| CSCS | 0 | 0.5 | 2.2702 | 2.1949 | 2.1305 | 2.0639 | 2.0299 |
| 0 | 1 | 2.4889 | 2.4125 | 2.3402 | 2.2608 | 2.2229 | |
| 0 | 5 | 2.6799 | 2.6551 | 2.6007 | 2.5159 | 2.4809 | |
| 0.5 | 0.5 | 2.3500 | 2.2855 | 2.2237 | 2.1542 | 2.1209 | |
| 0.5 | 1 | 2.5258 | 2.4619 | 2.3942 | 2.3144 | 2.2771 | |
| 0.5 | 5 | 2.6796 | 2.6609 | 2.6105 | 2.5266 | 2.4932 | |
| 2 | 0.5 | 2.4776 | 2.4404 | 2.3886 | 2.3152 | 2.2845 | |
| 2 | 1 | 2.5842 | 2.5476 | 2.4923 | 2.4127 | 2.3788 | |
| 2 | 5 | 2.6778 | 2.6715 | 2.6289 | 2.5474 | 2.5171 | |
| CCCC | 0 | 0.5 | 2.7695 | 2.6701 | 2.5885 | 2.5124 | 2.4665 |
| 0 | 1 | 3.0378 | 2.9312 | 2.8358 | 2.7455 | 2.6897 | |
| 0 | 5 | 3.2917 | 3.2401 | 3.1577 | 3.0599 | 2.9948 | |
| 0.5 | 0.5 | 2.8767 | 2.7864 | 2.7043 | 2.6239 | 2.5747 | |
| 0.5 | 1 | 3.0912 | 2.9977 | 2.9053 | 2.8136 | 2.7552 | |
| 0.5 | 5 | 3.2937 | 3.2499 | 3.1717 | 3.0748 | 3.0107 | |
| 2 | 0.5 | 3.0449 | 2.9835 | 2.9084 | 2.8226 | 2.7694 | |
| 2 | 1 | 3.1743 | 3.1116 | 3.0305 | 2.9380 | 2.8782 | |
| 2 | 5 | 3.2958 | 3.2674 | 3.1982 | 3.1032 | 3.0417 | |
| FCFC | 0 | 0.5 | 2.8951 | 2.7859 | 2.6987 | 2.6225 | 2.5716 |
| 0 | 1 | 3.1767 | 3.0559 | 2.9515 | 2.8615 | 2.7965 | |
| 0 | 5 | 3.4568 | 3.3879 | 3.2907 | 3.1924 | 3.1092 | |
| 0.5 | 0.5 | 3.0140 | 2.9116 | 2.8210 | 2.7402 | 2.6828 | |
| 0.5 | 1 | 3.2383 | 3.1298 | 3.0265 | 2.9346 | 2.8647 | |
| 0.5 | 5 | 3.4606 | 3.3999 | 3.3068 | 3.2091 | 3.1264 | |
| 2 | 0.5 | 3.1988 | 3.1233 | 3.0364 | 2.9495 | 2.8830 | |
| 2 | 1 | 3.3337 | 3.2555 | 3.1613 | 3.0677 | 2.9926 | |
| 2 | 5 | 3.4659 | 3.4215 | 3.3372 | 3.2410 | 3.1601 |
| Boundary Conditions | px | pz | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|---|
| SSSS | 0 | 0.5 | 3.6822 | 3.9704 | 4.2182 | 4.4049 | 4.6084 |
| 0 | 1 | 2.5836 | 2.9200 | 3.2324 | 3.4747 | 3.7533 | |
| 0 | 5 | 1.3291 | 1.5213 | 1.7898 | 2.0560 | 2.3673 | |
| 0.5 | 0.5 | 3.3400 | 3.6008 | 3.8391 | 4.0419 | 4.2426 | |
| 0.5 | 1 | 2.3939 | 2.6942 | 2.9871 | 3.2338 | 3.5029 | |
| 0.5 | 5 | 1.3132 | 1.4882 | 1.7421 | 2.0049 | 2.3062 | |
| 2 | 0.5 | 2.6494 | 2.8539 | 3.0711 | 3.3002 | 3.5003 | |
| 2 | 1 | 2.0109 | 2.2382 | 2.4909 | 2.7428 | 2.9958 | |
| 2 | 5 | 1.2799 | 1.4213 | 1.6460 | 1.9017 | 2.1826 | |
| CSCS | 0 | 0.5 | 6.8605 | 7.3953 | 7.8497 | 8.1872 | 8.5586 |
| 0 | 1 | 4.8432 | 5.4737 | 6.0517 | 6.4943 | 7.0067 | |
| 0 | 5 | 2.5016 | 2.8785 | 3.3849 | 3.8795 | 4.4612 | |
| 0.5 | 0.5 | 6.2201 | 6.7143 | 7.1567 | 7.5246 | 7.8959 | |
| 0.5 | 1 | 4.4844 | 5.0537 | 5.5993 | 6.0509 | 6.5494 | |
| 0.5 | 5 | 2.4677 | 2.8154 | 3.2956 | 3.7841 | 4.3477 | |
| 2 | 0.5 | 4.9270 | 5.3365 | 5.7488 | 6.1675 | 6.5439 | |
| 2 | 1 | 3.7581 | 4.2053 | 4.6824 | 5.1459 | 5.6195 | |
| 2 | 5 | 2.3949 | 2.6880 | 3.1153 | 3.5909 | 4.1184 | |
| CCCC | 0 | 0.5 | 9.2373 | 9.9552 | 10.5596 | 11.0035 | 11.4961 |
| 0 | 1 | 6.5513 | 7.4037 | 8.1779 | 8.7647 | 9.4479 | |
| 0 | 5 | 3.3941 | 3.9213 | 4.6095 | 5.2737 | 6.0585 | |
| 0.5 | 0.5 | 8.3721 | 9.0459 | 9.6401 | 10.1254 | 10.6224 | |
| 0.5 | 1 | 6.0623 | 6.8391 | 7.5736 | 8.1735 | 8.8414 | |
| 0.5 | 5 | 3.3439 | 3.8349 | 4.4887 | 5.1449 | 5.9063 | |
| 2 | 0.5 | 6.6247 | 7.2047 | 7.7675 | 8.3230 | 8.8337 | |
| 2 | 1 | 5.0717 | 5.6980 | 6.3470 | 6.9651 | 7.6049 | |
| 2 | 5 | 3.2349 | 3.6606 | 4.2447 | 4.8841 | 5.5985 | |
| FCFC | 0 | 0.5 | 10.8692 | 11.7121 | 12.4173 | 12.9312 | 13.5048 |
| 0 | 1 | 7.7331 | 8.7391 | 9.6467 | 10.3296 | 11.1282 | |
| 0 | 5 | 4.0148 | 4.6515 | 5.4666 | 6.2465 | 7.1712 | |
| 0.5 | 0.5 | 9.8488 | 10.6484 | 11.3463 | 11.9092 | 12.4918 | |
| 0.5 | 1 | 7.1529 | 8.0755 | 8.9396 | 9.6388 | 10.4219 | |
| 0.5 | 5 | 3.9521 | 4.5488 | 5.3239 | 6.0947 | 6.9926 | |
| 2 | 0.5 | 7.7875 | 8.4932 | 9.1618 | 9.8086 | 10.4127 | |
| 2 | 1 | 5.9771 | 6.7339 | 7.5029 | 8.2251 | 8.9797 | |
| 2 | 5 | 3.8149 | 4.3412 | 5.0358 | 5.7873 | 6.6313 |
| Boundary Conditions | px | pz | 1-0-1 | 2-1-2 | 1-1-1 | 2-2-1 | 1-2-1 |
|---|---|---|---|---|---|---|---|
| SSSS | 0 | 0.5 | 3.9158 | 3.6018 | 3.3496 | 3.1017 | 2.9770 |
| 0 | 1 | 4.9809 | 4.5812 | 4.2423 | 3.8888 | 3.7302 | |
| 0 | 5 | 6.3116 | 5.9908 | 5.6258 | 5.1429 | 4.9673 | |
| 0.5 | 0.5 | 4.2926 | 3.9860 | 3.7234 | 3.4429 | 3.3158 | |
| 0.5 | 1 | 5.2096 | 4.8331 | 4.4959 | 4.1236 | 3.9641 | |
| 0.5 | 5 | 6.3410 | 6.0394 | 5.6855 | 5.2028 | 5.0310 | |
| 2 | 0.5 | 5.0219 | 4.7482 | 4.4749 | 4.1298 | 3.9982 | |
| 2 | 1 | 5.6446 | 5.3254 | 5.0012 | 4.5931 | 4.4361 | |
| 2 | 5 | 6.3969 | 6.1343 | 5.8037 | 5.3219 | 5.1589 | |
| CSCS | 0 | 0.5 | 6.9651 | 6.3522 | 5.8856 | 5.4808 | 5.2319 |
| 0 | 1 | 8.8733 | 8.0495 | 7.3940 | 6.8224 | 6.4704 | |
| 0 | 5 | 11.4549 | 10.6674 | 9.8643 | 9.0650 | 8.5544 | |
| 0.5 | 0.5 | 7.7135 | 7.0766 | 6.5604 | 6.0956 | 5.8111 | |
| 0.5 | 1 | 9.3552 | 8.5479 | 7.8692 | 7.2585 | 6.8763 | |
| 0.5 | 5 | 11.5328 | 10.7791 | 9.9902 | 9.1863 | 8.6741 | |
| 2 | 0.5 | 9.1297 | 8.5002 | 7.9139 | 7.3319 | 6.9766 | |
| 2 | 1 | 10.2468 | 9.5073 | 8.8092 | 8.1261 | 7.6953 | |
| 2 | 5 | 11.6792 | 10.9948 | 10.2374 | 9.4264 | 8.9138 | |
| CCCC | 0 | 0.5 | 9.0716 | 8.2251 | 7.6020 | 7.1061 | 6.7586 |
| 0 | 1 | 11.5691 | 10.3968 | 9.4986 | 8.8027 | 8.2856 | |
| 0 | 5 | 15.1311 | 13.9037 | 12.7229 | 11.7333 | 10.9025 | |
| 0.5 | 0.5 | 10.1175 | 9.2048 | 8.4892 | 7.9139 | 7.4925 | |
| 0.5 | 1 | 12.2651 | 11.0898 | 10.1375 | 9.3863 | 8.8056 | |
| 0.5 | 5 | 15.2571 | 14.0721 | 12.9036 | 11.9041 | 11.0635 | |
| 2 | 0.5 | 12.0741 | 11.1201 | 10.2665 | 9.5369 | 8.9691 | |
| 2 | 1 | 13.5375 | 12.4139 | 11.3971 | 10.5446 | 9.8545 | |
| 2 | 5 | 15.4932 | 14.3959 | 13.2576 | 12.2414 | 11.3854 | |
| FCFC | 0 | 0.5 | 10.4404 | 9.4306 | 8.7022 | 8.1545 | 7.7373 |
| 0 | 1 | 13.3239 | 11.9014 | 10.8357 | 10.0699 | 9.4331 | |
| 0 | 5 | 17.5759 | 16.0092 | 14.5512 | 13.4495 | 12.3755 | |
| 0.5 | 0.5 | 11.6978 | 10.5847 | 9.7294 | 9.0892 | 8.5673 | |
| 0.5 | 1 | 14.1765 | 12.7309 | 11.5854 | 10.7529 | 10.0252 | |
| 0.5 | 5 | 17.7400 | 16.2199 | 14.7711 | 13.6554 | 12.5642 | |
| 2 | 0.5 | 14.0361 | 12.8349 | 11.7854 | 10.9667 | 10.2366 | |
| 2 | 1 | 15.7264 | 14.3105 | 13.0605 | 12.1066 | 11.2195 | |
| 2 | 5 | 18.0477 | 16.6251 | 15.2018 | 14.0618 | 12.9413 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadji, L.; Plevris, V.; Madan, R.; Ait Atmane, H. Multi-Directional Functionally Graded Sandwich Plates: Buckling and Free Vibration Analysis with Refined Plate Models under Various Boundary Conditions. Computation 2024, 12, 65. https://doi.org/10.3390/computation12040065
Hadji L, Plevris V, Madan R, Ait Atmane H. Multi-Directional Functionally Graded Sandwich Plates: Buckling and Free Vibration Analysis with Refined Plate Models under Various Boundary Conditions. Computation. 2024; 12(4):65. https://doi.org/10.3390/computation12040065
Chicago/Turabian StyleHadji, Lazreg, Vagelis Plevris, Royal Madan, and Hassen Ait Atmane. 2024. "Multi-Directional Functionally Graded Sandwich Plates: Buckling and Free Vibration Analysis with Refined Plate Models under Various Boundary Conditions" Computation 12, no. 4: 65. https://doi.org/10.3390/computation12040065
APA StyleHadji, L., Plevris, V., Madan, R., & Ait Atmane, H. (2024). Multi-Directional Functionally Graded Sandwich Plates: Buckling and Free Vibration Analysis with Refined Plate Models under Various Boundary Conditions. Computation, 12(4), 65. https://doi.org/10.3390/computation12040065







