Absorption by a Layered Microbolometer Pixel’s Active Element
Abstract
1. Introduction
2. System Model and Analytical Optimization Approach
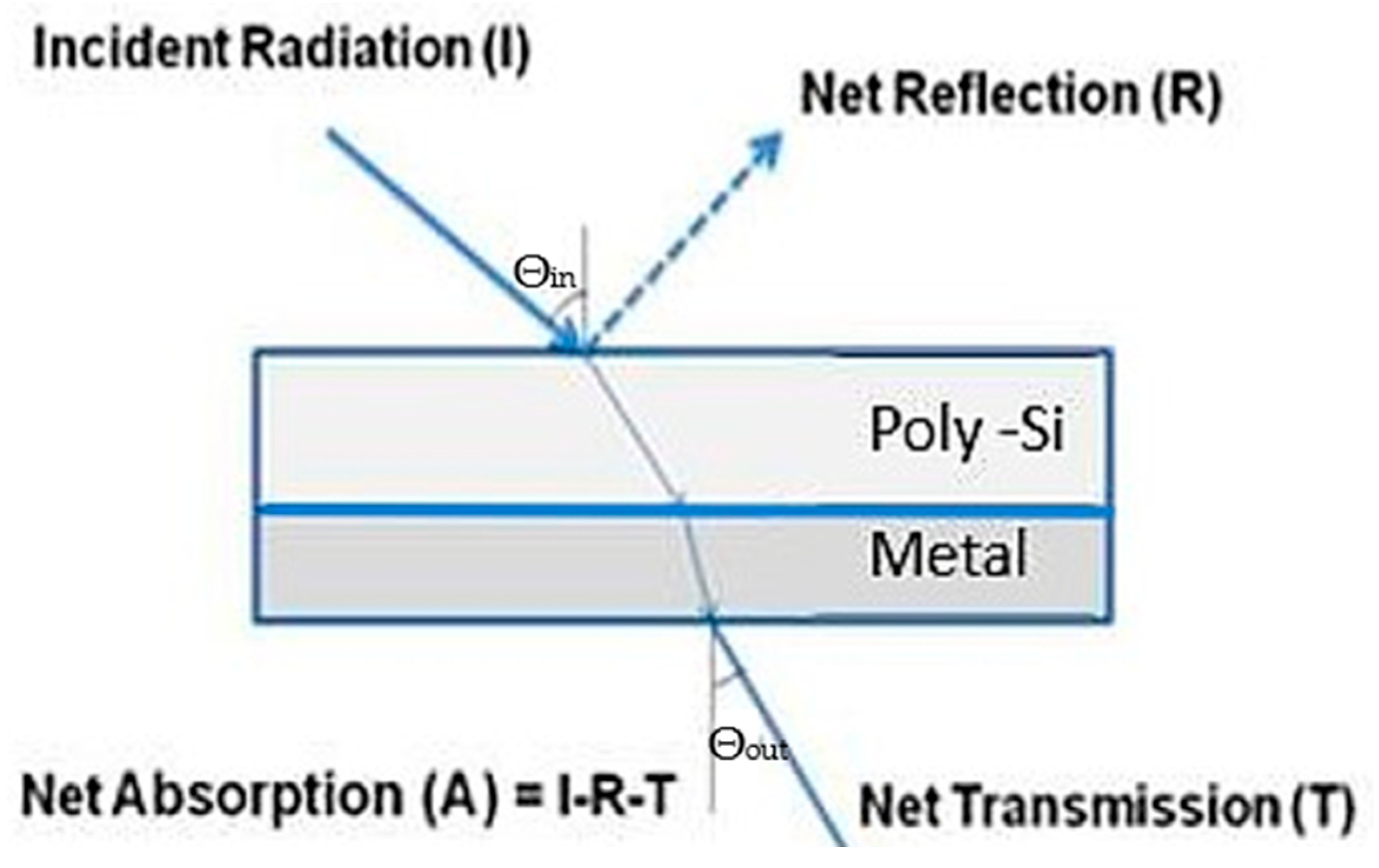
2.1. Absorber Setup
2.2. A Generalized Analytical Solution
3. Results and Comparison with Numerical Optimization Approach
3.1. Numerical Optimization Procedure
3.2. Numerical Calculation of the Optimized Absorber Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lynch, D. Introduction to RF Stealth; SciTech Publishing: Raleigh, NC, USA, 2004. [Google Scholar]
- Brun, M.-A.; Formanek, F.; Yasuda, A.; Sekine, M.; Ando, N.; Eishii, Y. Terahertz imaging applied to cancer diagnosis. Phys. Med. Biol. 2010, 55, 4615–4623. [Google Scholar] [CrossRef] [PubMed]
- Ashworth, P.C.; Pickwell-MacPherson, E.; Provenzano, E.; Pinder, S.E.; Purushotham, A.D.; Pepper, M.; Wallace, V.P. Terahertz pulsed spectroscopy of freshly excised human breast cancer. Opt. Express 2009, 17, 12444–12454. [Google Scholar] [CrossRef] [PubMed]
- Kruse, P.W. Uncooled Thermal Imaging: Arrays, Systems, and Applications; SPIE Press: Bellingham, WA, USA, 2002. [Google Scholar]
- Dewitte, S.; Abdul Nazar, A.A.; Zhang, Y.; Smeesters, L. A Multispectral Camera Suite for the Observation of Earth’s Outgoing Radiative Energy. Remote Sens. 2023, 15, 5487. [Google Scholar] [CrossRef]
- López-Alonso, J.M. Noise Equivalent Temperature Difference (NETD). In Encyclopedia of Optical and Photonic Engineering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 1766–1773. [Google Scholar]
- Bardalen, E.; Bouchouri, A.; Akram, M.N.; Nguyen, H.-V. Black Silicon as Anti-Reflective Structure for Infrared Imaging Applications. Nanomaterials 2024, 14, 20. [Google Scholar] [CrossRef] [PubMed]
- Yadav, P.V.K.; Yadav, I.; Ajitha, B.; Rajasekar, A.; Gupta, S.; Reddy, Y.A.K. Advancements of Uncooled Infrared Microbolometer Materials: A Review. Sens. Actuators A Phys. 2022, 342, 113611. [Google Scholar] [CrossRef]
- Shin, C.; Pham, D.P.; Park, J.; Kim, S.; Lee, Y.-J.; Yi, J. Structure and electrical properties of boron doped hydrogenated mixed-phase silicon films for uncooled microbolometer. Infrared Phys. Technol. 2018, 96, 84–88. [Google Scholar] [CrossRef]
- Audhkhasi, R.; Povinelli, M.L. Gold-black phosphorus nanostructured absorbers for efficient light trapping in the mid-infrared. Opt. Express 2020, 28, 19562–19570. [Google Scholar] [CrossRef] [PubMed]
- Yadav, I.; Jain, S.; Joshi, S.R.; Goyal, A.; Tomar, M.; Gupta, S.; Dutta, S.; Chatterjee, R. Compositional, electrical and thermal properties of nonstoichiometric titanium oxide thin films for MEMS bolometer applications. Mater. Sci. Semicond. Process. 2022, 148, 106779. [Google Scholar] [CrossRef]
- Bolakis, C.; Karanasiou, I.S.; Grbovic, D.; Karunasiri, G.; Uzunoglu, N. Optimizing detection methods for terahertz bio imaging applications. Opt. Eng. 2015, 54, 067107. [Google Scholar] [CrossRef]
- Bolakis, C.; Karanasiou, I.S.; Grbovic, D.; Vazouras, C.; Karunasiri, G.; Uzunoglu, N. Optimizing the Absorption Capability of a Microbolometer Pixel’s Active Element. Int. J. Electromagn. Appl. 2019, 9, 1–6. [Google Scholar]
- Lecaruyer, P.; Maillart, E.; Canva, M.; Rolland, J. Generalization of the Rouard method to an absorbing thin-film stack and application to surface plasmon resonance. Appl. Opt. 2006, 45, 8419–8423. [Google Scholar] [CrossRef] [PubMed]
- Müllerová, J.; Jurečka, S.; Šutta, P. Optical characterization of polysilicon thin films for solar applications. Sol. Energy 2006, 80, 667–674. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E.; Bhatia, A.B.; Clemmow, P.C.; Gabor, D.; Stokes, A.R.; Taylor, A.M.; Wayman, P.A.; Wilcock, W.L. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Balanis, C. Advanced Engineering Electromagnetics, 2nd ed.; Wiley: Ney York, NY, USA, 2012. [Google Scholar]
- Feynman, R. The Feynman Lectures on Physics. new millennium, Ed.; California Institute of Technology: Pasadena, CA, USA, 2010; Volume 2, pp. 3211–3213. [Google Scholar]






| Fixed Values | Wavelength of Interest [μm] | Required Poly-Si Thickness [μm] |
|---|---|---|
| 120 (2.5 THz) | 5.743 |
| 60 (5 THz) | 2.863 | |
| 40 (7.5 THz) | 1.903 | |
| 30 (10 THz) | 1.423 |
| Fixed Values | Wavelength of Interest [μm] | Required Poly-Si Thickness [μm] |
|---|---|---|
| 14 | 0.655 |
| 8 | 0.367 | |
| 5 | 0.223 | |
| 3 | 0.127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolakis, C.; Vazouras, C.N. Absorption by a Layered Microbolometer Pixel’s Active Element. Computation 2024, 12, 108. https://doi.org/10.3390/computation12050108
Bolakis C, Vazouras CN. Absorption by a Layered Microbolometer Pixel’s Active Element. Computation. 2024; 12(5):108. https://doi.org/10.3390/computation12050108
Chicago/Turabian StyleBolakis, Christos, and Christos N. Vazouras. 2024. "Absorption by a Layered Microbolometer Pixel’s Active Element" Computation 12, no. 5: 108. https://doi.org/10.3390/computation12050108
APA StyleBolakis, C., & Vazouras, C. N. (2024). Absorption by a Layered Microbolometer Pixel’s Active Element. Computation, 12(5), 108. https://doi.org/10.3390/computation12050108





