Computational Analysis of Hemodynamic Indices in Multivessel Coronary Artery Disease in the Presence of Myocardial Perfusion Dysfunction
Abstract
1. Introduction
2. Mathematical Model of Coronary Hemodynamics
2.1. The Model of Bood Flow in a Single Vessel
2.2. Boundary Conditions at Vascular Connections
2.3. Inflow Boundary Conditions
2.4. Outflow Boundary Conditions
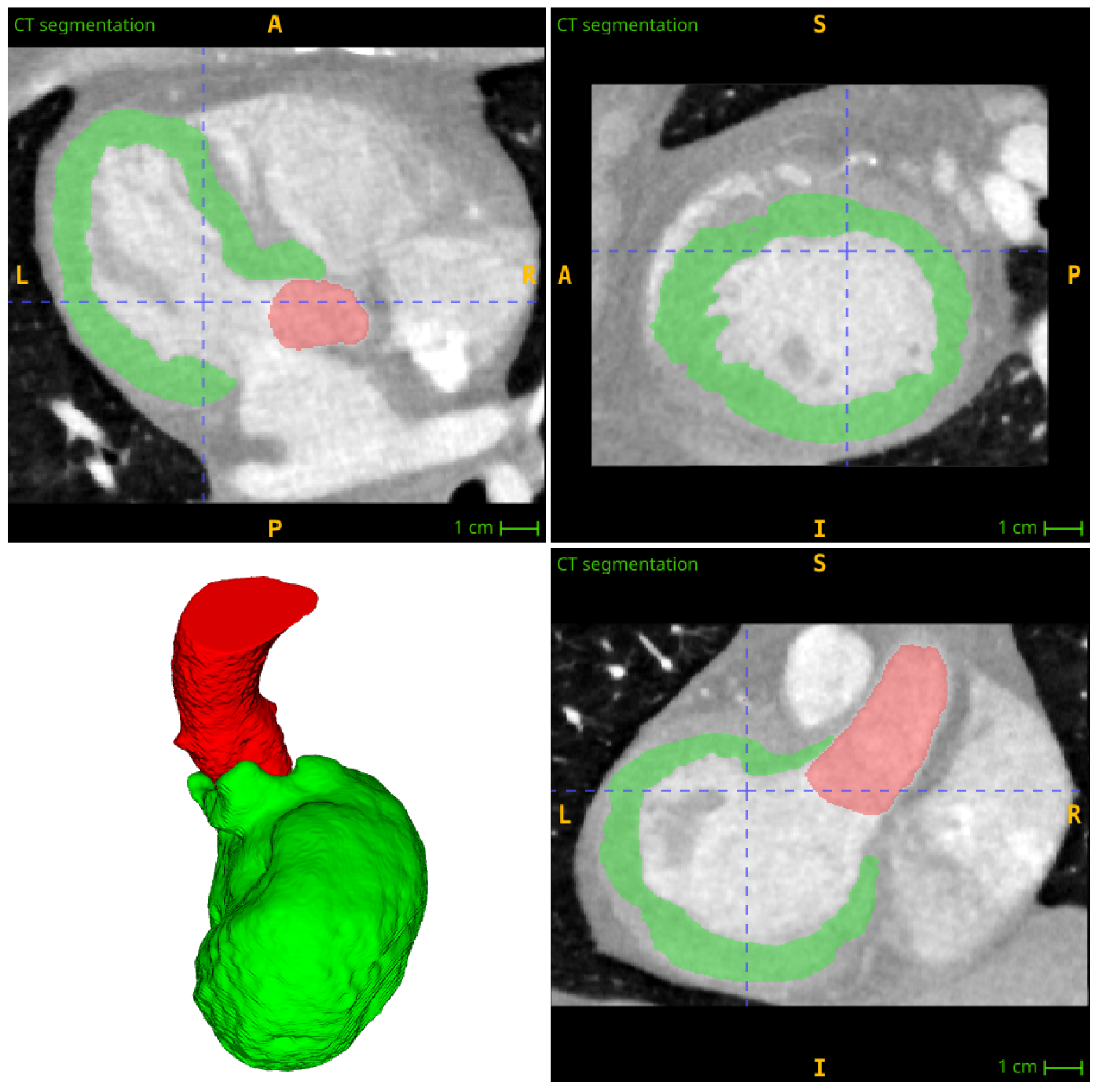
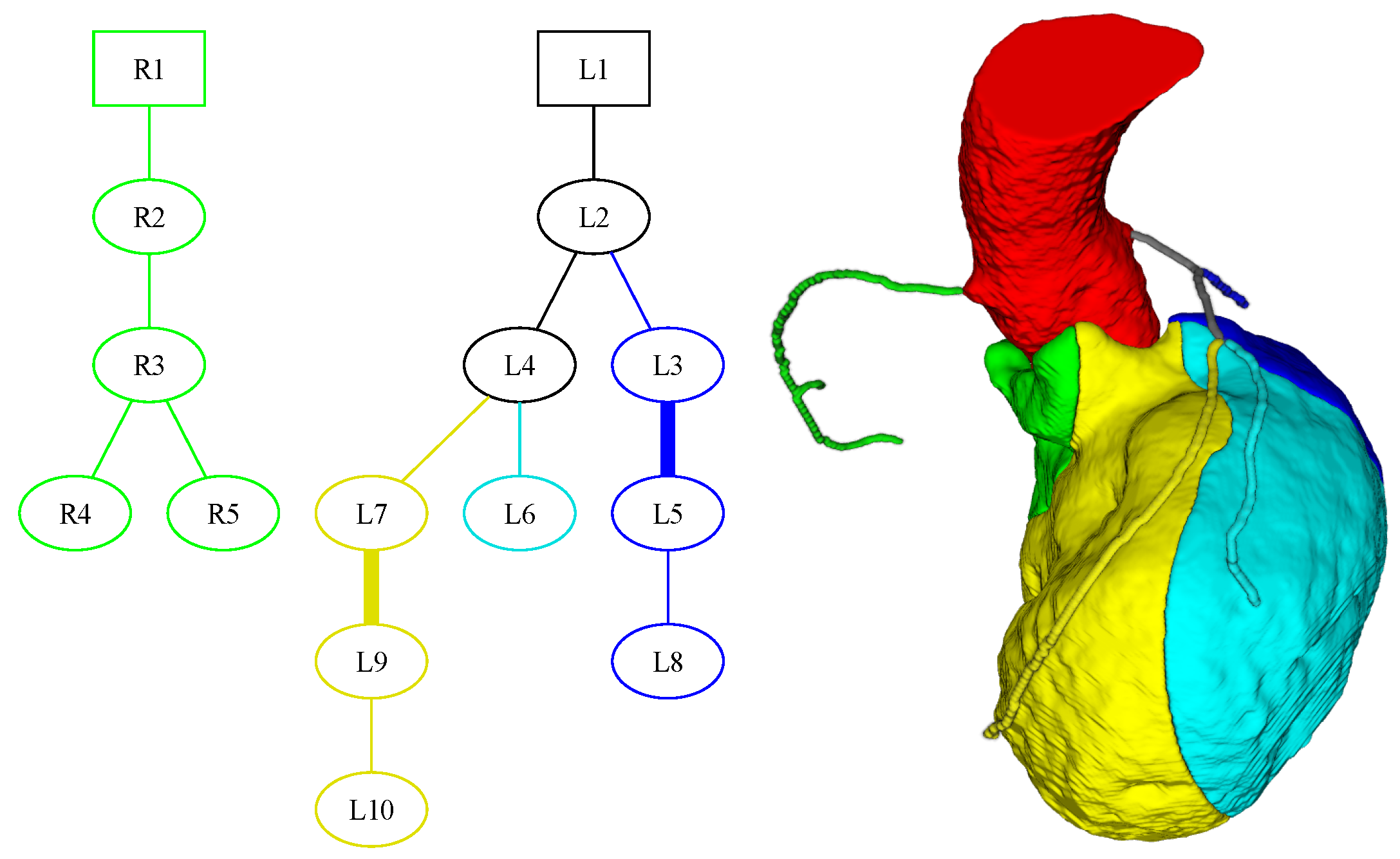
3. Segmentation and Partitioning of Coronary Vessels and Microcirculation
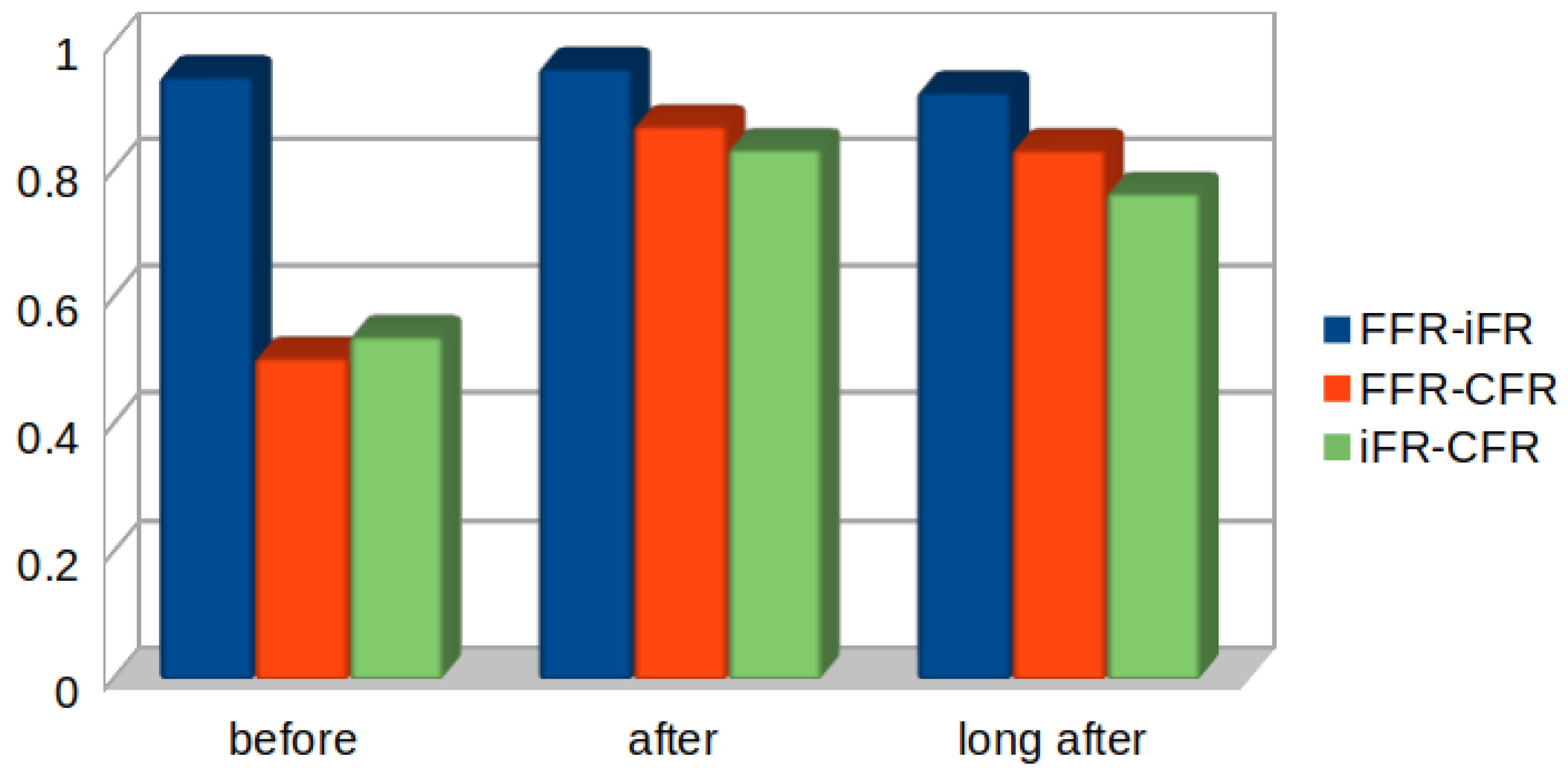
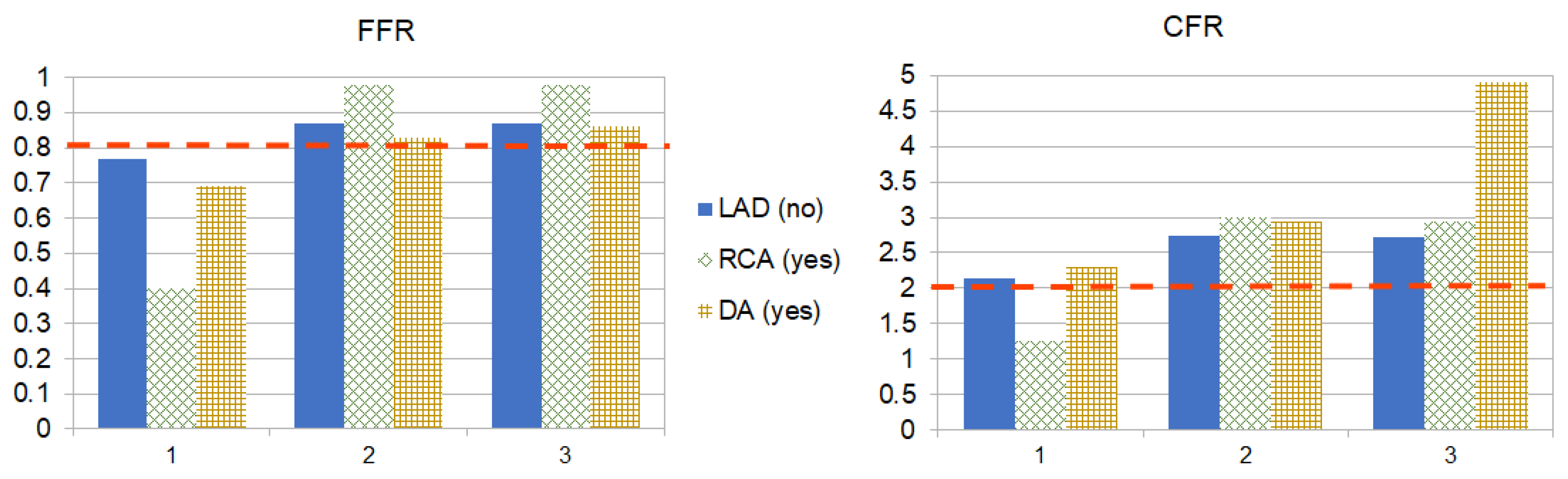
4. Results
5. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AoPWV | Aortic pulse wave velocity |
| PCI | Percutaneous coronary intervention |
| SV | Stroke volume |
| HR | Heart rate |
| FFR | Fractional flow reserve |
| iFR | Instanteneous wave-free ratio |
| CFR | Coronary flow reserve |
| TPR | Transmural perfusion ratio |
| LAD | Left anterior decending artery |
| LADp | Proximal part of the left anterior descending artery |
| LADd | Distal part of the left anterior descending artery |
| RCA | Right coronary artery |
| RCAp | Proximal part of the right coronary artery |
| RCAd | Distal part of the right coronary artery |
| LCx | Circumflex branch of left coronary artery |
| DA | Diagonal artery |
| OM | Obtuse marginal artery |
References
- Pijls, N.H.J.; de Bruyne, B.; Peels, K.; van der Voort, P.H.; Bonnier Hans, J.R.M.; Bartunek, J.; Koolen, J.J. Measurement of Fractional Flow Reserve to Assess the Functional Severity of Coronary-Artery Stenoses. N. Engl. J. Med. 1996, 334, 1703–1708. [Google Scholar] [CrossRef]
- Gould, K.L.; Kirkeeide, R.L.; Buchi, M. Coronary flow reserve as a physiologic measure of stenosis severity. J. Am. Coll. Cardiol. 1990, 15, 459–474. [Google Scholar] [CrossRef]
- Sen, S.; Escaned, J.; Malik, I.S.; Mikhail, G.W.; Foale, R.A.; Mila, R.; Tarkin, J.; Petraco, R.; Broyd, C.; Jabbou, R.; et al. Development and validation of a new adenosine–independent index of stenosis severity from coronary wave-intensity analysis: Results of the ADVISE (ADenosine Vasodilator Independent Stenosis Evaluation) study. J. Am. Coll. Cardiol. 2012, 59, 1392–1402. [Google Scholar] [CrossRef]
- Seitun, S.; De Lorenzi, C.; Cademartiri, F.; Buscaglia, A.; Travaglio, N.; Balbi, M.; Bezante, G.P. CT Myocardial perfusion imaging: A new frontier in cardiac imaging. BioMed Res. Int. 2018, 2018, 7295460. [Google Scholar] [CrossRef]
- Zaman, M.M.; Haque, S.S.; Siddique, M.A.; Banerjee, S.; Ahmed, C.M.; Sharma, A.K.; Rahman, M.F.; Haque, M.H.; Joarder, A.I.; Sultan, A.U.; et al. Correlation between severity of coronary artery stenosis and perfusion defect assessed by SPECT myocardial perfusion imaging. Mymensingh Med. J. 2010, 19, 608–613. [Google Scholar] [PubMed]
- Camici, P.G.; Magnoni, M. How important is microcirculation in clinical practice? Eur. Heart. J. Suppl. 2019, 21, B25–B27. [Google Scholar] [CrossRef] [PubMed]
- Sambuceti, G.; L’Abbate, A.; Marzilli, M. Why should we study the coronary microcirculation? Am. J.-Physiol.-Heart Circ. Physiol. 2000, 279, H2581–H2584. [Google Scholar] [CrossRef]
- George, R.T.; Arbab-Zadeh, A.; Miller, J.M.; Kitagawa, K.; Chang, H.J.; Bluemke, D.A.; Becker, L.; Yousuf, O.; Texter, J.; Lardo, A.C.; et al. Adenosine stress 64- and 256-row detector computed tomography angiography and perfusion imaging: A pilot study evaluating the transmural extent of perfusion abnormalities to predict atherosclerosis causing myocardial ischemia. Circ. Cardiovasc. Imaging 2009, 2, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Cury, R.C.; Magalhães, T.A.; Paladino, A.T.; Shiozaki, A.A.; Perini, M.; Senra, T.; Lemos, P.A.; Rochitte, C.E. Dipyridamole stress and rest transmural myocardial perfusion ratio evaluation by 64 detector-row computed tomography. J. Cardiovasc. Comput. Tomogr. 2011, 5, 443–448. [Google Scholar] [CrossRef]
- Coenen, A.; Rossi, A.; Lubbers, M.M.; Kurata, A.; Kono, A.K.; Chelu, R.G.; Segreto, S.; Dijkshoorn, M.L.; Wragg, A.; van Geuns, R.-J.M.; et al. Integrating CT Myocardial Perfusion and CT-FFR in the Work-Up of Coronary Artery Disease. JACC Cardiovasc. Imaging 2017, 10, 760–770. [Google Scholar] [CrossRef]
- Ihdayhid, A.R.; Sakaguchi, T.; Linde, J.J.; Sørgaard, M.H.; Kofoed, K.F.; Fujisawa, Y.; Hislop-Jambrich, J.; Nerlekar, N.; Cameron, J.D.; Munnur, R.K.; et al. Performance of computed tomography-derived fractional flow reserve using reduced-order modelling and static computed tomography stress myocardial perfusion imaging for detection of haemodynamically significant coronary stenosis. Eur. Heart J. Cardiovasc. Imaging 2018, 19, 1234–1243. [Google Scholar] [CrossRef] [PubMed]
- Lo, E.W.; Menezes, L.J.; Torii, R. On outflow boundary conditions for CT-based computation of FFR: Examination using PET images. Med. Eng. Phys. 2020, 76, 79–87. [Google Scholar] [CrossRef]
- Simakov, S.; Gamilov, T.; Liang, F.; Gognieva, D.G.; Gappoeva, M.K.; Kopylov, P.Y. Numerical evaluation of the effectiveness of coronary revascularization. Russ. J. Numer. Anal. Math. Model. 2021, 36, 303–312. [Google Scholar] [CrossRef]
- Ge, X.; Liu, Y.; Tu, S.; Simakov, S.; Vassilevski, Y.; Liang, F. Model-based analysis of the sensitivities and diagnostic implications of FFR and CFR under various pathological conditions. Int. J. Numer. Methods Biomed. Eng. 2019, 37, e3257. [Google Scholar] [CrossRef] [PubMed]
- Carson, J.M.; Pant, S.; Roobottom, C.; Alcock, R.; Blanco, P.J.; Carlos Bulant, C.A.; Vassilevski, Y.; Simakov, S.; Gamilov, T.; Pryamonosov, R.; et al. Non-invasive coronary CT angiography-derived fractional flow reserve: A benchmark study comparing the diagnostic performance of four different computational methodologies. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3235. [Google Scholar] [CrossRef] [PubMed]
- Carson, J.M.; Roobottom, C.; Alcock, R.; Nithiarasu, P. Computational instantaneous wave-free ratio (IFR) for patient-specific coronary artery stenoses using 1D network models. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3255. [Google Scholar] [CrossRef]
- Gamilov, T.M.; Kopylov, P.Y.; Pryamonosov, R.A.; Simakov, S.S. Virtual fractional flow reserve assessment in patient-specific coronary networks by 1D haemodynamic model. Russ. J. Numer. Anal. Math. Model. 2015, 30, 269–276. [Google Scholar] [CrossRef]
- Lu, M.T.; Ferencik, M.; Roberts, R.S.; Lee, K.L.; Ivanov, A.; Adami, E.; Mark, D.B.; Jaffer, F.A.; Leipsic, J.A.; Douglas, P.S.; et al. Noninvasive FFR Derived From Coronary CT Angiography: Management and Outcomes in the PROMISE Trial. JACC Cardiovasc. Imaging 2017, 10, 1350–1358. [Google Scholar] [CrossRef]
- Feng, Y.; Ruisen, F.; Li, B.; Li, N.; Yang, H.; Liu, J.; Liu, Y. Prediction of fractional flow reserve based on reduced-order cardiovascular model. Comput. Methods Appl. Mech. Eng. 2022, 400, 115473. [Google Scholar] [CrossRef]
- Gamilov, T.; Kopylov, P.; Serova, M.; Syunyaev, R.; Pikunov, A.; Belova, S.; Liang, F.; Alastruey, J.; Simakov, S. Computational analysis of coronary blood flow: The role of asynchronous pacing and arrhythmias. Mathematics 2020, 8, 1205. [Google Scholar] [CrossRef]
- Simakov, S.; Gamilov, T.; Liang, F.; Kopylov, P. Computational analysis of haemodynamic indices in synthetic atherosclerotic coronary netwroks. Mathematics 2021, 9, 2221. [Google Scholar] [CrossRef]
- Vassilevski, Y.; Olshanskii, M.; Simakov, S.; Kolobov, A.; Danilov, A. Personalized Computational Hemodynamics. Models, Methods, and Applications for Vascular Surgery and Antitumor Therapy, 1st ed.; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Vassilevski, Y.V.; Salamatova, V.Y.; Simakov, S.S. On the elasticity of blood vessels in one-dimensional problems of haemodynamics. Comput. Math. Math. Phys. 2015, 55, 1567–1578. [Google Scholar] [CrossRef]
- Coenen, A.; Lubbers, M.M.; Kurata, A.; Kono, A.; Dedic, A.; Chelu, R.G.; Dijkshoorn, M.L.; Rossi, A.; van Geuns, R.M.; Nieman, K. Diagnostic value of transmural perfusion ratio derived from dynamic CT-based myocardial perfusion imaging for the detection of haemodynamically relevant coronary artery stenosis. Eur. Radiol. 2017, 27, 2309–2316. [Google Scholar] [CrossRef] [PubMed]
- Magomedov, K.M.; Kholodov, A.S. Grid–Characteristic Numerical Methods; Nauka: Moscow, Russia, 2018. (In Russian) [Google Scholar]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. Acm 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Grady, L.K. Fast, quality, segmentation of large volumes—Isoperimetric distance trees. In Computer Vision—ECCV 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 449–462. [Google Scholar]
- Danilov, A.; Ivanov, Y.; Pryamonosov, R.; Vassilevski, Y. Methods of graph network reconstruction in personalized medicine. Int. J. Num. Met. Biomed. Engn. 2015, 32, e02754. [Google Scholar] [CrossRef] [PubMed]
- Frangi, A.F.; Niessen, W.J.; Vincken, K.L.; Viergever, M.A. Multiscale vessel enhancement filtering. In Medical Image Computing and Computer-Assisted Intervention—MICCAI’98; Springer: Berlin/Heidelberg, Germany, 1998; pp. 130–137. [Google Scholar]
- Pudney, C. Distance-ordered homotopic thinning: A skeletonization algorithm for 3D digital images. Comput. Vis. Image Underst. 1998, 72, 404–413. [Google Scholar] [CrossRef]
- McCormick, M.; Liu, X.; Jomier, J.; Marion, C.; Ibanez, L. ITK: Enabling reproducible research and open science. Front. Neuroinform. 2014, 8, 13. [Google Scholar] [CrossRef] [PubMed]
- Sugawara, J.; Hayashi, K.; Yokoi, T.; Cortez-Cooper, M.Y.; DeVan, A.E.; Anton, M.A.; Tanaka, H. Brachial–ankle pulse wave velocity: An index of central arterial stiffness? J. Hum. Hypertens 2005, 19, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Charlton, P.H.; Mariscal Harana, J.; Vennin, S.; Li, Y.; Chowienczyk, P.; Alastruey, J. Modeling arterial pulse waves in healthy aging: A database for in silico evaluation of hemodynamics and pulse wave indexes. Am. J.-Physiol. Circ. Physiol. 2019, 317, H1062–H1085. [Google Scholar] [CrossRef]
- Charlton, P.H. Pulse Wave Database. Available online: https://peterhcharlton.github.io/pwdb/pwdb.html (accessed on 31 March 2024).
- Gamilov, T.; Liang, F.; Kopylov, P.; Kuznetsova, N.; Rogov, A.; Simakov, S. Computational analysis of hemodynamic indices based on personalized identification of aortic pulse wave velocity by a neural network. Mathematics 2023, 11, 1358. [Google Scholar] [CrossRef]
- Jin, W.; Chowienczyk, P.; Alastruey, J. Estimating pulse wave velocity from the radial pressure wave using machine learning algorithms. PLoS ONE 2021, 16, e0245026. [Google Scholar] [CrossRef] [PubMed]
- Tavallali, P.; Razavi, M.; Pahlevan, N.M. Artificial Intelligence Estimation of Carotid-Femoral Pulse Wave Velocity using Carotid Waveform. Sci. Rep. 2018, 8, 1014. [Google Scholar] [CrossRef] [PubMed]
- Garcia, D.; Harbaoui, B.; van de Hoef, T.P.; Meuwissen, M.; Nijjer, S.S.; Echavarria-Pinto, M.; Davies, J.E.; Piek, J.J.; Lantelme, P. Relationship between FFR, CFR and coronary microvascular resistance—Practical implications for FFR-guided percutaneous coronary intervention. PLoS ONE 2019, 14, e0208612. [Google Scholar] [CrossRef] [PubMed]
- Fearon, W.F. 14—Invasive Testing. In Chronic Coronary Artery Disease; de Lemos, J.A., Omland, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 194–203. [Google Scholar]
- Morris, P.D.; Ryan, D.; Morton, A.C. Virtual fractional flow reserve from coronary angiography: Modeling the significance of coronary lesions: Results from the VIRTU-1 (VIRTUal Fractional Flow Reserve from Coronary Angiography) study. JACC Cardiovasc. Interv. 2013, 6, 149–157. [Google Scholar] [CrossRef]
- Tu, S.; Barbato, E.; Köszegi, Z.; Yang, J.; Sun, Z.; Holm, N.R.; Tar, B.; Li, Y.; Rusinaru, D.; Wijns, W.; et al. Fractional flow reserve calculation from 3 to dimensional quantitative coronary angiography and TIMI frame count: A fast computer model to quantify the functional significance of moderately obstructed coronary arteries. JACC Cardiovasc. Interv. 2014, 7, 768–777. [Google Scholar] [CrossRef] [PubMed]
- Koo, B.-K.; Erglis, A.; Doh, J.-H.; Daniels, D.V.; Jegere, S.; Kim, H.-S.; Dunning, A.; DeFrance, T.; Lansky, A.; Leipsic, J.; et al. Diagnosis of Ischemia-Causing Coronary Stenoses by Noninvasive Fractional Flow Reserve Computed from Coronary Computed Tomographic Angiograms: Results from the Prospective Multicenter DISCOVER-FLOW (Diagnosis of Ischemia-Causing Stenoses Obtained Via Noninvasive Fractional Flow Reserve) Study. JACC 2011, 58, 1989–1997. [Google Scholar] [PubMed]
- Nakazato, R.; Park, H.-B.; Berman, D.S.; Gransar, H.; Koo, B.-K.; Erglis, A.; Lin, F.Y.; Dunning, A.M.; Budoff, M.J.; Malpeso, J.; et al. Noninvasive fractional flow reserve derived from computed tomography angiography for coronary lesions of intermediate stenosis severity. Circ. Cardiovasc. Imaging 2013, 6, 881–889. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.; Liu, Y.; Yin, Z.; Tu, S.; Fan, Y.; Vassilevski, Y.; Simakov, S.; Liang, F. Comparison of instantaneous wave-free Ratio (iFR) and fractional flow reserve (FFR) with respect to their sensitivities to cardiovascular factors: A computational model-based study. J. Interv. Cardiol. 2020, 2020, 4094121. [Google Scholar] [CrossRef]
- Kern, M.J.; Seto, A.H. Vive la difference: Factors and mechanisms predicting discrepancy between iFR and FFR. Catheter. Cardiovasc. Interv. 2019, 94, 364–366. [Google Scholar] [CrossRef] [PubMed]
- Simakov, S.S.; Gamilov, T.M.; Kopylov, F.Y.; Vasilevskii, Y.V. Evaluation of Hemodynamic Significance of Stenosis in Multiple Involvement of the Coronary Vessels by Mathematical Simulation. Bull. Exp. Biol. Med. 2016, 162, 111–114. [Google Scholar] [CrossRef]
- Morris, P.D.; van de Vosse, F.N.; Lawford, P.V.; Hose, D.R.; Gunn, J.P. “Virtual” (Computed) Fractional Flow Reserve: Current Challenges and Limitations. JACC Cardiovasc. Interv. 2015, 8, 1009–1017. [Google Scholar] [CrossRef] [PubMed]


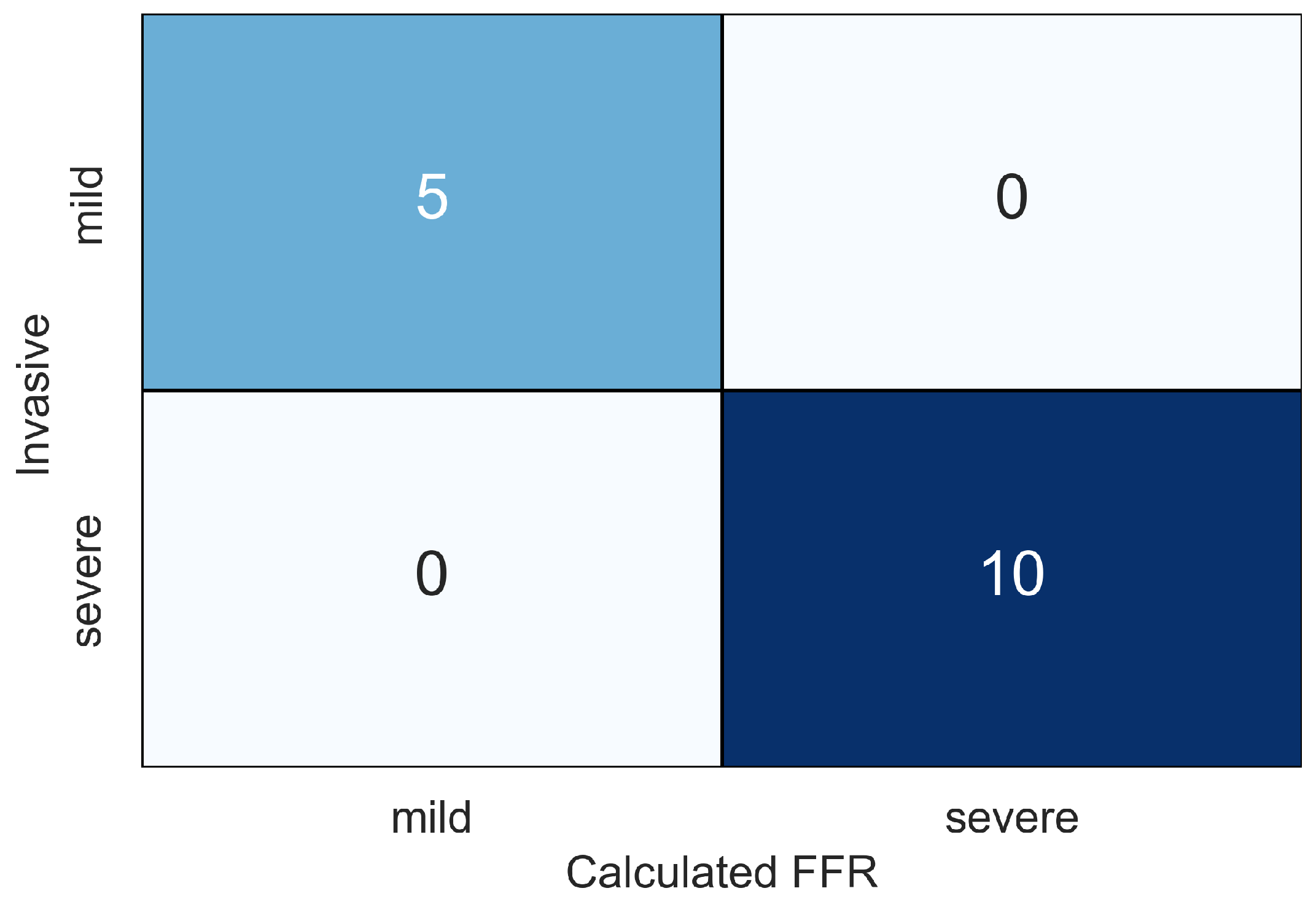

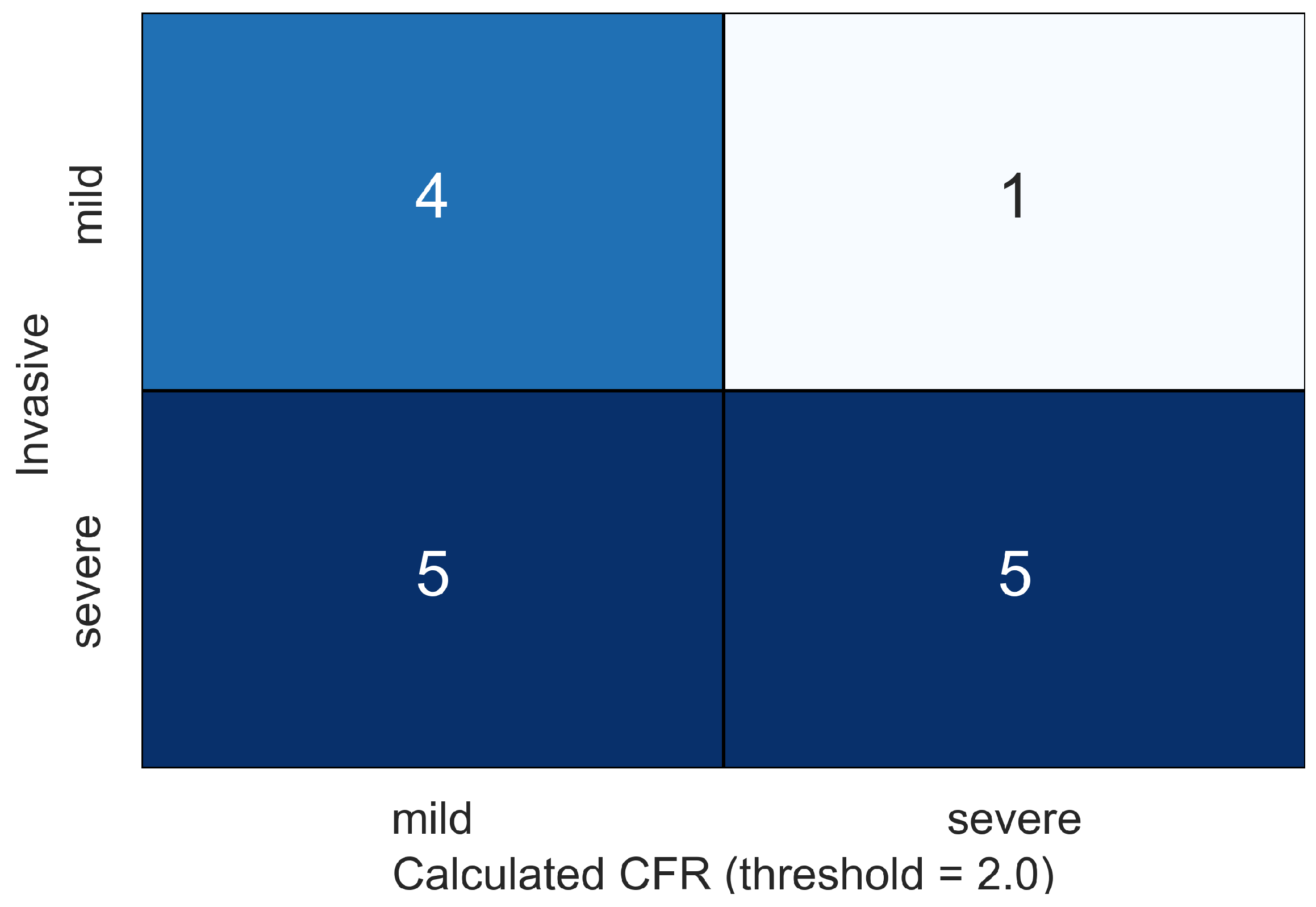
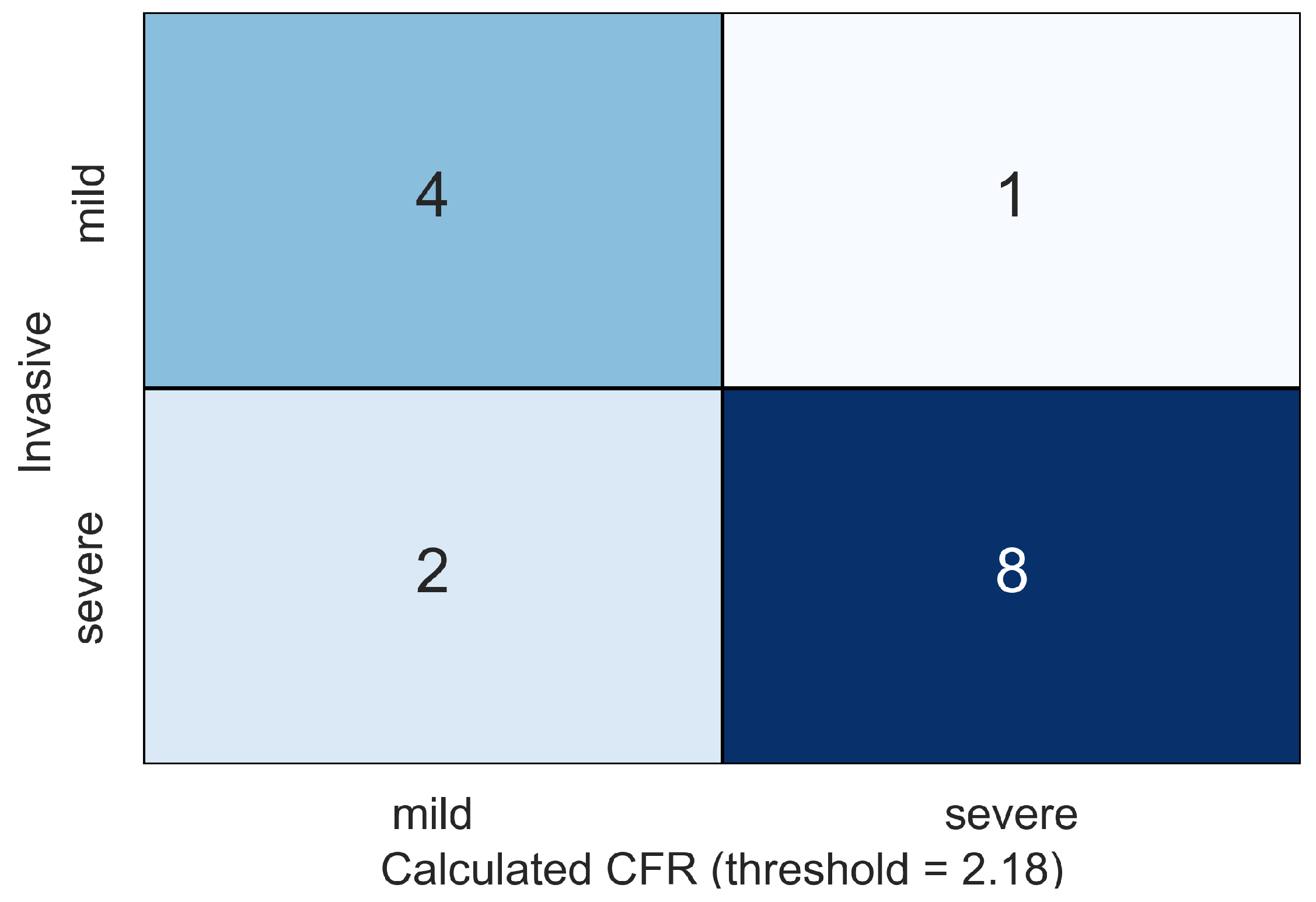


| ID | Age, Years | Sex | , mmHg | , mmHg | , mL | , bpm |
|---|---|---|---|---|---|---|
| 1 | 73 | m | 140 | 80 | 47 | 85 |
| 2 | 67 | m | 130 | 80 | 82 | 80 |
| 3 | 49 | f | 135 | 72 | 56 | 78 |
| 4 | 57 | m | 120 | 70 | 73 | 80 |
| 5 | 60 | f | 120 | 80 | 72 | 60 |
| 6 | 62 | m | 130 | 80 | 83 | 70 |
| 7 | 70 | m | 140 | 80 | 65 | 84 |
| 8 | 70 | m | 135 | 81 | 33 | 89 |
| 9 | 68 | f | 120 | 70 | 53 | 62 |
| 10 | 56 | m | 107 | 76 | 35 | 64 |
| 11 | 50 | m | 120 | 75 | 93 | 57 |
| Patient 1 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LADp (yes) | Before PCI | 0.41 (0.43) | 0.72 | 2.16 |
| After PCI | 0.99 | 0.99 | 2.99 | |
| Long term | 0.98 | 0.99 | 2.72 | |
| Patient 2 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| RCA (no) | Before PCI | 0.32 | 0.37 | 1.21 |
| After PCI | 0.31 | 0.37 | 1.17 | |
| Long term | 0.24 | 0.23 | 1.25 | |
| LAD (yes) | Before PCI | 0.80 (0.81) | 0.81 | 2.18 |
| After PCI | 0.99 | 0.99 | 2.61 | |
| Long term | 0.98 | 0.99 | 3.07 | |
| LCx (no) | Before PCI | 0.20 | 0.29 | 1.13 |
| After PCI | 0.19 | 0.29 | 1.14 | |
| Long term | 0.32 | 0.10 | 1.33 | |
| Patient 3 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LAD (yes) | Before PCI | 0.58 (0.58) | 0.69 (0.53) | 1.91 |
| After PCI | 0.98 | 1.00 | 2.96 | |
| Long term | 0.99 | 1.00 | 2.91 | |
| LCx (yes) | Before PCI | 0.56 | 0.58 | 1.83 |
| After PCI | 0.98 | 1.00 | 3.01 | |
| Long term | 0.99 | 1.00 | 3.89 | |
| Patient 4 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| RCAp (no) | Before PCI | 0.99 | 0.99 | 1.60 |
| After PCI | 0.96 | 0.98 | 2.89 | |
| Long term | 0.96 | 0.97 | 2.94 | |
| RCAd (yes) | Before PCI | 0.50 | 0.57 (0.56) | 1.60 |
| After PCI | 0.95 | 0.98 | 2.89 | |
| Long term | 0.96 | 0.98 | 2.94 | |
| LCx (no) | Before PCI | 0.92 | 0.94 | 1.22 |
| After PCI | 0.92 | 0.94 | 2.53 | |
| Long term | 0.89 | 0.95 | 2.55 | |
| DA (no) | Before PCI | 0.70 | 0.86 | 1.38 |
| After PCI | 0.70 | 0.86 | 2.14 | |
| Long term | 0.86 | 0.93 | 2.63 | |
| Patient 5 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LAD (yes) | Before PCI | 0.75 | 0.87 | 1.60 |
| After PCI | 0.99 | 1.00 | 2.77 | |
| Long term | 0.96 | 0.99 | 3.05 | |
| Patient 6 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LAD (yes) | Before PCI | 0.15 | 0.25 | 1.07 |
| After PCI | 0.98 | 0.99 | 2.83 | |
| Long term | 0.88 | 0.95 | 2.35 | |
| RCA (no) | Before PCI | 0.93 (0.94) | 0.95 | 2.68 |
| After PCI | 0.93 | 0.95 | 2.60 | |
| Long term | 0.95 | 0.96 | 2.84 | |
| OM (no) | Before PCI | 0.75 (0.74) | 0.91 (0.91) | 2.42 |
| After PCI | 0.75 | 0.91 | 2.34 | |
| Long term | 0.76 | 0.90 | 2.31 | |
| Patient 7 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LAD (no) | Before PCI | 0.76 | 0.95 | 1.71 |
| After PCI | 0.76 | 0.96 | 2.10 | |
| Long term | 0.65 | 0.98 | 2.19 | |
| RCA (yes) | Before PCI | 0.12 | 0.23 | 1.68 |
| After PCI | 0.99 | 1.00 | 2.80 | |
| Long term | 0.98 | 0.99 | 3.01 | |
| LCx (yes) | Before PCI | 0.11 | 0.38 | 1.82 |
| After PCI | 0.99 | 0.99 | 3.70 | |
| Long term | 0.99 | 0.99 | 3.39 | |
| Patient 8 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LAD (no) | Before PCI | 0.77 (0.77) | 0.86 | 2.14 |
| After PCI | 0.87 | 0.95 | 2.74 | |
| Long term | 0.87 | 0.89 | 2.71 | |
| RCA (yes) | Before PCI | 0.40 | 0.60 | 1.25 |
| After PCI | 0.98 | 0.99 | 3.00 | |
| Long term | 0.98 | 0.99 | 2.95 | |
| DA (yes) | Before PCI | 0.69 (0.69) | 0.89 | 2.30 |
| After PCI | 0.83 | 0.96 | 2.95 | |
| Long term | 0.86 | 0.93 | 4.9 | |
| Patient 9 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LCx (yes) | Before PCI | 0.64 | 0.74 (0.74) | 1.9 |
| After PCI | 0.99 | 0.99 | 2.75 | |
| Long term | 0.97 | 0.98 | 2.81 | |
| RCA (no) | Before PCI | 0.91 | 0.96 | 2.95 |
| After PCI | 0.96 | 0.96 | 2.92 | |
| Long term | 0.95 | 0.96 | 1.98 | |
| OM (no) | Before PCI | 0.58 | 0.73 | 1.74 |
| After PCI | 0.86 | 0.94 | 2.56 | |
| Long term | 0.88 | 0.95 | 2.74 | |
| Patient 10 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| OM (no) | Before PCI | 0.91 (0.91) | 0.96 | 1.98 |
| After PCI | 0.91 | 0.96 | 1.96 | |
| Long term | 0.96 | 0.99 | 3.34 | |
| RCA (yes) | Before PCI | 0.71 (0.71) | 0.75 | 2.09 |
| After PCI | 0.98 (0.98) | 0.99 | 2.92 | |
| Long term | 0.97 | 0.99 | 3.16 | |
| Patient 11 | ||||
| Vessel (stented) | Period | FFR | iFR | CFR |
| LAD (yes) | Before PCI | 0.52 (0.52) | 0.66 | 1.66 |
| After PCI | 0.93 (0.88) | 0.98 | 2.71 | |
| Long term | 0.99 | 0.99 | 3.03 | |
| OM (yes) | Before PCI | 0.41 (0.40) | 0.66 | 1.50 |
| After PCI | 0.93 | 0.98 | 2.81 | |
| Long term | 0.99 | 0.99 | 3.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamilov, T.; Danilov, A.; Chomakhidze, P.; Kopylov, P.; Simakov, S. Computational Analysis of Hemodynamic Indices in Multivessel Coronary Artery Disease in the Presence of Myocardial Perfusion Dysfunction. Computation 2024, 12, 110. https://doi.org/10.3390/computation12060110
Gamilov T, Danilov A, Chomakhidze P, Kopylov P, Simakov S. Computational Analysis of Hemodynamic Indices in Multivessel Coronary Artery Disease in the Presence of Myocardial Perfusion Dysfunction. Computation. 2024; 12(6):110. https://doi.org/10.3390/computation12060110
Chicago/Turabian StyleGamilov, Timur, Alexander Danilov, Peter Chomakhidze, Philipp Kopylov, and Sergey Simakov. 2024. "Computational Analysis of Hemodynamic Indices in Multivessel Coronary Artery Disease in the Presence of Myocardial Perfusion Dysfunction" Computation 12, no. 6: 110. https://doi.org/10.3390/computation12060110
APA StyleGamilov, T., Danilov, A., Chomakhidze, P., Kopylov, P., & Simakov, S. (2024). Computational Analysis of Hemodynamic Indices in Multivessel Coronary Artery Disease in the Presence of Myocardial Perfusion Dysfunction. Computation, 12(6), 110. https://doi.org/10.3390/computation12060110






