The Effect of Critical Distance in Digital Levelling
Abstract
:1. Introduction
2. An Overview of Levelling Error Theories
3. Basic Formulas for an Analysis of Levelling Accuracy
- Lallemand’s deviations of the cumulative height differences in bidirectional levelling are caused not only by systematic errors but also by random noise.
- The influence of systematic errors defined by Lallemand is valid only within a certain distance (limited length) of the levelling route, beyond which they behave as variable systematic errors dispersed around the mean systematic error.
- Levelling variance is expressed as a root square of the total variance:
4. Analysis of Experimental Data
4.1. Identification of the Type of Elementary Errors
- Bad illumination caused by various intensities of natural light or inhomogeneous light intensity caused by shadows at the levelling bar.
- Atmospheric influences such as turbulences cause blurred images, and refraction, which causes deviation of the line of sight.
- Mechanical influences such as vibrations (deviation of the line of sight), settlement of the instrument and bar and bar centring and inclination.
- Instrumental behaviour such as thermal effects (deviation of the line of sight), interference of code element size and pixels (wrong results at certain distances) and bad compensator function.
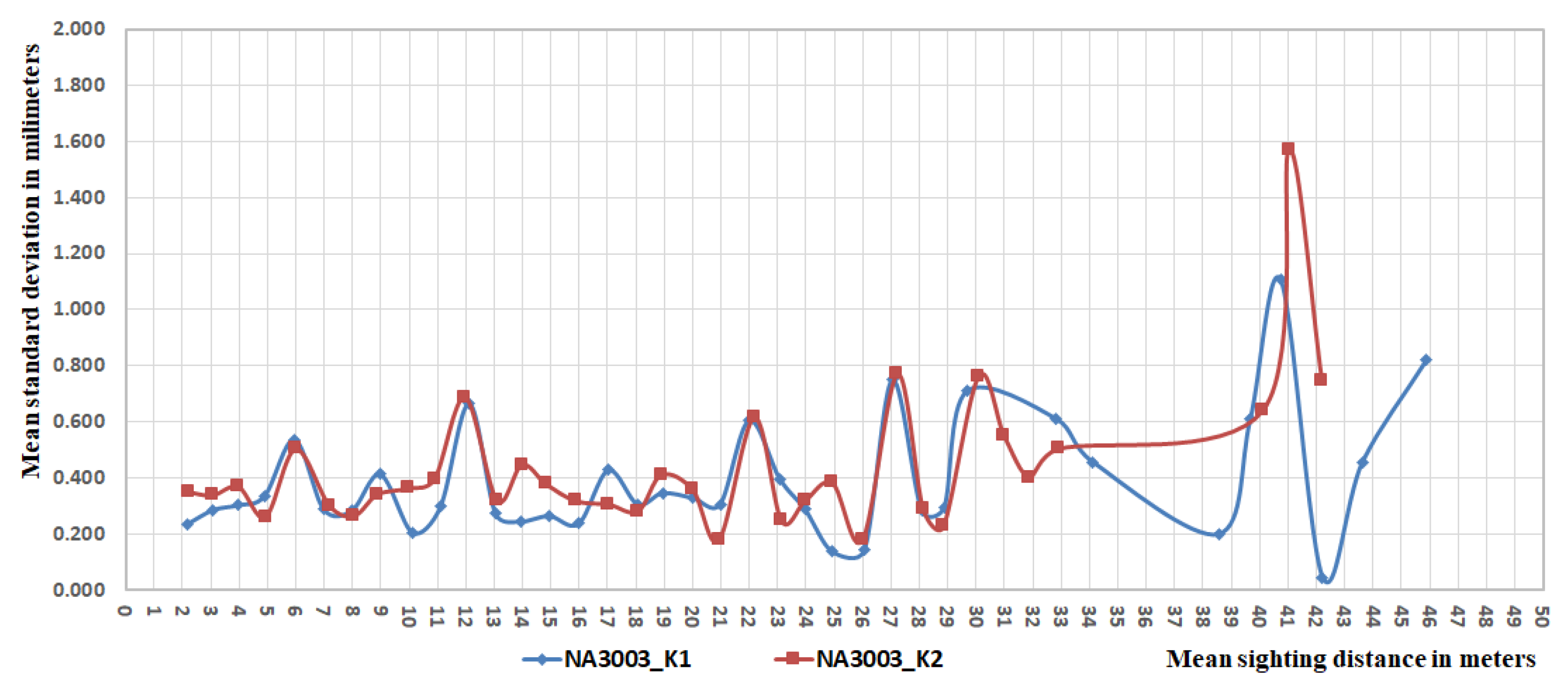
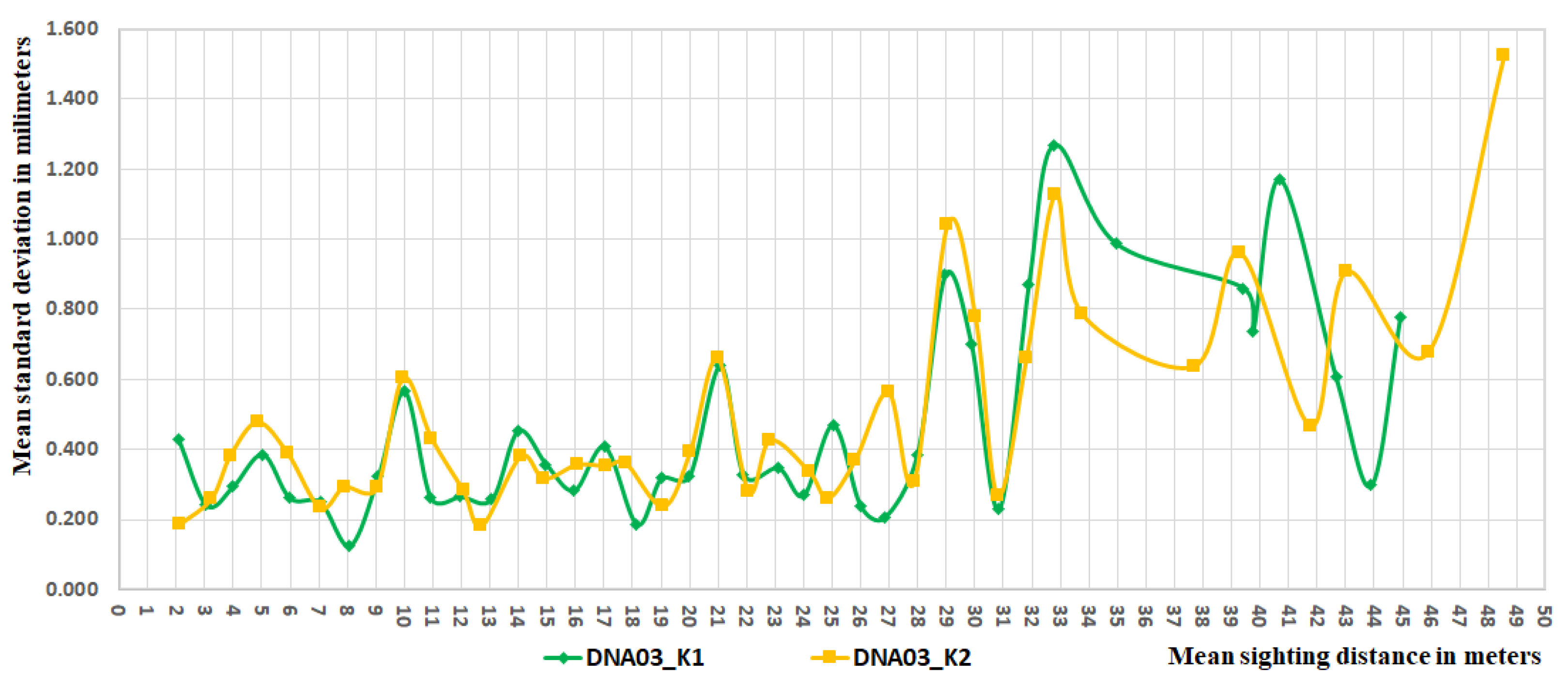
4.2. Detection of the Influence of Critical Sighting Distance
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gassner, G.L.; Ruland, R.; Dix, B. Investigations of digital levels at the SLAC vertical comparator. In Proceedings of the 8th International Workshop on Accelerator Alignment (IWAA2004), CERN, Geneva, Switzerland, 4–7 October 2004. [Google Scholar]
- Gassner, G.L.; Ruland, R.E. Investigations of Levelling Equipment for High Precision Measurements; SLAC, Stanford University: Menlo Park, CA, USA, 2005; pp. 1–8. Available online: https://www.slac.stanford.edu/pubs/slacpubs/12250/slac-pub-12326.pdf (accessed on 18 May 2024).
- Baričevič, S.; Satroveški, T.; Barkovič, D.; Zrinjsti, M. Measuring Uncertainty Analysis of the New Leveling Staff Calibration System. Sensors 2023, 23, 6358. [Google Scholar] [CrossRef] [PubMed]
- Kuchmister, J.; Gołuch, P.; Ćmielewski, K.; Rzepka, J.; Budzyń, G. A functional-precision analysis of the Vertical Comparator for the Calibration of geodetic Levelling Systems. Measurement 2020, 163, 107951. [Google Scholar] [CrossRef]
- Takalo, M.; Rouhiainen, P. On System Calibration of Digital Level. In Proceedings of the 14th International Conference on Engineering Surveying, Zürich, Switzerland, 15–19 March 2004; p. 10. [Google Scholar]
- Woschitz, H.F.K.; Brunner, F.K. Development of a Vertical Comparator for System Calibration of Digital Levels. Osterr. Z. Vermess. Geoinf. 2003, 91, 68–76. [Google Scholar]
- Woschitz, H.; Brunner, F.; Heister, H. Scale Determination of Digital Levelling Systems using a Vertical Comparator. In Fachbeiträge; Graz University of Technology and Bundeswehr University Munich, FIG XXII International Congress: Washington, DC, USA, 2002; zfv 1/2003; pp. 1–13 (2003). [Google Scholar]
- Woschitz, H.; Brunner, F.K. System Calibration of Digital Levels—Experimental Results of Systematic Effects; Graz University of Technology: Graz, Austria; pp. 1–8. Available online: https://www.tugraz.at/fileadmin/user_upload/Institute/IGMS/laboratory/diglevelcal/2002_WHD_FKB_ingeo_reprint.pdf (accessed on 18 May 2024).
- Rekus, D.; Aksamitauskas, V.C.; Giniotis, V. Application of Digital Automatic Levels and Impact of their Accuracy on Construction Measurements. In Proceedings of the 25th International Symposium ISARC, Vilnius, Lithuania, 26–29 June 2008; pp. 625–631. [Google Scholar]
- Sjöberg, L. An Analysis of Systematic and Random Errors in the Swedish Motorized Levelling Technique; Lantmäteriet, National Land Survey: Gävle, Sweden, 1981; 25p, Available online: https://www.lantmateriet.se/globalassets/geodata/gps-och-geodetisk-matning/rapporter/1981-2.pdf (accessed on 18 May 2024).
- Yaprak, S. Accuracy of a Second-Order First-Class Precise Levelling Project, Bollettino di Geofisica Teorica ed Applicata, Vl. 60; Department of Geomatics, Gaziosmanpas a University: Tokat, Turkey, 2019; pp. 39–48. [Google Scholar]
- Zilkovski, D.B. A Priori Estimates of Standard Errors of Levelling Data; National Geodetic Survey: Silver Spring, MD, USA, 1991; 12p, (Nationa Geodetic Survey June 2018). Available online: https://www.ngs.noaa.gov/wp-content/uploads/2018/06/Zilkoski1991-2.pdf (accessed on 19 June 2023).
- Errors in Levelling: Types and Their Correction. Different Types of Errors Encountered in Surveying Operations. Available online: https://testbook.com (accessed on 19 June 2023).
- Böhm, J.; Svoboda, J. Geometrická Nivelase; SNTL: Praha, Czechoslovak Republic, 1960; 288p. [Google Scholar]
- Craymer, M.R. Data Series Analysis and Systematic Effects in Levelling. Master’s Thesis, Department of Civil Engineering University Toronto, Toronto, ON, Canada, 1984; p. 126. Available online: https://gge.ext.unb.ca/Research/GRL/LSSA/Literature/Craymer1984.pdf (accessed on 5 May 2018).
- Craymer, M.R.; Vaníček, P. Further analysis of the 1981 Southern California field test for levelling refraction. J. Geophys. Res. 1986, 91, 9045–9055. [Google Scholar] [CrossRef]
- Saaranen, V. Robotization of Precise Levelling Measurements. Available online: https://mycoordinates.org/robotization-of-precise-levelling-measurements/ (accessed on 5 May 2018).
- Cvetkov, V. Two Adjustments of the Second Levelling of Finland by Using Nonconventional Weights. Available online: https://www.degruyter.com/document/doi/10.1515/jogs-2022-0148/html (accessed on 14 March 2023).
- Elhassan, I. Comparison of indoor and outdoor Accuracy Performance of Optical Automatic, Digital and Laser Levels. IJERT 2022, 11, 6. Available online: https://www.ijert.org/comparison-of-indoor-and-outdoor-accuracy-performance-of-optical-automatic-digital-and-laser-levels (accessed on 14 November 2022).
- Vignal, J. Evaluation de la Précision d’une Méthode de Nivellement; Bulletin Géodesique: Paris, France, 1936; pp. 1–159. [Google Scholar]
- Bomford, G. Geodesy, 3rd ed.; Clarendon Press: Oxford, UK, 1971; 731p. [Google Scholar]
- Ingesand, H. Check of Digital Levels. FIG XXII International Congress, TS5.11 Standards, Quality Assurance and Calibration, Washington, DC, USA. 2002, p. 10. Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig_2002/Ts5-11/TS5_11_ingensand.pdf (accessed on 14 March 2023).
- Ingensand, H. The Evolution of Digital Levelling Techniques—Limitations and New Solutions; FIG Report Activities, Comm 5; FIG Report: Zürich, Switzerland, 1999. [Google Scholar]
- Clarke, B.R. Linear Models: The Theory and Application of Analysis of Variance; Wiley: Hoboken, NJ, USA; Toronto, ON, Canada, 2008; 241p, ISBN 978-0-470-02566-6. [Google Scholar]
- Koch, K.R. Introduction to Bayesian Statistics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007; 249p, ISBN 978-3-540-72723-1. [Google Scholar]
- Niemeier, W. Ausgleichungs-Rechnung; Walter de Gruyter: Berlin, Germany; NewYork, NY, USA, 2002; 407p, ISBN 3-11-014080-2. [Google Scholar]
- Cochran Variance Outlier Test. Available online: https://www.itl.nist.gov/div898/software/dataplot/refman1/auxillar/cochvari.htm (accessed on 12 November 2023).
| Digital Level | Leica NA3003 | Leica DNA03 | ||||||
|---|---|---|---|---|---|---|---|---|
| Observational cycle | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Experimental locality K1 | ||||||||
| Number of intermediate sights | 188 | 188 | 186 | 186 | 178 | 184 | 180 | 185 |
| a | −0.26407 | 0.45756 | −0.69547 | 0.22898 | 0.10331 | 0.31647 | 0.49213 | −0.08210 |
| b | 0.42427 | −0.05980 | 0.69575 | −0.14731 | 0.01063 | −0.05351 | −0.18453 | 0.33137 |
| c | −0.08039 | −0.01296 | −0.01444 | 0.03605 | −0.02693 | −0.02658 | 0.02166 | −0.07674 |
| d | 0.00058 | 0.00070 | 0.00154 | −0.00045 | −0.00002 | 0.00036 | 0.00018 | 0.00093 |
| Experimental locality K2 | ||||||||
| Number of intermediate sights | 197 | 184 | 179 | 182 | 198 | 202 | 195 | 187 |
| a | −0.34173 | 0.07882 | −0.38973 | 0.33365 | 0.29877 | 0.14602 | −0.17625 | 0.29808 |
| b | 0.44522 | 0.24325 | 0.54661 | −0.18530 | −0.17068 | 0.12873 | 0.36003 | 0.08367 |
| c | −0.08643 | −0.06662 | −0.01247 | 0.03919 | 0.03827 | −0.04239 | −0.09337 | −0.01715 |
| d | 0.00087 | 0.00094 | 0.00142 | −0.00036 | −0.00042 | 0.00078 | 0.00138 | 0.00006 |
| Cochran Test | Estimated Unit Variances in mm | Cochran Arguments for α = 0.05 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Leica NA3003 | |||||||||
| Locality | σ12 | σ22 | σ32 | σ42 | σ2max | n | Fα | C | Cu |
| K1 | 0.030 | 0.016 | 0.017 | 0.006 | 0.030 | 32 | 1.85336 | 0.43450 | 0.38187 |
| K2 | 0.021 | 0.029 | 0.019 | 0.005 | 0.029 | 33 | 1.83633 | 0.39036 | 0.37970 |
| Leica DNA03 | |||||||||
| Locality | σ52 | σ62 | σ72 | σ82 | σ2max | n | Fα | C | Cu |
| K1 | 0.005 | 0.012 | 0.012 | 0.017 | 0.017 | 32 | 1.85336 | 0.36314 | 0.38187 |
| K2 | 0.014 | 0.017 | 0.012 | 0.020 | 0.020 | 32 | 1.85336 | 0.31727 | 0.38187 |
| NA3003 | DNA03 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Locality K1 | Locality K2 | Locality K1 | Locality K2 | ||||||||
| Sighting Distance [m] | Number of Sights | Weighted Stdev [mm] | Sighting Distance [m] | Number of Sights | Weighted Stdev [mm] | Sighting Distance [m] | Number of Sights | Weighted Stdev [mm] | Sighting Distance [m] | Number of Sights | Weighted Stdev [mm] |
| 2.186 | 11 | 0.24 | 2.241 | 7 | 0.35 | 2.065 | 25 | 0.43 | 2.151 | 19 | 0.19 |
| 3.090 | 42 | 0.29 | 3.072 | 28 | 0.34 | 3.042 | 25 | 0.24 | 3.256 | 23 | 0.26 |
| 3.976 | 48 | 0.30 | 3.991 | 58 | 0.37 | 3.970 | 37 | 0.29 | 3.911 | 40 | 0.38 |
| 4.901 | 32 | 0.34 | 4.942 | 23 | 0.26 | 5.014 | 34 | 0.39 | 4.863 | 47 | 0.48 |
| 5.962 | 16 | 0.54 | 6.000 | 22 | 0.50 | 5.966 | 33 | 0.26 | 5.920 | 17 | 0.39 |
| 6.990 | 24 | 0.29 | 7.193 | 19 | 0.30 | 7.046 | 20 | 0.25 | 7.062 | 49 | 0.23 |
| 7.980 | 56 | 0.28 | 8.058 | 50 | 0.27 | 8.073 | 23 | 0.13 | 7.907 | 24 | 0.29 |
| 8.994 | 24 | 0.41 | 8.890 | 22 | 0.34 | 9.071 | 15 | 0.32 | 9.044 | 29 | 0.29 |
| 10.130 | 8 | 0.21 | 9.986 | 8 | 0.36 | 9.990 | 22 | 0.56 | 9.956 | 16 | 0.60 |
| 11.109 | 14 | 0.30 | 10.901 | 30 | 0.40 | 10.910 | 23 | 0.26 | 10.964 | 13 | 0.43 |
| 12.121 | 12 | 0.67 | 11.983 | 12 | 0.69 | 11.953 | 21 | 0.27 | 12.078 | 27 | 0.28 |
| 13.048 | 40 | 0.27 | 13.105 | 47 | 0.32 | 13.059 | 25 | 0.26 | 12.720 | 13 | 0.18 |
| 13.925 | 45 | 0.25 | 13.987 | 39 | 0.45 | 13.978 | 17 | 0.45 | 14.082 | 43 | 0.38 |
| 14.948 | 15 | 0.27 | 14.843 | 10 | 0.38 | 14.960 | 24 | 0.36 | 14.907 | 28 | 0.32 |
| 15.983 | 9 | 0.24 | 15.889 | 22 | 0.32 | 15.940 | 39 | 0.28 | 16.059 | 11 | 0.36 |
| 17.032 | 28 | 0.43 | 17.048 | 15 | 0.31 | 17.013 | 18 | 0.41 | 17.092 | 50 | 0.35 |
| 18.057 | 48 | 0.31 | 18.082 | 59 | 0.28 | 18.141 | 27 | 0.19 | 17.761 | 21 | 0.36 |
| 18.942 | 35 | 0.35 | 18.903 | 22 | 0.41 | 18.999 | 19 | 0.32 | 19.086 | 31 | 0.24 |
| 20.018 | 4 | 0.33 | 20.010 | 19 | 0.36 | 19.988 | 27 | 0.32 | 20.024 | 30 | 0.39 |
| 20.974 | 16 | 0.31 | 20.932 | 13 | 0.18 | 21.061 | 24 | 0.64 | 20.995 | 9 | 0.66 |
| 21.991 | 18 | 0.61 | 22.182 | 13 | 0.62 | 21.879 | 13 | 0.33 | 22.063 | 23 | 0.28 |
| 23.077 | 32 | 0.40 | 23.139 | 32 | 0.25 | 23.098 | 20 | 0.35 | 22.825 | 18 | 0.43 |
| 23.965 | 51 | 0.29 | 23.964 | 43 | 0.32 | 23.986 | 16 | 0.27 | 24.197 | 25 | 0.34 |
| 24.922 | 10 | 0.14 | 24.938 | 10 | 0.38 | 25.024 | 20 | 0.47 | 24.857 | 39 | 0.26 |
| 26.062 | 8 | 0.14 | 25.996 | 8 | 0.18 | 25.984 | 27 | 0.24 | 25.808 | 13 | 0.37 |
| 27.041 | 21 | 0.75 | 27.228 | 7 | 0.77 | 26.821 | 11 | 0.21 | 26.971 | 15 | 0.56 |
| 28.081 | 19 | 0.28 | 28.134 | 28 | 0.29 | 27.972 | 22 | 0.38 | 27.877 | 38 | 0.31 |
| 28.877 | 23 | 0.30 | 28.851 | 21 | 0.23 | 28.956 | 9 | 0.90 | 29.051 | 2 | 1.04 |
| 29.678 | 5 | 0.71 | 30.100 | 4 | 0.76 | 29.867 | 15 | 0.70 | 30.021 | 5 | 0.78 |
| 32.833 | 3 | 0.61 | 31.001 | 11 | 0.55 | 30.835 | 12 | 0.23 | 30.805 | 8 | 0.27 |
| 34.124 | 9 | 0.46 | 31.895 | 6 | 0.40 | 31.939 | 6 | 0.99 | 31.811 | 2 | 0.66 |
| Total standard deviation | 0.31 | Total standard deviation | 0.37 | Total standard deviation | 0.35 | Total standard deviation | 0.38 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izvoltova, J.; Chromcak, J.; Bacova, D. The Effect of Critical Distance in Digital Levelling. Computation 2024, 12, 111. https://doi.org/10.3390/computation12060111
Izvoltova J, Chromcak J, Bacova D. The Effect of Critical Distance in Digital Levelling. Computation. 2024; 12(6):111. https://doi.org/10.3390/computation12060111
Chicago/Turabian StyleIzvoltova, Jana, Jakub Chromcak, and Dasa Bacova. 2024. "The Effect of Critical Distance in Digital Levelling" Computation 12, no. 6: 111. https://doi.org/10.3390/computation12060111







