Minimizing Cohort Discrepancies: A Comparative Analysis of Data Normalization Approaches in Biomarker Research

Abstract

Biological variance among samples across different cohorts can pose challenges for the long-term validation of developed models. Data-driven normalization methods offer promising tools for mitigating inter-sample biological variance. We applied seven data-driven normalization methods to quantitative metabolome data extracted from rat dried blood spots in the context of the Rice–Vannucci model of hypoxic–ischemic encephalopathy (HIE) in rats. The quality of normalization was assessed through the performance of Orthogonal Partial Least Squares (OPLS) models built on the training datasets; the sensitivity and specificity of these models were calculated by application to validation datasets. PQN, MRN, and VSN demonstrated a higher diagnostic quality of OPLS models than the other methods studied. The OPLS model based on VSN demonstrated superior performance (86% sensitivity and 77% specificity). After VSN, the VIP-identified potential biomarkers notably diverged from those identified using other normalization methods. Glycine consistently emerged as the top marker in six out of seven models, aligning perfectly with our prior research findings. Likewise, alanine exhibited a similar pattern. Notably, VSN uniquely highlighted pathways related to the oxidation of brain fatty acids and purine metabolism. Our findings underscore the widespread utility of VSN in metabolomics, suggesting its potential for use in large-scale and cross-study investigations.

1. Introduction

The biological condition of an organism profoundly impacts the qualitative and quantitative molecular profiles of its tissues and fluids, thereby facilitating the development of personalized medicine and molecular-profile-based diagnostics [1]. However, factors such as external conditions, variations in age–gender compositions, and the relatively small size of cohorts (often just a few dozen samples) can lead to experimental-condition-associated molecular profile variances that overshadow those attributed to individual subjects [2,3,4]. Considering that biological variances are distinct from technical variances associated with sample preparation and analysis conditions, traditional normalization methods utilizing internal standards or quality control samples may prove ineffective. Instead, data-driven approaches such as median/mean normalization, scaling methods, quantile normalization [5], probabilistic quotient normalization (PQN) [6], variance stabilizing normalization (VSN) [7], median ratio normalization (MRN) [8], and trimmed mean m-value normalization (TMM) [9] offer viable alternatives. Based on recent comparative studies conducted by Brix F. et al. [10] and Chua A.E. et al. [11], it is evident that PQN, VSN, and quantile normalization are three commonly employed methods in the field of metabolomics [10,11] . These normalization techniques have been extensively utilized in various research studies to enhance the accuracy and reliability of metabolomic data analysis.

In this study, we evaluate the effectiveness of these normalization methods in correcting validation dataset discrepancies at the level of training datasets, focusing on the molecular markers of the rat hypoxic–ischemic encephalopathy (HIE) model [12]. This study presents several strengths. First, a controlled and easily manipulable model was utilized to induce hypoxic–ischemic injury, aiming to simplify the study of HIE. This model, proposed by Rice J.E. et al. in 1981, remains the most commonly used pre-clinical model for investigating HIE [13]. Over the last four decades, the Rice–Vannucci model has been employed in various laboratories globally. Nonetheless, it exhibits significant inter-subject variability in terms of the severity of brain damage [14]. Second, the study involved conducting three sequential experiments, where each experiment consisted of both a control group and an HIE group. Furthermore, the inclusion of a standard neonatal screening platform, which involved the quantitative analysis of 57 metabolites in blood spots, enhances the translational potential of this research in neonatology. This approach not only brings the study closer to real-world clinical application but also reduces potential technical variability, specifically that stemming from inter-batch effects.

2. Materials and Methods

The dataset utilized in our study was obtained from Shevtsova et al.’s research [12] which comprised three experimental models. From these models, we selected samples from two experiments: “HIE with sampling at different times”, which consisted of intact rats (n = 10), rats with HIE, and sampling at 6 h post-hypoxia (n = 12) as a train dataset; and “Modeling of therapeutic hypothermia”, comprising intact rats (n = 13) and rats with HIE undergoing recovery for 6 h at 37 °C (n = 14) as a test dataset.

The following methods were used for normalization:

• Normalization by total concentration:

Concentrations from the training set were transformed using the following formula:

$$C_i^{j^{\prime }}=\frac{C_i^j\ast mean\left({{\displaystyle \sum }}_i{C}_i^j\right)}{{{\displaystyle \sum }}_i{C}_i^j}$$

where $C_i^j$ represents the original concentration of compound i in sample j and $C_i^{j^{\prime }}$ represents the normalized concentration of compound i in sample j.

Concentrations from test set were transformed using the following formula:

$$C_i^{j^{\prime }}=\frac{C_i^j\ast mean\left({{\displaystyle \sum }}_i{C}_i^t\right)}{{{\displaystyle \sum }}_i{C}_i^j}$$

where $C_i^j$ represents the original concentration of compound i in sample j in the test set, $C_i^{j^{\prime }}$ is the normalized concentration of compound i in sample j in the test set, and $C_i^t$ is the normalized concentration of compound i in sample t in the training set.

2.

Autoscaling normalization:

Concentrations from the test dataset were transformed using the following formula:

$$C_i^{j^{\prime }}=\frac{C_i^j-mea{n}_i\left(C_i^j\right)}{s{d}_i\left(C_i^j\right)}\ast s{d}_i\left(C_i^t\right)+mea{n}_i\left(C_i^t\right)$$

where $C_i^j$ represents the original concentration of compound i in sample j of the test set, $C_i^{j^{\prime }}$ signifies the normalized concentration of compound i in sample j of the test set, $C_i^t$ indicates the concentration of compound i in sample t of the training set, and $mea{n}_i$ and $s{d}_i$ denote the mean and standard deviation of the concentration of compound i in the test set or training set, respectively.

3.

Quantile normalization:

Quantile normalization is achieved by rearranging and transforming the distribution of values for each species in the samples to match the same distribution across all species [15]. The training dataset underwent normalization using its intrinsic values as the reference for standardization. The normalization process for the test dataset involved a step-by-step procedure. Initially, each sample from the non-normalized test dataset was precisely incorporated into the normalized training dataset. Subsequently, a fresh round of quantile normalization was executed on this merged dataset, which contained both the original test sample and the normalized training dataset. Lastly, the resulting normalized test samples were aggregated to construct the final normalized test dataset.

4.

Probabilistic quotient normalization:

The PQN method hinges on deriving a correction factor, which is uniformly applied to all species within a sample. This correction factor is computed by evaluating the median relative signal intensity of the normalized sample in relation to the signal intensity present in a reference sample or pseudo-sample. This reference sample can either be a quality control sample or the mean/median values of intensity across all samples [6]. The training dataset underwent normalization using median concentration values as the reference. Next, the test dataset was normalized by iteratively adding each sample from the non-normalized test dataset to the normalized training dataset. For each addition, a new PQN was performed with median values as the reference for the newly created dataset (the non-normalized test sample combined with the normalized training dataset). Finally, the normalized test samples were aggregated to construct the normalized test dataset.

5.

Median ratio normalization:

The MRN method shares similarities with PQN, although it distinguishes itself by employing geometric averages of sample concentrations as the reference values for normalization [8]. The training dataset underwent normalization using its own values as the reference point for standardization. Next, the test dataset was normalized by iteratively adding each sample from the non-normalized test dataset to the normalized training dataset. A new median ratio normalization was performed on the combined dataset, containing both the original test sample and the normalized training dataset. Finally, the normalized test samples were aggregated to construct the normalized test dataset.

6.

Trimmed median-m value normalization:

The TMM method involves the utilization of a correction factor, the influence of which is determined by its relative contribution to the overall signal intensity [9,16]. The training dataset underwent normalization using its own values as the reference point for standardization. Next, the test dataset was normalized by iteratively adding each sample from the non-normalized test dataset to the normalized training dataset. A subsequent TMM normalization process was applied to the combined dataset, containing the original test sample with the normalized training data. Finally, the normalized test samples were aggregated to construct the normalized test dataset.

7.

Variance stabilizing normalization.

This approach hinges on determining optimal parameters for glog transformation that effectively reduce signal intensity variation relative to the mean signal intensity. When applied to test samples, these parameters are derived from the pre-existing variation values computed from the training dataset [7,17].

Each normalized training dataset served as the foundation for constructing an Orthogonal Partial Least Squares (OPLS) model, executed through the ropls package [18]) with dependent values (HIE or healthy) acting as pivotal factors. The efficacy of these models was assessed based on the explained variance (R²Y) and predicted variance (Q²Y), alongside sensitivity and specificity metrics derived from validation models applied to the normalized test datasets (Refer to Figure S1 Supplementary). Following this evaluation, blood metabolites exhibiting a variable importance projection (VIP) exceeding 1 were evaluated as potential markers for HIE, with associated metabolite pathways delineated in alignment with prior research [12].

Moreover, the results of principal component analysis (PCA) conducted on raw data sourced from control samples across three distinct experiments [12] were compared with VSN-normalized control samples’ data.

In the context of this study, R 4.3.2 scripts were leveraged within RStudio to execute various normalization techniques. Quantile normalization was administered through the preprocessCore package (https://github.com/bmbolstad/preprocessCore), PQN was implemented using the Rcpm package, MRN was executed utilizing the Ebseq package (https://bioconductor.org/packages/release/bioc/html/EBSeq.html), TMM normalization was performed using the edgeR package [19], and lastly, VSN was executed through the vsn2 package [7].

3. Results

OPLS models constructed using non-normalized data, as well as datasets normalized through total sum of concentrations normalization, probabilistic quotient normalization (PQN), median ratio normalization (MRN), and trimmed mean of m-values (TMM), yielded models of sufficient quality for application in biological studies (with R²Y > 0.5 and Q²Y > 0.4). Notably, the model based on variance stabilizing normalization (VSN) exhibited the highest proportion of prediction-dependent variables and the lowest proportion of described independent variables (

Table 1. The characteristics and diagnostic power of OPLS models constructed using different normalization methods.

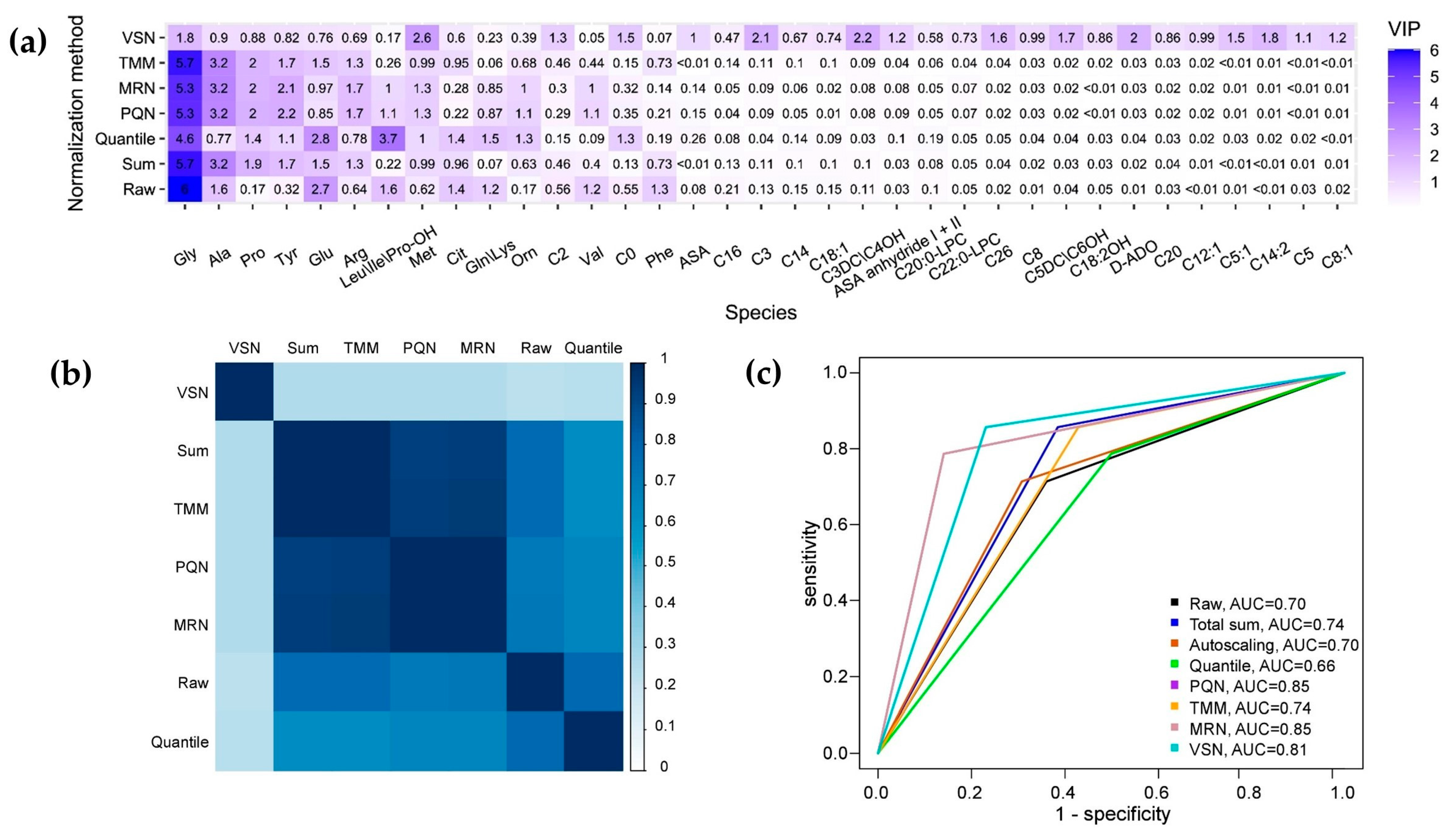
Normalization Method	R2X	R2Y	Q2Y	Accuracy	Sensitivity	Specificity
Raw	0.69	0.68	0.56	0.70	0.71	0.64
Total sum	0.76	0.62	0.47	0.74	0.86	0.57
Autoscaling	0.69	0.68	0.56	0.70	0.71	0.69
Quantile normalization	0.59	0.66	0.38	0.70	0.71	0.69
PQN	0.56	0.72	0.55	0.67	0.79	0.5
MRN	0.58	0.72	0.55	0.85	0.79	0.86
TMM	0.78	0.62	0.47	0.85	0.79	0.86
VSN	0.26	0.89	0.72	0.74	0.86	0.57

).

Normalization greatly influences the variable importance projection (VIP) distribution. The VIP distribution from the non-normalized dataset-based OPLS model significantly differed from the VIP distributions of the normalized datasets (Figure 1a,b). Total sum normalization, TMM normalization, PQN, and MRN resulted in very similar VIP distributions, with almost identical pairs of distributions between total sum normalization and TMM normalization, and between PQN and MRN (Figure 1a,b). The VIP-determined potential biomarkers after VSN differed dramatically from the other normalization methods (Figure 1a,b).

The total sum of concentrations, PQN, MRN, and TMM-normalized test datasets demonstrated higher accuracy compared to the non-normalized datasets. Furthermore, the PQN and MRN normalized test datasets exhibited the highest accuracy, while the VSN normalized dataset showed the highest sensitivity coupled with good specificity, as depicted in Figure 1c and Table 1.

The combination of OPLS model parameters and the quality of the test set validation indicates that VSN is the most promising method for reducing intra-study diagnostic variability. After VSN, fewer variables contribute to the discriminative components PC1 and PC2. In the non-normalized dataset, PC1 described 63% of the variables and PC2 described 21% (Figure S2a), while in the VSN-normalized dataset, PC1 described 36% and PC2 described 18% (Figure S2c). Additionally, VSN resulted in a more balanced loading of features onto the principal components (Figure S2b,d).

Alanine, arginine, and proline metabolism is enriched across all normalization methods, as depicted in Figure S3 and detailed in Table S1. Notably, total sum normalization, TMM normalization, PQN, and MRN resulted in identical sets of statistically significant enriched pathways (p < 0.1). Moreover, VSN highlighted the oxidation of brain fatty acids and purine metabolism pathways as unique findings, underscoring its distinctive contribution. On the other hand, quantile normalization specifically pinpointed the spermine and spermidine biosynthesis pathway.

4. Discussion

VSN, PQN, and MRN emerge as the most effective methods for reducing intra-study variation. However, OPLS models based on VSN-normalized datasets exhibit exceptionally high R²Y and Q²Y values and an extremely low R²X value. Furthermore, VIP distributions from the PQN and MRN normalized datasets differ significantly from those of the VSN-normalized dataset’s OPLS model. The PQN and MRN methods also yield identical R²X, R²Y, and Q²Y parameters for OPLS models. This similarity may be due to the inherent similarities in the principles of PQN and MRN—they both involve calculating correction factors. However, PQN uses mean or median values, while MRN utilizes the average geometric value of feature intensity or concentration within the cohort [6,8]. On the other hand, VSN operates on the principle of glog transformation, yielding different results.

Total sum normalization and TMM normalization also yield similar parameters and quality in OPLS models. These methods leverage information about total signal or concentration, with total sum normalization utilizing the absolute value of the sum in transformation, while TMM employs information about the ratio of each feature to the total sum [9]. TMM is primarily employed in genomics studies, and there is limited information regarding its use in metabolomic studies.

Quantile normalization of the dataset yields the closest VIP distribution in the OPLS model to the one based on raw data, yet the quality and diagnostic potential decrease after normalization (

Table 2. Summary of results from various normalization methods applied.

Normalization Method	Advantages	Disadvantages
Total sum	The OPLS model performed well, displaying a close distribution of the biomarkers’ importance compared to the other normalized datasets (TMM, PQN, MRN)	The OPLS model’s performance is adversely affected by imbalances in the training data, resulting in a lower quality outcome compared to when the model is trained on raw data.
Autoscaling	None	The application of this approach does not lead to an improvement in the validation results with the test data.
Quantile normalization	The distribution of the biomarkers’ importance closely aligns with the distribution observed in the raw data.	The performance of the OPLS model is found to be unsatisfactory, particularly as it demonstrates sensitivity to imbalances within the training data.
PQN	The OPLS model performed well, displaying a close distribution of the biomarkers’ importance compared to the other normalized datasets (TMM, total sum, MRN), resulting in an enhanced validation outcome for the test data	None
MRN	The OPLS model performed well, displaying a close distribution of the biomarkers’ importance compared to the other normalized datasets (TMM, total sum, PQN), resulting in an enhanced validation outcome for the test data	None
TMM	The OPLS model performed well, displaying a close distribution of biomarkers’ importance compared to the other normalized datasets (PQN, total sum, MRN), resulting in an enhanced validation outcome for the test data	The OPLS model’s performance is adversely affected by imbalances in the training data, resulting in a lower quality outcome compared to when the model is trained on raw data.
VSN	The model’s exceptional quality is demonstrated by achieving the highest sensitivity during the validation on test data, indicating its robust performance and reliability in accurately predicting outcomes.	There has been a significant change in the distribution of the biomarkers’ importance, reflecting a notable shift in the key factors influencing the model’s outcomes.

). O’Connell et al. demonstrated that quantile normalization, MRN, and TMM have the potential to obscure the biological structure of samples [20]. However, in our study, MRN yielded better results than quantile normalization, TMM normalization, or using non-normalized data. Similarly, in Abbas-Aghababazadeh F. et al.’s (2018) study, MRN improved the differentiation of RNA sequences from various tomato phenotypes compared to non-normalized, TMM-normalized, and quantile-normalized datasets [21].

VSN, quantile normalization, PQN, and autoscaling were employed in Cook T. et al.’s study for metabolome profile normalization but did not significantly improve sample differentiation between cancer patients (prostate and bladder cancer) and control group patients. This may be attributed to the low number of species analyzed (four species) [22]. Studies by Dressler F.F. et al. and Narasimhan M. et al. indicate that the comparative effectiveness of the VSN and quantile normalization methods depends on the original datasets that were normalized [23,24]. The dataset used for training in our study possessed some imbalance, with 10 samples from the control group and 12 samples from the HIE group. This imbalance may have influenced the normalization process, potentially causing the normalization levels to lean closer to those of the HIE samples rather than the control samples. This imbalance could contribute to the poor specificity observed in validation based on total-sum-normalized, quantile-normalized, and TMM-normalized datasets (Table 2).

Glycine emerges as the predominant marker in six out of seven models and retains significance in the VSN-normalized dataset-based model. This observation aligns with our prior research, which highlighted the correlation between glycine and hypoxic conditions as well as brain ischemia [12]. Similarly, alanine stands out as a crucial marker in five of the seven models, with the associated alanine metabolism pathway consistently represented across all analyses. Notably, the presence of alanine aminotransferase within this pathway underscores its significance as a marker for HIE. Furthermore, the arginine and proline metabolism pathway consistently demonstrates statistically significant enrichment across all normalization methods, signaling its potential relevance to hypoxic injury as indicated in previous studies [25,26]. While the oxidation of branched-chain fatty acids and purine metabolism pathways emerge as uniquely enriched pathways in the VSN-normalized dataset, it is worth noting that oxidative stress has been implicated in hypoxic conditions [27]. Several studies suggest a potential link between purine metabolism and hypoxia, further emphasizing the sophisticated connections that exist between blood metabolites and responses to hypoxic conditions [28,29].

Overall, the comprehensive exploration of these diverse normalization strategies unveiled specific metabolic pathways, shedding light on the interplay between normalization techniques and the identification of enriched pathways in the context of metabolite analysis.

5. Limitations, Future Prospects, and Suggestions

This study is subject to certain limitations that warrant consideration. Firstly, it focused solely on a single task (HIE/health), utilizing only two distinct datasets for analysis. This narrow scope may restrict the generalizability of the findings and the applicability of the normalization methods across diverse biological contexts. Furthermore, the balance of “case/control” samples is a critical factor in ensuring the representativeness and reliability of the data. It is imperative to acknowledge the potential impact of sample proportion imbalance on the quality of normalization procedures. Addressing these limitations and conducting further studies to evaluate the effects of sample proportions on normalization quality are crucial steps toward enhancing the robustness and reliability of data normalization practices in routine research and clinical applications.

Determining the best method for a particular type of biological sample can be a complex process that requires careful consideration of various factors that can influence the experimental outcomes. When it comes to normalization methods in biological sample analysis, several key factors should be taken into account to reach a reliable conclusion: sample features, analytical technique, biological variability, infrastructure and resources, and statistical considerations. In particular, the statistical assumptions underlying different normalization methods should be carefully evaluated. Some methods may introduce bias or distort the data if they are applied incorrectly or if the data do not meet the method’s assumptions. To come to a conclusion about the best method for a particular type of biological sample, it is essential to conduct a thorough evaluation of these factors and perform a meta-analysis to assess the performance of different normalization approaches. Ultimately, the choice of normalization method should be driven by the specific characteristics of the samples and the research objectives to ensure accurate and reliable results.

6. Conclusions

Evaluating the quality of normalization methods in biological sample analysis involves considering several key points. Firstly, the quality of the created model is crucial, with VSN showing promise by generating the best model based on OPLS-model metrics. Secondly, the robustness of the model across datasets is essential for reliability, and methods such as VSN, PQN, and MRN demonstrate the ability to create reliable models across different datasets. Finally, the adequacy in capturing changes in biological marker patterns is a significant factor to consider. VSN has been shown to significantly alter the distribution of biomarker importance, potentially revealing enriched pathways associated with specific conditions like HIE.

In comparison, the PQN and MRN methods maintain a closer alignment in biomarker distribution between themselves and the raw distribution, highlighting their consistency in handling biomarker patterns. In conclusion, VSN emerges as an attractive choice for routine use in reducing between-study biological variation due to its ability to create robust models, significant impact on biomarker importance distribution, and potential for uncovering relevant biological pathways associated with specific conditions like HIE.