Numerical Simulation and Comparison of Different Steady-State Tumble Measuring Configurations for Internal Combustion Engines
Abstract
:1. Introduction
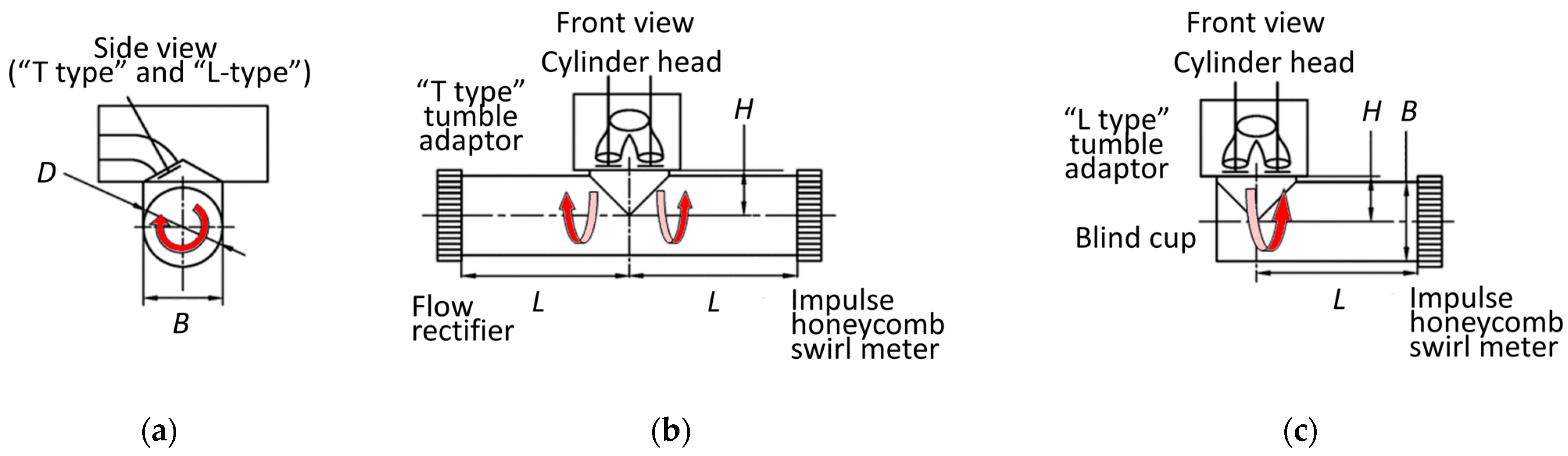
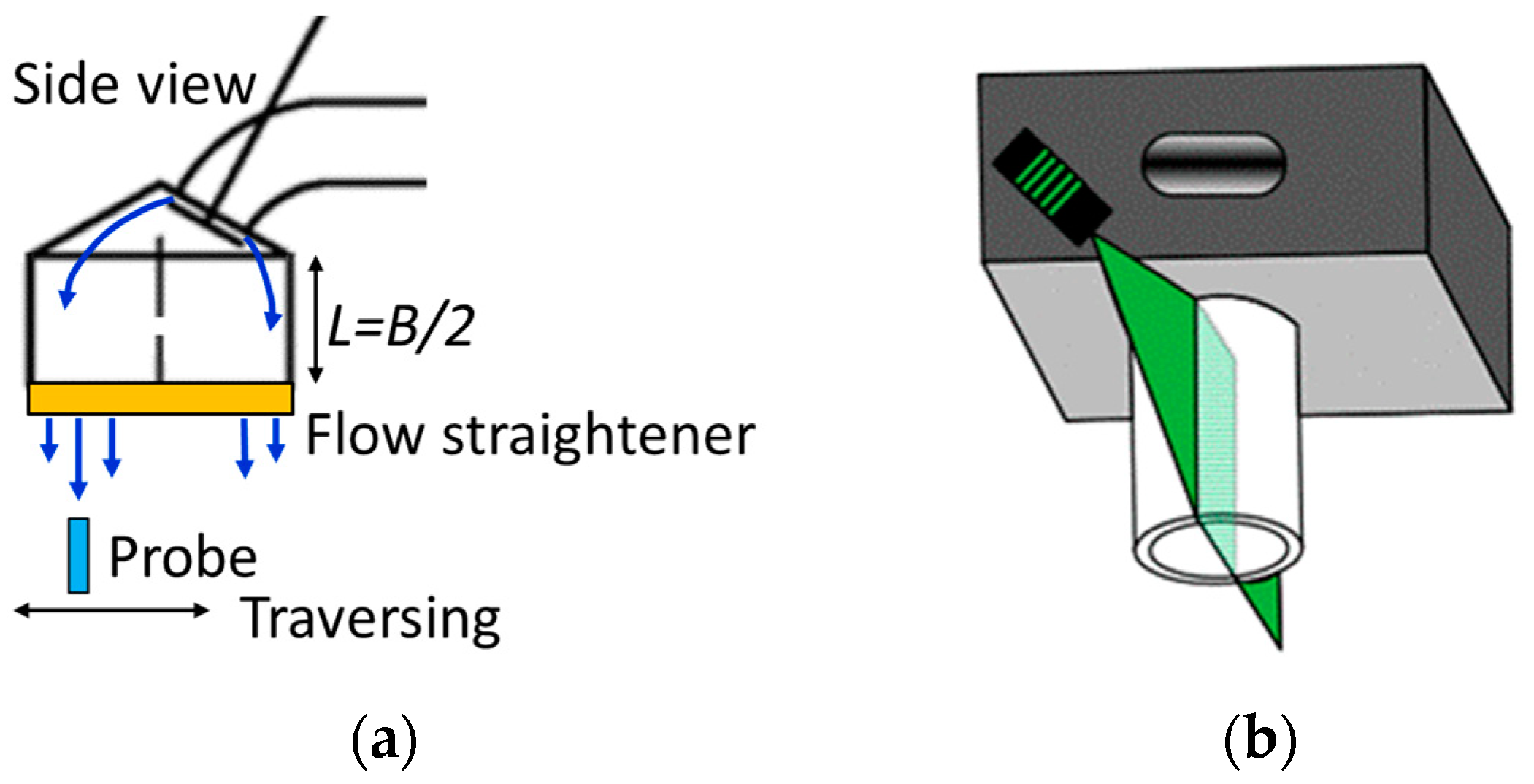
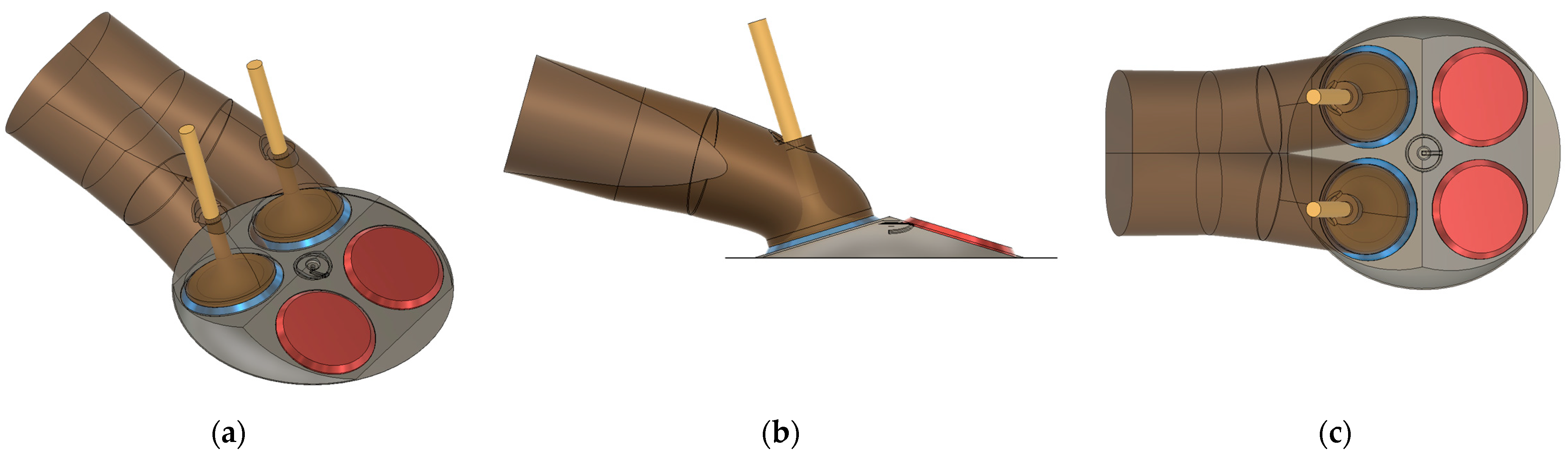
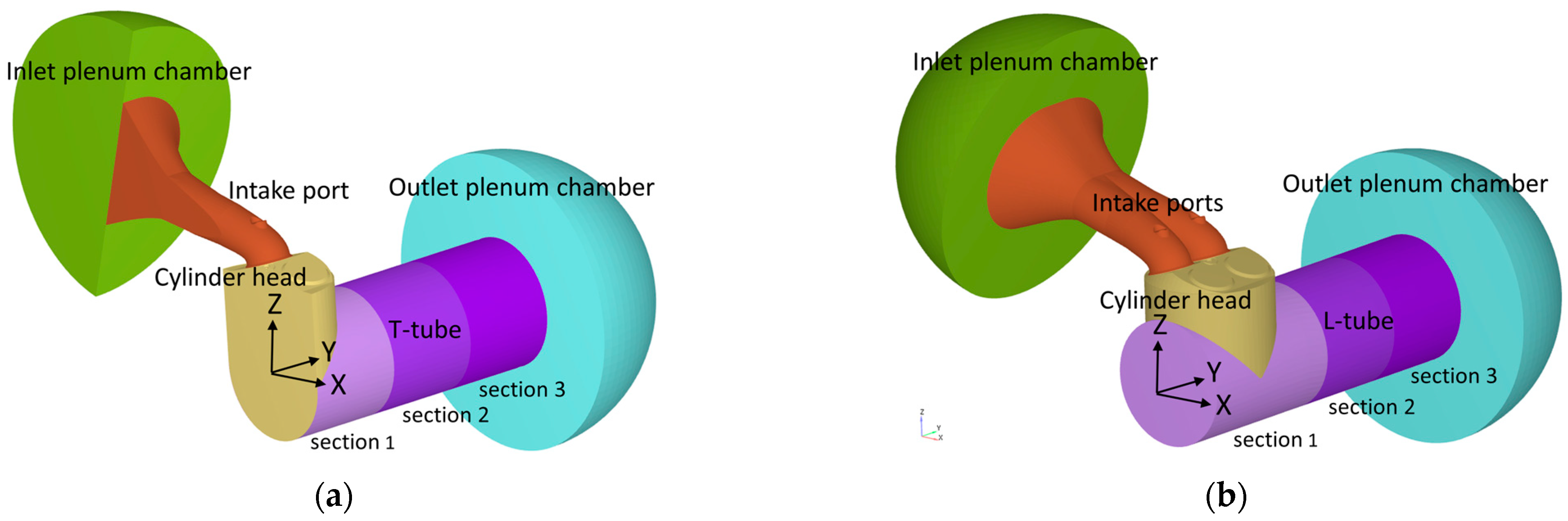
2. Materials and Methods
3. Results
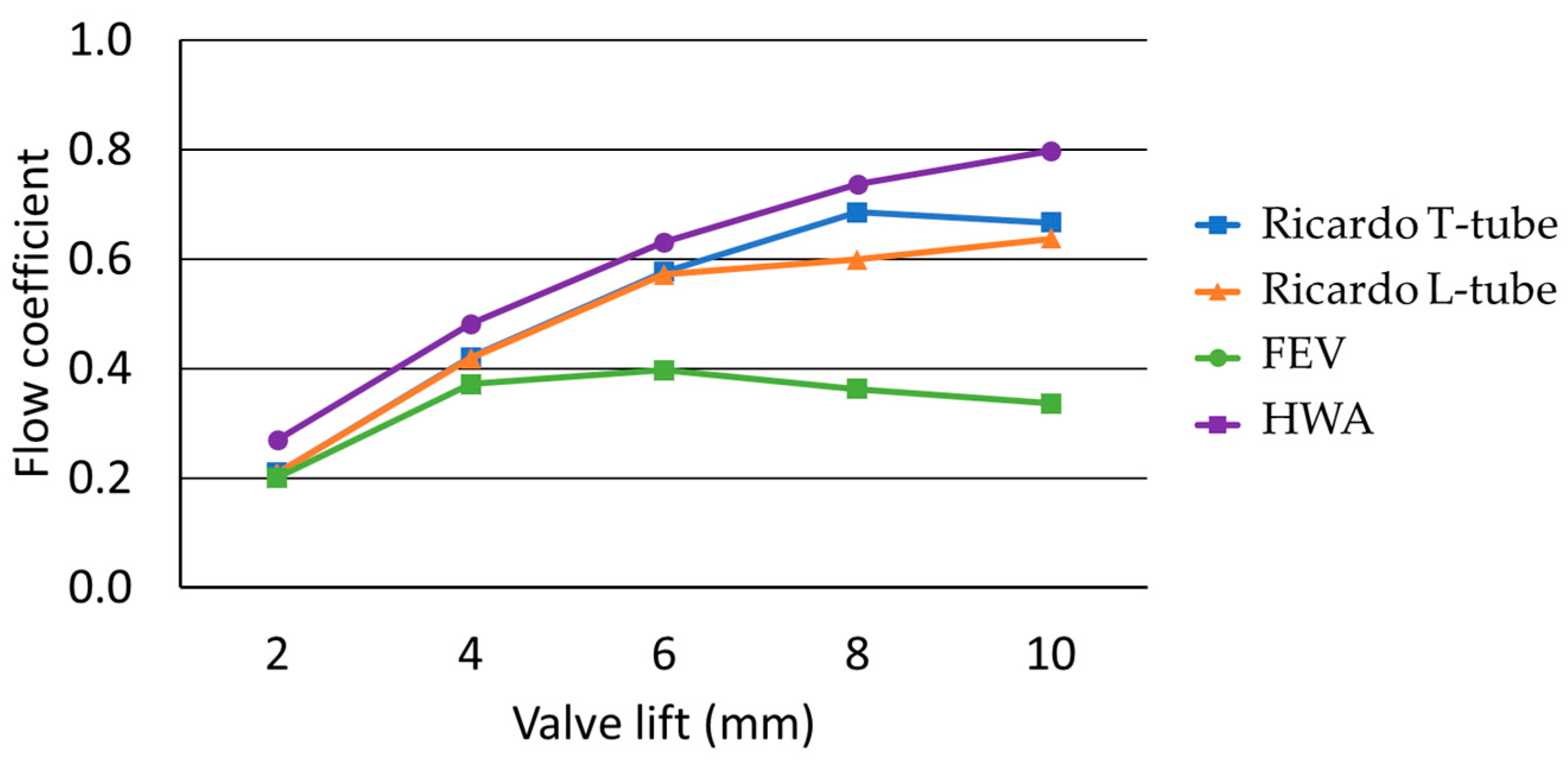
3.1. Flow Coefficients and Tumble Ratios
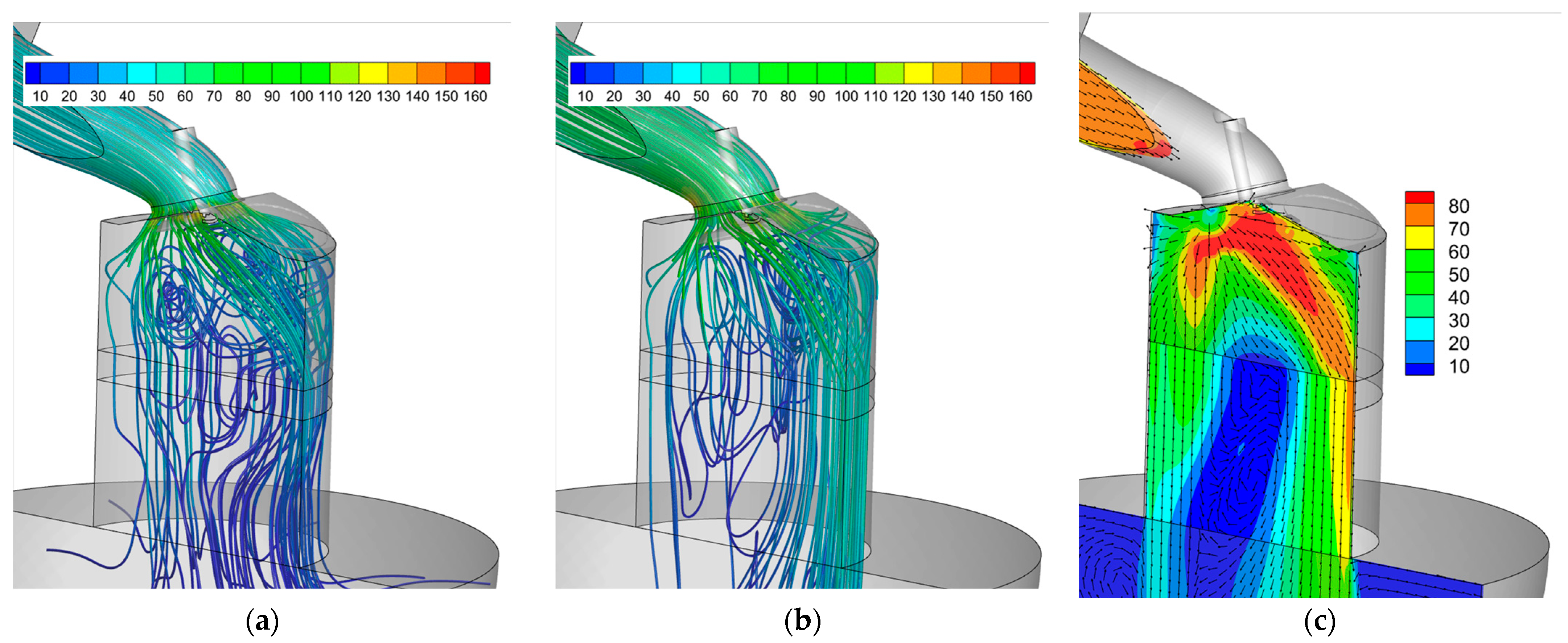
3.2. HWA Configuration
3.3. Ricardo T-Tube and L-Tube Configurations
3.4. FEV Configuration
4. Discussion
5. Conclusions
- The Ricardo L-tube configuration generates a non-symmetrical flow field inside the cylinder even if the cylinder head and the inlet valve lifts are symmetrical.
- Both Ricardo configurations, in place of the piston, have the exit tubes’ bottom side, which affects the angular momentum of the flow.
- The FEV configuration is technically more demanding than the Ricardo configurations, having the rotating paddle wheel inside the cylinder. The use of the rotating paddle wheel has also the disadvantage that affects the flow field. The small diameter of the exit tube restricts the flow. On the other hand, it allows for the use of a real production piston and can assess how its crown shape affects the tumble.
- All integral methods can be effectively used only when the axis of the tumbling flow inside the cylinder is parallel with the exit tubes or the axis of the rotating paddle wheel. That is not always the case (i.e., when the lift of the inlet valves is not equal or one of the inlet valves is deactivated).
- HWA measurements for tumble ratio estimation require more expensive equipment and effort. The flow field inside the cylinder in regions away from the cylinder head is not relevant with the flow field inside the cylinder of a motored engine.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ibham, V.; Mohd Farid Muhamad, S.; Mohd Azman, A.; Zulkarnain Abdul, L.; Mohd Rozi Mohd, P.; Djati Wibowo, D.; Djamari, D.W. Future Direction of Microalgae Biodiesel in Indonesia. J. Adv. Res. Appl. Sci. Eng. Technol. 2021, 25, 1–6. [Google Scholar] [CrossRef]
- Gheidan, A.A.S.; Abdul Wahid, M.; Abdul Munir, F.; Anthony Chukwunonso, O. Feasibility Study of Bio-fuel As a Sustainable Product of Biomass: An Overview of Its Fundamentals, Application and Environmental Impact. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 88, 106–122. [Google Scholar] [CrossRef]
- Mohsin, R.; Majid, Z.A.; Shihnan, A.H.; Nasri, N.S.; Sharer, Z.; Mat, R.C. Effects of Multi-Variant Biofuel on Engine Performance and Exhaust Emission of DDF Engine System. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 6, 1–18. [Google Scholar]
- Wouters, C.; Lehrheuer, B.; Pischinger, S.; Seifert, P.; Raabe, T.; Kolbeck, M.; Rausch, B.; Menger, L.; Kulzer, A.C. Evaluation of Synthetic Gasoline Fuels and Alcohol Blends in a Spark-Ignition Engine. SAE Int. J. Fuels Lubr. 2022, 15, 333–347. [Google Scholar] [CrossRef]
- Shadidi, B.; Najafi, G.; Yusaf, T. A Review of Hydrogen as a Fuel in Internal Combustion Engines. Energies 2021, 14, 6209. [Google Scholar] [CrossRef]
- Sementa, P.; de Vargas Antolini, J.B.; Tornatore, C.; Catapano, F.; Vaglieco, B.M.; Sánchez, J.J.L. Exploring the potentials of lean-burn hydrogen SI engine compared to methane operation. Int. J. Hydrogen Energy 2022, 2, 5044–5056. [Google Scholar] [CrossRef]
- Mat Taib, N.; Abu Mansor, M.R.; Wan Mahmood, W.M.F. Simulation of Hydrogen Fuel Combustion in Neon-oxygen Circulated Compression Ignition Engine. J. Adv. Res. Numer. Heat Transf. 2020, 3, 25–36. [Google Scholar] [CrossRef]
- Hill, P.G.; Zhang, D. The effects of swirl and tumble on combustion in spark-ignition engines. Prog. Energy Combust. Sci. 1994, 20, 373–429. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.; Kwon, H.; Lee, J.; Park, S. Effects of the swirl ratio and injector hole number on the combustion and emission characteristics of a light duty diesel engine. Appl. Therm. Eng. 2018, 142, 68–78. [Google Scholar] [CrossRef]
- Wang, G.; Yu, W.; Li, X.; Yang, R. Influence of fuel injection and intake port on combustion characteristics of controllable intake swirl diesel engine. Fuel 2020, 262, 116548. [Google Scholar] [CrossRef]
- Heywood, J. Internal Combustion Engine Fundamentals; McGraw-Hill Education: Berkshire, UK, 2018. [Google Scholar]
- Kim, M.J.; Lee, S.H.; Kim, W.T. Correlation study of the measured tumble ratios using three different methods: Steady flow rig; 2-dimensional PIV; and 3-dimensional PTV water flow rig. Int. J. Automot. Technol. 2006, 7, 441–448. [Google Scholar]
- Kaplan, M. Influence of swirl, tumble and squish flows on combustion characteristics and emissions in internal combustion engine-review. Int. J. Automot. Eng. Technol. 2019, 8, 83–102. [Google Scholar] [CrossRef]
- Duronio, F.; Vita, A.D.; Allocca, L.; Anatone, M. Gasoline direct injection engines—A review of latest technologies and trends. Part 1: Spray breakup process. Fuel 2020, 265, 116948. [Google Scholar] [CrossRef]
- Saw, O.P.; Addepalli, S.K.; Mallikarjuna, J.M. (Eds.) Effects of Cylinder Head Geometry on Mixture Stratification, Combustion and Emissions in a GDI Engine—A CFD Analysis. International Powertrains, Fuels & Lubricants Meeting; SAE International: Warrendale PA, USA, 2019. [Google Scholar]
- Jamil, A.; Baharom, M.B.; Aziz, A.R.A. IC engine in-cylinder cold-flow analysis—A critical review. Alex. Eng. J. 2021, 60, 2921–2945. [Google Scholar] [CrossRef]
- El Adawy, M.; Heikal, M.R.; A Aziz, A.R. Experimental Investigation of the In-Cylinder Tumble Motion inside GDI Cylinder at Different Planes under Steady-State Condition using Stereoscopic-PIV. J. Appl. Fluid Mech. 2019, 12, 41–49. [Google Scholar] [CrossRef]
- El Adawy, M.; Heikal, M.R.; Aziz, A.A.R.; Siddiqui, M.; Munir, S. Characterization of the Inlet Port Flow under Steady-State Conditions Using PIV and POD. Energies 2017, 10, 1950. [Google Scholar] [CrossRef]
- Mohammadebrahim, A.; Hannani, S.; Shafii, M. Investigation into the effect of intake port geometric parameters and blockage on flow coefficient and in-cylinder flow: Application to engine port design. Sci. Iran. 2014, 21, 438–448. [Google Scholar]
- El-Adawy, M.; Heikal, M.R.; Aziz, A.R.A.; Siddiqui, M.I.; Wahhab, H.A.A. Experimental study on an IC engine in-cylinder flow using different steady-state flow benches. Alex. Eng. J. 2017, 56, 727–736. [Google Scholar] [CrossRef]
- Ramajo, D.; Zanotti, A.; Nigro, N. In-cylinder flow control in a four-valve spark ignition engine: Numerical and experimental steady rig tests. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2011, 225, 813–828. [Google Scholar] [CrossRef]
- Ramajo, D.E.; Nigro, N.M. In-Cylinder Flow Computational Fluid Dynamics Analysis of a Four-Valve Spark Ignition Engine: Comparison between Steady and Dynamic Tests. J. Eng. Gas Turbines Power 2010, 132, 052804. [Google Scholar] [CrossRef]
- Wahono, B.; Setiawan, A.; Lim, O. Effect of the intake port flow direction on the stability and characteristics of the in-cylinder flow field of a small motorcycle engine. Appl. Energy 2021, 288, 116659. [Google Scholar] [CrossRef]
- Xu, H. (Ed.) Some Critical Technical Issues on the Steady Flow Testing of Cylinder Heads; SAE Technical Paper Series; SAE International: Warrendale PA, USA, 2001. [Google Scholar]
- Ballapu, H.; Mallikarjuna, J.M. Effect of piston shape on in-cylinder flows and air–fuel interaction in a direct injection spark ignition engine—A CFD analysis. Energy 2015, 81, 361–372. [Google Scholar]
- Baratta, M.; Misul, D.; Spessa, E.; Viglione, L.; Carpegna, G.; Perna, F. Experimental and numerical approaches for the quantification of tumble intensity in high-performance SI engines. Energy Convers. Manag. 2017, 138, 435–451. [Google Scholar] [CrossRef]
- Wahono, B.; Setiawan, A.; Lim, O. Experimental study and numerical simulation on in-cylinder flow of small motorcycle engine. Appl. Energy 2019, 255, 113863. [Google Scholar] [CrossRef]
- Yang, X.; Kuo, T.-W.; Guralp, O.; Grover, R.O.; Najt, P. (Eds.) In-Cylinder Flow Correlations Between Steady Flow Bench and Motored Engine Using Computational Fluid Dynamics. J. Eng. Gas Turbines Power 2017, 139, 072802. [Google Scholar] [CrossRef]
- Ricardo, J. Steady State Flowbench Port Performance Measurement and Analysis Techniques; Report DP93/0704; 1993. [Google Scholar]
- Richards, K.J.; Senecal, P.K.; Pomraning, E. CONVERGE 3.0*; Convergent Science: Madison, WI, USA, 2022. [Google Scholar]
- Theodorakakos, A. Numerical Study of Different Steady-State Flow Rigs for the Tumble Motion Characterization of a Four-Valve Cylinder Head. CFD Lett. 2023, 15, 18–31. [Google Scholar] [CrossRef]
- Menter, F. (Ed.) Zonal Two Equation k-w Turbulence Models For Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1993. [Google Scholar]


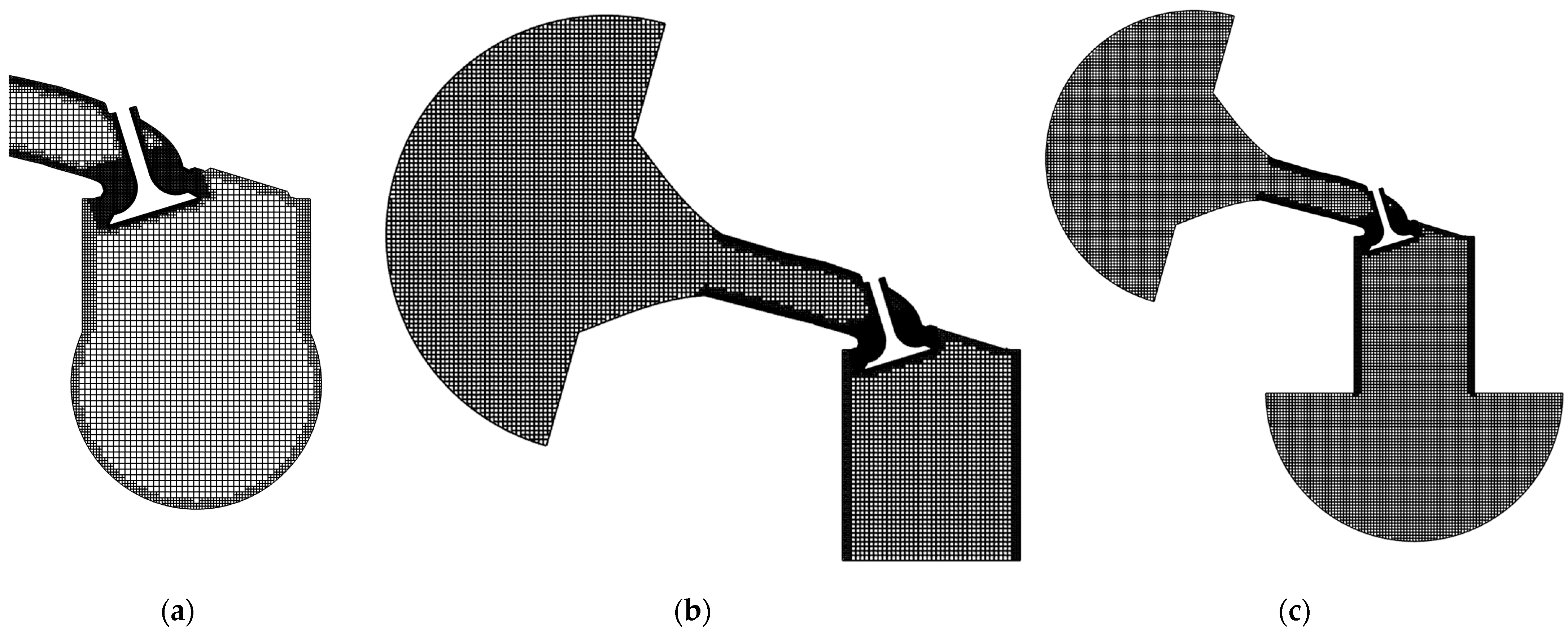





| Stroke (mm) | 89.7 |
| Bore (mm) | 87.5 |
| Pentroof angle (deg) | 17° |
| Diameter of inlet valves (mm) | 32 |
| Angle of valve’s seat (deg) | 45° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Theodorakakos, A. Numerical Simulation and Comparison of Different Steady-State Tumble Measuring Configurations for Internal Combustion Engines. Computation 2024, 12, 138. https://doi.org/10.3390/computation12070138
Theodorakakos A. Numerical Simulation and Comparison of Different Steady-State Tumble Measuring Configurations for Internal Combustion Engines. Computation. 2024; 12(7):138. https://doi.org/10.3390/computation12070138
Chicago/Turabian StyleTheodorakakos, Andreas. 2024. "Numerical Simulation and Comparison of Different Steady-State Tumble Measuring Configurations for Internal Combustion Engines" Computation 12, no. 7: 138. https://doi.org/10.3390/computation12070138
APA StyleTheodorakakos, A. (2024). Numerical Simulation and Comparison of Different Steady-State Tumble Measuring Configurations for Internal Combustion Engines. Computation, 12(7), 138. https://doi.org/10.3390/computation12070138




