Computational Analysis of the Performance Characteristics of a Supercritical CO2 Centrifugal Compressor
Abstract
:1. Introduction
2. Materials and Methods
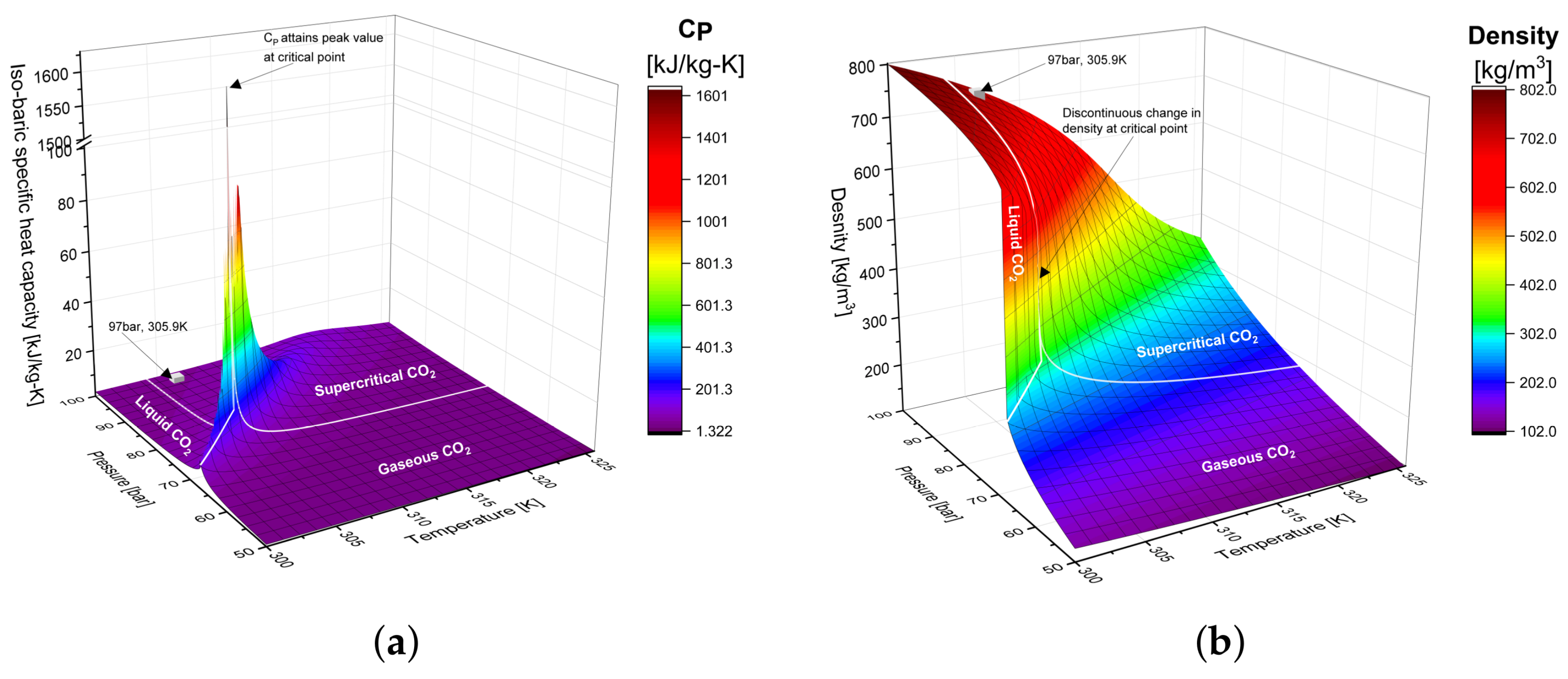
2.1. Real Gas Property Table
2.2. Compressor Geometry and Mesh
2.3. Numerical Methodology
3. Validation
4. Results and Discussion
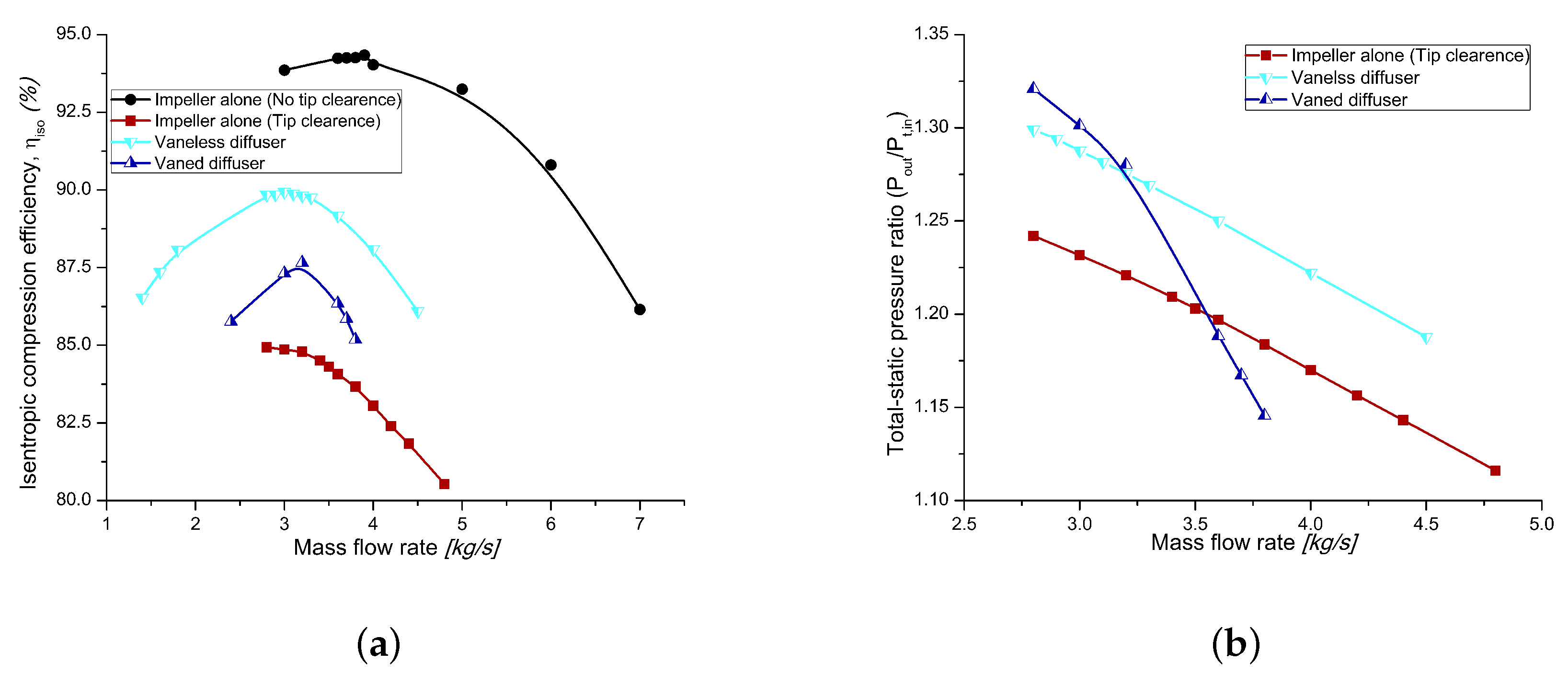
4.1. Effect of Tip Clearance
4.2. Effect of Diffuser
4.3. Flow Field Near the Impeller and Diffuser Interface
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cabeza, L.F.; de Gracia, A.; Fernández, A.I.; Farid, M.M. Supercritical CO2 as heat transfer fluid: A review. Appl. Therm. Eng. 2017, 125, 799–810. [Google Scholar] [CrossRef]
- Ayub, Z. Recent developments in CO2 heat transfer. Heat Transf. Eng. 2005, 26, 3–6. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Y.; Zhou, Y.; Chen, J.; Huang, Y.; Wang, J. Experimental study of supercritical CO2 leakage behavior from pressurized vessels. Energy 2018, 150, 342–350. [Google Scholar] [CrossRef]
- Tokanai, H.; Ohtomo, Y.; Horiguchi, H.; Harada, E.; Kuriyama, M. Heat transfer of supercritical CO2 flow in natural convection circulation system. Heat Transf. Eng. 2010, 31, 750–756. [Google Scholar] [CrossRef]
- Shu, G.; Shi, L.; Tian, H.; Chang, L. Comparison and Selection Research of CO2-Based Transcritical Rankine Cycle Using for Gasoline and Diesel Engine’s Waste Heat Recovery. Heat Transf. Eng. 2017, 7632, 1–15. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, Z.; Tian, H. A review of transcritical carbon dioxide heat pump and refrigeration cycles. Energy 2013, 55, 156–172. [Google Scholar] [CrossRef]
- Lee, J.; Baik, S.; Cho, S.K.; Cha, J.E.; Lee, J.I. Issues in performance measurement of CO2 compressor near the critical point. Appl. Therm. Eng. 2016, 94, 111–121. [Google Scholar] [CrossRef]
- Assael, M.J. The importance of thermophysical properties in optimum design and energy saving. In Energy and Environment; Mori, Y.H., Ohnishi, K., Eds.; Springer: Tokyo, Japan, 2001; pp. 162–178. [Google Scholar]
- Hosseini, M.; Sun, Z.; He, X.; Zheng, X. Effects of Radial Gap Ratio between Impeller and Vaned Diffuser on Performance of Centrifugal Compressors. Appl. Sci. 2017, 7, 728. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, D.; Zhang, D.; Xie, Y. Investigation on Unsteady Flow Characteristics of a SCO2 Centrifugal Compressor. Appl. Sci. 2017, 7, 310. [Google Scholar] [CrossRef]
- Baltadjiev, N.D.; Lettieri, C.; Spakovszky, Z.S. An Investigation of Real Gas Effects in Supercritical CO2 Centrifugal Compressors. J. Turbomach. 2015, 137, 091003. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Li, P.Y.; Gu, C.W.; Song, Y. A New Optimization Method for Centrifugal Compressors Based on 1D Calculations and Analyses. Energies 2015, 8, 4317–4334. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Luo, W.; Zhao, Q.; Zhao, W.; Xu, J. Preliminary Design and Model Assessment of a Supercritical CO2 Compressor. Appl. Sci. 2018, 8, 595. [Google Scholar] [CrossRef]
- Fuller, R.L.; Eisemann, K. Centrifugal Compressor Off-Design Performance for Super-Critical CO2. In Proceedings of the Supercritical CO2 Power Cycle Symposium, Boulder, CO, USA, 24–25 May 2011; pp. 1–20. [Google Scholar]
- Pecnik, R.; Rinaldi, E.; Colonna, P. Computational Fluid Dynamics of a Radial Compressor Operating with Supercritical CO2. J. Eng. Gas Turbines Power 2012, 134, 122301. [Google Scholar] [CrossRef]
- Pham, H.S.; Alpy, N.; Ferrasse, J.H.; Boutin, O.; Tothill, M.; Quenaut, J.; Gastaldi, O.; Cadiou, T.; Saez, M. An approach for establishing the performance maps of the sc-CO2 compressor: Development and qualification by means of CFD simulations. Int. J. Heat Fluid Flow 2016, 61, 379–394. [Google Scholar] [CrossRef]
- Wright, S.A.; Radel, R.F.; Vernon, M.E.; Rochau, G.E.; Pickard, P.S. Operation and Analysis of a Supercritical CO2 Brayton Cycle; SANDIA Report SAND 2010-0171; Sandia National Laboratories: Livermore, CA, USA, 2010; p. 101.
- Ameli, A.; Afzalifar, A.; Turunen-Saaresti, T.; Backman, J. Effects of Real Gas Model Accuracy and Operating Conditions on Supercritical CO2 Compressor Performance and Flow Field. J. Eng. Gas Turbines Power 2018, 140, 062603. [Google Scholar] [CrossRef]

















| Number of main blades | 6 | Blade thickness at impeller trailing edge | 0.762 mm |
| Number of splitter blades | 6 | Blade height at impeller leading edge | 1.7 mm |
| Impeller inlet radius at hub | 2.537585 mm | Blade angle of the impeller leading edge at hub | 17.88 |
| Impeller inlet radius at shroud | 9.372047 mm | Blade angle of the impeller leading edge at mean radius | 37.13 |
| Impeller exit radius | 18.68170 mm | Blade angle of the impeller leading edge at shroud | 50 |
| Full blade length | 25 mm | Blade angle of the impeller trailing edge | –50 |
| Splitter blade length | 12.5 mm | Angle between streamlines and shaft at impeller inlet | 0 |
| Axial length of the impeller | 15.9 mm | Angle between streamlines and shaft at impeller exit | 90 |
| Clearance gap at impeller tip | 0.254 mm | Blade thickness at impeller leading edge | 0.762 mm |
| Number of vanes | 17 | Blade height at diffuser exit | 1.8 mm |
| Diffuser inlet radius | 18.5 mm | Diffuser channel length | 10.6 mm |
| Diffuser exit radius | 26.0 mm | Blade thickness at diffuser inlet | 0.0 mm |
| Blade angle at diffuser inlet | 71.5 | Blade thickness at diffuser exit | 3.35 mm |
| Blade height at diffuser inlet | 1.8 mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raman, S.K.; Kim, H.D. Computational Analysis of the Performance Characteristics of a Supercritical CO2 Centrifugal Compressor. Computation 2018, 6, 54. https://doi.org/10.3390/computation6040054
Raman SK, Kim HD. Computational Analysis of the Performance Characteristics of a Supercritical CO2 Centrifugal Compressor. Computation. 2018; 6(4):54. https://doi.org/10.3390/computation6040054
Chicago/Turabian StyleRaman, Senthil Kumar, and Heuy Dong Kim. 2018. "Computational Analysis of the Performance Characteristics of a Supercritical CO2 Centrifugal Compressor" Computation 6, no. 4: 54. https://doi.org/10.3390/computation6040054
APA StyleRaman, S. K., & Kim, H. D. (2018). Computational Analysis of the Performance Characteristics of a Supercritical CO2 Centrifugal Compressor. Computation, 6(4), 54. https://doi.org/10.3390/computation6040054





