Spatial Diversity for CDMA RoFSO Links over M Turbulence Channels with Nonzero Boresight Pointing Errors
Abstract
:1. Introduction
2. The CDMA RoFSO System with Spatial Diversity
2.1. Forward Link
2.2. Reverse Link
2.3. Spatial Diversity Receivers
3. The M-Distribution with Nonzero Boresight Pointing Errors
4. Average Bit Error Rate Estimation
5. Outage Probability Estimation
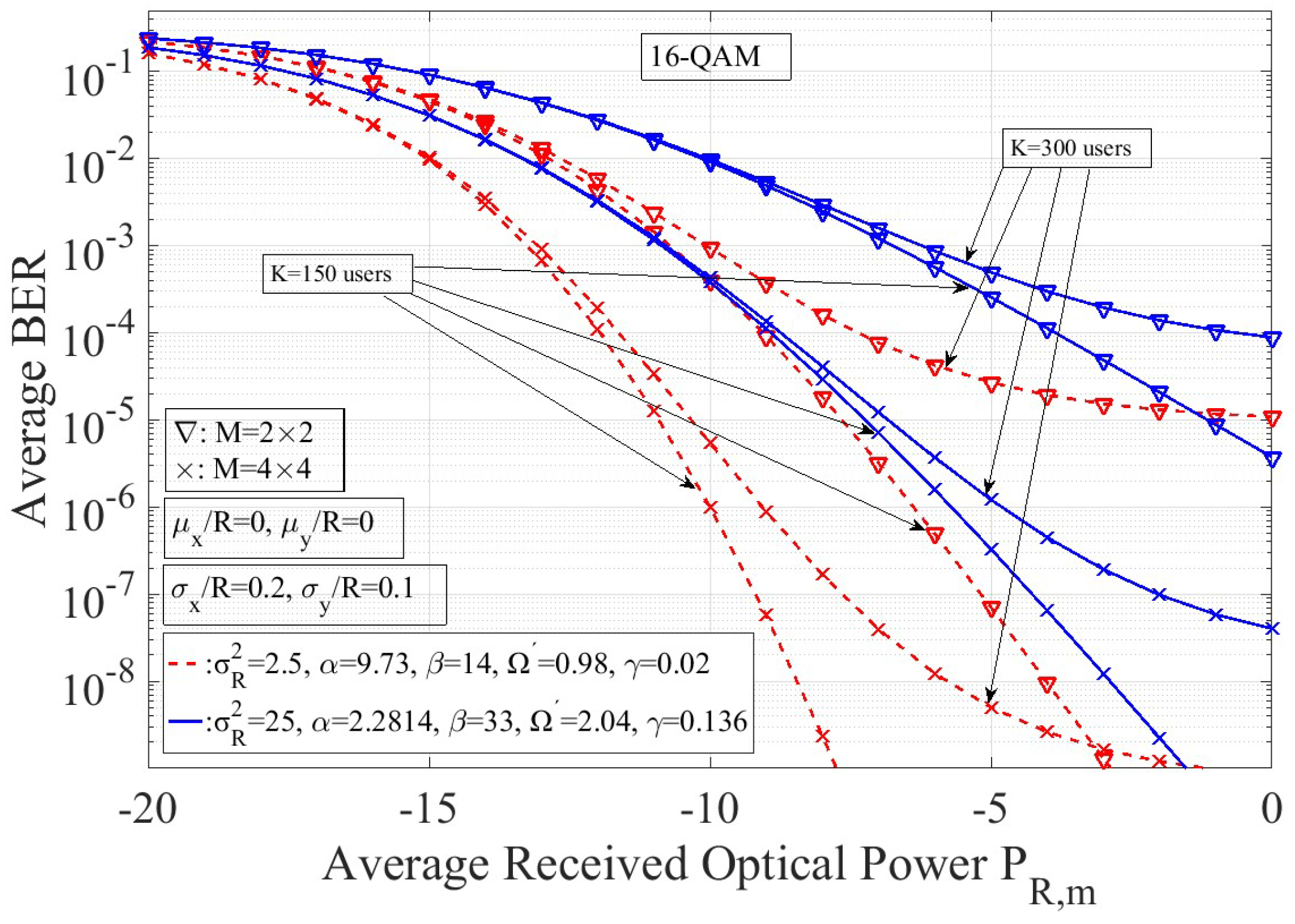
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Uysal, M.; Capsoni, C.; Ghassemlooy, Z.; Boucouvalas, A.; Udvary, E. (Eds.) Optical Wireless Communications: An Emerging Technology; Springer: Cham, Switzerland, 2016; ISBN 978-3-319-30201-0. [Google Scholar]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with Matlab; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2012; ISBN 9781138074804. [Google Scholar]
- Kazaura, K.; Wakamori, K.; Matsumoto, M.; Higashino, T.; Tsukamoto, K.; Komaki, S. RoFSO: A universal platform for convergence of fiber and free space optical communication networks. IEEE Commun. Mag. 2010, 48, 130–137. [Google Scholar] [CrossRef]
- Fernando, X.N. Radio over Fiber for Wireless Communications: From Fundamentals to Advanced Topics; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-3-319-30201-0. [Google Scholar]
- Andrews, L.C.; Philips, R.L. Laser Beam Propagation through Random Media; SPIE: Bellingham, WA, USA, 2005; ISBN 9780819459480. [Google Scholar]
- Jurado-Navas, A.; Garrido-Balsells, J.M.; Paris, J.F.; Puerta-Notario, A. A unifying statistical model for atmospheric optical scintillation. In Numerical Simulation in Physics and Engineering; Intech Publisher: Rijeka, Croatia, 2011; pp. 181–206. [Google Scholar]
- Farid, A.; Hranilovic, S. Outage capacity optimization for free-space optical links with pointing errors. J. Lightw. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Jurado-Navas, A.; Garrido-Balsells, J.M.; Paris, J.F.; Castillo-Vasquez, M.; Puerta-Notario, A. Impact of pointing errors on the performance of generalized atmospheric optical channels. Opt. Express 2012, 20, 12550–12562. [Google Scholar] [CrossRef] [PubMed]
- Boluda Ruiz, R.; Garcia-Zambrana, A.; Castillo-Vazquez, C.; Castillo-Vázquez, B. Novel approximation of misalignment fading modeled by Beckmann distribution on free-space optical links. Opt. Express 2016, 24, 22635–22649. [Google Scholar] [CrossRef] [PubMed]
- Ansari, I.S.; Yilmaz, F.; Alouini, M.S. Performance Analysis of Free-Space Optical Links over Málaga (M) Turbulence Channels with Pointing Errors. IEEE Trans. Wirel. Commun. 2016, 15, 91–102. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Tombras, G.S. SIMO optical wireless links with nonzero boresight pointing errors over M modeled turbulence channels. Opt. Commun. 2017, 403, 391–400. [Google Scholar] [CrossRef]
- Muhammad, S.S.; Kohldolfer, P.; Leitgeb, E. Channel Modeling for Terrestrial Free Space Optical Links. In Proceedings of the 7th International Conference of Transparent Optical Networks, Barcelona, Spain, 3–7 July 2005. [Google Scholar]
- Ales, P. Atmospheric effects on availability of free space optics systems. Opt. Eng. 2009, 48, 066001. [Google Scholar] [CrossRef] [Green Version]
- Navidpour, S.M.; Uysal, M.; Kavehrad, M. BER performance of free space optical transmission with spatial diversity. IEEE Trans. Wirel. Commun. 2007, 6, 2813–2819. [Google Scholar] [CrossRef]
- Tsiftsis, T.A.; Sandalidis, H.G.; Karagiannidis, G.K.; Uysal, M. Optical wireless links with spatial diversity over strong atmospheric turbulence channels. IEEE Trans. Wirel. Commun. 2009, 8, 951–957. [Google Scholar] [CrossRef] [Green Version]
- Zixiong, W.; Wen-De, Z.; Songnian, F.; Chinlon, L. Performance comparison of different modulation formats over free-space optical (FSO) turbulence links with space diversity reception technique. IEEE Photonics J. 2009, 1, 277–285. [Google Scholar] [CrossRef]
- Nistazakis, H.E. A time-diversity scheme for wireless optical links over exponentially modeled turbulence channels. Optik 2013, 124, 1386–1391. [Google Scholar] [CrossRef]
- Abu-Rgheff, M.A. Introduction to CDMA Wireless Communications; Academic Press: New York, NY, USA, 2007; ISBN 978-0-7506-5252-0. [Google Scholar]
- Ninos, M.P.; Nistazakis, H.E.; Sandalidis, H.G.; Tombras, G.S. CDMA RoFSO links with nonzero boresight pointing errors over M turbulence channels. IEEE Photonics J. 2018, 10. [Google Scholar] [CrossRef]
- Simon, Μ.Κ.; Alouini, M.S. Digital Communications over Fading Channels, 2nd ed.; Wiley-IEEE: Hoboken, NJ, USA, 2004; pp. 401–415. ISBN 978-0-471-64953-3. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007; ISBN 978-0-7506-5252-0. [Google Scholar]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill: New York, NY, USA, 2008; ISBN 978-0072957167. [Google Scholar]
- Sadhwani, D.; Yadav, R.N.; Aggrawal, S. Tighter bounds on the Gaussian Q function and its application in Nakagami-m fading channel. IEEE Wirel. Commun. Lett. 2017, 6, 574–577. [Google Scholar] [CrossRef]
- Alouini, M.S.; Simon, Μ.Κ. An MGF-based performance analysis of generalized selection combining over Rayleigh fading channels. IEEE Trans. Commun. 2000, 48, 401–415. [Google Scholar] [CrossRef]
- Adamchik, V.S.; Marichev, O.I. The Algorithm for calculating integrals of hypergeometric type function and its realization in reduce system. In Proceedings of the International Symposium on Symbolic and Algebraic Computation, Tokyo, Japan, 20–24 August 1990; pp. 212–214. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ninos, M.P.; Nistazakis, H.E. Spatial Diversity for CDMA RoFSO Links over M Turbulence Channels with Nonzero Boresight Pointing Errors. Computation 2018, 6, 55. https://doi.org/10.3390/computation6040055
Ninos MP, Nistazakis HE. Spatial Diversity for CDMA RoFSO Links over M Turbulence Channels with Nonzero Boresight Pointing Errors. Computation. 2018; 6(4):55. https://doi.org/10.3390/computation6040055
Chicago/Turabian StyleNinos, Michalis P., and Hector E. Nistazakis. 2018. "Spatial Diversity for CDMA RoFSO Links over M Turbulence Channels with Nonzero Boresight Pointing Errors" Computation 6, no. 4: 55. https://doi.org/10.3390/computation6040055
APA StyleNinos, M. P., & Nistazakis, H. E. (2018). Spatial Diversity for CDMA RoFSO Links over M Turbulence Channels with Nonzero Boresight Pointing Errors. Computation, 6(4), 55. https://doi.org/10.3390/computation6040055





