Nonlinear Dynamics and Performance Analysis of a Buck Converter with Hysteresis Control
Abstract
:1. Introduction
- The constant hysteresis control is applied to a nonlinear and fast dynamic power converter system.
- A mathematical model is derived and used to characterize the nonlinear dynamics induced by the hysteresis control.
- A cost-effective voltage control strategy is implemented using few analog electronic components.
2. Materials and Methods
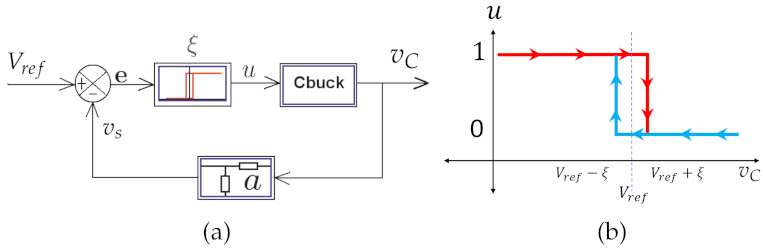
2.1. Model of the Buck Converter
2.2. Buck Converter Voltage Control with Constant Hysteresis
2.3. Physical Considerations
2.4. System Parameters for Simulation
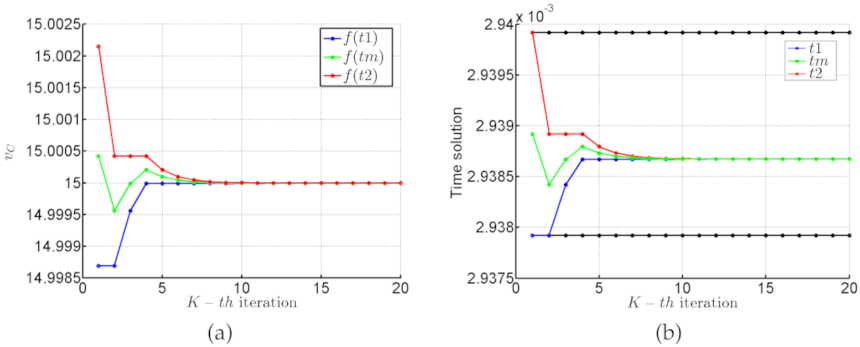
2.5. Model Simulations and Numerical Methods
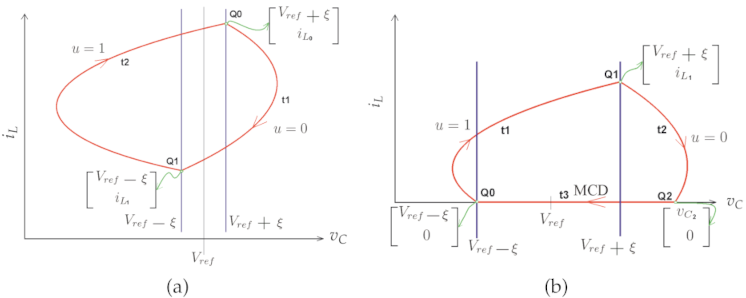
2.6. Nonlinear Dynamics for the Zero Hysteresis Control
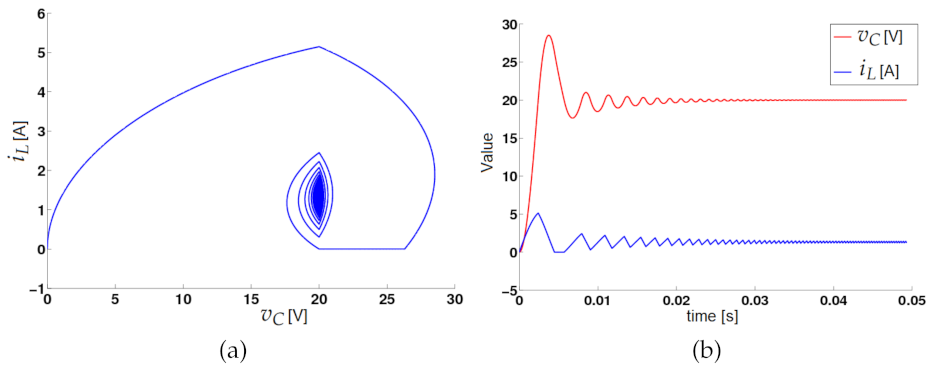
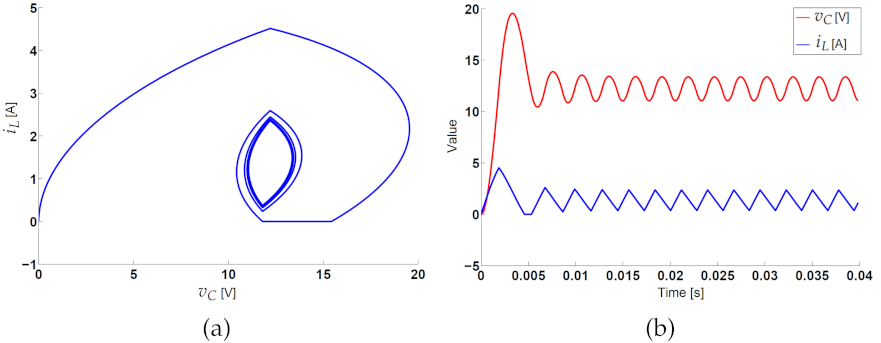
2.6.1. Steady- and Transient-State Simulations
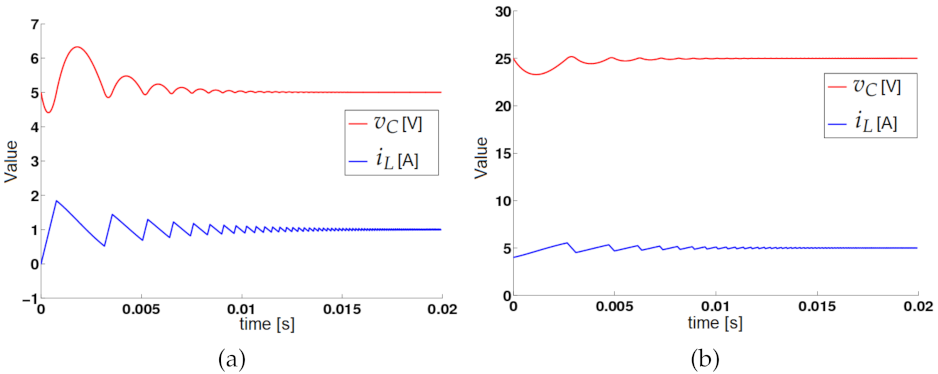
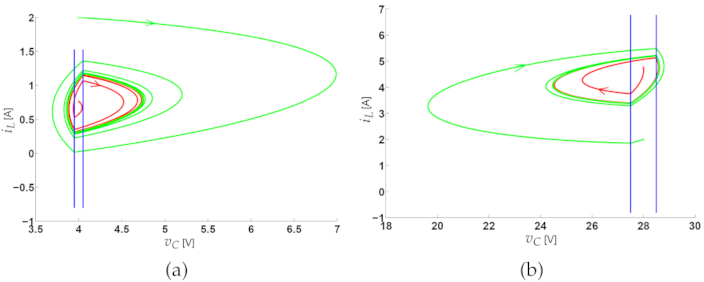
2.6.2. Regulation for Different Voltage Set Points
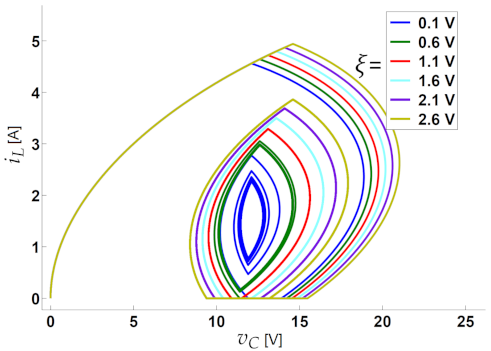
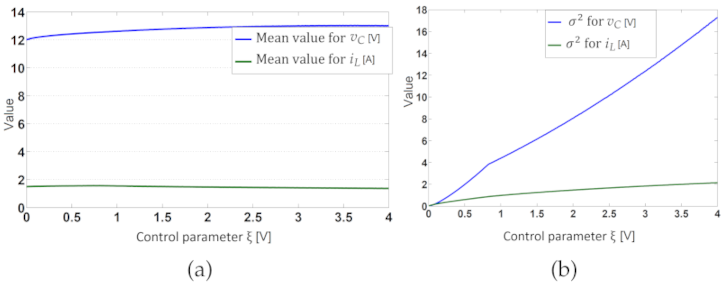
2.7. Nonlinear Dynamics for the Constant Hysteresis Control
3. Experimental Results
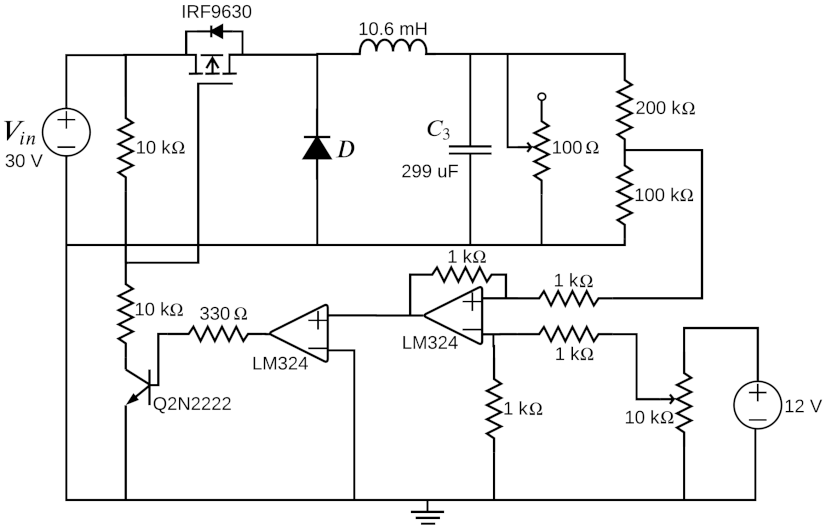
3.1. Experimental Implementation of the Zero Hysteresis Control
Comparison of Experimental Observation with Simulations
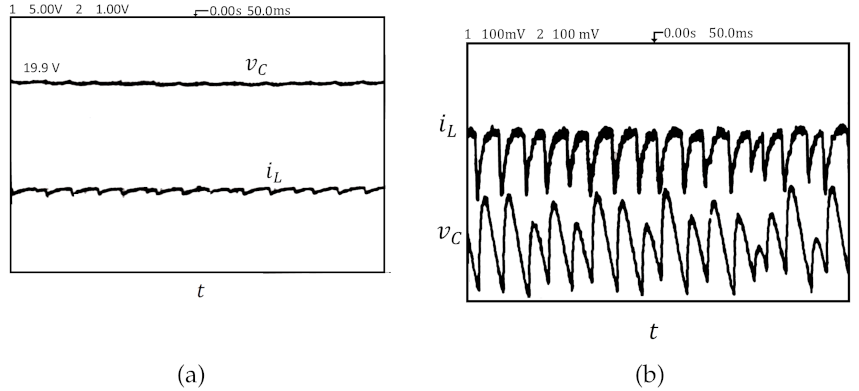
3.2. Steady- and Transient-State Operation
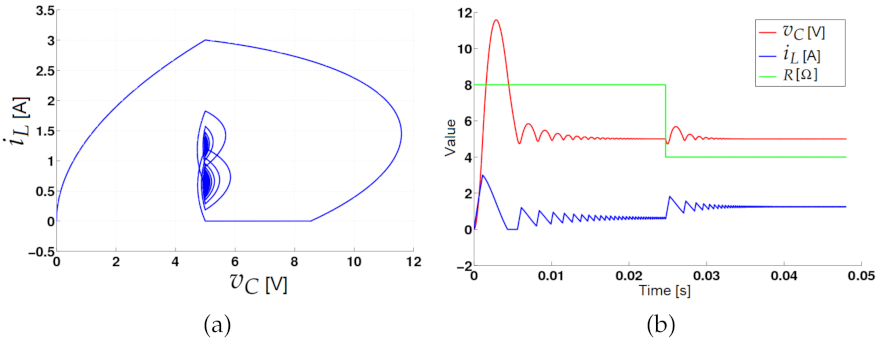
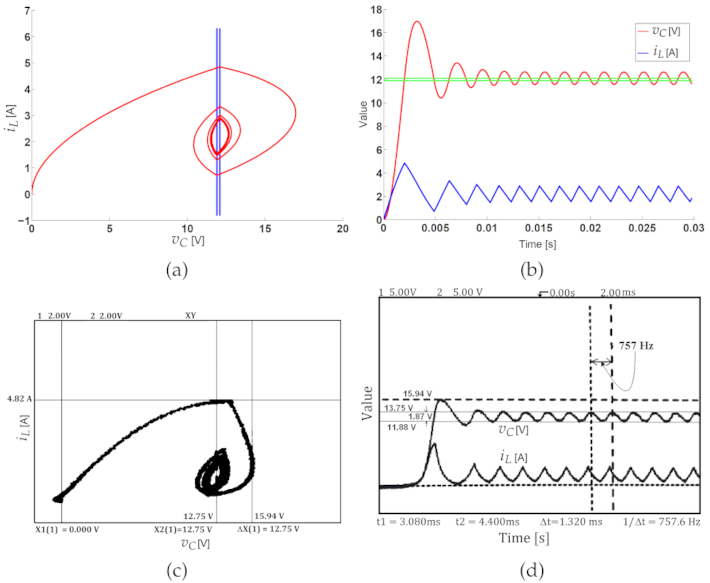
3.2.1. Load Disturbance
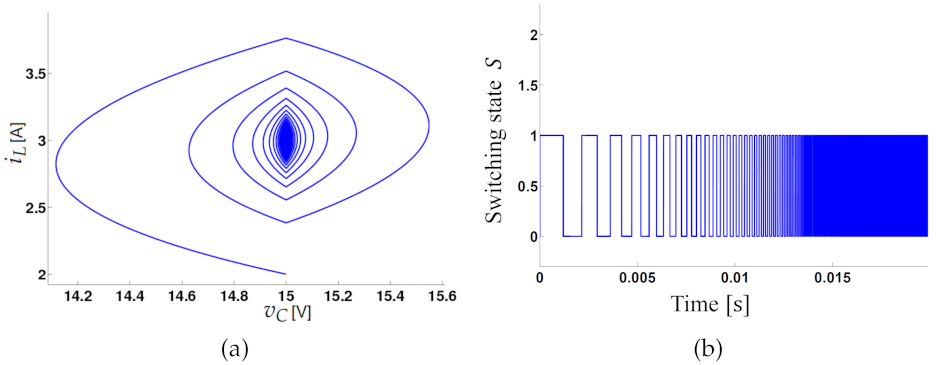
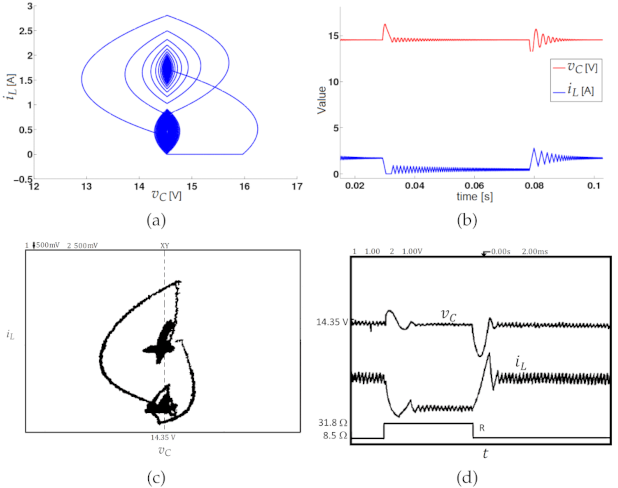
3.2.2. Chaos with the Zero Hysteresis Control
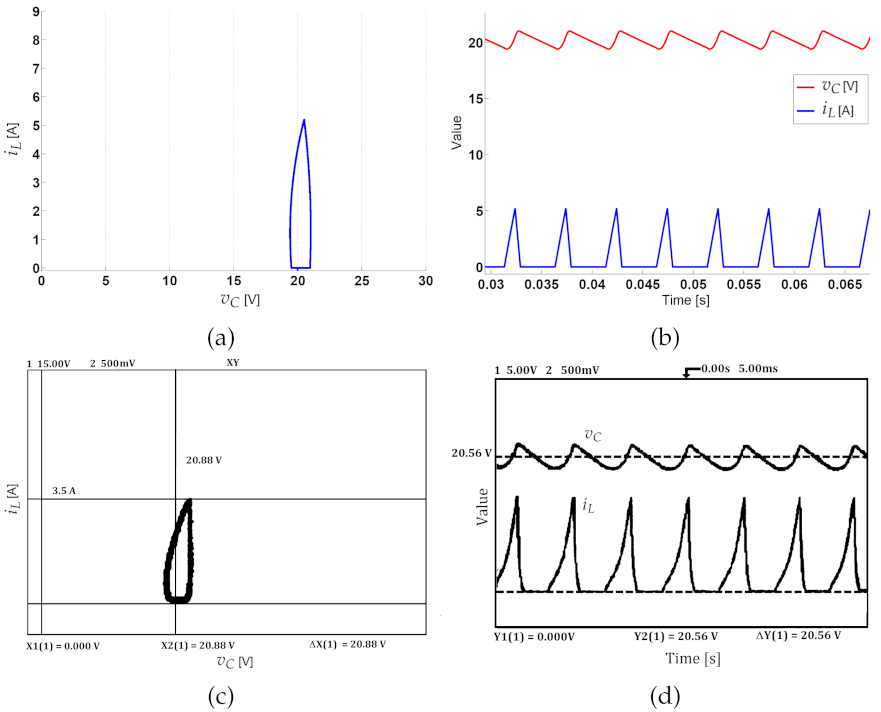
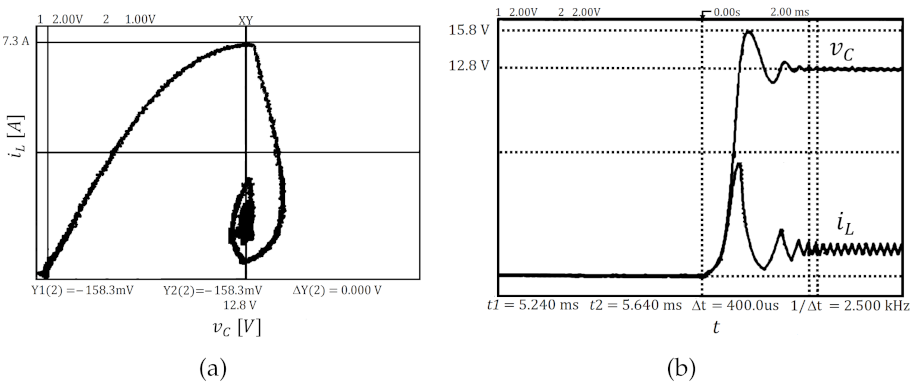
3.3. Experimental Validation of the Constant Hysteresis Control
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Bisection Numerical Method

| Algorithm A1 Bisection numerical Method |
| 1: Time interval initial value |
| 2: Time interval corresponds to , the Time simulation step |
| 3: Reference value to reach and find the time value (solution) |
| 4: Tolerance criteria for convergence |
| 5: error as initial value |
| 6: while do |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: if then |
| 12: |
| 13: else |
| 14: |
| 15: end |
| 16: return |
References
- El Aroudi, A.; Giaouris, D.; Iu, H.H.C.; Hiskens, I.A. A Review on Stability Analysis Methods for Switching Mode Power Converters. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 302–315. [Google Scholar] [CrossRef]
- Choi, K.; Kim, D.S.; Kim, S.K. Disturbance Observer-Based Offset-Free Global Tracking Control for Input-Constrained LTI Systems with DC/DC Buck Converter Applications. Energies 2020, 13, 4079. [Google Scholar] [CrossRef]
- Vilathgamuwa, M.; Nayanasiri, D.; Gamini, S. Power Electronics for Photovoltaic Power Systems. Synth. Lect. Power Electron. 2015, 5, 1–131. [Google Scholar] [CrossRef]
- Zhou, S.; Rincon-Mora, G. A high efficiency, soft switching DC-DC converter with adaptive current-ripple control for portable applications. IEEE Trans. Circuits Syst. II 2006, 53, 319–323. [Google Scholar] [CrossRef]
- Zhong, Z. Tracking Synchronization for DC Microgrid With Multiple-Photovoltaic Arrays: An Even-Based Fuzzy Control Scheme. IEEE Access 2018, 6, 24996–25006. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Sliding-Mode Control of PWM Dual Inverter-Based Grid-Connected PV System: Modeling and Performance Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 435–444. [Google Scholar] [CrossRef]
- Restrepo, C.; González-Castaño, C. Digital control strategies of DC–DC converters in automotive hybrid powertrains. In Modeling, Operation, and Analysis of DC Grids; Garcés, A., Ed.; Academic Press: New York, NY, USA, 2021; pp. 245–287. [Google Scholar] [CrossRef]
- Nan, C.; Ayyanar, R. A 1 MHz bi-directional soft-switching DC-DC converter with planar coupled inductor for dual voltage automotive systems. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 432–439. [Google Scholar] [CrossRef]
- Reatti, A.; Corti, F.; Tesi, A.; Torlai, A.; Kazimierczuk, M.K. Effect of Parasitic Components on Dynamic Performance of Power Stages of DC-DC PWM Buck and Boost Converters in CCM. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- You, S.H.; Bonn, K.; Kim, D.S.; Kim, S.K. Cascade-Type Pole-Zero Cancellation Output Voltage Regulator for DC/DC Boost Converters. Energies 2021, 14, 3824. [Google Scholar] [CrossRef]
- Choi, K.; Kim, K.S.; Kim, S.K. Proportional-Type Sensor Fault Diagnosis Algorithm for DC/DC Boost Converters Based on Disturbance Observer. Energies 2019, 12, 1412. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.-J.; Shieh, H.-J.; Huang, P.-K.; Teng, L.-T. Adaptive control with hysteresis estimation and compensation using RFNN for piezo-actuator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1649–1661. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Xu, C.; Shao, S.; Xu, W.; Wang, Z.; Wang, Y.; Sun, X.; Yang, Q. Field experimental investigation on partial-load dynamic performance with variable hysteresis control of air-to-water heat pump (AWHP) system. Appl. Therm. Eng. 2021, 182, 116072. [Google Scholar] [CrossRef]
- Li, Y.; Ruan, X.; Zhang, L.; Lo, Y.K. Multipower-Level Hysteresis Control for the Class E DC–DC Converters. IEEE Trans. Power Electron. 2020, 35, 5279–5289. [Google Scholar] [CrossRef]
- Ling, R.; Maksimovic, D.; Leyva, R. Second-Order Sliding-Mode Controlled Synchronous Buck DC–DC Converter. IEEE Trans. Power Electron. 2016, 31, 2539–2549. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Calvente, J.; Giral, R. Hysteretic Transition Method for Avoiding the Dead-Zone Effect and Subharmonics in a Noninverting Buck–Boost Converter. IEEE Trans. Power Electron. 2015, 30, 3418–3430. [Google Scholar] [CrossRef] [Green Version]
- Revelo-Fuelagán, J.; Candelo-Becerra, J.E.; Hoyos, F.E. Power Factor Correction of Compact Fluorescent and Tubular LED Lamps by Boost Converter with Hysteretic Control. J. Daylight. 2020, 7, 73–83. [Google Scholar] [CrossRef]
- Mehrabian-Nejad, H.; Farhangi, B.; Farhangi, S.; Vaez-Zadeh, S. DC-DC converter for energy loss compensation and maximum frequency limitation in capacitive deionization systems. In Proceedings of the 2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 16–18 February 2016; pp. 211–216. [Google Scholar] [CrossRef]
- Aroudi, A.E.; Martinez-Tribiño, B.A.; Calvente, J.; Cid-Pastor, A.; Martínez-Salamero, L. Sliding-mode control of a boost converter feeding a buck converter operating as a constant power load. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017. [Google Scholar] [CrossRef]
- Viswadev, R.; Mudlapur, A.; Ramana, V.V.; Venkatesaperumal, B.; Mishra, S. A Novel AC Current Sensorless Hysteresis Control for Grid-Tie Inverters. IEEE Trans. Circuits Syst. II 2020, 67, 2577–2581. [Google Scholar] [CrossRef]
- Kumar.Ch, S.V.S.P.; Jain, S.; Hota, A.; Sonti, V. Performance analysis of Closed Loop Hysteresis Control of a PV based 8/6 Pole and 10/8 Pole Switched Reluctance Motor for EV Application. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, J.; Qu, K.; Li, F.; Cao, W. A new hysteresis control buck converter with enhanced feedback ripple. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 972–976. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, J.; Qu, K.; Li, F. Dynamic analysis of hysteresis control buck converter with enhanced feedback ripple. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 2663–2668. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Control of Dual Inverter Based PV System Through Double-Band Adaptive SMC. In Proceedings of the 2019 IEEE International Conference on Sustainable Energy Technologies and Systems (ICSETS), Bhubaneswar, India, 26 February–1 March 2019; pp. 156–160. [Google Scholar] [CrossRef]
- Hilairet, M.; Auger, F. Speed sensorless control of a DC-motor via adaptive filters. IET Electric Power Appl. 2007, 1, 601. [Google Scholar] [CrossRef]
- S. Buso, P.M. Digital Control in Power Electronics; Morgan & Claypool Publishers: San Rafael, CA, USA, 2015. [Google Scholar]
- Aguilera, R.P.; Quevedo, D.E. Predictive Control of Power Converters: Designs With Guaranteed Performance. IEEE Trans. Ind. Inform. 2015, 11, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Peterchev, A.; Sanders, S. Quantization resolution and limit cycling in digitally controlled PWM converters. IEEE Trans. Power Electron. 2003, 18, 301–308. [Google Scholar] [CrossRef] [Green Version]
- Corradini, L.; Mattavelli, P. Analysis of Multiple Sampling Technique for Digitally Controlled DC-DC Converters. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Fernandez-Alvarez, A.; Portela-Garcia, M.; Garcia-Valderas, M.; Lopez, J.; Sanz, M. HW/SW Co-Simulation System for Enhancing Hardware-in-the-Loop of Power Converter Digital Controllers. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1779–1786. [Google Scholar] [CrossRef]
- Taborda, J.A.; Angulo, F.; Olivar, G. Characterization of chaotic attractors inside band-merging scenario in a ZAD-controlled buck converter. Int. J. Bifurc. Chaos 2012, 22, 1230034. [Google Scholar] [CrossRef]
- Ashita, S.; Uma, G.; Deivasundari, P. Chaotic dynamics of a zero average dynamics controlled DC–DC Ćuk converter. IET Power Electron. 2014, 7, 289–298. [Google Scholar] [CrossRef]
- Angulo, F.; Jorge, E.B.; Olivar, G. Study of Nonlinear Dynamics in a Buck Converter Controlled by Lateral PWM and ZAD. In Modeling, Simulation and Control of Nonlinear Engineering Dynamical Systems; Springer: Dordrecht, the Netherlands, 2008; pp. 313–325. [Google Scholar] [CrossRef]
- Hoyos, F.E.; Candelo-Becerra, J.E.; Hoyos Velasco, C.I. Application of Zero Average Dynamics and Fixed Point Induction Control Techniques to Control the Speed of a DC Motor with a Buck Converter. Appl. Sci. 2020, 10, 1807. [Google Scholar] [CrossRef] [Green Version]
- Hoyos, F.E.; Candelo, J.E.; Taborda, J.A. Selection and Validation of Mathematical Models of Power Converters using Rapid Modeling and Control Prototyping Methods. Int. J. Electr. Comput. Eng. 2018, 8, 1551. [Google Scholar] [CrossRef]
- Ding, S.; Zheng, W.X.; Sun, J.; Wang, J. Second-Order Sliding-Mode Controller Design and Its Implementation for Buck Converters. IEEE Trans. Ind. Inform. 2018, 14, 1990–2000. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.; Wu, B.; Li, S.; Li, Q. Extended state observer-based sliding mode control for PWM-based DC–DC buck power converter systems with mismatched disturbances. IET Control Theory Appl. 2015, 9, 579–586. [Google Scholar] [CrossRef]
- Hoyos Velasco, F.E.; Hoyos Velasco, C.I.; Candelo-Becerra, J.E. DC-AC power inverter controlled analogically with zero hysteresis. Int. J. Electr. Comput. Eng. 2019, 9, 4767–4776. [Google Scholar] [CrossRef]
- Baek, J.; Lee, J.H.; Shin, S.U.; Jung, M.y.; Cho, G.H. Switched inductor capacitor buck converter with gt; 85% power efficiency in 100uA-to-300mA loads using a bang-bang zero-current detector. In Proceedings of the 2018 IEEE Custom Integrated Circuits Conference (CICC), San Diego, CA, USA, 8–11 April 2018; pp. 1–4. [Google Scholar] [CrossRef]
- di Gaeta, A.; Hoyos Velasco, C.I.; Montanaro, U. Cycle-by-Cycle Adaptive Force Compensation for the Soft-Landing Control of an Electro-Mechanical Engine Valve Actuator. Asian J. Control 2015, 17, 1–18. [Google Scholar] [CrossRef]
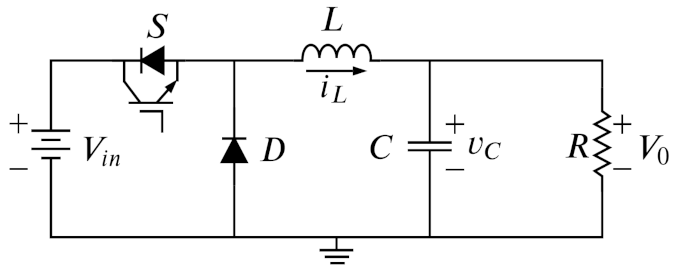
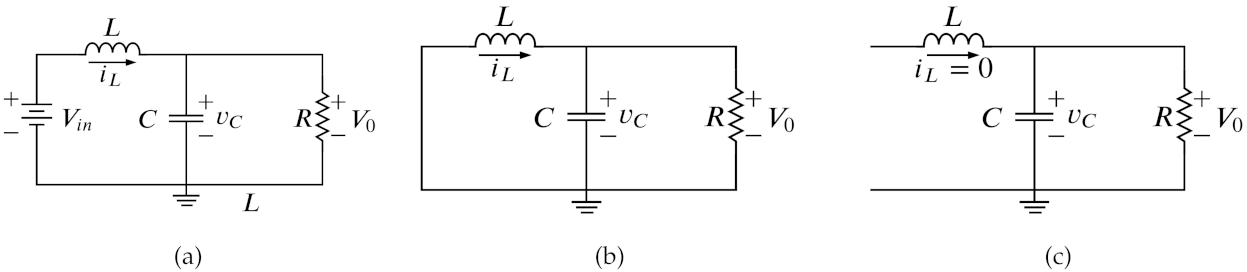
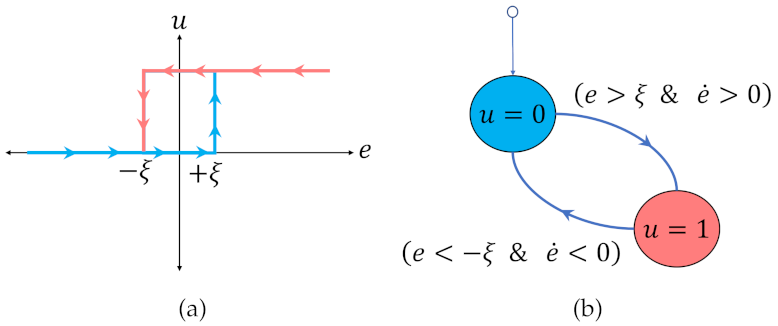

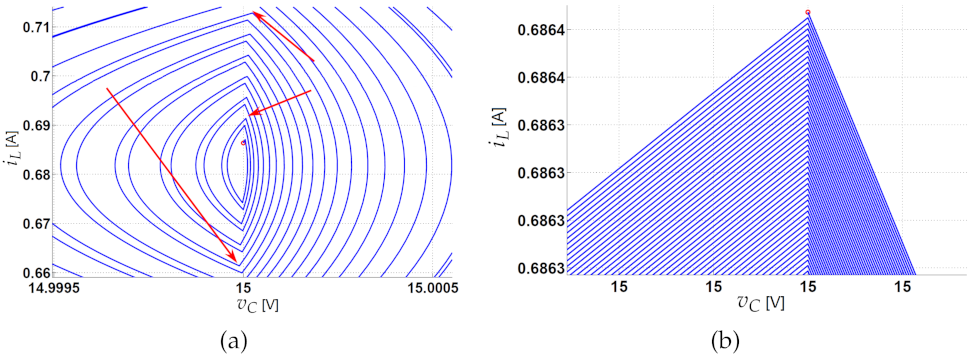





| Parameter | Description | Value |
|---|---|---|
| Input voltage | 20 V | |
| Reference voltage | 15 V | |
| R | Resistance | 22 |
| C | Capacitance | 1000 f |
| L | Inductance | 7 mH |
| Initial conditions | 0 V; 0 A | |
| Hysteresis band | 0 V | |
| Time discrete steps | s | |
| Initial simulation time | 0.0 s | |
| Final simulation time | 0.4 s |
| Parameter | Description | Value |
|---|---|---|
| Input voltage | 30 V | |
| Reference voltage | ||
| a | Constant of the sensor | 1/3 |
| R | Load resistance | |
| C | Capacitance | f |
| L | Inductance | mH |
| Resistance of the inductor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoyos Velasco, C.I.; Hoyos Velasco, F.E.; Candelo-Becerra, J.E. Nonlinear Dynamics and Performance Analysis of a Buck Converter with Hysteresis Control. Computation 2021, 9, 112. https://doi.org/10.3390/computation9100112
Hoyos Velasco CI, Hoyos Velasco FE, Candelo-Becerra JE. Nonlinear Dynamics and Performance Analysis of a Buck Converter with Hysteresis Control. Computation. 2021; 9(10):112. https://doi.org/10.3390/computation9100112
Chicago/Turabian StyleHoyos Velasco, Carlos I., Fredy Edimer Hoyos Velasco, and John E. Candelo-Becerra. 2021. "Nonlinear Dynamics and Performance Analysis of a Buck Converter with Hysteresis Control" Computation 9, no. 10: 112. https://doi.org/10.3390/computation9100112
APA StyleHoyos Velasco, C. I., Hoyos Velasco, F. E., & Candelo-Becerra, J. E. (2021). Nonlinear Dynamics and Performance Analysis of a Buck Converter with Hysteresis Control. Computation, 9(10), 112. https://doi.org/10.3390/computation9100112








