Multidimensional Scaling of Cognitive Ability and Academic Achievement Scores
Abstract
:Author Note
Abstract
1. Introduction
1.1. Intelligence and Academic Achievement Tests Are Multidimensional and Related
1.2. Validity Evidence from Multidimensional Scaling
1.3. MDS with Intelligence and Academic Achievement
1.4. Facet Theory
1.5. Purpose of the Study
- Are complex tests in the center of the MDS configuration with less complex tests farther from the center of the MDS configuration?
- Intelligence and academic achievement tests of higher complexity were predicted to be near the center of the configuration and tests of lower complexity were predicted to be on the periphery (Marshalek et al. 1983). However, tests were not necessarily expected to all radiate outward from complex to simple tests in exact order by complexity as indicated by g-loadings (e.g., McGrew et al. 2014). Are intelligence tests and academic achievement tests clustered by CHC ability and academic content, respectively?
- Ga, Gc, Gv, Gf, and Gsm or Gwm tests were expected to cluster by CHC ability, and reading, writing, math, and oral language tests were expected to cluster by academic achievement area. Certain regions of academic achievement tests were predicted to align more closely with CHC ability factors. Reading and writing tests were predicted to be close to the Gc, Ga, and oral language tests. Math tests were predicted to be closer to the Gsm or Gwm, Gv, and Gf clusters.
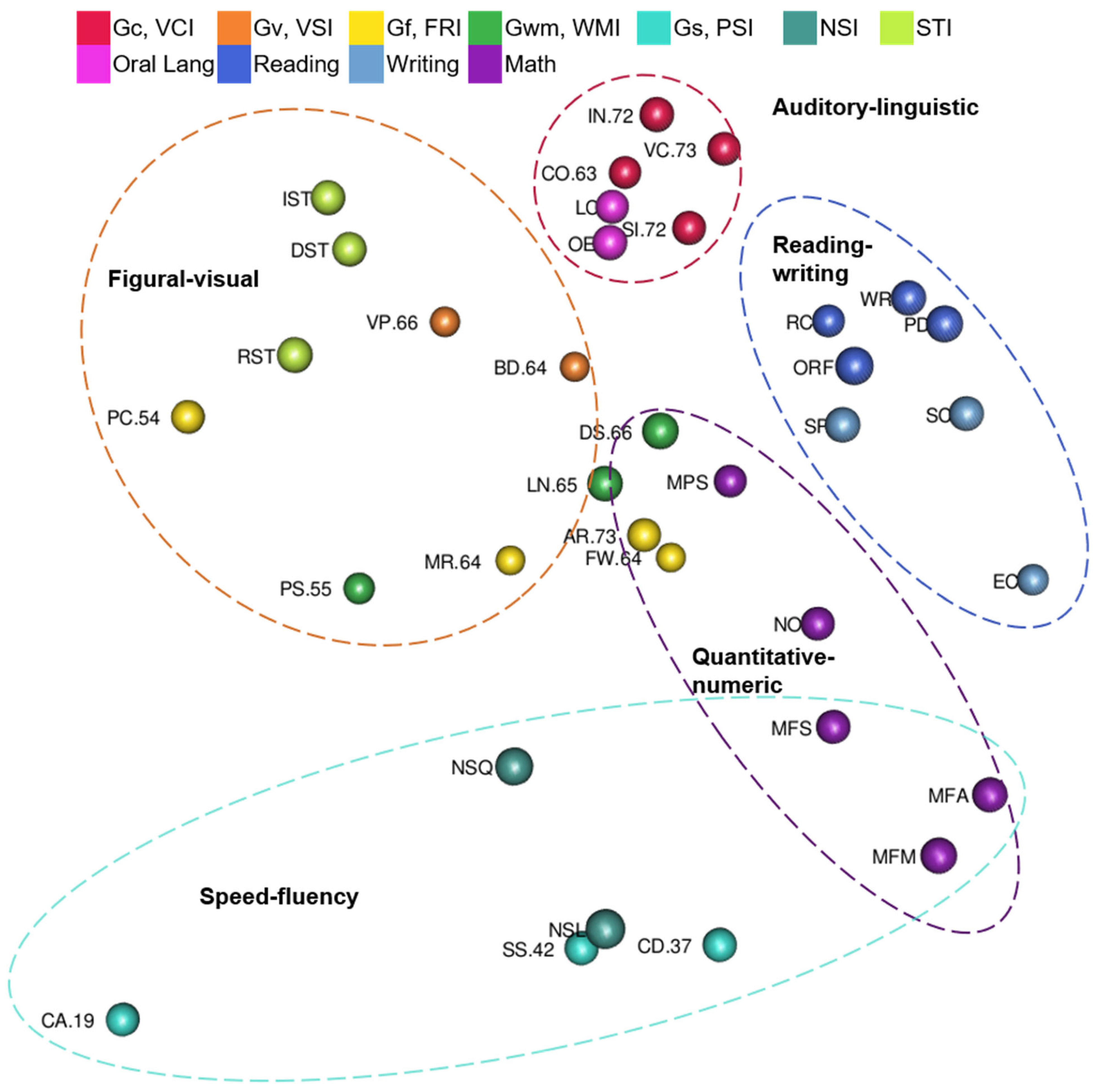
- Are tests organized into auditory-linguistic, figural-visual, reading-writing, quantitative-numeric, and speed-fluency regions?
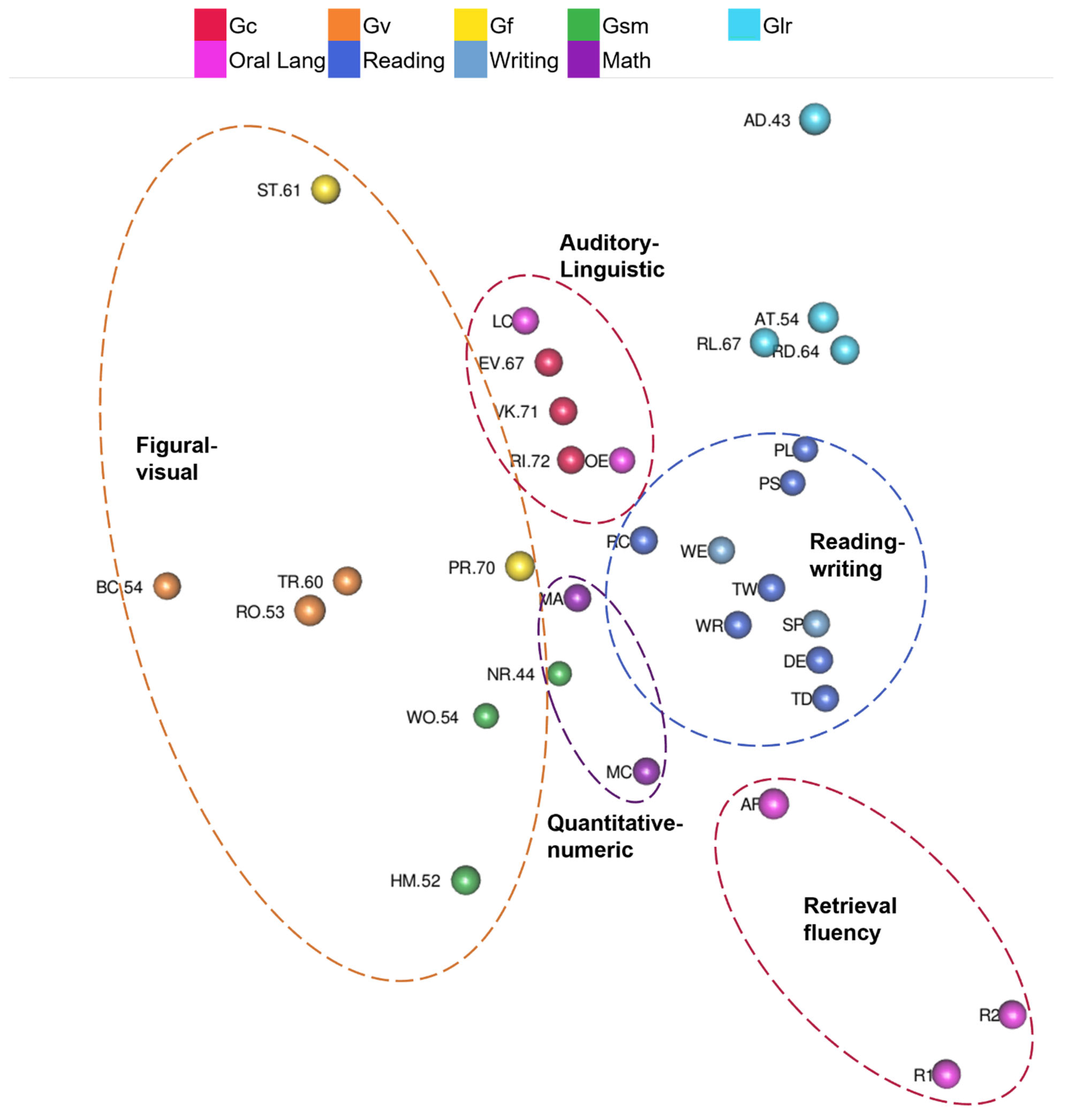
- Auditory-linguistic, figural-visual, reading-writing, quantitative-numeric, and speed-fluency regions were investigated in this study (McGrew et al. 2014). Gc tests, Ga tests, and oral language tests were predicted to cluster together with each other within an auditory-linguistic region. Reading and writing tests were predicted to be located in a reading-writing region. Gf tests were predicted to be in figural-visual or quantitative-numeric regions. Gv tests were predicted to be in a figural-visual region. Gsm or Gwm tests were predicted to be in the region that corresponded to the figural or numeric content (i.e., tests with pictures in the figural-visual region and tests with numbers in the quantitative-numeric region). Glr tests were not expected to be in just one region or in the same region of every configuration (McGrew et al. 2014).
2. Materials and Methods
2.1. Participants
2.1.1. Wechsler Sample Participants
2.1.2. Kaufman Sample Participants
2.2. Measures
2.2.1. WISC-V and WIAT-III
2.2.2. KABC-II and KTEA-II
2.3. Data Preparation Prior to MDS Analysis
2.4. MDS Analysis
2.4.1. Model Selection
2.4.2. Preparation for Interpretation
3. Results
3.1. Preliminary Analysis and Model Selection
3.2. Primary Analyses
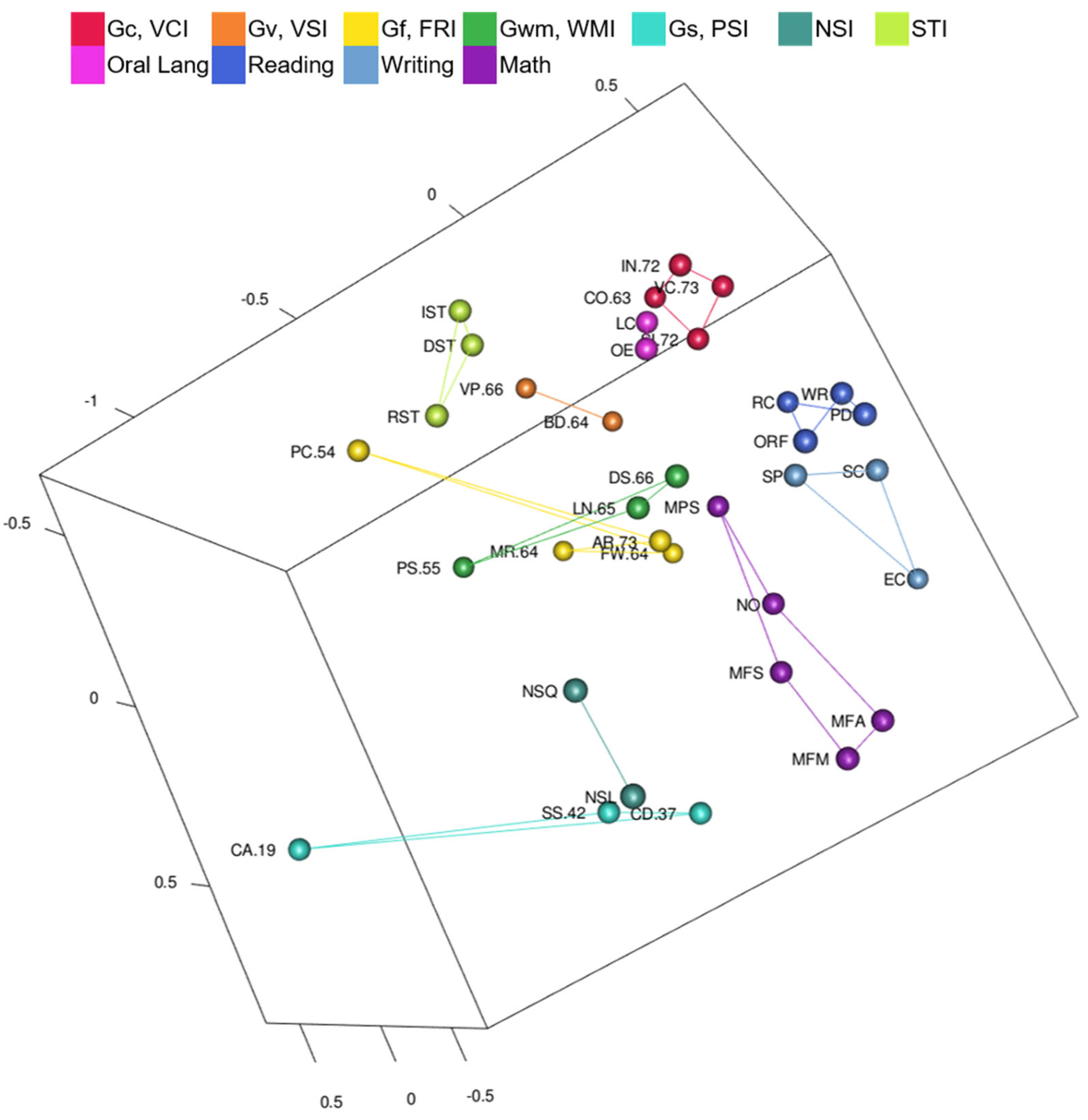
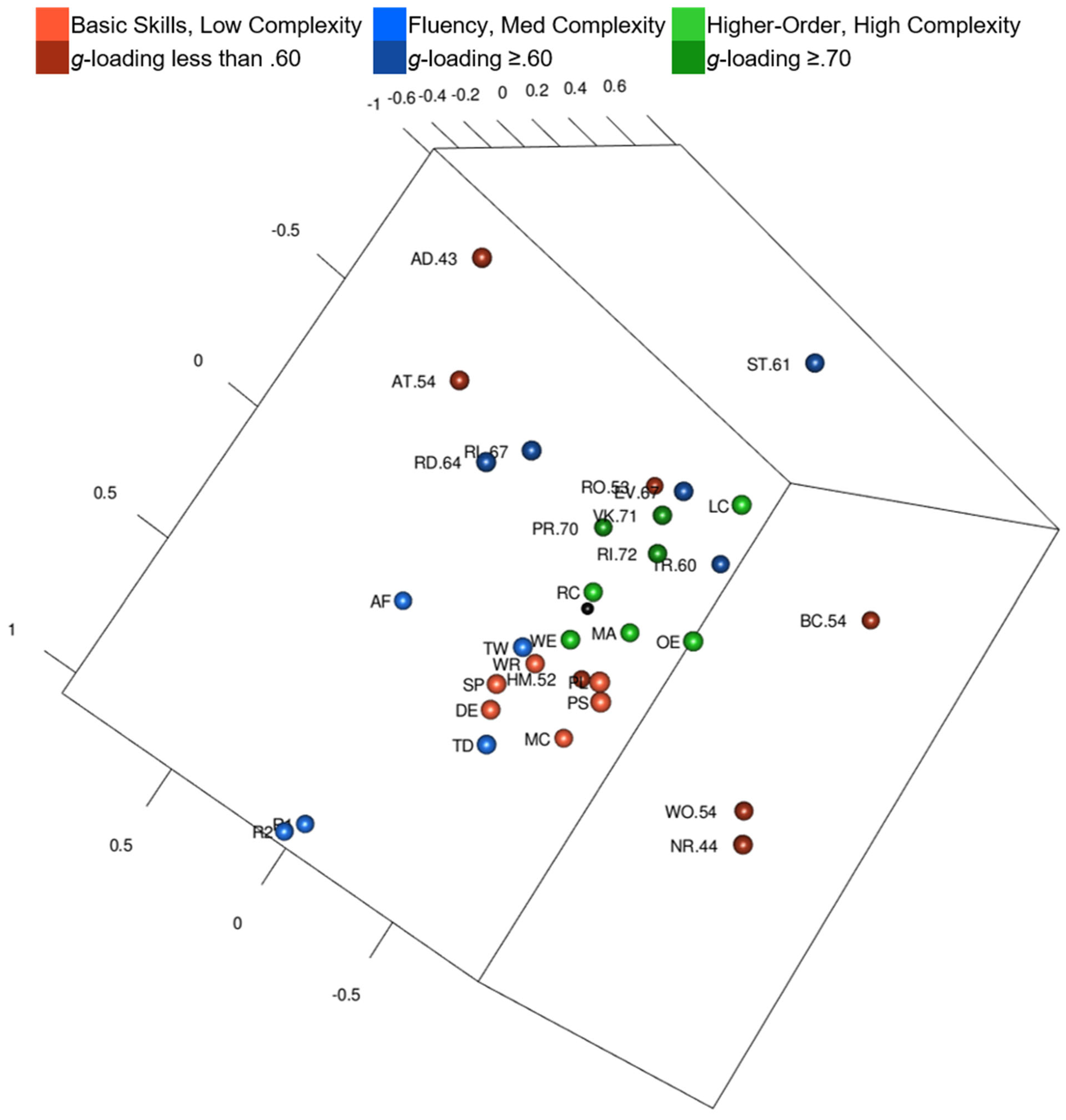
3.2.1. WISC-V and WIAT-III Model Results
- Are complex tests in the center of the MDS configuration with less complex tests farther from the center of the MDS configuration?
- 2.
- Are intelligence tests and academic achievement tests clustered by CHC ability and academic content, respectively?
- 3.
- Are tests organized into auditory-linguistic, figural-visual, reading-writing, quantitative-numeric, and speed-fluency regions?
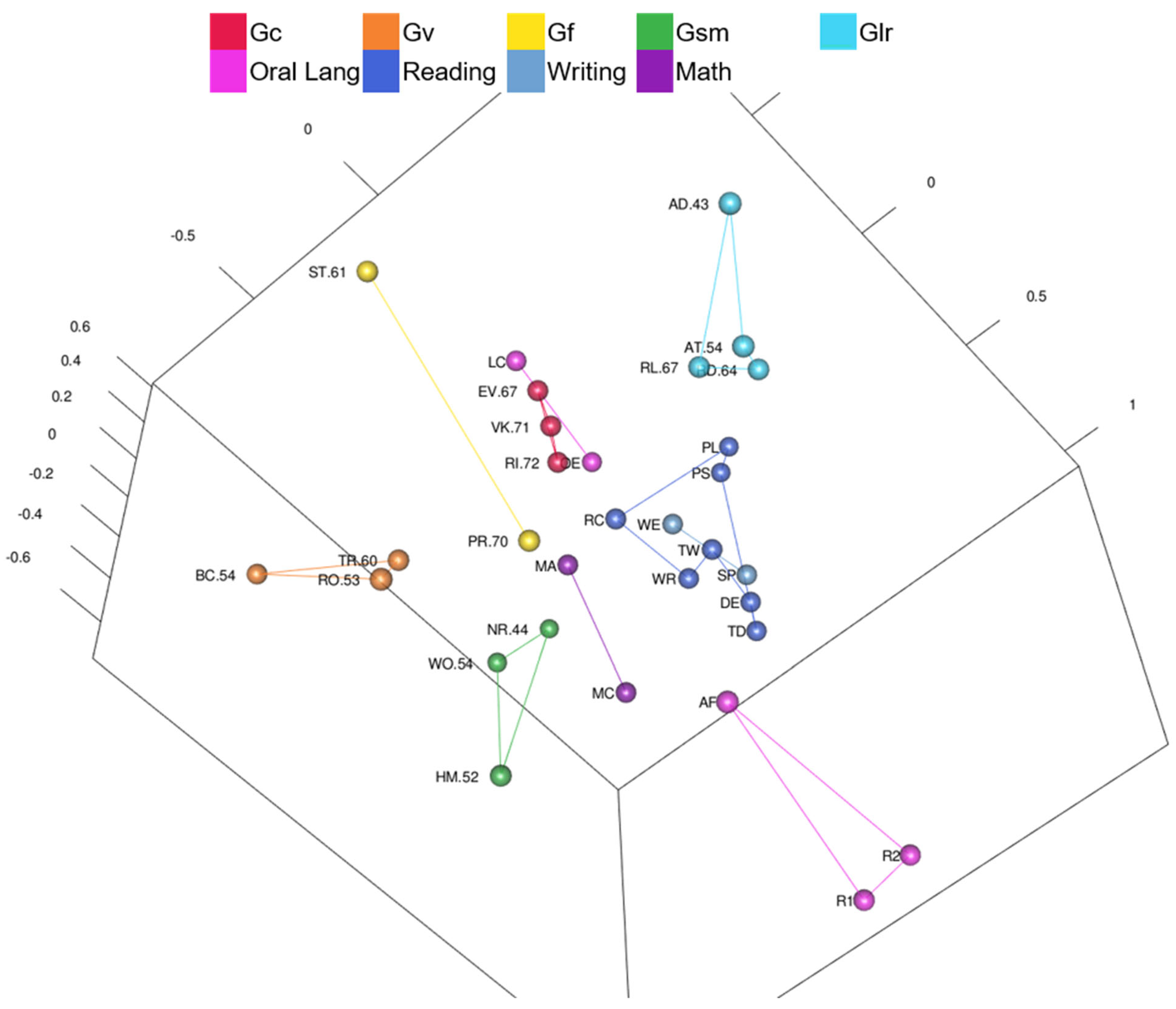
3.2.2. Kaufman Grades 4–6 Model Results
- Are complex tests in the center of the MDS configuration with less complex tests farther from the center of the MDS configuration?
- 2.
- Are intelligence tests and academic achievement tests clustered by CHC ability and academic content, respectively?
- 3.
- Are tests organized into auditory-linguistic, figural-visual, reading-writing, quantitative-numeric, and speed-fluency regions?
3.3. Secondary Analyses
3.3.1. Kaufman Grade Groups
3.3.2. WISC-V and WIAT-III Content and Response Modes
4. Discussion
4.1. Complexity
4.1.1. Wechsler Models
4.1.2. Kaufman Models
4.2. CHC and Academic Clusters
4.3. Regions and Fluency
4.4. Content and Response Process Facets
4.5. Limitations
4.6. Future Research
4.7. Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Acosta Caballero, Karen. 2012. The Reading Comprehension Strategies of Second Langauge Learners: A Spanish-English Study. Ph.D. thesis, University of Kansas, Kansas City, KS, USA. [Google Scholar]
- Adler, Daniel, and Duncan Murdoch. 2021. rgl: 3D Visualization Using OpenGL. Version 0.105.22. Available online: https://CRAN.R-project.org/package=rgl (accessed on 2 November 2021).
- Ambinder, Michael, Ranxiao Wang, James Crowell, George Francis, and Peter Brinkmann. 2009. Human Four-Dimensional Spatial Intuition in Virtual Reality. Psychonomic Bulletin & Review 16: 818–23. [Google Scholar]
- American Educational Research Association, American Psychological Association, National Council on Measurement in Education, Joint Committee on Standards for Educational, and Psychological Testing. 2014. Standards for Educational and Psychological Testing. American Educational Research Association. Available online: https://books.google.com/books?id=clI_mAEACAAJ (accessed on 23 January 2021).
- Beauducel, André, and Martin Kersting. 2002. Fluid and Crystallized Intelligence and the Berlin Model of Intelligence Structure (Bis). European Journal of Psychological Assessment 18: 97–112. [Google Scholar] [CrossRef] [Green Version]
- Benson, Nicholas, Randy Floyd, John Kranzler, Tanya Eckert, Sarah Fefer, and Grant Morgan. 2019. Test Use and Assessment Practices of School Psychologists in the United States: Findings from the 2017 National Survey. Journal of School Psychology 72: 29–48. [Google Scholar] [CrossRef]
- Benson, Nicholas, John Kranzler, and Randy Floyd. 2016. Examining the Integrity of Measurement of Cognitive Abilities in the Prediction of Achievement: Comparisons and Contrasts across Variables from Higher-Order and Bifactor Models. Journal of School Psychology 58: 1–19. [Google Scholar] [CrossRef] [PubMed]
- Borg, Ingwer, and Patrick Groenen. 2005. Modern Multidimensional Scaling: Theory and Applications, 2nd ed. Springer Series in Statistics; Berlin and Heidelberg: Springer. [Google Scholar]
- Borg, Ingwer, Patrick Groenen, and Patrick Mair. 2018. Applied Multidimensional Scaling and Unfolding, 2nd ed. Springer Briefs in Statistics. Berlin and Heidelberg: Springer. [Google Scholar]
- Breaux, Kristina. 2009. Wechsler Individual Achievement Test, 3rd ed. Technical Manual. Chicago: NCS Pearson. [Google Scholar]
- Caemmerer, Jacqueline, Timothy Keith, and Matthew Reynolds. 2020. Beyond Individual Intelligence Tests: Application of Cattell-Horn-Carroll Theory. Intelligence 79: 101433. [Google Scholar] [CrossRef]
- Caemmerer, Jacqueline, Danika Maddocks, Timothy Keith, and Matthew Reynolds. 2018. Effects of Cognitive Abilities on Child and Youth Academic Achievement: Evidence from the WISC-V and WIAT-III. Intelligence 68: 6–20. [Google Scholar] [CrossRef]
- Carroll, John. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies. Cambridge: Cambridge University Press. [Google Scholar]
- Cattell, Raymond. 1943. The Measurement of Adult Intelligence. Psychological Bulletin 40: 153–93. [Google Scholar] [CrossRef]
- Cohen, Arie, Catherine Fiorello, and Frank Farley. 2006. The Cylindrical Structure of the Wechsler Intelligence Scale for Children-IV: A Retest of the Guttman Model of Intelligence. Intelligence 34: 587–91. [Google Scholar] [CrossRef]
- Conway, Andrew, Kristof Kovacs, Han Hao, Kevin P. Rosales, and Jean-Paul Snijder. 2021. Individual Differences in Attention and Intelligence: A United Cognitive/Psychometric Approach. Journal of Intelligence 9: 34. [Google Scholar] [CrossRef]
- Cormier, Damien, Okan Bulut, Kevin McGrew, and Jessica Frison. 2016. The Role of Cattell-Horn-Carroll (Chc) Cognitive Abilities in Predicting Writing Achievement During the School-Age Years. Psychology in the Schools 53: 787–803. [Google Scholar] [CrossRef]
- Cormier, Damien, Kevin McGrew, Okan Bulut, and Allyson Funamoto. 2017. Revisiting the Relations between the Wj-Iv Measures of Cattell-Horn-Carroll (Chc) Cognitive Abilities and Reading Achievement During the School-Age Years. Journal of Psychoeducational Assessment 35: 731–54. [Google Scholar] [CrossRef]
- Finlayson, Nonie, Xiaoli Zhang, and Julie Golomb. 2017. Differential Patterns of 2d Location Versus Depth Decoding Along the Visual Hierarchy. NeuroImage 147: 507–16. [Google Scholar] [CrossRef] [PubMed]
- Floyd, Randy, Jeffrey Evans, and Kevin McGrew. 2003. Relations between Measures of Cattell-Horn-Carroll (Chc) Cognitive Abilities and Mathematics Achievement across the School-Age Years. Psychology in the Schools 40: 155–71. [Google Scholar] [CrossRef]
- Floyd, Randy, Timothy Keith, Gordon Taub, and Kevin McGrew. 2007. Cattell-Horn-Carroll Cognitive Abilities and Their Effects on Reading Decoding Skills: G Has Indirect Effects, More Specific Abilities Have Direct Effects. School Psychology Quarterly 22: 200–33. [Google Scholar] [CrossRef] [Green Version]
- Garcia, Gailyn, and Mary Stafford. 2000. Prediction of Reading by Ga and Gc Specific Cognitive Abilities for Low-Ses White and Hispanic English-Speaking Children. Psychology in the Schools 37: 227–35. [Google Scholar] [CrossRef]
- Gerst, Elyssa, Paul Cirino, Kelly Macdonald, Jeremy Miciak, Hanako Yoshida, Steven Woods, and Cullen Gibbs. 2021. The Structure of Processing Speed in Children and Its Impact on Reading. Journal of Cognition and Development 22: 84–107. [Google Scholar] [CrossRef] [PubMed]
- Graham, John. 2009. Missing Data Analysis: Making It Work in the Real World. Annual Review of Psychology 60: 549–76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Graves, Scott, Leanne Smith, and Kayla Nichols. 2020. Is the WISC-V a Fair Test for Black Children: Factor Structure in an Urban Public School Sample. Contemporary School Psychology 25: 157–69. [Google Scholar] [CrossRef]
- Gustafsson, Jan-Eric. 1984. A Unifying Model for the Structure of Intellectual Abilities. Intelligence 8: 179–203. [Google Scholar] [CrossRef]
- Gustafsson, Jan-Eric, and Gudrun Balke. 1993. General and Specific Abilities as Predictors of School Achievement. Multivariate Behavioral Research 28: 407–34. [Google Scholar] [CrossRef]
- Guttman, Louis, and Shlomit Levy. 1991. Two Structural Laws for Intelligence Tests. Intelligence 15: 79–103. [Google Scholar] [CrossRef]
- Hajovsky, Daniel, Ethan Villeneuve, Joel Schneider, and Jacqueline Caemmerer. 2020. An Alternative Approach to Cognitive and Achievement Relations Research: An Introduction to Quantile Regression. Journal of Pediatric Neuropsychology 6: 83–95. [Google Scholar] [CrossRef]
- Hajovsky, Daniel, Matthew Reynolds, Randy Floyd, Joshua Turek, and Timothy Keith. 2014. A Multigroup Investigation of Latent Cognitive Abilities and Reading Achievement Relations. School Psychology Review 43: 385–406. [Google Scholar] [CrossRef]
- Jacobson, Lisa, Matthew Ryan, Rebecca Martin, Joshua Ewen, Stewart Mostofsky, Martha Denckla, and Mark Mahone. 2011. Working Memory Influences Processing Speed and Reading Fluency in Adhd. Child Neuropsychology 17: 209–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jensen, Aarthur. 1998. The G Factor: The Science of Mental Ability. Westport: Praeger Publishing. [Google Scholar]
- Jewsbury, Paul, and Stephen Bowden. 2016. Construct Validity of Fluency and Implications for the Factorial Structure of Memory. Journal of Psychoeducational Assessment 35: 460–81. [Google Scholar] [CrossRef]
- Kaufman, Alan, and Nadeen Kaufman. 2004. Kaufman Assessment Battery for Children—Second Edition (KABC-II) Manual. Circle Pines: American Guidance Service. [Google Scholar]
- Kaufman, Alan. 2004. Kaufman Test of Educational Achievement, Second Edition Comprehensive Form Manual. Circle Pines: American Guidance Service. [Google Scholar]
- Kaufman, Alan, Nadeen Kaufman, and Kristina Breaux. 2014. Technical & Interpretive Manual. Kaufman Test of Educational Achievement—Third Edition. Bloomington: NCS Pearson. [Google Scholar]
- Kaufman, Scott, Matthew Reynolds, Xin Liu, Alan Kaufman, and Kevin McGrew. 2012. Are Cognitive G and Academic Achievement G One and the Same G? An Exploration on the Woodcock-Johnson and Kaufman Tests. Intelligence 40: 123–38. [Google Scholar] [CrossRef]
- Keith, Timothy. 1999. Effects of General and Specific Abilities on Student Achievement: Similarities and Differences across Ethnic Groups. School Psychology Quarterly 14: 239–62. [Google Scholar] [CrossRef]
- Keith, Timothy, and Matthew Reynolds. 2010. Cattell-Horn-Carroll Abilities and Cognitive Tests: What We’ve Learned from 20 Years of Research. Psychology in the Schools 47: 635–50. [Google Scholar] [CrossRef]
- Koponen, Tuire, Mikko Aro, Anna-Maija Poikkeus, Pekka Niemi, Marja-Kristilina Lerkkanen, Timo Ahonen, and Jari-Erik Nurmi. 2018. Comorbid Fluency Difficulties in Reading and Math: Longitudinal Stability across Early Grades. Exceptional Children 84: 298–311. [Google Scholar] [CrossRef] [Green Version]
- Kruskal, Joseph. 1964. Nonmetric Multidimensional Scaling: A Numerical Method. Psychometrika 29: 115–29. [Google Scholar] [CrossRef]
- Li, Xueming, and Stephen Sireci. 2013. A New Method for Analyzing Content Validity Data Using Multidimensional Scaling. Educational and Psychological Measurement 73: 365–85. [Google Scholar] [CrossRef]
- Lichtenberger, Elizabeth, and Kristina Breaux. 2010. Essentials of WIAT-III and KTEA-II Assessment. Hoboken: John Wiley & Sons. [Google Scholar]
- Lohman, David, and Joni Lakin. 2011. Intelligence and Reasoning. In The Cambridge Handbook of Intelligence. Edited by Robert Sternberg and Scott Kaufman. Cambridge: Cambridge University Press, pp. 419–41. [Google Scholar]
- Lovett, Benjamin, Allyson Harrison, and Irene Armstrong. 2020. Processing Speed and Timed Academic Skills in Children with Learning Problems. Applied Neuropsychology Child 11: 320–27. [Google Scholar] [CrossRef] [PubMed]
- Mair, Patrick, Ingwer Borg, and Thomas Rusch. 2016. Goodness-of-Fit Assessment in Multidimensional Scaling and Unfolding. Multivariate Behavioral Research 51: 772–89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mair, Patric, Jan de Leeuw, Patrick Groenen, and Ingwer Borg. 2021. Smacof R Package Version 2.1-2. Available online: https://cran.r-project.org/web/packages/smacof/smacof.pdf (accessed on 28 September 2022).
- Marshalek, Brachia, David Lohman, and Richard Snow. 1983. The Complexity Continuum in the Radex and Hierarchical Models of Intelligence. Intelligence 7: 107–27. [Google Scholar] [CrossRef]
- Mather, Nancy, and Bashir Abu-Hamour. 2013. Individual Assessment of Academic Achievement. In Apa Handbook of Testing and Assessment in Psychology: Testing and Assessment in School Psychology and Education. Edited by Kurt Geisinger. Washington: American Psychological Association, pp. 101–28. [Google Scholar]
- Mather, Nancy, and Barbara Wendling. 2015. Essentials of Wj Iv Tests of Achievement. Hoboken: John Wiley & Sons. [Google Scholar]
- McGill, Ryan. 2020. An Instrument in Search of a Theory: Structural Validity of the Kaufman Assessment Battery for Children—Second Edition Normative Update at School-Age. Psychology in the Schools 57: 247–64. [Google Scholar] [CrossRef]
- McGrew, Kevin. 2012. Implications of 20 Years of Chc Cognitive-Achievement Research: Back-to-the-Future and Beyond. Medford: Richard Woodcock Institute, Tufts University. [Google Scholar]
- McGrew, Kevin, Erica LaForte, and Fredrick Schrank. 2014. Technical Manual. Woodcock-Johnson Iv. Rolling Meadows: Riverside. [Google Scholar]
- McGrew, Kevin, and Barbara Wendling. 2010. Cattell-Horn-Carroll Cognitive-Achievement Relations: What We Have Learned from the Past 20 Years of Research. Psychology in the Schools 47: 651–75. [Google Scholar] [CrossRef]
- McGrew, Kevin. 2009. CHC Theory and the Human Cognitive Abilities Project: Standing on the Shoulders of the Giants of Psychometric Intelligence Research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- Meyer, Emily, and Matthew Reynolds. 2018. Scores in Space: Multidimensional Scaling of the WISC-V. Journal of Psychoeducational Assessment 36: 562–75. [Google Scholar] [CrossRef]
- Niileksela, Christopher, and Matthew Reynolds. 2014. Global, Broad, or Specific Cognitive Differences? Using a Mimic Model to Examine Differences in Chc Abilities in Children with Learning Disabilities. Journal of Learning Disabilities 47: 224–36. [Google Scholar] [CrossRef]
- Niileksela, Christopher, Matthew Reynolds, Timothy Keith, and Kevin McGrew. 2016. A Special Validity Study of the Woodcock-Johnson IV: Acting on Evidence for Specific Abilities. In WJ IV Clinical Use and Interpretation: Scientist-Practitioner Perspectives (Practical Resources for the Mental Health Professional). Edited by Dawn P. Flanagan and Vincent C. Alfonso. San Diego: Elsevier, chp. 3. pp. 65–106. [Google Scholar]
- Norton, Elizabeth, and Maryanne Wolf. 2012. Rapid Automatized Naming (Ran) and Reading Fluency: Implications for Understanding and Treatment of Reading Disabilities. Annual Review of Psychology 63: 427–52. [Google Scholar] [CrossRef] [Green Version]
- Ortiz, Samuel, Nicole Piazza, SSalvador Hector Ochoa, and Agnieszka Dynda. 2018. Testing with Culturally and Linguistically Diverse Populations: New Directions in Fairness and Validity. In Contemporary Intellectual Assessment: Theories, Tests, and Issues. Edited by Dawn Flanagan and Erin McDonough. New York: Guilford Publications, pp. 684–712. [Google Scholar]
- Paige, David, and Theresa Magpuri-Lavell. 2014. Reading Fluency in the Middle and Secondary Grades. International Electronic Journal of Elementary Education 7: 83–96. [Google Scholar]
- Qian, Jiehui, and Ke Zhang. 2019. Working Memory for Stereoscopic Depth Is Limited and Imprecise—Evidence from a Change Detection Task. Psychonomic Bulletin & Review 26: 1657–65. [Google Scholar]
- R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Rabin, Laura, Emily Paolillo, and William Barr. 2016. Stability in Test-Usage Practices of Clinical Neuropsychologists in the United States and Canada over a 10-Year Period: A Follow-up Survey of Ins and Nan Members. Archives of Clinical Neuropsychology 31: 206–30. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, Matthew, Timothy Keith, Jodene Goldenring Fine, Melissa Fisher, and Justin Low. 2007. Confirmatory Factor Structure of the Kaufman Assessment Battery for Children—Second Edition: Consistency with Cattell-Horn-Carroll Theory. School Psychology Quarterly 22: 511–39. [Google Scholar] [CrossRef]
- Reynolds, Matthew, and Timothy Keith. 2007. Spearman’s Law of Diminishing Returns in Hierarchical Models of Intelligence for Children and Adolescents. Intelligence 35: 267–81. [Google Scholar] [CrossRef]
- Reynolds, Matthew, and Timothy Keith. 2017. Multi-Group and Hierarchical Confirmatory Factor Analysis of the Wechsler Intelligence Scale for Children-Fifth Edition: What Does It Measure? Intelligence 62: 31–47. [Google Scholar] [CrossRef]
- Schneider, Joel, and Kevin McGrew. 2018. The Cattell-Horn-Carroll Theory of Cognitive Abilities. In Contemporary Intellectual Assessment: Theories, Tests, and Issues. Edited by Dawn Flanagan and Erin McDonough. New York: Guilford Press, pp. 73–164. [Google Scholar]
- Snow, Richard, Patrick Kyllonen, and Brachia Marshalek. 1984. The Topography of Learning and Ability Correlations. Advances in the Psychology of Human Intelligence 2: 47–103. [Google Scholar]
- Süß, Heinz-Martin, and André Beauducel. 2015. Modeling the Construct Validity of the Berlin Intelligence Structure Model. Estudos de Psicologia 32: 13–25. [Google Scholar] [CrossRef] [Green Version]
- Swanson, Lee, and Linda Siegel. 2011. Learning Disabilities as a Working Memory Deficit. Experimental Psychology 49: 5–28. [Google Scholar]
- Thurstone, Louis. 1938. Primary mental abilities. Psychometric Monographs 1: 270–75. [Google Scholar]
- Tucker-Drob, Elliot, and Timothy Salthouse. 2009. Confirmatory Factor Analysis and Multidimensional Scaling for Construct Validation of Cognitive Abilities. International Journal of Behavioral Development 33: 277–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanderwood, Michael, Kevin McGrew, Dawn Flanagan, and Timothy Keith. 2002. The Contribution of General and Specific Cognitive Abilities to Reading Achievement. Learning and Individual Differences 13: 159–88. [Google Scholar] [CrossRef]
- Vernon, Philip E. 1950. The Structure of Human Abilities. London: Methuen. [Google Scholar] [CrossRef]
- Wechsler, David. 2014. Technical and Interpretive Manual for the Wechsler Intelligence Scale for Children–Fifth Edition (WISC-V). Bloomington: Pearson. [Google Scholar]
- Wickham, Hadley. 2016. Ggplot2: Elegant Graphics for Data Analysis Version. Abingdon: Taylor & Francis. [Google Scholar]



| Demographic Variable | % of Validity Sample N = 181 |
|---|---|
| Sex | |
| Female | 44.8 |
| Male | 55.2 |
| Race/Ethnicity | |
| Asian | 1.7 |
| Black | 19.9 |
| Hispanic | 21.0 |
| Other | 7.2 |
| White | 50.3 |
| Highest Parental Education | |
| Grade 8 or less | 2.2 |
| Grade 9–12, no diploma | 8.3 |
| Graduated high school or GED | 24.9 |
| Some College/Associate Degree | 35.4 |
| Undergraduate, Graduate, or Professional degree | 29.3 |
| Kaufman Test Demographic Information: KABC-II and KTEA-II Grade Subsamples | ||||
|---|---|---|---|---|
| Grades 1–3 | Grades 4–6 | Grades 7–9 | Grades 10–12 | |
| Sex | (n = 592) | (n = 558) | (n = 566) | (n = 401) |
| Female | 49.3 | 48.9 | 49.5 | 50.9 |
| Male | 50.7 | 51.1 | 50.5 | 49.1 |
| Ethnicity | ||||
| Black | 15.5 | 13.8 | 15.5 | 13.7 |
| Hispanic | 19.9 | 18.3 | 15.4 | 17.2 |
| Other | 4.7 | 6.1 | 5.7 | 5.5 |
| White | 59.8 | 61.8 | 63.4 | 63.6 |
| Highest Parent Ed. | ||||
| Grade 11 or less | 13.0 | 16.5 | 14.8 | 15.5 |
| HS graduate | 32.6 | 31.9 | 32.2 | 33.4 |
| 1–3 years college | 31.9 | 28.7 | 29.3 | 28.4 |
| 4 year degree+ | 22.5 | 22.9 | 23.7 | 22.7 |
| Geographic Region | ||||
| Northeast | 16.6 | 16.5 | 11.3 | 9.5 |
| North central | 23.6 | 27.1 | 23.0 | 27.9 |
| South | 35.5 | 33.2 | 35.0 | 35.9 |
| West | 24.3 | 23.3 | 30.7 | 26.7 |
| Age Band | ||||
| 6:00–6:11 | 20.6 | |||
| 7:00–7:11 | 30.1 | |||
| 8:00–8:11 | 31.9 | 0.2 | ||
| 9:00–9:11 | 16.7 | 16.8 | ||
| 10:00–10:11 | 0.7 | 33.7 | ||
| 11:00–11:11 | 33.3 | 0.2 | ||
| 12:00–12:11 | 14.7 | 20.5 | ||
| 13:00–13:11 | 1.1 | 32.3 | ||
| 14:00–14:11 | 0.2 | 32.0 | 0.5 | |
| 15:00–15:11 | 13.4 | 15.5 | ||
| 16:00–16:11 | 0.9 | 32.9 | ||
| 17:00–17:11 | 0.4 | 33.4 | ||
| 18:00–18:11 | 0.2 | 17.5 | ||
| 19:00–19:11 | 0.2 | 0.2 | ||
| Correlation Matrix | Ordinal, Two Dimensions | Interval, Two Dimensions | Ordinal, Three Dimensions | Interval, Three Dimensions |
|---|---|---|---|---|
| WISC-V and WIAT-III | 0.22 | 0.26 | 0.15 | 0.18 |
| Kaufman Grades 1–3 | 0.24 | 0.29 | 0.14 | 0.20 |
| Kaufman Grades 4–6 | 0.24 | 0.29 | 0.14 | 0.20 |
| Kaufman Grades 7–9 | 0.18 | 0.20 | 0.11 | 0.18 |
| Kaufman Grades 10–12 | 0.18 | 0.20 | 0.13 | 0.18 |
| Subtest Abbr. | Subtest | Composite | g-Loading or Complexity | Distance from Center |
|---|---|---|---|---|
| AR | Arithmetic | Fluid Reasoning | .73 | 0.09 |
| MPS | Math Problem Solving | Mathematics | High | 0.24 |
| LN | Letter-Number Sequencing | Working Memory | .65 | 0.26 |
| NO | Numerical Operations | Mathematics | Low | 0.39 |
| SP | Spelling | Written Expression | Low | 0.40 |
| DS | Digit Span | Working Memory | .66 | 0.40 |
| OE | Oral Expression | Oral Language | High | 0.43 |
| SI | Similarities | Verbal Comprehension | .72 | 0.45 |
| LC | Listening Comprehension | Oral Language | High | 0.50 |
| RC | Reading Comprehension | Reading Comp. & Fluency | High | 0.50 |
| MFS | Math Fluency Subtraction | Math Fluency | Medium | 0.53 |
| WR | Word Reading | Basic Reading | Low | 0.56 |
| SC | Sentence Composition | Written Expression | High | 0.56 |
| VC | Vocabulary | Verbal Comprehension | .73 | 0.62 |
| IN | Information | Verbal Comprehension | .72 | 0.63 |
| CO | Comprehension | Verbal Comprehension | .63 | 0.63 |
| DST | Delayed Symbol Translation | Symbol Translation | 0.66 | |
| PD | Pseudoword Decoding | Basic Reading | Low | 0.67 |
| ORF | Oral Reading Fluency | Reading Comp. & Fluency | Medium | 0.68 |
| RST | Recognition Symbol Translation | Symbol Translation | 0.68 | |
| PS | Picture Span | Working Memory | .55 | 0.70 |
| IST | Immediate Symbol Translation | Symbol Translation | 0.74 | |
| FW | Figure Weights | Fluid Reasoning | .64 | 0.78 |
| NSQ | Naming Speed Quantity | Naming Speed | 0.78 | |
| BD | Block Design | Visual Spatial | .64 | 0.80 |
| MFA | Math Fluency Addition | Math Fluency | Medium | 0.80 |
| CD | Coding | Processing Speed | .37 | 0.81 |
| VP | Visual Puzzles | Visual Spatial | .66 | 0.82 |
| MR | Matrix Reasoning | Fluid Reasoning | .64 | 0.82 |
| PC | Picture Concepts | Fluid Reasoning | .54 | 0.82 |
| SS | Symbol Search | Processing Speed | .42 | 0.82 |
| MFM | Math Fluency Multiplication | Math Fluency | Medium | 0.85 |
| EC | Essay Composition | Written Expression | High | 0.86 |
| NSL | Naming Speed Literacy | Naming Speed | 1.06 | |
| CA | Cancellation | Processing Speed | .19 | 1.33 |
| Subtest Abbr. | Subtest | Composite | g-Loading or Complexity | Distance from Center |
|---|---|---|---|---|
| RC | Reading Comprehension | Reading | High | 0.05 |
| MA | Math Concepts & Applications | Mathematics | High | 0.18 |
| WE | Written Expression | Written Language | High | 0.21 |
| WR | Letter & Word Recognition | Reading, Decoding | Low | 0.24 |
| TW | Word Recognition Fluency | Reading Fluency | Medium | 0.27 |
| RI | Riddles | Gc | 0.72 | 0.28 |
| VK | Verbal Knowledge | Gc | 0.71 | 0.37 |
| SP | Spelling | Written Language | Low | 0.41 |
| PR | Pattern Reasoning | Gf | 0.7 | 0.43 |
| DE | Nonsense Word Decoding | Sound-Symbol, Decoding | Low | 0.45 |
| MC | Math Computation | Mathematics | Low | 0.46 |
| EV | Expressive Vocabulary | Gc | 0.67 | 0.47 |
| OE | Oral Expression | Oral Language | High | 0.47 |
| TD | Decoding Fluency | Reading Fluency | Medium | 0.53 |
| RL | Rebus | Glr | 0.67 | 0.56 |
| LC | Listening Comprehension | Oral Language | High | 0.61 |
| RD | Rebus Delayed | Glr | 0.64 | 0.63 |
| TR | Triangles | Gv | 0.6 | 0.64 |
| PS | Phonological Awareness | Sound-Symbol | Low | 0.66 |
| PL | Phonological Awareness (Long) | Sound-Symbol | Low | 0.69 |
| AF | Associational Fluency | Oral Fluency | Low | 0.77 |
| HM | Hand Movements | Gsm | 0.52 | 0.79 |
| AT | Atlantis | Glr | 0.54 | 0.8 |
| WO | Word Order | Gsm | 0.54 | 0.8 |
| NR | Number Recall | Gsm | 0.44 | 0.86 |
| RO | Rover | Gv | 0.53 | 0.89 |
| ST | Story Completion | Gf | 0.61 | 1.03 |
| BC | Block Counting | Gv | 0.54 | 1.06 |
| AD | Atlantis Delayed | Glr | 0.43 | 1.12 |
| R2 | Naming Facility: Objects, Colors, & Letters | Oral Fluency | Low | 1.21 |
| R1 | Naming Facility: Objects & Colors | Oral Fluency | Low | 1.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meyer, E.M.; Reynolds, M.R. Multidimensional Scaling of Cognitive Ability and Academic Achievement Scores. J. Intell. 2022, 10, 117. https://doi.org/10.3390/jintelligence10040117
Meyer EM, Reynolds MR. Multidimensional Scaling of Cognitive Ability and Academic Achievement Scores. Journal of Intelligence. 2022; 10(4):117. https://doi.org/10.3390/jintelligence10040117
Chicago/Turabian StyleMeyer, Em M., and Matthew R. Reynolds. 2022. "Multidimensional Scaling of Cognitive Ability and Academic Achievement Scores" Journal of Intelligence 10, no. 4: 117. https://doi.org/10.3390/jintelligence10040117
APA StyleMeyer, E. M., & Reynolds, M. R. (2022). Multidimensional Scaling of Cognitive Ability and Academic Achievement Scores. Journal of Intelligence, 10(4), 117. https://doi.org/10.3390/jintelligence10040117





