I Choose to Opt-Out of Answering: Individual Differences in Giving Up Behaviour on Cognitive Tests
Abstract
1. Introduction
1.1. Cognition and Metacognition
1.2. Opting Out or Giving Up Behaviour
1.3. Academic Performance
1.4. Uncertainty–Monitoring Paradigm from Animal Metacognition
1.5. Aims and Hypotheses
- We postulate and compare four models: (1) a one-factor model with all performance accuracy, on-task confidence and giving up metrics defining one factor; (2) a two-factor model with performance accuracy defining one factor with confidence and giving up scores converging to define the second factor; (3) a three-factor model with a giving up factor, defined by all giving up scores across the three tasks, a confidence factor, defined by all confidence ratings, and a cognitive ability factor, defined by all performance accuracy variables; and finally, (4) a four-factor model with the broad accuracy factor splitting into two possible factors, accuracy for the tests with the embedded giving up scores and accuracy for the tests with the embedded confidence ratings. We expect that a three-factor solution would fit the data best.
- The giving up factor will (a) correlate negatively with the confidence and (b) positively with the cognitive ability factors. It will also correlate positively with (c) rational and (d) avoidant decision-making styles, and negatively or not at all with (e) dependent, (f) intuitive, and (g) spontaneous decision-making styles. Finally, the giving up factor will (h) correlate positively with academic performance.
2. Materials and Methods
2.1. Participants
2.2. Measures
2.3. Procedure
3. Results
3.1. Descriptive Statistics, Reliabilities, and Correlations between Giving Up, Confidence, Performance Accuracy and Life Outcome Measures
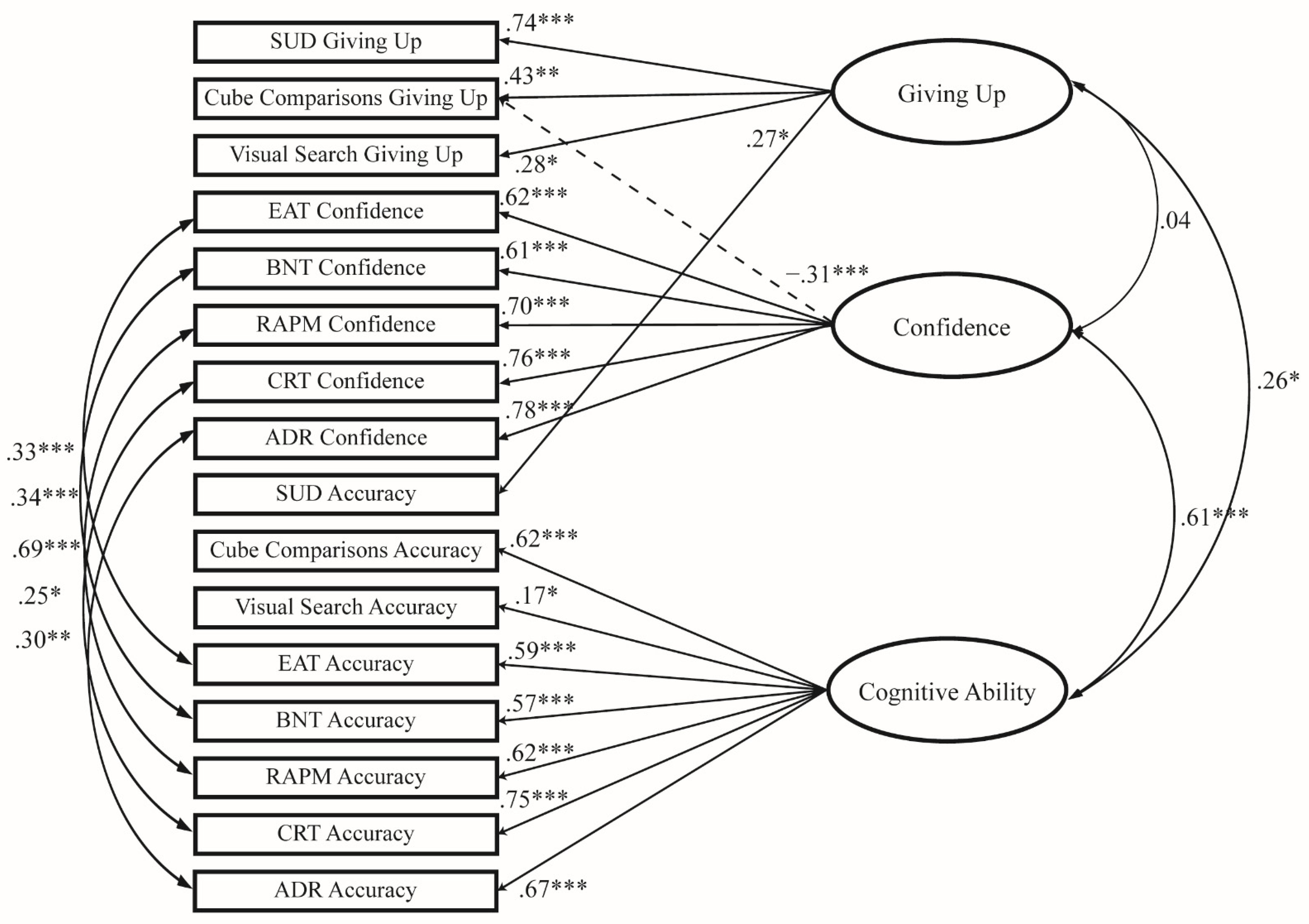
3.2. Confirmatory Factor Analysis (CFA) of Cognitive and Metacognitive Variables Using Maximum-Likelihood Method
3.3. Comparisons between Giving Up, Confidence, and Cognitive Ability Factors with All Other Variables
4. Discussion
4.1. Are Giving Up Tendencies Systematic?
4.2. Correlations with Other Variables
4.3. Limitations and Future Direction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Mean | SD | α | |
|---|---|---|---|
| GDMS Avoidant | 3.15 | 0.89 | .87 |
| GDMS Dependent | 3.82 | 0.65 | .75 |
| GDMS Intuitive | 3.64 | 0.61 | .76 |
| GDMS Rational | 3.86 | 0.59 | .75 |
| GDMS Spontaneous | 2.90 | 0.69 | .80 |
| Academic Performance | 70.77 | 9.88 | - |
| Mean | SD | α | Correlations | |||
|---|---|---|---|---|---|---|
| Giving Up | Confidence | Cognitive Ability | ||||
| Executive Function | ||||||
| Flanker Difference Score | 0.10 | 0.09 | - | −.05 | −.15 | −.16 * |
| Task Switching Difference Score | 0.08 | 0.15 | - | −.10 | −.01 | −.05 |
| Running Letters Accuracy | 0.47 | 0.19 | .71 | .15 * | .26 ** | .38 ** |
| Heuristics and Biases | ||||||
| Risky Gambles | 0.42 | 0.17 | .66 | .09 | .08 | .04 |
| Resistance to Framing | 36.18 | 4.85 | .62 | .10 | .06 | .09 |
| Social Norms Rank Score | 0.51 | 0.22 | .37 | .00 | .07 | .16 * |
| Consistency in Risk Perception | 0.87 | 0.12 | .51 | .00 | .18 * | .12 |
| Personality | ||||||
| Mini-IPIP Extraversion | 3.05 | 1.01 | .87 | −.01 | −.07 | −.15 * |
| Mini-IPIP Agreeableness | 4.00 | 0.72 | .72 | .03 | −.13 | −.14 |
| Mini-IPIP Conscientiousness | 3.22 | 0.81 | .68 | .10 | .04 | −.06 |
| Mini-IPIP Neuroticism | 3.09 | 0.81 | .65 | −.06 | −.17 * | −.03 |
| Mini-IPIP Intellect | 3.86 | 0.69 | .69 | .03 | .06 | .11 |
| BAS Drive | 2.72 | 0.59 | .80 | −.01 | .10 | −.13 |
| BAS Fun Seeking | 3.00 | 0.54 | .70 | −.05 | .03 | −.10 |
| BAS Reward Responsiveness | 3.39 | 0.42 | .72 | −.10 | −.02 | −.25 ** |
| BIS | 3.15 | 0.51 | .79 | −.01 | −.10 | −.07 |
| Need for Closure | 3.83 | 0.64 | .82 | −.05 | .03 | −.02 |
| Other Variables | ||||||
| Medical Decision-Making Test Accuracy | 0.49 | 0.24 | .78 | .01 | .15 * | .34 ** |
| Adapted Decision Outcomes Inventory Score | −0.15 | 0.08 | - | −.03 | .14 | .13 |


| 1 | Whilst the animal psychology literature labels this paradigm as “uncertainty monitoring”, this terminology may be confusing due to the metacognitive and decision-making literatures’ use of certainty judgements (i.e., confidence). In such fields, uncertainty is treated synonymously as the antithesis of certainty (e.g., 0% confidence on a response being correct). Thus, to increase clarity, we refer to the “uncertainty monitoring” variables measured in the current study as “giving up” behaviour to align with terminology which is more commonly used in the cognitive and decision-making literature. |
| 2 | When factor analyses were conducted with the paid participants removed, the pattern of results was analogous to the full sample analyses. Thus, both samples were combined to improve power (analyses conducted without paid participants can be provided upon request from the corresponding author). |
References
- Ackerman, Rakefet. 2014. The Diminishing Criterion Model for Metacognitive Regulation of Time Investment. Journal of Experimental Psychology: General 143: 1349–68. [Google Scholar] [CrossRef]
- Ackerman, Rakefet, and Yael Beller. 2017. Shared and Distinct Cue Utilization for Metacognitive Judgements during Reasoning and Memorisation. Thinking & Reasoning 23: 376–408. [Google Scholar] [CrossRef]
- Ackerman, Rakefet, and Valerie A. Thompson. 2017. Meta-Reasoning: Monitoring and Control of Thinking and Reasoning. Trends in Cognitive Sciences 21: 607–17. [Google Scholar] [CrossRef]
- Ackerman, Rakefet, Elad Yom-Tov, and Ilan Torgovitsky. 2020. Using Confidence and Consensuality to Predict Time Invested in Problem Solving and in Real-Life Web Searching. Cognition 199: 104248. [Google Scholar] [CrossRef] [PubMed]
- Basu, Sabnam, and Shikha Dixit. 2022. Role of Metacognition in Explaining Decision-Making Styles: A Study of Knowledge about Cognition and Regulation of Cognition. Personality and Individual Differences 185: 111318. [Google Scholar] [CrossRef]
- Beran, Michael J., J. David Smith, Mariana V. C. Coutinho, Justin J. Couchman, and Joseph Boomer. 2009. The Psychological Organization of ‘Uncertainty’ Responses and ‘Middle’ Responses: A Dissociation in Capuchin Monkeys (Cebus Apella). Journal of Experimental Psychology. Animal Behavior Processes 35: 371–81. [Google Scholar] [CrossRef]
- Blanchard, Matthew D., Simon A. Jackson, and Sabina Kleitman. 2020. Collective Decision Making Reduces Metacognitive Control and Increases Error Rates, Particularly for Overconfident Individuals. Journal of Behavioral Decision Making 33: 348–75. [Google Scholar] [CrossRef]
- Boekaerts, Monique. 1999. Self-Regulated Learning: Where We Are Today. International Journal of Educational Research 31: 445–57. [Google Scholar] [CrossRef]
- Brown, Timothy A. 2015. Confirmatory Factor Analysis for Applied Research, Second Edition. New York: Guilford Publications. [Google Scholar]
- Buratti, Sandra, Carl Martin Allwood, and Sabina Kleitman. 2013. First- and Second-Order Metacognitive Judgments of Semantic Memory Reports: The Influence of Personality Traits and Cognitive Styles. Metacognition and Learning 8: 79–102. [Google Scholar] [CrossRef]
- Cokely, Edward T., Mirta Galesic, Eric Schulz, Rocio Garcia-Retamero, and Saima Ghazal. 2012. Measuring Risk Literacy: The Berlin Numeracy Test. Judgment and Decision Making 7: 23. [Google Scholar]
- Coutinho, Mariana V. C., Joshua S. Redford, Barbara A. Church, Alexandria C. Zakrzewski, Justin J. Couchman, and J. David Smith. 2015. The Interplay between Uncertainty Monitoring and Working Memory: Can Metacognition Become Automatic? Memory & Cognition 43: 990–1006. [Google Scholar] [CrossRef]
- Cronbach, Lee J. 1951. Coefficient Alpha and the Internal Structure of Tests. Psychometrika 16: 297–334. [Google Scholar] [CrossRef]
- de Bruin, Wandi Bruine, Andrew M. Parker, and Baruch Fischhoff. 2007. Individual Differences in Adult Decision-Making Competence. Journal of Personality and Social Psychology 92: 938–56. [Google Scholar] [CrossRef] [PubMed]
- Ekstrom, Ruth B., John W. French, Harry H. Harmon, and Diran Dermen. 1976. Manual for Kit of Factor-Referenced Cognitive Tests. Princeton: Educational Testing Service. [Google Scholar]
- Frederick, Shane. 2005. Cognitive Reflection and Decision Making. Journal of Economic Perspectives 19: 25–42. [Google Scholar] [CrossRef]
- Goldsmith, Morris. 2016. Metacognitive Quality-Control Processes in Memory Retrieval and Reporting. In The Oxford Handbook of Metamemory. Oxford: Oxford Academic. [Google Scholar] [CrossRef]
- Goldsmith, Morris, Ainat Pansky, and Asher Koriat. 2014. Metacognitive Control of Memory Reporting. In The SAGE Handbook of Applied Memory. Edited by Timothy J. Perfect and D. Stephen Lindsay. London: SAGE Publications, pp. 481–500. [Google Scholar]
- Graham, John W., Patricio E. Cumsille, and Allison E. Shevock. 2013. Methods for Handling Missing Data. In Handbook of Psychology: Research Methods in Psychology, 2nd ed. Edited by Irving B. Weiner, John A. Schinka and Wayne F. Velicer. Hoboken: John Wiley & Sons, Inc., vol. 2, pp. 109–41. [Google Scholar]
- Grice, Herbert. P. 1975. Logic and Conversation. Leiden: Brill. [Google Scholar] [CrossRef]
- Hanczakowski, Maciej, Tomasz Pasek, Katarzyna Zawadzka, and Giuliana Mazzoni. 2013. Cue Familiarity and ‘Don’t Know’ Responding in Episodic Memory Tasks. Journal of Memory and Language 69: 368–83. [Google Scholar] [CrossRef]
- Händel, Marion, Anique B. H. de Bruin, and Markus Dresel. 2020. Individual Differences in Local and Global Metacognitive Judgments. Metacognition and Learning 15: 51–75. [Google Scholar] [CrossRef]
- Hu, Li-tze, and Peter M. Bentler. 1999. Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Structural Equation Modeling: A Multidisciplinary Journal 6: 1–55. [Google Scholar] [CrossRef]
- IBM Corp. 2020. IBM SPSS Statistics for Windows. version 27.0. Armonk: IBM Corp. [Google Scholar]
- Jackson, Simon A., Sabina Kleitman, Pauline Howie, and Lazar Stankov. 2016. Cognitive Abilities, Monitoring Confidence, and Control Thresholds Explain Individual Differences in Heuristics and Biases. Frontiers in Psychology 7: 1559. [Google Scholar] [CrossRef]
- Jackson, Simon A., Sabina Kleitman, Lazar Stankov, and Pauline Howie. 2017. Individual Differences in Decision Making Depend on Cognitive Abilities, Monitoring and Control: Individual Differences in Decision Making. Journal of Behavioral Decision Making 30: 209–23. [Google Scholar] [CrossRef]
- Kleitman, Sabina, Marvin K. H. Law, and Judy Kay. 2018. It’s the Deceiver and the Receiver: Individual Differences in Phishing Susceptibility and False Positives with Item Profiling. PLoS ONE 13: e0205089. [Google Scholar] [CrossRef]
- Kleitman, Sabina, Jessica Sik-Wai Hui, and Yixin Jiang. 2019. Confidence to Spare: Individual Differences in Cognitive and Metacognitive Arrogance and Competence. Metacognition and Learning 14: 479–508. [Google Scholar] [CrossRef]
- Koriat, Asher, and Morris Goldsmith. 1996. Monitoring and Control Processes in the Strategic Regulation of Memory Accuracy. Psychological Review 103: 497–517. [Google Scholar] [CrossRef] [PubMed]
- Kozhevnikov, Maria, and Mary Hegarty. 2001. A Dissociation between Object Manipulation Spatial Ability and Spatial Orientation Ability. Memory & Cognition 29: 745–56. [Google Scholar] [CrossRef]
- Lauterman, Tirza, and Rakefet Ackerman. 2019. Initial Judgment of Solvability in Non-Verbal Problems—A Predictor of Solving Processes. Metacognition and Learning 14: 365–83. [Google Scholar] [CrossRef]
- Law, Marvin K. H., Simon A. Jackson, Eugene Aidman, Mattis Geiger, Sally Olderbak, and Sabina Kleitman. 2018. It’s the Deceiver, Not the Receiver: No Individual Differences When Detecting Deception in a Foreign and a Native Language. PLoS ONE 13: e0196384. [Google Scholar] [CrossRef] [PubMed]
- Lichtenstein, Sarah, and Baruch Fischhoff. 1977. Do Those Who Know More Also Know More about How Much They Know? Organizational Behavior and Human Performance 20: 159–83. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2009. CHC Theory and the Human Cognitive Abilities Project: Standing on the Shoulders of the Giants of Psychometric Intelligence Research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- Moore, Don A., and Paul J. Healy. 2008. The Trouble with Overconfidence. Psychological Review 115: 502–17. [Google Scholar] [CrossRef] [PubMed]
- Neisser, Ulric, Gwyneth Boodoo, Thomas J. Bouchard, A. Wade Boykin, Nathan Brody, Stephen J. Ceci, Diane E. Halpern, John C. Loehlin, Robert Perloff, Robert Sternberg, and et al. 1996. Intelligence: Knowns and Unknowns. American Psychologist 51: 77–101. [Google Scholar] [CrossRef]
- Nelson, Thomas O., and Louis Narens. 1990. Metamemory: A Theoretical Framework and New Findings. Psychology of Learning and Motivation 26: 125–73. [Google Scholar] [CrossRef]
- Nusbaum, Emily C., and Paul J. Silvia. 2011. Are Intelligence and Creativity Really so Different?: Fluid Intelligence, Executive Processes, and Strategy Use in Divergent Thinking. Intelligence 39: 36–45. [Google Scholar] [CrossRef]
- Parker, Andrew M., and Baruch Fischhoff. 2005. Decision-Making Competence: External Validation through an Individual-Differences Approach. Journal of Behavioral Decision Making 18: 1–27. [Google Scholar] [CrossRef]
- Payne, Stephen J., and Geoffrey B. Duggan. 2011. Giving Up Problem Solving. Memory & Cognition 39: 902–13. [Google Scholar] [CrossRef]
- R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Raven, John C. 1938. Progressive Matrices. New York: The Psychological Corporation. [Google Scholar]
- Rohde, Treena Eileen, and Lee Anne Thompson. 2007. Predicting Academic Achievement with Cognitive Ability. Intelligence 35: 83–92. [Google Scholar] [CrossRef]
- Rosseel, Yves. 2012. Lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software 48: 1–36. [Google Scholar] [CrossRef]
- Schlösser, Thomas, David Dunning, Kerri L. Johnson, and Justin Kruger. 2013. How Unaware Are the Unskilled? Empirical Tests of the ‘Signal Extraction’ Counterexplanation for the Dunning–Kruger Effect in Self-Evaluation of Performance. Journal of Economic Psychology 39: 85–100. [Google Scholar] [CrossRef]
- Scott, Susanne G., and Reginald A. Bruce. 1995. Decision-Making Style: The Development and Assessment of a New Measure. Educational and Psychological Measurement 55: 818–31. [Google Scholar] [CrossRef]
- Smith, J. David, Wendy E. Shields, Jonathan Schull, and David A. Washburn. 1997. The Uncertain Response in Humans and Animals. Cognition 62: 75–97. [Google Scholar] [CrossRef]
- Smith, J. David, Michael J. Beran, Joshua S. Redford, and David A. Washburn. 2006. Dissociating Uncertainty Responses and Reinforcement Signals in the Comparative Study of Uncertainty Monitoring. Journal of Experimental Psychology: General 135: 282–97. [Google Scholar] [CrossRef]
- Spicer, David P., and Eugene Sadler-Smith. 2005. An Examination of the General Decision Making Style Questionnaire in Two UK Samples. Journal of Managerial Psychology 20: 137–49. [Google Scholar] [CrossRef]
- Stankov, Lazar. 1997. Gf–Gc Quickie Test Battery. Unpublished Test Battery Available from the School of Psychology, University of Sydney. Sydney: University of Sydney. [Google Scholar]
- Stankov, Lazar. 2013. Noncognitive Predictors of Intelligence and Academic Achievement: An Important Role of Confidence. Personality and Individual Differences 55: 727–32. [Google Scholar] [CrossRef]
- Stankov, Lazar, and Jihyun Lee. 2008. Confidence and Cognitive Test Performance. Journal of Educational Psychology 100: 961–76. [Google Scholar] [CrossRef]
- Stankov, Lazar, Jihyun Lee, Wenshu Luo, and David J. Hogan. 2012. Confidence: A Better Predictor of Academic Achievement than Self-Efficacy, Self-Concept and Anxiety? Learning and Individual Differences 22: 747–58. [Google Scholar] [CrossRef]
- Stankov, Lazar, Suzanne Morony, and Yim Ping Lee. 2014. Confidence: The Best Non-Cognitive Predictor of Academic Achievement? Educational Psychology 34: 9–28. [Google Scholar] [CrossRef]
- Stankov, Lazar, Sabina Kleitman, and Simon A. Jackson. 2015. Measures of the Trait of Confidence. In Measures of Personality and Social Psychological Constructs. Edited by Gregory J. Boyle, Donald H. Saklofske and Gerald Matthews. Cambridge: Academic Press, pp. 158–89. [Google Scholar] [CrossRef]
- Suantak, Liana, Fergus Bolger, and William R. Ferrell. 1996. The Hard–Easy Effect in Subjective Probability Calibration. Organizational Behavior and Human Decision Processes 67: 201–21. [Google Scholar] [CrossRef]
- Tabachnick, Barbara, and Linda Fidell. 2013. Using Multivariate Statistics: Pearson New International Edition PDF EBook, 6th ed. Harlow: Pearson Education, Limited. [Google Scholar]
- Toplak, Maggie E., Richard F. West, and Keith E. Stanovich. 2017. Real-World Correlates of Performance on Heuristics and Biases Tasks in a Community Sample. Journal of Behavioral Decision Making 30: 541–54. [Google Scholar] [CrossRef]
- Toplak, Maggie E., Richard F. West, and Keith E. Stanovich. 2014. Assessing Miserly Information Processing: An Expansion of the Cognitive Reflection Test. Thinking & Reasoning 20: 147–68. [Google Scholar] [CrossRef]
- Undorf, Monika, Iris Livneh, and Rakefet Ackerman. 2021. Metacognitive Control Processes in Question Answering: Help Seeking and Withholding Answers. Metacognition and Learning 16: 431–58. [Google Scholar] [CrossRef]
- Waschl, Nicolette A., Ted Nettelbeck, Simon A. Jackson, and Nicholas R. Burns. 2016. Dimensionality of the Raven’s Advanced Progressive Matrices: Sex Differences and Visuospatial Ability. Personality and Individual Differences 100: 157–66. [Google Scholar] [CrossRef]
- Washburn, David A., J. David Smith, and Lauren A. Taglialatela. 2005. Individual Differences in Metacognitive Responsiveness: Cognitive and Personality Correlates. The Journal of General Psychology 132: 446–61. [Google Scholar] [CrossRef]
- Waters, Erika A., Jennifer L. Hay, Heather Orom, Marc T. Kiviniemi, and Bettina F. Drake. 2013. ‘Don’t Know’ Responses to Risk Perception Measures: Implications for Underserved Populations. Medical Decision Making: An International Journal of the Society for Medical Decision Making 33: 271–81. [Google Scholar] [CrossRef] [PubMed]
- Weber, Nathan, and Neil Brewer. 2008. Eyewitness Recall: Regulation of Grain Size and the Role of Confidence. Journal of Experimental Psychology: Applied 14: 50–60. [Google Scholar] [CrossRef] [PubMed]
- Weber, Nathan, and Timothy J. Perfect. 2011. Improving Eyewitness Identification Accuracy by Screening Out Those Who Say They Don’t Know. Law and Human Behavior 36: 28–36. [Google Scholar] [CrossRef]
- West, Richard F., Maggie E. Toplak, and Keith E. Stanovich. 2008. Heuristics and Biases as Measures of Critical Thinking: Associations with Cognitive Ability and Thinking Dispositions. Journal of Educational Psychology 100: 930–41. [Google Scholar] [CrossRef]
- Wilhelm, Oliver, Andrea Hildebrandt, Karsten Manske, Annekathrin Schacht, and Werner Sommer. 2014. Test Battery for Measuring the Perception and Recognition of Facial Expressions of Emotion. Frontiers in Psychology 5: 404. [Google Scholar] [CrossRef]

| Measure | Example Item | Reliability from Previous Studies |
|---|---|---|
| Cognitive Tasks with embedded giving up options | ||
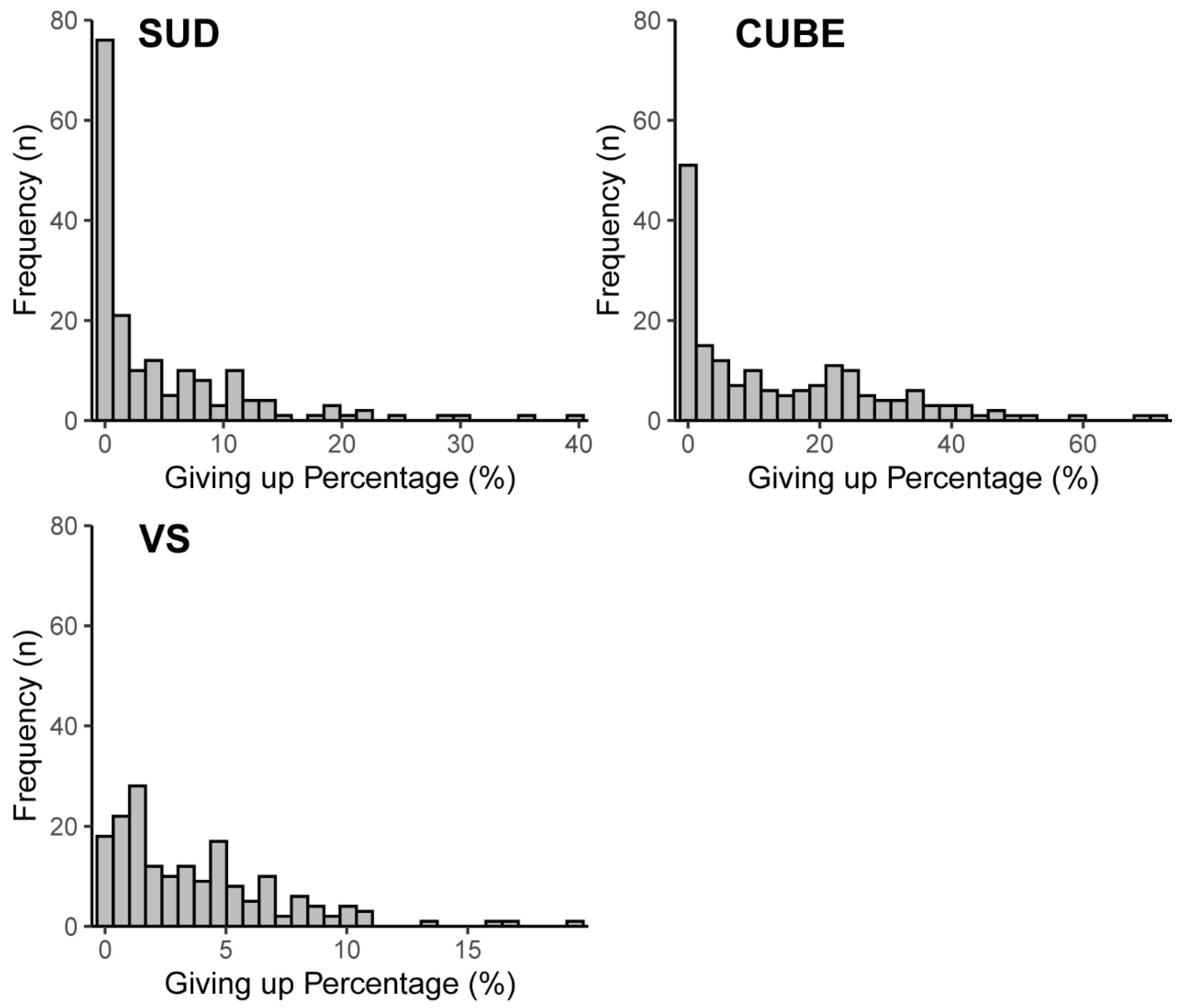
| Sparse-Uncertainty-Dense (SUD) Task—Beran et al. (2009). A visual processing task which was developed within animal psychology research to examine metacognition in animals and humans (Beran et al. 2009; Smith et al. 2006). For this task, participants are shown pixel density boxes and were asked to decide whether the number of pixels in the box constitutes as sparse or dense with correct responses eliciting rewards and incorrect responses eliciting punishments. The most sparse and dense items were given to participants as practise prior to the task. For the current study, a point system and item time delays were used as reward and punishment incentives with correct responses leading to a point increase and time delays between items of one second whilst incorrect responses had a point reduction and a time delay of eight seconds a. To measure giving up, participants were given a third option to select that they are uncertain about the answer, which will skip over the current item, eliciting no point change and a time delay of two seconds. Following prior studies, pixel density plots were 200 × 100 pixels in area with pixel densities ranging from 1085 to 2255 with a 1.8% increase in pixel density per level (Beran et al. 2009). Ultimately, 42 levels were constructed with the first 21 defined as sparse and the latter 21 defined as dense. These pixel boxes were constructed using a pixel density randomisation script in JavaScript (source code available by request). Participants were shown each level three times over the task. Overall accuracy and giving up scores were measured for this task, with accuracy being the percentage of correct responses out of all attempted items and giving up scores, being the percentage of uncertain responses out of all items (126—three repetitions of the 42 items). | see Figure 1 | - |
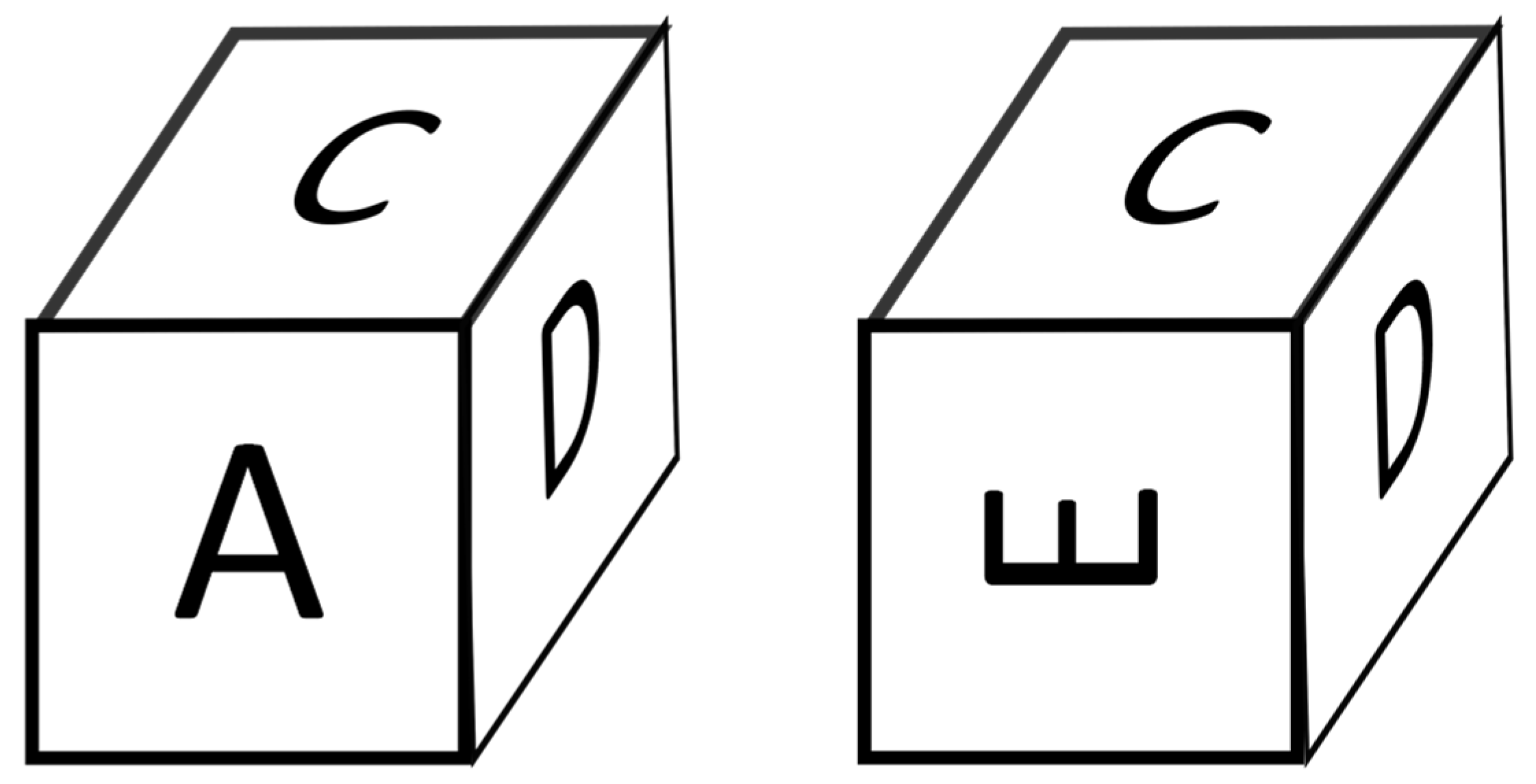
| Cube Comparisons—Ekstrom et al. (1976). The Cube Comparisons Task is a measure of visual processing from the ETS’s Kit of Factor Referenced Cognitive Tests with 42 items. For each item, participants are shown three faces of two cubes and must decide if they think that the cubes could potentially be the same cube or are definitely different. Similar to the SUD task, a third “uncertain” option was added for when participants were uncertain about answering. Prior to the task, participants were shown some practise items with feedback. Overall accuracy and giving up scores were calculated in the same way as that in the SUD task. For this task, there was no feedback nor reward/punishment for responding. | See Ekstrom et al. (1976) and Figure A1 in the Appendix A. | Original measure: .84 (Kozhevnikov and Hegarty 2001). |
| Visual Search for Faces with Corresponding Emotion Expressions of Different Intensity—Short Form—Wilhelm et al. (2014). This task is a short 20-item measure of emotion perception. For each of the twenty items, participants are shown 9 different faces of the same individual in a 3 × 3 grid, with each face displaying a certain emotion. Participants must discern which of the faces do not express the same emotion as the majority of the faces. Adapting to measure giving up, an “uncertain” option was provided for each of the faces in the items, with participants being allowed to choose uncertain rather than make a decision on whether the face was part of the majority emotion or not. As a result, participants were not allowed to select uncertain and make a decision on the same face. Participants were shown an example item before the task. Following prior research, accuracy on the task was measured using Unbiased Hit Rates which control for both Hit and False rates. Akin to the other two tasks measuring giving up, overall giving up scores were measured as the percentage of uncertain responses out of all possible face selections (180). | See Wilhelm et al. (2014) and Figure A2 in the Appendix A. | .89 (Law et al. 2018) |
| Cognitive tasks with embedded confidence ratings | ||
| Esoteric Analogies Test (EAT)—Stankov (1997). The EAT is a measure of both fluid and crystallised intelligence with the current study using a twenty-item version. For each item, participants are shown a pair of words and an additional word. They are then given four multiple choice options and must decide which option relates to the additional word in the same way that the pair of words relate to each other. Accuracy on this score is measured by the percentage of items correct. | SPACE is to POINT as TIME is to: CLOCK, ETERNITY, MOMENT*, POSITION | .70 to .72 (Kleitman et al. 2018; Stankov 1997) |
| Berlin Numeracy Test (BNT)—Cokely et al. (2012). The BNT is a measure of numerical ability, more specifically, statistical and risk literacy. We used the four-item version of the BNT, with every item being a mathematical question which asks for an open-ended numeric answer. Accuracy was measured through percentage of items correct. Although the measure only consists of four items, it has been shown to predict risk understanding more effectively than other longer numeric and intelligence measures. | Imagine we are throwing a five-sided die 50 times. On average, out of these 50 throws how many times would this five-sided die show an odd number (1, 3 or 5)? ____ out of 50 throws | Test-retest reliability: .91 (Cokely et al. 2012). |
| Raven’s Advanced Progressive Matrices (RAPM)—Raven (1938) and Waschl et al. (2016). RAPM is a measure of fluid intelligence which has been used frequently within the individual differences literature (McGrew 2009; Waschl et al. 2016). For each item, participants are shown a 3 × 3 grid of abstract figures with the bottom right figure being left blank. The participants are shown eight different options and must decide which option best fits the pattern shown in the grid. Based on previous research, the current study used a 15-item version which has been validated in prior research (Waschl et al. 2016). Accuracy is measured as the percentage of correct items. | See Raven (1938) and Figure A3 in the Appendix A for example. | .80 (Jackson et al. 2017) |
| Cognitive Reflection Test (CRT)—Frederick (2005) and Toplak et al. (2014). The CRT is a reasoning measure of susceptibility to heuristics and biases where participants must answer open-ended questions which have been constructed to prompt incorrect intuitive answers. The current study used the extended 7-item CRT (Toplak et al. 2014). Accuracy on the CRT is measured by percentage correct. | A bat and a ball cost $1.10 in total. The bat costs a dollar more than the ball. How much does the ball cost? ____ cents. | .70 (Jackson et al. 2016) |
| Applying Decision Rules (ADR)—(de Bruin et al. 2007). The ADR is a reasoning measure testing heuristics and biases susceptibility where participants are shown attribute information on five different DVD players, with four different attributes (e.g., sound quality) each with varying levels of performance ratings from 1 (very low) to 5 (very high). For each of the ten items, participants are given a scenario and must then select the DVD player/s which best fit the scenario. An accuracy score is computed by the percentage of answers correct. | LaToya only wants a DVD player that has got a “Very High” rating on Sound Quality | .60 (Jackson et al. 2016) |
| Decision-Making Styles | ||
| General Decision-Making Styles (GDMS) Scale—(Scott and Bruce 1995). The GDMS scale measures people’s decision-making tendencies with 25 self-report items with 5 items each relating to 5 different decision-making styles: rational, avoidant, dependent, intuitive, and spontaneous. Participants must respond from 1 (strongly disagree) to 5 (strongly agree) for each item. Average scores for each decision-making style are calculated, with higher scores indicating higher style propensity. | Rational: I make decisions in a logical and systematic way. Avoidant: I avoid making important decisions until the pressure is on. Dependent: I rarely make important decisions without consulting other people. Intuitive: When making decisions, I rely upon my instincts. Spontaneous: I often make impulsive decisions | .67 to .87 (Scott and Bruce 1995; Spicer and Sadler-Smith 2005) |
| Real-Life Outcomes | ||
| Academic performance. To measure academic performance, overall weighted average marks (WAM) from consenting participants were collected (n = 130). | - | - |
| Mean | SD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Giving Up Score | ||||||||||||||||||
| 1. SUD | 4.61 | 7.01 | (.94) | |||||||||||||||
| 2. CUBE | 14.02 | 15.35 | .32 ** | (.91) | ||||||||||||||
| 3. VS | 3.73 | 3.45 | .21 ** | .03 | (.78) | |||||||||||||
| Confidence | ||||||||||||||||||
| 4. EAT | 68.96 | 11.22 | .02 | −.21 ** | .06 | (.83) | ||||||||||||
| 5. BNT | 63.38 | 24.93 | .07 | −.17 * | .06 | .29 ** | (.83) | |||||||||||
| 6. RAPM | 65.60 | 19.93 | −.01 | −.16 * | .05 | .46 ** | .46 ** | (.91) | ||||||||||
| 7. CRT | 76.70 | 17.77 | .00 | −.29 ** | .03 | .47 ** | .54 ** | .52 ** | (.79) | |||||||||
| 8. ADR | 83.65 | 14.69 | .02 | −.22 ** | .02 | .53 ** | .41 ** | .57 ** | .61 ** | (.87) | ||||||||
| Performance Accuracy | ||||||||||||||||||
| 9. SUD | 87.17 | 3.80 | .20 ** | .07 | .16 * | −.01 | −.02 | −.02 | −.04 | −.02 | (.79) | |||||||
| 10. CUBE | 74.55 | 13.39 | .14 | .10 | .07 | .24 ** | .36 ** | .36 ** | .17 * | .21 ** | .02 | (.85) | ||||||
| 11. VS | 70.61 | 12.10 | −.01 | −.05 | .00 | .01 | .11 | .05 | −.04 | −.10 | .07 | .12 | (.86) | |||||
| 12. EAT | 64.13 | 16.06 | .09 | −.05 | .11 | .43 ** | .25 ** | .30 ** | .30 ** | .29 ** | .02 | .36 ** | .15 * | (.69) | ||||
| 13. BNT | 42.61 | 30.39 | .16 * | −.07 | .12 | .17 * | .52 ** | .29 ** | .31 ** | .19 * | .09 | .30 ** | .18 * | .39 ** | (.55) | |||
| 14. RAPM | 60.68 | 22.75 | .05 | .02 | .12 | .23 ** | .38 ** | .69 ** | .30 ** | .30 ** | .06 | .52 ** | .10 | .37 ** | .39 ** | (.79) | ||
| 15. CRT | 46.43 | 32.16 | .11 | −.04 | .15 * | .27 ** | .50 ** | .40 ** | .45 ** | .31 ** | −.02 | .44 ** | .13 | .39 ** | .53 ** | .49 ** | (.78) | |
| 16. ADR | 62.69 | 21.55 | .11 | −.09 | .05 | .21 ** | .36 ** | .23 ** | .19 * | .37 ** | .01 | .44 ** | .12 | .43 ** | .38 ** | .38 ** | .50 ** | (.64) |
| χ2 | df | χ2/df | TLI | CFI | RMSEA (90% CI) | AIC | SRMR | |
|---|---|---|---|---|---|---|---|---|
| One-factor model | 387.502 | 104 | 3.726 | .618 | .669 | .124 (.111–.138) | 22,370.5 | .092 |
| Two-factor model | 309.666 | 103 | 3.006 | .719 | .759 | .107 (.093–.121) | 22,294.7 | .084 |
| Three-factor model | 284.124 | 101 | 2.813 | .746 | .786 | .101 (.088–.116) | 22,273.1 | .080 |
| Four-factor model | 277.246 | 98 | 2.829 | .744 | .791 | .102 (.088–.116) | 22,272.2 | .079 |
| Three-factor model—Modified | 123.273 | 95 | 1.298 | .958 | .967 | .041 (.015–.060) | 22,124.3 | .060 |
| Giving Up | Confidence | Cognitive Ability | |
|---|---|---|---|
| GDMS Avoidant | .05 | −.15 * | −.03 |
| GDMS Dependent | .08 | −.01 | .00 |
| GDMS Intuitive | −.11 | −.08 | −.16 * |
| GDMS Rational | .18 * | .20 ** | .10 |
| GDMS Spontaneous | .01 | .05 | .02 |
| Academic Performance | .19 * | .18 * | .35 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Law, M.K.H.; Stankov, L.; Kleitman, S. I Choose to Opt-Out of Answering: Individual Differences in Giving Up Behaviour on Cognitive Tests. J. Intell. 2022, 10, 86. https://doi.org/10.3390/jintelligence10040086
Law MKH, Stankov L, Kleitman S. I Choose to Opt-Out of Answering: Individual Differences in Giving Up Behaviour on Cognitive Tests. Journal of Intelligence. 2022; 10(4):86. https://doi.org/10.3390/jintelligence10040086
Chicago/Turabian StyleLaw, Marvin K. H., Lazar Stankov, and Sabina Kleitman. 2022. "I Choose to Opt-Out of Answering: Individual Differences in Giving Up Behaviour on Cognitive Tests" Journal of Intelligence 10, no. 4: 86. https://doi.org/10.3390/jintelligence10040086
APA StyleLaw, M. K. H., Stankov, L., & Kleitman, S. (2022). I Choose to Opt-Out of Answering: Individual Differences in Giving Up Behaviour on Cognitive Tests. Journal of Intelligence, 10(4), 86. https://doi.org/10.3390/jintelligence10040086






