Carroll’s Three-Stratum (3S) Cognitive Ability Theory at 30 Years: Impact, 3S-CHC Theory Clarification, Structural Replication, and Cognitive–Achievement Psychometric Network Analysis Extension
Abstract
1. Introduction
2. Carroll’s 3S Theory Impact on CHC Theory and Intelligence Testing
2.1. Carroll’s 3S Theory’s Connection with CHC Theory: An Arranged Marriage of Convenience
2.2. Criticisms of Carroll’s 3S and CHC Theory
2.3. A Recommended Name Change: CHC Theories—Not CHC Theory
2.4. Summary Comments
3. A Replication and Extension of Carroll’s (2003) Comparison of the Three Primary Structural Models of Cognitive Abilities
3.1. Carroll’s (2003) Analyses That Supported His Standard Multifactorial 3S View of Intelligence
3.2. Confirmation of Carroll’s 3S Multifactorial View with 46 WJ III Tests
3.3. A Note on Factor Analysis as per Carroll: Art and Science
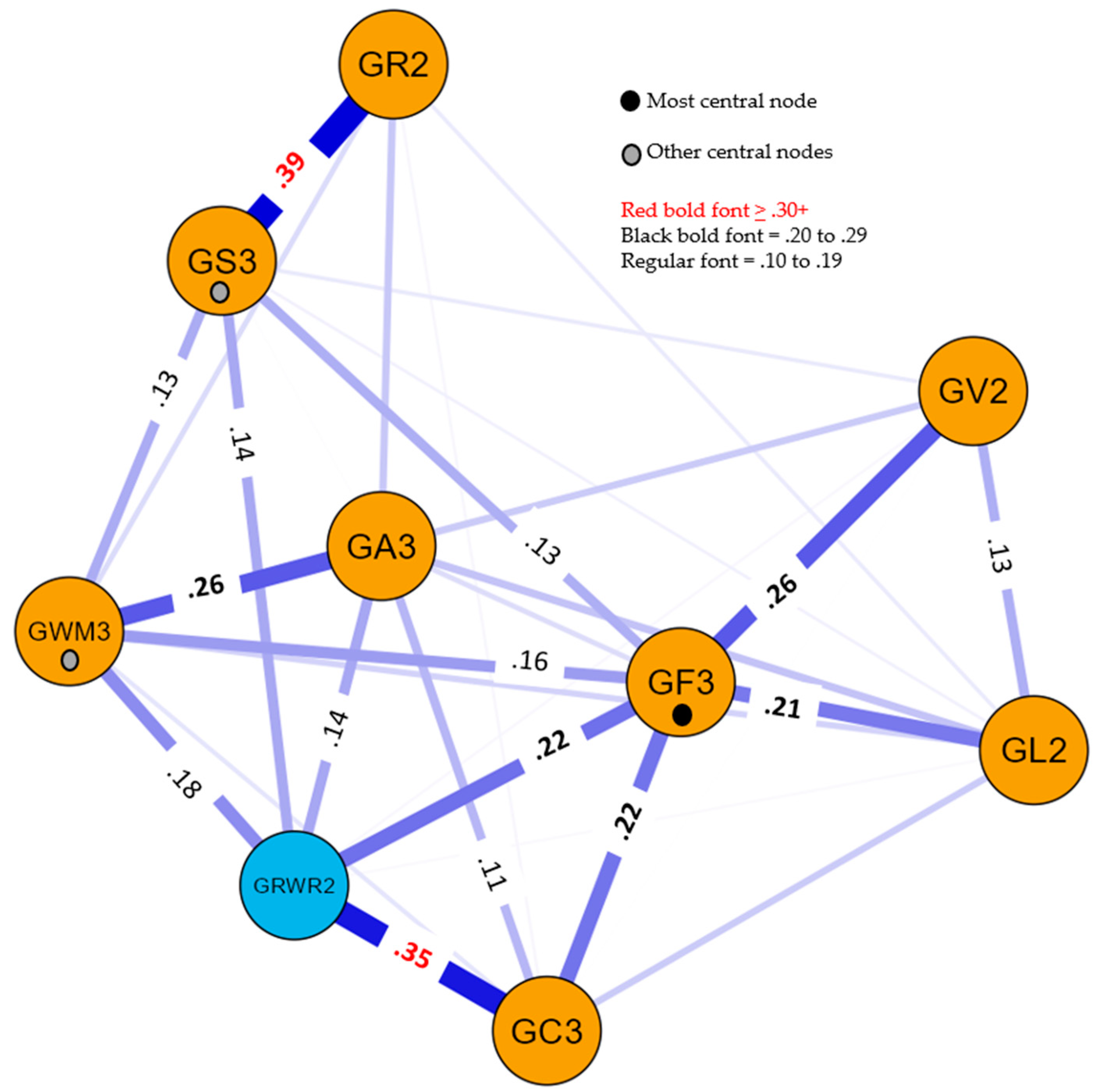
4. In Search of Cognitive and Achievement Causal Mechanisms: A Carroll Higher-Stratum Psychometric Network Analysis
After talking with Carroll, I began to worry that none of us really knew very much about the mental mechanisms and processes involved with 3S and Horn–Cattell broad abilities. I was floored when I later learned that Carroll (1974, 1976, 1981) had made serious efforts to characterize cognitive factors in terms of their constituent cognitive processes, and that he had developed a complete taxonomy of cognitive processes used in the performance of elementary cognitive tasks before he started his famous survey of mental abilities. Carroll’s ultimate goal, I believe, was to survey the full range of cognitive factors with each factor broken down into its constituent elementary cognitive processes. It would be analogous to setting up Linnaeus’s eighteenth-century binomial nomenclature—which introduced the standard hierarchy of class, order, genus, and species—to classify species based on their DNA!(p. 254)
4.1. Psychometric Network Analysis Methods: A Brief Introduction
4.2. A Carroll-Inspired Higher-Stratum PNA Analysis of Cognitive–Achievement Variables
4.2.1. Methodology
4.2.2. Results and Discussion
5. Summary
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | |
| 2 | The broad CHC ability names, definitions, and abbreviations are drawn from Schneider and McGrew (2018): Gc (Comprehension-Knowledge), Grw (Reading and Writing), Gq (Quantitative Knowledge), Gf (Fluid Reasoning), Gwm (Short-term Working Memory), Gv (Visual–spatial Processing), Ga (Auditory Processing), Gl (Learning Efficiency), Gr (Retrieval Fluency), and Gs (Processing Speed). Definitions for these broad and narrow CHC abilities are included in Supplementary Materials Section S1. |
| 3 | See the personal reflections of Julian Stanley, David Lubinski, A. T. Panter, and Lyle V. Jones published by the Association for Psychological Science (APS) on 9 November 2003 (https://www.psychologicalscience.org/observer/in-appreciation-john-b-carroll (accessed on 4 October 2021)). |
| 4 | The lower-case italic subscripted notation (e.g., gf and gc) recognizes that Cattell’s general capacities were more consistent with (but different from) Spearman’s general intelligence (g). The more common upper case CHC theory ability notation (e.g., Gf and Gc) acknowledges both Horn and Carroll’s notions of broad abilities. See Schneider and McGrew (2018) for a brief discussion. |
| 5 | Carroll used the older Glr and Gsm notation for two factors. These CHC factor labels, where appropriate, have been changed to Gl and Gr (formerly together as Glr), and Gwm as per the most recent iteration of CHC theory (Schneider and McGrew 2018). |
| 6 | In Carroll’s (2003) analyses, he used the complete variable names in the correlation matrices presented in that publication (Tables 1.1 and 1.4), but used his own test variable name abbreviations when presenting the results of his factor analysis (Tables 1.2, 1.3, and 1.5). His test name abbreviations are included here for those interested in linking the current discussion with the formal factor analysis output presented in his 2003 chapter. In this section, MC factor loadings from Table 1 are in regular font, while Carroll analysis factor loadings (Table 1.5 in Carroll 2003) are in italic font. |
| 7 | As defined by Schneider and McGrew (2018), “Major factors are those that represent the core characteristics of the domain, typically represent more complex cognitive processing, tend to display higher loadings on the g factor when present in the analysis, and are more predictive and clinically useful. Minor factors typically are less useful, less cognitively complex, and less g-loaded.” (p. 141; emphasis added). |
| 8 | As would be expected, each test’s loadings on the nine CHC factors in the hierarchical g and Horn no-g models had identical factor loadings (save for a few differences to the second decimal place) and only differed in the specification of the covariance of the first-order latent CHC factors (see Supplementary Materials Section S5, Tables S4 and S6) as correlated factors or as loadings on the second-order g factor. Furthermore, inspection of fit statistics found that the MC analysis bifactor (CFI = .890; TLI = .878; RMSEA = .063 [90% CI 0.62–0.65]), hierarchical g (CFI = .871; TLI = .862; RMSEA = .067 [90% CI 0.66–0.69]), and Horn no-g (CFI = .880; TLI = .868; RMSEA = .066 [90% CI 0.65–0.67]) models did not differ substantially in model fit (see Supplementary Materials Section S4, Tables S3, S5 and S8). Substantive theoretical considerations would be important in determining which of the three models was a “better” model, a discussion beyond the scope of the current paper. |
| 9 | Supplementary Materials Section S6 includes a copy of Carroll’s last known recorded thoughts regarding the psychometric g factor (copy of hand printed note dated 6-11-03 and a transcribed version). This note includes the referenced personal communication statement. |
| 10 | Carroll used the phrase “computer scientists … [as a] shorthand label, as it were, for a wide class of educational research specialists. Not all of those I refer to in this way are necessarily computer scientists in the strict sense”(Carroll 1985, p. 384). Instead, Carroll used this label to characterize a class of researchers as described in this paragraph (i.e., the hard-nosed methodologists). |
References
- Ackerman, Philip L. 1996. A theory of adult intellectual development: Process, personality, interests, and knowledge. Intelligence 22: 227–57. [Google Scholar] [CrossRef]
- Ackerman, Philip L. 2018. Intelligence-as-process, personality, interests, and intelligence-as-knowledge: A framework for adult intellectual development. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 4th ed. Edited by Dawn P. Flanagan and Erin M. McDonough. New York: The Guilford Press, pp. 225–41. [Google Scholar]
- Alexander, William P. 1934. Research in guidance: A theoretical basis. Occupations: The Vocational Guidance Magazine 12: 75–91. [Google Scholar] [CrossRef]
- Anderson, Lorin. W. 1985. Perspectives on School Learning: Selected Writings of John B. Carroll. Hillsdale: Lawrence Erlbaum Associates. [Google Scholar]
- Angelelli, Paola, Daniele L. Romano, Chiara V. Marinelli, Luigi Macchitella, and Pierluigi Zoccolotti. 2021. The simple view of reading in children acquiring a regular orthography (Italian): A network analysis approach. Frontiers in Psychology 12: 686914. [Google Scholar] [CrossRef] [PubMed]
- Baddeley, Alan. 2012. Working memory: Theories, models, and controversies. Annual Review of Psychology 63: 1–29. [Google Scholar] [CrossRef] [PubMed]
- Barbey, Aron K. 2018. Network neuroscience theory of human intelligence. Trends in Cognitive Sciences 22: 8–20. [Google Scholar] [CrossRef]
- Barrouillet, Pierre. 2011. Dual-process theories and cognitive development: Advances and challenges. Developmental Review 31: 79–85. [Google Scholar] [CrossRef]
- Beaujean, A. Alexander. 2015. John Carroll’s views on intelligence: Bi-factor vs. higher-order models. Journal of Intelligence 3: 121–36. [Google Scholar] [CrossRef]
- Benson, Nicholas F., A. Alexander Beaujean, Ryan J. McGill, and Stefan C. Dombrowski. 2018. Revisiting Carroll’s survey of factor-analytic studies: Implications for the clinical assessment of intelligence. Psychological Assessment 30: 1028. [Google Scholar] [CrossRef]
- Borsboom, Denny, Marie K. Deserno, Mike Rhemtulla, Sacha Epskamp, Eiko I. Fried, Richard J. McNally, Donald J. Robinaugh, Marco Perugini, Jonas Dalege, Giulio Costantini, and et al. 2021. Network analysis of multivariate data in psychological science. Nature Reviews Methods Primers 1: 58. [Google Scholar] [CrossRef]
- Bulut, Okan, Damien C. Cormier, Alexandra M. Aquilina, and Hatice C. Bulut. 2021. Age and sex invariance of the Woodcock-Johnson IV tests of cognitive abilities: Evidence from psychometric network modeling. Journal of Intelligence 9: 35. [Google Scholar] [CrossRef]
- Caemmerer, Jacqueline M., Timothy Z. Keith, and Matthew R. Reynolds. 2020. Beyond individual intelligence tests: Application of Cattell-Horn-Carroll Theory. Intelligence 79: 101433. [Google Scholar] [CrossRef]
- Carroll, John B. 1974. Psychometric Tests as Cognitive Tasks: A New “Structure of Intellect”. Technical Report No. 4. Princeton: Educational Testing Service. [Google Scholar]
- Carroll, John B. 1976. Psychometric tests as cognitive tasks: A new “structure of intellect”. In The Nature of Intelligence. Edited by Lauren B. Resnick. Hillsdale: Lawrence Erlbaum, pp. 27–56. [Google Scholar]
- Carroll, John B. 1978. How shall we study individual differences in cognitive abilities? Methodological and theoretical perspectives. Intelligence 2: 87–115. [Google Scholar] [CrossRef]
- Carroll, John B. 1980. Individual Differences in Psychometric and Experimental Cognitive Tasks. Chapel Hill: The L. L. Thurstone Psychometric Laboratory, University of North Carolina, Report No. 163. [NTIS Doc. AD-A086 057; ERIC Doc. ED 191 891]. [Google Scholar]
- Carroll, John B. 1981. Ability and task difficulty in cognitive psychology. Educational Researcher 10: 11–21. [Google Scholar] [CrossRef]
- Carroll, John B. 1985. The educational researcher: Computer scientist or renaissance man. In Perspectives on School Learning: Selected Writings of John B. Carroll. Edited by Lorin W. Anderson. Hillsdale: Lawrence Erlbaum Associates, pp. 383–90. [Google Scholar]
- Carroll, John B. 1991. No demonstration that g is not unitary, but there’s more to the story: Comment on Kranzler and Jensen. Intelligence 15: 423–36. [Google Scholar] [CrossRef]
- Carroll, John B. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Carroll, John B. 1995. On methodology in the study of cognitive abilities. Multivariate Behavioral Research 30: 429–52. [Google Scholar] [CrossRef] [PubMed]
- Carroll, John B. 1996. A three-stratum theory of intelligence: Spearman’s contribution. In Human Abilities: Their Nature and Measurement. Edited by Ian Dennis and Patrick Tapsfield. Mahway: Lawrence Erlbaum Associates, pp. 1–17. [Google Scholar] [CrossRef]
- Carroll, John B. 1997. Psychometrics, intelligence, and public perception. Intelligence 24: 25–52. [Google Scholar] [CrossRef]
- Carroll, John B. 1998. Human cognitive abilities: A critique. In Human Cognitive Abilities in Theory and Practice. Edited by John. J. McArdle and Richard. W. Woodcock. Mahway: Lawrence Erlbaum Associates, pp. 5–24. [Google Scholar]
- Carroll, John B. 2003. The higher-stratum structure of cognitive abilities: Current evidence supports g and about ten broad factors. In The Scientific Study of General Intelligence: Tribute to Arthur R. Jensen. Edited by Helmuth Nyborg. Oxford: Pergamon, pp. 5–22. [Google Scholar]
- Cattell, Raymond B. 1971. Abilities: Their Structure, Growth, and Action. Boston: Houghton Mifflin. [Google Scholar]
- Cattell, Raymond B. 1987. Intelligence: Its Structure, Growth and Action. Amsterdam: Elsevier. [Google Scholar]
- Conway, Andrew R. A., Kristof Kovacs, Han Hao, Kevin P. Rosales, and Jean-Paul Snijder. 2021. Individual differences in attention and intelligence: A united cognitive/psychometric approach. Journal of Intelligence 9: 34. [Google Scholar] [CrossRef] [PubMed]
- Conway, Christopher, David B. Pisoni, and William G. Kronenberger. 2009. The importance of sound for cognitive sequencing abilities: The auditory scaffolding hypothesis. Current Directions in Psychological Science 18: 275–79. [Google Scholar] [CrossRef]
- Corno, Lyn, Lee J. Cronbach, Haggai Kupermintz, David F. Lohman, Ellen B. Mandinach, Ann W. Porteus, and Joan E. Talbert. 2002. Remaking the Concept of Aptitude: Extending the Legacy of Richard E. Snow. New York: Routledge. [Google Scholar]
- Daniel, Mark H. 1997. Intelligence testing: Status and trends. American Psychologist 52: 1038–45. [Google Scholar] [CrossRef]
- De Alwis, Duneesha, Sarah Hale, and Joel Myerson. 2014. Extended cascade models of age and individual differences in children’s fluid intelligence. Intelligence 46: 84–93. [Google Scholar] [CrossRef]
- Decker, Scott L. 2021. Don’t use a bifactor model unless you believe the true structure is bifactor. Journal of Psychoeducational Assessment 39: 39–49. [Google Scholar] [CrossRef]
- Decker, Scott L., Rachel M. Bridges, Jessica C. Luedke, and Michael J. Eason. 2021. Dimensional evaluation of cognitive measures: Methodological confounds and theoretical concerns. Journal of Psychoeducational Assessment 39: 3–27. [Google Scholar] [CrossRef]
- Demetriou, Andreas, George Spanoudis, Michael Shayer, Sanne van der Ven, Christopher R. Brydges, Evelyn Kroesbergen, Gal Podjarny, and H. Lee Swanson. 2014. Relations between speed, working memory, and intelligence from preschool to adulthood: Structural equation modeling of 14 studies. Intelligence 46: 107–21. [Google Scholar] [CrossRef]
- De Neys, Wim, and Gordon Pennycook. 2019. Logic, fast and slow: Advances in dual-process theorizing. Current Directions in Psychological Science 28: 503–9. [Google Scholar] [CrossRef]
- Epskamp, Sacha, and Eiko I. Fried. 2018. A tutorial on regularized partial correlation networks. Psychological Methods 23: 617–34. [Google Scholar] [CrossRef]
- Epskamp, Sacha, Mijke Rhemtulla, and Denny Borsboom. 2017. Generalized network psychometrics: Combining network and latent variable models. Psychometrika 82: 904–27. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, Dawn P., Judy L. Genshaft, and Patti L. Harrison. 1997. Contemporary Intellectual Assessment. New York: Guilford. [Google Scholar]
- Flanagan, Dawn P., and Kevin S. McGrew. 1997. A cross-battery approach to assessing and interpreting cognitive abilities. Narrowing the gap between practice and science. In Contemporary Intellectual Assessment. Theories, Tests, and Issues. Edited by Dawn. P. Flanagan, Judy L. Genshaft and Patti L. Harrison. New York: Guilford, pp. 314–25. [Google Scholar]
- Flanagan, Dawn P., Kevin S. McGrew, and Samuel O. Ortiz. 2000. The Wechsler Intelligence Scales and Gf-Gc Theory: A Contemporary Approach to Interpretation. Boston: Allyn and Bacon. [Google Scholar]
- Flanagan, Dawn P., Samuel O. Ortiz, and Vincent C. Alfonso. 2013. Essentials of Cross-Battery Assessment. Hoboken: John Wiley and Sons. [Google Scholar]
- Forthmann, Boris, David Jendryczko, Jana Scharfen, Ruben Kleinkorres, Mathias Benedek, and Heinz Holling. 2019. Creative ideation, broad retrieval ability, and processing speed: A confirmatory study of nested cognitive abilities. Intelligence 75: 59–72. [Google Scholar] [CrossRef]
- Fried, Eiko I. 2020. Lack of theory building and testing impedes progress in the factor and network literature. Psychological Inquiry 31: 271–88. [Google Scholar] [CrossRef]
- Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2008. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9: 432–41. [Google Scholar] [CrossRef]
- Fry, Astrid F., and Sandra Hale. 1996. Processing speed, working memory, and fluid intelligence: Evidence for a developmental cascade. Psychological Science 7: 237–41. [Google Scholar] [CrossRef]
- Fry, Astrid F., and Sandra Hale. 2000. Relationships among processing speed, working memory, and fluid intelligence in children. Biological Psychology 54: 1–34. [Google Scholar] [CrossRef] [PubMed]
- Goodale, Melvyn A., and David A. Milner. 2018. Two visual pathways—Where have they taken use and where will they lead in the future. Cortex 98: 283–92. [Google Scholar] [CrossRef] [PubMed]
- Golino, Hudson F., and Sacha Epskamp. 2017. Exploratory graph analysis: A new approach for estimating the number of dimensions in psychological research. PloS ONE 12: e0174035. [Google Scholar] [CrossRef] [PubMed]
- Hajovsky, Daniel B., Christopher R. Niileksela, Dawn P. Flanagan, Vincent C. Alfonso, W. Joel Schneider, and Craig J. Zinkiewicz. 2022. Toward a consensus model of cognitive-achievement relations using meta-SEM [Poster]. Paper presented at American Psychological Association Annual Conference 2022, Minneapolis, MN, USA, August 4–6. [Google Scholar]
- Hampshire, Adam, Roger R. Highfield, Beth L. Parkin, and Adrian M. Owen. 2012. Fractionating human intelligence. Neuron 76: 1225–37. [Google Scholar] [CrossRef] [PubMed]
- Haslbeck, Jonas M. B., Oisín Ryan, Donald J. Robinaugh, Lourens J. Waldorp, and Denny Borsboom. 2021. Modeling psychopathology: From data models to formal theories. Psychological Methods 27: 930–57. [Google Scholar] [CrossRef]
- Horn, John L. 1985. Remodeling old models of intelligence. In Handbook of Intelligence: Theories, Measurements, and Applications. Edited by Benjamin B. Wolman. New York: Wiley, pp. 267–300. [Google Scholar]
- Horn, John L. 1998. A basis for research on age differences in cognitive abilities. In Human Cognitive Abilities in Theory and Practice. Edited by John J. McArdle and Richard W. Woodcock. Mahway: Lawrence Erlbaum Associates, pp. 57–92. [Google Scholar]
- Horn, John L., and Jennie Noll. 1997. Human cognitive capabilities: Gf-Gc theory. In Contemporary Intellectual Assessment: Theories, Tests, and Issues. Edited by Dawn P. Flanagan, Judy L. Genshaft and Patti L. Harrison. New York: Guilford Press, pp. 53–91. [Google Scholar]
- JASP Team. 2022. JASP (0.16.3). Available online: https://jasp-stats.org/ (accessed on 4 October 2021).
- Jensen, Arthur R. 2004. Obituary: John Bissell Carroll. Intelligence 32: 1–5. [Google Scholar] [CrossRef]
- Jewsbury, Paul A., Stephen C. Bowden, and Kevin Duff. 2017. The Cattell–Horn–Carroll model of cognition for clinical assessment. Journal of Psychoeducational Assessment 35: 547–67. [Google Scholar] [CrossRef]
- Jones, Payton J., Patrick Mair, and Richard J. McNally. 2018. Visualizing psychological networks: A tutorial in R. Frontiers in Psychology 9: 1742. [Google Scholar] [CrossRef]
- Kamphaus, Randy W., Anne Pierce Winsor, Ellen W. Rowe, and Sangwon Kim. 2012. A history of intelligence test interpretation. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 3rd ed. Edited by Dawn P. Flanagan and Patti L. Harrison. New York: Guilford, pp. 56–70. [Google Scholar]
- Kahneman, Daniel. 2011. Thinking, Fast and Slow. Basingstoke: Macmillan. [Google Scholar]
- Kail, Robert V. 2007. Longitudinal evidence that increases in processing speed and working memory enhance children’s reasoning. Psychological Science 18: 312–13. [Google Scholar] [CrossRef]
- Kail, Robert V., Arne Lervåg, and Charles Hulme. 2016. Longitudinal evidence linking processing speed to the development of reasoning. Developmental Science 19: 1067–74. [Google Scholar] [CrossRef]
- Kan, Kees-Jan, Han L. J. van der Maas, and Stephen Z. Levine. 2019. Extending psychometric network analysis: Empirical evidence against g in favor of mutualism? Intelligence 73: 52–62. [Google Scholar] [CrossRef]
- Kaufman, Alan S. 2009. IQ Testing 101. New York: Springer. ISBN 978-0-8261-2236-0. [Google Scholar]
- Kaufman, Alan S. 1979. Intelligent Testing with the WISC-R. New York: Wiley-Interscience. [Google Scholar]
- Kaufman, Alan S., and Nadeen L. Kaufman. 1983. Kaufman Assessment Battery for Children (KABC). Circle Pines: American Guidance Services. [Google Scholar]
- Keith, Timothy Z., and Mathew R. Reynolds. 2010. Cattell-Horn-Carroll abilities and cognitive tests: What we’ve learned from 20 years of research. Psychology in the Schools 47: 635–50. [Google Scholar] [CrossRef]
- Klauer, Karl J., Klaus Willmes, and Gary D. Phye. 2002. Inducing inductive reasoning: Does it transfer to fluid intelligence? Contemporary Educational Psychology 27: 1–25. [Google Scholar] [CrossRef]
- Kovacs, Kristof, and Andrew R. Conway. 2016. Process overlap theory: A unified account of the general factor of intelligence. Psychological Inquiry 27: 151–77. [Google Scholar] [CrossRef]
- Kovacs, Kristof, and Andrew R. Conway. 2019. A unified cognitive/differential approach to human intelligence: Implications for IQ testing. Journal of Applied Research in Memory and Cognition 8: 255–72. [Google Scholar] [CrossRef]
- Lubinski, David. 2004. Introduction to the special section on cognitive abilities: 100 years after Spearman’s (1904) “‘General intelligence,’ objectively determined and measured”. Journal of Personality and Social Psychology 86: 96. [Google Scholar] [CrossRef]
- Lunansky, Gabriela, Jasper Naberman, Claudia D. van Borkulo, Chen Chen, Li Wang, and Denny Borsboom. 2022. Intervening on psychopathology networks: Evaluating intervention targets through simulations. Methods 204: 29–37. [Google Scholar] [CrossRef]
- Masten, Ann S., and D. Dante Cicchetti. 2010. Developmental cascades. Development and Psychopathology 22: 491–95. [Google Scholar] [CrossRef]
- McArdle, John J. 2007. John L. Horn (1928–2006). American Psychologist 62: 596–97. [Google Scholar] [CrossRef]
- McArdle, John J., and Scott M. Hofer. 2014. Fighting for intelligence: A brief overview of the academic work of John L. Horn. Multivariate Behavioral Research 49: 1–16. [Google Scholar] [CrossRef]
- McGill, Ryan J., and Stefan C. Dombrowski. 2019. Critically reflecting on the origins, evolution, and impact of the Cattell-Horn-Carroll (CHC) model. Applied Measurement in Education 32: 216–31. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 1997. Analysis of the major intelligence batteries according to a proposed comprehensive Gf-Gc framework. In Contemporary Intellectual Assessment: Theories, Tests, and Issues. Edited by Dawn P. Flanagan, Judy L. Genshaft and Patti. L. Harrison. New York: Guilford Press, pp. 151–79. [Google Scholar]
- McGrew, Kevin S. 2005. The Cattell-Horn-Carroll theory of cognitive abilities: Past, present, and future. In Contemporary Intellectual Assessment. Theories, Tests, and Issues, 2nd ed. Edited by Dawn P. Flanagan and Patti L. Harrison. New York: Guilford Press, pp. 136–81. [Google Scholar]
- McGrew, Kevin S. 2009. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2022. The cognitive-affective-motivation model of learning (CAMML): Standing on the shoulders of giants. Canadian Journal of School Psychology 37: 117–34. [Google Scholar] [CrossRef]
- McGrew, Kevin S., and Jeffery J. Evans. 2004. Carroll Human Cognitive Abilities Project: Research Report No. 2, Internal and External Factorial Extensions to the Cattell-Horn-Carroll (CHC) Theory of Cognitive Abilities: A Review of Factor Analytic Research Since Carroll’s Seminal 1993 Treatise. St. Cloud, MN: Institute for Applied Psychometrics. Available online: http://www.iapsych.com/HCARR2.pdf (accessed on 4 October 2021).
- McGrew, Kevin S., Erica M. LaForte, and Fredrick A. Schrank. 2014. Woodcock-Johnson IV Technical Manual. Rolling Meadows: Riverside. [Google Scholar]
- McGrew, Kevin S., and Dawn P. Flanagan. 1998. The Intelligence Test Desk Reference (ITDR): Gf-Gc Cross-Battery Assessment. Boston: Allyn and Bacon. [Google Scholar]
- McGrew, Kevin S., and Richard W. Woodcock. 2001. Technical Manual. Woodcock-Johnson Psycho-Educational Battery-Revised. Rolling Meadows: Riverside. [Google Scholar]
- McGrew, Kevin S., and Barbara J. Wendling. 2010. Cattell-Horn-Carroll cognitive-achievement relations: What we have learned from the past 20 years of research. Psychology in the Schools 47: 651–75. [Google Scholar] [CrossRef]
- McGrew, Kevin. S., Judy. K. Werder, and R. W. Woodcock. 1991. WJ-R Technical Manual. Rolling Meadows: Riverside. [Google Scholar]
- McGrew, Kevin S., W. Joel Schneider, Scott L. Decker, and Okan Bulut. 2023. A psychometric network analysis of CHC intelligence measures: Implications for Research, Theory, and Interpretation of Broad CHC Scores “Beyond g”. Journal of Intelligence 11: 19. [Google Scholar] [CrossRef] [PubMed]
- Meyer, Em M., and Matthew R. Reynolds. 2022. Multidimensional scaling of cognitive ability and academic achievement scores. Journal of Intelligence 10: 117. [Google Scholar] [CrossRef] [PubMed]
- Milner, David A., and Melvyn A. Goodale. 2006. The Visual Brain in Action. New York: Oxford University Press, ISBN-10: 0198524722. [Google Scholar]
- Naglieri, Jack. A., and J. P. Das. 1997. Cognitive Assessment System. Itasca: Riverside. [Google Scholar]
- Neal, Zacharly P., and Jennifer W. Neal. 2021. Out of bounds? The boundary specification problem for centrality in psychological networks. Psychological Methods. Advance online publication. [Google Scholar] [CrossRef]
- Ortiz, Samuel O. 2015. CHC theory of intelligence. In Handbook of intelligence: Evolutionary Theory, Historical Perspective, and Current Concepts. Edited by Sam Goldstein, Dana Princiotta and Jack A. Naglieri. New York: Springer, pp. 209–27. [Google Scholar]
- Procopio, Francesca, Quan Zhou, Ziye Wang, Agnieska Gidziela, Kaili Rimfeld, Margherita Malanchini, and Robert Plomin. 2022. The genetics of specific cognitive abilities. Intelligence 95: 101689. [Google Scholar] [CrossRef]
- Protzko, John, and Roberto Colom. 2021. Testing the structure of human cognitive ability using evidence obtained from the impact of brain lesions over abilities. Intelligence 89: 101581. [Google Scholar] [CrossRef]
- Rappaport, David, Merton Gil, and R. Schafer. 1945–1946. Diagnositc Psychological Testing. Chicago: Year Book Medical, 2 Vols.
- Robinaugh, Donald J., Alexander J. Millner, and Richard J. McNally. 2016. Identifying highly influential nodes in the complicated grief network. Journal of Abnormal Psychology 125: 747–57. [Google Scholar] [CrossRef]
- Savi, Alexander O., Maarten Marsman, and Han L. J. van der Maas. 2021. Evolving networks of human intelligence. Intelligence 88: 101567. [Google Scholar] [CrossRef]
- Schneider, W. Joel. 2016. Strengths and weaknesses of the Woodcock-Johnson IV Tests of Cognitive Abilities: Best practice from a scientist-practitioner perspective. In WJ IV Clinical Use and Interpretation. Edited by Dawn P. Flanagan and Vincent C. Alfonso. Amsterdam: Academic Press, pp. 191–210. [Google Scholar]
- Schneider, W. Joel, and Dawn P. Flanagan. 2015. The relationship between theories of intelligence and intelligence tests. In Handbook of Intelligence: Evolutionary Theory, Historical Perspective, and Current Concepts. Edited by Sam Goldstein, Dana Princiotta and Jack A. Naglieri. New York: Springer, pp. 317–39. [Google Scholar]
- Schneider, W. Joel, and Kevin S. McGrew. 2012. The Cattell-Horn-Carroll model of intelligence. In Contemporary Intellectual Assessment: Theories, Tests and Issues, 2nd ed. Edited by Dawn P. Flanagan and Patti L. Harrison. New York: Guilford Press, pp. 99–144. [Google Scholar]
- Schneider, W. Joel, and Kevin S. McGrew. 2018. The Cattell-Horn-Carroll theory of cognitive abilities. In Contemporary Intellectual Assessment: Theories, Tests and Issues, 3rd ed. Edited by Dawn P. Flanagan and Erin M. McDonough. New York: Guilford Press, pp. 73–130. [Google Scholar]
- Tourva, Anna, and George Spanoudis. 2020. Speed of processing, control of processing, working memory and crystallized and fluid intelligence: Evidence for a developmental cascade. Intelligence 83: 101503. [Google Scholar] [CrossRef]
- van der Maas, Han L. J., Conor V. Dolan, Raoul P. P. P. Grasman, Jelte M. Wicherts, Hilde M. Huizenga, and Maartje E. J. Raijmakers. 2006. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review 113: 842–61. [Google Scholar] [CrossRef] [PubMed]
- van der Maas, Han L. J., Kees-Jan Kan, and Denny Borsboom. 2014. Intelligence is what the intelligence test measures. Seriously. Journal of Intelligence 2: 12–15. [Google Scholar] [CrossRef]
- van der Maas, Han L. J., Alexander O. Savi, Abe Hofman, Kees-Jan Kan, and Maarten Marsman. 2019. The network approach to general intelligence. In General and Specific Mental Abilities. Edited by D. J. McFarland. Cambridge: Cambridge Scholars Publishing, pp. 108–31, ISBN13: 978-1-5275-3310-3. [Google Scholar]
- Vernon, Philip E. 1950. The Structure of Human Abilities. London: Methuen and Co. LTD. [Google Scholar]
- Wasserman, John D. 2019. Deconstructing CHC. Applied Measurement in Education 32: 249–68. [Google Scholar] [CrossRef]
- Whilhelm, O., and P. Kyllonen. 2021. To predict the future, consider the past: Revisiting Carroll (1993) as a guide to the future of intelligence research. Intelligence 89: 101585. [Google Scholar] [CrossRef]
- Woodcock, Richard W. 1990. Theoretical foundations of the WJ-R measures of cognitive ability. Journal of Psychoeducational Assessment 8: 231–58. [Google Scholar] [CrossRef]
- Woodcock, Richard W., and Mary B. Johnson. 1989. Woodcock-Johnson Psycho-Educational Battery–Revised. Allen: DLM. [Google Scholar]
- Woodcock, R. W., K. S. McGrew, and N. Mather. 2001. Woodcock-Johnson III. Itasca: Riverside Publishing. [Google Scholar]


| WJ III Test Name | Factors | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TM CHC | O2 g | O1 Grw | O1 Gc | O1 Gl 1 | O1 Gsc 2 | O1 Gf | O1 Gsa 2 | O1 Gwm 1 | O1 Gq | O1 Gv | O1 Ga | ||
| Word Attack | Grw | 0.62 | 0.58 | ||||||||||
| Spelling of Sounds | Grw | 0.70 | 0.46 | 0.30 | |||||||||
| Spelling | Grw | 0.65 | 0.32 | ||||||||||
| Letter–Word Identification | Grw | 0.74 | 0.32 | ||||||||||
| Editing | Grw | 0.70 | 0.22 | ||||||||||
| Writing Samples | Grw | 0.67 | 0.14 | ||||||||||
| Picture Vocabulary | Gc | 0.65 | 0.65 | ||||||||||
| Verbal Comprehension | Gc | 0.86 | 0.45 | ||||||||||
| General Information | Gc | 0.82 | 0.34 | ||||||||||
| Academic Knowledge | Gc | 0.83 | 0.26 | ||||||||||
| Reading Vocabulary | Grw | 0.81 | 0.20 | ||||||||||
| Story Recall | Gl | 0.82 | 0.14 | ||||||||||
| Oral Comprehension | Gc | 0.66 | 0.14 | ||||||||||
| Passage Comprehension | Grw | 0.68 | 0.08 | ||||||||||
| Memory for Names | Gl | 0.57 | 0.48 | ||||||||||
| Visual–Auditory Learning | Gl | 0.70 | 0.44 | ||||||||||
| Picture Recognition | Gv | 0.44 | 0.23 | ||||||||||
| Visual Closure | Gv | 0.25 | 0.16 | ||||||||||
| Pair Cancellation | Gs | 0.42 | 0.79 | ||||||||||
| Visual Matching | Gs | 0.48 | 0.68 | ||||||||||
| Decision Speed | Gs | 0.39 | 0.64 | ||||||||||
| Cross Out | Gs | 0.51 | 0.57 | ||||||||||
| Retrieval Fluency | Gr | 0.54 | 0.25 | ||||||||||
| Concept Formation | Gf | 0.73 | 0.54 | ||||||||||
| Understanding Directions | Gwm | 0.81 | 0.22 | 0.40 | |||||||||
| Reading Fluency | Grw | 0.66 | 0.38 | 0.47 | |||||||||
| Math Fluency | Gq | 0.50 | 0.46 | 0.37 | 0.33 | ||||||||
| Rapid Picture Naming | Gr | 0.43 | 0.43 | 0.25 | |||||||||
| Writing Fluency | Grw | 0.58 | 0.27 | 0.25 | |||||||||
| Memory for Words | Gwm | 0.57 | 0.50 | ||||||||||
| Numbers Reversed | Gwm | 0.58 | 0.40 | ||||||||||
| Memory for Sentences | Gwm | 0.66 | 0.14 | 0.37 | |||||||||
| Auditory Working Memory | Gwm | 0.70 | 0.37 | ||||||||||
| Calculation | Gq | 0.59 | 0.42 | ||||||||||
| Number Series 3 | Gf | 0.73 | 0.39 | ||||||||||
| Number Matrices 3 | Gf | 0.72 | 0.38 | ||||||||||
| Applied Problems | Gq | 0.76 | 0.34 | ||||||||||
| Analysis-Synthesis | Gf | 0.73 | 0.18 | 0.20 | |||||||||
| Spatial Relations | Gv | 0.50 | 0.52 | ||||||||||
| Block Rotation | Gv | 0.49 | 0.39 | ||||||||||
| Planning | Gv | 0.38 | 0.29 | ||||||||||
| Sound Blending | Ga | 0.56 | 0.58 | ||||||||||
| Auditory Attention | Ga | 0.42 | 0.23 | 0.41 | |||||||||
| Incomplete Words | Ga | 0.48 | 0.34 | ||||||||||
| Sound Patterns–Voice | Ga | 0.49 | 0.20 | ||||||||||
| Sound Awareness | Ga | 0.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McGrew, K.S. Carroll’s Three-Stratum (3S) Cognitive Ability Theory at 30 Years: Impact, 3S-CHC Theory Clarification, Structural Replication, and Cognitive–Achievement Psychometric Network Analysis Extension. J. Intell. 2023, 11, 32. https://doi.org/10.3390/jintelligence11020032
McGrew KS. Carroll’s Three-Stratum (3S) Cognitive Ability Theory at 30 Years: Impact, 3S-CHC Theory Clarification, Structural Replication, and Cognitive–Achievement Psychometric Network Analysis Extension. Journal of Intelligence. 2023; 11(2):32. https://doi.org/10.3390/jintelligence11020032
Chicago/Turabian StyleMcGrew, Kevin S. 2023. "Carroll’s Three-Stratum (3S) Cognitive Ability Theory at 30 Years: Impact, 3S-CHC Theory Clarification, Structural Replication, and Cognitive–Achievement Psychometric Network Analysis Extension" Journal of Intelligence 11, no. 2: 32. https://doi.org/10.3390/jintelligence11020032
APA StyleMcGrew, K. S. (2023). Carroll’s Three-Stratum (3S) Cognitive Ability Theory at 30 Years: Impact, 3S-CHC Theory Clarification, Structural Replication, and Cognitive–Achievement Psychometric Network Analysis Extension. Journal of Intelligence, 11(2), 32. https://doi.org/10.3390/jintelligence11020032




