Metacognitive Cues, Working Memory, and Math Anxiety: The Regulated Attention in Mathematical Problem Solving (RAMPS) Framework
Abstract
1. Introduction
2. The Role of Working Memory in Mathematical Problem Solving
3. Processes Involved in Mathematical Problem Solving
3.1. Metacognition and Mathematical Problem Solving
3.2. Math Anxiety and Mathematical Problem Solving
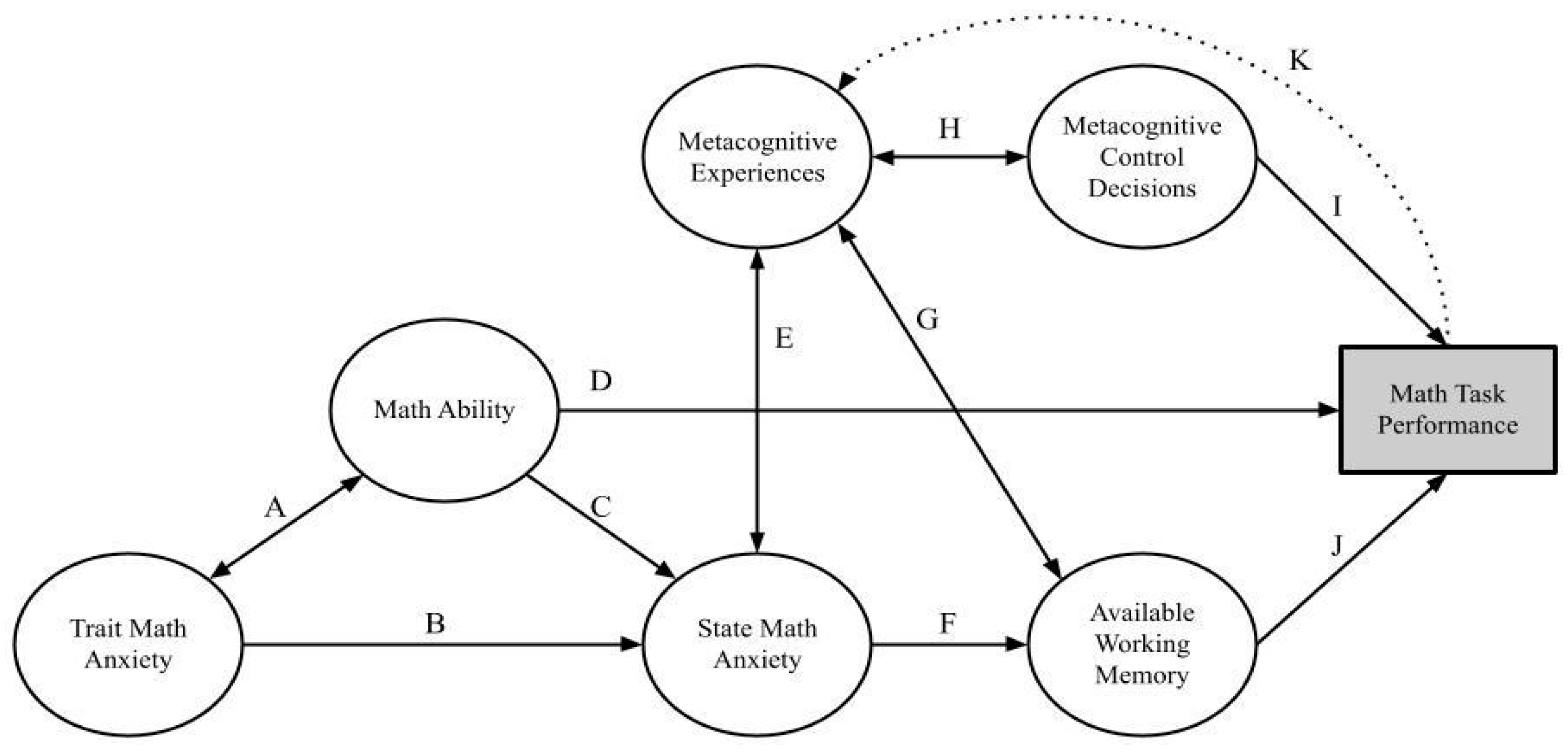
4. Working Memory and Math Anxiety
4.1. The Mechanism of State Math Anxiety
4.1.1. The Disruption Account of Math Anxiety
4.1.2. Factors Inducing State Math Anxiety
“For me, it’s being called on by a teacher. Just remembering this now, I remember one day in elementary I had this one teacher who called on me to answer a simple fraction problem and I didn’t know the answer to it. The teacher became frustrated at this, and she kept demanding the right answer. Every single time, I would guess and get the answer wrong, eventually to the point where she started yelling at me and I started crying. I think from this point on, I just avoided being picked on, even if I knew the answer, it really took a toll on my confidence towards math.”
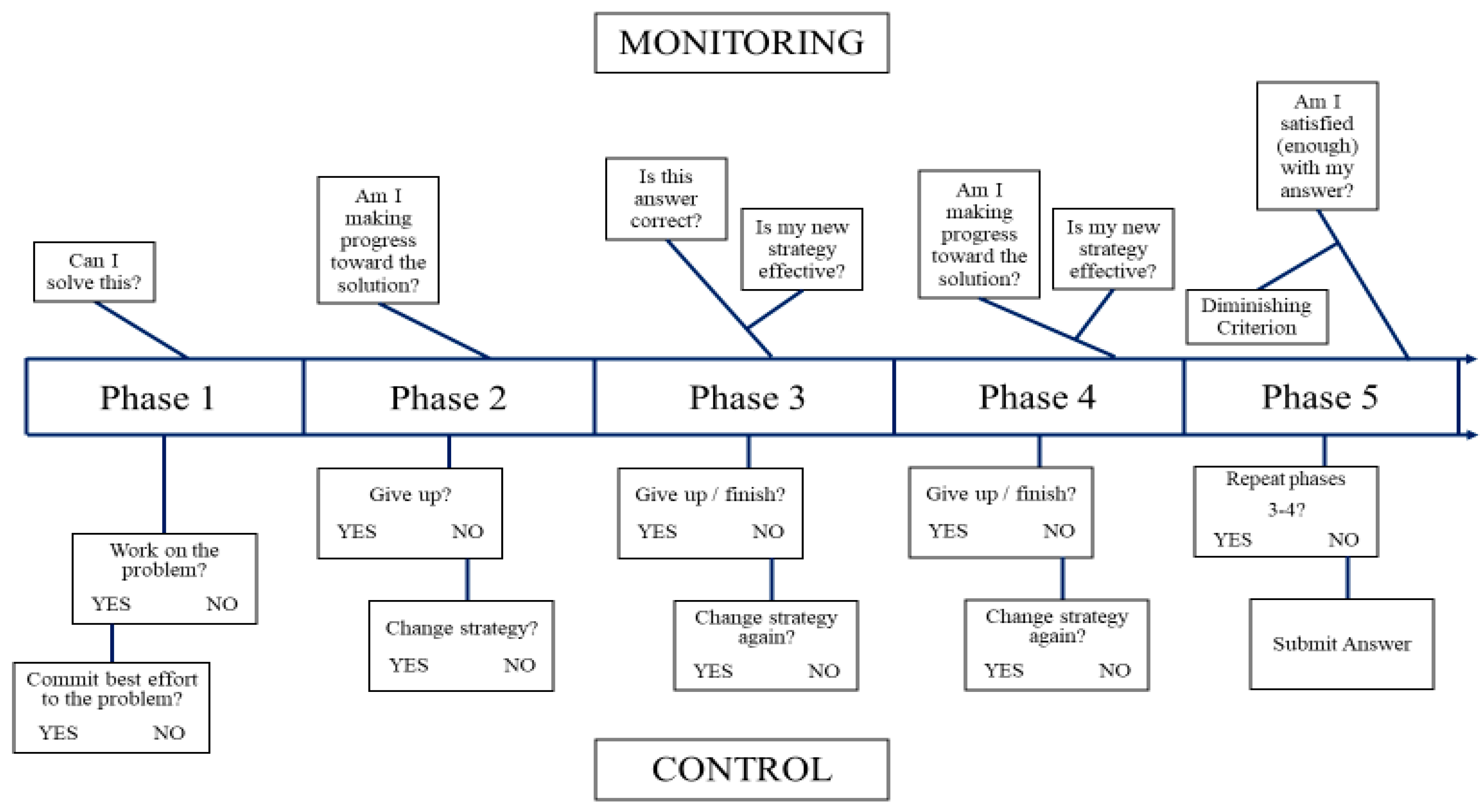
4.2. Phase Approach to Relations between Working Memory and Metacognitive Experiences
4.2.1. Phase 1: Initial Evaluation
4.2.2. Phase 2: Progress Evaluation
4.2.3. Phase 3: Intermediate Evaluation
4.2.4. Phase 4: Second Progress Evaluation
4.2.5. Phase 5: Final Answer Evaluation
5. Conclusions and Future Directions
5.1. Extending Meta-Reasoning into Mathematics
5.2. Extensions, Interventions, and Future Directions
5.3. Final Thoughts
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The qualitative data presented herein (see Table 1) were analyzed using codes generated separately from Scheibe et al. (2023) and have not been analyzed or published in any other outlet. |
References
- Ackerman, Rakefet. 2014. The diminishing criterion model for metacognitive regulation of time investment. Journal of Experimental Psychology: General 143: 1349–68. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, Rakefet, and Yael Beller. 2017. Shared and distinct cue utilization for metacognitive judgements during reasoning and memorisation. Thinking and Reasoning 23: 376–408. [Google Scholar] [CrossRef]
- Ackerman, Rakefet, and Valerie A. Thompson. 2015. Meta-reasoning: What can we learn from meta-memory? In Reasoning as Memory. Edited by Aidan Feeney and Valerie Thompson. London: Psychology Press, pp. 164–82. [Google Scholar]
- Ackerman, Rakefet, and Valerie A. Thompson. 2017. Meta-Reasoning: Monitoring and Control of Thinking and Reasoning. Trends in Cognitive Sciences 21: 607–17. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, Wondimu, Alexander Minnaert, Hans Kuyper, and Margaretha Van der Werf. 2012. Reciprocal relationships between math self-concept and math anxiety. Learning and Individual Differences 22: 385–89. [Google Scholar] [CrossRef]
- Ashcraft, Mark H. 2002. Math Anxiety: Personal, Educational, and Cognitive Consequences. Current Directions in Psychological Science 11: 181–85. [Google Scholar] [CrossRef]
- Ashcraft, Mark H. 2019. Models of math anxiety. In Mathematics Anxiety: What Is Known and What Is Still to Be Understood. Edited by Irene C. Mammarella, Sara Caviola and Ann Dowker. Abingdon: Routledge, pp. 1–19. [Google Scholar]
- Ashcraft, Mark H., and Michael W. Faust. 1994. Mathematics anxiety and mental arithmetic performance: An exploratory investigation. Cognition & Emotion 8: 97–125. [Google Scholar] [CrossRef]
- Ashcraft, Mark H., and Elizabeth P. Kirk. 2001. The relationships among working memory, math anxiety, and performance. Journal of Experimental Psychology: General 130: 224–37. [Google Scholar] [CrossRef]
- Ashcraft, Mark H., and Jeremy A. Krause. 2007. Working memory, math performance, and math anxiety. Psychonomic Bulletin & Review 14: 243–48. [Google Scholar] [CrossRef]
- Ashcraft, Mark H., and Kelly S. Ridley. 2005. Math anxiety and its cognitive consequences: A tutorial review. In Handbook of Mathematical Cognition. Edited by Jamie I. D. Campbell. London: Psychology Press, pp. 315–27. [Google Scholar]
- Baddeley, A. 2001. Is working memory still working? American Psychologist 56: 851–64. [Google Scholar] [CrossRef]
- Baddeley, Alan D., and Graham Hitch. 1974. Psychology of Learning and Motivation. Working Memory 8: 47–89. [Google Scholar] [CrossRef]
- Baddeley, Alan D., and Robert H. Logie. 1999. Working memory: The multiple-component model. In Models of Working Memory: Mechanisms of Active Maintenance and Executive Control. Edited by Akira Miyake and Priti Shah. Cambridge: Cambridge University Press, pp. 28–61. [Google Scholar] [CrossRef]
- Barroso, Connie, Colleen M. Ganley, Amanda L. McGraw, Elyssa A. Geer, Sara A. Hart, and Mia C. Daucourt. 2021. A meta-analysis of the relation between math anxiety and math achievement. Psychological Bulletin 147: 134–68. [Google Scholar] [CrossRef] [PubMed]
- Beilock, Sian L., and Thomas H. Carr. 2005. When High-Powered People Fail. Psychological Science 16: 101–5. [Google Scholar] [CrossRef]
- Bellon, Elien, Wim Fias, and Bert De Smedt. 2019. More than number sense: The additional role of executive functions and metacognition in arithmetic. Journal of Experimental Child Psychology 182: 38–60. [Google Scholar] [CrossRef]
- Bellon, Elien, Wim Fias, and Bert De Smedt. 2021. Too anxious to be confident? A panel longitudinal study into the interplay of mathematics anxiety and metacognitive monitoring in arithmetic achievement. Journal of Educational Psychology 113: 1550–64. [Google Scholar] [CrossRef]
- Berardi-Coletta, Bernadette, Linda S. Buyer, Roger L. Dominowski, and Elizabeth R. Rellinger. 1995. Metacognition and problem solving: A process-oriented approach. Journal of Experimental Psychology: Learning, Memory, and Cognition 21: 205–23. [Google Scholar] [CrossRef]
- Boaler, Jo. 2014. Research Suggests that Timed Tests Cause Math Anxiety. Teaching Children Mathematics 20: 469–74. [Google Scholar] [CrossRef]
- Burgoyne, Alexander P., and Randall W. Engle. 2020. Attention Control: A Cornerstone of Higher-Order Cognition. Current Directions in Psychological Science 29: 624–30. [Google Scholar] [CrossRef]
- Carey, Emma, Francesca Hill, Amy Devine, and Dénes Szucs. 2016. The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Frontiers in Psychology 6. [Google Scholar] [CrossRef]
- Carver, Charles. 2003. Pleasure as a sign you can attend to something else: Placing positive feelings within a general model of affect. Cognition and Emotion 17: 241–61. [Google Scholar] [CrossRef]
- Carver, Charles S., and Michael F. Scheier. 1998. On the Self-Regulation of Behavior. Cambridge: Cambridge University Press. [Google Scholar]
- Caviola, Sara, Enrico Toffalini, David Giofrè, Jessica Mercader Ruiz, Dénes Szűcs, and Irene C. Mammarella. 2022. Math Performance and Academic Anxiety Forms, from Sociodemographic to Cognitive Aspects: A Meta-analysis on 906,311 Participants. Educational Psychology Review 34: 363–99. [Google Scholar] [CrossRef]
- Chen, Edward H., and Drew H. Bailey. 2021. Dual-task studies of working memory and arithmetic performance: A meta-analysis. Journal of Experimental Psychology: Learning, Memory, and Cognition 47: 220–33. [Google Scholar] [CrossRef]
- Cowan, Nelson. 2017. The many faces of working memory and short-term storage. Psychonomic Bulletin & Review 24: 1158–70. [Google Scholar] [CrossRef]
- Dehaene, Stanislas. 2011. The Number Sense, 2nd ed. Oxford: Oxford University Press. [Google Scholar]
- Devine, Amy, Kayleigh Fawcett, Dénes Szűcs, and Ann Dowker. 2012. Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and Brain Functions 8: 33–33. [Google Scholar] [CrossRef]
- Dowker, Ann, Amar Sarkar, and Chung Yen Looi. 2016. Mathematics anxiety: What have we learned in 60 Years? Frontiers in Psychology 7: 508. [Google Scholar] [CrossRef]
- Dreger, Ralph Mason, and Lewis R. Aiken. 1957. The identification of number anxiety in a college population. Journal of Educational Psychology 48: 344–51. [Google Scholar] [CrossRef]
- Dunlosky, John, and Janet Metcalfe. 2009. Metacognition. Thousand Oaks: Sage Publications. [Google Scholar]
- Dunlosky, John, and Thomas O. Nelson. 1992. Importance of the kind of cue for judgments of learning (JOL) and the delayed-JOL effect. Memory & Cognition 20: 374–80. [Google Scholar] [CrossRef]
- Efklides, Anastasia. 2002. Feelings and judgments as subjective evaluations of cognitive processing: How reliable are they? Psychology: The Journal of the Hellenic Psychological Society 9: 163–84. [Google Scholar]
- Efklides, Anastasia, and Chryssoula Petkaki. 2005. Effects of mood on students’ metacognitive experiences. Learning and Instruction 15: 415–31. [Google Scholar] [CrossRef]
- Efklides, Anastasia. 2006. Metacognition and affect: What can metacognitive experiences tell us about the learning process? Educational Research Review 1: 3–14. [Google Scholar] [CrossRef]
- Efklides, Anastasia, Akilina Samara, and Marina Petropoulou. 1999. Feeling of difficulty: An aspect of monitoring that influences control. European Journal of Psychology of Education 14: 461–76. [Google Scholar] [CrossRef]
- Engle, Randall W. 2002. Working memory capacity as executive attention. Current Directions in Psychological Science 11: 19–23. [Google Scholar] [CrossRef]
- Erickson, Shanna, and Evan Heit. 2015. Metacognition and confidence: Comparing math to other academic subjects. Frontiers in Psychology 6: 742. [Google Scholar] [CrossRef]
- Eysenck, Michael W. 1992. Anxiety: The Cognitive Perspective. Hove: Erlbaum. [Google Scholar]
- Eysenck, Michael W., and Manuel G. Calvo. 1992. Anxiety and performance: The processing efficiency theory. Cognition and Emotion 6: 409–34. [Google Scholar] [CrossRef]
- Faust, Michael W., Mark H Ashcraft, and David E. Fleck. 1996. Mathematics Anxiety Effects in Simple and Complex Addition. Mathematical Cognition 2: 25–62. [Google Scholar] [CrossRef]
- Fitzsimmons, Charles J., and Clarissa A. Thompson. 2022. Developmental differences in monitoring accuracy and cue use when estimating whole-number and fraction magnitudes. Cognitive Development 61: 101148. [Google Scholar] [CrossRef]
- Fitzsimmons, Charles J., and Clarissa A. Thompson. 2023. Why is monitoring accuracy so poor in number line estimation? The importance of valid cues and systematic variability for U.S. college students. Metacognition and Learning, 1–32. [Google Scholar] [CrossRef]
- Fitzsimmons, Charles J., Clarissa A. Thompson, and Pooja G. Sidney. 2020. Confident or familiar? The role of familiarity ratings in adults’ confidence judgments when estimating fraction magnitudes. Metacognition and Learning 15: 215–31. [Google Scholar] [CrossRef]
- Flavell, John H. 1979. Metacognition and cognitive monitoring: A new area of cognitive–developmental inquiry. American Psychologist 34: 906–11. [Google Scholar] [CrossRef]
- Frederick, Shane. 2005. Cognitive reflection and decision making. Journal of Economic Perspectives 19: 25–42. [Google Scholar] [CrossRef]
- Gangemi, Amelia, Sacha Bourgeois-Gironde, and Francesco Mancini. 2015. Feelings of error in reasoning—In search of a phenomenon. Thinking & Reasoning 21: 383–96. [Google Scholar] [CrossRef]
- Ganley, Colleen M., Rachel A. Conlon, Amanda L. McGraw, Connie Barroso, and Elyssa A. Geer. 2021. The effect of brief anxiety interventions on reported anxiety and math test performance. Journal of Numerical Cognition 7: 4–19. [Google Scholar] [CrossRef]
- Hacker, Douglas J. 1998. Self-regulated comprehension during normal reading. In Metacognition in Educational Theory and Practice. Edited by Douglas J. Hacker, John Dunlosky and Arthur C. Graesser. Hillsdale: Lawrence Erlbaum Associates Publishers, pp. 165–91. [Google Scholar]
- Handel, Michael J. 2016. What do people do at work? Journal for Labour Market Research 49: 177–97. [Google Scholar] [CrossRef]
- Hembree, Ray. 1990. The Nature, Effects, and Relief of Mathematics Anxiety. Journal for Research in Mathematics Education 21: 33. [Google Scholar] [CrossRef]
- Hertzog, Christopher, and Roger A. Dixon. 1994. Metacognitive development in adulthood and old age. In Metacognition: Knowing about Knowing. Edited by Janet Metcalfe and Arthur Shimamura. Bradford: MIT Press, pp. 227–51. [Google Scholar]
- Justicia-Galiano, José M., Eva M. Martín-Puga, Rocío Linares, and Santiago Pelegrina. 2017. Math anxiety and math performance in children: The mediating roles of working memory and math self-concept. British Journal of Educational Psychology 87: 573–89. [Google Scholar] [CrossRef] [PubMed]
- Kellogg, Jeffry S., Derek R. Hopko, and Mark H. Ashcraft. 1999. The Effects of Time Pressure on Arithmetic Performance. Journal of Anxiety Disorders 13: 591–600. [Google Scholar] [CrossRef]
- Koriat, Asher, and Ravit Levy-Sadot. 1999. Processes underlying metacognitive judgments: Information-based and experience-based monitoring of one’s own knowledge. In Dual-Process Theories in Social Psychology. Edited by Shelly Chaiken and Yaacov Trope. New York: The Guilford Press, pp. 483–502. [Google Scholar]
- Lee, Jihyun. 2009. Universals and specifics of math self-concept, math self-efficacy, and math anxiety across 41 PISA 2003 participating countries. Learning and Individual Differences 19: 355–65. [Google Scholar] [CrossRef]
- Lester, Frank K., and Jinfa Cai. 2016. Can Mathematical Problem Solving Be Taught? Preliminary Answers from 30 Years of Research. In Posing and Solving Mathematical Problems. Edited by Patricio Felmer, Erkki Pehkonen, Jeremy Kilpatrick. Berlin and Heidelberg: Springer, pp. 117–35. [Google Scholar] [CrossRef]
- Ma, Xin. 1999. A Meta-Analysis of the Relationship between Anxiety toward Mathematics and Achievement in Mathematics. Journal for Research in Mathematics Education 30: 520. [Google Scholar] [CrossRef]
- Maloney, Erin A. 2016. Math anxiety: Causes, consequences, and remediation. In Handbook of Motivation at School, 2nd ed. Edited by Kathryn R. Wentzel and David B. Miele. Abingdon: Routledge, pp. 408–23. [Google Scholar]
- Mammarella, Irene C., Sara Caviola, and Ann Dowker. 2019. Concluding remarks. In Mathematics Anxiety: What Is Known and What Is Still to Be Understood. Edited by Irene C. Mammarella, Sara Caviola and Ann Dowker. Abingdon: Routledge, pp. 211–21. [Google Scholar]
- Matlin, Margaret W. 2013. Cognitive Psychology. Hoboken: Wiley. [Google Scholar]
- Mednick, Sarnoff A. 1962. The associative basis of the creative process. Psychological Review 69: 220–32. [Google Scholar] [CrossRef]
- Mielicki, Marta K., Lauren K. Schiller, Charles J. Fitzsimmons, Daniel Scheibe, and Clarissa A. Thompson. 2022. Perceptions of ease and difficulty, but not growth mindset, relate to specific math attitudes. British Journal of Educational Psychology 92: e12472. [Google Scholar] [CrossRef]
- Miyake, Akira, Naomi Friedman, Michael J. Emerson, Alexander H. Witzki, Amy Howerter, and Tor D. Wager. 2000. The Unity and Diversity of Executive Functions and Their Contributions to Complex “Frontal Lobe” Tasks: A Latent Variable Analysis. Cognitive Psychology 41: 49–100. [Google Scholar] [CrossRef] [PubMed]
- Morsanyi, Kinga, Irene C. Mammarella, Dénes Szücs, Carlo Tomasetto, Caterina Primi, and Erin A. Maloney. 2016. Editorial: Mathematical and Statistics Anxiety: Educational, Social, Developmental and Cognitive Perspectives. Frontiers in Psychology 7: 1083. [Google Scholar] [CrossRef] [PubMed]
- Morsanyi, Kinga, Niamh Ní Cheallaigh, and Rakafet Ackerman. 2019. Mathematics Anxiety and Metacognitive Processes: Proposal for a new line of inquiry. Psihologijske Teme 28: 147–69. [Google Scholar] [CrossRef]
- Namkung, Jessica M., Peng Peng, and Xin Lin. 2019. The Relation between Mathematics Anxiety and Mathematics Performance Among School-Aged Students: A Meta-Analysis. Review of Educational Research 89: 459–96. [Google Scholar] [CrossRef]
- Nelson, Thomas O., Arie W. Kruglanski, and John Jost. 1998. Knowing thyself and others: Progress in metacognitive social psychology. In Metacognition: Cognitive and Social Dimensions. Edited by Vincent Y. Yzerbyt, Guy Lories and Benoit Dardenne. Wallsend: Sage, pp. 69–89. [Google Scholar]
- Nelson, Thomas O., and Louis Narens. 1990. Metamemory: A Theoretical Framework and New Findings. The Psychology of Learning and Motivation 26: 125–73. [Google Scholar] [CrossRef]
- Ng, Ee Lynn, and Kerry Lee. 2019. The different involvement of working memory in math and test anxiety. In Mathematics Anxiety: What Is Known and What Is Still to Be Understood. Edited by Irene C. Mammarella, Sara Caviola and Ann Dowker. Abingdon: Routledge. [Google Scholar]
- Özcan, Zeynep Çiğdem, and Aynur Eren Gümüş. 2019. A modeling study to explain mathematical problem-solving performance through metacognition, self-efficacy, motivation, and anxiety. Australian Journal of Education 63: 116–34. [Google Scholar] [CrossRef]
- Pajares, Frank, and M. David Miller. 1996. Role of self-efficacy and self-concept beliefs in mathematical problem solving: A path analysis. Journal of Educational Psychology 86: 193–203. [Google Scholar] [CrossRef]
- Passolunghi, Maria Chiara, Marija Zivkovic, and Sandra Pellizzoni. 2019. Mathematics anxiety and working memory: What is the relationship? In Mathematics Anxiety: What Is Known and What is Still to Be Understood. Edited by Irene C. Mammarella, Sara Caviola and Ann Dowker. Abingdon: Routledge, pp. 103–25. [Google Scholar]
- Pellizzoni, Sandra, Martina Fontana, and Maria Chiara Passolunghi. 2021. Exploring the effect of cool and hot EFs training in four-year-old children. European Journal of Developmental Psychology 18: 731–46. [Google Scholar] [CrossRef]
- Peng, Peng, Jessica Namkung, Marcia Barnes, and Congying Sun. 2016. A meta-analysis of mathematics and working memory: Moderating effects of working memory domain, type of mathematics skill, and sample characteristics. Journal of Educational Psychology 108: 455–73. [Google Scholar] [CrossRef]
- Peters, Ellen. 2020. Innumeracy in the Wild: Misunderstanding and Misusing Numbers. Oxford: Oxford University Press. [Google Scholar]
- Pizzie, Rachel G., and David J. M. Kraemer. 2021. The Association between Emotion Regulation, Physiological Arousal, and Performance in Math Anxiety. Frontiers in Psychology 12: 639448. [Google Scholar] [CrossRef]
- Ramirez, Gerardo, Elizabeth A. Gunderson, Susan C. Levine, and Sian L. Beilock. 2013. Math Anxiety, Working Memory, and Math Achievement in Early Elementary School. Journal of Cognition and Development 14: 187–202. [Google Scholar] [CrossRef]
- Ramirez, Gerardo, Stacy T. Shaw, and Erin A. Maloney. 2018. Math Anxiety: Past Research, Promising Interventions, and a New Interpretation Framework. Educational Psychologist 53: 145–64. [Google Scholar] [CrossRef]
- Rhodes, Matthew G. 2019. Metacognition. Teaching of Psychology 46: 168–75. [Google Scholar] [CrossRef]
- Richardson, Frank C., and Richard M. Suinn. 1972. The Mathematics Anxiety Rating Scale: Psychometric data. Journal of Counseling Psychology 19: 551–54. [Google Scholar] [CrossRef]
- Rivers, Michelle L., Charles J. Fitzsimmons, Susan R. Fisk, John Dunlosky, and Clarissa A. Thompson. 2020. Gender differences in confidence during number-line estimation. Metacognition and Learning 16: 157–78. [Google Scholar] [CrossRef]
- Scheibe, Daniel A., Charles J. Fitzsimmons, Marta K. Mielicki, Jennifer M. Taber, Pooja G. Sidney, Karin Coifman, and Clarissa A. Thompson. 2022. Confidence in COVID problem solving: What factors predict adults’ item-level metacognitive judgments on health-related math problems before and after an educational intervention? Metacognition and Learning 17: 989–1023. [Google Scholar] [CrossRef]
- Scheibe, Daniel A., Christopher A. Was, Pooja G.. Sidney, and Clarissa A. Thompson. 2023. How Does Math Anxiety Affect Math Performance? An Experimental Two-Study Investigation into the Mechanism Driving Math Anxiety Interventions. Manuscript submitted for publication. Kent: The Psychological Sciences, Kent State University. [Google Scholar]
- Schneider, Wolfgang, Hans Gruber, Andreas Gold, and Klaus Opwis. 1993. Chess Expertise and Memory for Chess Positions in Children and Adults. Journal of Experimental Child Psychology 56: 328–49. [Google Scholar] [CrossRef]
- Schoenfeld, Alan H. 2016. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics (Reprint). Journal of Education 196: 1–38. First published 1985. [Google Scholar] [CrossRef]
- Sidney, Pooja G., Clarissa A. Thompson, Charles Fitzsimmons, and Jennifer M. Taber. 2021. Children’s and Adults’ Math Attitudes Are Differentiated by Number Type. The Journal of Experimental Education 89: 1–32. [Google Scholar] [CrossRef]
- Thompson, Clarissa A., Marta K. Mielicki, Ferdinand Rivera, Charles J. Fitzsimmons, Daniel A. Scheibe, Pooja G. Sidney, Lauren K. Schiller, Jennifer M. Taber, and Erika A. Waters. 2023. Leveraging Math Cognition to Combat Health Innumeracy. Perspectives on Psychological Science 18: 152–77. [Google Scholar] [CrossRef]
- Thompson, Valerie A. 2009. Dual-process theories: A metacognitive perspective. In In Two Minds: Dual Processes and Beyond. Edited by Jonathan Evans and Keith Frankish. Oxford: Oxford University Press, pp. 171–95. [Google Scholar]
- Thompson, Valerie A., and Aidan Feeney. 2015. Reasoning and memory: A case for integration. In Reasoning as Memory. Edited by Aidan Feeney and Valerie A. Thompson. London: Psychology Press, pp. 1–8. [Google Scholar]
- Thompson, Valerie A., and Stephen C. Johnson. 2014. Conflict, metacognition, and analytic thinking. Thinking & Reasoning 20: 215–44. [Google Scholar] [CrossRef]
- Thompson, Valerie A., Jamie A. Prowse Turner, and Gordon Pennycook. 2011. Intuition, reason, and metacognition. Cognitive Psychology 63: 107–40. [Google Scholar] [CrossRef] [PubMed]
- Thompson, Valerie A., Jamie A. Prowse Turner, Pennycook Gordon, Linden J. Ball, Hannah Brack, Yael Ophir, and Rakefet Ackerman. 2013. The role of answer fluency and perceptual fluency as metacognitive cues for initiating analytic thinking. Cognition 128: 237–51. [Google Scholar] [CrossRef] [PubMed]
- Topolinski, Sascha, and Fritz Strack. 2009. The analysis of intuition: Processing fluency and affect in judgements of semantic coherence. Cognition and Emotion 23: 1465–503. [Google Scholar] [CrossRef]
- Unsworth, Nash, and Randall W. Engle. 2007. The nature of individual differences in working memory capacity: Active maintenance in primary memory and controlled search from secondary memory. Psychological Review 114: 104–32. [Google Scholar] [CrossRef]
- Widaman, Keith F., David C. Geary, Pierre Cormier, and Todd D. Little. 1989. A componential model for mental addition. Journal of Experimental Psychology: Learning, Memory, and Cognition 15: 898–919. [Google Scholar] [CrossRef][Green Version]
- Zepeda, Cristina D., and Timothy J. Nokes-Malach. 2023. Assessing Metacognitive Regulation during Problem Solving: A Comparison of Three Measures. Journal of Intelligence 11: 16. [Google Scholar] [CrossRef]
- Zhang, Jing, Nan Zhao, and Qi-Ping Kong. 2019. The Relationship Between Math Anxiety and Math Performance: A Meta-Analytic Investigation. Frontiers in Psychology 10: 1613. [Google Scholar] [CrossRef]
| Code | Code Definition | Examples | Prevalence |
|---|---|---|---|
| Testing or High Stakes | Any mention of (a) testing situations or (b) high-stake ramifications inducing anxiety. | “Important exams and [the] ACT because the grade matters a lot.” | 46.1% |
| “Exams. I hate tests.” | |||
| Social Pressure or Embarrassment | Any mention of (a) being watched, (b) being judged, or (c) being embarrassed due to social comparison inducing anxiety. | “When people depend on me or people are watching me because I don’t want to disappoint them.” | 30.5% |
| “When I have to express my math abilities to others. It’s easy to mess up, and that would be embarrassing.” | |||
| Specific Type of Math | Any mention of a specific type of math inducing anxiety (as opposed to math anxiety as more of a generality). | “Anything that requires percentages and needs to be quickly determined.” | 20.3% |
| “Fractions and word problems. I have never been good at fractions and word problems can be very confusing.” | |||
| Surprise or Lack of Preparation | Any mention of being put on the spot to complete math or having to do math without the chance for proper preparation inducing anxiety. | “When I am put on the spot because I do my best work when I have time to prepare and study.” | 10.4% |
| “Pop quizzes because it is unexpected.” | |||
| Time Constraints | Any mention of a specific allotted amount of time inducing anxiety. | “Anything that requires percentages and needs to be quickly determined.” | 7.7% |
| “When I have to do it in a time limit.” |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scheibe, D.A.; Was, C.A.; Dunlosky, J.; Thompson, C.A. Metacognitive Cues, Working Memory, and Math Anxiety: The Regulated Attention in Mathematical Problem Solving (RAMPS) Framework. J. Intell. 2023, 11, 117. https://doi.org/10.3390/jintelligence11060117
Scheibe DA, Was CA, Dunlosky J, Thompson CA. Metacognitive Cues, Working Memory, and Math Anxiety: The Regulated Attention in Mathematical Problem Solving (RAMPS) Framework. Journal of Intelligence. 2023; 11(6):117. https://doi.org/10.3390/jintelligence11060117
Chicago/Turabian StyleScheibe, Daniel A., Christopher A. Was, John Dunlosky, and Clarissa A. Thompson. 2023. "Metacognitive Cues, Working Memory, and Math Anxiety: The Regulated Attention in Mathematical Problem Solving (RAMPS) Framework" Journal of Intelligence 11, no. 6: 117. https://doi.org/10.3390/jintelligence11060117
APA StyleScheibe, D. A., Was, C. A., Dunlosky, J., & Thompson, C. A. (2023). Metacognitive Cues, Working Memory, and Math Anxiety: The Regulated Attention in Mathematical Problem Solving (RAMPS) Framework. Journal of Intelligence, 11(6), 117. https://doi.org/10.3390/jintelligence11060117






