Conditional Dependence across Slow and Fast Item Responses: With a Latent Space Item Response Modeling Approach
Abstract
1. Introduction
1.1. Background
1.2. Current Study
1.3. Structure
2. Latent-Space Item-Response Theory
3. Our Approach
3.1. Classification of Item Responses into Slow and Fast Responses
3.2. Estimation of Separate Latent Positions of Slow and Fast Responses for an Item
- The constrained model—same item easiness across slow and fast responses for an item: We constrain the item parameter (in Equation (2)) to be equal across fast and slow conditions. That is, we constrain to be equal to so that each item has a single easiness parameter regardless of the response-speed conditions. Such a constraint will allow the interaction map to capture the heterogeneity in the item–respondent interactions across response times that may be due to either items or persons or both. For instance, the distances we observe from the interaction map may reflect how each item performs differently depending on whether it is answered faster or slower by respondents and how individuals behave differently on different items depending on response times.
- The unconstrained model—separate item easiness across slow and fast responses for an item: We allow for a separate estimation of the item-easiness parameters for slow and fast conditions to examine the remaining heterogeneity after accounting for the differences in item properties across slow and fast responses. This approach removes the heterogeneity across slow and fast responses that is consistent across respondents from the interaction map and helps us explore the heterogeneity that cannot be explained by the items themselves by inspecting the interaction map. Thus, we anticipate that the former model (i.e., the constrained model) captures the heterogeneity in item–person interactions due to the differences in item properties across fast and slow responses as a part of residual dependence, whereas the latter model (i.e., the unconstrained model) captures any potential heterogeneity that remains even after accounting for the item-difficulty differences across response times.
4. Empirical Analysis
4.1. Data
4.1.1. Verbal Analogies
4.1.2. Pattern Matrices
4.1.3. Amsterdam Chess Test
4.2. Analytic Methods
4.2.1. Model Estimation
4.2.2. Model Identifiability
4.2.3. Model Evaluation
5. Results
5.1. Constrained Model: Heterogeneity of Item–Respondent Interactions across Slow and Fast Responses
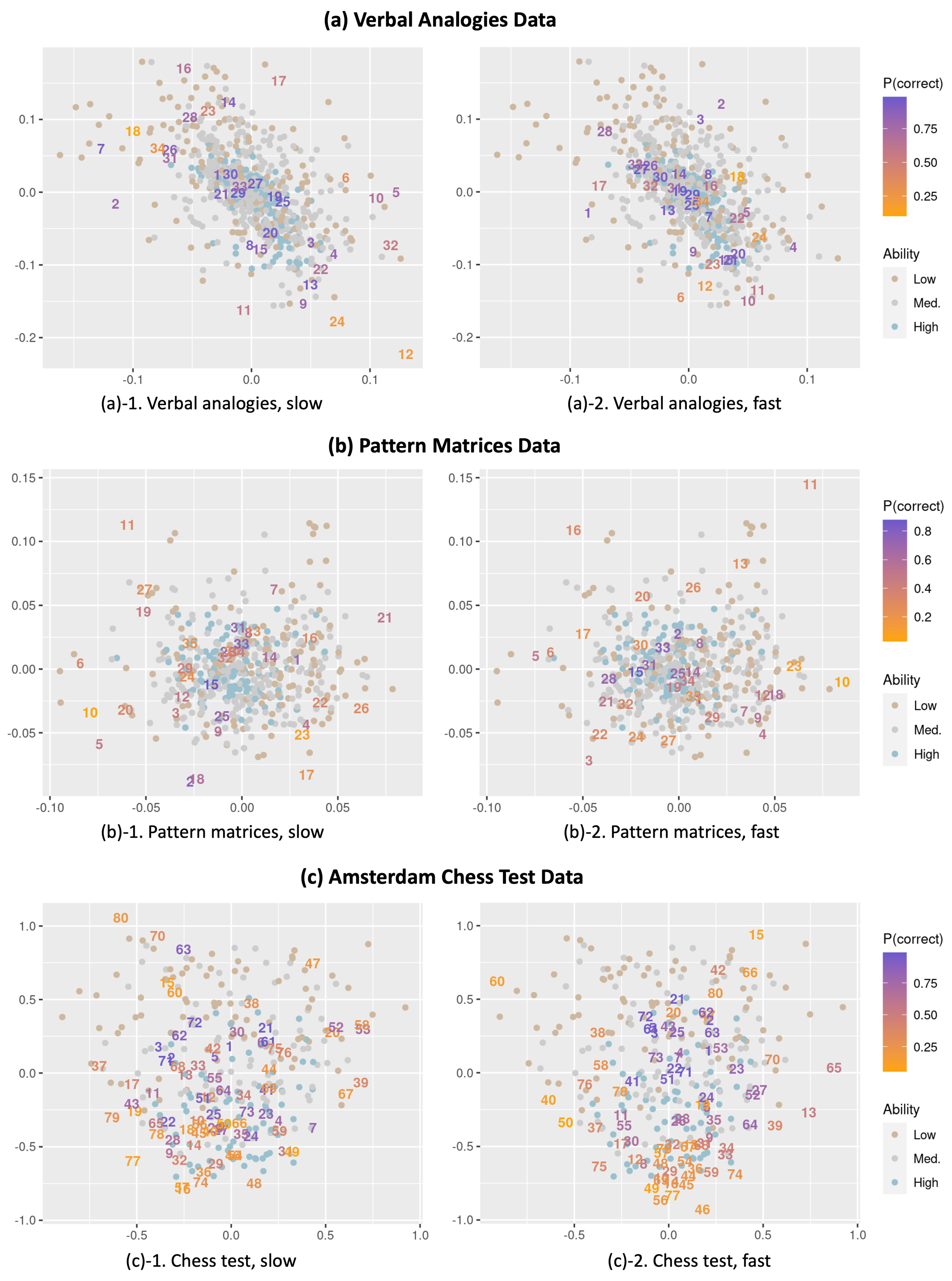
- We present the interaction map for the slow- and fast-response conditions separately for ease of interpretation. Note that the positions from the two maps are obtained from a single model for the same dataset. Therefore, the positions of the respondents (represented as dots) are the same in the two maps.
- Items are represented as their original item number for both the slow and fast conditions (instead of the item numbers in the expanded data format) so that the item positions for slow and fast responses can be easily compared. Thus, for example, by comparing the positions for the same item number in the interaction maps for the slow- and fast-response conditions, we can observe how an item behaves differently depending on whether it was responded to slower or faster than expected.
- We color the respondents and items each based on their levels of ability estimates and the proportion that each item is correct (the overall item easiness). We define the respondents’ ability as low, medium, and high if the estimates are below , between and , and above , respectively, and each group is colored differently. There are 162, 377, and 187 respondents each in the low, medium, and high groups for the verbal analogies data, respectively; 137, 240, and 126 respondents for the matrices data, respectively; and 83, 91, and 75 respondents for the ACT data, respectively. For the items, easier items (with a higher proportion correct) are colored purple while more difficult items (with a lower proportion correct) are colored orange.
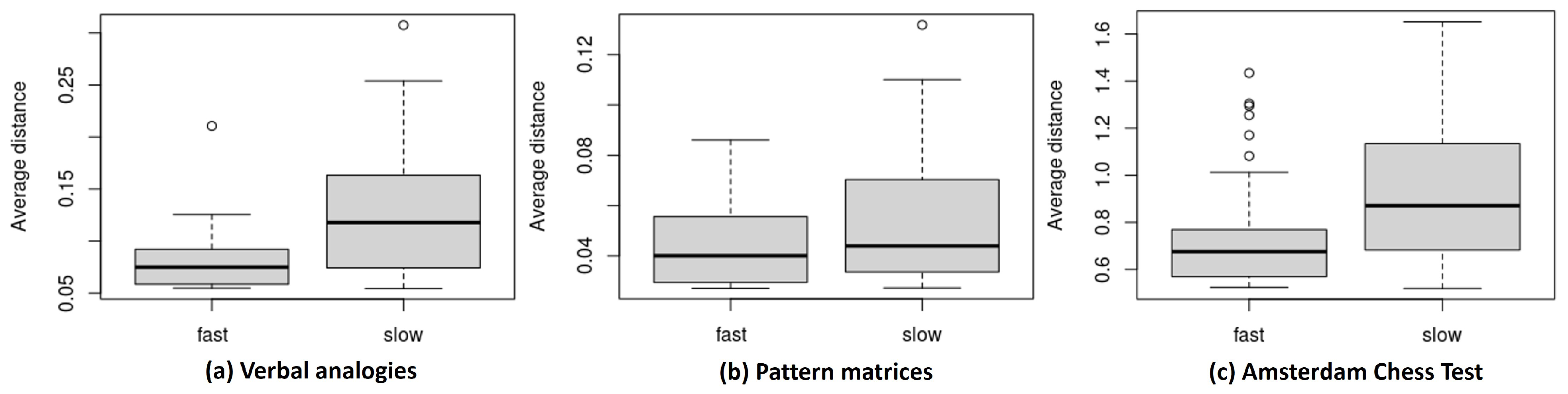
- Items with slow responses are farther away from respondents. One common observation across the three datasets is that item positions are generally more scattered under the slow-response condition than the fast-response condition. Such a result possibly indicates that items tend to show more heterogeneity in item–person interactions when responded to slower than expected, while the interaction is less heterogeneous when responded to faster. As items for slow responses are more spread out, we can naturally expect slow responses, on average, to have a greater distance from the positions of respondents compared to fast responses.
- Item 13 in the verbal analogies data (a relatively easy item located at the top left of plot (a)-1 and in the middle of plot (a)-2 in Figure 1), the proportion correct is .865 for the slow responses (of which the average item–respondent distance is .251) and .987 for faster responses (the average distance is .056).
- Likewise, Item 63 in the ACT data (located on the left side of plot (c)-1 and toward the center of plot (c)-2) produces a relatively lower proportion correct (.820) for the slow responses (average distance = 1.002) than for the fast responses (proportion correct = .949, average distance = .544).
- The pattern of association varies by the overall item difficulty. The observed pattern above is particularly apparent and consistent for easier items (purple-colored items) while some relatively difficult items (orange-colored items) show a weak or even an opposite pattern. For example,
- Item 29 with a moderate difficulty (overall proportion correct = .404) in the pattern matrices data is located inside the item cluster around the middle of plot (b)-1 and in the upper right of plot (b)-2 in Figure 1, showing a higher proportion correct (.519) for the slow responses (average distance = 0.033) and a lower proportion correct (.250) for the fast responses (average distance = .086).
- Item 76 in the ACT data, which is relatively difficult (overall proportion correct = .378) and located toward the center of plot (c)-1 and at the top of plot (c)-2 in Figure 1, appears to be easier for the slow responses (proportion correct = .566, average distance = .527) and more difficult for the fast responses (proportion correct = .150, average distance = 1.434).
- Item–respondent interactions vary across respondents. While we observe differences in item difficulty across response times, it is important to highlight that such a pattern only explains a part of the residual dependency between responses and response times captured in the interaction map. Every individual interacts with items in different ways, and thus the relationship between responses and response times may not be the same for all respondents and items. For instance, an item that is easier when responded to faster for some respondents can be easier when responded to slower for other respondents and vice versa. Such heterogeneity can be examined by looking at the positions of individual respondents and items in the interaction map across fast and slow responses. The heterogeneity is expected to be more apparently demonstrated by items exhibiting very different positions in the interaction map across fast and slow responses. For example,
- Although Item 63 in the ACT data is shown to be generally easier for fast responses (as described above), respondents who are located around the position of Item 63 in plot (c)-1 of Figure 1 would show a lower accuracy for fast responses (as manifested by larger distances between these individuals and Item 63 in plot (c)-2).
- Item 27 in the pattern matrices data is located at the lower left part of plot (b)-1 and the upper right part of plot (b)-2 in Figure 1, which possibly suggests that respondents with positions around the lower left are more likely to get the item correct when responding slower than faster whereas those located around the upper right tend to have a higher probability of getting the item correct when responding faster.
5.2. Unconstrained Model: Residual Dependency between Item Responses and RT after Accounting for the Heterogeneity in Item Difficulty across Fast and Slow Responses
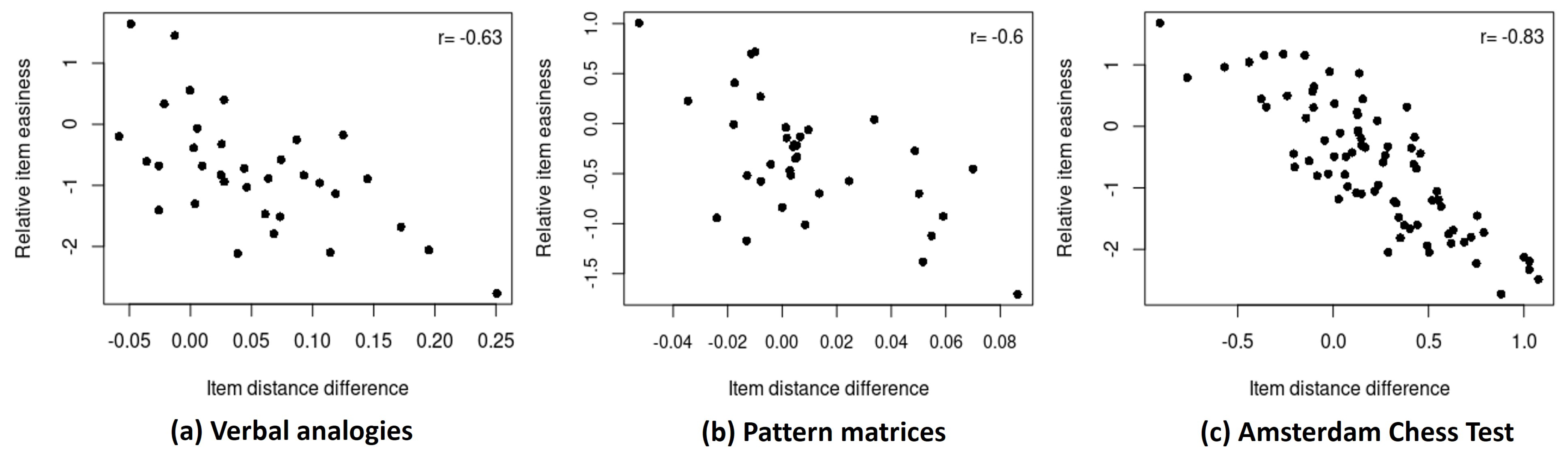
- More difficult items tend to be more spread out. As a result of removing the overall item differences in difficulty across the response times from the interaction map, we observe in Figure 4 that the items are now relatively equally spread out across the fast and slow responses compared to Figure 1. In addition, for both the fast and slow responses, the more difficult items (orange-colored) appear generally more spread out in the interaction map than the easier items (purple-colored) that are more clustered. This indicates that the more difficult items tend to show more heterogeneous interactions with respondents that cannot be explained by the person and item parameters, involving a greater amount of residual variation (e.g., item–respondent specificities). A related observation is a larger distance between the slow and fast responses for more difficult items. The distance between the slow and fast responses for an item tends to negatively correlate with the overall item difficulty in all three examples (ranging from to ). This suggests that more difficult items may exhibit a greater heterogeneity in item–respondent interactions across response times.
- The conditional dependence between responses and response times is heterogeneous. As implied above, some items are located very closely across the fast- and slow-response conditions (e.g., Item 30 in the verbal analogies data) while some other items show a larger distance between the positions for the slow- and fast-response conditions. Such variability suggests that the amount of residual dependency between the responses and response times is different across items. A shorter distance implies that there is not much conditional dependence remaining between the responses and response times; thus, respondents would behave similarly for the slow and fast responses (in a way captured by the item-difficulty differences between the slow and fast responses). In contrast, a larger distance between the fast and slow responses indicates a greater residual dependency unexplained by item-difficulty differences. Thus, these items may involve more person and item specificities in the conditional dependence and consequently show a more heterogeneous conditional dependence between the responses and response times.
- Item 23 in the verbal analogies data has item-easiness estimates of 1.250 for the slow and 2.930 for the fast responses, indicating that the item is generally easier when responded to faster. However, we observe the opposite pattern for the respondents who are located around the slow-response position in plot (a) of Figure 5; the response accuracy is higher when the response is given slower (proportion correct = .57) than faster (proportion correct = .00).
- The item-easiness estimates for Item 22 in the pattern matrices data are 1.315 and 1.272 for the slow and fast responses, respectively, and .643 and .714 for Item 58 in the ACT data. Although the item-easiness estimates do not have a large difference between the slow and fast responses, we can see from plots (b) and (c) in Figure 5 that the respondents are showing a disproportionately higher correct proportion for the slow or fast responses depending on their distances from the item’s slow- and fast-response positions in the interaction map.
- Item 70 in the ACT data has item-easiness estimates of 1.546 for the slow and 1.103 for the fast responses, suggesting that the item is in general slightly easier when responded to slower. We, however, observe that the respondents located near the fast-response position are performing better when they respond to the item faster than slower.

6. Conclusions
6.1. Summary and Discussion
6.2. Limitations and Future Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
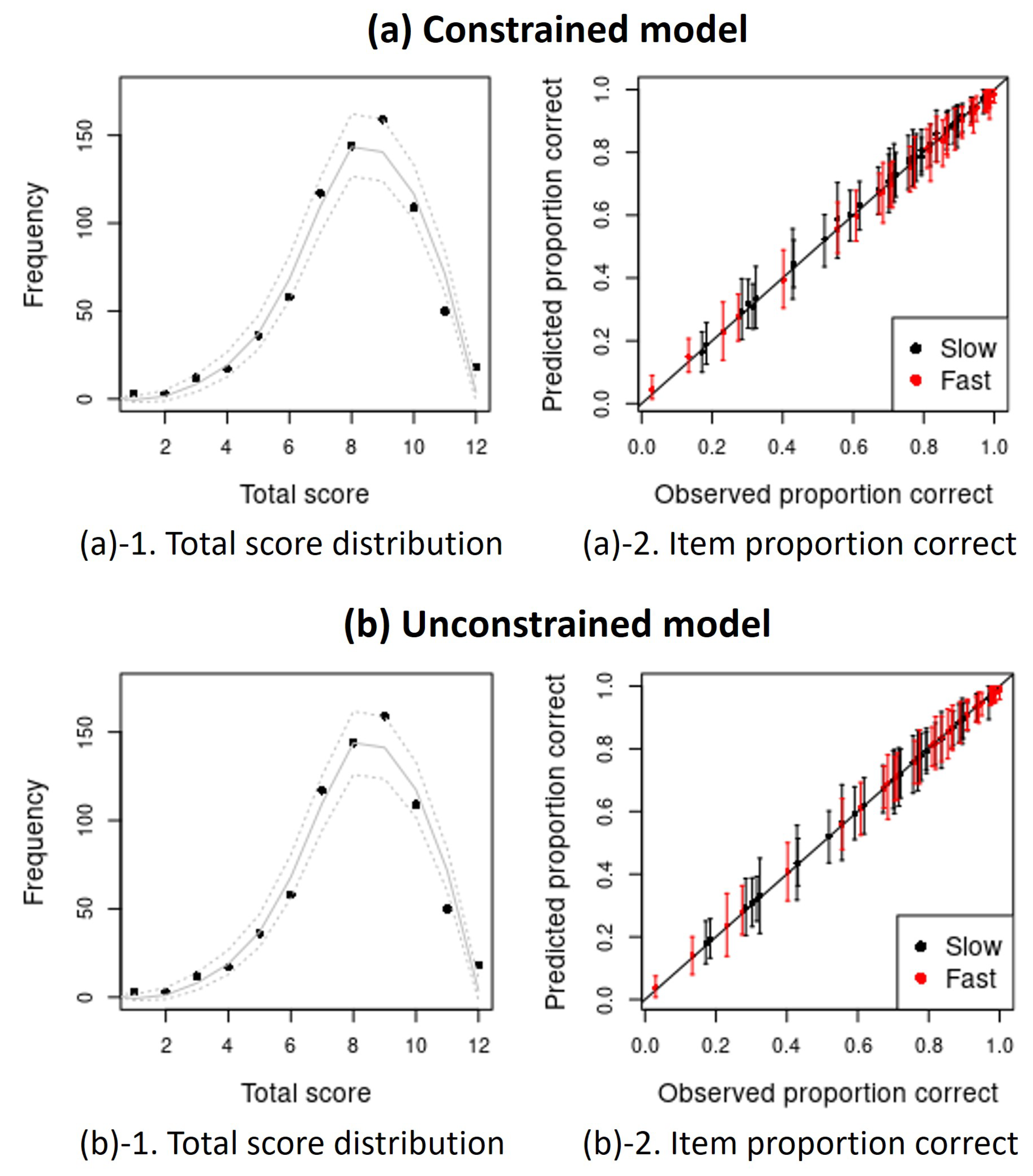
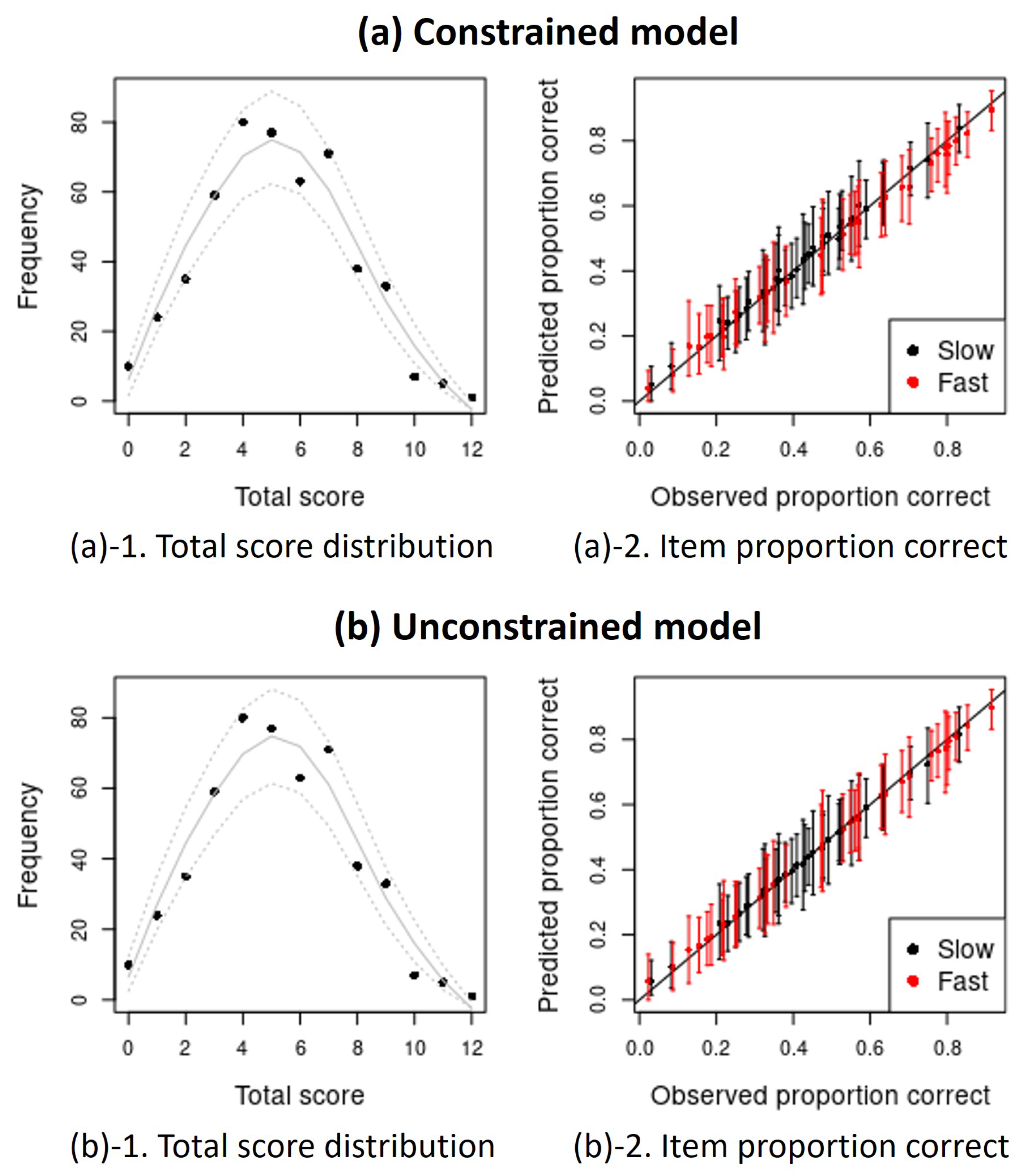
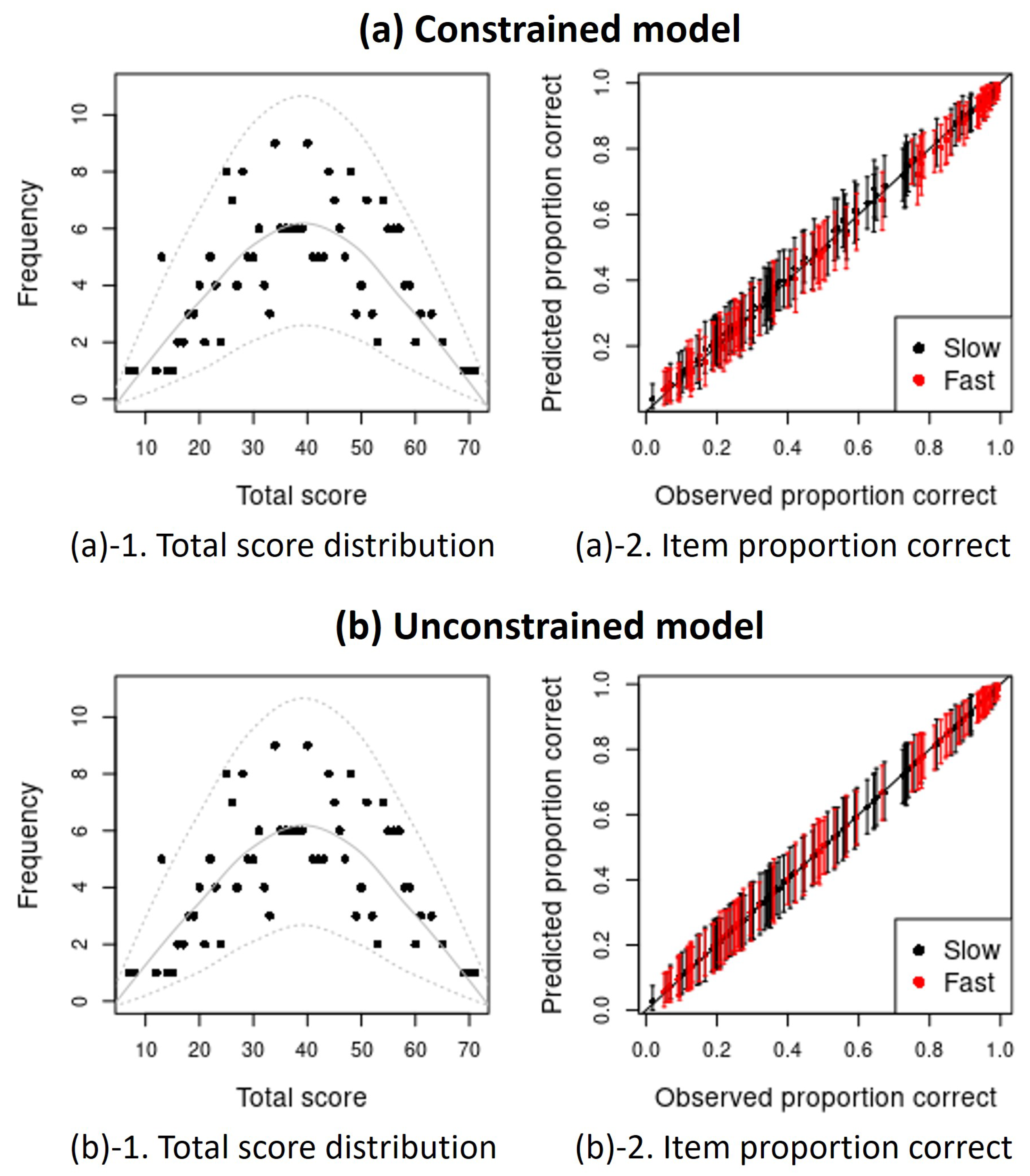
Appendix A. Posterior Predictive Checks (PPCs) Plots
References
- Bates, Douglas, Martin Mächler, Ben Bolker, and Steve Walker. 2015. Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67: 1–48. [Google Scholar] [CrossRef]
- Bejar, Isaac I., Roger Chaffin, and Susan Embretson. 1991. Cognitive and Psychometric Analysis of Analogical Problem Solving. New York: Springer. [Google Scholar] [CrossRef]
- Böckenholt, Ulf. 2012. Modeling multiple response processes in judgment and choice. Psychological Methods 17: 665–78. [Google Scholar] [CrossRef]
- Bolsinova, Maria, and Jesper Tijmstra. 2018. Improving precision of ability estimation: Getting more from response times. The British Journal of Mathematical and Statistical Psychology 71: 13–38. [Google Scholar] [CrossRef]
- Bolsinova, Maria, Jesper Tijmstra, and Dylan Molenaar. 2017a. Response moderation models for conditional dependence between response time and response accuracy. British Journal of Mathematical and Statistical Psychology 70: 257–79. [Google Scholar] [CrossRef] [PubMed]
- Bolsinova, Maria, Jesper Tijmstra, Dylan Molenaar, and Paul De Boeck. 2017b. Conditional dependence between response time and accuracy: An overview of its possible sources and directions for distinguishing between them. Frontiers in Psychology 8: 202. [Google Scholar] [CrossRef]
- Bolsinova, Maria, Paul De Boeck, and Jesper Tijmstra. 2017c. Modelling conditional dependence between response time and accuracy. Psychometrika 82: 1126–48. [Google Scholar] [CrossRef]
- Borg, Ingwer, and Patrick J. F. Groenen. 2005. Modern Multidimensional Scaling: Theory and Applications, 2nd ed. New York: Springer. [Google Scholar] [CrossRef]
- Chen, Haiqin, Paul De Boeck, Matthew Grady, Chien-Lin Yang, and David Waldschmidt. 2018. Curvilinear dependency of response accuracy on response time in cognitive tests. Intelligence 69: 16–23. [Google Scholar] [CrossRef]
- De Boeck, Paul, and Ivailo Partchev. 2012. Irtrees: Tree-based item response models of the glmm family. Journal of Statistical Software 48: 1–28. [Google Scholar] [CrossRef]
- De Boeck, Paul, and Minjeong Jeon. 2019. An overview of models for response times and processes in cognitive tests. Frontiers in Psychology 10: 102. [Google Scholar] [CrossRef]
- DiTrapani, Jack, Minjeong Jeon, Paul De Boeck, and Ivailo Partchev. 2016. Attempting to differentiate fast and slow intelligence: Using generalized item response trees to examine the role of speed on intelligence tests. Intelligence 56: 82–92. [Google Scholar] [CrossRef]
- Friel, Nial, Riccardo Rastelli, Jason Wyse, and Adrian E. Raftery. 2016. Interlocking directorates in Irish companies using a latent space model for bipartite networks. Proceedings of the National Academy of Sciences 113: 6629–34. [Google Scholar] [CrossRef]
- Gelman, Andrew, and Donald B. Rubin. 1992. Inference from iterative simulation using multiple sequences. Statistical Science 7: 457–72. [Google Scholar] [CrossRef]
- Gelman, Andrew, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin. 2013. Bayesian Data Analysis, 3rd ed. London: Chapman & Hall/CRC Press. [Google Scholar]
- Goldhammer, Frank, Johannes Naumann, Annette Stelter, Krisztina Tóth, Heiko Rölke, and Eckhard Klieme. 2014. The time on task effect in reading and problem solving is moderated by task difficulty and skill: Insights from a computer-based large-scale assessment. Journal of Educational Psychology 106: 608–26. [Google Scholar] [CrossRef]
- Hoffman, Matthew D., and Andrew Gelman. 2014. The No-U-Turn Sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research 15: 1351–81. [Google Scholar]
- Hoff, Peter D., Adrian E. Raftery, and Mark S. Handcock. 2002. Latent space approaches to social network analysis. Journal of the American Statistical Association 97: 1090–98. [Google Scholar] [CrossRef]
- Hornke, Lutz F. 1999. Benefits from computerized adaptive testing as seen in simulation studies. European Journal of Psychological Assessment 15: 91–98. [Google Scholar] [CrossRef]
- Hornke, Lutz F. 2002. Item generation models for higher order cognitive functions. In Item Generation for Test Development. Edited by Sidney H. Irvine and Patrick C. Kyllonen. Mahwah: Lawrence Erlbaum Associates Publishers, pp. 159–78. [Google Scholar]
- Hornke, Lutz F., and Klaus Rettig. 1993. Evaluation und revision einer itembank von analogieaufgaben [evaluation and revision ofan item bank of verbal analogy items]. Zeitschrift für Differentielle und Diagnostische Psychologie 14: 113–28. [Google Scholar]
- Hornke, Lutz F., and Michael W. Habon. 1986. Rule-based item bank construction and evaluation within the linear logistic framework. Applied Psychological Measurement 10: 369–80. [Google Scholar] [CrossRef]
- Jeon, Minjeong, and Paul De Boeck. 2016. A generalized item response tree model for psychological assessments. Behavior Research Methods 48: 1070–85. [Google Scholar] [CrossRef]
- Jeon, Minjeong, Ick Hoon Jin, Michael Schweinberger, and Samuel Baugh. 2021. Mapping unobservd item-respondent interactions: A latent space item response model with interaction map. Psychometrika 86: 378–403. [Google Scholar] [CrossRef]
- Jin, Ick Hoon, and Minjeong Jeon. 2019. A doubly latent space joint model for local item and person dependence in the analysis of item response data. Psychometrika 84: 236–60. [Google Scholar] [CrossRef] [PubMed]
- Kang, Inhan, Paul De Boeck, and Ivailo Partchev. 2022a. A randomness perspective on intelligence processes. Intelligence 91: 101632. [Google Scholar] [CrossRef]
- Kang, Inhan, Paul De Boeck, and Roger Ratcliff. 2022b. Modeling conditional dependence of response accuracy and response time with the diffusion item response theory model. Psychometrika 87: 725–48. [Google Scholar] [CrossRef] [PubMed]
- Kang, Inhan, Minjeong Jeon, and Ivailo Partchev. 2023. A latent space diffusion item response theory model to explore conditional dependence between responses and response times. Psychometrika 88: 830–64. [Google Scholar] [CrossRef]
- Kim, Nana, and Daniel M. Bolt. 2023. Evaluating psychometric differences between fast versus slow responses on rating scale items. Journal of Educational and Behavioral Statistics. [Google Scholar] [CrossRef]
- Levine, Abraham S. 1950. Construction and use of verbal analogy items. Journal of Applied Psychology 34: 105–7. [Google Scholar] [CrossRef] [PubMed]
- Luo, Jinwen, and Minjeong Jeon. 2023. Procrustes Matching for Latent Space Item Response Model. Available online: https://CRAN.R-project.org/package=prolsirm (accessed on 10 February 2024).
- Meng, Xiang-Bin, Jian Tao, and Hua-Hua Chang. 2015. A conditional joint modeling approach for locally dependent item responses and response times. Journal of Educational Measurement 52: 1–27. [Google Scholar] [CrossRef]
- Meyer, Patrick J. 2010. A mixture rasch model with item response time components. Applied Psychological Measurement 34: 521–38. [Google Scholar] [CrossRef]
- Molenaar, Dylan, and Paul De Boeck. 2018. Response mixture modeling: Accounting for heterogeneity in item characteristics across response times. Psychometrika 83: 279–97. [Google Scholar] [CrossRef]
- Naumann, Johannes, and Frank Goldhammer. 2017. Time-on-task effects in digital reading are non-linear and moderated by persons’ skills and tasks’ demands. Learning and Individual Differences 53: 1–16. [Google Scholar] [CrossRef]
- Oh, Man-Suk, and Adrian E. Raftery. 2007. Model-based clustering with dissimilarities: A bayesian approach. Journal of Computational and Graphical Statistics 16: 559–85. [Google Scholar] [CrossRef]
- Partchev, Ivailo, and Paul De Boeck. 2012. Can fast and slow intelligence be differentiated? Intelligence 40: 23–32. [Google Scholar] [CrossRef]
- Partchev, Ivailo, Paul De Boeck, and Rolf Steyer. 2013. How much power and speed is measured in this test? Assessment 20: 242–52. [Google Scholar] [CrossRef]
- Rasch, Georg. 1980. Probabilistic Models for Some Intelligence and Attainment Tests. Chicago: University of Chicago Press, Originally published as 1960. [Google Scholar]
- R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Schneider, Walter, and Richard M. Shiffrin. 1977. Controlled and automatic human information processing: I. detection, search, and attention. Psychological Review 84: 1–66. [Google Scholar] [CrossRef]
- Shiffrin, Richard M., and Walter Schneider. 1977. Controlled and automatic human information processing: Ii. perceptual learning, automatic attending, and a general theory. Psychological Review 84: 127–90. [Google Scholar] [CrossRef]
- Shortreed, Susan, Mark S. Handcock, and Peter Hoff. 2006. Positional estimation within a latent space model for networks. Methodology: European Journal of Research Methods for the Behavioral and Social Sciences 2: 24–33. [Google Scholar] [CrossRef]
- Stan Development Team. 2023a. RStan: The R Interface to Stan. R Package Version 2.26.21. Available online: https://mc-stan.org/ (accessed on 10 February 2024).
- Stan Development Team. 2023b. Stan Modeling Language Users Guide and Reference Manual. Version 2.26.1. Available online: https://mc-stan.org/ (accessed on 10 February 2024).
- Tuerlinckx, Francis, and Paul De Boeck. 2005. Two interpretations of the discrimination parameter. Psychometrika 70: 629–50. [Google Scholar] [CrossRef]
- Tuerlinckx, Francis, Dylan Molenaar, and Han L. J. van der Maas. 2016. Diffusion-based response-time models. In Handbook of Item Response Theory. Edited by Wim J. van der Linden. New York: Chapman & Hall/CRC, pp. 283–300. [Google Scholar]
- Ulitzsch, Esther, Matthias von Davier, and Steffi Pohl. 2020. Response times for joint modeling of response and omission behavior. Multivariate Behavioral Research 55: 425–53. [Google Scholar] [CrossRef]
- Ullstadius, Eva, Berit Carlstedt, and Jan-Eric Gustafsson. 2008. The multidimensionality of verbal analogy items. International Journal of Testing 8: 166–79. [Google Scholar] [CrossRef]
- van der Linden, Wim J. 2007. A hierarchical framework for modeling speed and accuracy on test items. Psychometrika 72: 287–308. [Google Scholar] [CrossRef]
- van der Linden, Wim J., and Fanmin Guo. 2008. Bayesian procedures for identifying aberrant response-time patterns in adaptive testing. Pyschometrika 73: 365–84. [Google Scholar] [CrossRef]
- van der Maas, Han L. J., and Eric-Jan Wagenmakers. 2005. A psychometric analysis of chess expertise. The American Journal of Psychology 118: 29–60. [Google Scholar] [CrossRef] [PubMed]
- van der Maas, Han L. J., Dylan Molenaar, Gunter Maris, Rogier A. Kievit, and Denny Borsboom. 2011. Cognitive psychology meets psychometric theory: On the relation between process models for decision making and latent variable models for individual differences. Psychological Review 118: 339–56. [Google Scholar] [CrossRef] [PubMed]
- van Harreveld, Frank, Eric-Jan Wagenmakers, and Han L. J. van der Maas. 2007. The effects of time pressure on chess skill: An investigation into fast and slow processes underlying expert performance. Psychological Research 71: 591–97. [Google Scholar] [CrossRef] [PubMed]
- Wang, Chun, and Gongjun Xu. 2015. A mixture hierarchical model for response times and response accuracy. British Journal of Mathematical and Statistical Psychology 68: 456–77. [Google Scholar] [CrossRef] [PubMed]
- Wang, Chun, Gongjun Xu, Zhuoran Shang, and Nathan Kuncel. 2018. Detecting aberrant behavior and item preknowledge: A comparison of mixture modeling method and residual method. Journal of Educational and Behavioral Statistics 43: 469–501. [Google Scholar] [CrossRef]
- Wise, Steven L., and Christine E. DeMars. 2006. An application of item response time: The effort-moderated IRT model. Journal of Educational Measurement 43: 19–38. [Google Scholar] [CrossRef]
- Wise, Steven L., and Xiaojing Kong. 2005. Response time effort: A new measure of examinee motivation in computer-based tests. Applied Measurement in Education 18: 163–83. [Google Scholar] [CrossRef]

| Person | Slow Responses | Fast Responses | ||||||
|---|---|---|---|---|---|---|---|---|
| Item 1 | Item 2 | ⋯ | Item I | Item | Item | ⋯ | Item | |
| 1 | 0 | NA | NA | NA | 1 | |||
| 0 | NA | 0 | NA | 1 | NA | |||
| NA | 1 | NA | 1 | NA | 1 | |||
| ⋮ | ||||||||
| NA | NA | 1 | 0 | 1 | NA | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, N.; Jeon, M.; Partchev, I. Conditional Dependence across Slow and Fast Item Responses: With a Latent Space Item Response Modeling Approach. J. Intell. 2024, 12, 23. https://doi.org/10.3390/jintelligence12020023
Kim N, Jeon M, Partchev I. Conditional Dependence across Slow and Fast Item Responses: With a Latent Space Item Response Modeling Approach. Journal of Intelligence. 2024; 12(2):23. https://doi.org/10.3390/jintelligence12020023
Chicago/Turabian StyleKim, Nana, Minjeong Jeon, and Ivailo Partchev. 2024. "Conditional Dependence across Slow and Fast Item Responses: With a Latent Space Item Response Modeling Approach" Journal of Intelligence 12, no. 2: 23. https://doi.org/10.3390/jintelligence12020023
APA StyleKim, N., Jeon, M., & Partchev, I. (2024). Conditional Dependence across Slow and Fast Item Responses: With a Latent Space Item Response Modeling Approach. Journal of Intelligence, 12(2), 23. https://doi.org/10.3390/jintelligence12020023





