The Worst Performance Rule, or the Not-Best Performance Rule? Latent-Variable Analyses of Working Memory Capacity, Mind-Wandering Propensity, and Reaction Time
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Reaction Time (Outcome) Tasks
2.2.1. SART
2.2.2. Number Stroop
2.2.3. Spatial Stroop
2.2.4. Arrow Flanker
2.2.5. Letter Flanker
2.2.6. Circle Flanker
2.3. Cognitive Predictor Measures
2.3.1. Working Memory Capacity (WMC)
2.3.2. Thought Reports of TUT
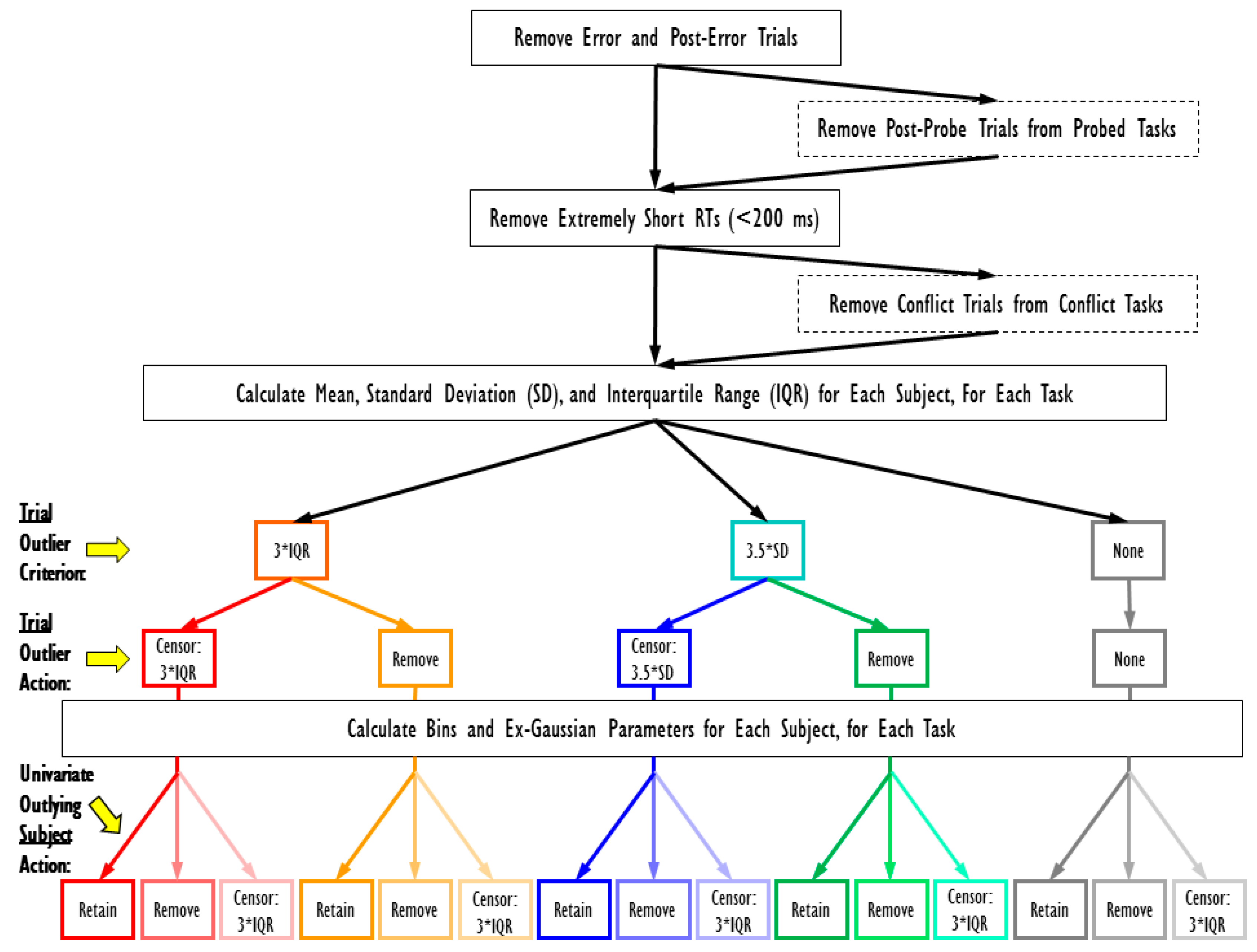
2.4. RT Data Cleaning Procedure
3. Results
3.1. Ranked-Bin Analyses
3.1.1. Descriptive Statistics and Zero-Order Correlations
3.1.2. Regression Evidence for the Worst Performance Rule
3.1.3. Confirmatory Factor Analyses of Ranked Bins
3.2. Ex-Gaussian Analyses
3.2.1. Descriptive Statistics and Zero-Order Correlations
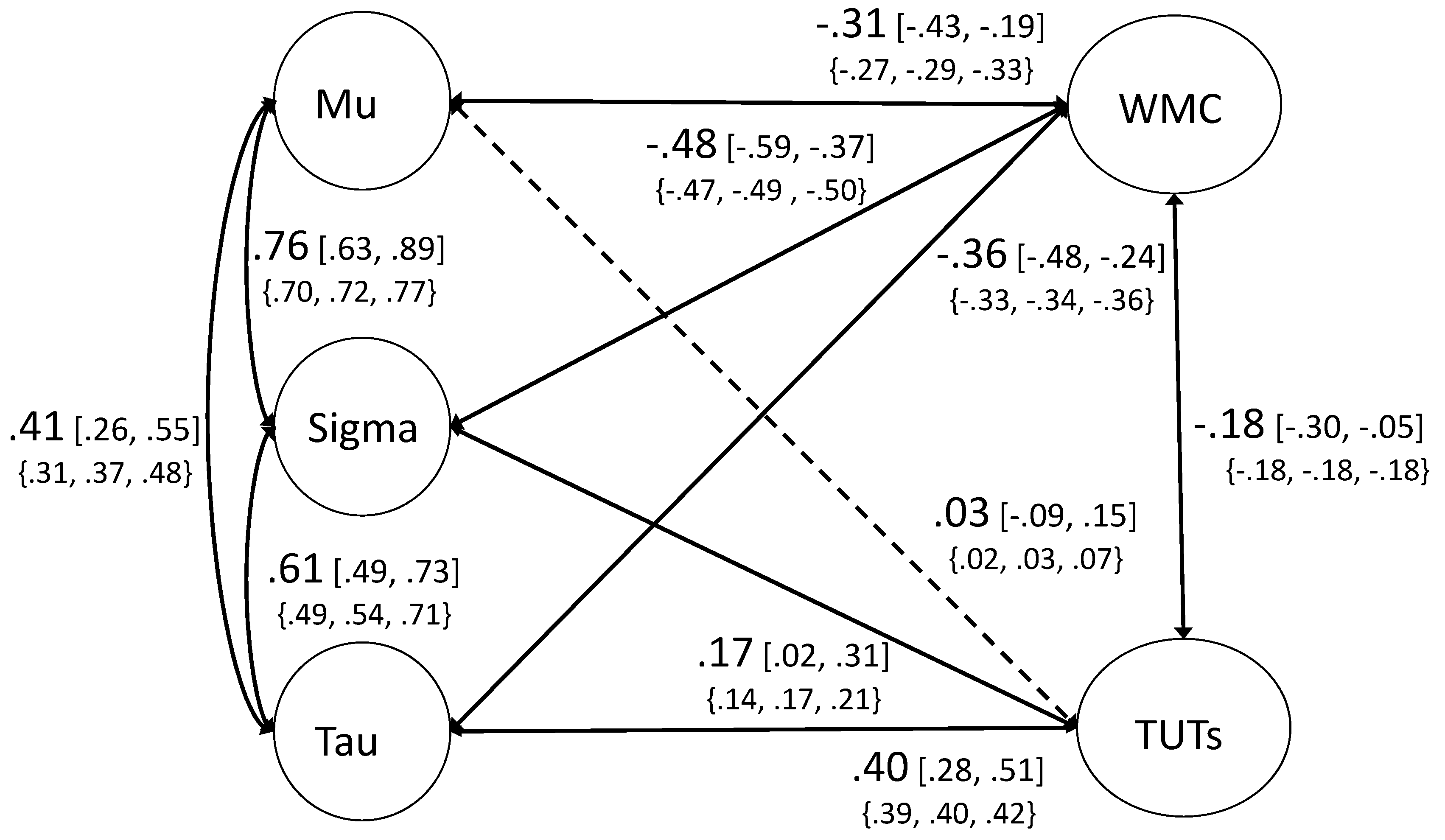
3.2.2. Ex-Gaussian Structural Models
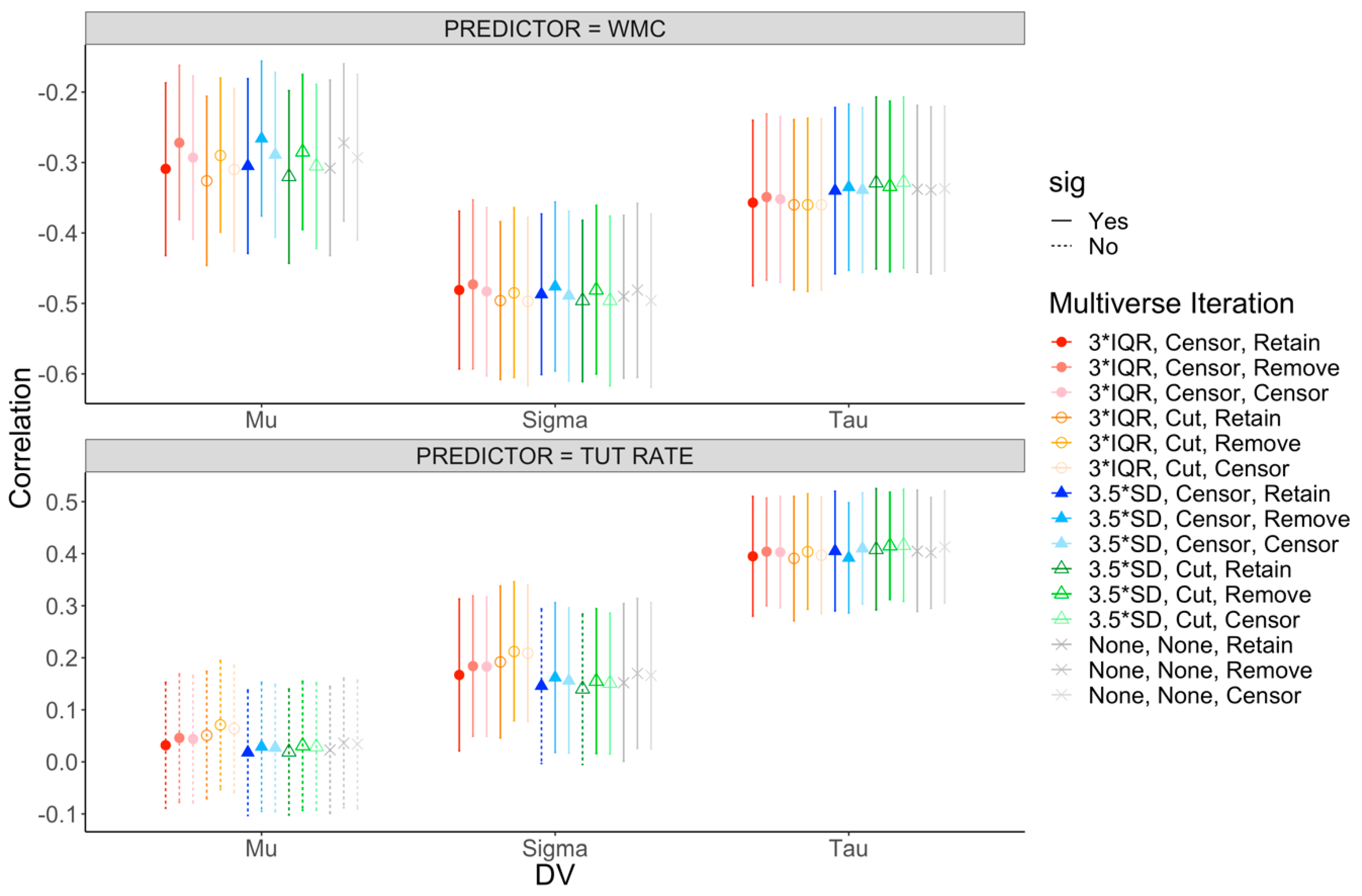
3.3. Mini-Multiverse Analysis of WPR Findings
3.3.1. Mini-Multiverse Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arnau, Stefan, Christoph Löffler, Jan Rummel, Dirk Hagemann, Edmund Wascher, and Anna-Lena Schubert. 2020. Inter-trial alpha power indicates mind wandering. Psychophysiology 57: e13581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bakker, Marjan, and Jelte M. Wicherts. 2014. Outlier removal and the relation with reporting errors and quality of psychological research. PLoS ONE 9: e103360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baldwin, Carryl L., Daniel M. Roberts, Daniela Barragan, John D. Lee, Neil Lerner, and James S. Higgins. 2017. Detecting and quantifying mind wandering during simulated driving. Frontiers in Human Neuroscience 11: 1–15. [Google Scholar] [CrossRef] [PubMed]
- Banks, Jonathan B., Matthew S. Welhaf, Audrey V. B. Hood, Adriel Boals, and Jaime L. Tartar. 2016. Examining the role of emotional valence of mind wandering: All mind wandering is not equal. Consciousness and Cognition 43: 167–76. [Google Scholar] [CrossRef] [PubMed]
- Bastian, Mikaël, and Jérôme Sackur. 2013. Mind wandering at the fingertips: Automatic parsing of subjective states based on response time variability. Frontiers in Psychology 4: 573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baumeister, Alfred A., and George Kellas. 1968. Intrasubject response variability in relation to intelligence. Journal of Abnormal Psychology 73: 421–23. [Google Scholar] [CrossRef] [Green Version]
- Cheyne, J. Allan, Grayden J. F. Solman, Jonathan S. A. Carriere, and Daniel Smilek. 2009. Anatomy of an error: A bidirectional state model of task engagement/disengagement and attention-related errors. Cognition 111: 98–113. [Google Scholar] [CrossRef]
- Christoff, Kalina, Alan M. Gordon, Jonathan Smallwood, Rachelle Smith, and Jonathan W. Schooler. 2009. Experience sampling during fMRI reveals default network and executive system contributions to mind wandering. Proceedings of the National Academy of Sciences USA 106: 8719–24. [Google Scholar] [CrossRef] [Green Version]
- Coyle, Thomas R. 2001. IQ is related to the worst performance rule in a memory task involving children. Intelligence 29: 117–29. [Google Scholar] [CrossRef]
- Coyle, Thomas R. 2003a. A review of the worst performance rule: Evidence, theory, and alternative hypotheses. Intelligence 6: 567–87. [Google Scholar] [CrossRef]
- Coyle, Thomas R. 2003b. IQ, the worst performance rule, and Spearman’s law: A reanalysis and extension. Intelligence 31: 473–89. [Google Scholar] [CrossRef]
- Doebler, Philipp, and Barbara Scheffler. 2016. The relationship of choice reaction time variability and intelligence: A meta-analysis. Learning and Individual Differences 52: 157–66. [Google Scholar] [CrossRef]
- Duncan, Terry E., Susan C. Duncan, and Lisa A. Strycker. 2006. An Introduction to Latent Variable Growth Curve Modeling: Concepts, Issues, and Applications. Mahwah: Erlbaum. [Google Scholar]
- Dutilh, Gilles, Joachim Vandekerckhove, Alexander Ly, Dora Matzke, Andreas Pedroni, Renato Frey, Jörg Rieskamp, and Eric-Jan Wagenmakers. 2017. A test of diffusion model explanation of the worst performance rule using preregistration and blinding. Attention, Perception, Psychophysics 79: 713–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engle, Randall W., and Michael J. Kane. 2004. Executive attention, working memory capacity, and a two-factor theory of cognitive control. In The Psychology of Learning and Motivation. Edited by Bower Gordon H. New York: Academic Press. [Google Scholar]
- Fernandez, Sébastien, Delphine Fagot, Judith Dirk, and Anik De Ribaupierre. 2014. Generalization of the worst performance rule across the lifespan. Intelligence 42: 31–43. [Google Scholar] [CrossRef]
- Fox, Kieran C.R., and Kalina Christoff. 2018. The Oxford Handbook of Spontaneous Thought: Mind-Wandering, Creativity, and Dreaming, 1st ed. New York: Oxford University Press. [Google Scholar]
- Frischkorn, Gidon T., Anna-Lena Schubert, Andreas B. Neubauer, and Dirk Hagemann. 2016. The worst performance rule as moderation: New methods for worst performance analysis. Journal of Intelligence 4: 9. [Google Scholar] [CrossRef] [Green Version]
- Heathcote, Andrew, Scott Brown, and Denis Cousineau. 2004. QMPE: Estimating lognormal, Wald, and Weibull RT distributions with a parameter-dependent lower bound. Behavior Research Methods, Instruments, Computers 36: 277–90. [Google Scholar] [CrossRef] [Green Version]
- Jensen, Arthur R. 1982. Reaction time and psychometric “g”. In A Model for Intelligence. Edited by Eysenck Hans Jurgen. New York: Plenum. [Google Scholar]
- Jensen, Arthur R. 1987. Individual differences in the Hick paradigm. In Speed of Information-Processing and Intelligence. Edited by Vernon Philip A. Norwood: Ablex. [Google Scholar]
- Jensen, Arthur R. 1992. The importance of intraindividual variation in reaction time. Personality and Individual Differences 13: 869–81. [Google Scholar] [CrossRef]
- Kam, Julia W. Y., and Todd C. Handy. 2013. The neurocognitive consequences of the wandering mind: A mechanistic account of sensory-motor decoupling. Frontiers in Psychology 4: 725. [Google Scholar] [CrossRef] [Green Version]
- Kane, Michael J., and Jennifer C. McVay. 2012. What mind wandering reveals about executive-control abilities and failures. Current Directions in Psychological Science 21: 348–54. [Google Scholar] [CrossRef] [Green Version]
- Kane, Michael J., Leslie H. Brown, Jennifer C. McVay, Paul J. Silvia, Inez Myin-Germeys, and Thomas R. Kwapil. 2007. For whom the mind wanderings and when: An experience-sampling study of working memory and executive control in daily life. Psychological Science 18: 614–21. [Google Scholar] [CrossRef]
- Kane, Michael J., Matt E. Meier, Bridget A. Smeekens, Georgina M. Gross, Charlotte A. Chun, Paul J. Silvia, and Thomas R. Kwapil. 2016. Individual differences in the executive control of attention, memory, thought, and their associations with schizotypy. Journal of Experimental Psychology: General 145: 1017–48. [Google Scholar] [CrossRef] [PubMed]
- Kovacs, Kristof, and Andrew R. A. Conway. 2016. Process Overlap Theory: A unified account of the general factor of intelligence. Psychological Inquiry 27: 151–77. [Google Scholar] [CrossRef]
- Kranzler, John H. 1992. A test of Larson and Alderton’s (1990) worst performance rule of reaction time variability. Personality and Individual Differences 13: 255–61. [Google Scholar] [CrossRef]
- Larson, Gerald E., and David L. Alderton. 1990. Reaction time variability and intelligence: A “worst performance” analysis of individual differences. Intelligence 14: 309–25. [Google Scholar] [CrossRef]
- Larson, Gerald E., and Dennis P. Saccuzzo. 1989. Cognitive correlates of general intelligence: Toward a process theory of g. Intelligence 13: 5–31. [Google Scholar] [CrossRef]
- Leys, Christophe, Marie Delacre, Youri L. Mora, Daniël Lakens, and Christophe Ley. 2019. How to classify, detect, and manage univariate and multivariate outliers, with emphasis on pre-registration. International Review of Social Psychology 32: 1–10. [Google Scholar] [CrossRef]
- Mason, Malia F., Michael I. Norton, John D. Van Horn, Daniel M. Wegner, Scott T. Grafton, and C. Neil Macrae. 2007. Wandering minds: The default network and stimulus-independent thought. Science 315: 393–95. [Google Scholar] [CrossRef] [Green Version]
- Massidda, Davide. 2013. Retimes: Reaction Time Analysis (Version 0.1–2). Available online: https://CRAN.R-project.org/package=retimes (accessed on 6 March 2019).
- Matzke, Dora, and Eric-Jan Wagenmakers. 2009. Psychology interpretation of the ex-Gaussian and shift Wald parameters: A diffusion model analysis. Psychonomic Bulletin Review 16: 798–817. [Google Scholar] [CrossRef]
- McVay, Jennifer C., and Michael J. Kane. 2009. Conducting the train of thought: Working memory capacity, goal neglect, and mind wandering in an executive-control task. Journal of Experimental Psychology: Learning, Memory, and Cognition 35: 196–204. [Google Scholar] [CrossRef] [Green Version]
- McVay, Jennifer C., and Michael J. Kane. 2010. Does mind wandering reflect executive function or executive failure? Comment on Smallwood and Schooler (2006) and Watkins (2008). Psychological Bulletin 136: 188–97. [Google Scholar] [CrossRef] [Green Version]
- McVay, Jennifer C., and Michael J. Kane. 2012a. Drifting from slow to “d’oh!”: Working memory capacity and mind wandering predict extreme reaction times and executive control. Journal of Experimental Psychology: Learning, Memory, and Cognition 38: 525–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McVay, Jennifer C., and Michael J. Kane. 2012b. Why does working memory capacity predict variation in reading comprehension? On the influence of mind wandering and executive attention. Journal of Experimental Psychology: General 141: 302–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meiran, Nachshon, and Nitzan Shahar. 2018. Working memory involvement in reaction time and intelligence: An examination of individual differences in reaction-time distributions. Intelligence 69: 176–85. [Google Scholar] [CrossRef]
- Mrazek, Michael D., Jonathan Smallwood, Michael S. Franklin, Jason M. Chin, Benjamin Baird, and Jonathan W. Schooler. 2012. The role of mind-wandering in measurements of general aptitude. Journal of Experimental Psychology: General 141: 788–98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Preacher, Kristopher J., Aaron L. Wichman, Robert C. MacCallum, and Nancy E. Briggs. 2008. Latent Growth Curve Modeling. Los Angeles: Sage. [Google Scholar]
- R Core Team. 2018. R: A Language and Environment for Statistical Computing. Vienna: R Foundationg for Statistical Computing. [Google Scholar]
- Rammsayer, Thomas H., and Stefan J. Troche. 2016. Validity of the worst performance rule as a function of task complexity and psychometric g: On the crucial role of g saturation. Journal of Intelligence 4: 5. [Google Scholar] [CrossRef] [Green Version]
- Randall, Jason G., Frederick L. Oswald, and Margaret E. Beier. 2014. Mind-wandering, cognition, and performance: A theory-driven meta-analysis of attention regulation. Psychological Bulletin 140: 1411–31. [Google Scholar] [CrossRef]
- Ratcliff, Roger, Anjali Thapar, and Gail McKoon. 2010. Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology 60: 127–57. [Google Scholar] [CrossRef] [Green Version]
- Robison, Matthew K., and Nash Unsworth. 2018. Cognitive and contextual correlates of spontaneous and deliberate mind-wandering. Journal of Experimental Psychology: Learning, Memory, and Cognition 44: 85–98. [Google Scholar] [CrossRef]
- Robison, Matthew K., Katherine I. Gath, and Nash Unsworth. 2017. The neurotic wandering mind: An individual differences investigation of neuroticism, mind-wandering, and executive control. The Quarterly Journal of Experimental Psychology 70: 649–66. [Google Scholar] [CrossRef]
- Schmiedek, Florian, Klaus Oberauer, Oliver Wilhelm, Heinz-Martin Süß, and Werner W. Wittmann. 2007. Individual differences in components of reaction time distributions and their relations to working memory and intelligence. Journal of Experimental Psychology: General 136: 414–29. [Google Scholar] [CrossRef] [Green Version]
- Schooler, Jonathan W., E. D. Reichle, and D. V. Halpern. 2004. Zoning out while reading: Evidence for dissociations between experience and metaconsciousness. In Thinking and Seeing: Visual Metacognition in Adults and Children. Cambridge: MIT Press. [Google Scholar]
- Schubert, Anna-Lena. 2019. A meta-analysis of the worst performance rule. Intelligence 73: 88–100. [Google Scholar] [CrossRef] [Green Version]
- Seli, Paul, James Allan Cheyne, and Daniel Smilek. 2013. Wandering minds and wavering rhythms: Linking mind wandering and behavioral variability. Journal of Experimental Psychology: Human Perception and Performance 39: 1–5. [Google Scholar] [CrossRef] [PubMed]
- Shahar, Nitzan, Andrei R. Teodorescu, Marius Usher, Maayan Pereg, and Nachshon Meiran. 2014. Selective influences of working memory load on exceptionally slow reaction times. Journal of Experimental Psychology: General 143: 1837–60. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, Leah D., and Philip A. Vernon. 2008. Intelligence and speed of information-processing: A review of 50 years of research. Personality and Individual Differences 44: 535–51. [Google Scholar] [CrossRef]
- Silberzahn, Raphael, Eric L. Uhlmann, Daniel P. Martin, Pasquale Anselmi, Frederik Aust, Eli Awtrey, and Štěpán Bahník. 2018. Many analysts, one data set: Making transparent how variations in analytic choices affect results. Advances in Methods and Practices in Psychological Science 1: 337–56. [Google Scholar] [CrossRef] [Green Version]
- Smallwood, Jonathan, and Jonathan W. Schooler. 2006. The restless mind. Psychological Bulletin 132: 946–58. [Google Scholar] [CrossRef]
- Smallwood, Jonathan, and Jonathan W. Schooler. 2015. The science of mind wandering: Empirically navigating the stream of consciousness. Annual Review of Psychology 66: 487–518. [Google Scholar] [CrossRef]
- Stawarczyk, David, Steve Majerus, Michalina Maj, Martial Van der Linden, and Arnaud D’Argembeau. 2011. Mind-wandering: Phenomenology and function as assessed with a novel experience sampling method. Acta Psychologica 136: 370–81. [Google Scholar] [CrossRef]
- Steegen, Sara, Francis Tuerlinckx, Andrew Gelman, and Wolf Vanpaemel. 2017. Increasing transparency through a multiverse analysis. Perspectives on Psychological Science 11: 702–12. [Google Scholar] [CrossRef]
- Ulrich, Rolf, and Jeff Miller. 1993. Effects of truncation on reaction time analysis. Journal of Experimental Psychology: General 123: 34–80. [Google Scholar] [CrossRef]
- Unsworth, Nash, and Gregory J. Spillers. 2010. Working memory capacity: Attention control, secondary memory, or both? A direct test of the dual-component model. Journal of Memory and Language 62: 392–406. [Google Scholar] [CrossRef]
- Unsworth, Nash, and Matthew K. Robison. 2015. Individual differences in the allocation of attention to items in working memory: Evidence from pupillometry. Psychonomic Bulletin Review 22: 757–65. [Google Scholar] [CrossRef] [PubMed]
- Unsworth, Nash, and Matthew K. Robison. 2016. Pupillary correlates of lapses of sustained attention. Cognitive, Affective, Behavioral Neuroscience 16: 601–15. [Google Scholar] [CrossRef] [PubMed]
- Unsworth, Nash, and Matthew K. Robison. 2017a. The importance of arousal for variation in working memory capacity and attention control: A latent variable pupillometry study. Journal of Experimental Psychology: Learning, Memory, and Cognition 43: 1962–87. [Google Scholar] [CrossRef] [PubMed]
- Unsworth, Nash, and Matthew K. Robison. 2017b. A locus Coeruleus-Norepinephrine account of individual differences in working memory capacity and attention control. Psychonomic Bulletin Review 43: 1282–311. [Google Scholar] [CrossRef]
- Unsworth, Nash, and Matthew K. Robison. 2018. Tracking mind-wandering and arousal state with pupillometry. Cognitive, Affective, & Behavioral Neuroscience 18: 638–664. [Google Scholar]
- Unsworth, Nash, and Randall W. Engle. 2008. Speed and accuracy of accessing information in working memory: An individual differences investigation of focus switching. Journal of Experimental Psychology: Learning, Memory, and Cognition 34: 616–30. [Google Scholar] [CrossRef] [Green Version]
- Unsworth, Nash, Matthew K. Robison, and Ashley L. Miller. 2018. Pupillary correlates of fluctuations in sustained attention. Journal of Cognitive Neuroscience 30: 1241–53. [Google Scholar] [CrossRef]
- Unsworth, Nash, Thomas S. Redick, Chad E. Lakey, and Diana L. Young. 2010. Lapses of sustained attention and their relation to executive control and fluid abilities: An individual differences investigation. Intelligence 38: 111–22. [Google Scholar] [CrossRef]
- Unsworth, Nash, Thomas S. Redick, Gregory J. Spillers, and Gene A. Brewer. 2012. Variation in working memory capacity and cognitive control: Goal maintenance and microadjustments of control. The Quarterly Journal of Experimental Psychology 65: 326–55. [Google Scholar] [CrossRef]
- Unsworth, Nash, Gregory J. Spillers, Gene A. Brewer, and Brittany McMillan. 2011. Attention control and the antisaccade task: A response time distribution analysis. Acta Psychological 137: 90–100. [Google Scholar] [CrossRef] [PubMed]
- Unsworth, Nash. 2015. Consistency of attentional control as an important cognitive trait: A latent-variable analysis. Intelligence 49: 110–28. [Google Scholar] [CrossRef]
- Van Zandt, Trisha. 2000. How to fit a response time distribution. Psychonomic Bulletin Review 7: 424–65. [Google Scholar] [CrossRef] [PubMed]
- Wickham, Hadley, Romain Francois, Lionel Henry, and Kirill Müller. 2018. Dplyr: A Grammar of Data Manipulation. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 3 March 2019).
- Wiemers, Elizabeth A., and Thomas S. Redick. 2019. The influence of thought probes on performance: Does the mind wander more if you ask it? Psychonomic Bulletin Review 26: 367–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilhelm, Oliver, and Klaus Oberauer. 2006. Why are reasoning ability and working memory capacity related to mental speed? An investigation of stimulus-response compatibility in choice reaction time tasks. European Journal of Cognitive Psychology 18: 18–50. [Google Scholar] [CrossRef]


| Variable | Mean | SD | Min | Max | Skew | Kurtosis |
|---|---|---|---|---|---|---|
| SART Bin 1 | 337 | 72 | 213 | 639 | 0.726 | 0.562 |
| SART Bin 2 | 421 | 95 | 237 | 823 | 0.506 | 0.202 |
| SART Bin 3 | 491 | 107 | 258 | 979 | 0.265 | 0.177 |
| SART Bin 4 | 576 | 122 | 279 | 1048 | 0.367 | 1.002 |
| SART Bin 5 | 781 | 182 | 326 | 1419 | 0.870 | 1.412 |
| Letter Flanker Bin 1 | 437 | 59 | 292 | 627 | 0.608 | 0.417 |
| Letter Flanker Bin 2 | 498 | 75 | 339 | 773 | 0.651 | 0.372 |
| Letter Flanker Bin 3 | 547 | 91 | 367 | 864 | 0.778 | 0.574 |
| Letter Flanker Bin 4 | 611 | 118 | 405 | 1028 | 0.982 | 1.157 |
| Letter Flanker Bin 5 | 778 | 202 | 450 | 1488 | 1.168 | 1.467 |
| Arrow Flanker Bin 1 | 389 | 37 | 260 | 527 | 0.306 | 0.486 |
| Arrow Flanker Bin 2 | 437 | 45 | 311 | 584 | 0.552 | 0.195 |
| Arrow Flanker Bin 3 | 471 | 53 | 343 | 669 | 0.691 | 0.476 |
| Arrow Flanker Bin 4 | 515 | 67 | 373 | 750 | 0.776 | 0.536 |
| Arrow Flanker Bin 5 | 636 | 113 | 427 | 1048 | 0.949 | 0.744 |
| Circle Flanker Bin 1 | 426 | 46 | 293 | 595 | 0.668 | 0.930 |
| Circle Flanker Bin 2 | 489 | 57 | 351 | 699 | 0.629 | 0.516 |
| Circle Flanker Bin 3 | 536 | 69 | 389 | 799 | 0.776 | 1.010 |
| Circle Flanker Bin 4 | 600 | 96 | 421 | 941 | 1.131 | 1.794 |
| Circle Flanker Bin 5 | 768 | 180 | 466 | 1360 | 1.339 | 1.938 |
| Number Stroop Bin 1 | 411 | 40 | 309 | 557 | 0.590 | 0.940 |
| Number Stroop Bin 2 | 478 | 47 | 366 | 658 | 0.490 | 0.831 |
| Number Stroop Bin 3 | 523 | 53 | 405 | 724 | 0.480 | 0.687 |
| Number Stroop Bin 4 | 574 | 64 | 441 | 824 | 0.648 | 0.790 |
| Number Stroop Bin 5 | 716 | 125 | 502 | 1167 | 1.228 | 1.799 |
| Spatial Stroop Bin 1 | 516 | 95 | 293 | 880 | 1.013 | 1.507 |
| Spatial Stroop Bin 2 | 596 | 118 | 382 | 1010 | 1.151 | 1.716 |
| Spatial Stroop Bin 3 | 661 | 139 | 410 | 1133 | 1.216 | 1.714 |
| Spatial Stroop Bin 4 | 751 | 179 | 432 | 1333 | 1.334 | 1.900 |
| Spatial Stroop Bin 5 | 991 | 307 | 514 | 1955 | 1.408 | 1.765 |
| Model 1 (WMC) | Model 2 (TUTs) | |||
|---|---|---|---|---|
| SART | B (SE) | ß | B (SE) | ß |
| Bin | 104.655 (1.743) | 0.759 *** | 104.655 (1.743) | 0.759 *** |
| WMC | −3.677 (7.795) | −0.009 | ||
| Bin X WMC | −20.330 (3.556) | −0.169 *** | ||
| TUT | −5.470 (9.427) | −0.011 | ||
| Bin X TUT | 24.743 (4.299) | 0.171 *** | ||
| Letter Flanker | ||||
| Bin | 79.654 (1.857) | 0.665 *** | 79.724 (1.824) | 0.759 *** |
| WMC | −31.405 (7.331) | −0.089 *** | ||
| Bin X WMC | −9.604 (3.851) | −0.090 * | ||
| TUT | 50.355 (8.434) | 0.123 *** | ||
| Bin X TUT | 20.369 (4.403) | 0.165 *** | ||
| Arrow Flanker | B (SE) | ß | B (SE) | ß |
| Bin | 57.324 (1.030) | 0.748 *** | 57.268 (1.044) | 0.747 *** |
| WMC | −26.804 (4.547) | −0.120 *** | ||
| Bin X WMC | −9.373 (2.115) | −0.139 * | ||
| TUT | 17.039 (5.480) | 0.064 ** | ||
| Bin X TUT | 8.411 (2.571) | 0.104 ** | ||
| Circle Flanker | ||||
| Bin | 80.380 (1.594) | 0.714 *** | 80.441 (1.606) | 0.714 *** |
| WMC | −47.011 (6.587) | −0.146 *** | ||
| Bin X WMC | −15.938 (3.220) | −0.169 *** | ||
| TUT | 46.040 (7.929) | 0.119 *** | ||
| Bin X TUT | 19.843 (3.890) | 0.170 *** | ||
| Number Stroop | ||||
| Bin | 70.970 (1.098) | 0.795 *** | 70.998 (1.102) | 0.795 *** |
| WMC | −32.507 (5.342) | −0.125 *** | ||
| Bin X WMC | −12.222 (2.261) | −0.156 *** | ||
| TUT | 32.592 (6.274) | 0.107 *** | ||
| Bin X TUT | 16.167 (2.661) | 0.176 *** | ||
| Spatial Stroop | ||||
| Bin | 112.604 (2.980) | 0.616 *** | 112.817 (3.012) | 0.618 *** |
| WMC | −59.276 (10.940) | −0.113 *** | ||
| Bin X WMC | −21.361 (6.060) | −0.139 *** | ||
| TUT | 13.043 (13.129) | 0.021 | ||
| Bin X TUT | 25.725 (7.301) | 0.136 *** | ||
| Model 1 | Model 2 | Model 3 | ||||
|---|---|---|---|---|---|---|
| SART | B (SE) | ß | B (SE) | ß | B (SE) | ß |
| Bin 1 | 0.001 (0.000) | 0.159 *** | 0.003 (0.001) | 0.394 *** | 0.002 (0.001) | 0.220 * |
| Bin 3 | −0.001 (0.000) | −0.276 *** | 0.000 (0.000) | 0.018 | ||
| Bin 5 | −0.001 (0.000) | −0.247 * | ||||
| R2 | 0.025 | 0.047 | 0.079 | |||
| ∆R2 | 0.022 | 0.032 | ||||
| Letter Flanker | ||||||
| Bin 1 | −0.001 (0.000) | −0.105 * | 0.002 (0.001) | 0.244 * | 0.003 (0.001) | 0.329 ** |
| Bin 3 | −0.002 (0.001) | −0.381 *** | −0.003 (0.001) | −0.619 *** | ||
| Bin 5 | 0.000 (0.000) | 0.182 ^ | ||||
| R2 | 0.011 | 0.034 | 0.041 | |||
| ∆R2 | 0.022 | 0.007 | ||||
| Arrow Flanker | ||||||
| Bin 1 | −0.002 (0.001) | −0.138 ** | 0.003 (0.001) | 0.217 * | 0.003 (0.001) | 0.202 * |
| Bin 3 | −0.004 (0.001) | −0.407 *** | −0.003 (0.001) | −0.356 * | ||
| Bin 5 | −0.000 (0.000) | −0.041 | ||||
| R2 | 0.019 | 0.058 | 0.059 | |||
| ∆R2 | 0.039 | 0.001 | ||||
| Circle Flanker | ||||||
| Bin 1 | −0.002 (0.000) | −0.230 *** | 0.001 (0.001) | 0.049 | 0.001 (0.001) | 0.048 |
| Bin 3 | −0.002 (0.001) | −0.317 *** | −0.002 (0.001) | −0.315 * | ||
| Bin 5 | −0.000 (0.000) | −0.002 | ||||
| R2 | 0.053 | 0.076 | 0.076 | |||
| ∆R2 | 0.023 | 0.000 | ||||
| Number Stroop | ||||||
| Bin 1 | −0.002 (0.001) | −0.135 ** | 0.005 (0.001) | 0.410 *** | 0.006 (0.001) | 0.457 *** |
| Bin 3 | −0.006 (0.001) | −0.621 *** | −0.007 (0.001) | −0.730 *** | ||
| Bin 5 | 0.000 (0.000) | 0.083 | ||||
| R2 | 0.018 | 0.106 | 0.108 | |||
| ∆R2 | 0.088 | 0.002 | ||||
| Spatial Stroop | B (SE) | ß | B (SE) | ß | B (SE) | ß |
| Bin 1 | −0.001 (0.000) | −0.128 ** | 0.001 (0.001) | 0.149 | 0.000 (0.001) | 0.092 |
| Bin 3 | −0.001 (0.000) | −0.300 * | −0.001 (0.001) | −0.185 | ||
| Bin 5 | −0.000 (0.000) | −0.074 | ||||
| R2 | 0.016 | 0.030 | 0.031 | |||
| ∆R2 | 0.014 | 0.001 | ||||
| Model 1 | Model 2 | Model 3 | ||||
|---|---|---|---|---|---|---|
| SART | B (SE) | ß | B (SE) | ß | B (SE) | ß |
| Bin 1 | −0.001 (0.000) | −0.210 *** | −0.003 (0.000) | −0.453 *** | −0.002 (0.001) | −0.291 ** |
| Bin 3 | 0.001 (0.000) | 0.287 *** | 0.000 (0.000) | 0.012 | ||
| Bin 5 | 0.001 (0.000) | 0.231 *** | ||||
| R2 | 0.044 | 0.067 | 0.094 | |||
| ∆R2 | 0.020 | 0.027 | ||||
| Letter Flanker | ||||||
| Bin 1 | 0.001 (0.000) | 0.136 ** | −0.001 (0.001) | −0.191 ^ | −0.001 (0.001) | −0.092 |
| Bin 3 | 0.002 (0.001) | 0.358 ** | 0.000 (0.001) | 0.080 | ||
| Bin 5 | 0.000 (0.000) | 0.213 * | ||||
| R2 | 0.019 | 0.039 | 0.048 | |||
| ∆R2 | 0.020 | 0.009 | ||||
| Arrow Flanker | ||||||
| Bin 1 | 0.000 (0.001) | 0.031 | −0.003 (0.001) | −0.241 ** | −0.002 (0.001) | −0.180 ^ |
| Bin 3 | 0.002 (0.001) | 0.312 *** | 0.001 (0.001) | 0.112 | ||
| Bin 5 | 0.001 (0.000) | 0.165 | ||||
| R2 | 0.001 | 0.024 | 0.029 | |||
| ∆R2 | 0.023 | 0.005 | ||||
| Circle Flanker | ||||||
| Bin 1 | 0.001 (0.000) | 0.155 *** | −0.001 (0.001) | −0.067 | 0.000 (0.001) | 0.031 |
| Bin 3 | 0.001 (0.001) | 0.252 ** | −0.000 (0.001) | −0.018 | ||
| Bin 5 | 0.000 (0.000) | 0.220 * | ||||
| R2 | 0.024 | 0.038 | 0.051 | |||
| ∆R2 | 0.014 | 0.013 | ||||
| Number Stroop | B (SE) | ß | B (SE) | ß | B (SE) | ß |
| Bin 1 | 0.001 (0.00) | 0.089 ^ | −0.003 (0.001) | −0.295 ** | −0.001 (0.001) | −0.101 |
| Bin 3 | 0.003 (0.001) | 0.437 *** | −0.000 (0.001) | −0.020 | ||
| Bin 5 | 0.001 (0.000) | 0.345 *** | ||||
| R2 | 0.008 | 0.052 | 0.080 | |||
| ∆R2 | 0.044 | 0.028 | ||||
| Spatial Stroop | ||||||
| Bin 1 | −0.000 (0.000) | − 0.107 * | −0.003 (0.001) | −0.672 *** | −0.002 (0.001) | −0.513 *** |
| Bin 3 | 0.002 (0.000) | 0.612 *** | 0.001 (0.001) | 0.286 | ||
| Bin 5 | 0.000 (0.000) | 0.209 ^ | ||||
| R2 | 0.011 | 0.068 | 0.075 | |||
| ∆R2 | 0.057 | 0.007 | ||||
| Variable | Mean | SD | Min | Max | Skew | Kurtosis |
|---|---|---|---|---|---|---|
| SART Mu | 447 | 49 | 330 | 646 | 0.678 | 0.927 |
| SART Sigma | 49 | 19 | 0 | 119 | 0.309 | 0.571 |
| SART Tau | 114 | 61 | 1 | 303 | 1.263 | 1.704 |
| Letter Flanker Mu | 376 | 108 | 200 | 871 | 0.465 | 0.109 |
| Letter Flanker Sigma | 69 | 41 | 0 | 252 | 0.758 | 0.460 |
| Letter Flanker Tau | 144 | 71 | 3 | 386 | 1.147 | 1.670 |
| Arrow Flanker Mu | 446 | 42 | 356 | 608 | 0.446 | 0.639 |
| Arrow Flanker Sigma | 58 | 14 | 22 | 108 | 0.523 | 0.456 |
| Arrow Flanker Tau | 94 | 42 | 5 | 237 | 1.335 | 1.801 |
| Circle Flanker Mu | 407 | 39 | 309 | 533 | 0.506 | 0.300 |
| Circle Flanker Sigma | 39 | 15 | 0 | 91 | 0.917 | 1.366 |
| Circle Flanker Tau | 82 | 36 | 3 | 203 | 0.968 | 0.796 |
| Number Stroop Mu | 534 | 105 | 329 | 917 | 1.046 | 1.593 |
| Number Stroop Sigma | 58 | 30 | 0 | 167 | 1.024 | 1.852 |
| Number Stroop Tau | 165 | 98 | 3 | 486 | 1.353 | 1.816 |
| Spatial Stroop Mu | 456 | 65 | 310 | 702 | 0.645 | 0.444 |
| Spatial Stroop Sigma | 47 | 21 | 0 | 127 | 0.730 | 0.879 |
| Spatial Stroop Tau | 115 | 64 | 2 | 345 | 1.210 | 1.851 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Welhaf, M.S.; Smeekens, B.A.; Meier, M.E.; Silvia, P.J.; Kwapil, T.R.; Kane, M.J. The Worst Performance Rule, or the Not-Best Performance Rule? Latent-Variable Analyses of Working Memory Capacity, Mind-Wandering Propensity, and Reaction Time. J. Intell. 2020, 8, 25. https://doi.org/10.3390/jintelligence8020025
Welhaf MS, Smeekens BA, Meier ME, Silvia PJ, Kwapil TR, Kane MJ. The Worst Performance Rule, or the Not-Best Performance Rule? Latent-Variable Analyses of Working Memory Capacity, Mind-Wandering Propensity, and Reaction Time. Journal of Intelligence. 2020; 8(2):25. https://doi.org/10.3390/jintelligence8020025
Chicago/Turabian StyleWelhaf, Matthew S., Bridget A. Smeekens, Matt E. Meier, Paul J. Silvia, Thomas R. Kwapil, and Michael J. Kane. 2020. "The Worst Performance Rule, or the Not-Best Performance Rule? Latent-Variable Analyses of Working Memory Capacity, Mind-Wandering Propensity, and Reaction Time" Journal of Intelligence 8, no. 2: 25. https://doi.org/10.3390/jintelligence8020025
APA StyleWelhaf, M. S., Smeekens, B. A., Meier, M. E., Silvia, P. J., Kwapil, T. R., & Kane, M. J. (2020). The Worst Performance Rule, or the Not-Best Performance Rule? Latent-Variable Analyses of Working Memory Capacity, Mind-Wandering Propensity, and Reaction Time. Journal of Intelligence, 8(2), 25. https://doi.org/10.3390/jintelligence8020025





