Model-Based Design to Enhance Neotissue Formation in Additively Manufactured Calcium-Phosphate-Based Scaffolds
Abstract
:1. Introduction
2. Materials and Methods
2.1. In Silico Model
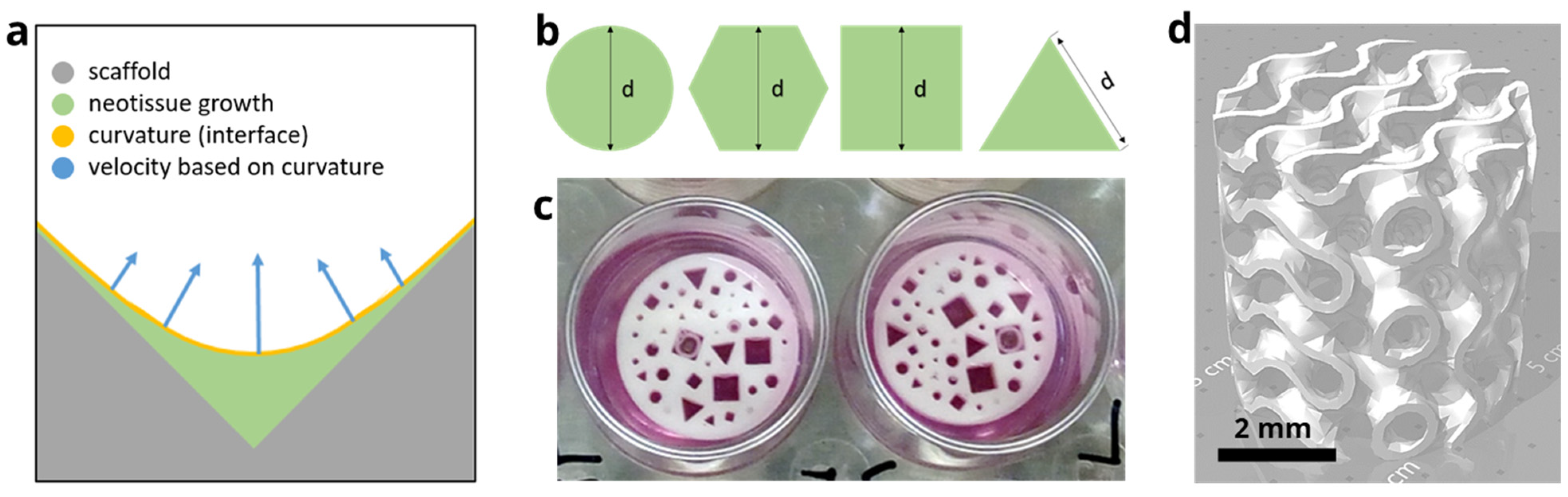
2.1.1. Level Set Method
2.1.2. Implementation of the Model
2.1.3. Optimization of the Velocity Control Value
2.2. In Vitro Experiments
2.2.1. Design of the Disk
2.2.2. Design of the Gyroid Scaffold
2.2.3. Production of the Disk and Scaffold
2.2.4. Cell Culture and Analysis
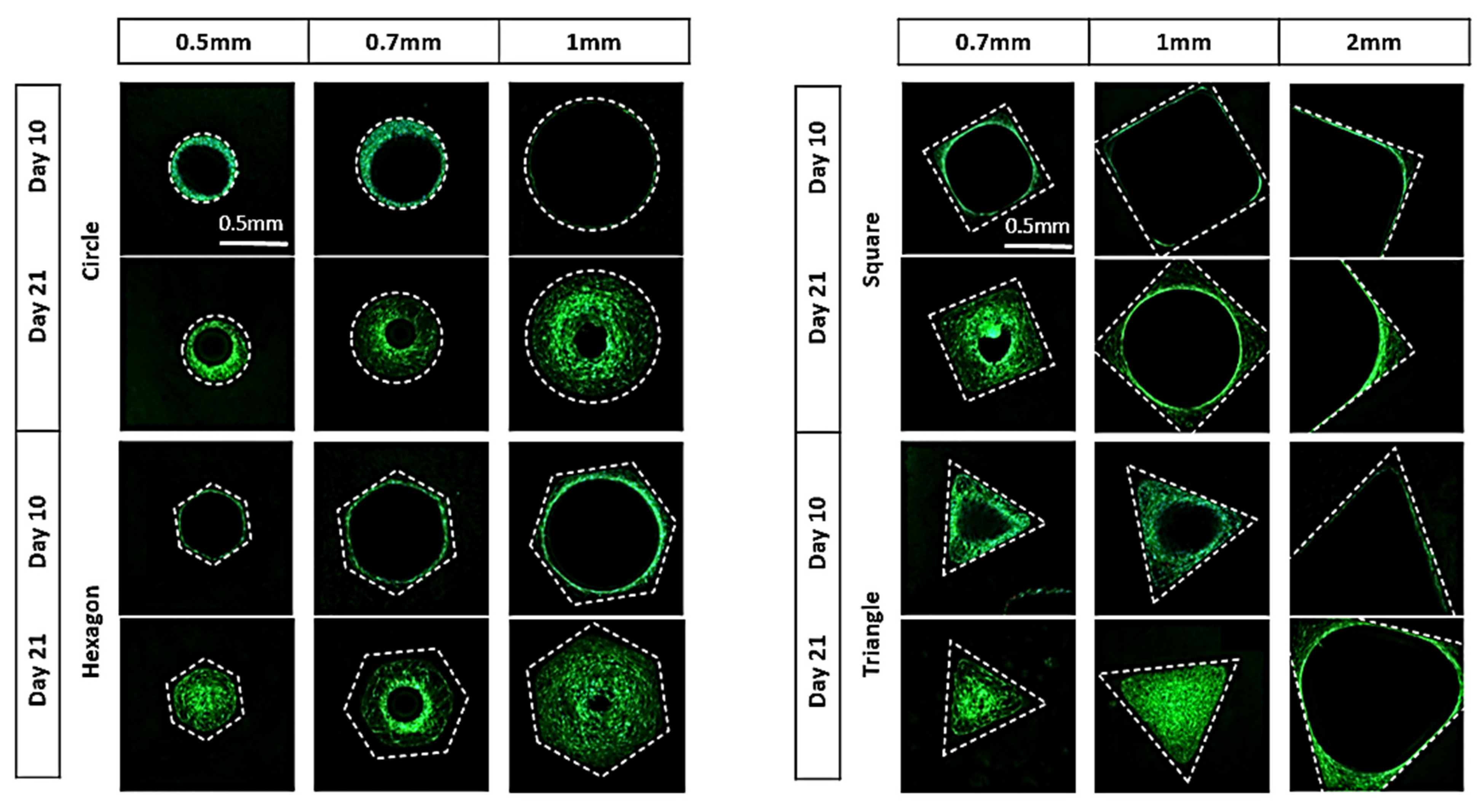
2.2.5. Image Processing
2.2.6. Statistical Analysis
3. Results
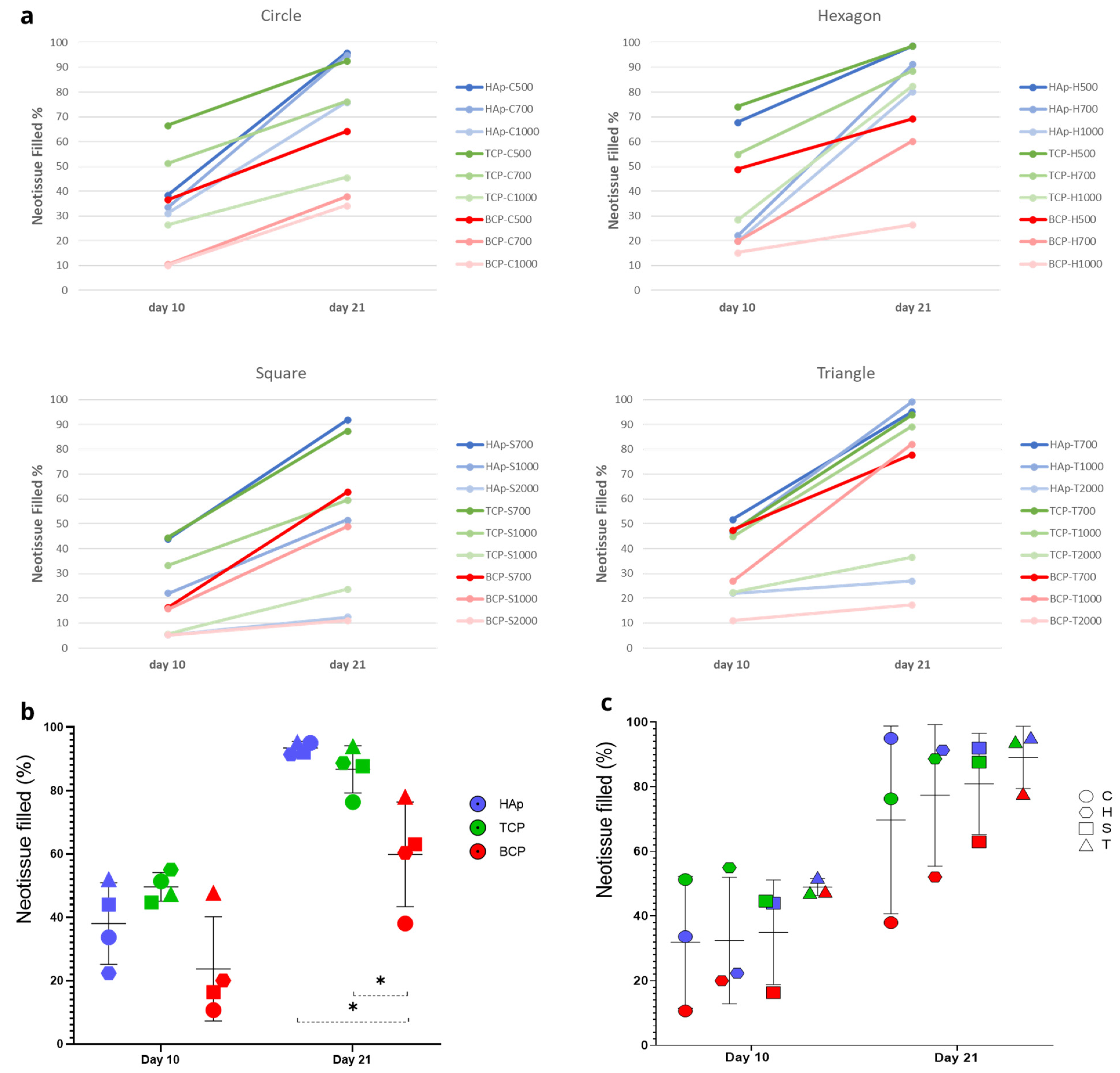
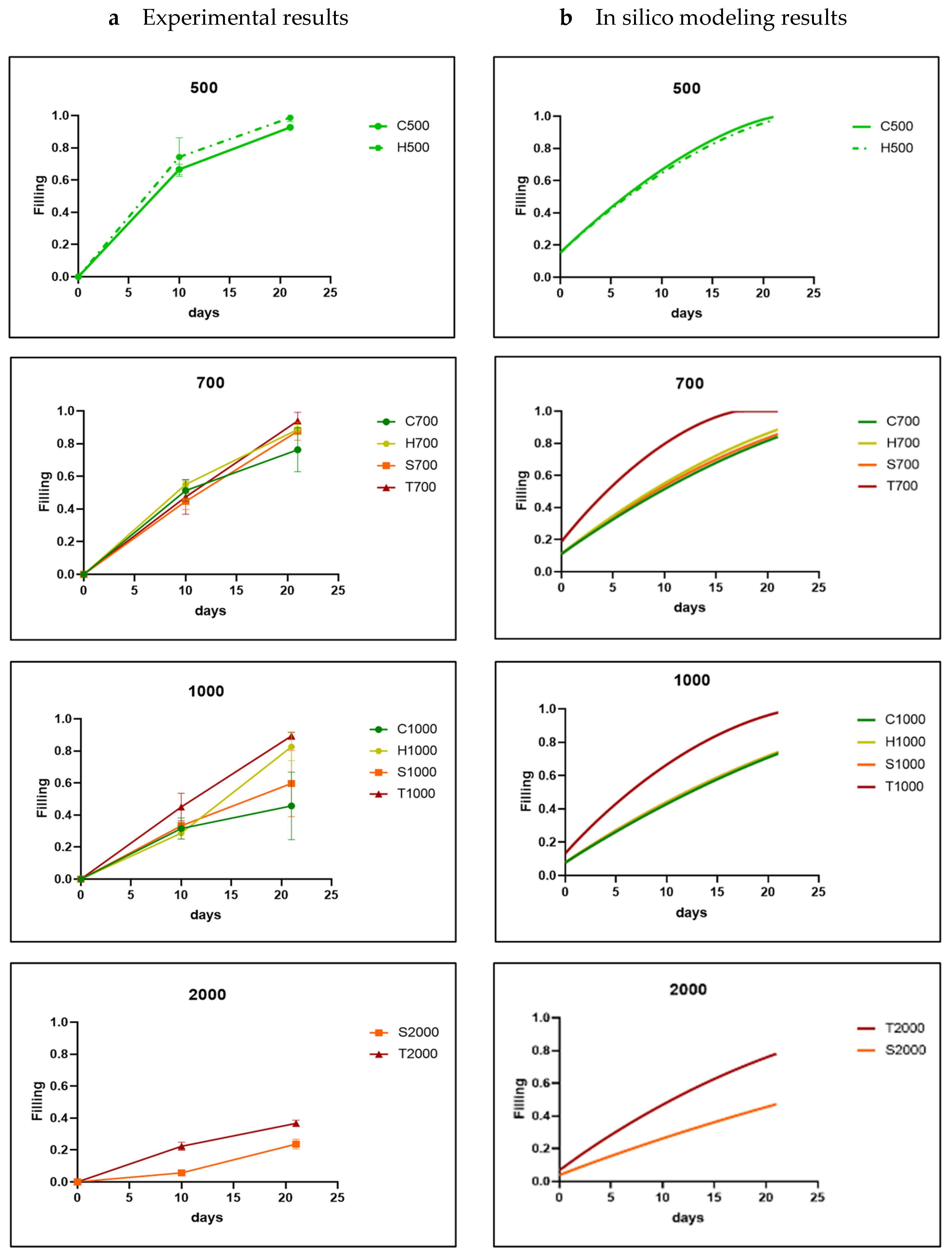
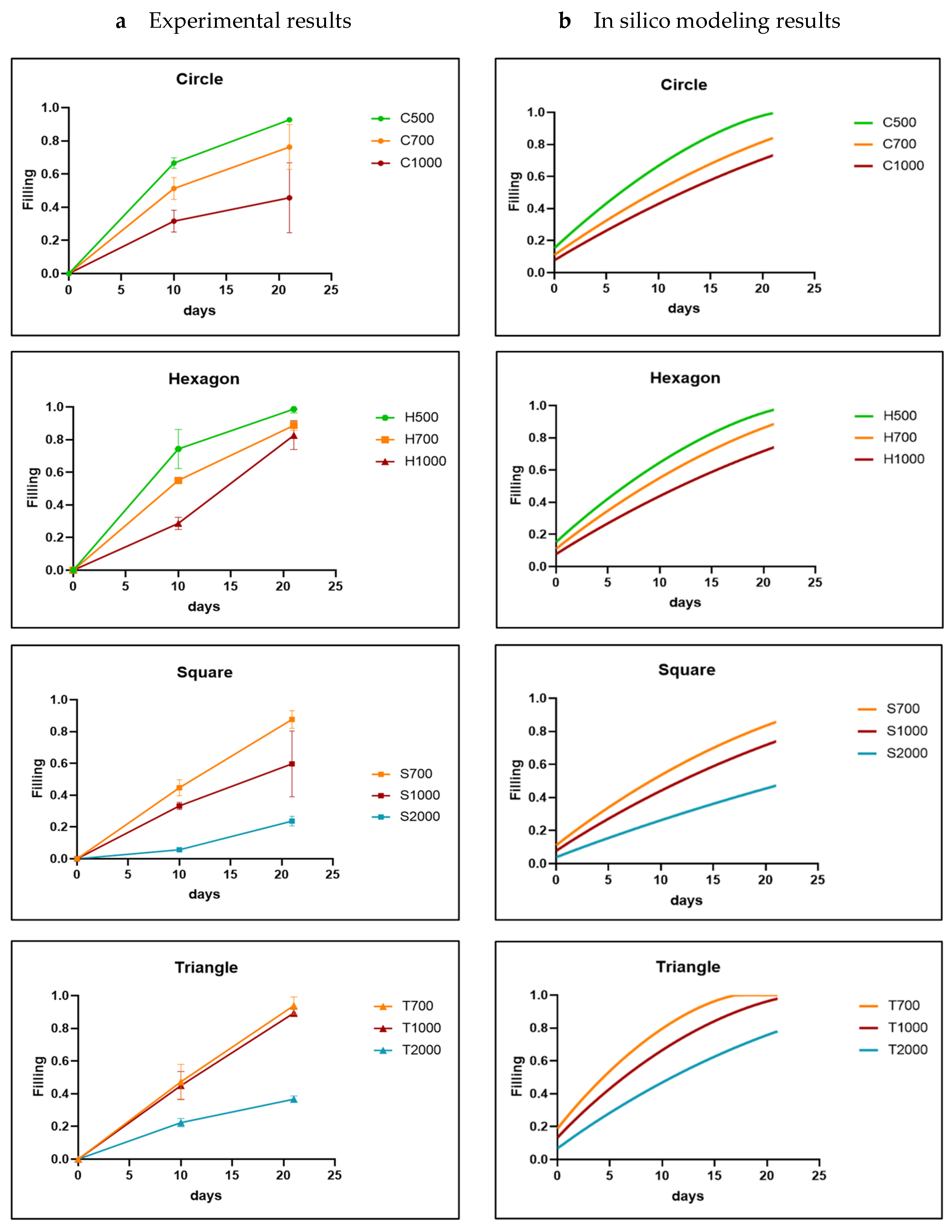
3.1. Analysis of In Vitro Cell Behavior
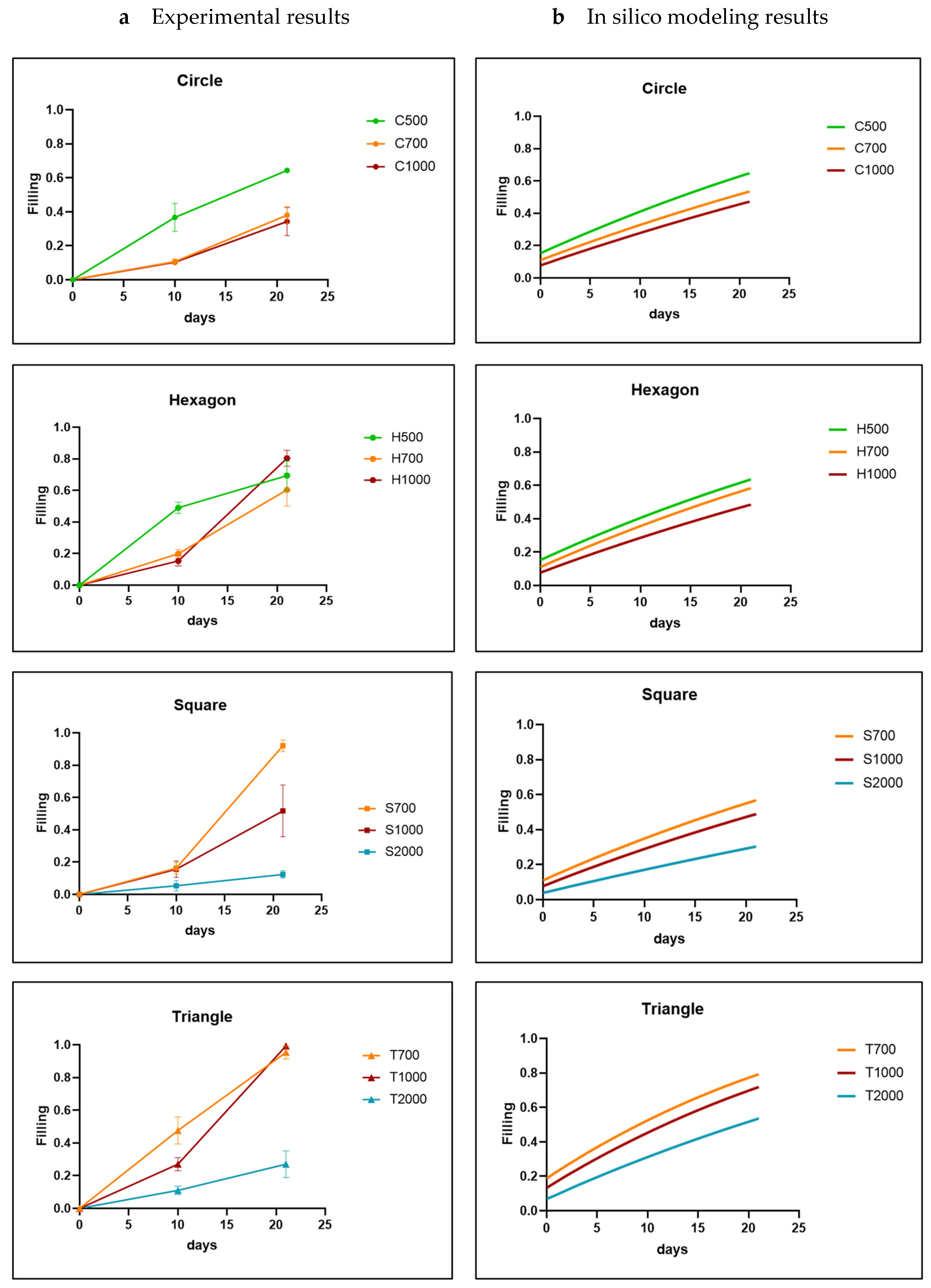
3.2. In Silico Modeling
3.3. Model-Informed 3D Scaffold Design and Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| [%] | S1 | S2 | S3 | Average | S1 | S2 | S3 | Average | S1 | S2 | S3 | Average | S1 | S2 | S3 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HAp-C500 | HAp-C700 | HAp-C1000 | ||||||||||||||
| day 10 | 43 | 35 | 38 | 38.67 | 37 | 31 | 33 | 33.67 | 34 | 35 | 25 | 31.33 | ||||
| day 21 | 97 | 91 | 100 | 96.00 | 97 | 95 | 93 | 95.00 | 86 | 75 | 67 | 76.00 | ||||
| HAp-H500 | HAp-H700 | HAp-H1000 | ||||||||||||||
| day 10 | 62 | 66 | 76 | 68.00 | 24 | 20 | 23 | 22.33 | 18 | 24 | 18 | 20.00 | ||||
| day 21 | 100 | 96 | 100 | 98.67 | 93 | 90 | 91 | 91.33 | 75 | 81 | 85 | 80.33 | ||||
| HAp-S700 | HAp-S1000 | HAp-S2000 | ||||||||||||||
| day 10 | 51 | 39 | 42 | 44.00 | 19 | 25 | 22 | 22.00 | 5 | 5 | 6 | 5.33 | ||||
| day 21 | 96 | 91 | 89 | 92.00 | 53 | 67 | 35 | 51.67 | 15 | 11 | 11 | 12.33 | ||||
| HAp-T700 | HAp-T1000 | HAp-T2000 | ||||||||||||||
| day 10 | 59 | 46 | 51 | 52.00 | 49 | 41 | 50 | 46.67 | 26 | 23 | 17 | 22.00 | ||||
| day 21 | 93 | 100 | 93 | 95.33 | 98 | 100 | 100 | 99.33 | 34 | 18 | 29 | 27.00 | ||||
| TCP-C500 | TCP-C700 | TCP-C1000 | ||||||||||||||
| day 10 | 63 | 69 | 68 | 66.67 | 53 | 44 | 57 | 51.33 | 30 | 24 | 26 | 26.67 | ||||
| day 21 | 93 | 93 | 92 | 92.67 | 69 | 68 | 92 | 76.33 | 32 | 70 | 35 | 45.67 | ||||
| TCP-H500 | TCP-H700 | TCP-H1000 | ||||||||||||||
| day 10 | 63 | 87 | 73 | 74.33 | 57 | 53 | 55 | 55.00 | 26 | 33 | 27 | 28.67 | ||||
| day 21 | 96 | 100 | 100 | 98.67 | 86 | 92 | 88 | 88.67 | 90 | 73 | 85 | 82.67 | ||||
| TCP-S700 | TCP-S1000 | TCP-S2000 | ||||||||||||||
| day 10 | 40 | 50 | 44 | 44.67 | 36 | 32 | 32 | 33.33 | 7 | 5 | 5 | 5.67 | ||||
| day 21 | 85 | 94 | 84 | 87.67 | 41 | 82 | 56 | 59.67 | 21 | 27 | 23 | 23.67 | ||||
| TCP-T700 | TCP-T1000 | TCP-T2000 | ||||||||||||||
| day 10 | 36 | 49 | 57 | 47.33 | 35 | 50 | 50 | 45.00 | 20 | 22 | 25 | 22.33 | ||||
| day 21 | 92 | 100 | 90 | 94.00 | 88 | 88 | 92 | 89.33 | 35 | 36 | 39 | 36.67 | ||||
| BCP-C500 | BCP-C700 | BCP-C1000 | ||||||||||||||
| day 10 | 46 | 30 | 34 | 36.67 | 12 | 9 | 11 | 10.67 | 10 | 11 | 10 | 10.33 | ||||
| day 21 | 63 | 65 | 65 | 64.33 | 33 | 43 | 38 | 38.00 | 41 | 37 | 25 | 34.33 | ||||
| BCP-H500 | BCP-H700 | BCP-H1000 | ||||||||||||||
| day 10 | 45 | 52 | 50 | 49.00 | 21 | 22 | 17 | 20.00 | 13 | 14 | 19 | 15.33 | ||||
| day 21 | 65 | 80 | 63 | 69.33 | 69 | 49 | 63 | 60.33 | 26 | 27 | 27 | 26.67 | ||||
| BCP-S700 | BCP-S1000 | BCP-S2000 | ||||||||||||||
| day 10 | 20 | 16 | 13 | 16.33 | 17 | 20 | 10 | 15.67 | 3 | 9 | 4 | 5.33 | ||||
| day 21 | 79 | 44 | 66 | 63.00 | 42 | 60 | 45 | 49.00 | 13 | 11 | 9 | 11.00 | ||||
| BCP-T700 | BCP-T1000 | BCP-T2000 | ||||||||||||||
| day 10 | 57 | 41 | 45 | 47.67 | 23 | 27 | 31 | 27.00 | 9 | 10 | 14 | 11.00 | ||||
| day 21 | 85 | 65 | 84 | 78.00 | 84 | 78 | 85 | 82.33 | 21 | 16 | 15 | 17.33 | ||||



References
- Baldwin, P.; Li, D.J.; Auston, D.A.; Mir, H.S.; Yoon, R.S.; Koval, K.J. Autograft, Allograft, and Bone Graft Substitutes: Clinical Evidence and Indications for Use in the Setting of Orthopaedic Trauma Surgery. J. Orthop. Trauma 2019, 33, 203–213. [Google Scholar] [CrossRef]
- Schmidt, A.H. Autologous Bone Graft: Is It Still the Gold Standard? Injury 2021, 52, S18–S22. [Google Scholar] [CrossRef] [PubMed]
- Bone|Definition, Anatomy, & Composition|Britannica. Available online: https://www.britannica.com/science/bone-anatomy (accessed on 30 October 2023).
- Peacock, M. Calcium Metabolism in Health and Disease. J. Am. Soc. Nephr 2010, 5, S23–S30. [Google Scholar] [CrossRef] [PubMed]
- Foreman, M.A.; Gu, Y.; Howl, J.; Jones, S.; Publicover, S.J. Group III Metabotropic Glutamate Receptor Activation Inhibits Ca2+ Influx and Nitric Oxide Synthase Activity in Bone Marrow Stromal Cells. J. Cell. Physiol. 2005, 204, 704–713. [Google Scholar] [CrossRef] [PubMed]
- Riddle, R.C.; Taylor, A.F.; Genetos, D.C.; Donahue, H.J. MAP Kinase and Calcium Signaling Mediate Fluid Flow-induced Human Mesenchymal Stem Cell Proliferation. Am. J. Physiol. Cell Physiol. 2006, 290, C776–C784. [Google Scholar] [CrossRef]
- Hou, X.-D.; Zhang, L.; Zhou, Z.; Luo, X.; Wang, T.-L.; Zhao, X.-Y.; Lu, B.-Q.; Chen, F.; Zheng, L. Calcium Phosphate-based Biomaterials for Bone Repair. J. Funct. Biomater. 2022, 13, 187. [Google Scholar] [CrossRef] [PubMed]
- Garot, C.; Bettega, G.; Picart, C.; Picart, C. Additive Manufacturing of Material Scaffolds for Bone Regeneration: Toward Application in the Clinics. Adv. Funct. Mat. 2021, 31, 2006967. [Google Scholar] [CrossRef]
- Lin, K.; Sheikh, R.; Romanazzo, S.; Roohani, I. 3D Printing of Bioceramic Scaffolds—Barriers to the Clinical Translation: From Promise to Reality, and Future Perspectives. Materials 2019, 12, 2660. [Google Scholar] [CrossRef]
- Van hede, D.; Liang, B.; Anania, S.; Barzegari, M.; Verlee, B.; Nolens, G.; Pirson, J.; Geris, L. 3d-printed Synthetic Hydroxyapatite Scaffold with in silico Optimized Macrostructure Enhances Bone Formation in vivo. Adv. Funct. Mat. 2022, 32, 2105002. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, T.; Bei, H.P.; Zhang, L.; Tang, C.Y.; Zhang, M.Y.; Xu, C.; Bian, L.; Yeung, K.W.K.; Fuh, J.Y.H. Gaussian Curvature–driven Direction of Cell Fate Toward Osteogenesis with Triply Periodic Minimal Surface Scaffolds. Proc. Natl. Acad. Sci. USA 2022, 119, e2206684119. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Zhong, C.; Zhao, C.C.; Shen, J.; Chen, H.; Ye, M.; Zhou, J.; Yang, X.; Gou, Z. The Design of Strut/tpms-based Pore Geometries in Bioceramic Scaffolds Guiding Osteogenesis and Angiogenesis in Bone Regeneration. Mater. Today Bio 2023, 20, 100667. [Google Scholar] [CrossRef]
- Carlier, A.; Lammens, J.; Van Oosterwyck, H.; Geris, L.; Geris, L. Computational Modeling of Bone Fracture Non-unions: Four Clinically Relevant Case Studies. Silico Cell Tissue Sci. 2015, 2, 1. [Google Scholar] [CrossRef] [PubMed]
- Perier-Metz, C.; Duda, G.N.; Checa, S. Mechano-biological Computer Model of Scaffold-supported Bone Regeneration: Effect of Bone Graft and Scaffold Structure on Large Bone Defect Tissue Patterning. Front. Bioeng. Biotechnol. 2020, 8, 585799. [Google Scholar] [CrossRef] [PubMed]
- Sandino, C.; Checa, S.; Prendergast, P.J.; Lacroix, D. Simulation of Angiogenesis and Cell Differentiation in a Cap Scaffold Subjected to Compressive Strains Using a Lattice Modeling Approach. Biomaterials 2010, 31, 2446–2452. [Google Scholar] [CrossRef]
- Sandino, C.; Lacroix, D. A Dynamical Study of the Mechanical Stimuli and Tissue Differentiation Within a Cap Scaffold Based on Micro-ct Finite Element Models. Biomech. Model. Mechanobiol. 2011, 10, 565–576. [Google Scholar] [CrossRef] [PubMed]
- Coelho, P.; Hollister, S.J.; Flanagan, C.L.; Fernandes, P.R. Bioresorbable Scaffolds for Bone Tissue Engineering: Optimal Design, Fabrication, Mechanical Testing and Scale-size Effects Analysis. Med. Eng. Phys. 2015, 37, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Dias, M.; Guedes, J.M.; Flanagan, C.L.; Hollister, S.J.; Fernandes, P.R. Optimization of Scaffold Design for Bone Tissue Engineering: A Computational and Experimental Study. Med. Eng. Phys. 2014, 36, 448–457. [Google Scholar] [CrossRef] [PubMed]
- Schamberger, B.; Roschger, A.; Ziege, R.; Anselme, K.; Ben Amar, M.; Bykowski, M.; Castro, A.P.G.; Cipitria, A.; Coles, R.; Dimova, R.; et al. Curvature in Biological Systems: Its Quantification, Emergence, and Implications Across the Scales. Adv. Mater. 2023, 35, e2206110. [Google Scholar] [CrossRef]
- Rumpler, M.; Woesz, A.; Dunlop, J.; van Dongen, J.; Fratzl, P. The Effect of Geometry on Three-dimensional Tissue Growth. J. R. Soc. Interface 2008, 5, 1173–1180. [Google Scholar] [CrossRef]
- Bidan, C.M.; Kommareddy, K.P.; Rumpler, M.; Kollmannsberger, P.; Fratzl, P.; Dunlop, J.W.C. Geometry as a Factor for Tissue Growth: Towards Shape Optimization of Tissue Engineering Scaffolds. Adv. Healthc. Mat. 2013, 2, 186–194. [Google Scholar] [CrossRef]
- Guyot, Y.; Guyot, Y.; Papantoniou, I.; Chai, Y.C.; Bael, S.V.; Schrooten, J.; Geris, L.; Geris, L. A Computational Model for Cell/ecm Growth on 3D Surfaces Using the Level Set Method: A Bone Tissue Engineering Case Study. Biomech. Model. Mechanobiol. 2014, 13, 1361–1371. [Google Scholar] [CrossRef] [PubMed]
- Alias, M.A.; Alias, M.A.; Buenzli, P.R. Modeling the Effect of Curvature on the Collective Behavior of Cells Growing New Tissue. Biophys. J. 2017, 112, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Blanquer, S.; Werner, M.; Hannula, M.; Sharifi, S.; Lajoinie, G.; Eglin, D.; Hyttinen, J.; Poot, A.A.; Grijpma, D.W. Surface Curvature in Triply-periodic Minimal Surface Architectures as a Distinct Design Parameter in Preparing Advanced Tissue Engineering Scaffolds. Biofabrication 2017, 9, 025001. [Google Scholar] [CrossRef] [PubMed]
- Buenzli, P.R.; Lanaro, M.; Wong, C.S.; McLaughlin, M.P.; Allenby, M.C.; Woodruff, M.A.; Simpson, M.J. Cell Proliferation and Migration Explain Pore Bridging Dynamics in 3D Printed Scaffolds of Different Pore Size. Acta Biomater. 2020, 114, 285–295. [Google Scholar] [CrossRef]
- Bidan, C.M.; Kommareddy, K.P.; Rumpler, M.; Kollmannsberger, P.; Bréchet, Y.J.M.; Fratzl, P.; Dunlop, J.W.C. How Linear Tension Converts to Curvature: Geometric Control of Bone Tissue Growth. PLoS ONE 2012, 7, e36336. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts Propagating with Curvature-dependent Speed: Algorithms Based on Hamilton-jacobi Formulations. J. Comp. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Hecht, F. New development in FREEfem++. J. Num. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef]
- Ribes, A.; Caremoli, C. Salomé platform component model for numerical simulation. In Proceedings of the 31st Annual International Computer Software and Applications Conference (COMPSAC 2007), Beijing, China, 24–27 July 2007; Volume 2, pp. 553–564. [Google Scholar] [CrossRef]
- Dapogny, C.; Frey, P. Computation of the signed distance function to a discrete contour on adapted triangulation. Calcolo 2012, 49, 193–219. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F.; Moussiaux, A. Handbook of First-Order Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Amestoy, P.R.; Duff, I.S.; L’Excellent, J.Y.; Koster, J. MUMPS: A general purpose distributed memory sparse solver. In Applied Parallel Computing. New Paradigms for HPC in Industry and Academia; Sørevik, T., Manne, F., Gebremedhin, A.H., Moe, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1947, PARA 2000. Lecture Notes in Computer Science. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. Paraview: An End-User Tool for Large Data Visualization. In The Visualization Handbook; Elsevier: Amsterdam, The Netherlands, 2005; pp. 717–731. [Google Scholar] [CrossRef]
- Mockus, J. Bayesian approach to global optimization: Theory and applications. Springer Sci. Bus. Media 2012, 37. [Google Scholar]
- Goffard, R.; Sforza, T.; Clarinval, A.-M.; Dormal, T.; Boilet, L.; Hocquet, S.; Cambier, F. Additive Manufacturing of Biocompatible Ceramics. Adv. Prod. Eng. Manag. 2013, 8, 96. [Google Scholar] [CrossRef]
- Champion, E. Sintering of calcium phosphate bioceramics. Acta Biomater. 2013, 9, 5855–5875. [Google Scholar] [CrossRef]
- Bouakaz, I.; Sadeghian Dehkord, E.; Meille, S.; Schrijnemakers, A.; Boschini, F.; Preux, N.; Hocquet, S.; Geris, L.; Nolens, G.; Grossin, D.; et al. 3D printed triply periodic minimal surfaces calcium phosphate bone substitute: The effect of porosity design on mechanical properties. Ceram. Interntl. 2023. [Google Scholar] [CrossRef]
- Barzegari, M.; Geris, L. An Open Source Crash Course on Parameter Estimation of Computational Models Using a Bayesian Optimization Approach. J. Open Source Ed. 2021, 4, 89. [Google Scholar] [CrossRef]
- Mehrian, M.; Mehrian, M.; Guyot, Y.; Guyot, Y.; Papantoniou, I.; Olofsson, S.; Sonnaert, M.; Misener, R.; Geris, L.; Geris, L. Maximizing Neotissue Growth Kinetics in a Perfusion Bioreactor: An in silico Strategy Using Model Reduction and Bayesian Optimization. Biotech. Bioeng. 2018, 115, 617–629. [Google Scholar] [CrossRef] [PubMed]
- Kerckhofs, G.; Chai, Y.C.; Luyten, F.P.; Geris, L. Combining microCT-based characterization with empirical modelling as a robust screening approach for the design of optimized CaP-containing scaffolds for progenitor cell-mediated bone formation. Acta Biomater. 2016, 35, 330–340. [Google Scholar] [CrossRef] [PubMed]
- Kommareddy, K.P.; Lange, C.; Rumpler, M.; Dunlop, J.W.C.; Manjubala, I.; Cui, J.; Kratz, K.; Lendlein, A.; Fratzl, P. Two stages in three-dimensional in vitro growth of tissue generated by osteoblastlike cells. Biointerphases 2010, 5, 45–52. [Google Scholar] [CrossRef] [PubMed]
- Van Bael, S.; Chai, Y.C.; Chai, Y.C.; Truscello, S.; Moesen, M.; Kerckhofs, G.; Van Oosterwyck, H.; Kruth, J.-P.; Schrooten, J. The Effect of Pore Geometry on the in vitro Biological Behavior of Human Periosteum-derived Cells Seeded on Selective Laser-melted Ti6al4v Bone Scaffolds. Acta Biomater. 2012, 8, 2824–2834. [Google Scholar] [CrossRef] [PubMed]
- Winning, L.; Robinson, L.; Boyd, A.; El Karim, I.A.; Lundy, F.; Meenan, B.J. Osteoblastic Differentiation of Periodontal Ligament Stem Cells on Non-stoichiometric Calcium Phosphate and Titanium Surfaces. J. Biomed. Mater. Res. A 2017, 105, 1692–1702. [Google Scholar] [CrossRef]
- Cun, X.; Hosta-Rigau, L. Topography: A Biophysical Approach to Direct the Fate of Mesenchymal Stem Cells in Tissue Engineering Applications. Nanomaterials 2020, 10, 2070. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, J.H.; Shim, J.H.; Hwang, N.S.; Heo, C.Y.; Heo, C.Y. Bioactive Calcium Phosphate Materials and Applications in Bone Regeneration. Biomater. Res. 2019, 23, 4. [Google Scholar] [CrossRef]
- Milazzo, M.; Milazzo, M.; Contessi Negrini, N.; Contessi Negrini, N.; Scialla, S.; Marelli, B.; Farè, S.; Danti, S.; Danti, S.; Danti, S. Additive Manufacturing Approaches for Hydroxyapatite-reinforced Composites. Adv. Funct. Mater. 2019, 29, 1903055. [Google Scholar] [CrossRef]
- Bal, Z.; Kaito, T.; Korkusuz, F.; Yoshikawa, H. Bone Regeneration with Hydroxyapatite-based Biomaterials. Emerg. Mater. 2020, 3, 521–544. [Google Scholar] [CrossRef]
- Tavoni, M.; Dapporto, M.; Tampieri, A.; Sprio, S. Bioactive Calcium Phosphate-based Composites for Bone Regeneration. J. Compos. Sci. 2021, 5, 227. [Google Scholar] [CrossRef]
- Han, Y.; Wei, Q.; Chang, P.; Hu, K.; Okoro, O.V.; Shavandi, A.; Nie, L. Three-dimensional Printing of Hydroxyapatite Composites for Biomedical Application. Crystals 2021, 11, 353. [Google Scholar] [CrossRef]
- Yazdanpanah, Z.; Johnston, G.D.; Cooper, D.M.L.; Chen, X. 3D Bioprinted Scaffolds for Bone Tissue Engineering: State-of-the-art and Emerging Technologies. Front. Bioeng. Biotechnol. 2022, 10, 824156. [Google Scholar] [CrossRef]
- Nik Md Noordin Kahar, N.N.F.; Ahmad, N.; Jaafar, M.; Yahaya, B.H.; Sulaiman, A.R.; Abdul Hamid, Z.A. A Review of Bioceramics Scaffolds for Bone Defects in Different Types of Animal Models: HA and Β -TCP. Biomed. Phys. Eng. Express 2022, 8, 052002. [Google Scholar] [CrossRef]
- Callens, S.J.P. Emergent Collective Organization of Bone Cells in Complex Curvature Fields. Nat. Commun. 2023, 14, 855. [Google Scholar] [CrossRef]
- Callens, S.J.P.; Uyttendaele, R.J.C.; Fratila-Apachitei, L.E.; Zadpoor, A.A. Substrate Curvature as a Cue to Guide Spatiotemporal Cell and Tissue Organization. Biomaterials 2020, 232, 119739. [Google Scholar] [CrossRef]
- Hayashi, K.; Kishida, R.; Tsuchida, A.; Ishikawa, A. Superiority of Triply Periodic Minimal Surface Gyroid Structure to Strut-based Grid Structure in Both Strength and Bone Regeneration. ACS Appl. Mater. Interfaces 2023, 15, 34570–34577. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Chen, X.; Zhao, R. Effect of Surface Curvature on the Mechanical and Mass-transport Properties of Additively Manufactured Tissue Scaffolds with Minimal Surfaces. ACS Biomater. Sci. Eng. 2022, 8, 1623–1643. [Google Scholar] [CrossRef]
- Pires, T.H.V.; Dunlop, J.W.C.; Castro, A.P.G.; Fernandes, P.R. Wall Shear Stress Analysis and Optimization in Tissue Engineering TPMS Scaffolds. Materials 2022, 15, 7375. [Google Scholar] [CrossRef] [PubMed]

| Property | Description |
|---|---|
| Pore shapes | Triangle, square, hexagon, and circle |
| Pore size | 0.5 mm, 0.7 mm, 1 mm, and 2 mm |
| Distribution | Randomly |
| Materials | Hydroxyapatite (HAp, 100%), Tricalcium phosphate (TCP, 100%), and mixed HAp 60%–TCP 40% pastes (supplier Cerhum) |
| Sintering temperature | 1030 °C for TCP100 and HAp60-TCP40 and 1130 °C for HAp100 |
| Time points analysis | 10 days and 21 days |
| Cell type | Human telomerase reverse transcriptase-immortalized bone marrow mesenchymal stem cells (hTERT-BMMSCs) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, B.; Sadeghian Dehkord, E.; Van Hede, D.; Barzegari, M.; Verlée, B.; Pirson, J.; Nolens, G.; Lambert, F.; Geris, L. Model-Based Design to Enhance Neotissue Formation in Additively Manufactured Calcium-Phosphate-Based Scaffolds. J. Funct. Biomater. 2023, 14, 563. https://doi.org/10.3390/jfb14120563
Liang B, Sadeghian Dehkord E, Van Hede D, Barzegari M, Verlée B, Pirson J, Nolens G, Lambert F, Geris L. Model-Based Design to Enhance Neotissue Formation in Additively Manufactured Calcium-Phosphate-Based Scaffolds. Journal of Functional Biomaterials. 2023; 14(12):563. https://doi.org/10.3390/jfb14120563
Chicago/Turabian StyleLiang, Bingbing, Ehsan Sadeghian Dehkord, Dorien Van Hede, Mojtaba Barzegari, Bruno Verlée, Justine Pirson, Grégory Nolens, France Lambert, and Liesbet Geris. 2023. "Model-Based Design to Enhance Neotissue Formation in Additively Manufactured Calcium-Phosphate-Based Scaffolds" Journal of Functional Biomaterials 14, no. 12: 563. https://doi.org/10.3390/jfb14120563
APA StyleLiang, B., Sadeghian Dehkord, E., Van Hede, D., Barzegari, M., Verlée, B., Pirson, J., Nolens, G., Lambert, F., & Geris, L. (2023). Model-Based Design to Enhance Neotissue Formation in Additively Manufactured Calcium-Phosphate-Based Scaffolds. Journal of Functional Biomaterials, 14(12), 563. https://doi.org/10.3390/jfb14120563






