Free Vibration of Functionally Graded Graphene Platelets Reinforced Magnetic Nanocomposite Beams Resting on Elastic Foundation
Abstract
1. Introduction
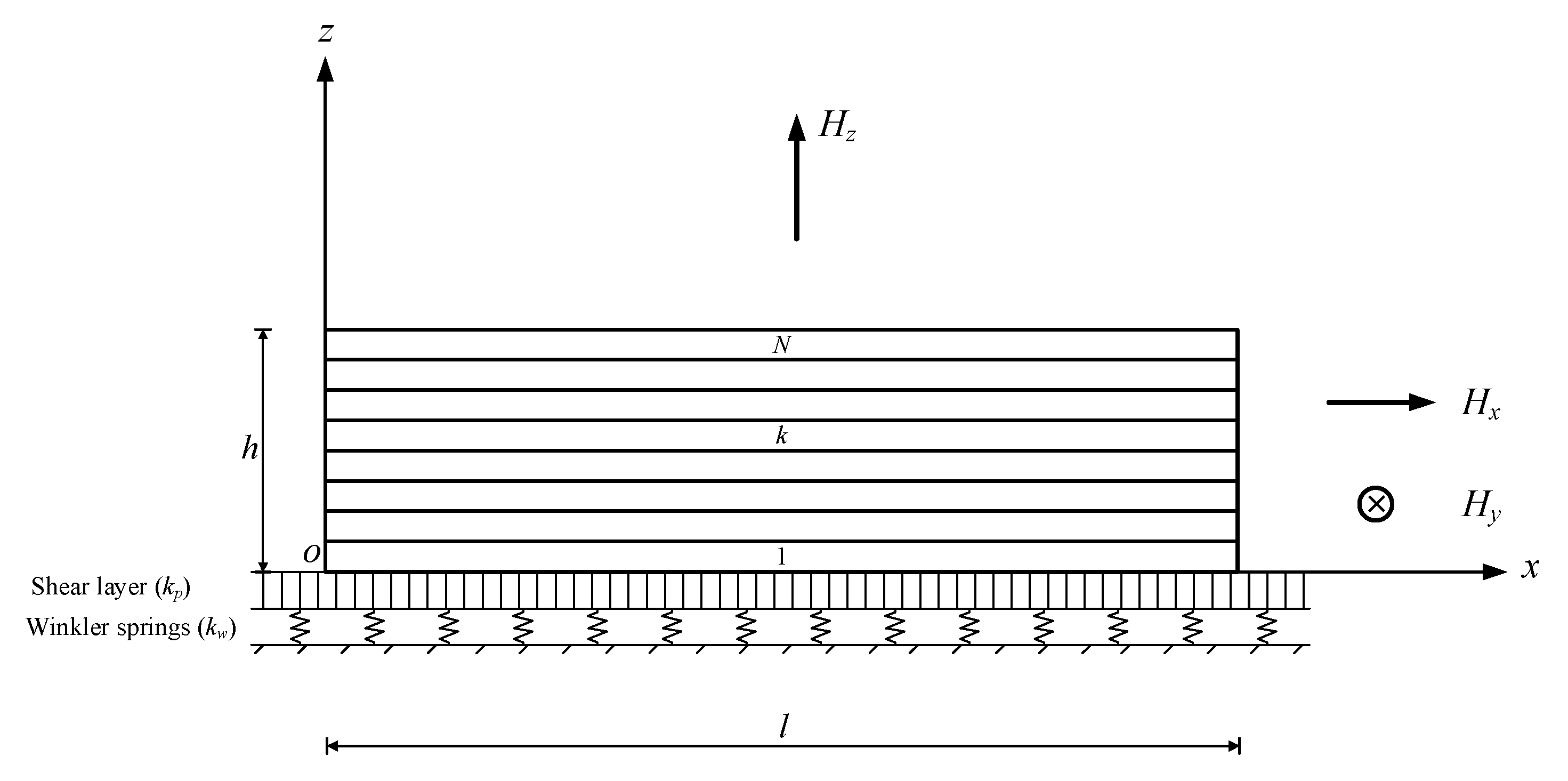
2. Theoretical Formulation
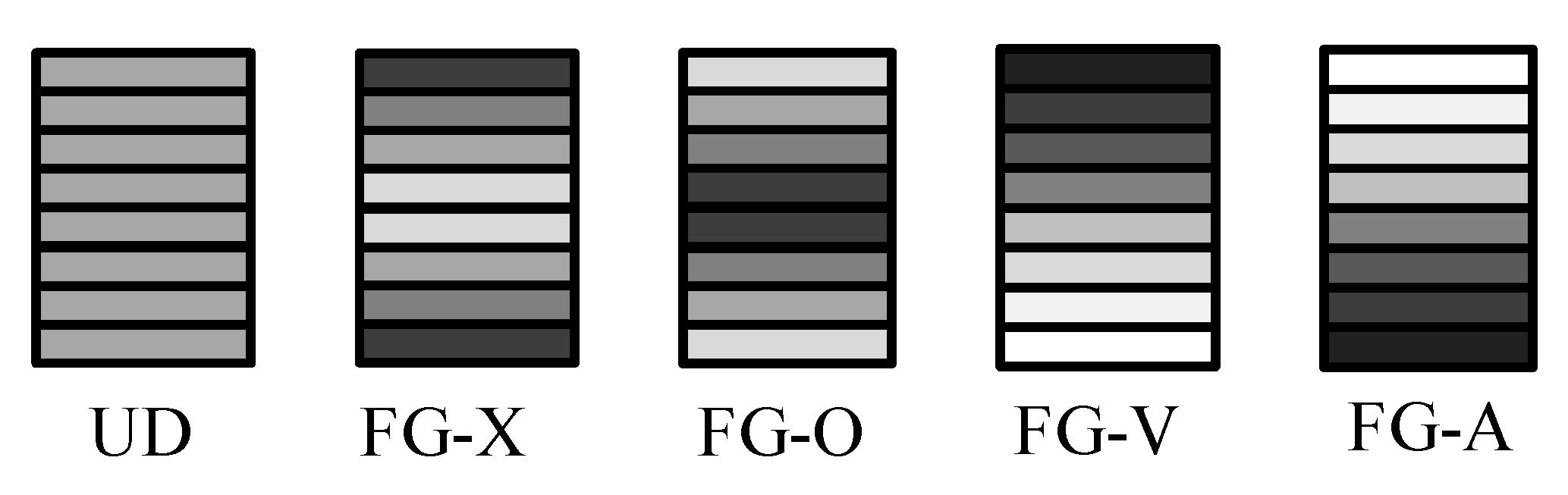
2.1. Micromechanics Model of the FG-GPLRCs
2.2. Maxwell’s Relation
2.3. Structural Problem Formulation
3. Results and Discussion
3.1. Validation of the Present Method
3.2. Free Vibration of Epoxy/GPLs Beams in Magnetic Fields
4. Conclusions
- (1)
- A low content of GPLs dispersed into the matrix can increase the vibration frequencies significantly, and the pattern FG-X holds the highest fundamental frequency among all GPL distribution patterns.
- (2)
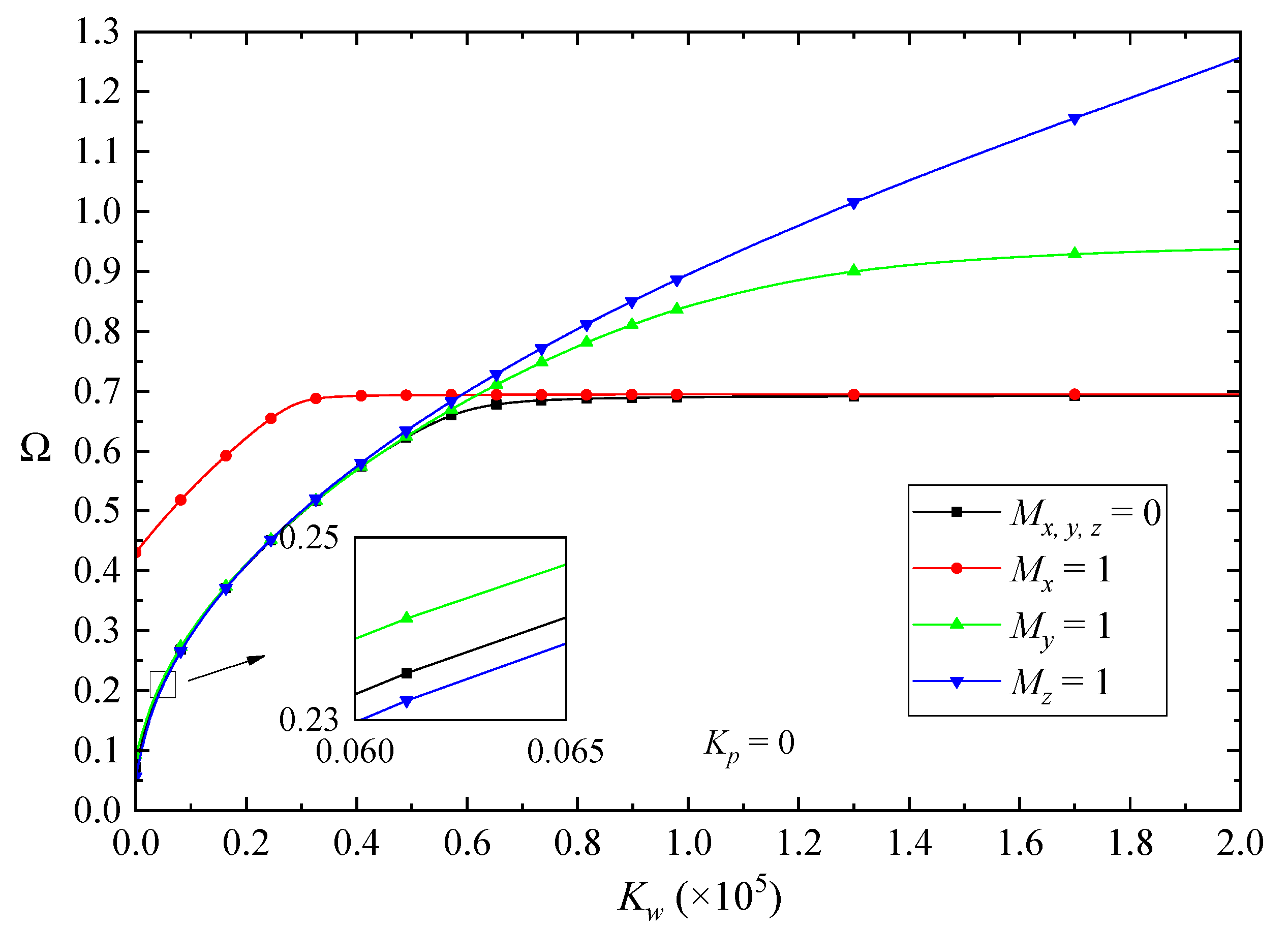
- The results show that an increase in the elastic coefficients of the elastic foundation promotes the frequency characteristics of the FG-GPLRC beams.
- (3)
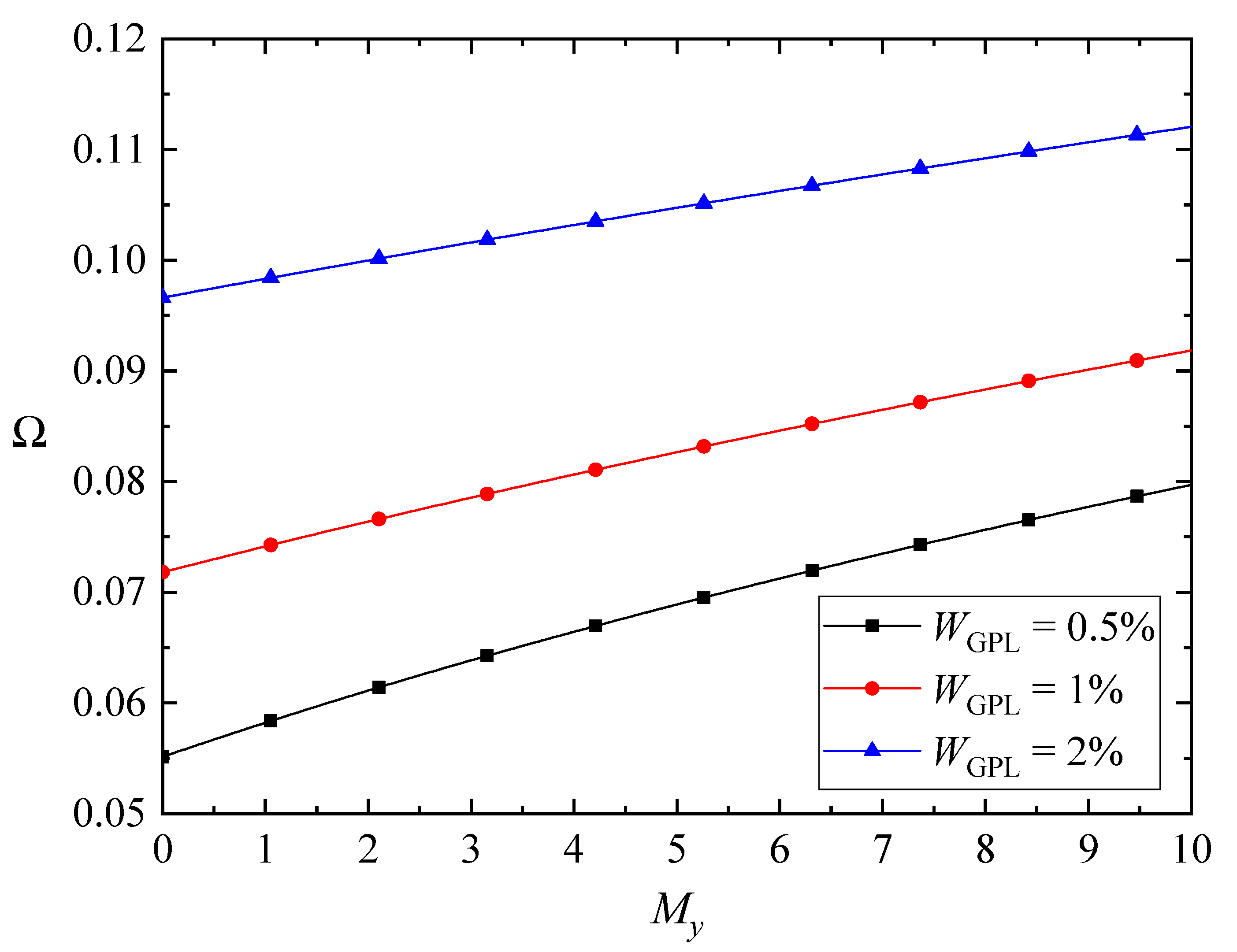
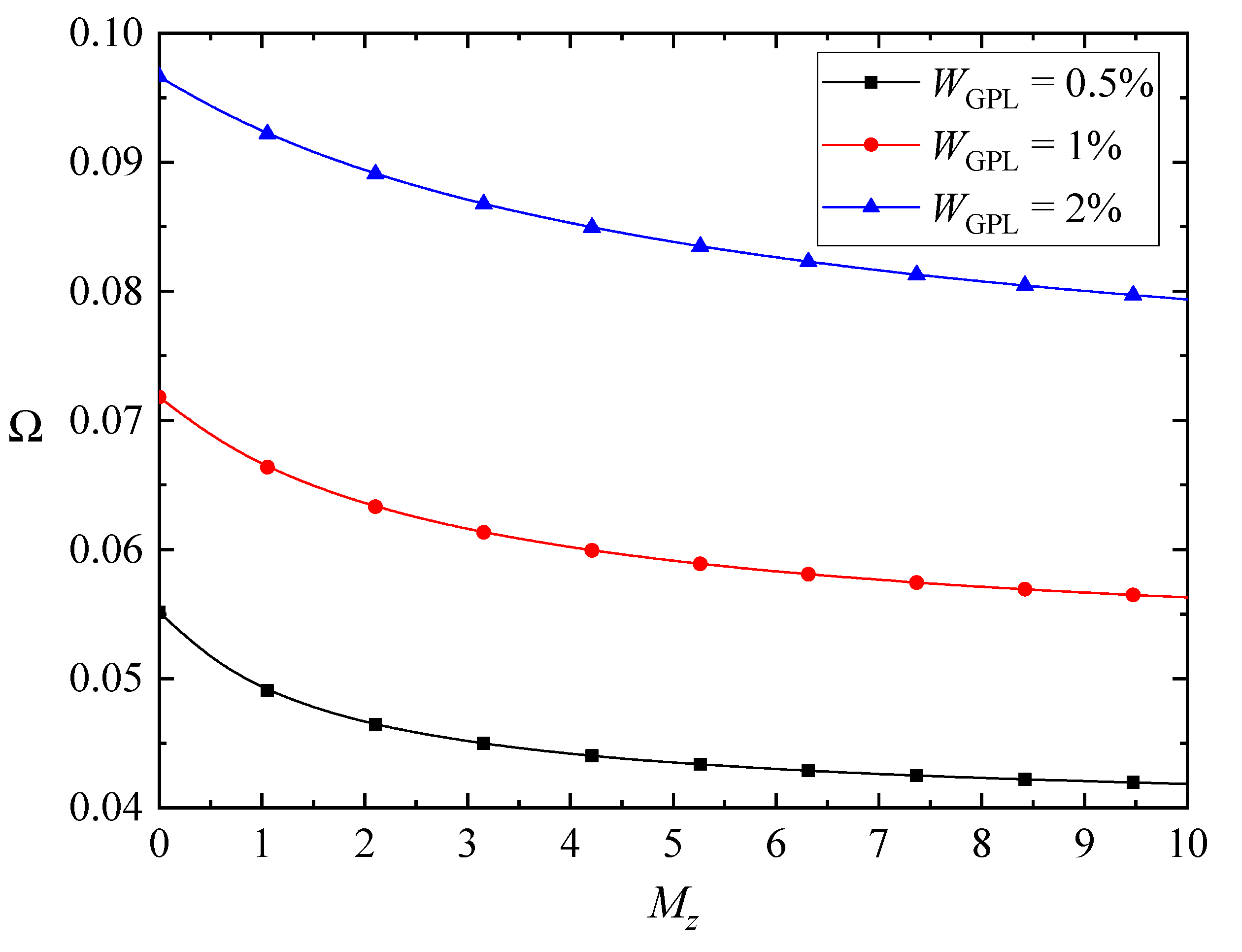
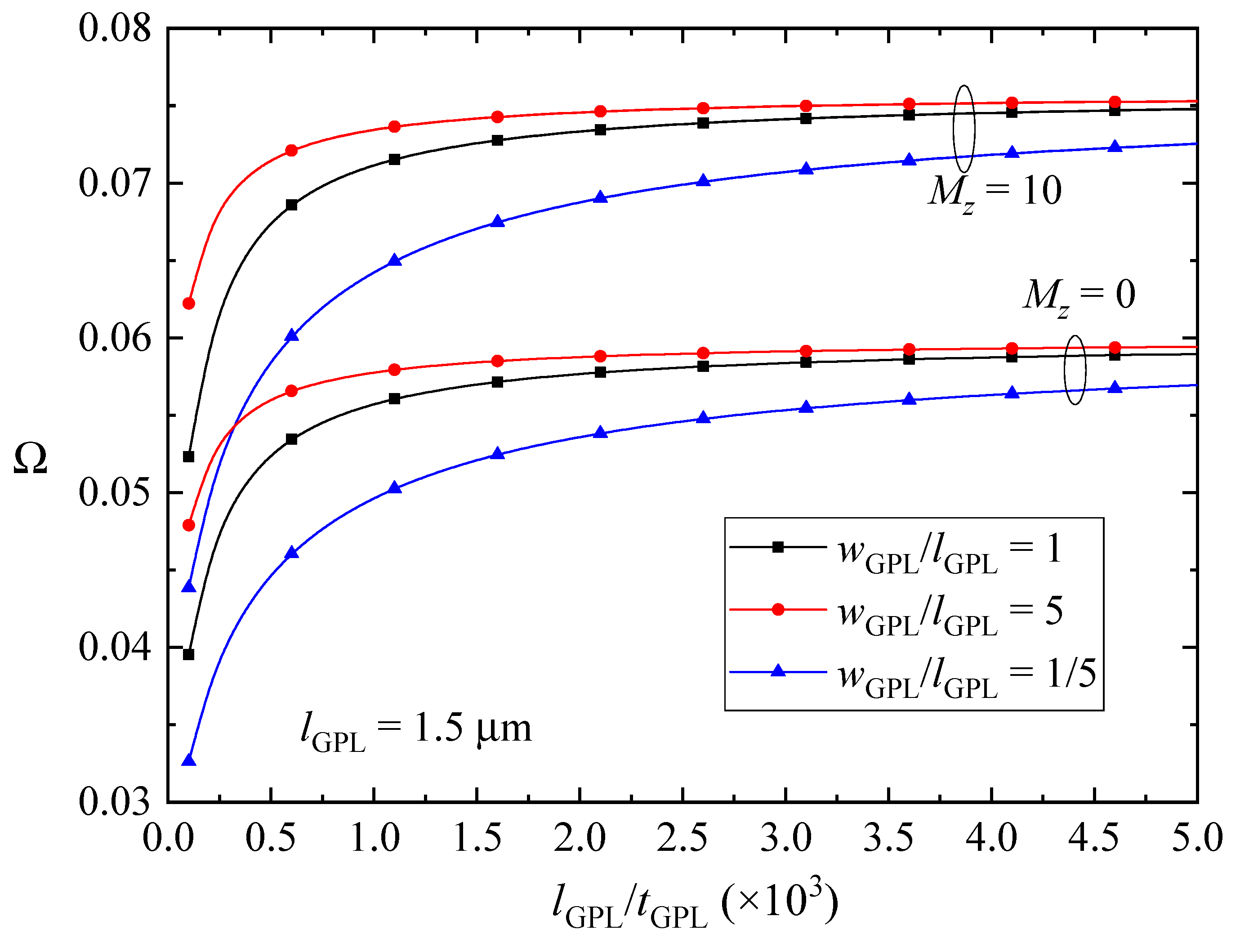
- The results show that an increase in the magnetic fields of the x direction and y direction increases the fundamental frequencies of the FG-GPLRC beams. However, it reverses for the case of z-direction magnetic field.
- (4)
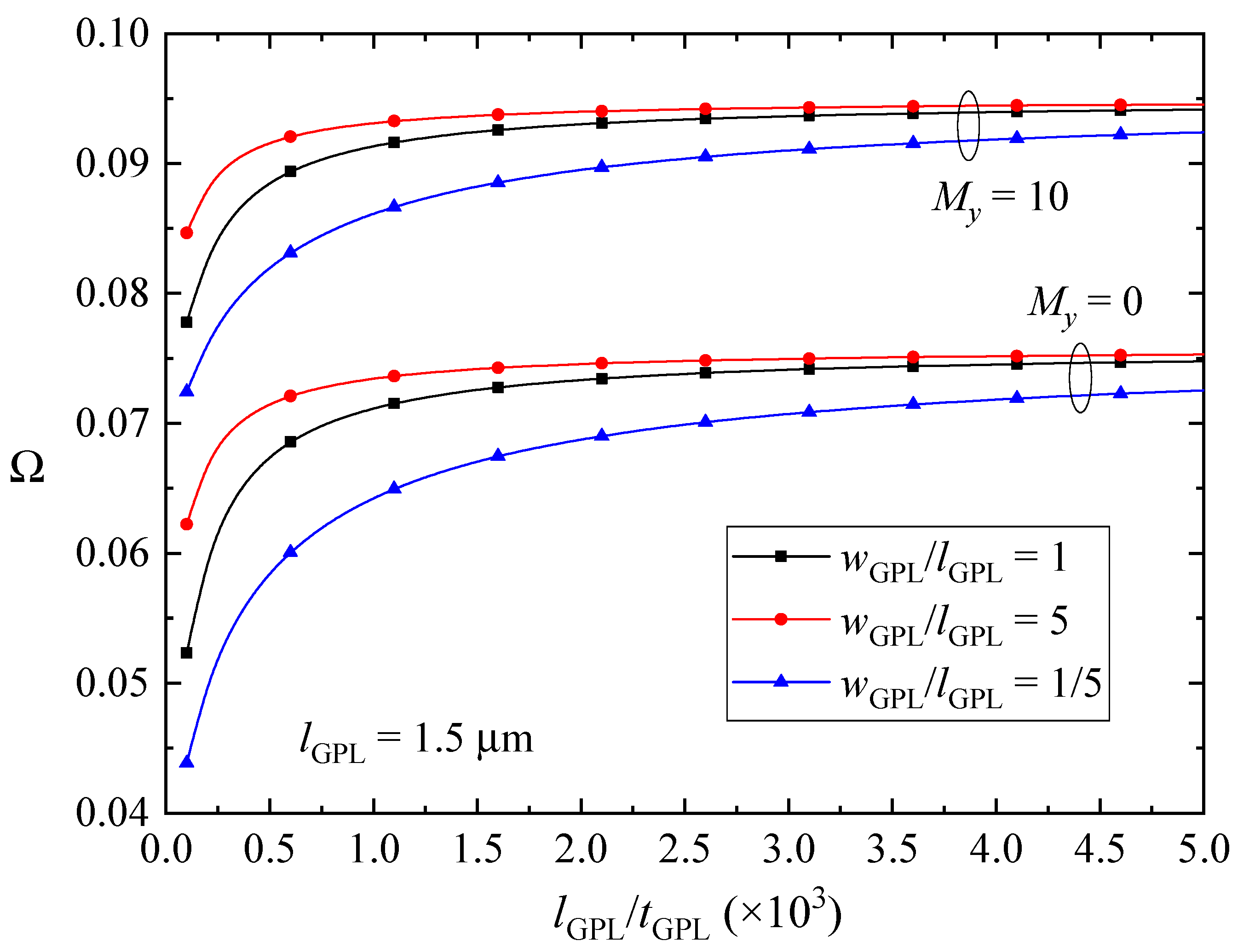
- Thinner and larger GPL nanofillers are preferred as nano-reinforcements to increase the fundamental frequencies of FG-GPLRC beams in the y- and z-direction magnetic fields. However, it reverses for the case of the beams in x-direction magnetic field.
Funding
Conflicts of Interest
References
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, T.; Abdala, A.; Stankovich, S.; Dikin, D.; Herreraalonso, M.; Piner, R.D.; Adamson, D.H.; Schniepp, H.C.; Chen, X.; Ruoff, R.S.; et al. Functionalized graphene sheets for polymer nanocomposites. Nat. Nanotechnol. 2008, 3, 327–331. [Google Scholar] [CrossRef] [PubMed]
- Eda, G.; Chhowalla, M. Graphene-based Composite Thin Films for Electronics. Nano Lett. 2009, 9, 814–818. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Qi, X.; Boey, F.; Zhang, H. Graphene-based composites. Chem. Soc. Rev. 2012, 41, 666–686. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Abdala, A.A.; Macosko, C.W. Graphene/Polymer Nanocomposites. Macromolecules 2010, 43, 6515–6530. [Google Scholar] [CrossRef]
- Shi, G.; Araby, S.; Gibson, C.T.; Meng, Q.; Bokhari, S.W.; Ma, J. Graphene Platelets and Their Polymer Composites: Fabrication, Structure, Properties, and Applications. Adv. Funct. Mater. 2018, 28, 1706705. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.; Koratkar, N. Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Ji, X.-Y.; Cao, Y.-P.; Feng, X.-Q. Micromechanics prediction of the effective elastic moduli of graphene sheet-reinforced polymer nanocomposites. Model. Simul. Mater. Sci. Eng. 2010, 18, 045005. [Google Scholar] [CrossRef]
- Chandra, Y.; Chowdhury, R.; Scarpa, F.; Adhikari, S.; Sienz, J.; Arnold, C.; Murmu, T.; Bould, D. Vibration frequency of graphene based composites: A multiscale approach. Mater. Sci. Eng. B 2012, 177, 303–310. [Google Scholar] [CrossRef]
- Koizumi, M. The concept of FGM. Ceram. Trans. 1993, 34, 3–10. [Google Scholar]
- Loy, C.; Lam, K.; Reddy, J. Vibration of functionally graded cylindrical shells. Int. J. Mech. Sci. 1999, 41, 309–324. [Google Scholar] [CrossRef]
- Chen, W.; Bian, Z.; Ding, H. Three-dimensional vibration analysis of fluid-filled orthotropic FGM cylindrical shells. Int. J. Mech. Sci. 2004, 46, 159–171. [Google Scholar] [CrossRef]
- Trinh, M.-C.; Mukhopadhyay, T.; Kim, S.-E. A semi-analytical stochastic buckling quantification of porous functionally graded plates. Aerosp. Sci. Technol. 2020, 105, 105928. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Express 2018, 5, 095006. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. A new hyperbolic-polynomial higher-order elasticity theory for mechanics of thick FGM beams with imperfection in the material composition. Compos. Struct. 2020, 249, 112486. [Google Scholar] [CrossRef]
- Sayyad, A.; Ghumare, S. A new quasi-3D model for functionally graded plates. J. Appl. Compu. Mech. 2019, 5, 367–380. [Google Scholar]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. Part B Eng. 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Yang, J.; Wu, H.; Kitipornchai, S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos. Struct. 2017, 161, 111–118. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J.; Kitipornchai, S. Thermoelastic analysis of functionally graded graphene reinforced rectangular plates based on 3D elasticity. Meccanica 2016, 52, 2275–2292. [Google Scholar] [CrossRef]
- Wu, H.; Kitipornchai, S.; Yang, J. Thermal buckling and postbuckling of functionally graded graphene nanocomposite plates. Mater. Des. 2017, 132, 430–441. [Google Scholar] [CrossRef]
- Yang, B.; Kitipornchai, S.; Yang, Y.-F.; Yang, J. 3D thermo-mechanical bending solution of functionally graded graphene reinforced circular and annular plates. Appl. Math. Model. 2017, 49, 69–86. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Liu, D.; Li, Z.; Kitipornchai, S.; Yang, J. Three-dimensional free vibration and bending analyses of functionally graded graphene nanoplatelets-reinforced nanocomposite annular plates. Compos. Struct. 2019, 229, 111453. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Y.; Chen, D.; Yang, J. Vibration characteristics of functionally graded graphene reinforced porous nanocomposite cylindrical shells with spinning motion. Compos. Part B Eng. 2018, 145, 1–13. [Google Scholar] [CrossRef]
- Liu, D.; Kitipornchai, S.; Chen, W.; Yang, J. Three-dimensional buckling and free vibration analyses of initially stressed functionally graded graphene reinforced composite cylindrical shell. Compos. Struct. 2018, 189, 560–569. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, Y.; Zhu, J. On the free vibration and bending analysis of functionally graded nanocomposite spherical shells reinforced with graphene nanoplatelets: Three-dimensional elasticity solutions. Eng. Struct. 2021, 226, 111376. [Google Scholar] [CrossRef]
- Lin, F.; Xiang, Y.; Shen, H.-S. Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites—A molecular dynamics simulation. Compos. Part B Eng. 2017, 111, 261–269. [Google Scholar] [CrossRef]
- Shen, H.-S.; Lin, F.; Xiang, Y. Nonlinear vibration of functionally graded graphene-reinforced composite laminated beams resting on elastic foundations in thermal environments. Nonlinear Dyn. 2017, 90, 899–914. [Google Scholar] [CrossRef]
- Shen, H.-S.; Lin, F.; Xiang, Y. Nonlinear bending and thermal postbuckling of functionally graded graphene-reinforced composite laminated beams resting on elastic foundations. Eng. Struct. 2017, 140, 89–97. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y.; Lin, F. Thermal buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations. Thin-Walled Struct. 2017, 118, 229–237. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y.; Lin, F. Nonlinear bending of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations in thermal environments. Compos. Struct. 2017, 170, 80–90. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y.; Fan, Y. Nonlinear vibration of functionally graded graphene-reinforced composite laminated cylindrical shells in thermal environments. Compos. Struct. 2017, 182, 447–456. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y.; Fan, Y.; Hui, D. Nonlinear vibration of functionally graded graphene-reinforced composite laminated cylindrical panels resting on elastic foundations in thermal environments. Compos. Part B Eng. 2018, 136, 177–186. [Google Scholar] [CrossRef]
- Périgo, E.A.; Weidenfeller, B.; Kollár, P.; Füzer, J. Past, present, and future of soft magnetic composites. Appl. Phys. Rev. 2018, 5, 031301. [Google Scholar] [CrossRef]
- Kharissova, O.V.; García, B.O.; Kharisov, B.I.; Méndez, U.O. Magnetic-Graphene-Based Nanocomposites and Respective Applications. In Advances in Carbon Nanostructures; Silva, A.M.T., Carabineiro, S.A.C., Eds.; IntechOpen: London, UK, 2016. [Google Scholar]
- Sun, Y.; Pan, H.; Zheng, Y.; Zhang, K.; Fu, L.; Chen, J.; Zhang, W.; Tang, N. The effect of thermal annealing on the magnetic properties of graphene oxide quantum dots. Appl. Surf. Sci. 2020, 501, 144234. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Matte, H.S.S.R.; Subrahmanyam, K.S.; Maitra, U. Unusual magnetic properties of graphene and related materials. Chem. Sci. 2012, 3, 45–52. [Google Scholar] [CrossRef]
- Murmu, T.; McCarthy, M.; Adhikari, S. In-plane magnetic field affected transverse vibration of embedded single-layer graphene sheets using equivalent nonlocal elasticity approach. Compos. Struct. 2013, 96, 57–63. [Google Scholar] [CrossRef]
- Karličić, D.; Kozić, P.; Adhikari, S.; Cajić, M.; Murmu, T.; Lazarević, M. Nonlocal mass-nanosensor model based on the damped vibration of single-layer graphene sheet influenced by in-plane magnetic field. Int. J. Mech. Sci. 2015, 132–142. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Chen, J. Nonlinear dynamic responses of triple-layered graphene sheets under moving particles and an external magnetic field. Int. J. Mech. Sci. 2018, 136, 413–423. [Google Scholar] [CrossRef]
- Malikan, M.; Krasheninnikov, M.; Eremeyev, V.A. Torsional stability capacity of a nano-composite shell based on a nonlocal strain gradient shell model under a three-dimensional magnetic field. Int. J. Eng. Sci. 2020, 148, 103210. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V. Buckling analysis of piezo-magnetoelectric nanoplates in hygrothermal environment based on a novel one variable plate theory combining with higher-order nonlocal strain gradient theory. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 102, 8–28. [Google Scholar] [CrossRef]
- Sobhy, M. Buckling and vibration of FG graphene platelets/aluminum sandwich curved nanobeams considering the thickness stretching effect and exposed to a magnetic field. Results Phys. 2020, 16, 102865. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Mehrabi, M.; Mousavinejad, F.S. Magneto-mechanical vibration analysis of single-/three-layered micro-Timoshenko porous beam and graphene platelet as reinforcement based on modified strain gradient theory and differential quadrature method. J. Vib. Control 2020, 1–18. [Google Scholar] [CrossRef]
- Kiani, K. Free vibration of conducting nanoplates exposed to unidirectional in-plane magnetic fields using nonlocal shear deformable plate theories. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 57, 179–192. [Google Scholar] [CrossRef]
- Ying, J.; Lü, C.; Chen, W. Two-dimensional elasticity solutions for functionally graded beams resting on elastic foundations. Compos. Struct. 2008, 84, 209–219. [Google Scholar] [CrossRef]
- Chen, W.; Lü, C.; Bian, Z. A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation. Appl. Math. Model. 2004, 28, 877–890. [Google Scholar] [CrossRef]
- Orlita, M.; Escoffier, W.; Plochocka, P.; Raquet, B.; Zeitler, U. Graphene in high magnetic fields. C. R. Phys. 2013, 14, 78–93. [Google Scholar] [CrossRef]




| Present | Reference [48] | Present | Reference [48] | Present | Reference [48] | ||
|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 3.14143 | 3.14143 | 3.13024 | 3.13024 | 3.04799 | 3.04799 |
| 0.5 | 3.47659 | 3.47659 | 3.46670 | 3.46671 | 3.39458 | 3.39458 | |
| 1.0 | 3.73587 | 3.73587 | 3.72656 | 3.72656 | 3.65801 | 3.65802 | |
| 2.5 | 4.29686 | 4.29686 | 4.28808 | 4.28809 | 4.21833 | 4.21834 | |
| 102 | 0.0 | 3.74823 | 3.74823 | 3.73894 | 3.73894 | 3.67049 | 3.67050 |
| 0.5 | 3.96067 | 3.96067 | 3.95167 | 3.95168 | 3.88397 | 3.88397 | |
| 1.0 | 4.14356 | 4.14356 | 4.13471 | 4.13471 | 4.06635 | 4.06636 | |
| 2.5 | 4.58226 | 4.58226 | 4.57346 | 4.57347 | 4.49913 | 4.49913 | |
| 104 | 0.0 | 10.02403 | 10.02403 | 9.99581 | 9.99582 | 7.34080 | 7.34081 |
| 0.5 | 10.03610 | 10.03610 | 10.00777 | 10.00778 | 7.34087 | 7.34088 | |
| 1.0 | 10.04813 | 10.04813 | 10.01968 | 10.01969 | 7.34094 | 7.34095 | |
| 2.5 | 10.08394 | 10.08394 | 10.05518 | 10.05519 | 7.34115 | 7.34116 |
| Present | Reference [49] | Present | Reference [49] | Present | Reference [49] | ||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 2.9449 | 2.9449 | 2.8773 | 2.8773 | 2.7026 | 2.7026 |
| 10 | 3.1644 | 3.1644 | 3.0979 | 3.0979 | 2.9194 | 2.9194 | |
| 25 | 3.4264 | 3.4264 | 3.3578 | 3.3578 | 3.1450 | 3.1450 | |
| 102 | 0 | 3.1670 | 3.1670 | 3.1005 | 3.1005 | 2.9219 | 2.9219 |
| 10 | 3.3480 | 3.3480 | 3.2804 | 3.2804 | 3.0809 | 3.0809 | |
| 25 | 3.5743 | 3.5743 | 3.5030 | 3.5030 | 3.2583 | 3.2583 | |
| 104 | 0 | 7.1422 | 7.1422 | 6.5058 | 6.5058 | 4.2742 | 4.2742 |
| 10 | 7.1592 | 7.1592 | 6.5163 | 6.5163 | 4.2753 | 4.2753 | |
| 25 | 7.1844 | 7.1844 | 6.5319 | 6.5319 | 4.2770 | 4.2770 |
| Material Properties | GPLs | Epoxy |
|---|---|---|
| Young’s modulus (GPa) | 1010 | 3.0 |
| Density (kg/m3) | 1060 | 1200 |
| Poisson’s ratio | 0.186 | 0.34 |
| λ | n | Epoxy | UD | FG-X | FG-O | FG-V | FG-A |
|---|---|---|---|---|---|---|---|
| 1/20 | 1 | 0.0075 | 0.0157 (109%) | 0.0184 (145%) | 0.0124 (65%) | 0.0141 (88%) | 0.0141 (88%) |
| 2 | 0.0298 | 0.0621 (108%) | 0.0718 (141%) | 0.0491 (65%) | 0.0558 (87%) | 0.0558 (87%) | |
| 3 | 0.0656 | 0.1369 (109%) | 0.1554 (137%) | 0.1091 (66%) | 0.1233 (88%) | 0.1233 (88%) | |
| 4 | 0.1134 | 0.2367 (109%) | 0.2628 (132%) | 0.1906 (68%) | 0.2140 (89%) | 0.2140 (89%) | |
| 5 | 0.1714 | 0.3579 (109%) | 0.3882 (126%) | 0.2915 (70%) | 0.3249 (90%) | 0.3249 (90%) | |
| 1/10 | 1 | 0.0298 | 0.0621 (108%) | 0.0718 (141%) | 0.0491 (65%) | 0.0558 (87%) | 0.0558 (87%) |
| 2 | 0.1134 | 0.2367 (109%) | 0.2628 (132%) | 0.1906 (68%) | 0.2140 (89%) | 0.2140 (89%) | |
| 3 | 0.2380 | 0.4968 (109%) | 0.5266 (121%) | 0.4097 (72%) | 0.4530 (90%) | 0.4530 (90%) | |
| 4 | 0.3903 | 0.8149 (109%) | 0.8283 (112%) | 0.6890 (77%) | 0.7502 (92%) | 0.7502 (92%) | |
| 5 | 0.5602 | 1.1699 (109%) | 1.1491 (105%) | 1.0131 (81%) | 1.0871 (94%) | 1.0871 (94%) | |
| 1/5 | 1 | 0.1134 | 0.2367 (109%) | 0.2628 (132%) | 0.1906 (68%) | 0.2140 (89%) | 0.2140 (89%) |
| 2 | 0.3903 | 0.8149 (109%) | 0.8283 (112%) | 0.6890 (77%) | 0.7502 (92%) | 0.7502 (92%) | |
| 3 | 0.7409 | 1.5474 (109%) | 1.4803 (100%) | 1.3694 (85%) | 1.4507 (96%) | 1.4507 (96%) | |
| 4 | 1.1191 | 2.3376 (109%) | 2.1622 (93%) | 2.1452 (92%) | 2.2242 (99%) | 2.2242 (99%) | |
| 5 | 1.5060 | 3.1461 (109%) | 2.8653 (90%) | 2.9689 (97%) | 3.0225 (101%) | 3.0225 (101%) |
| Kw | Kp | Epoxy | UD | FG-X | FG-O | FG-V | FG-A |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.0298 | 0.0621 | 0.0718 | 0.0492 | 0.0558 | 0.0558 |
| 10 | 0.0412 | 0.0683 | 0.0772 | 0.0568 | 0.0626 | 0.0627 | |
| 50 | 0.0702 | 0.0889 | 0.0960 | 0.0804 | 0.0845 | 0.0848 | |
| 100 | 0.0947 | 0.1094 | 0.1152 | 0.1026 | 0.1056 | 0.1061 | |
| 102 | 0 | 0.0413 | 0.0684 | 0.0773 | 0.0569 | 0.0627 | 0.0628 |
| 10 | 0.0501 | 0.0741 | 0.0824 | 0.0637 | 0.0688 | 0.0690 | |
| 50 | 0.0758 | 0.0934 | 0.1002 | 0.0854 | 0.0891 | 0.0895 | |
| 100 | 0.0989 | 0.1131 | 0.1187 | 0.1065 | 0.1094 | 0.1099 | |
| 103 | 0 | 0.0952 | 0.1099 | 0.1156 | 0.1031 | 0.1061 | 0.1066 |
| 10 | 0.0994 | 0.1135 | 0.1191 | 0.1069 | 0.1098 | 0.1104 | |
| 50 | 0.1144 | 0.1269 | 0.1320 | 0.1211 | 0.1235 | 0.1242 | |
| 100 | 0.1308 | 0.1420 | 0.1465 | 0.1368 | 0.1388 | 0.1396 | |
| 105 | 0 | 0.3302 | 0.4076 | 0.4091 | 0.4050 | 0.4026 | 0.4086 |
| 10 | 0.3303 | 0.4086 | 0.4100 | 0.4060 | 0.4036 | 0.4095 | |
| 50 | 0.3304 | 0.4125 | 0.4139 | 0.4098 | 0.4073 | 0.4134 | |
| 100 | 0.3324 | 0.6910 | 0.6898 | 0.6908 | 0.6818 | 0.6936 |
| Magnetic Parameter | Epoxy | UD | FG-X | FG-O | FG-V | FG-A | |
|---|---|---|---|---|---|---|---|
| Mx | 0 | 0.0298 | 0.0621 | 0.0718 | 0.0492 | 0.0558 | 0.0558 |
| 2 | 0.3351 | 0.6481 | 0.6959 | 0.6960 | 0.6878 | 0.6878 | |
| 5 | 0.3371 | 0.6983 | 0.6977 | 0.6980 | 0.6964 | 0.6964 | |
| 10 | 0.3400 | 0.6999 | 0.6997 | 0.6993 | 0.6982 | 0.6982 | |
| My | 0 | 0.0298 | 0.0621 | 0.0718 | 0.0492 | 0.0558 | 0.0558 |
| 2 | 0.0401 | 0.0678 | 0.0764 | 0.0564 | 0.0631 | 0.0631 | |
| 5 | 0.0513 | 0.0754 | 0.0827 | 0.0656 | 0.0721 | 0.0721 | |
| 10 | 0.0649 | 0.0864 | 0.0918 | 0.0784 | 0.0843 | 0.0843 | |
| Mz | 0 | 0.0298 | 0.0621 | 0.0718 | 0.0492 | 0.0558 | 0.0558 |
| 2 | 0.0228 | 0.0532 | 0.0636 | 0.0409 | 0.0471 | 0.0471 | |
| 5 | 0.0220 | 0.0495 | 0.0591 | 0.0382 | 0.0441 | 0.0441 | |
| 10 | 0.0216 | 0.0474 | 0.0563 | 0.0369 | 0.0424 | 0.0424 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D. Free Vibration of Functionally Graded Graphene Platelets Reinforced Magnetic Nanocomposite Beams Resting on Elastic Foundation. Nanomaterials 2020, 10, 2193. https://doi.org/10.3390/nano10112193
Liu D. Free Vibration of Functionally Graded Graphene Platelets Reinforced Magnetic Nanocomposite Beams Resting on Elastic Foundation. Nanomaterials. 2020; 10(11):2193. https://doi.org/10.3390/nano10112193
Chicago/Turabian StyleLiu, Dongying. 2020. "Free Vibration of Functionally Graded Graphene Platelets Reinforced Magnetic Nanocomposite Beams Resting on Elastic Foundation" Nanomaterials 10, no. 11: 2193. https://doi.org/10.3390/nano10112193
APA StyleLiu, D. (2020). Free Vibration of Functionally Graded Graphene Platelets Reinforced Magnetic Nanocomposite Beams Resting on Elastic Foundation. Nanomaterials, 10(11), 2193. https://doi.org/10.3390/nano10112193





