Calculation of Hole Concentrations in Zn Doped GaAs Nanowires
Abstract
:1. Introduction
2. Materials and Methods
2.1. Density Functional Theory Calculations
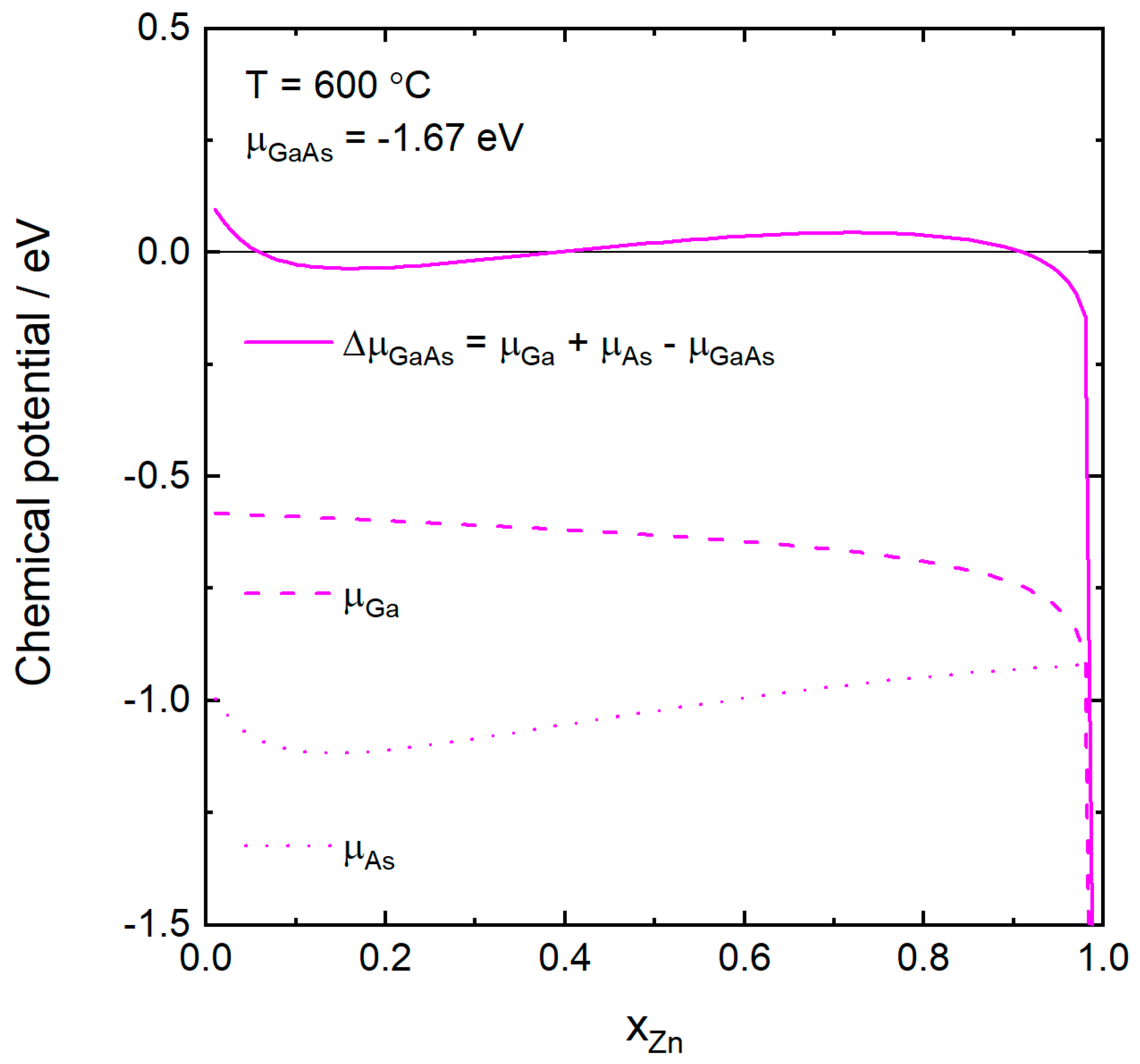
2.2. Calculation of Chemical Potentials
2.3. Aerotaxy Growth
2.4. Doping Characterization
2.5. Catalyst Particle Composition
3. Theoretical Model
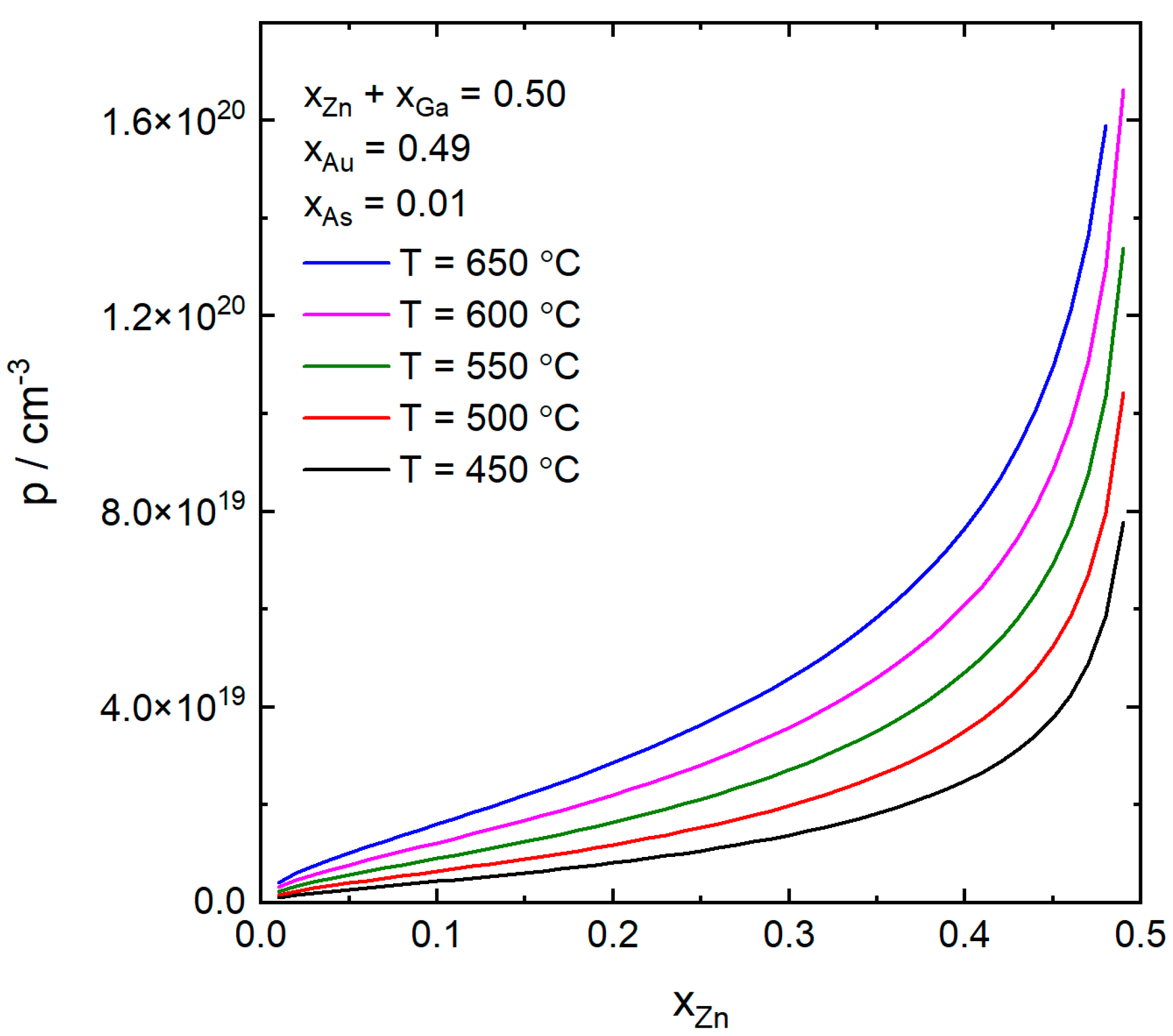
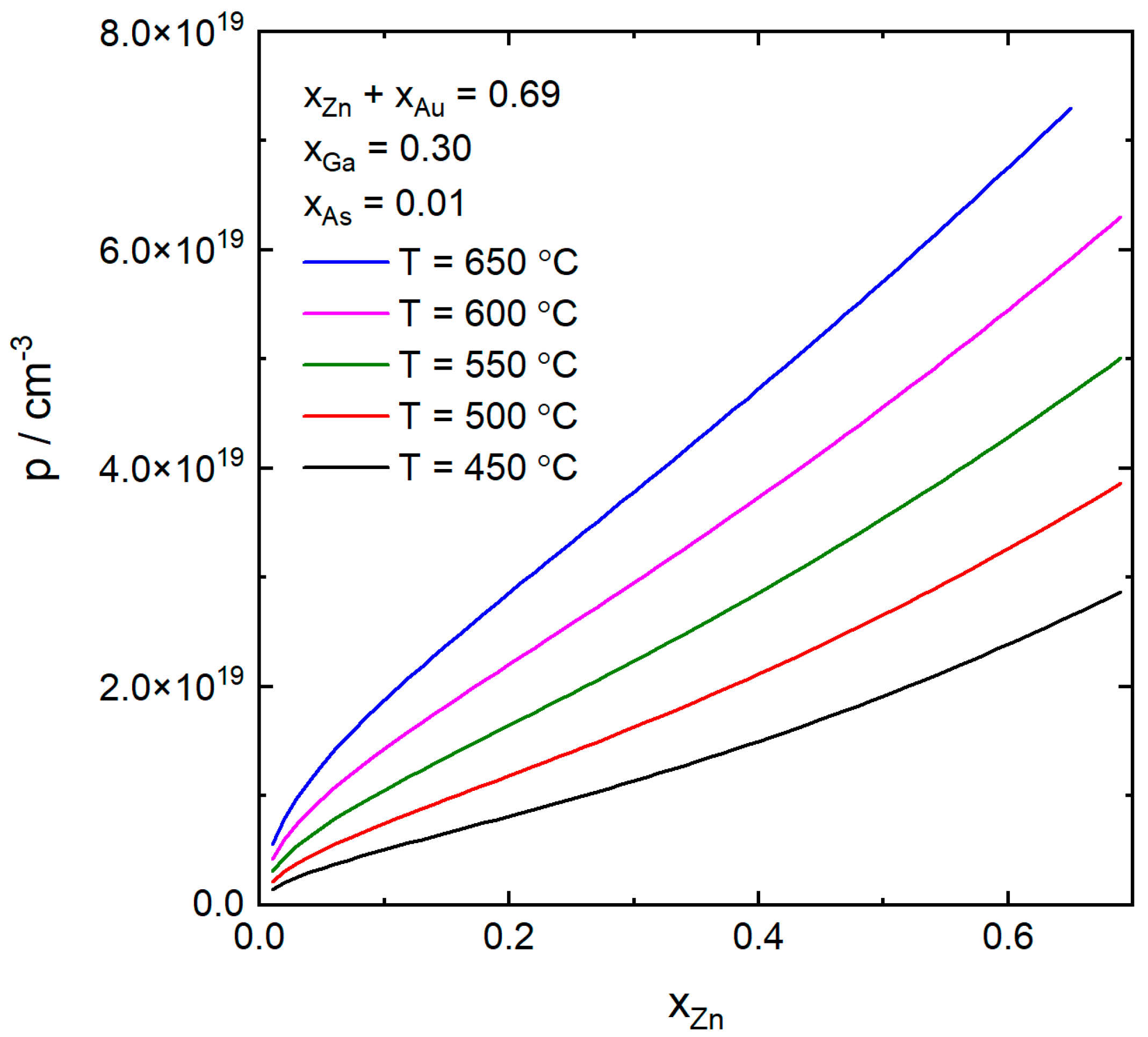
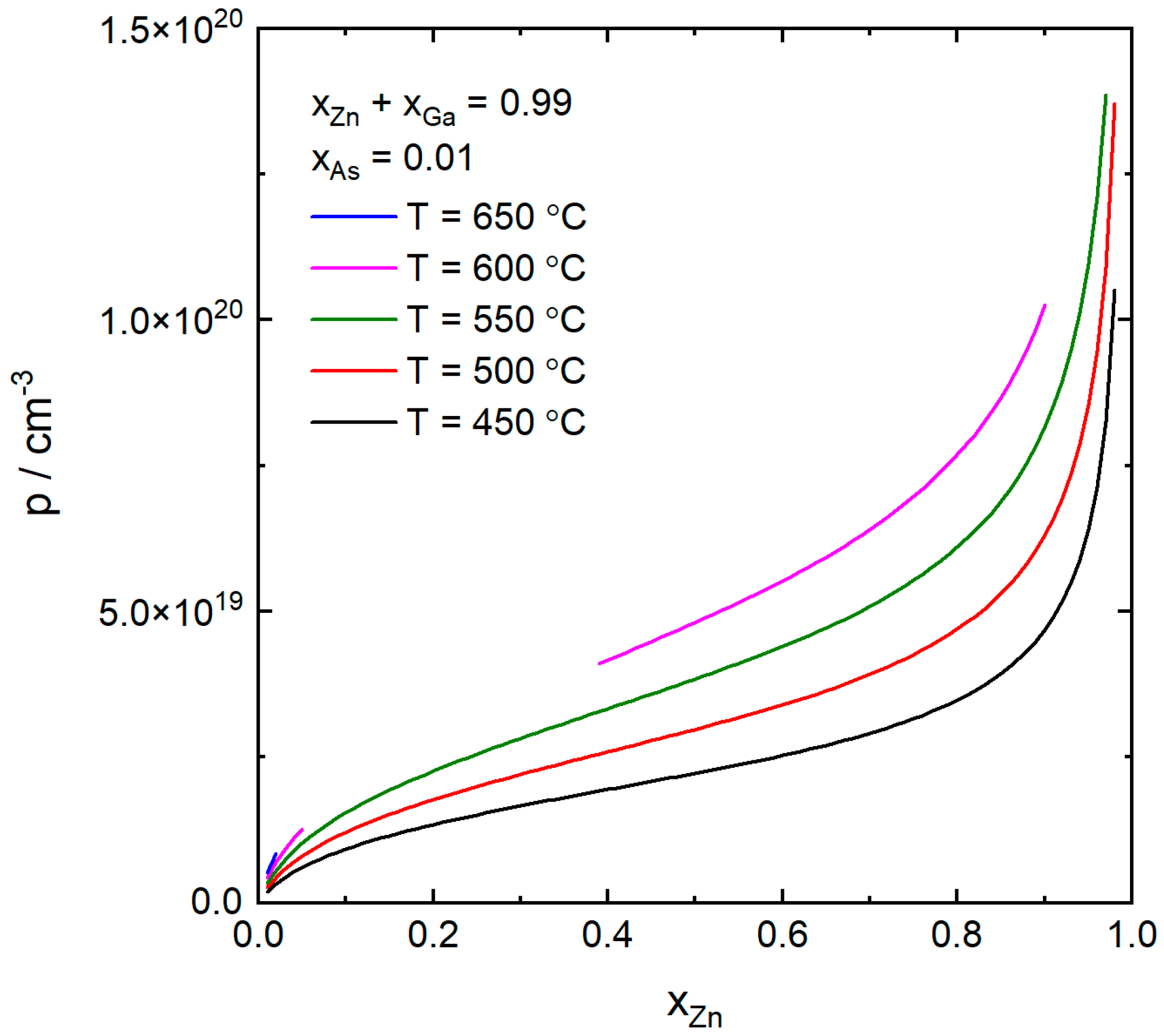
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rahong, S.; Yasui, T.; Kaji, N.; Baba, Y. Recent developments in nanowires for bio-applications from molecular to cellular levels. Lab Chip 2016, 16, 1126–1138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wernersson, L.E.; Thelander, C.; Lind, E.; Samuelson, L. III-V Nanowires-Extending a Narrowing Road. Proc. IEEE 2010, 98, 2047–2060. [Google Scholar] [CrossRef]
- Quan, L.N.; Kang, J.; Ning, C.Z.; Yang, P.D. Nanowires for Photonics. Chem. Rev. 2019, 119, 9153–9169. [Google Scholar] [CrossRef] [PubMed]
- Guan, N.; Dai, X.; Julien, F.H.; Eymery, J.; Durant, C.; Tchernycheva, M. Nitride Nanowires for Light Emitting Diodes. In Light-Emitting Diodes; Solid State Lighting Technology and Application Series; Li, J., Zhang, G., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Borgstrom, M.T.; Magnusson, M.H.; Dimroth, F.; Siefer, G.; Hohn, O.; Riel, H.; Schmid, H.; Wirths, S.; Bjork, M.; Aberg, I.; et al. Towards Nanowire Tandem Junction Solar Cells on Silicon. IEEE J. Photovolt. 2018, 8, 733–740. [Google Scholar] [CrossRef] [Green Version]
- Kolasinski, K.W. Catalytic Growth of Nanowires: Vapor-Liquid-Solid, Vapor-Solid-Solid, Solution-Liquid-Solid and Solid-Liquid-Solid Growth. Curr. Opin. Solid State Mater. Sci. 2006, 10, 182–191. [Google Scholar] [CrossRef]
- Guniat, L.; Caroff, P.; Morral, A.F.I. Vapor Phase Growth of Semiconductor Nanowires: Key Developments and Open Questions. Chem. Rev. 2019, 119, 8958–8971. [Google Scholar] [CrossRef] [Green Version]
- Wallentin, J.; Borgstrom, M.T. Doping of semiconductor nanowires. J. Mater. Res. 2011, 26, 2142–2156. [Google Scholar] [CrossRef] [Green Version]
- Dayeh, S.A.; Chen, R.; Ro, Y.G.; Sim, J. Progress in doping semiconductor nanowires during growth. Mater. Sci. Semicon. Proc. 2017, 62, 135–155. [Google Scholar] [CrossRef] [Green Version]
- Schwalbach, E.J.; Voorhees, P.W. Doping nanowires grown by the vapor-liquid-solid mechanism. Appl. Phys. Lett. 2009, 95, 063105. [Google Scholar] [CrossRef]
- Hijazi, H.; Monier, G.; Gil, E.; Trassoudaine, A.; Bougerol, C.; Leroux, C.; Castellucci, D.; Robert-Goumet, C.; Hoggan, P.E.; Andre, Y.; et al. Si Doping of Vapor-Liquid-Solid GaAs Nanowires: n-Type or p-Type? Nano Lett. 2019, 19, 4498–4504. [Google Scholar] [CrossRef]
- Hannay, N.B. Solid State Chemistry; Prentice-Hall: Englewood Cliffs, NJ, USA, 1967. [Google Scholar]
- Dubrovskii, V.G.; Hijazi, H. Effect of Arsenic Depletion on the Silicon Doping of Vapor-Liquid-Solid GaAs Nanowires. Phys. Status Solidi R 2020, 14, 2000129. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Hijazi, H.; Goktas, N.I.; LaPierre, R.R. Be, Te, and Si Doping of GaAs Nanowires: Theory and Experiment. J. Phys. Chem. C 2020, 124, 17299–17307. [Google Scholar] [CrossRef]
- Zhang, S.B.; Northrup, J.E. Chemical-Potential Dependence of Defect Formation Energies in GaAs—Application to Ga Self-Diffusion. Phys. Rev. Lett. 1991, 67, 2339–2342. [Google Scholar] [CrossRef]
- Heurlin, M.; Magnusson, M.H.; Lindgren, D.; Ek, M.; Wallenberg, L.R.; Deppert, K.; Samuelson, L. Continuous gas-phase synthesis of nanowires with tunable properties. Nature 2012, 492, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Sivakumar, S.; Persson, A.R.; Metaferia, W.; Heurlin, M.; Wallenberg, R.; Samuelson, L.; Deppert, K.; Johansson, J.; Magnusson, M.H. Aerotaxy: Gas-phase epitaxy of quasi 1D nanostructures. Nanotechnology 2020, 32, 025605. [Google Scholar] [CrossRef] [PubMed]
- Gonze, X.; Amadon, B.; Anglade, P.M.; Beuken, J.M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Cote, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Slater, J.C. Wave functions in a periodic potential. Phys. Rev. 1937, 51, 0846–0851. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Andersson, J.O.; Helander, T.; Hoglund, L.H.; Shi, P.F.; Sundman, B. Thermo-Calc & Dictra, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar]
- Ghasemi, M.; Johansson, J. Thermodynamic assessment of the As-Zn and As-Ga-Zn systems. J. Alloys Compd. 2015, 638, 95–102. [Google Scholar] [CrossRef] [Green Version]
- Ansara, I.; Chatillon, C.; Lukas, H.L.; Nishizawa, T.; Ohtani, H.; Ishida, K.; Hillert, M.; Sundman, B.; Argent, B.B.; Watson, A.; et al. A Binary Database for III-V Compound Semiconductor Systems. Calphad 1994, 18, 177–222. [Google Scholar] [CrossRef]
- Ghasemi, M.; Johansson, J. Phase diagrams for understanding gold-seeded growth of GaAs and InAs nanowires. J. Phys. D 2017, 50, 134002. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.J.; Liu, L.B.; Zhou, H.Y.; Jin, Z.P. Thermodynamic assessment of the Au-Ga binary system. Calphad 2011, 35, 242–248. [Google Scholar] [CrossRef]
- Liu, H.S.; Ishida, K.; Jin, Z.P.; Du, Y. Thermodynamic assessment of the Au-Zn binary system. Intermetallics 2003, 11, 987–994. [Google Scholar] [CrossRef]
- Dutkiewicz, J.; Moser, Z.; Zabdyr, L.; Gohil, D.D.; Chart, T.G.; Ansara, I.; Girard, C. The Ga–Zn (Gallium–Zinc) system. Bull. Alloy Phase Diagr. 1990, 11, 77–82. [Google Scholar] [CrossRef]
- Magnusson, M.H.; Deppert, K.; Malm, J.O.; Bovin, J.O.; Samuelson, L. Size-selected gold nanoparticles by aerosol technology. Nanostruct. Mater. 1999, 12, 45–48. [Google Scholar] [CrossRef]
- Preger, C.; Overgaard, N.C.; Messing, M.E.; Magnusson, M.H. Predicting the deposition spot radius and the nanoparticle concentration distribution in an electrostatic precipitator. Aerosol Sci. Technol. 2020, 54, 718–728. [Google Scholar] [CrossRef]
- Borghs, G.; Bhattacharyya, K.; Deneffe, K.; Vanmieghem, P.; Mertens, R. Band-Gap Narrowing in Highly Doped n- and p-type GaAs Studied by Photoluminescence Spectroscopy. J. Appl. Phys. 1989, 66, 4381–4386. [Google Scholar] [CrossRef]
- Ermanis, F.; Wolfstir, K. Hall Effect and Resistivity of Zn-Doped GaAs. J. Appl. Phys. 1966, 37, 1963–1966. [Google Scholar] [CrossRef]
- Hurle, D.T.J. A comprehensive thermodynamic analysis of native point defect and dopant solubilities in gallium arsenide. J. Appl. Phys. 1999, 85, 6957–7022. [Google Scholar] [CrossRef]
- Böer, K.W.; Pohl, U.W. Semiconductor Physics; Springer: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Makov, G.; Payne, M.C. Periodic Boundary-Conditions in Ab-Initio Calculations. Phys. Rev. B 1995, 51, 4014–4022. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, F.F.; Messing, M.E.; Mergenthaler, K.; Ghasemi, M.; Johansson, J.; Wallenberg, L.R.; Pistol, M.E.; Deppert, K.; Samuelson, L.; Magnusson, M.H. Zn-doping of GaAs nanowires grown by Aerotaxy. J. Cryst. Growth 2015, 414, 181–186. [Google Scholar] [CrossRef]


| 8 | −8939.9832 | 402.9457 |
| 16 | −18,283.0257 | 402.8363 |
| 64 | −74,340.6705 | 402.7707 |
| 128 | −149,084.1712 | 402.7106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johansson, J.; Ghasemi, M.; Sivakumar, S.; Mergenthaler, K.; Persson, A.R.; Metaferia, W.; Magnusson, M.H. Calculation of Hole Concentrations in Zn Doped GaAs Nanowires. Nanomaterials 2020, 10, 2524. https://doi.org/10.3390/nano10122524
Johansson J, Ghasemi M, Sivakumar S, Mergenthaler K, Persson AR, Metaferia W, Magnusson MH. Calculation of Hole Concentrations in Zn Doped GaAs Nanowires. Nanomaterials. 2020; 10(12):2524. https://doi.org/10.3390/nano10122524
Chicago/Turabian StyleJohansson, Jonas, Masoomeh Ghasemi, Sudhakar Sivakumar, Kilian Mergenthaler, Axel R. Persson, Wondwosen Metaferia, and Martin H. Magnusson. 2020. "Calculation of Hole Concentrations in Zn Doped GaAs Nanowires" Nanomaterials 10, no. 12: 2524. https://doi.org/10.3390/nano10122524
APA StyleJohansson, J., Ghasemi, M., Sivakumar, S., Mergenthaler, K., Persson, A. R., Metaferia, W., & Magnusson, M. H. (2020). Calculation of Hole Concentrations in Zn Doped GaAs Nanowires. Nanomaterials, 10(12), 2524. https://doi.org/10.3390/nano10122524






