Numerical and Theoretical Study of Tunable Plasmonically Induced Transparency Effect Based on Bright–Dark Mode Coupling in Graphene Metasurface
Abstract
:1. Introduction
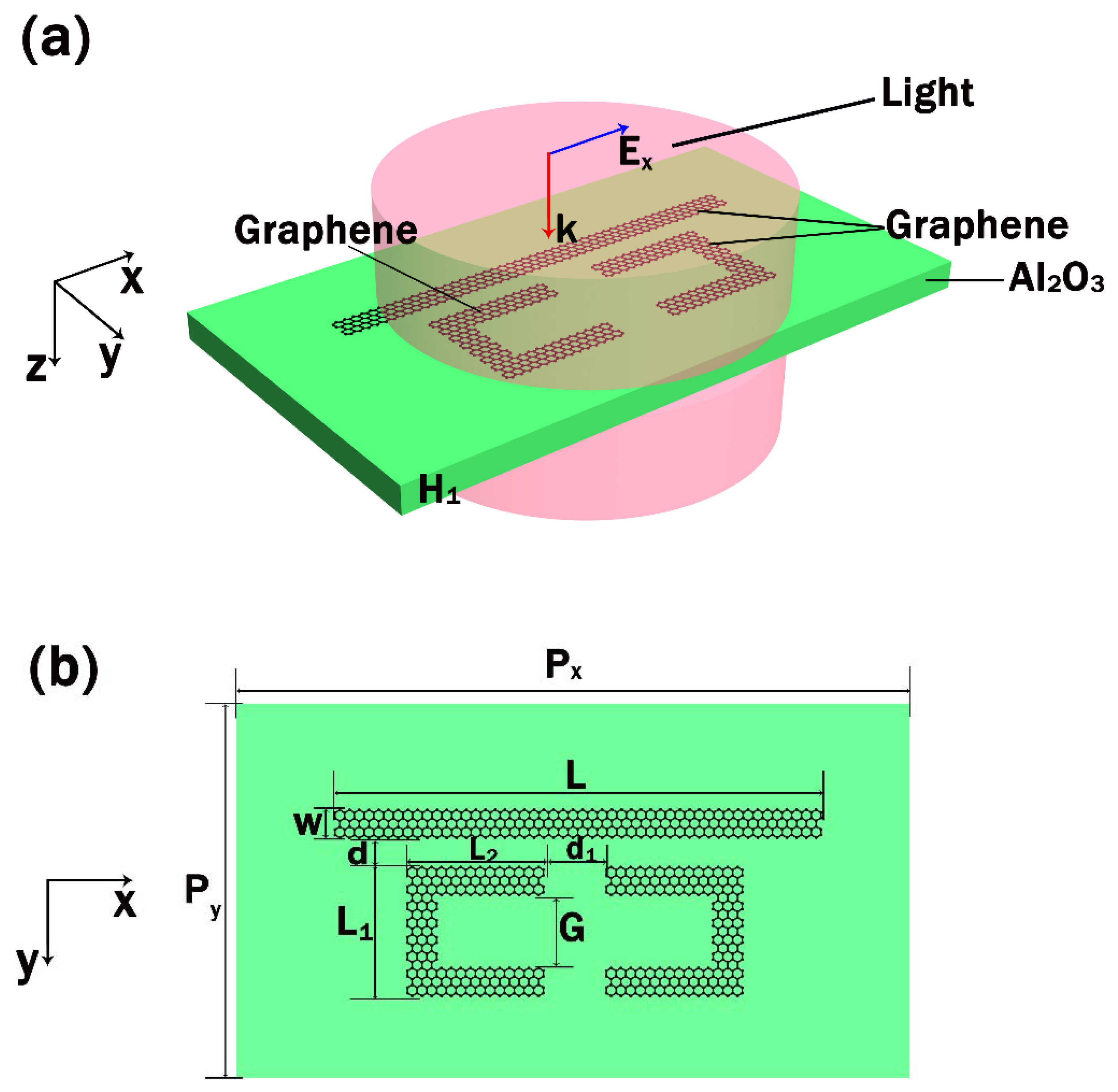
2. Materials and Methods
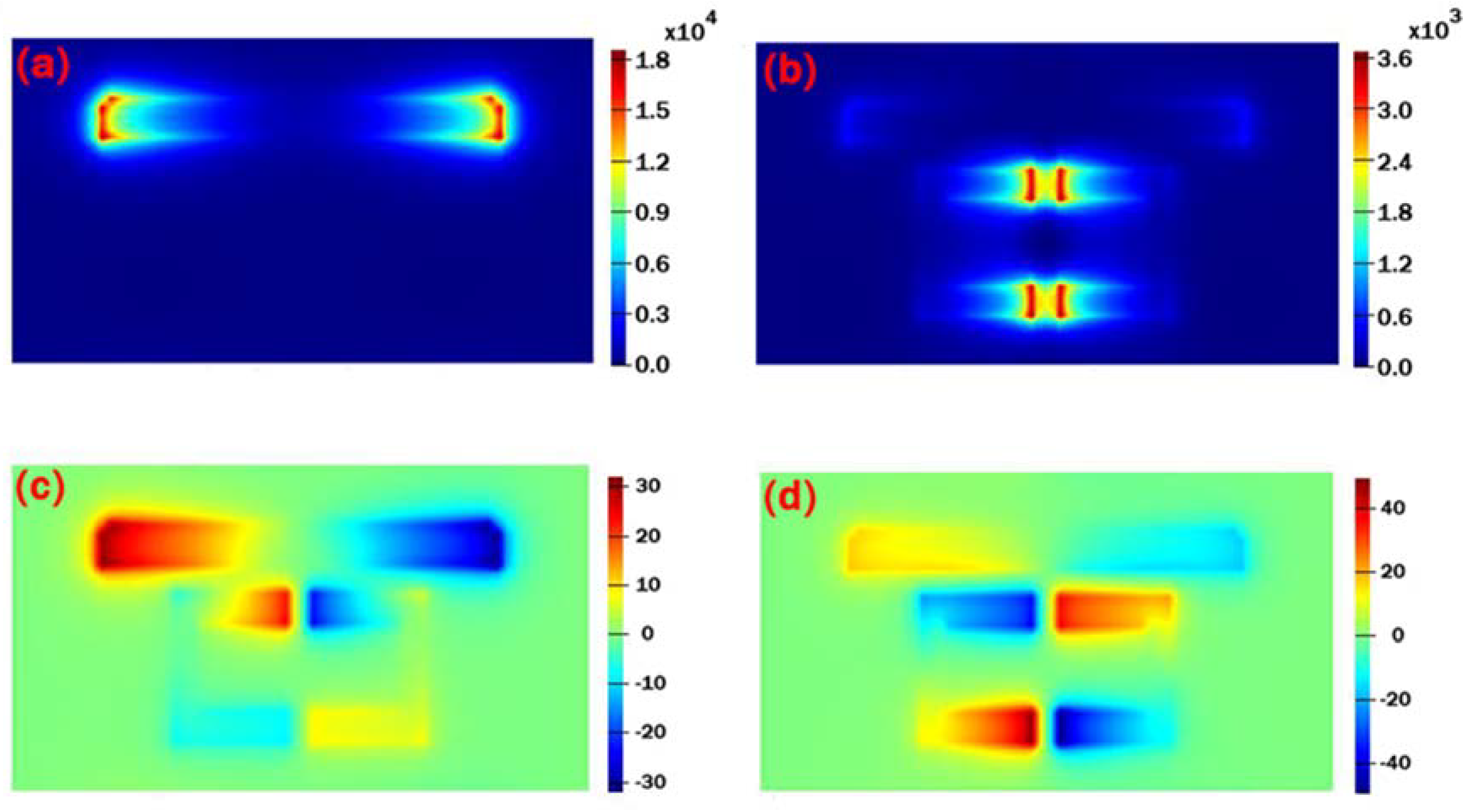
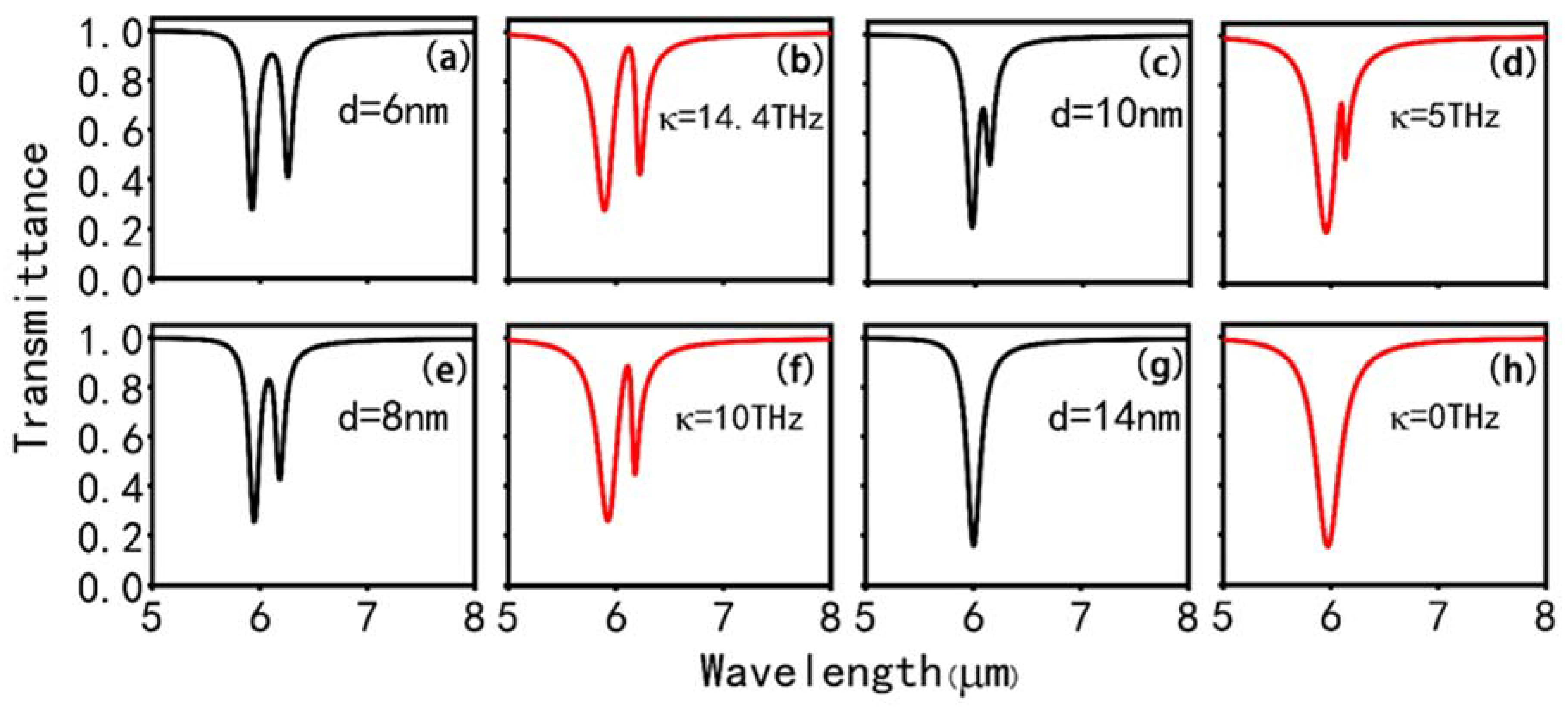
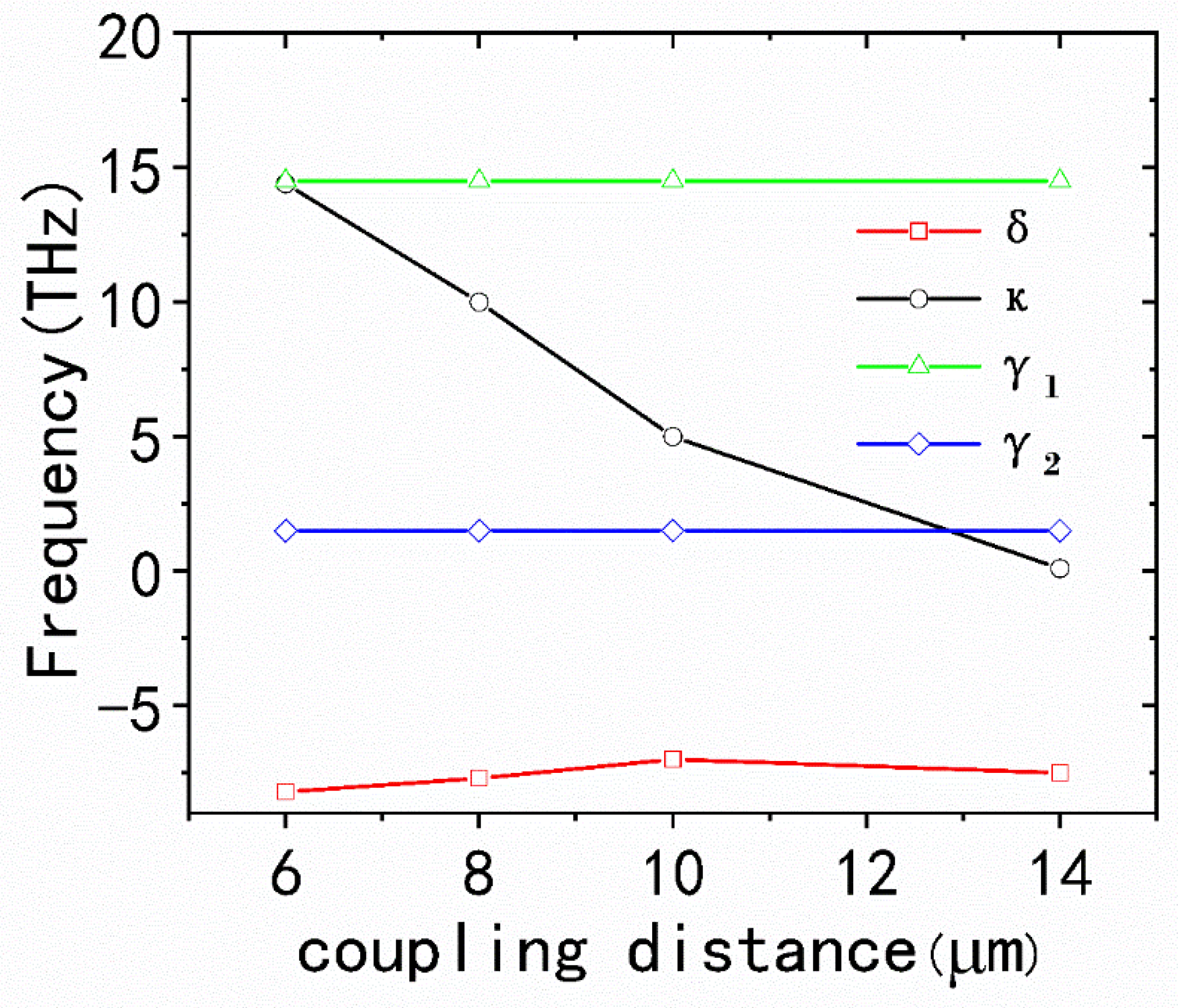
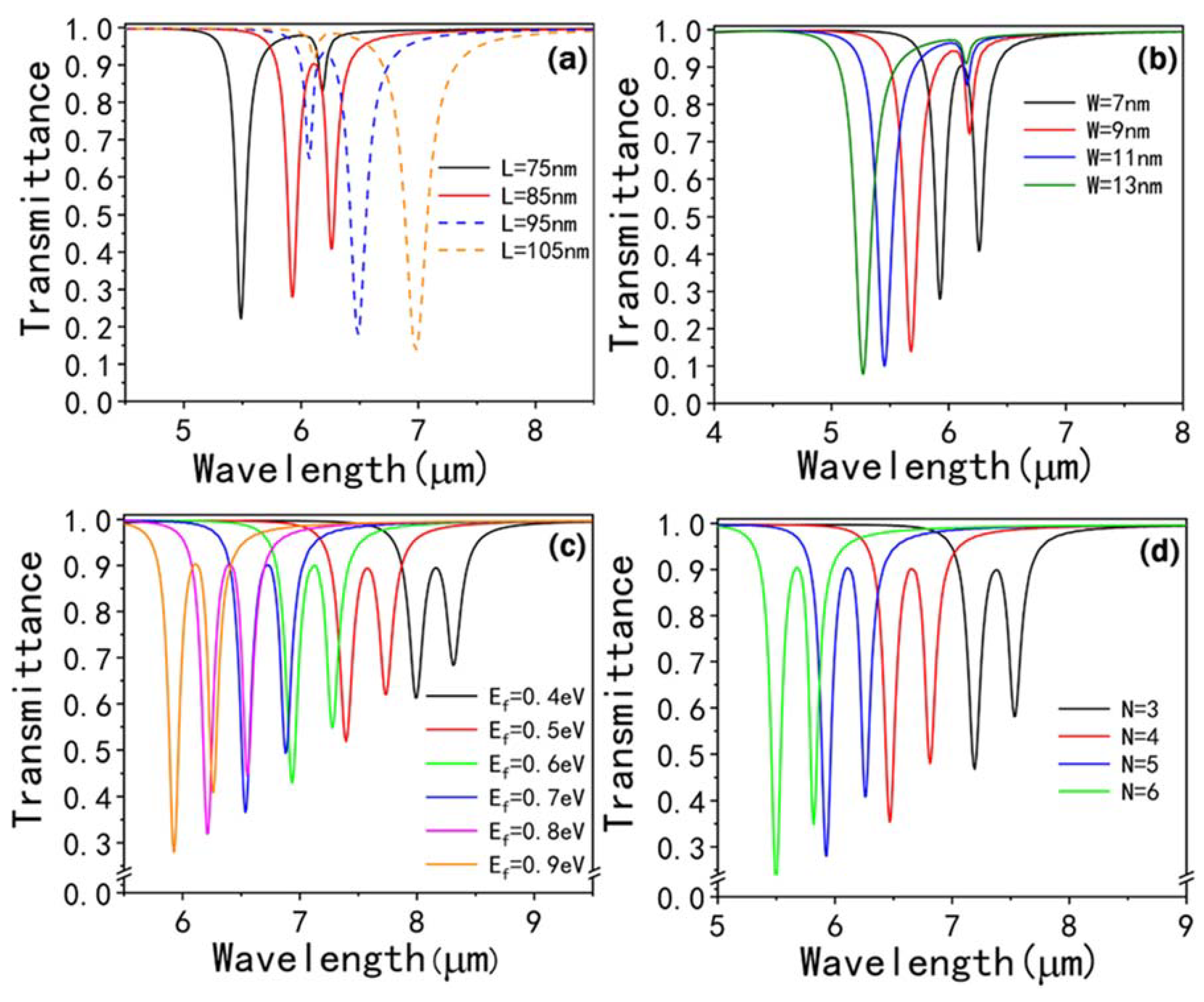
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boller, K.J.; Imamolu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593–2596. [Google Scholar] [CrossRef] [Green Version]
- Marangos, J.P. Electromagnetically induced transparency. J. Mod. Opt. 1998, 45, 471–503. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef] [Green Version]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon N. Y. 2018, 126, 271–278. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Xiao, G.; Liu, F.; Lin, F.; Shi, W. Flexible properties of THz graphene bowtie metamaterials structures. Opt. Mater. Express 2019, 9, 44–55. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Liu, C.; Wu, K. Absorption and slow-light analysis based on tunable plasmon-induced transparency in patterned graphene metamaterial. Opt. Express 2019, 27, 3598–3608. [Google Scholar] [CrossRef]
- Wang, J.; Fan, C.; He, J.; Ding, P.; Liang, E.; Xue, Q. Double Fano resonances due to interplay of electric and magnetic plasmon modes in planar plasmonic structure with high sensing sensitivity. Opt. Express 2013, 21, 2236–2244. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Mousavi, S.H.; Wu, C.; Dabidian, N.; Alici, K.B.; Shvets, G. Electromagnetically induced polarization conversion. Opt. Commun. 2012, 285, 3423–3427. [Google Scholar] [CrossRef]
- Tang, C.; Niu, Q.; Wang, B.-X.; Huang, W.-Q. Design of Dual-Band Plasmon-Induced Transparent Effect Based on Composite Structure of Closed-Ring and Square Patch. Plasmonics 2019, 14, 533–538. [Google Scholar] [CrossRef]
- Shen, N.-H.; Massaouti, M.; Gokkavas, M.; Manceau, J.-M.; Ozbay, E.; Kafesaki, M.; Koschny, T.; Tzortzakis, S.; Soukoulis, C.M. Optically Implemented Broadband Blueshift Switch in the Terahertz Regime. Phys. Rev. Lett. 2011, 106, 37403. [Google Scholar] [CrossRef]
- Gu, J.; Singh, R.; Liu, X.; Zhang, X.; Ma, Y.; Zhang, S.; Maier, S.A.; Tian, Z.; Azad, A.K.; Chen, H.-T.; et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 2012, 3, 1151. [Google Scholar] [CrossRef] [Green Version]
- Zharov, A.A.; Shadrivov, I.V.; Kivshar, Y.S. Nonlinear Properties of Left-Handed Metamaterials. Phys. Rev. Lett. 2003, 91, 37401. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Gu, C.; Li, Z.; Liu, L.; Niu, Z. A Novel Absorber with Tunable Bandwidth Based on Graphene. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 822–825. [Google Scholar]
- García de Abajo, F.J. Graphene Plasmonics: Challenges and Opportunities. ACS Photonics 2014, 1, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Liu, X.; He, L.; Yin, Y.; Wu, D.; Shi, J. Manipulating Graphene Mobility and Charge Neutral Point with Ligand-Bound Nanoparticles as Charge Reservoir. Nano Lett. 2010, 10, 4989–4993. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 64302. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Shen, N.-H.; Koschny, T.; Soukoulis, C.M. Tunable Terahertz Meta-Surface with Graphene Cut-Wires. ACS Photonics 2015, 2, 151–156. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.-H.; Zhang, F.; Wei, Z.; Li, H.; Zhao, Q.; Fu, Q.; Zhang, P.; Koschny, T.; Soukoulis, C.M. Electrically Tunable Goos–Hänchen Effect with Graphene in the Terahertz Regime. Adv. Opt. Mater. 2016, 4, 1824–1828. [Google Scholar] [CrossRef]
- Tasolamprou, A.C.; Koulouklidis, A.D.; Daskalaki, C.; Mavidis, C.P.; Kenanakis, G.; Deligeorgis, G.; Viskadourakis, Z.; Kuzhir, P.; Tzortzakis, S.; Kafesaki, M.; et al. Experimental Demonstration of Ultrafast THz Modulation in a Graphene-Based Thin Film Absorber through Negative Photoinduced Conductivity. ACS Photonics 2019, 6, 720–727. [Google Scholar] [CrossRef] [Green Version]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: New York, NY, USA, 1998; Volume 3, p. 662. [Google Scholar]
- Chang, Y.-C.; Liu, C.-H.; Liu, C.-H.; Zhong, Z.; Norris, T.B. Mid-infrared Hyperbolic Metamaterial Based on Graphene-dielectric Multilayers. Proc. SPIE 2015, 9544, 954417. [Google Scholar]
- Park, S.; Ruoff, R.S. Chemical methods for the production of graphenes. Nat. Nanotechnol. 2009, 4, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Z.; Kim, P.; Zhang, L.; Zhou, C. Anisotropic Hydrogen Etching of Chemical Vapor Deposited Graphene. ACS Nano 2012, 6, 126–132. [Google Scholar] [CrossRef] [PubMed]
- Suk, J.W.; Kitt, A.; Magnuson, C.W.; Hao, Y.; Ahmed, S.; An, J.; Swan, A.K.; Goldberg, B.B.; Ruoff, R.S. Transfer of CVD-Grown Monolayer Graphene onto Arbitrary Substrates. ACS Nano 2011, 5, 6916–6924. [Google Scholar] [CrossRef] [PubMed]
- Lao, J.; Tao, J.; Wang, Q.J.; Huang, X.G. Tunable graphene-based plasmonic waveguides: Nano modulators and nano attenuators. Laser Photon. Rev. 2014, 8, 569–574. [Google Scholar] [CrossRef]
- Yao, J.; Chen, Y.; Ye, L.; Liu, N.; Cai, G.; Liu, Q.H. Multiple resonant excitations of surface plasmons in a graphene stratified slab by Otto configuration and their independent tuning. Photon. Res. 2017, 5, 377–384. [Google Scholar] [CrossRef]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of Plasmonic Waves in Graphene by Guided-Mode Resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef]
- Chen, Z.H.; Tao, J.; Gu, J.H.; Li, J.; Hu, D.; Tan, Q.L.; Zhang, F.; Huang, X.G. Tunable metamaterial-induced transparency with gate-controlled on-chip graphene metasurface. Opt. Express 2016, 24, 29216–29225. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation Optics Using Graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.S.; How Gan, C. Active plasmonic switching at mid-infrared wavelengths with graphene ribbon arrays. Appl. Phys. Lett. 2013, 102, 231107. [Google Scholar] [CrossRef] [Green Version]
- Casiraghi, C.; Hartschuh, A.; Lidorikis, E.; Qian, H.; Harutyunyan, H.; Gokus, T.; Novoselov, K.S.; Ferrari, A.C. Rayleigh Imaging of Graphene and Graphene Layers. Nano Lett. 2007, 7, 2711–2717. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Li, X.; Chandra, B.; Tulevski, G.; Wu, Y.; Freitag, M.; Zhu, W.; Avouris, P.; Xia, F. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol. 2012, 7, 330. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-Induced Transparency in Metamaterials. Phys. Rev. Lett. 2008, 101, 47401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, N.; Langguth, L.; Weiss, T.; Kästel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef]
- Ding, J.; Arigong, B.; Ren, H.; Zhou, M.; Shao, J.; Lu, M.; Chai, Y.; Lin, Y.; Zhang, H. Tuneable complementary metamaterial structures based on graphene for single and multiple transparency windows. Sci. Rep. 2014, 4, 6128. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Cai, W.; Xiang, Y.; Wang, L.; Ren, M.; Zhang, X.; Xu, J. Flexible modulation of plasmon-induced transparency in a strongly coupled graphene grating-sheet system. Opt. Express 2016, 24, 5784–5793. [Google Scholar] [CrossRef]
- Fang, Z.; Thongrattanasiri, S.; Schlather, A.; Liu, Z.; Ma, L.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J.; García de Abajo, F.J. Gated Tunability and Hybridization of Localized Plasmons in Nanostructured Graphene. ACS Nano 2013, 7, 2388–2395. [Google Scholar] [CrossRef]
- Asgari, S.; Shokati, E.; Granpayeh, N. High-efficiency tunable plasmonically induced transparency-like effect in metasurfaces composed of graphene nano-rings and ribbon arrays and its application. Appl. Opt. 2019, 58, 3664–3670. [Google Scholar] [CrossRef]
- Jiang, T.; Huang, D.; Cheng, J.; Fan, X.; Zhang, Z.; Shan, Y.; Yi, Y.; Dai, Y.; Shi, L.; Liu, K.; et al. Gate-tunable third-order nonlinear optical response of massless Dirac fermions in graphene. Nat. Photonics 2018, 12, 430–436. [Google Scholar] [CrossRef] [Green Version]
- Susan, M.A.B.H.; Kaneko, T.; Noda, A.; Watanabe, M. Ion Gels Prepared by in Situ Radical Polymerization of Vinyl Monomers in an Ionic Liquid and Their Characterization as Polymer Electrolytes. J. Am. Chem. Soc. 2005, 127, 4976–4983. [Google Scholar] [CrossRef]
- Lee, S.-K.; Humayun Kabir, S.M.; Sharma, B.K.; Kim, B.J.; Cho, J.H.; Ahn, J.-H. Photo-patternable ion gel-gated graphene transistors and inverters on plastic. Nanotechnology 2013, 25, 14002. [Google Scholar] [CrossRef]
- Cho, J.H.; Lee, J.; Xia, Y.; Kim, B.; He, Y.; Renn, M.J.; Lodge, T.P.; Daniel Frisbie, C. Printable ion-gel gate dielectrics for low-voltage polymer thin-film transistors on plastic. Nat. Mater. 2008, 7, 900–906. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Zhai, F.; Hu, D.; Li, Z.; Bai, B.; Yang, X.; Dai, Q. Broadly tunable graphene plasmons using an ion-gel top gate with low control voltage. Nanoscale 2015, 7, 19493–19500. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Chen, S.; Yu, P.; Duan, X.; Xie, B.; Tian, J. Dynamically tunable plasmonically induced transparency in periodically patterned graphene nanostrips. Appl. Phys. Lett. 2013, 103, 203112. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Dai, J.; Luo, A.; Hong, W. Numerical and Theoretical Study of Tunable Plasmonically Induced Transparency Effect Based on Bright–Dark Mode Coupling in Graphene Metasurface. Nanomaterials 2020, 10, 232. https://doi.org/10.3390/nano10020232
Ma Q, Dai J, Luo A, Hong W. Numerical and Theoretical Study of Tunable Plasmonically Induced Transparency Effect Based on Bright–Dark Mode Coupling in Graphene Metasurface. Nanomaterials. 2020; 10(2):232. https://doi.org/10.3390/nano10020232
Chicago/Turabian StyleMa, Qichang, Jianan Dai, Aiping Luo, and Weiyi Hong. 2020. "Numerical and Theoretical Study of Tunable Plasmonically Induced Transparency Effect Based on Bright–Dark Mode Coupling in Graphene Metasurface" Nanomaterials 10, no. 2: 232. https://doi.org/10.3390/nano10020232
APA StyleMa, Q., Dai, J., Luo, A., & Hong, W. (2020). Numerical and Theoretical Study of Tunable Plasmonically Induced Transparency Effect Based on Bright–Dark Mode Coupling in Graphene Metasurface. Nanomaterials, 10(2), 232. https://doi.org/10.3390/nano10020232




