Nonlinear Vibration of a Pre-Stressed Water-Filled Single-Walled Carbon Nanotube Using Shell Model
Abstract
:1. Introduction
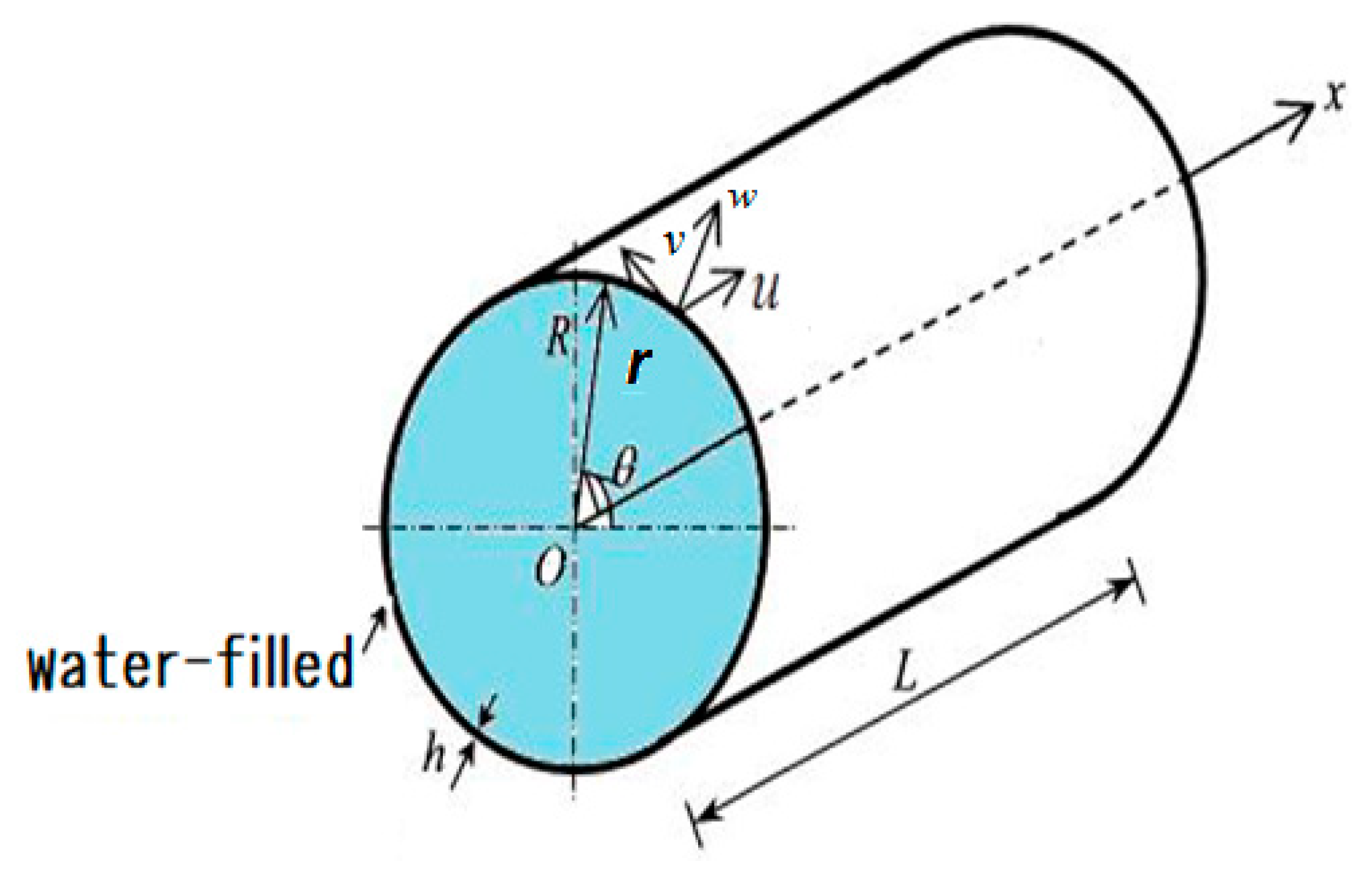
2. Formulation of the Problem
3. Solution of the Problem
3.1. Application of Galerkin’s Method
3.2. The Method of Averaging
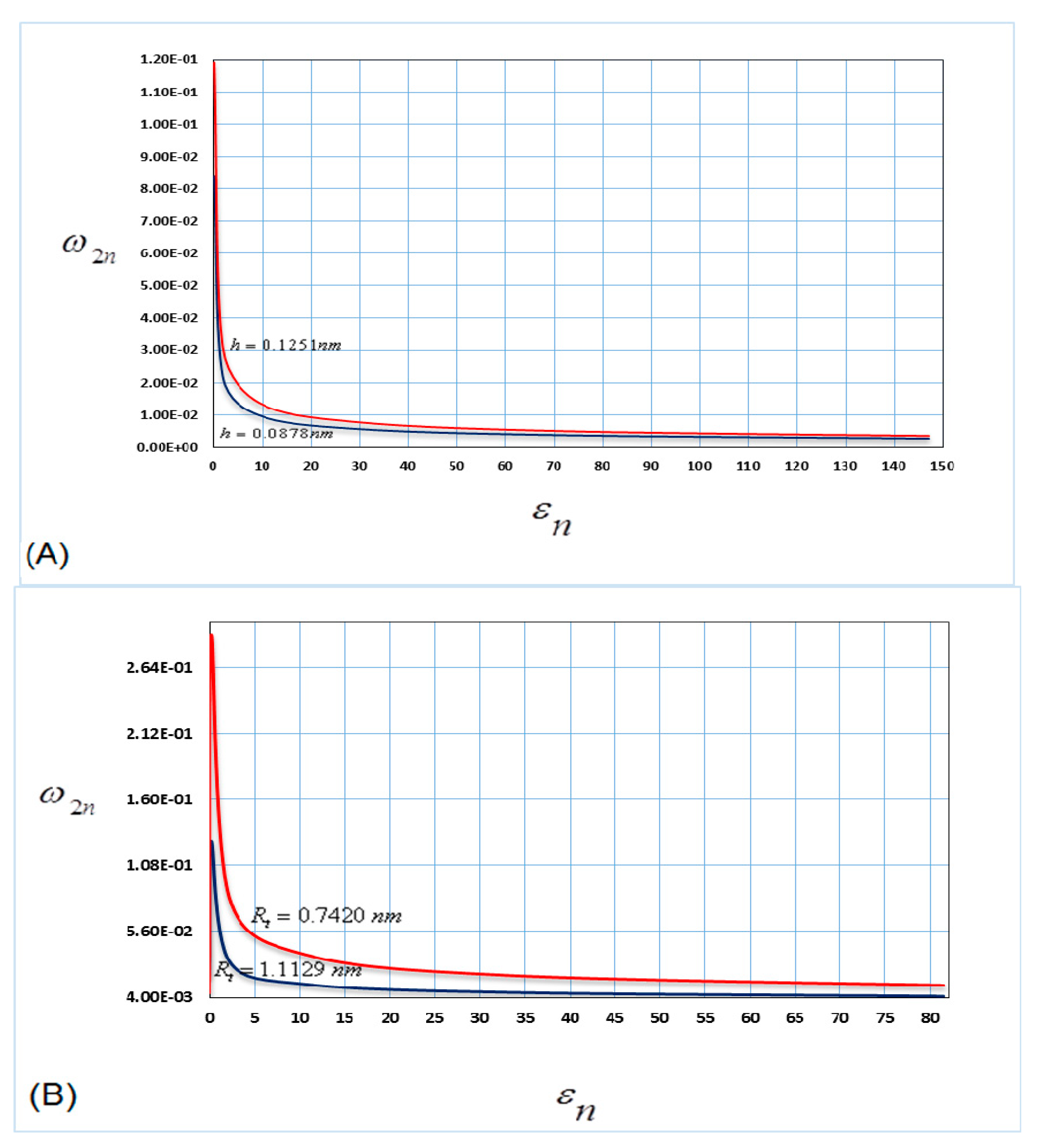
4. Numerical Simulation Procedure
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Ball, P. Roll up for the revolution. Nature 2001, 414, 142. [Google Scholar] [CrossRef]
- Baughman, R.H.; Zakhidov, A.A.; de Heer, W.A. Carbon nanotubes-the route toward applications. Science 2002, 297, 787–792. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Chou, T.W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Shen, L.; Li, J. Transversely isotropic elastic properties of single-walled carbon nanotubes. Phys. Rev. B 2004, 69, 045414. [Google Scholar] [CrossRef]
- Shen, L.; Li, J. Transversely isotropic elastic properties of multiwalled carbon nanotubes. Phys. Rev. B 2005, 71, 035412. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Buckling behavior of FG-CNT reinforced composite conical shells subjected to a combined loading. Nanomaterials 2020, 10, 419. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Hu, T.; Chen, G.; Jiang, Q. Bending instability characteristics of double-walled carbon nanotubes. Phys. Rev. B 2005, 71, 045403. [Google Scholar] [CrossRef] [Green Version]
- Yoon, J.; Ru, C.Q.; Mioduchowski, A. Vibration of an embedded multiwall carbon nanotube. Compos. Sci. Technol. 2003, 63, 1533–1542. [Google Scholar] [CrossRef]
- Yoon, J.; Ru, C.Q.; Mioduchowski, A. Sound wave propagation in multiwall carbon nanotubes. J. Appl. Phys. 2003, 93, 4801–4806. [Google Scholar] [CrossRef]
- Natsuki, T.; Hayashi, T.; Endo, M. Wave propagation of carbon nanotubes embedded in an elastic medium. J. Appl. Phys. 2005, 97, 044307. [Google Scholar] [CrossRef]
- Wang, X.; Cai, H. Effects of initial stress on non-coaxial resonance of multi-wall carbon nanotubes. Acta Mater. 2006, 54, 2067–2074. [Google Scholar] [CrossRef]
- Sun, C.; Liu, K. Vibration of multi-walled carbon nanotubes with initial axial loading. Solid State Commun. 2007, 143, 202–207. [Google Scholar] [CrossRef]
- Asghar, S.; Naeem, M.N.; Hussain, M. Non-local effect on the vibration analysis of double walled carbon nanotubes based on Donnell shell theory. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 116, 113726. [Google Scholar] [CrossRef]
- Yan, K.; Zhang, Y.; Cai, H.; Tahouneh, V. Vibrational characteristic of FG porous conical shells using Donnell’s shell theory. Steel Compos. Struct. 2020, 35, 249–260. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, C.M.; Duan, W.; Xiang, Y.; Zong, Z. Assessment of Continuum mechanics model in predicting buckling strain of single-walled carbon nanotubes. Nanotechnology 2009, 20, 395707. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, L.X.; Wang, W.Q. Dynamical mode transitions of simply supported double-walled carbon nanotubes based on an elastic shell model. J. Appl. Phys. 2008, 103, 113523. [Google Scholar] [CrossRef]
- Lee, S.M.; An, K.H.; Lee, Y.H.; Seifert, G.; Frauenheim, T.J. A hydrogen storage mechanism in single-walled carbon nanotubes. Am. Chem. Soc. 2001, 21, 5059–5063. [Google Scholar] [CrossRef]
- Yan, Y.; He, X.Q.; Zhang, L.X.; Wang, Q. Flow-induced instability of double-walled carbon nanotubes based on an elastic shell model. J. Appl. Phys. 2007, 102, 044307. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, W.Q.; Zhang, L.X. Dynamical behaviors of fluid-conveyed multi-walled carbon nanotubes. Appl. Math. Model. 2009, 33, 1430–1440. [Google Scholar] [CrossRef]
- Wang, L.; Ni, Q.; Li, M. Buckling instability of double-wall carbon nanotubes conveying fluid. Comput. Mater. Sci. 2008, 44, 821–825. [Google Scholar] [CrossRef]
- Khosravian, N.; Rafii-Tabar, H. Computational modelling of a non-viscous fluid flow in a multi-walled carbon nanotube modelled as a Timoshenko beam. Nanotechnology 2008, 19, 275703. [Google Scholar] [CrossRef] [PubMed]
- Soltani, P.; Bahramian, R.; Saberian, J. Nonlinear vibration analysis of the fluid-filled single walled carbon nanotube with the shell model based on the nonlocal elacticity theory. J. Solid Mech. 2015, 7, 58–70. [Google Scholar]
- Wang, Q.; Varadan, V.K. Wave characteristics of carbon nanotubes. Int. J. Solids Struct. 2006, 43, 254–265. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y.; Zhang, L.C. An elastic shell model for characterizing single-walled carbon nanotubes. Nanotechnology 2008, 19, 195704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Z.G.; Wang, B. Non-local theory solution for an anti-plane shear permeable crack in functionally graded piezoelectric materials. Appl. Compos. Mater. 2006, 13, 345–367. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, G.; Han, X. Transverse vibrations of double-walled carbon nanotubes under compressive axial load. Phys. Lett. A 2005, 340, 258–266. [Google Scholar] [CrossRef]
- Lu, P.; Lee, H.P.; Lu, C.; Zhang, P.Q. Application of nonlocal beam models for carbon nanotubes. Int. J. Solids Struct. 2007, 44, 5289–5300. [Google Scholar] [CrossRef] [Green Version]
- Heireche, H.; Tounsi, A.; Benzair, A. Scale effect on wave propagation of double-walled carbon nanotubes with initial axial loading. Nanotechnology 2008, 19, 185703. [Google Scholar] [CrossRef]
- Dağlıoğlu, C. İlaç taşıma sistemleri olarak nanopartiküller kullanılarak pasif ve aktif tümör hedeflemelerinin karşılaştırmalı incelenmesi. Akad. Platf. Mühendislik Fen Bilimleri Derg. 2018, 6, 1–7. [Google Scholar] [CrossRef]
- Selim, M.M. Vibrational analysis of initially stressed carbon nanotubes. Acta Phys. Pol. A 2011, 119, 778–782. [Google Scholar] [CrossRef]
- Selim, M.M. Torsional vibration of carbon nanotubes under initial compression stress. Braz. J. Phys. 2010, 40, 283–287. [Google Scholar] [CrossRef]
- Selim, M.M. Dispersion of dilatation wave propagation in single-wall carbon nanotubes under initial stress using nonlocal scale effects. J. Comput. Theor. Nanosci. 2013, 10, 2547–2554. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Lv, Y.; Cheng, H.M.; Ma, Z.G. Fatigue performances of glass fiber reinforced concrete in flexure. Procedia Eng. 2012, 31, 550–556. [Google Scholar] [CrossRef] [Green Version]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley and Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Gupta, S.S.; Bosco, F.G.; Batra, R.C. Wall thickness and elastic moduli of single-walled carbon nanotubes from frequencies of axial, torsional and inextensional modes of vibration. Comput. Mater. Sci. 2010, 47, 1049–1059, Corpus ID: 30056031. [Google Scholar] [CrossRef]

| Young’s Modulus E(Gpa) | Mass Density | Poisson’s Ratio | Tube (n,m) | Tube Length L (nm) |
|---|---|---|---|---|
| 1060 | 2270 | 0.25 | (40,0) | 10 |
| Radius of Single-Walled Carbon Nanotube (Rt) (nm) | Nanotube Wall Thickness (h) (nm) |
|---|---|
| 0.7420 | 0.0878 |
| 1.1129 | 0.1340 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed Selim, M.; Musa, A. Nonlinear Vibration of a Pre-Stressed Water-Filled Single-Walled Carbon Nanotube Using Shell Model. Nanomaterials 2020, 10, 974. https://doi.org/10.3390/nano10050974
Mohamed Selim M, Musa A. Nonlinear Vibration of a Pre-Stressed Water-Filled Single-Walled Carbon Nanotube Using Shell Model. Nanomaterials. 2020; 10(5):974. https://doi.org/10.3390/nano10050974
Chicago/Turabian StyleMohamed Selim, Mahmoud, and Awad Musa. 2020. "Nonlinear Vibration of a Pre-Stressed Water-Filled Single-Walled Carbon Nanotube Using Shell Model" Nanomaterials 10, no. 5: 974. https://doi.org/10.3390/nano10050974





