Purcell Effect and Beaming of Emission in Hybrid AlGaAs Nanowires with GaAs Quantum Dots
Abstract
:1. Introduction
2. Materials and Methods
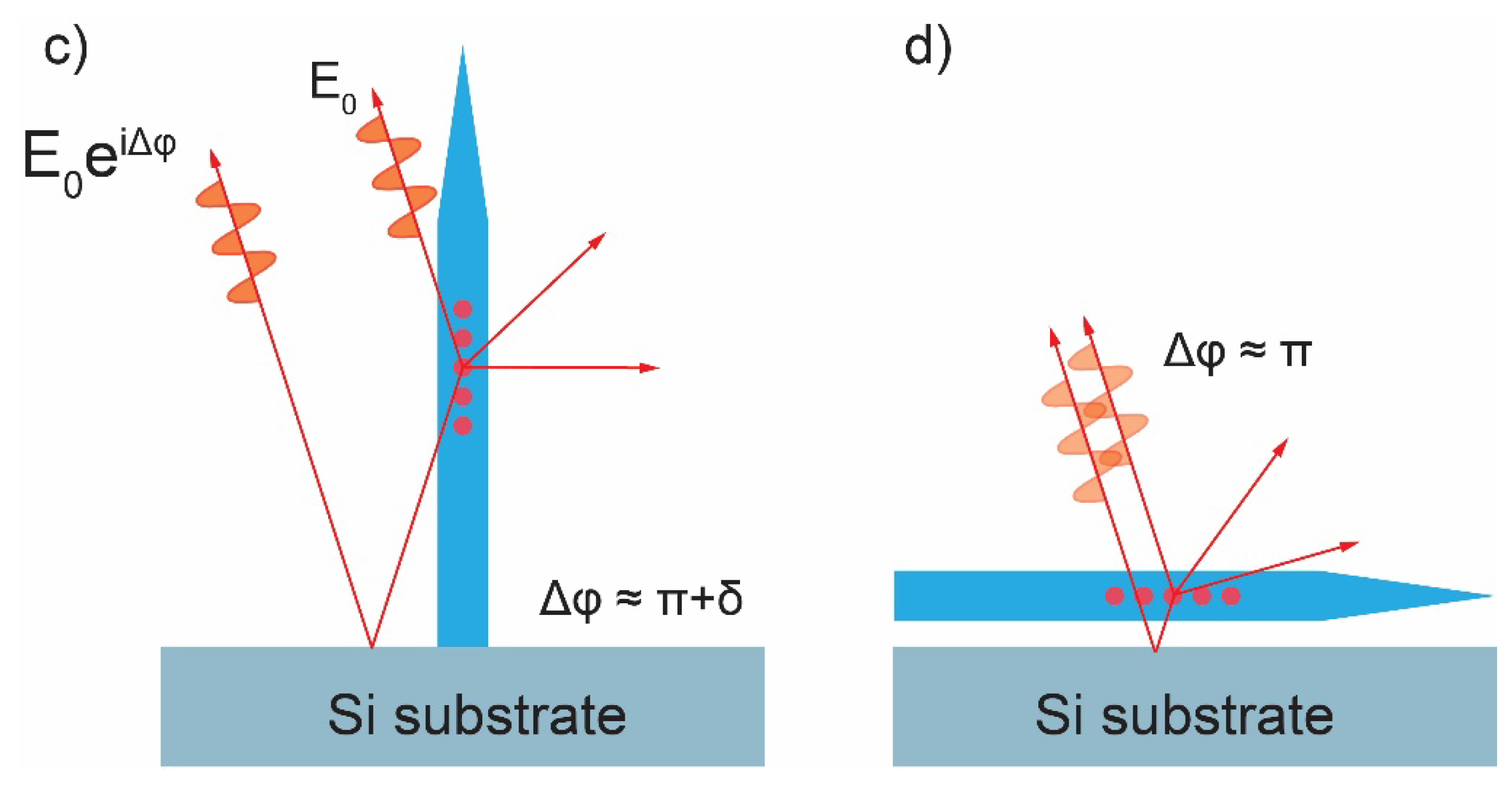
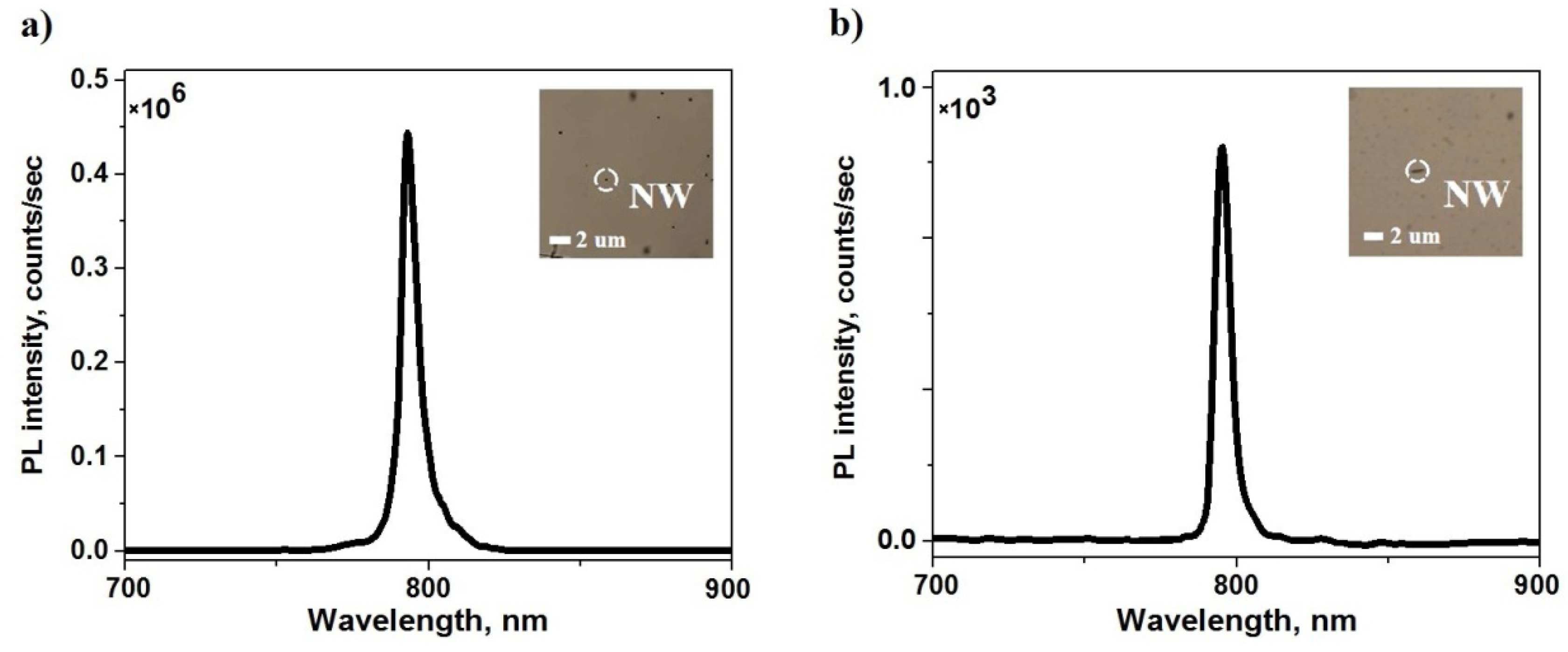
3. Results
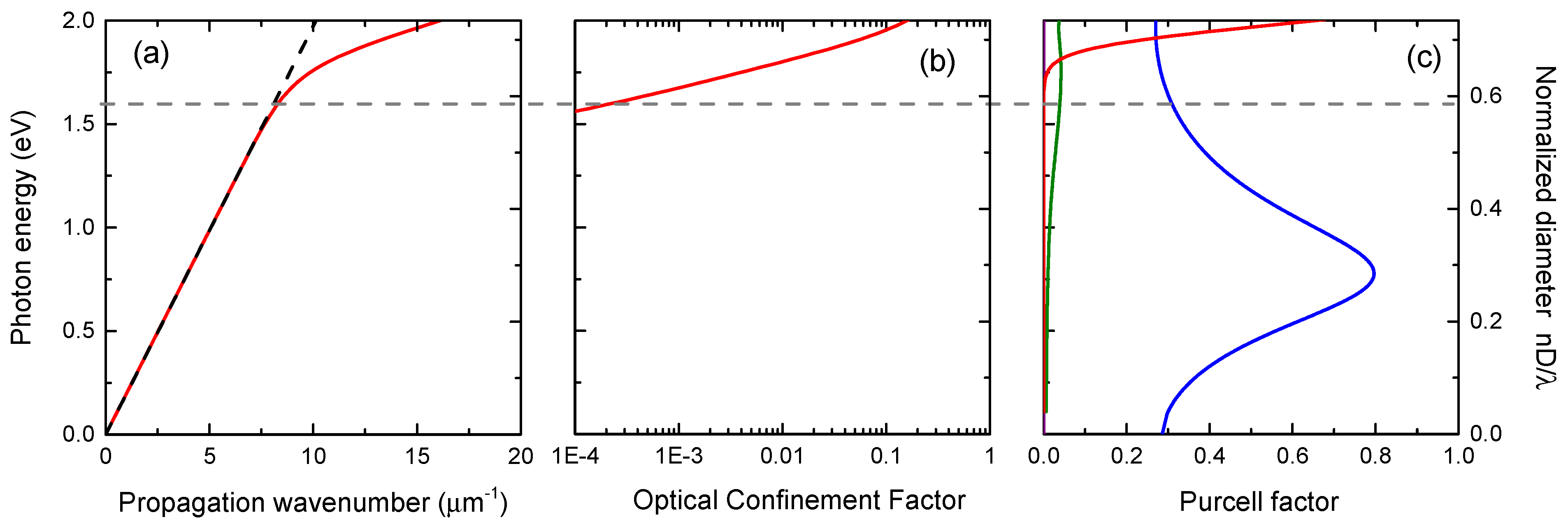
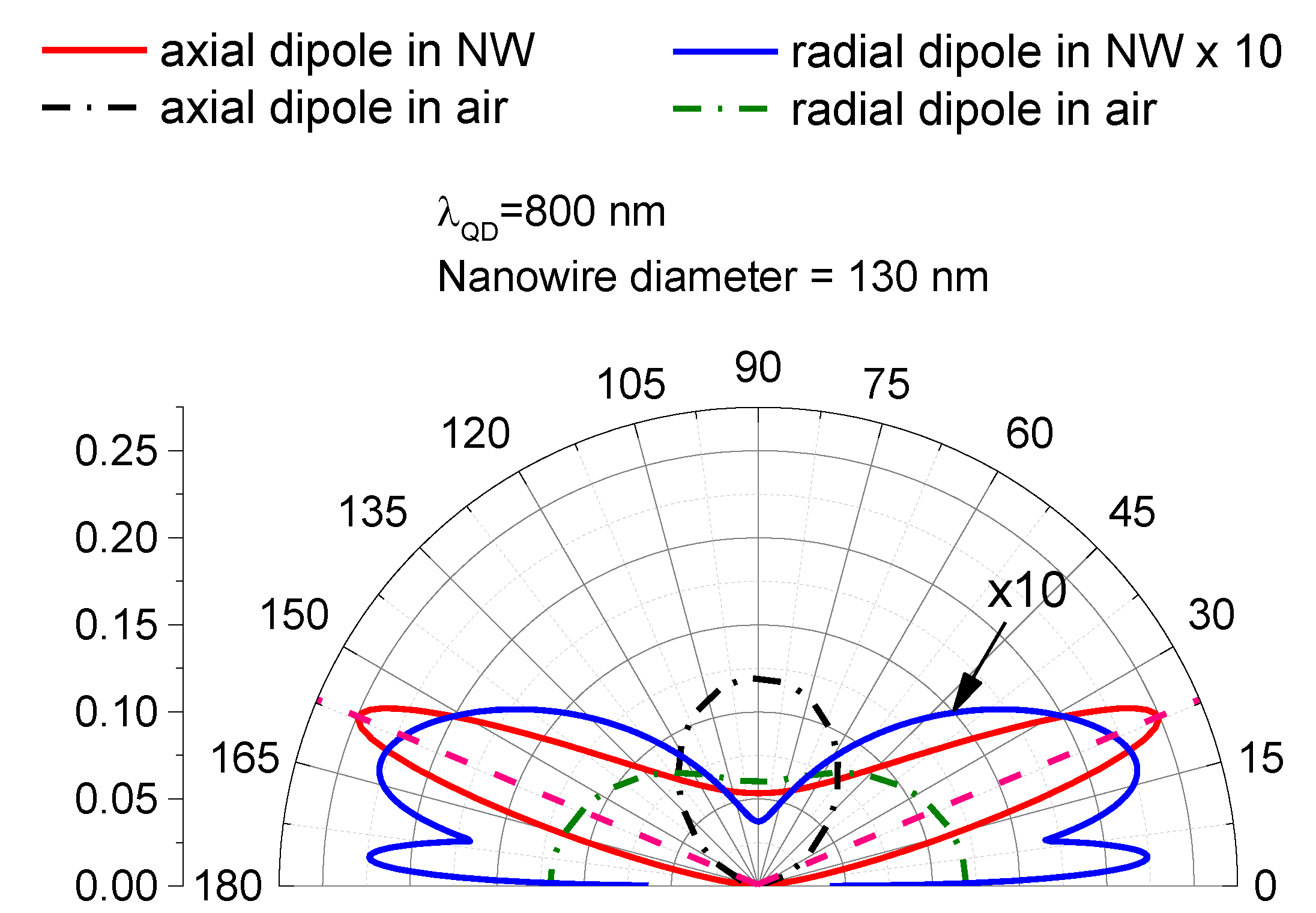
4. Theory
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cirlin, G.E.; Dubrovskii, V.G.; Samsonenko, Y.B.; Bouravleuv, A.D.; Durose, K.; Proskuryakov, Y.Y.; Mendes, B.; Bowen, L.; Kaliteevski, M.A.; Abram, R.A.; et al. Self-catalyzed, pure zincblende GaAs nanowires grown on Si(111) by molecular beam epitaxy. Phys. Rev. B. 2010, 82, 035302. [Google Scholar] [CrossRef] [Green Version]
- Kats, V.N.; Kochereshko, V.P.; Platonov, A.V.; Chizhova, T.V.; Cirlin, G.E.; Bouravleuv, A.D.; Samsonenko, Y.B.; Soshnikov, I.P.; Ubyivovk, E.V.; Bleuse, J.; et al. Optical study of GaAs quantum dots embedded into AlGaAs nanowires. Semicond. Sci. Technol. 2011, 27, 015009. [Google Scholar] [CrossRef] [Green Version]
- Leanrdo, L.; Hastrup, J.; Reznik, R.; Cirlin, G.; Akopian, N. Resonant excitation of nanowire quantum dots. NPJ Quantum Inf. 2020, 6, 93. [Google Scholar] [CrossRef]
- Leandro, L.; Gunnarsson, C.P.; Reznik, R.; Jöns, K.D.; Shtrom, I.V.; Khrebtov, A.I.; Kasama, T.; Zwiller, V.; Cirlin, G.E.; Akopian, N. Nanowire quantum dots tuned to atomic resonances. Nano Lett. 2018, 18, 7217–7221. [Google Scholar] [CrossRef] [Green Version]
- Heinrich, J.; Huggenberger, A.; Heindel, T.; Reitzenstein, S.; Höfling, S.; Worschech, L.; Forchel, A. Single photon emission from positioned GaAs/AlGaAs photonic nanowires. Appl. Phys. Lett. 2010, 96, 211117. [Google Scholar] [CrossRef]
- Bleuse, J.; Claudon, J.; Creasey, M.; Malik, N.S.; Gérard, J.-M.; Maksymov, I.; Hugonin, J.-P.; Lalanne, P. Inhibition, Enhancement, and Control of Spontaneous Emission in Photonic Nanowires. Phys. Rev. Lett. 2011, 10, 103601. [Google Scholar] [CrossRef] [PubMed]
- Bulgarini, G.; Reimer, M.E.; Zehender, T.; Hocevar, M.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Zwiller, V. Spontaneous emission control of single quantum dots in bottom-up nanowire waveguides. Appl. Phys. Lett. 2012, 100, 121106. [Google Scholar] [CrossRef]
- Claudon, J.; Gregersen, N.; Lalanne, P.; Gérard, J.-M. Harnessing Light with Photonic Nanowires: Fundamentals and Applications to Quantum Optics. ChemPhysChem 2013, 14, 2393–2402. [Google Scholar] [CrossRef]
- Claudon, J.; Bleuse, J.; Malik, N.S.; Bazin, M.; Jaffrennou, P.; Gregersen, N.; Sauvan, C.; Lalanne, P.; Gérard, J.-M. A highly efficient single-photon source based on a quantum dot in a photonic nanowire. Nat. Photonics 2010, 4, 174–177. [Google Scholar] [CrossRef]
- Jaffal, A.; Redjem, W.; Regreny, P.; Nguyen, H.-S.; Cueff, S.; Letartre, X.; Chauvin, N. InAs quantum dot in a needlelike tapered InP nanowire: A telecom band single photon source monolithically grown on silicon. Nanoscale 2019, 11, 21847–21855. [Google Scholar] [CrossRef] [Green Version]
- Gregersen, N.; Nielsen, T.R.; Claudon, J.; Gérard, J.-M.; Mørk, J. Controlling the emission profile of a nanowire with a conical taper. Opt. Lett. 2008, 33, 1693–1695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stepanov, P.; Delga, A.; Gregersen, N.; Peinke, E.; Munsch, M.; Teissier, J.; Mørk, J.; Richard, M.; Bleuse, J.; Gérard, J.-M.; et al. Highly directive and Gaussian far-field emission from “giant” photonic trumpets. Appl. Phys. Lett. 2015, 107, 141106. [Google Scholar] [CrossRef] [Green Version]
- Bulgarini, G.; Reimer, M.E.; Bouwes Bavinck, M.; Jöns, K.D.; Dalacu, D.; Poole, P.J.; Bakkers, E.P.A.M.; Zwiller, V. Nanowire Waveguides Launching Single Photons in a Gaussian Mode for Ideal Fiber Coupling. Nano Lett. 2014, 14, 4102–4106. [Google Scholar] [CrossRef] [Green Version]
- Cortez, S.; Krebs, O.; Voisin, P.; Gérard, J.M. Polarization of the interband optical dipole in InAs/GaAs self-organized quantum dots. Phys. Rev. B 2001, 63, 233306. [Google Scholar] [CrossRef]
- Ivchenko, E.L.; Pikus, G.E. Superlattices and Other Heterostructures: Symmetry and Optical Phenomena, 2nd ed.; Springer Science & Business Media: Berlin, Germany, 1997. [Google Scholar] [CrossRef]
- Ivchenko, E.L. Optical Spectroscopy of Semiconductor Nanostructures; Alpha Science: Harrow, UK, 2005; Available online: https://scholar.google.com/scholar_lookup?title=Optical%20Spectroscopy%20of%20Semiconductor%20Nanostructures&author=E.L..%20Ivchenko&publication_year=2005 (accessed on 5 July 2021).
- Heiss, M.; Fontana, Y.; Gustafsson, A.; Wüst, G.; Magen, C.; O’regan, D.D.; Luo, J.W.; Ketterer, B.; Conesa-Boj, S.; Kuhlmann, A.V.; et al. Self-assembled quantum dots in a nanowire system for quantum photonics. Nat. Mater. 2013, 12, 439–444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeannin, M.; Cremel, T.; Häyrynen, T.; Gregersen, N.; Bellet-Amalric, E.; Nogues, G.; Kheng, K. Enhanced Photon Extraction from a Nanowire Quantum Dot Using a Bottom-Up Photonic Shell. Phys. Rev. Appl. 2017, 8, 054022. [Google Scholar] [CrossRef] [Green Version]
- Haffouz, S.; Zeuner, K.D.; Dalacu, D.; Poole, P.J.; Lapointe, J.; Poitras, D.; Mnaymneh, K.; Wu, X.; Couillard, M.; Korkusinski, M.; et al. Bright Single InAsP Quantum Dots at Telecom Wavelengths in Position-Controlled InP Nanowires: The Role of the Photonic Waveguide. Nano Lett. 2018, 18, 3047–3052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Korkusinski, M.; Hawrylak, P. Atomistic theory of emission from dark excitons in self-assembled quantum dots. Phys. Rev. B 2013, 87, 115310. [Google Scholar] [CrossRef]
- Niquet, Y.M.; Mojica, D.C. Quantum dots and tunnel barriers in InAs∕InP nanowire heterostructures: Electronic and optical properties. Phys. Rev. B 2008, 77, 115316. [Google Scholar] [CrossRef] [Green Version]
- Zieliński, M. Fine structure of light-hole excitons in nanowire quantum dots. Phys. Rev. B 2013, 88, 115424. [Google Scholar] [CrossRef]
- Huo, Y.H.; Witek, B.J.; Kumar, S.; Cardenas, J.R.; Zhang, J.X.; Akopian, N.; Singh, R.; Zallo, E.; Grifone, R.; Kriegner, D.; et al. A light-hole exciton in a quantum dot. Nat. Phys. 2014, 10, 46–51. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Shtrom, I.V.; Reznik, R.R.; Samsonenko, Y.B.; Khrebtov, A.I.; Soshnikov, I.P.; Rouvimov, S.; Akopian, N.; Kasama, T.; Cirlin, G.E. Origin of spontaneous core–shell AlGaAs nanowires grown by molecular beam epitaxy. Cryst. Growth Des. 2016, 16, 7251–7255. [Google Scholar] [CrossRef]
- Leandro, L.; Reznik, R.; Clement, J.D.; Repän, J.; Reynolds, M.; Ubyivovk, E.V.; Shtrom, I.V.; Cirlin, G.; Akopian, N. Wurtzite AlGaAs Nanowires. Sci. Rep. 2020, 10, 735. [Google Scholar] [CrossRef] [PubMed] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reznik, R.R.; Cirlin, G.E.; Kotlyar, K.P.; Ilkiv, I.V.; Akopian, N.; Leandro, L.; Nikolaev, V.V.; Belonovski, A.V.; Kaliteevski, M.A. Purcell Effect and Beaming of Emission in Hybrid AlGaAs Nanowires with GaAs Quantum Dots. Nanomaterials 2021, 11, 2894. https://doi.org/10.3390/nano11112894
Reznik RR, Cirlin GE, Kotlyar KP, Ilkiv IV, Akopian N, Leandro L, Nikolaev VV, Belonovski AV, Kaliteevski MA. Purcell Effect and Beaming of Emission in Hybrid AlGaAs Nanowires with GaAs Quantum Dots. Nanomaterials. 2021; 11(11):2894. https://doi.org/10.3390/nano11112894
Chicago/Turabian StyleReznik, Rodion R., George E. Cirlin, Konstantin P. Kotlyar, Igor V. Ilkiv, Nika Akopian, Lorenzo Leandro, Valentin V. Nikolaev, Alexey V. Belonovski, and Mikhail A. Kaliteevski. 2021. "Purcell Effect and Beaming of Emission in Hybrid AlGaAs Nanowires with GaAs Quantum Dots" Nanomaterials 11, no. 11: 2894. https://doi.org/10.3390/nano11112894
APA StyleReznik, R. R., Cirlin, G. E., Kotlyar, K. P., Ilkiv, I. V., Akopian, N., Leandro, L., Nikolaev, V. V., Belonovski, A. V., & Kaliteevski, M. A. (2021). Purcell Effect and Beaming of Emission in Hybrid AlGaAs Nanowires with GaAs Quantum Dots. Nanomaterials, 11(11), 2894. https://doi.org/10.3390/nano11112894






