A Generalized Approach for Evaluating the Mechanical Properties of Polymer Nanocomposites Reinforced with Spherical Fillers
Abstract
:1. Introduction
2. Generalized Approach
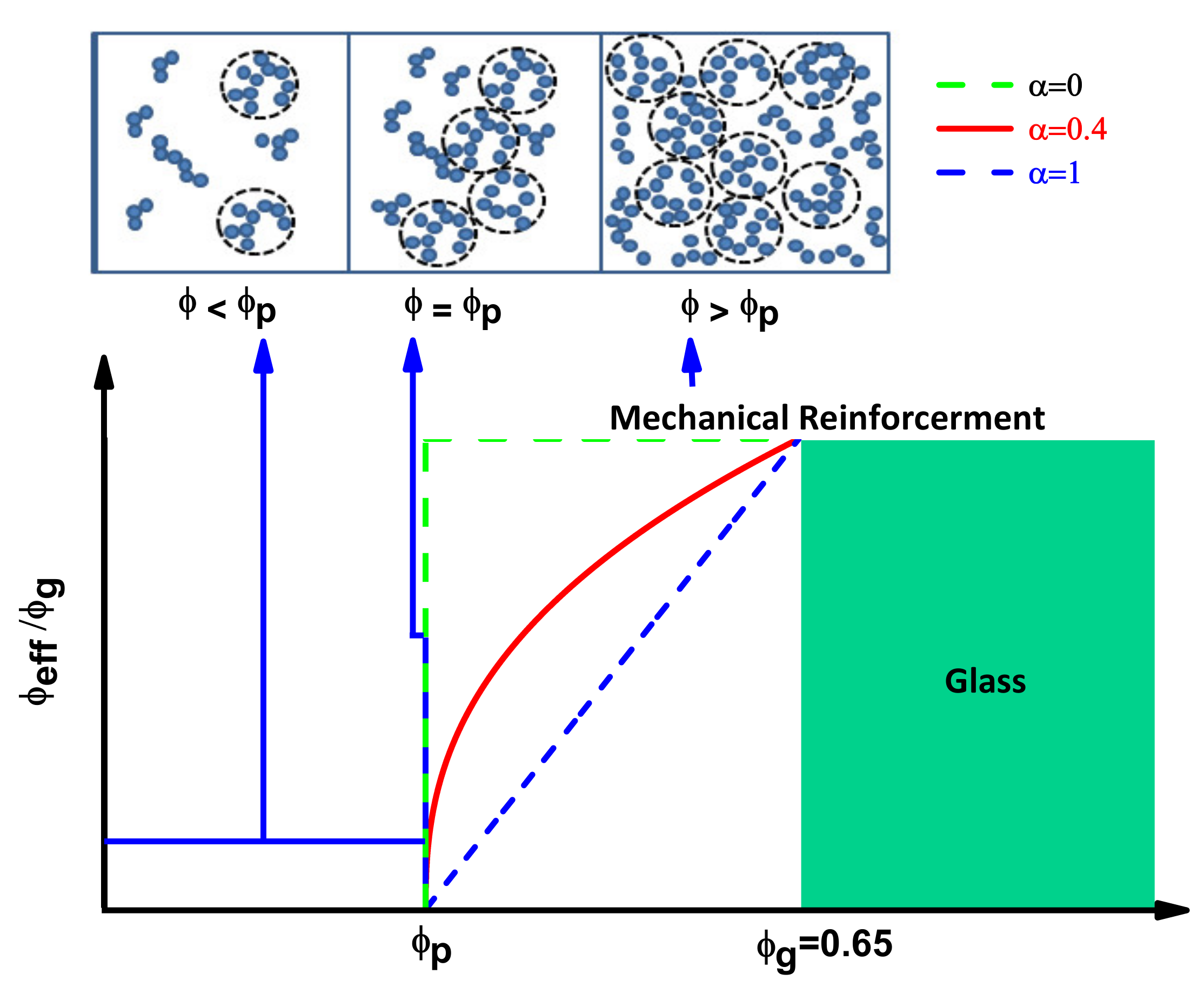
2.1. Effective Particles Contributing to the Mechanical Reinforcement
2.2. Percolation Threshold
2.3. Critical Percolation Exponent
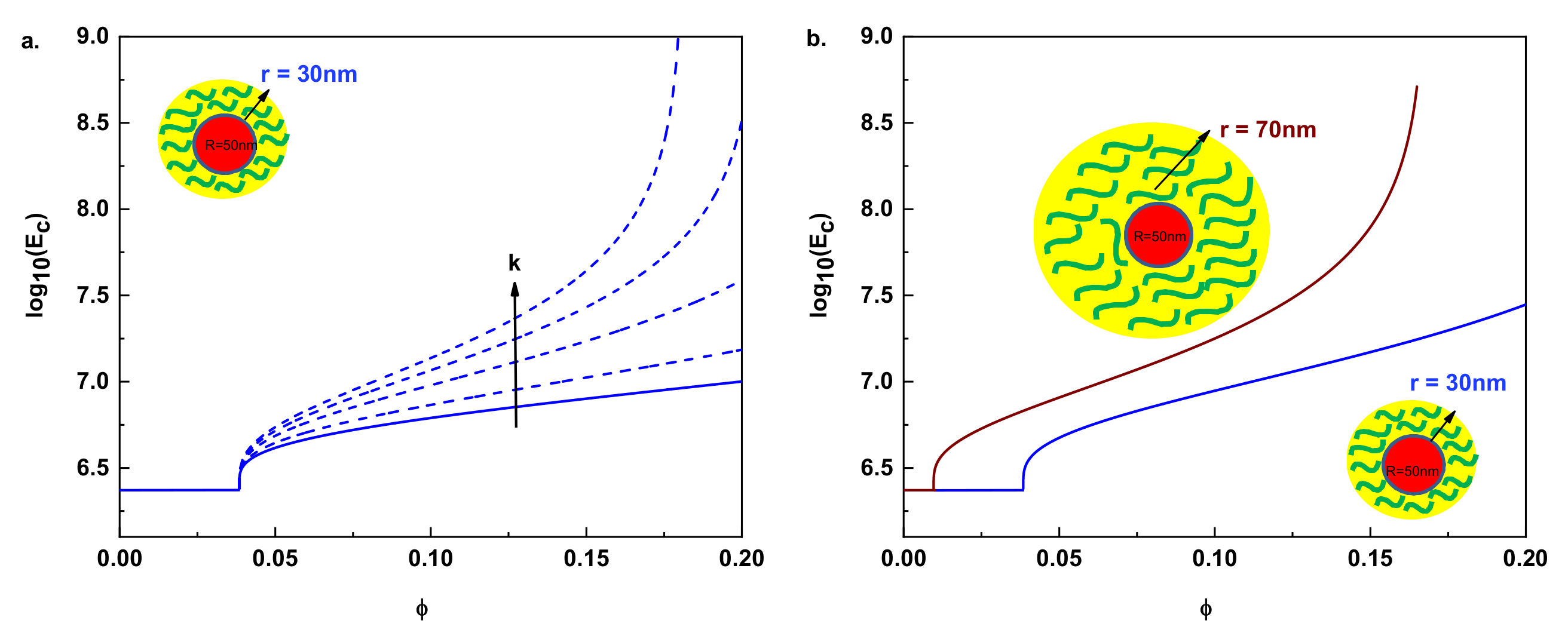
2.4. Tensile Modulus
3. Model Validation and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ji, X.L.; Jing, J.K.; Jiang, W.; Jiang, B.Z. Tensile modulus of polymer nanocomposites. Polym. Eng. Sci. 2002, 42, 983–993. [Google Scholar] [CrossRef]
- Schilling, T.; Miller, M.A.; Van der Schoot, P. Percolation in suspensions of hard nanoparticles: From spheres to needles. EPL 2015, 111, 56004. [Google Scholar] [CrossRef]
- Tjong, S.C.; Mai, Y.-W. Physical Properties and Applications of Polymer Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Mittal, V. Polymer Nanotubes Nanocomposites: Synthesis, Properties and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Mohanty, S.; Nayak, S.K.; Kaith, B.; Kalia, S. Polymer Nanocomposites Based On Inorganic and Organic Nanomaterials; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wypych, G. Handbook of Fillers; ChemTec Pub.: Toronto, TN, Canda, 2010; Volume 92. [Google Scholar]
- Rothon, R. Mineral Fillers in Thermoplastics I. In Mineral Fillers in Thermoplastics: Filler Manufacture and Characterisation; Springer: Berlin, Germany, 1999; pp. 67–107. [Google Scholar]
- Rothon, R. Mineral fillers in thermoplastics: Filler manufacture. J. Adhes. 1997, 64, 87–109. [Google Scholar]
- Mark, J.E.; Erman, B.; Roland, M. The Science and Technology of Rubber; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Nielsen, L.E.; Landel, R. Mechanical Properties of Polymers and Composites; Marcel Dekker Inc.: New York, NY, USA, 1994. [Google Scholar]
- Sapkota, J.; Gooneie, A.; Shirole, A.; Martinez Garcia, J.C. A refined model for the mechanical properties of polymer composites with nanorods having different length distributions. J. Appl. Polym. Sci. 2017, 134, 45279. [Google Scholar] [CrossRef]
- Sapkota, J.; Martinez Garcia, J.C.; Lattuada, M. Reinterpretation of the mechanical reinforcement of polymer nanocomposites reinforced with cellulose nanorods. J. Appl. Polym. Sci. 2017, 134, 45254. [Google Scholar] [CrossRef]
- Payne, A. A note on the existence of a yield point in the dynamic modulus of loaded vulcanizates. J. Appl. Polym. Sci. 1960, 3, 127. [Google Scholar] [CrossRef]
- Stöckelhuber, K.W.; Das, A.; Klüppel, M. Designing of elastomer Nanocomposites: From Theory to Applications; Springer: Berlin, Germany, 2017. [Google Scholar]
- Heinrich, G.; Klüppel, M. Recent advances in the theory of filler networking in elastomers. In Filled Elastomers Drug Delivery Systems; Springer: Berlin, Germany, 2002; pp. 1–44. [Google Scholar]
- Heinrich, G.; Klüppel, M.; Vilgis, T.A. Reinforcement of elastomers. Curr. Opin. Solid State Mater. Sci. 2002, 6, 195–203. [Google Scholar] [CrossRef]
- Ahmed, S.; Jones, F. A review of particulate reinforcement theories for polymer composites. J. Mater. Sci. 1990, 25, 4933–4942. [Google Scholar] [CrossRef]
- Einstein, A. A new determination of molecular dimensions. Ann. Phys. 1906, 19, 289–306. [Google Scholar] [CrossRef]
- Smallwood, H.M. Limiting law of the reinforcement of rubber. J. Appl. Phys. 1944, 15, 758–766. [Google Scholar] [CrossRef]
- Dewey, J.M. Theory of filler reìnforcement. J. Appl. Phys. 1945, 16, 55. [Google Scholar] [CrossRef]
- Kerner, E. The elastic and thermo-elastic properties of composite media. Proc. Phys. Soc. Sect. B 1956, 69, 808. [Google Scholar] [CrossRef]
- Halpin, J. Stiffness and expansion estimates for oriented short fiber composites. J. Compos. Mater. 1969, 3, 732–734. [Google Scholar] [CrossRef]
- Halpin, J.C. Effects of Environmental Factors on Composite Materials; Air Force Materials Lab Wright-Patterson AFB OH: Dyton, OH, USA, 1969. [Google Scholar]
- Nielsen, L.E. Generalized equation for the elastic moduli of composite materials. J. Appl. Phys. 1970, 41, 4626–4627. [Google Scholar] [CrossRef]
- Mooney, M. The viscosity of a concentrated suspension of spherical particles. J. Colloid Sci. 1951, 6, 162–170. [Google Scholar] [CrossRef]
- Christensen, R.; Lo, K. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Counto, U.J. The effect of the elastic modulus of the aggregate on the elastic modulus, creep and creep recovery of concrete. Mag. Concr. Res. 1964, 16, 129–138. [Google Scholar] [CrossRef]
- Verbeek, C. The influence of interfacial adhesion, particle size and size distribution on the predicted mechanical properties of particulate thermoplastic composites. Mater. Lett. 2003, 57, 1919–1924. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites. Compos. Part B Eng. 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Ren, N.; Matta, M.E.; Martinez, H.; Walton, K.L.; Munro, J.C.; Schneiderman, D.K.; Hillmyer, M.A. Filler-Reinforced Elastomers Based on Functional Polyolefin Prepolymers. Ind. Eng. Chem. Res. 2016, 55, 6106–6112. [Google Scholar] [CrossRef]
- Edwards, D. Polymer-filler interactions in rubber reinforcement. J. Mater. Sci. 1990, 25, 4175–4185. [Google Scholar] [CrossRef]
- Wang, M.-J. Effect of polymer-filler and filler-filler interactions on dynamic properties of filled vulcanizates. Rubber Chem. Technol. 1998, 71, 520–589. [Google Scholar] [CrossRef]
- Berriot, J.; Lequeux, F.; Monnerie, L.; Montes, H.; Long, D.; Sotta, P. Filler–elastomer interaction in model filled rubbers, a 1H NMR study. J. Non Cryst. Solids 2002, 307, 719–724. [Google Scholar] [CrossRef]
- Berriot, J.; Montes, H.; Lequeux, F.; Long, D.; Sotta, P. Evidence for the shift of the glass transition near the particles in silica-filled elastomers. Macromolecules 2002, 35, 9756–9762. [Google Scholar] [CrossRef]
- Berriot, J.; Montes, H.; Lequeux, F.; Long, D.; Sotta, P. Gradient of glass transition temperature in filled elastomers. EPL 2003, 64, 50. [Google Scholar] [CrossRef]
- Papon, A.; Saalwächter, K.; Schäler, K.; Guy, L.; Lequeux, F.; Montes, H. Low-field NMR investigations of nanocomposites: Polymer dynamics and network effects. Macromolecules 2011, 44, 913–922. [Google Scholar] [CrossRef]
- Papon, A.; Montes, H.; Hanafi, M.; Lequeux, F.; Guy, L.; Saalwächter, K. Glass-transition temperature gradient in nanocomposites: Evidence from nuclear magnetic resonance and differential scanning calorimetry. Phys. Rev. Lett. 2012, 108, 065702. [Google Scholar] [CrossRef]
- Struik, L. The mechanical and physical ageing of semicrystalline polymers: 1. Polymer 1987, 28, 1521–1533. [Google Scholar] [CrossRef]
- Struik, L. The mechanical behaviour and physical ageing of semicrystalline polymers: 2. Polymer 1987, 28, 1534–1542. [Google Scholar] [CrossRef]
- Qu, M.; Deng, F.; Kalkhoran, S.M.; Gouldstone, A.; Robisson, A.; Van Vliet, K.J. Nanoscale visualization and multiscale mechanical implications of bound rubber interphases in rubber–carbon black nanocomposites. Soft Matter 2011, 7, 1066–1077. [Google Scholar] [CrossRef]
- Lewis, T.; Nielsen, L. Dynamic mechanical properties of particulate-filled composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Vollenber, P.H.; Heikens, D. Influence of Particle Dimension on Young’s Modulus and Stress Strain Behaviour of Filled Polymers. In Proceedings of the Filler ‘86, UK; 1986. [Google Scholar]
- Takayanagi, M.; Ogata, T.; Morikawa, M.; Kai, T. Polymer composites of rigid and flexible molecules: System of wholly aromatic and aliphatic polyamides. J. Macromol. Sci. Part B Phys. 1980, 17, 591–615. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V.; Khalatur, P.G.; Khokhlov, A.R. Study of the mechanisms of filler reinforcement in elastomer nanocomposites. Macromolecules 2014, 47, 5400–5408. [Google Scholar] [CrossRef]
- Gusev, A.A. Micromechanical mechanism of reinforcement and losses in filled rubbers. Macromolecules 2006, 39, 5960–5962. [Google Scholar] [CrossRef]
- Lutz, M.P.; Zimmerman, R.W. Effect of an inhomogeneous interphase zone on the bulk modulus and conductivity of a particulate composite. Int. J. Solids Struct. 2005, 42, 429–437. [Google Scholar] [CrossRef]
- Ding, K.; Weng, G. The influence of moduli slope of a linearly graded matrix on the bulk moduli of some particle-and fiber-reinforced composites. J. Elast. 1998, 53, 1–22. [Google Scholar] [CrossRef]
- Herve, E.; Zaoui, A. N-layered inclusion-based micromechanical modelling. Int. J. Eng. Sci. 1993, 31, 1–10. [Google Scholar] [CrossRef]
- Nie, S.; Basaran, C. A micromechanical model for effective elastic properties of particulate composites with imperfect interfacial bonds. Int. J. Solids Struct. 2005, 42, 4179–4191. [Google Scholar] [CrossRef]
- Deng, F.; Van Vliet, K.J. Prediction of elastic properties for polymer–particle nanocomposites exhibiting an interphase. Nanotechnology 2011, 22, 165703. [Google Scholar] [CrossRef]
- Deng, F.; Zheng, Q.-S. An analytical model of effective electrical conductivity of carbon nanotube composites. Appl. Phys. Lett. 2008, 92, 071902. [Google Scholar] [CrossRef]
- Deng, F.; Zheng, Q.-S.; Wang, L.-F.; Nan, C.-W. Effects of anisotropy, aspect ratio, and nonstraightness of carbon nanotubes on thermal conductivity of carbon nanotube composites. Appl. Phys. Lett. 2007, 90, 021914. [Google Scholar] [CrossRef]
- Zheng, Q.-S.; Du, D.-X. An explicit and universally applicable estimate for the effective properties of multiphase composites which accounts for inclusion distribution. J. Mech. and Phys. Solids 2001, 49, 2765–2788. [Google Scholar] [CrossRef]
- Lindsay, H.; Chaikin, P. Elastic properties of colloidal crystals and glasses. J. Chem. Phys. 1982, 76, 3774–3781. [Google Scholar] [CrossRef]
- Pusey, P.N.; Van Megen, W. Phase behaviour of concentrated suspensions of nearly hard colloidal spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Pusey, P.N.; van Megen, W. Observation of a glass transition in suspensions of spherical colloidal particles. Phys. Rev. Lett. 1987, 59, 2083. [Google Scholar] [CrossRef] [PubMed]
- Hunter, G.L.; Weeks, E.R. The physics of the colloidal glass transition. Rep. Prog. Phys. 2012, 75, 066501. [Google Scholar] [CrossRef] [PubMed]
- Ouali, N.; Cavaillé, J.; Perez, J. Elastic, viscoelastic and plastic behavior of multiphase polymer blends. Plast. Rubber Compos. Process. Appl. (UK) 1991, 16, 55–60. [Google Scholar]
- Kyrylyuk, A.V.; van der Schoot, P. Continuum percolation of carbon nanotubes in polymeric and colloidal media. Proc. Natl. Acad. Sci. USA 2008, 105, 8221–8226. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- De Gennes, P.-G.; Gennes, P.-G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Bauhofer, W.; Kovacs, J.Z. A review and analysis of electrical percolation in carbon nanotube polymer composites. Compos. Sci. Technol. 2009, 69, 1486–1498. [Google Scholar] [CrossRef]
- Nawaz, K.; Khan, U.; Ul-Haq, N.; May, P.; O’Neill, A.; Coleman, J.N. Observation of mechanical percolation in functionalized graphene oxide/elastomer composites. Carbon 2012, 50, 4489–4494. [Google Scholar] [CrossRef]
- Capadona, J.R.; Shanmuganathan, K.; Tyler, D.J.; Rowan, S.J.; Weder, C. Stimuli-responsive polymer nanocomposites inspired by the sea cucumber dermis. Science 2008, 319, 1370–1374. [Google Scholar] [CrossRef]
- Capadona, J.R.; Van Den Berg, O.; Capadona, L.A.; Schroeter, M.; Rowan, S.J.; Tyler, D.J.; Weder, C. A versatile approach for the processing of polymer nanocomposites with self-assembled nanofibre templates. Nat. Nanotechnol. 2007, 2, 765–769. [Google Scholar] [CrossRef]
- Sydsaeter, K.; Hammond, P.J. Mathematics for Economic Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Grüneisen, E. Theorie des festen Zustandes einatomiger Elemente. Ann. Phys. 1912, 344, 257–306. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drozd-Rzoska, A.; Martinez-Garcia, J. A universal description of ultraslow glass dynamics. Nat. Commun. 2013, 4, 1823. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drzozd-Rzoska, A.; Martinez-Garcia, J.; Mauro, J.C. Divergent dynamics and the Kauzmann temperature in glass forming systems. Sci. Rep. 2014, 4, 5160. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drozd-Rzoska, A.; Starzonek, S.; Mauro, J.C. Fragility and basic process energies in vitrifying systems. Sci. Rep. 2015, 5, 8314. [Google Scholar] [CrossRef]
- Kuo, M.; Tsai, C.; Huang, J.; Chen, M. PEEK composites reinforced by nano-sized SiO2 and Al2O3 particulates. Mater. Chem. Phys. 2005, 90, 185–195. [Google Scholar] [CrossRef]
- Sarwar, M.I.; Zulfiqar, S.; Ahmad, Z. Preparation and properties of polyamide–titania nanocomposites. J. Sol Gel Sci. Technol. 2007, 44, 41–46. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Su, Q.; Zheng, J. Use of unmodified SiO2 as nanofiller to improve mechanical properties of polymer-based nanocomposites. Compos. Sci. Technol. 2013, 89, 52–60. [Google Scholar] [CrossRef]


| Our Model | X. Ling Ji et al. Model [1] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Composite [ref.] | R (nm) | R (nm) | Em (GPa) | K = Ei/Em | Ef (GPa) | R (nm) | K = Ei/Em | Ef (GPa) | ||
| 1 | Polyolefin 1/CB [31] | 50 | 51 | 2.4 × 10−3 | 1.66 | 364 | 0.75 | 0.0117 | 59 | 2.76 | 579 |
| 2 | Polyolefin 1/fumed silica [31] | 7.5 | 8 | 2.4 × 10−3 | 1.43 | 4.3 | 0.63 | 0.0153 | 8 | 4.09 | 4.1 |
| 3 | PEEK 2/Al2O3 [72] | 15 | 15 | 3.9 | 4.37 | 19.2 | 0.74 | 14 | 7.22 | 15.8 | |
| 4 | PEEK 2/SiO2 [72] | 15 | 17 | 3.9 | 4.76 | 16 | 0.72 | 0.0141 | 15 | 7.72 | 17 |
| 5 | PTMHMTA 3/TiO2 [73] | 4.5 | 4 | 1.82 | 2.04 | 9 | 0.64 | 0.0212 | 4 | 2.22 | 24.9 |
| 6 | P(MMA-MTC) 4/SiO2 [74] | 10 | 23 | 1.91 | 2.35 | 428 | 0.72 | 0.0036 | 21 | 5.59 | 271 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez-Garcia, J.C.; Serraïma-Ferrer, A.; Lopeandía-Fernández, A.; Lattuada, M.; Sapkota, J.; Rodríguez-Viejo, J. A Generalized Approach for Evaluating the Mechanical Properties of Polymer Nanocomposites Reinforced with Spherical Fillers. Nanomaterials 2021, 11, 830. https://doi.org/10.3390/nano11040830
Martinez-Garcia JC, Serraïma-Ferrer A, Lopeandía-Fernández A, Lattuada M, Sapkota J, Rodríguez-Viejo J. A Generalized Approach for Evaluating the Mechanical Properties of Polymer Nanocomposites Reinforced with Spherical Fillers. Nanomaterials. 2021; 11(4):830. https://doi.org/10.3390/nano11040830
Chicago/Turabian StyleMartinez-Garcia, Julio Cesar, Alexandre Serraïma-Ferrer, Aitor Lopeandía-Fernández, Marco Lattuada, Janak Sapkota, and Javier Rodríguez-Viejo. 2021. "A Generalized Approach for Evaluating the Mechanical Properties of Polymer Nanocomposites Reinforced with Spherical Fillers" Nanomaterials 11, no. 4: 830. https://doi.org/10.3390/nano11040830
APA StyleMartinez-Garcia, J. C., Serraïma-Ferrer, A., Lopeandía-Fernández, A., Lattuada, M., Sapkota, J., & Rodríguez-Viejo, J. (2021). A Generalized Approach for Evaluating the Mechanical Properties of Polymer Nanocomposites Reinforced with Spherical Fillers. Nanomaterials, 11(4), 830. https://doi.org/10.3390/nano11040830






