Modeling and Simulations of Buongiorno’s Model for Nanofluid in a Microchannel with Electro-Osmotic Effects and an Exothermal Chemical Reaction
Abstract
1. Introduction
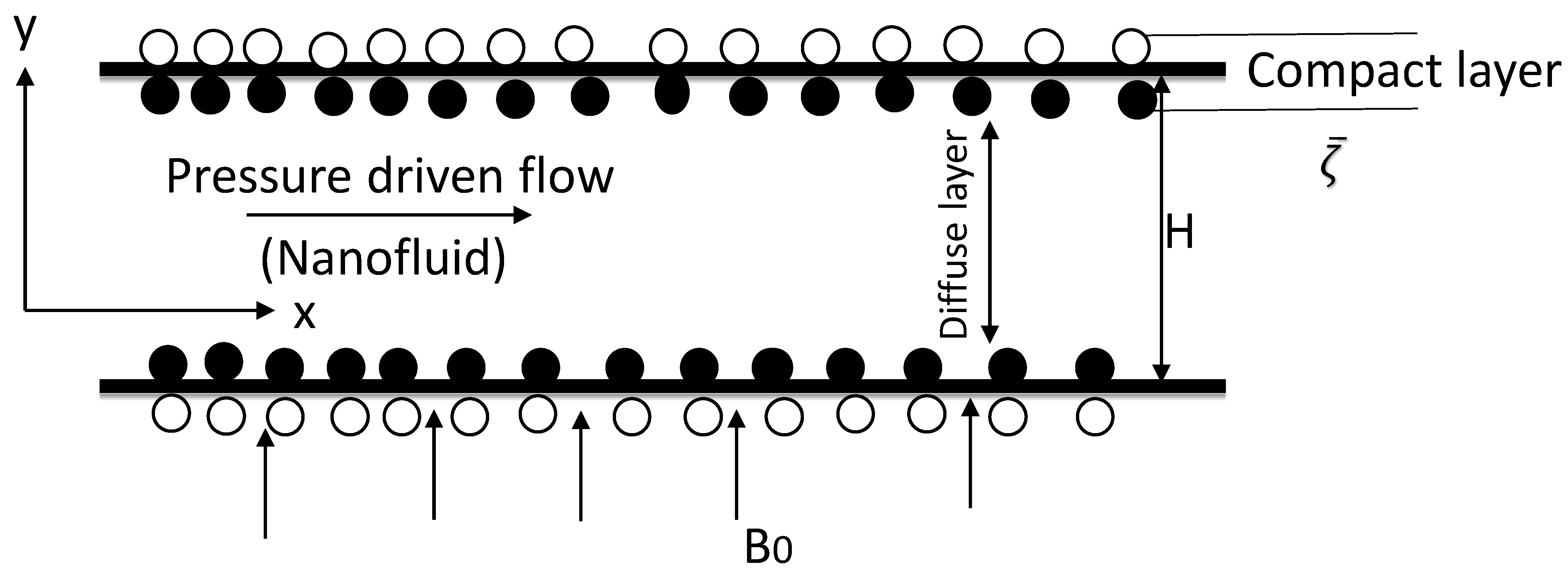
2. Governing Equations
Theory and Mathematical Modelling
- The electric force is due to the EDL and the electric field strength is directed towards x-axis (i.e., ) because the freely charged particles on surface of EDL will alter along the direction of fluid flow.
- The fluid flow in the microchannel is assumed parallel to the -axis. So only the velocity component of fluid along the -axis is non-zero.
- The induced magnetic field is neglected because the minimal magnetic Reynolds number () is considered. While the imposed magnetic field based on the Ohm’s law and these assumptions can be written as .
- The change in temperature and nanparticles volume fraction are kept constant along horizontal direction (i.e., ).
- The applied electric field is neglected and the fluid motion is pressure driven, that is, .
3. Results and Discussion
3.1. Solutions & Simulations
Numerical Procedure
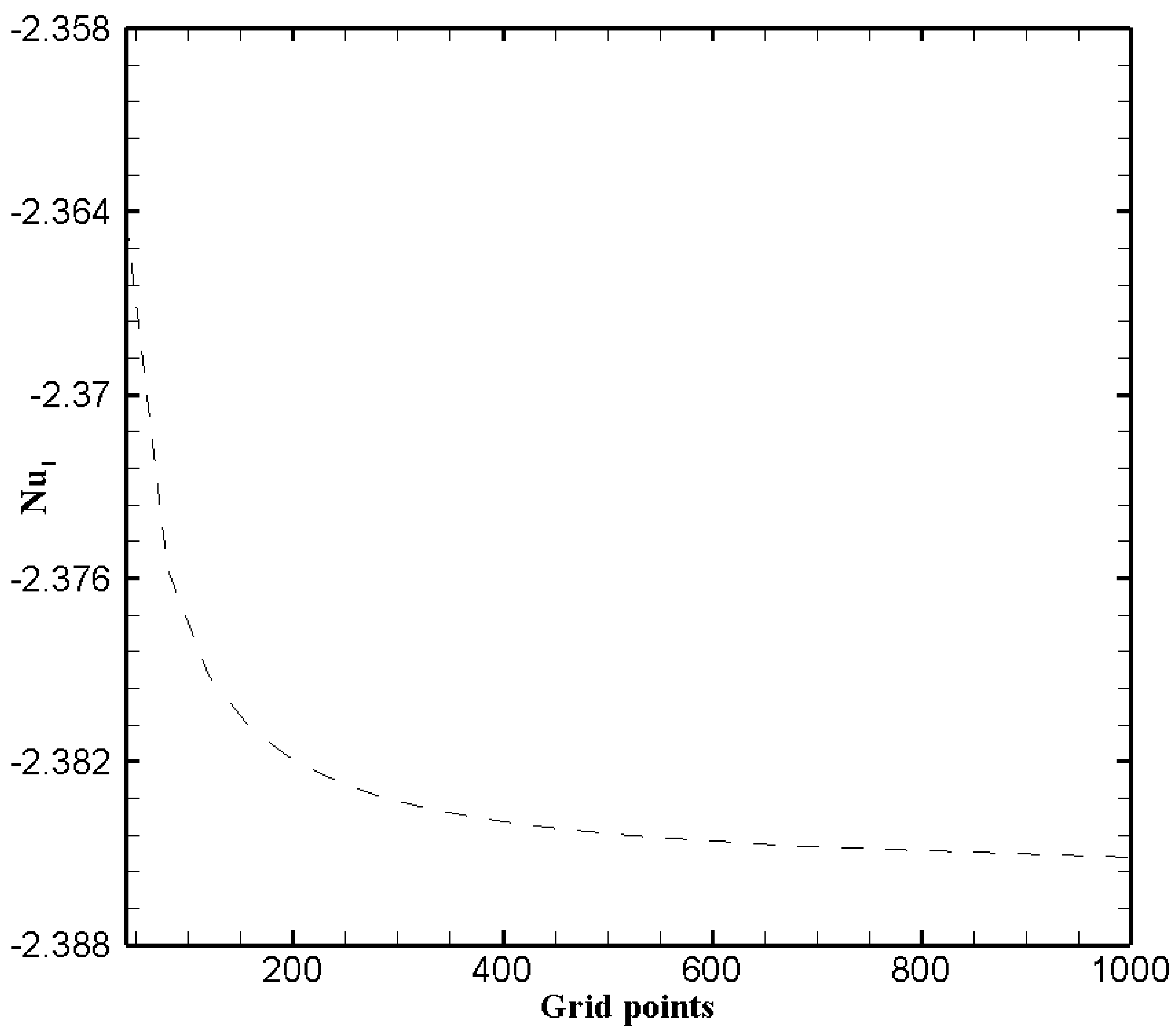
3.2. Grid Independence Test
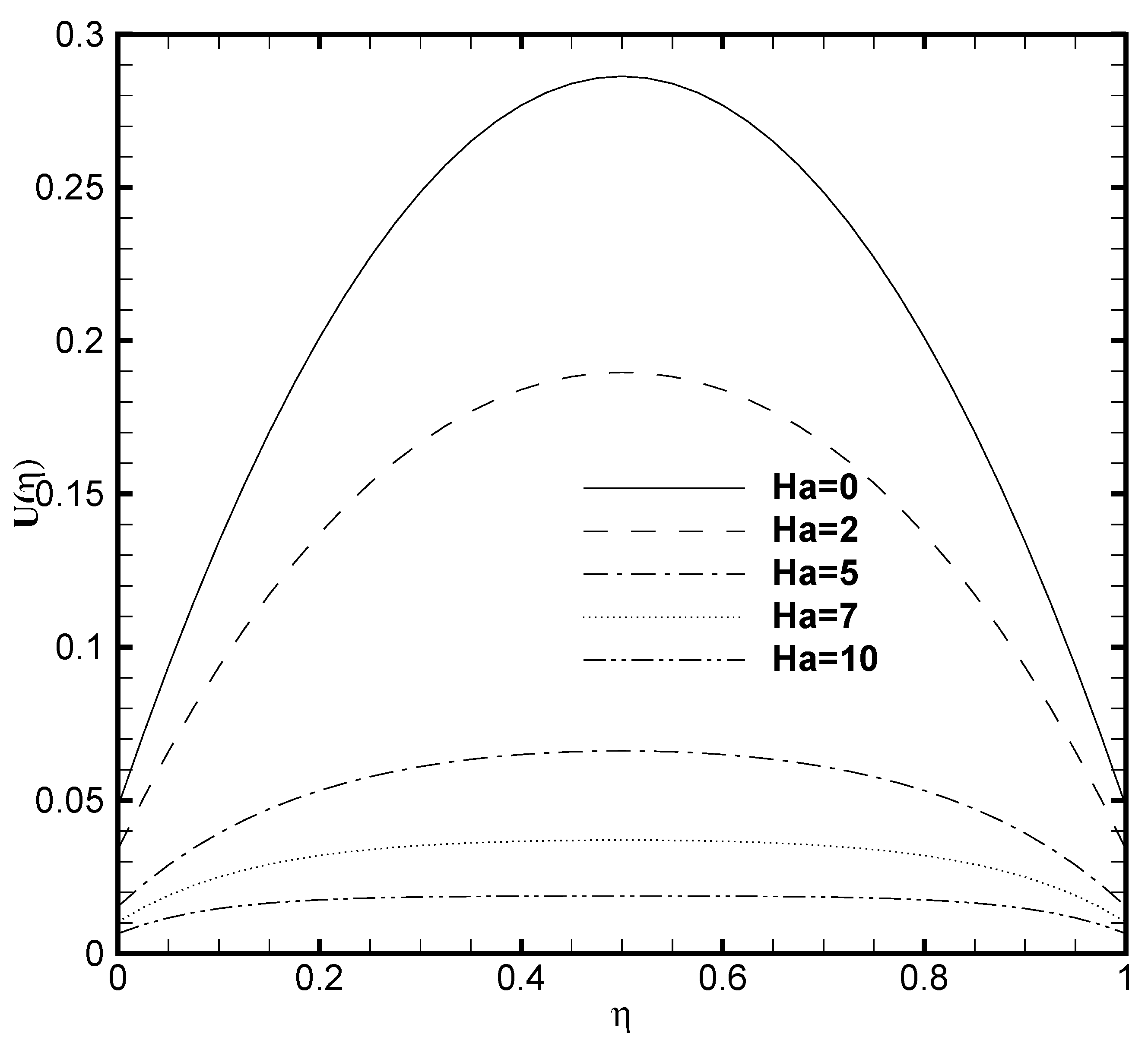
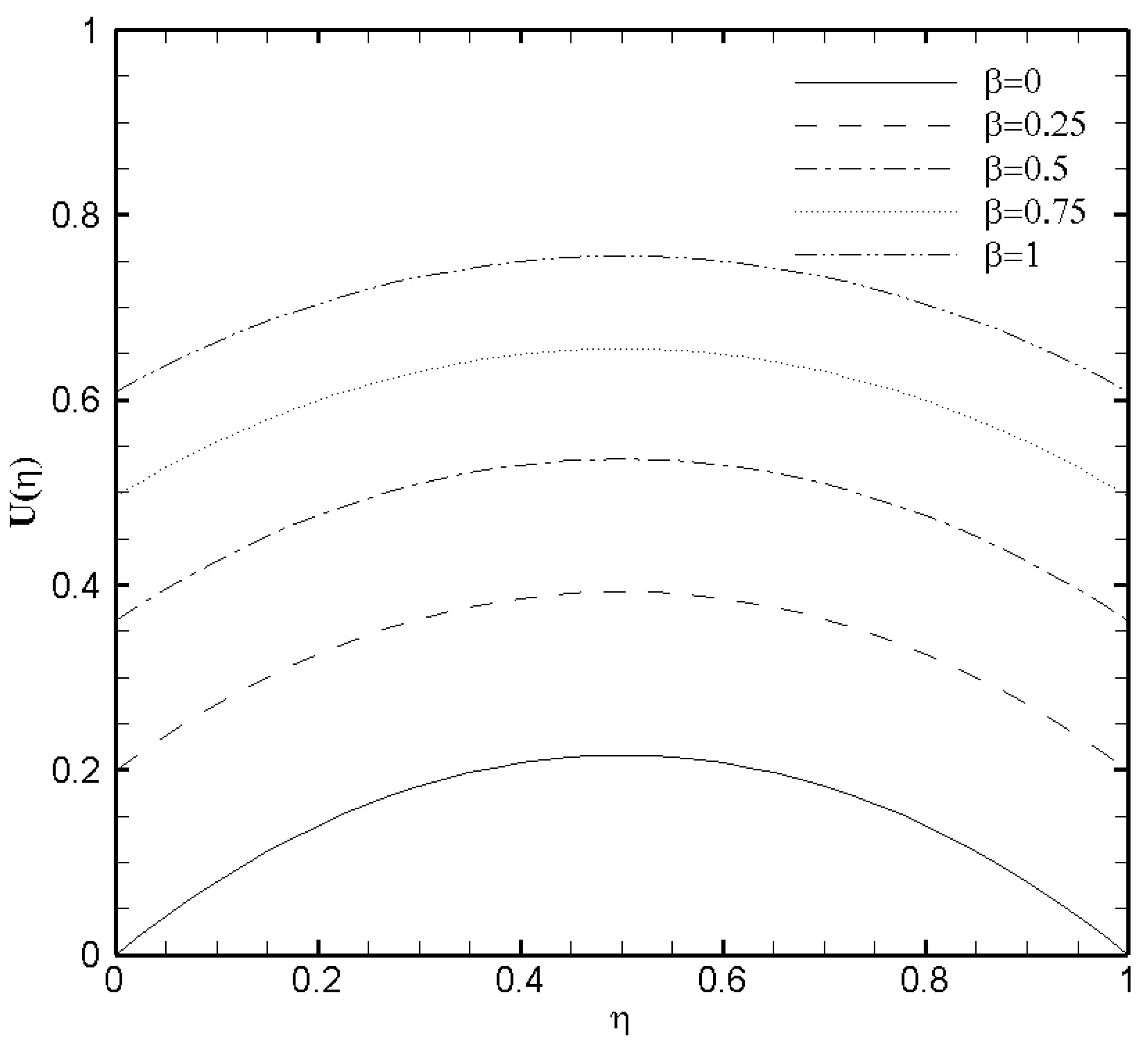
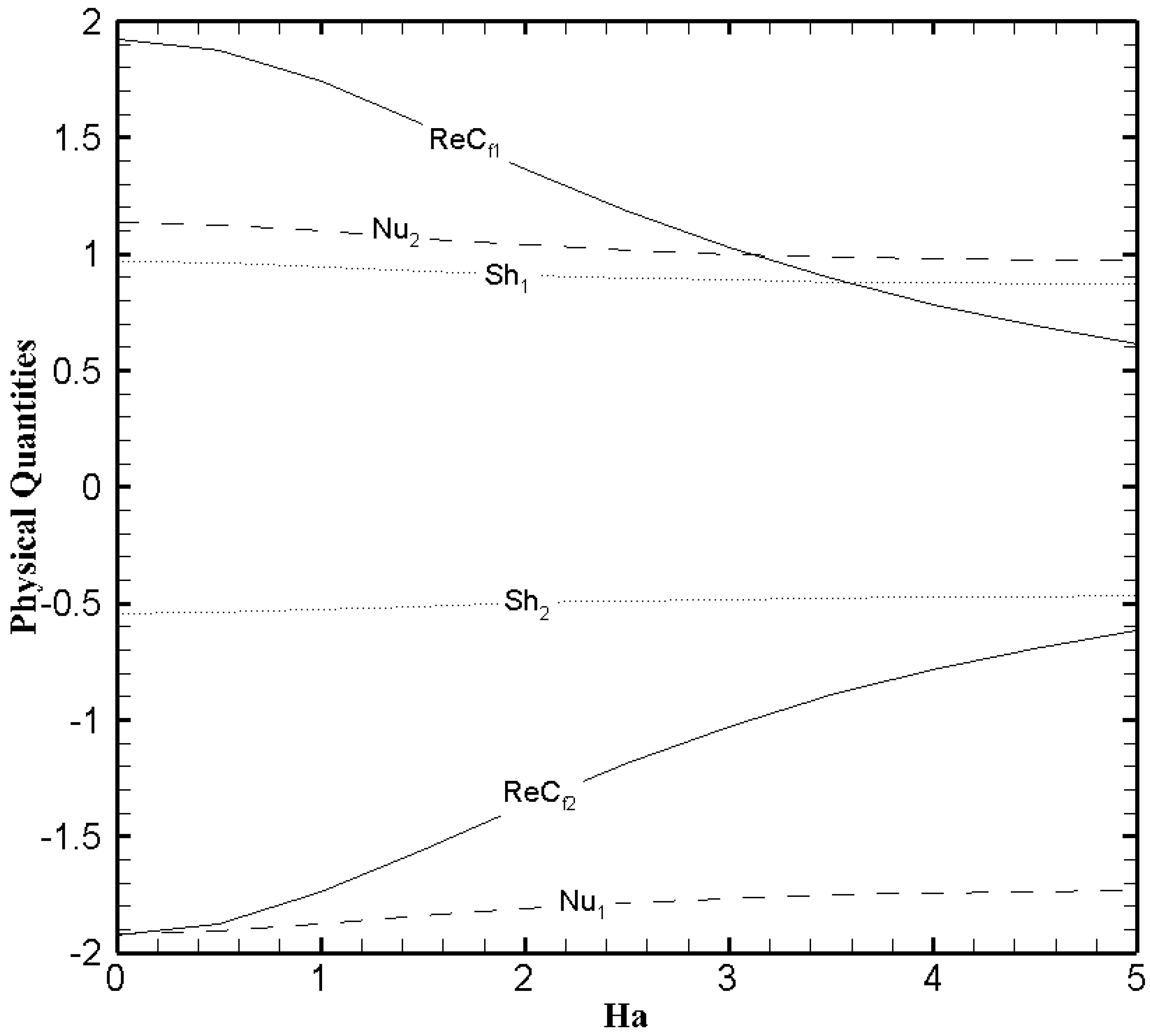
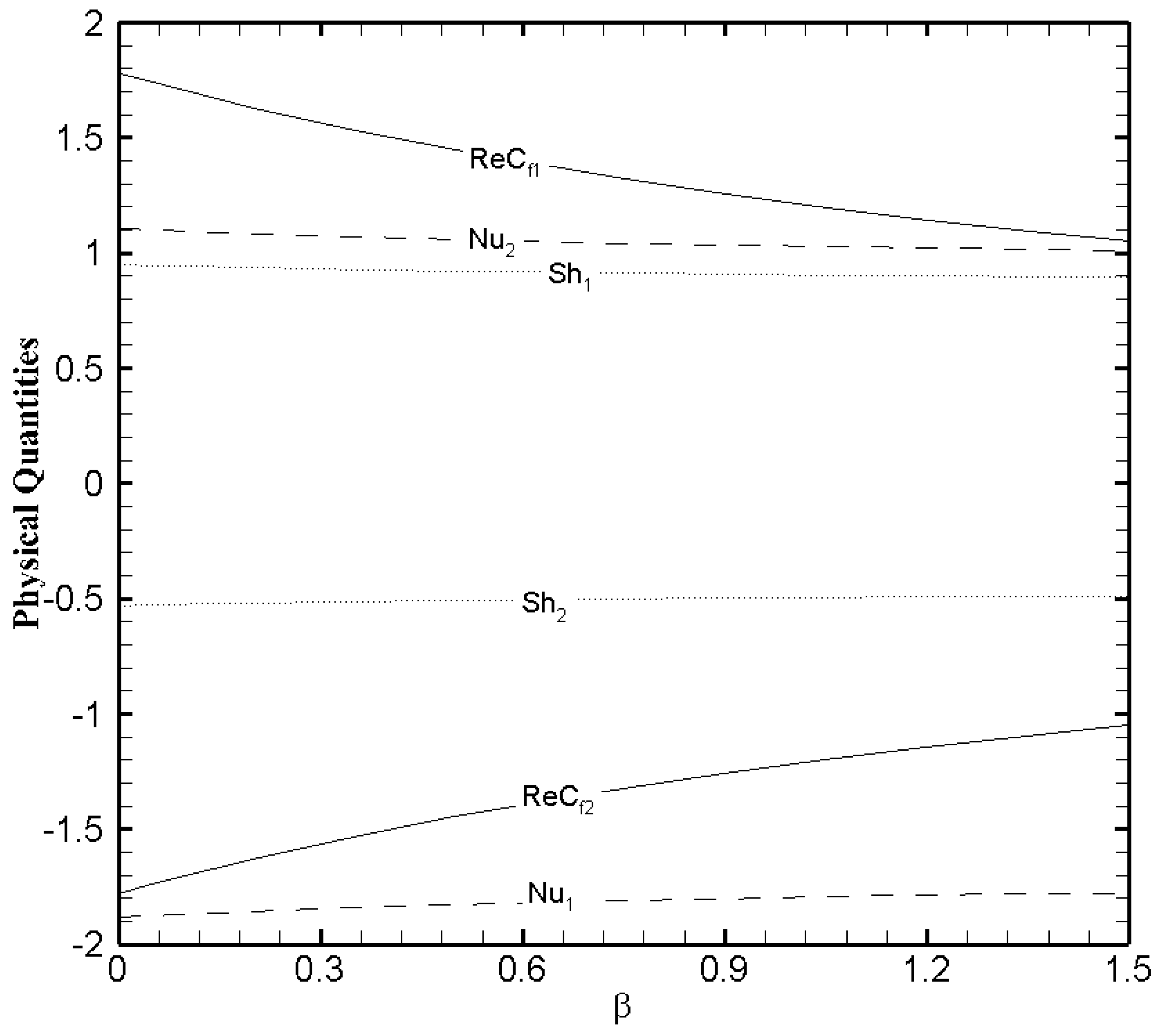
3.3. Effects of Hartmann Number () and Slip Parameter ()
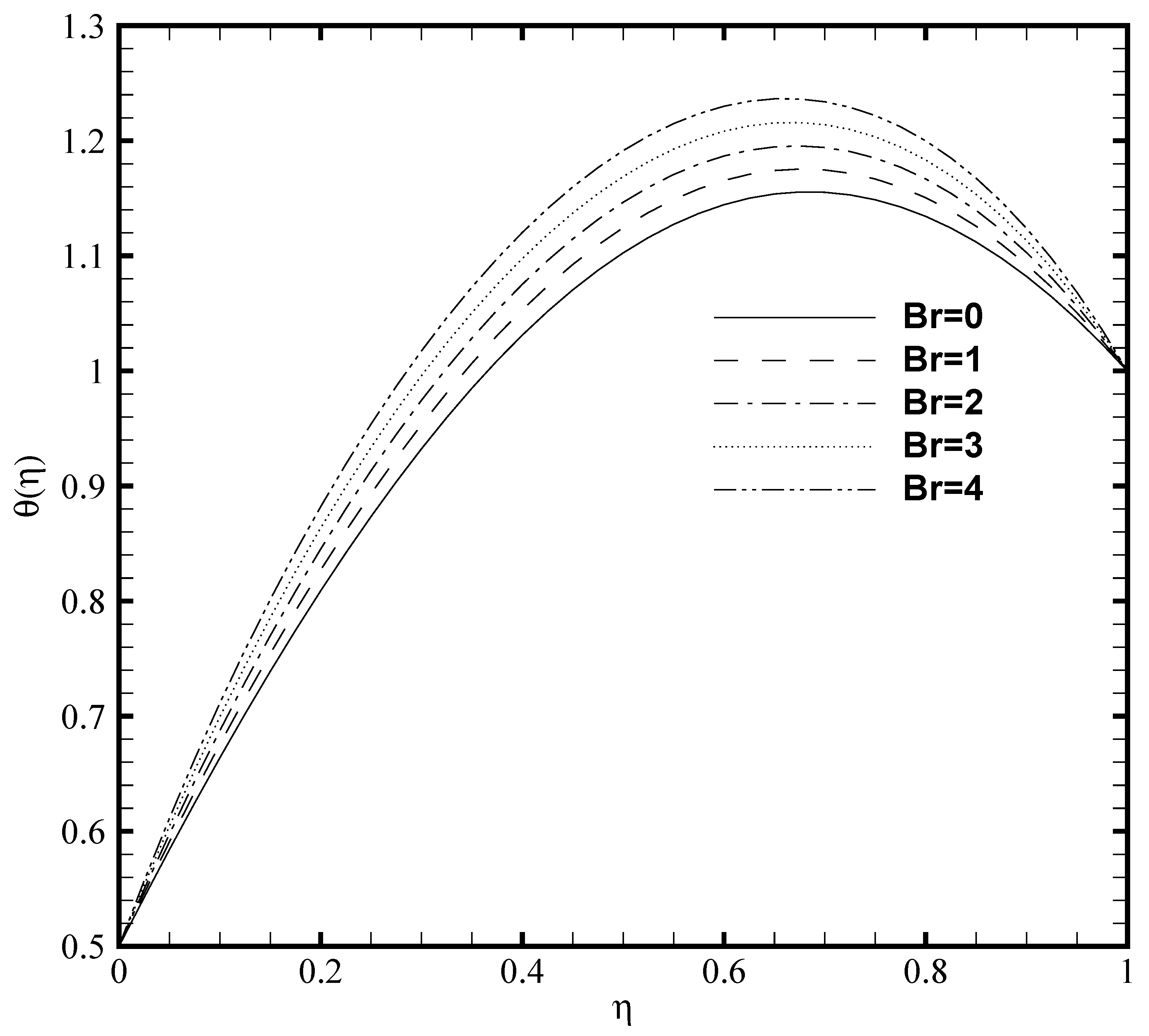
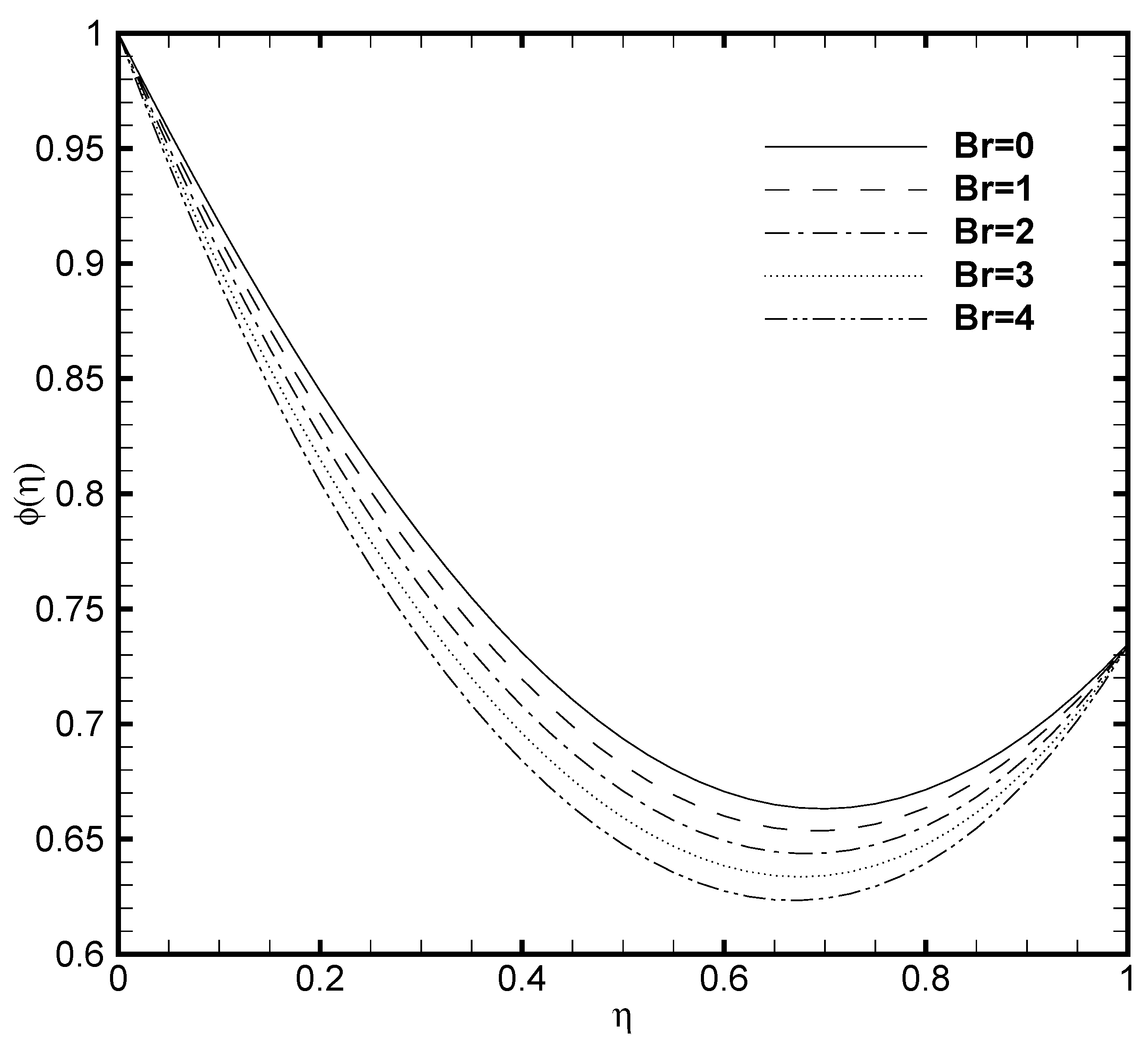
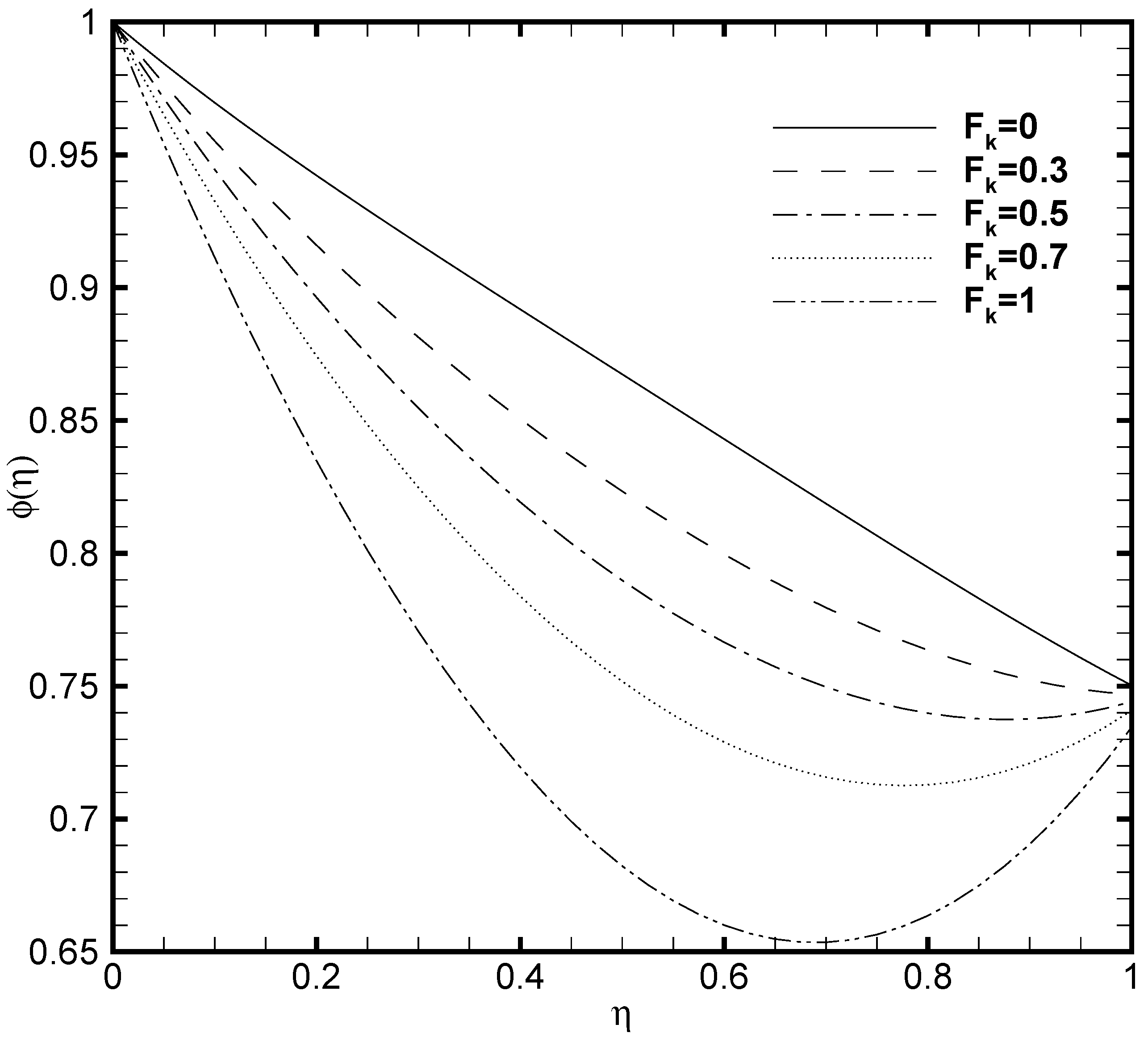
3.4. Effects of Brinkmann Number (Br) and Frank-Kamenetskii Number ()
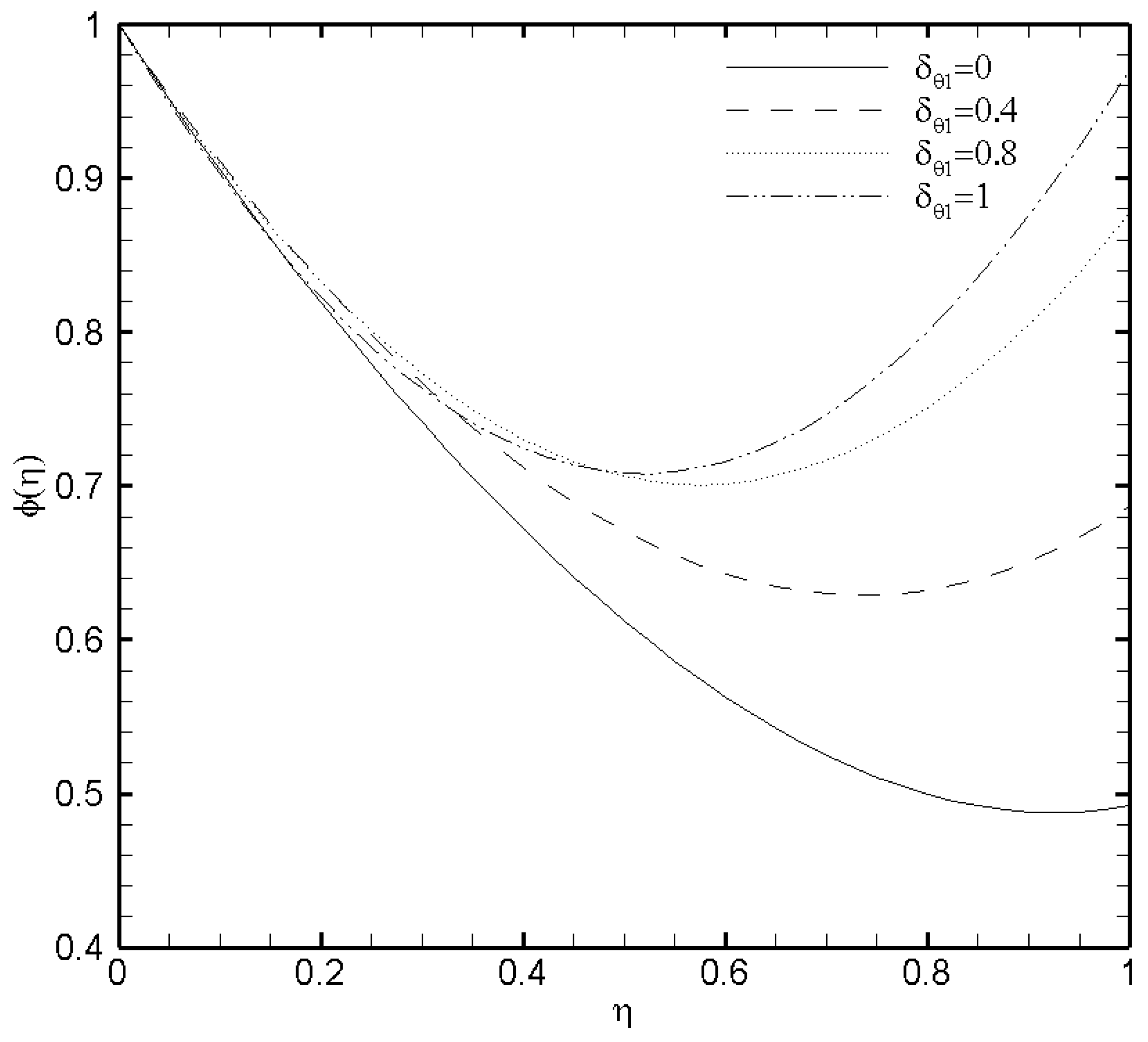
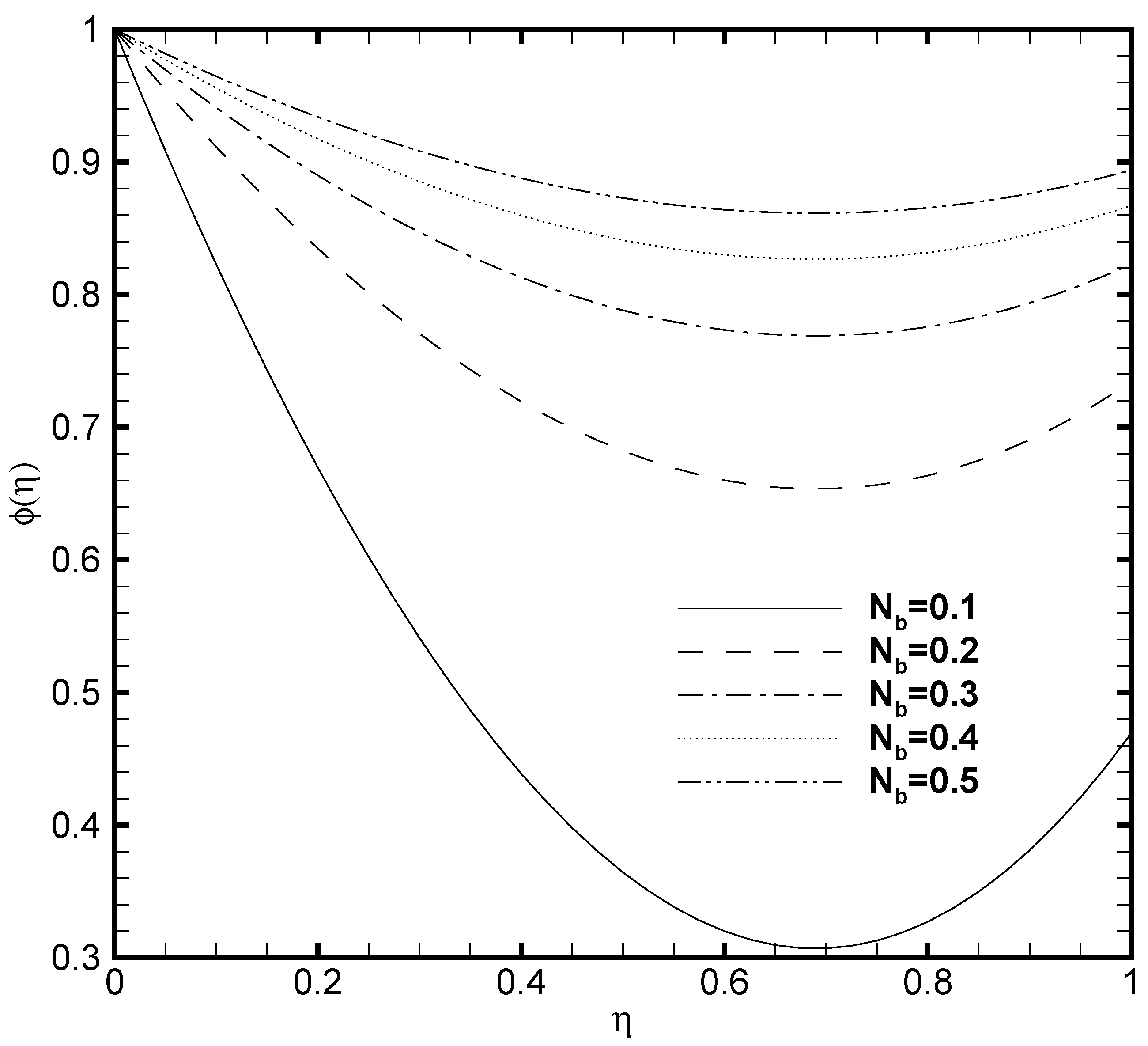
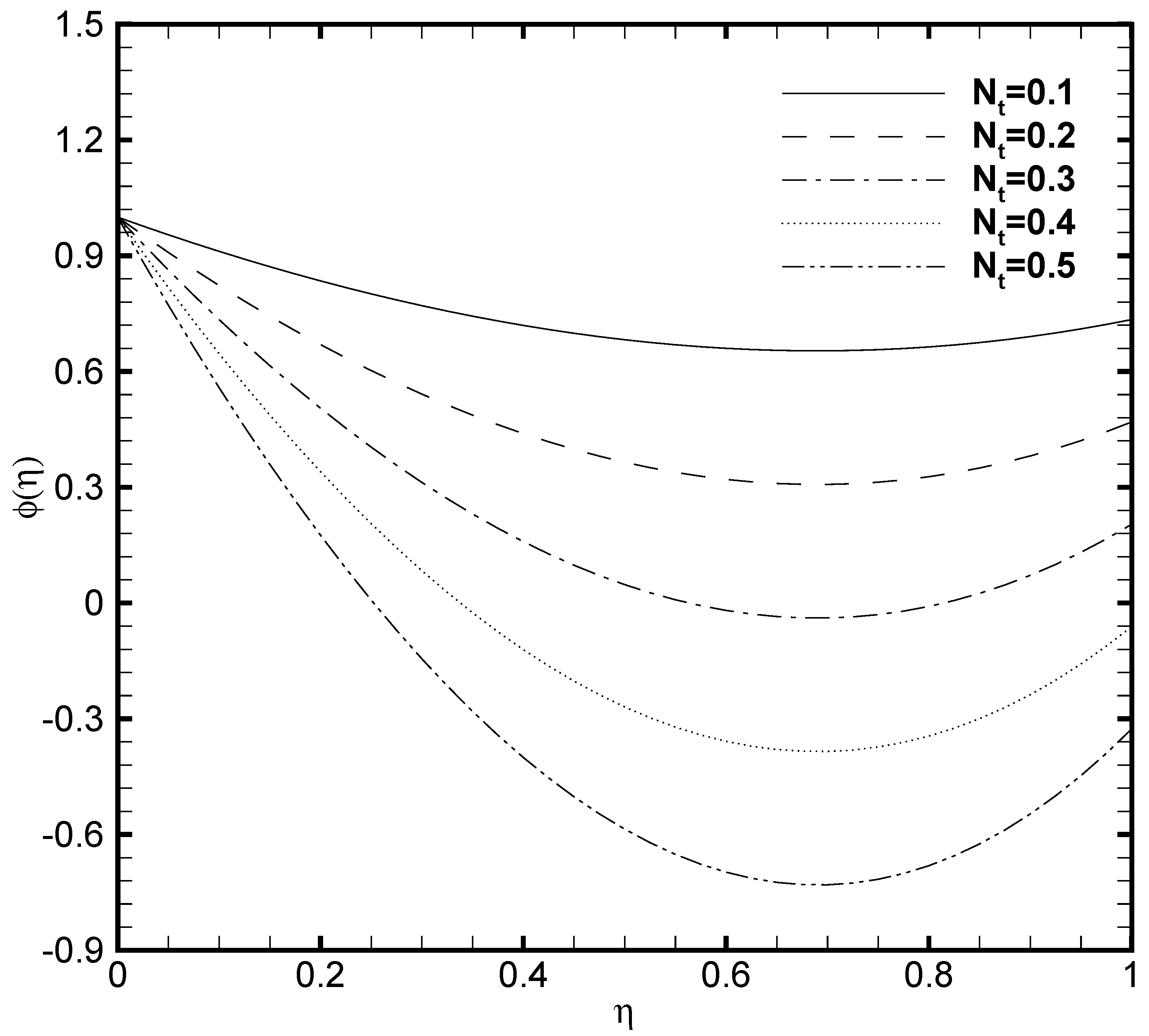
3.5. Effects of Temperature Constant (), Brownian Diffusion () and Thermophoresis () Parameters
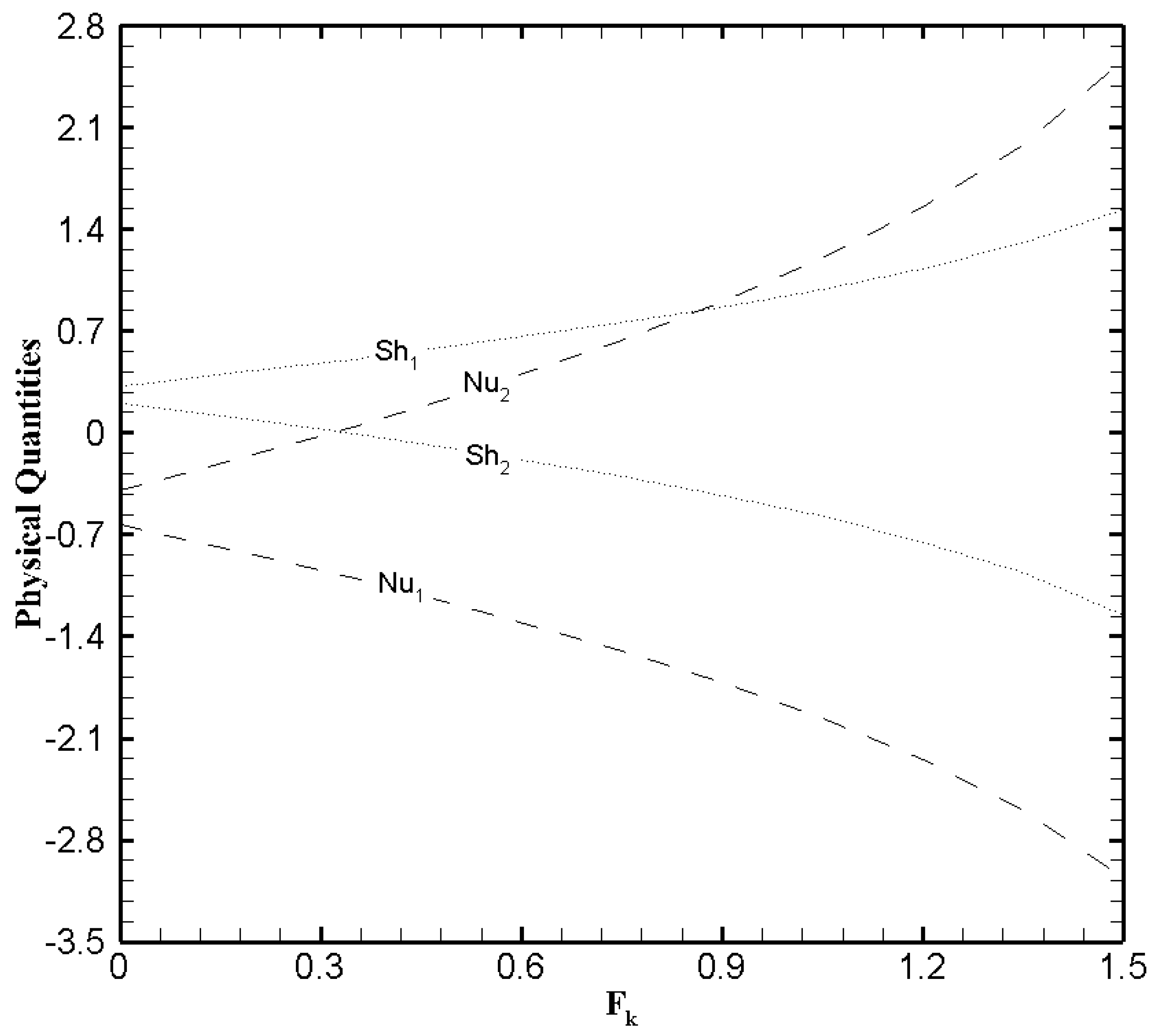
3.6. Analysis of Physical Quantities
4. Conclusions
- The exact solutions are obtained for both the electric potential and velocity field with the corresponding slip conditions.
- The slip parameter exercises a significant influence on the velocity field but the effectiveness of the boundary slip gets negligible when the value of zeta potential is large enough. This analysis supports the published findings by You and Guo [25].
- The temperature profile greatly elevates due to the heat generation caused by the exothermic chemical reaction. While for more elevated Frank-Kamenetskii number the nanoparticle volume fraction decreases.
- Frank-Kamenetskii number display a noticeable effect on the Nusselt number and Sherwood number. While and exert a significant effect on skin friction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| Brinkman number | |
| nano-particle volume fraction | |
| reference nano-particle volume fraction | |
| local skin friction coefficients | |
| specific heat capacity of fluid and nanoparticles | |
| local Nusselt numbers | |
| local Sherwood numbers | |
| Heat flux on the microchannel walls | |
| mass fluxes on the microchannel walls | |
| Brownian diffusion coefficient | |
| thermophoretic diffusion coefficient | |
| thermal conductivity of the fluid | |
| P | non-dimensional pressure gradient parameter |
| temperatures of nanofluid on microchannel walls | |
| reference temperature | |
| average velocity of the fluid | |
| Hartmann number | |
| Frank-Kamenetskii number | |
| Eckert number | |
| Prandtl number | |
| E | activation energy |
| electric field strength | |
| e | charge of proton |
| electric field in x-direction | |
| F | electrical body force from uniform electromagnetic field |
| Boltzmann constant | |
| the bulk ionic concentration | |
| Brownian motion parameter | |
| thermophoresis parameters | |
| Reynolds number | |
| the valences of ions | |
| Greek Symbols | |
| nanofluid’s thermal diffusivity | |
| ration of dielectric constants of the medium; | |
| permittivity of vacuum | |
| dielectric constant of the medium | |
| dynamic viscosity of the fluid | |
| non-dimensional electrostatic potential | |
| nanofluid density | |
| nanoparticles density | |
| charge density | |
| electrical conductivity of fluid | |
| dimensional slip parameter | |
| dimensionless slip parameter | |
| electro-osmotic parameter | |
| non-dimensional temperature parameter | |
| non-dimensional nanoparticles volume fraction | |
| constants on the microchannel walls | |
| non-dimensional zeta potential | |
| zeta potential | |
| wall shear stress on the microchannel |
References
- Song, H.; Tice, J.D.; Ismagilov, R.F. A microfluidic system for controlling reaction networks in time. Angew. Chem. Int. Ed. 2003, 42, 768–772. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Roach, L.S.; Ismagilov, R.F. Screening of protein crystallization conditions on a microfluidic chip using nanoliter-size droplets. J. Am. Chem. Soc. 2003, 125, 11170–11171. [Google Scholar] [CrossRef] [PubMed]
- Gravesen, P.; Branebjerg, J.; Jensen, O.S. Microfluidics—A review. J. Microdech. Microeng. 1993, 3, 168–182. [Google Scholar] [CrossRef]
- Ziaie, B.; Baldi, A.; Lei, M.; Gu, Y.; Siegel, R.A. Hard and soft micromachining for BioMEMS: Review of techniques and examples of applications in microfluidics and drug delivery. Adv. Drug Deliv. Rev. 2004, 56, 145–172. [Google Scholar] [CrossRef] [PubMed]
- Pfahler, J.; Harley, J.; Bau, H.; Zemel, J. Gas and liquid flow in small channels, micromechanical sensors, actuators and systems. In Proceedings of the Winter Meeting of ASME: Micromechanical Sensors, Actuators and Systems, Atlanta, GA, USA, 1–6 December 1991; Volume 32, pp. 49–60. [Google Scholar]
- You, X.Y.; Zheng, X.J.; Zheng, J.R. Molecular theory of liquid apparent viscosity in microchannels. Acta Phys. Sin. 2007, 56, 2323–2329. (In Chinese) [Google Scholar]
- Watanabe, K.; Udagawa, Y.; Mizunuma, H. Slip of Newtonian fluids at slid boundary. JSME Int. J. Ser. B 1998, 41, 525–529. [Google Scholar] [CrossRef]
- Tretheway, D.C.; Meinhart, C.D. Apparent fluid slip at hydrophobic microchannel walls. Phys. Fluids 2002, 14, L9–L12. [Google Scholar] [CrossRef]
- Soong, C.Y.; Wang, S.H. Theoretical analysis of electrokinetic flow and heat transfer in a microchannel under asymmetric boundary conditions. J. Colloid Interface Sci. 2003, 256, 202–213. [Google Scholar] [CrossRef]
- Yang, C.; Li, D. Analysis of electrokinetic effects on the liquid flow in rectangular microchannels. Physicochem. Eng. Asp. 1998, 143, 339–353. [Google Scholar] [CrossRef]
- You, X.Y.; Li, S.H.; Xiao, H.P. The effects surface roughness on drag reduction and control of laminar plane microchannel flows. Chem. Eng. 2008, 36, 25–27. (In Chinese) [Google Scholar]
- Shit, G.C.; Mondal, A.; Sinha, A.; Kundu, P.K. Electro-osmotically driven MHD flow and heat transfer in mirco-channel. Phys. A Stat. Mech. Appl. 2016, 449, 437–454. [Google Scholar] [CrossRef]
- Ganguly, S.; Sarkar, S.; Hota, T.K.; Mishra, M. Thermally developing combined electroosmotic and pressure-driven flow of nanofluids in microchannel under the effect of magnetic field. Chem. Eng. Sci. 2015, 126, 10–21. [Google Scholar] [CrossRef]
- Deshiikan, S.R.; Papadopoulos, K.D. Modified Booth equation for the calculation of zeta potential. Colloid Polym. Sci. 1998, 276, 117–124. [Google Scholar] [CrossRef]
- Ho, T.A.; Papavassiliou, D.V.; Lee, L.L.; Striolo, A. Liquid water can slip on a hydrophilic surface. Proc. Natl. Acad. Sci. USA 2011, 108, 16170–16175. [Google Scholar] [CrossRef] [PubMed]
- Ou, J.; Perot, B.; Rothstein, J.P. Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 2004, 16, 4635–4643. [Google Scholar] [CrossRef]
- Byun, D.; Kim, J.; Ko, H.S.; Park, H.C. Direct measurement of slip flows in superhydrophobic microchannels with transverse grooves. Phys. Fluids 2008, 20, 113601. [Google Scholar] [CrossRef]
- Tretheway, D.C.; Meinhart, C.D. A generating mechanism for apparent fluid slip in hydrophobic microchannels. Phys. Fluids 2004, 16, 1509–1515. [Google Scholar] [CrossRef]
- Chun, M.S.; Lee, S. Flow imaging of dilute colloidal suspension in PDMS-based microfluidic chip using fluorescence microscopy. Colloids Surf. A Physicochem. Eng. Asp. 2005, 267, 86–94. [Google Scholar] [CrossRef]
- Rosengarten, G.; Cooper-White, J.; Metcalfe, G. Experimental and analytical study of the effect of contact angle on liquid convective heat transfer in microchannels. Int. J. Heat Mass Transf. 2006, 49, 4161–4170. [Google Scholar] [CrossRef]
- Kundu, M.; Vamsee, K.; Maiti, D. Simulation and analysis of flow through microchannel. Asia Pac. J. Chem. Eng. 2009, 4, 450–461. [Google Scholar] [CrossRef]
- Bhagavatula, N.; Castro, J.M. Modelling and experimental verification of pressure prediction in the in-mould coating (IMC) process for injection moulded parts. Modell. Simul. Mater. Sci. Eng. 2007, 15, 171–189. [Google Scholar] [CrossRef]
- Babaie, A.; Saidi, M.H.; Sadeghi, A. Heat transfer characteristics of mixed electroosmotic and pressure driven flow of power-law fluids in a slit microchannel. Int. J. Therm. Sci. 2012, 53, 71–79. [Google Scholar] [CrossRef]
- Shojaeian, M.; Kosar, A. Convective heat transfer and entropy generation analysis on Newtonian and non-Newtonian fluid flows between parallel-plates under slip boundary conditions. Int. J. Heat Mass Transf. 2014, 70, 664–673. [Google Scholar] [CrossRef]
- You, X.-Y.; Guo, L. Combined effects of EDL and boundary slip on mean flow and its stability in microchannels. C. R. Mec. 2010, 338, 181–190. [Google Scholar] [CrossRef]
- Xie, Z.-Y.; Jian, Y.-J. Entropy generation of two-layer magnetohydrodynamic electroosmotic flow through microparallel channels. Energy 2017, 139, 1080–1093. [Google Scholar] [CrossRef]
- Jing, D.; Pan, Y.; Wang, X. The non-monotonic overlapping EDL-induced electroviscous effect with surface charge-dependent slip and its size dependence. Int. J. Heat Mass Transfer 2017, 113, 32–39. [Google Scholar] [CrossRef]
- Zhao, Q.; Xu, H.; Tao, L. Nanofluid flow and heat transfer in a microchannel with interfacial electrokinetic effects. Int. J. Heat Mass Transf. 2018, 124, 158–167. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective tranport in nanofluids. J. Heat Transf. Trans. ASME 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Zhao, Q.; Xu, H.; Tao, L. Flow and heat transfer of nanofluid through a horizontal microchannel with magnetic field and interfacial electrokinetic effects. Eur. J. Mech. B/Fluids 2020, 80, 72–79. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. The Cheng-Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: A revised model. Int. J. Heat Mass Transfer 2013, 65, 682–685. [Google Scholar] [CrossRef]
- Haq, M.R.U.; Xu, H.; Zhao, L. Study of electrokinetic effects for heat transfer in microchannel with sinusoidal thermal boundary conditions. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3872–3892. [Google Scholar]
- Niazi, M.D.K.; Hang, X. Modelling two-layer nanofluid flow in a micro-channel with electro-osmotic effects by means of Buongiorno’s model. Appl. Math. Mech. Engl. Ed. 2020, 41, 83–104. [Google Scholar] [CrossRef]
- Lazarovici, A.; Volpert, V.; Merkin, J.H. Steady states, oscillations and heat explosion in a combustion problem with convection. Eur. J. Mech. B/Fluids 2005, 2, 189–203. [Google Scholar] [CrossRef]
- Merkin, J.H.; Mahmood, T. Convective flows on reactive surfaces in porous media. Transp. Porous Media 1998, 33, 279–293. [Google Scholar] [CrossRef]
- Chaudhary, M.A.; Linan, A.; Merkin, J.H. Free convection boundary layers driven by exothermic surface reactions: Critical ambient temperatures. Mech. Eng. Ind. 1995, 5, 129–145. [Google Scholar]
- Merkin, J.H.; Pop, I. Stagnation point flow past a stretching/shrinking sheet driven by Arrhenius kinetics. Appl. Math. Comput. 2018, 337, 583–590. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, L.; Zhang, X.; Chen, G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction. Appl. Math. Modell. 2015, 39, 165–181. [Google Scholar] [CrossRef]
- Rahman, M.M.; Pop, I.; Saghir, M.Z. Steady free convection flow within a titled nanofluid saturated porous cavity in the presence of a sloping magnetic field energized by an exothermic chemical reaction administered by Arrhenius kinetics. Int. J. Heat Mass Transfer 2019, 129, 198–211. [Google Scholar] [CrossRef]
- Raees-ul-Haq, M. Analysis of Heat Transfer in a Triangular Enclosure Filled with a Porous Medium Saturated with Magnetized Nanofluid Charged by an Exothermic Chemical Reaction. Math. Probl. Eng. 2019, 2019, 1–19. [Google Scholar]
- Yang, W.Y.; Cao, W.; Chung, T.-S.; Morris, J. Applied Numerical Methods Using MATLAB; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raees, A.; Raees-ul-Haq, M.; Mansoor, M. Modeling and Simulations of Buongiorno’s Model for Nanofluid in a Microchannel with Electro-Osmotic Effects and an Exothermal Chemical Reaction. Nanomaterials 2021, 11, 905. https://doi.org/10.3390/nano11040905
Raees A, Raees-ul-Haq M, Mansoor M. Modeling and Simulations of Buongiorno’s Model for Nanofluid in a Microchannel with Electro-Osmotic Effects and an Exothermal Chemical Reaction. Nanomaterials. 2021; 11(4):905. https://doi.org/10.3390/nano11040905
Chicago/Turabian StyleRaees, Ammarah, Muhammad Raees-ul-Haq, and Muavia Mansoor. 2021. "Modeling and Simulations of Buongiorno’s Model for Nanofluid in a Microchannel with Electro-Osmotic Effects and an Exothermal Chemical Reaction" Nanomaterials 11, no. 4: 905. https://doi.org/10.3390/nano11040905
APA StyleRaees, A., Raees-ul-Haq, M., & Mansoor, M. (2021). Modeling and Simulations of Buongiorno’s Model for Nanofluid in a Microchannel with Electro-Osmotic Effects and an Exothermal Chemical Reaction. Nanomaterials, 11(4), 905. https://doi.org/10.3390/nano11040905





