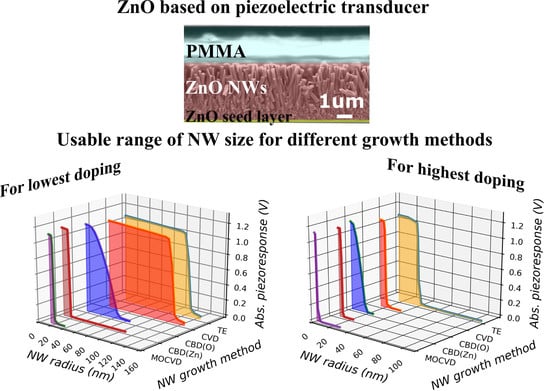
Dimensional Roadmap for Maximizing the Piezoelectrical Response of ZnO Nanowire-Based Transducers: Impact of Growth Method
Abstract
1. Introduction
2. Simulation Framework
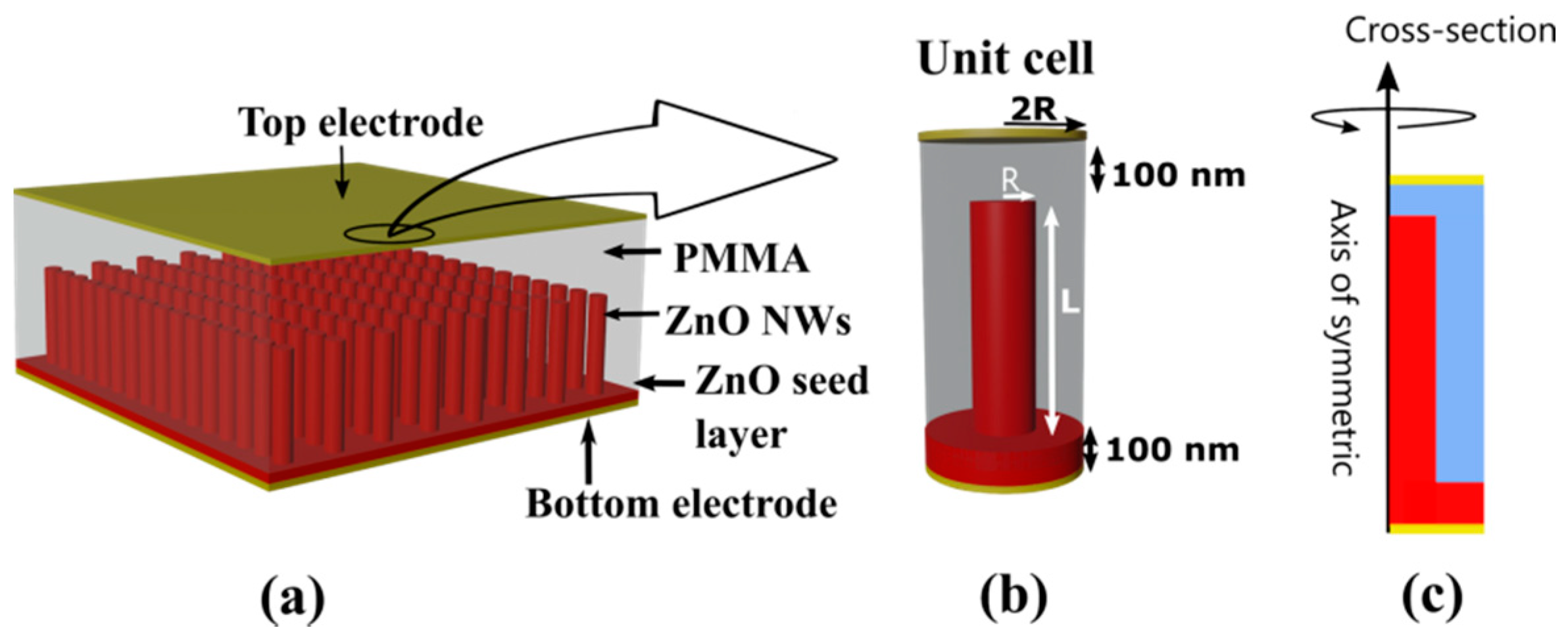
2.1. Device under Study and Simulated Structure
2.2. System of Equations
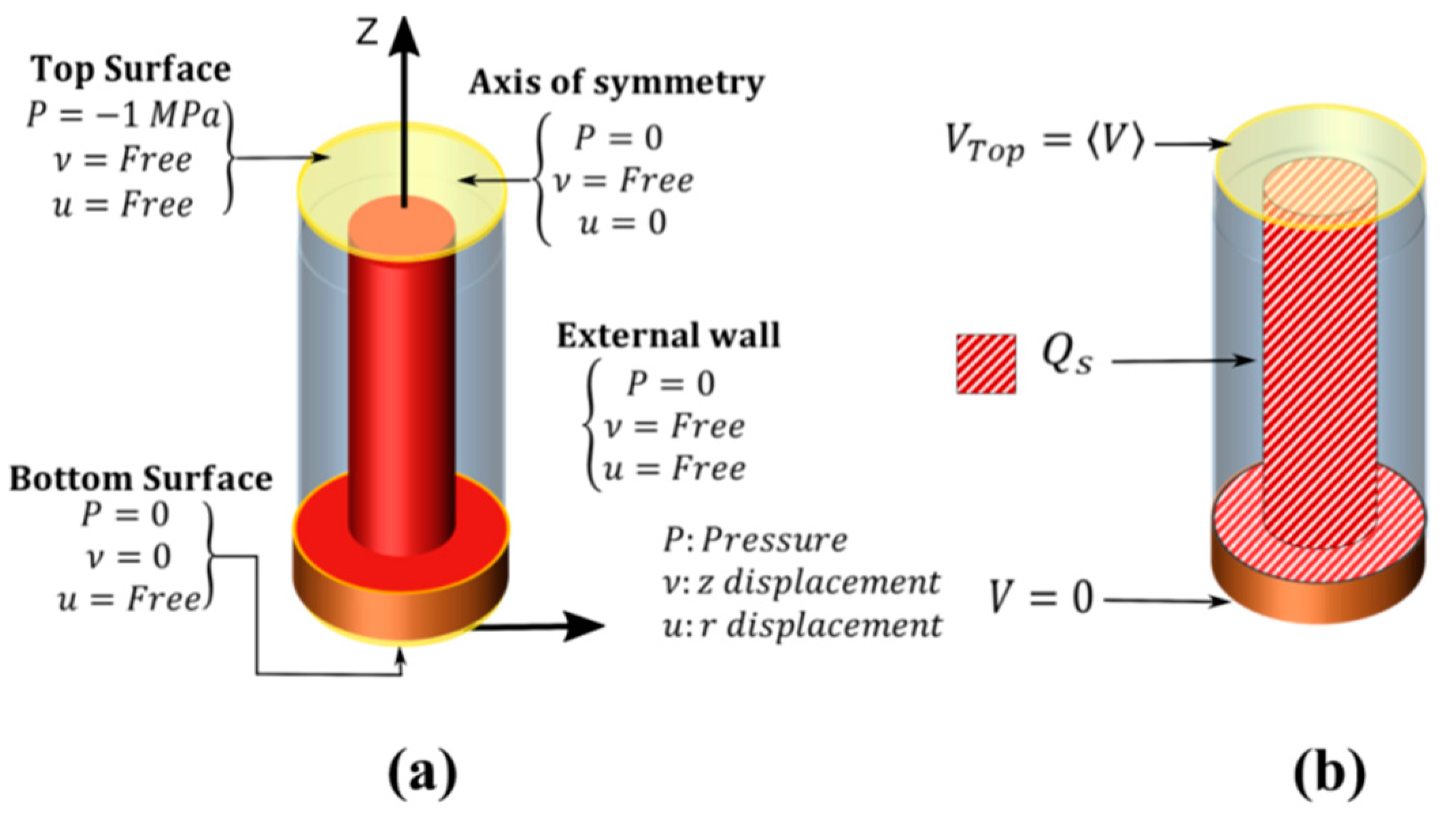
2.3. Boundary Conditions
3. Simulation Results and Discussions
3.1. Input Experimental Data for the Simulation
3.2. Piezoelectric Performance as a Function of the Nanowire Growth Method
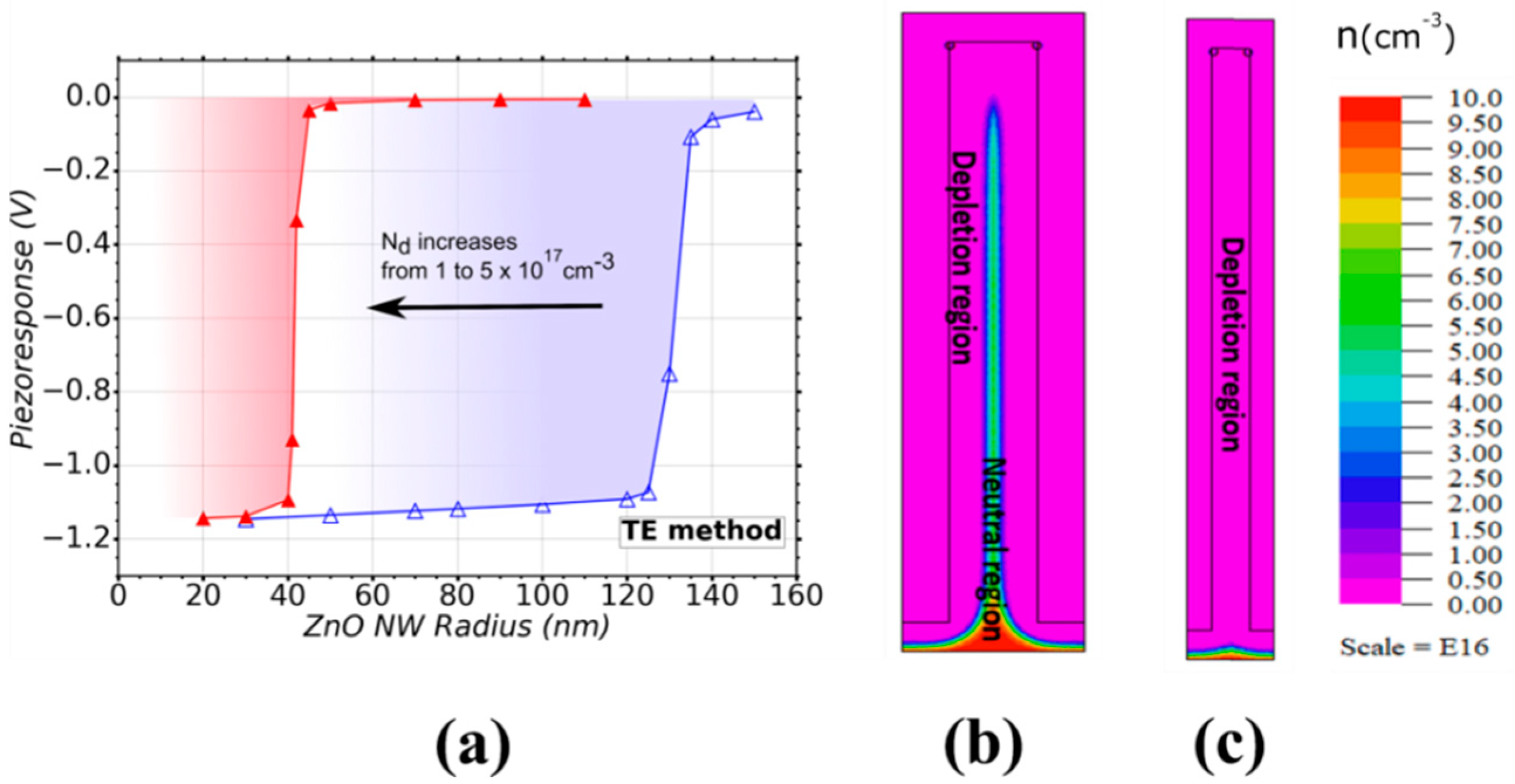
3.2.1. TE Method
3.2.2. CVD Method
3.2.3. MOCVD method
3.2.4. CBD Method
3.2.5. Electrodeposition: Analytical Evaluation of the Critical NW Radius
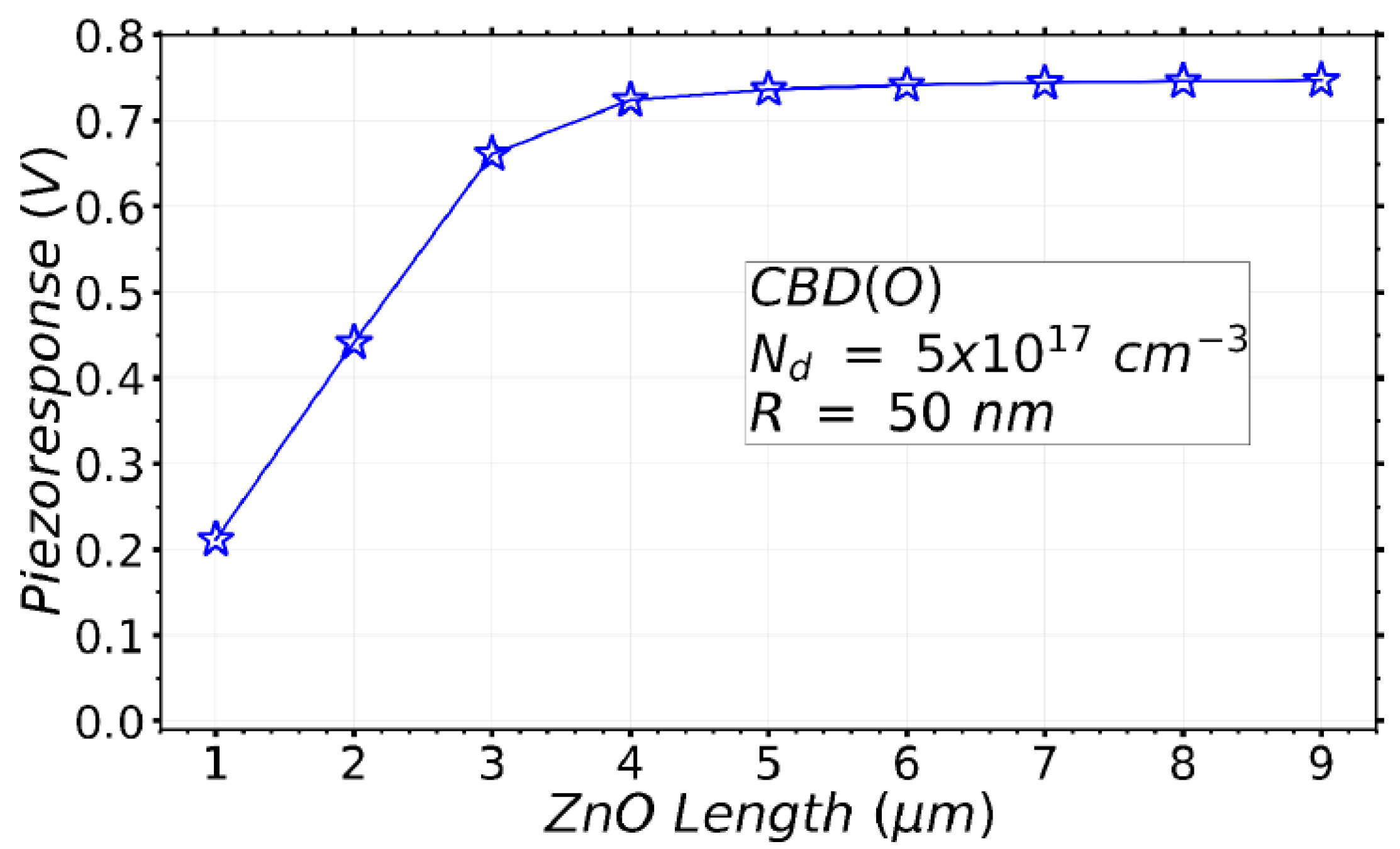
3.2.6. Effect of the Variation of NW Length on the VING Performance
3.3. Summary and Discussion about the Mechanisms at Work
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.L. Toward self-powered sensor networks. Nano Today 2010, 5, 512–514. [Google Scholar] [CrossRef]
- Lee, T.I.; Jang, W.S.; Lee, E.; Kim, Y.S.; Wang, Z.L.; Baik, H.K.; Myoung, J.M. Ultrathin self-powered artificial skin. Energy Environ. Sci. 2014, 7, 3994–3999. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1–R21. [Google Scholar] [CrossRef]
- Wang, Z.L. Piezoelectric Nanogenerators Based on Zinc Oxide Nanowire Arrays. Science 2006, 312, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Yang, R.; Wang, S.; Wang, Z.L. Flexible High-Output Nanogenerator Based on Lateral ZnO Nanowire Array. Nano Lett. 2010, 10, 3151–3155. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Qin, Y.; Xu, C.; Wei, Y.; Yang, R.; Wang, Z.L. Self-powered nanowire devices. Nat. Nanotechnol. 2010, 5, 366–373. [Google Scholar] [CrossRef] [PubMed]
- Yu, A.; Li, H.; Tang, H.; Liu, T.; Jiang, P.; Wang, Z.L. Vertically integrated nanogenerator based on ZnO nanowire arrays. Phys. Status Solidi RRL. 2011, 5, 162–164. [Google Scholar] [CrossRef]
- Tao, R.; Parmar, M.; Ardila, G.; Oliveira, P.; Marques, D.; Montès, L.; Mouis, M. Performance of ZnO based piezo-generators under controlled compression. Semicond. Sci. Technol. 2017, 32, 064003. [Google Scholar] [CrossRef]
- Hu, Y.; Lin, L.; Zhang, Y.; Wang, Z.L. Replacing a Battery by a Nanogenerator with 20 V Output. Adv. Mater. 2011, 24, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Wang, A.C.; Liu, Y.; Zhou, Y.; Wang, Z.L. Functional Electrical Stimulation by Nanogenerator with 58 V Output Voltage. Nano Lett. 2012, 12, 3086–3090. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, X.; He, Y.; Hu, Y.; Gu, H.; Wang, Y. Piezoelectric Nanowires in Energy Harvesting Applications. Adv. Mater. Sci. Eng. 2015, 2015, 165631. [Google Scholar] [CrossRef]
- Yang, R.; Qin, Y.; Li, C.; Zhu, G.; Wang, Z.L. Converting Biomechanical Energy into Electricity by a Muscle-Movement-Driven Nanogenerator. Nano Lett. 2009, 9, 1201–1205. [Google Scholar] [CrossRef] [PubMed]
- Yim, M.; Jeon, B.; Yoon, G. Fabrication of Tandem-type Vertically Integrated Nanogenerator by In-situ Deposition of AlN/ZnO Films. J. Semicond. Technol. Sci. 2019, 19, 233–238. [Google Scholar] [CrossRef]
- Dahiya, A.S.; Morini, F.; Boubenia, S.; Nadaud, K.; Alquier, D.; Poulin-Vittrant, G. Organic/Inorganic Hybrid Stretchable Piezoelectric Nanogenerators for Self-Powered Wearable Electronics. Adv. Mater. Technol. 2018, 3, 1–11. [Google Scholar] [CrossRef]
- Deng, W.; Jin, L.; Zhang, B.; Chen, Y.; Mao, L.; Zhang, H.; Yang, W. A flexible field-limited ordered ZnO nanorod-based self-powered tactile sensor array for electronic skin. Nanoscale 2016, 8, 16302–16306. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Hu, Y.; Xu, C.; Zhang, Y.; Zhang, R.; Wen, X.; Wang, Z.L. Transparent flexible nanogenerator as self-powered sensor for transportation monitoring. Nano Energy 2013, 2, 75–81. [Google Scholar] [CrossRef]
- Rivera, V.F.; Auras, F.; Motto, P.; Stassi, S.; Canavese, G.; Celasco, E.; Bein, T.; Onida, B.; Cauda, V. Length-Dependent Charge Generation from Vertical Arrays of High-Aspect-Ratio ZnO Nanowires. Chem. Eur. J. 2013, 19, 14665–14674. [Google Scholar] [CrossRef]
- Kammel, R.S.; Sabry, R.S. Effects of the aspect ratio of ZnO nanorods on the performance of piezoelectric nanogenerators. J. Sci. Adv. Mater. Devices 2019, 4, 420–424. [Google Scholar] [CrossRef]
- Riaz, M.; Song, J.; Nur, O.; Wang, Z.L.; Willander, M. Study of the Piezoelectric Power Generation of ZnO Nanowire Arrays Grown by Different Methods. Adv. Funct. Mater. 2010, 21, 628–633. [Google Scholar] [CrossRef]
- Tao, R.; Mouis, M.; Ardila, G. Unveiling the Influence of Surface Fermi Level Pinning on the Piezoelectric Response of Semiconducting Nanowires. Adv. Electron. Mater. 2018, 4, 1700299. [Google Scholar] [CrossRef]
- Schmidt-Mende, L.; MacManus-Driscoll, J.L. ZnO—nanostructures, defects, and devices. Mater. Today 2007, 10, 40–48. [Google Scholar] [CrossRef]
- Nobis, T.; Kaidashev, E.M.; Rahm, A.; Lorenz, M.; Lenzner, J.; Grundmann, M. Spatially Inhomogeneous Impurity Distribution in ZnO Micropillars. Nano Lett. 2004, 4, 797–800. [Google Scholar] [CrossRef]
- Yao, B.D.; Chan, Y.F.; Wang, N. Formation of ZnO nanostructures by a simple way of thermal evaporation. Appl. Phys. Lett. 2002, 81, 757–759. [Google Scholar] [CrossRef]
- Wu, J.-J.; Liu, S.-C. Low-Temperature Growth of Well-Aligned ZnO Nanorods by Chemical Vapor Deposition. Adv. Mater. 2002, 14, 215–218. [Google Scholar] [CrossRef]
- Park, W.I.; Kim, D.H.; Jung, S.-W.; Yi, G.-C. Metalorganic vapor-phase epitaxial growth of vertically well-aligned ZnO nanorods. Appl. Phys. Lett. 2002, 80, 4232–4234. [Google Scholar] [CrossRef]
- Peulon, S.; Lincot, D. Cathodic electrodeposition from aqueous solution of dense or open-structured zinc oxide films. Adv. Mater. 1996, 8, 166–170. [Google Scholar] [CrossRef]
- Vayssieres, L.; Keis, K.; Lindquist, S.-E.; Hagfeldt, A. Purpose-Built Anisotropic Metal Oxide Material: 3D Highly Oriented Microrod Array of ZnO. J. Phys. Chem. B 2001, 105, 3350–3352. [Google Scholar] [CrossRef]
- Lord, A.M.; Maffeis, T.G.; Walton, A.S.; Kepaptsoglou, D.M.; Ramasse, Q.M.; Ward, M.B.; Köble, J.; Wilks, S.P. Factors that determine and limit the resistivity of high-quality individual ZnO nanowires. Nanotechnology 2013, 24, 435706. [Google Scholar] [CrossRef] [PubMed]
- Chiu, S.-P.; Chung, H.-F.; Lin, Y.-H.; Kai, J.-J.; Chen, F.-R.; Lin, J.-J. Four-probe electrical-transport measurements on single indium tin oxide nanowires between 1.5 and 300 K. Nanotechnology 2009, 20, 105203. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.-K.; Yoon, J.; Lee, T. Hydrogen plasma-mediated modification of the electrical transport properties of ZnO nanowire field effect transistors. Nanotechnology 2015, 26, 125202. [Google Scholar] [CrossRef] [PubMed]
- Bugallo, A.D.L.; Donatini, F.; Sartel, C.; Sallet, V.; Pernot, J. Metallic core conduction in unintentionally doped ZnO nanowire. Appl. Phys. Express 2015, 8, 25001. [Google Scholar] [CrossRef]
- Wang, L.; Chauveau, J.-M.; Brenier, R.; Sallet, V.; Jomard, F.; Sartel, C.; Bremond, G. Access to residual carrier concentration in ZnO nanowires by calibrated scanning spreading resistance microscopy. Appl. Phys. Lett. 2016, 108, 132103. [Google Scholar] [CrossRef]
- den Hertog, M.; Donatini, F.; McLeod, R.; Monroy, E.; Sartel, C.; Sallet, V.; Pernot, J. In situ biasing and off-axis electron holography of a ZnO nanowire. Nanotechnology 2018, 29, 025710. [Google Scholar] [CrossRef] [PubMed]
- Baxter, J.B.; Schmuttenmaer, C.A. Conductivity of ZnO Nanowires, Nanoparticles, and Thin Films Using Time-Resolved Terahertz Spectroscopy†. J. Phys. Chem. B 2006, 110, 25229–25239. [Google Scholar] [CrossRef] [PubMed]
- Opoku, C.; Dahiya, A.S.; Cayrel, F.; Poulin-Vittrant, G.; Alquier, D.; Camara, N. Fabrication of field-effect transistors and functional nanogenerators using hydrothermally grown ZnO nanowires. RSC Adv. 2015, 5, 69925–69931. [Google Scholar] [CrossRef]
- Cossuet, T.; Donatini, F.; Lord, A.M.; Appert, E.; Pernot, J.; Consonni, V. Polarity-Dependent High Electrical Conductivity of ZnO Nanorods and Its Relation to Hydrogen. J. Phys. Chem. C 2018, 122, 22767–22775. [Google Scholar] [CrossRef]
- Villafuerte, J.; Donatini, F.; Kioseoglou, J.; Sarigiannidou, E.; Chaix-Pluchery, O.; Pernot, J.; Consonni, V. Zinc Vacancy–Hydrogen Complexes as Major Defects in ZnO Nanowires Grown by Chemical Bath Deposition. J. Phys. Chem. C 2020, 124, 16652–16662. [Google Scholar] [CrossRef]
- Könenkamp, R.; Boedecker, K.; Lux-Steiner, M.C.; Poschenrieder, M.; Zenia, F.; Levy-Clement, C.; Wagner, S. Thin film semiconductor deposition on free-standing ZnO columns. Appl. Phys. Lett. 2000, 77, 2575–2577. [Google Scholar] [CrossRef]
- Mora-Sero, I.; Fabregat-Santiago, F.; Denier, B.; Bisquert, J.; Tena-Zaera, R.; Elias, J.; Lévy-Clément, C. Determination of carrier density of ZnO nanowires by electrochemical techniques. Appl. Phys. Lett. 2006, 89, 203117. [Google Scholar] [CrossRef]
- Mallampati, B.; Singh, A.; Shik, A.; Ruda, H.E.; Philipose, U. Electro-physical characterization of individual and arrays of ZnO nanowires. J. Appl. Phys. 2015, 118, 34302. [Google Scholar] [CrossRef]
- Voss, T.; Bekeny, C.; Gutowski, J.; Tena-Zaera, R.; Elias, J.; Lévy-Clément, C.; Mora-Sero, I.; Bisquert, J. Localized versus delocalized states: Photoluminescence from electrochemically synthesized ZnO nanowires. J. Appl. Phys. 2009, 106, 054304. [Google Scholar] [CrossRef]
- Fan, J.; Shavel, A.; Zamani, R.; Fábrega, C.; Rousset, J.; Haller, S.; Güell, F.; Carrete, A.; Andreu, T.; Arbiol, J.; et al. Control of the doping concentration, morphology and optoelectronic properties of vertically aligned chlorine-doped ZnO nan-owires. Acta Mater. 2011, 59, 6790–6800. [Google Scholar] [CrossRef]
- Wang, L.; Guillemin, S.; Chauveau, J.-M.; Sallet, V.; Jomard, F.; Brenier, R.; Consonni, V.; Bremond, G. Characterization of carrier concentration in ZnO nanowires by scanning capacitance microscopy. Phys. Status Solidi C 2016, 13, 576–580. [Google Scholar] [CrossRef]
- Goldberger, J.; Sirbuly, D.J.; Law, M.; Yang, P.; Goldberger, J. ZnO Nanowire Transistors. J. Phys. Chem. B 2005, 109, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Chang, P.-C.; Chien, C.-J.; Stichtenoth, D.; Ronning, C.; Lu, J.G. Finite size effect in ZnO nanowires. Appl. Phys. Lett. 2007, 90, 113101. [Google Scholar] [CrossRef]
- Song, S.; Hong, W.-K.; Kwon, S.-S.; Lee, T. Passivation effects on ZnO nanowire field effect transistors under oxygen, ambient, and vacuum environments. Appl. Phys. Lett. 2008, 92, 263109. [Google Scholar] [CrossRef]
- Hong, W.-K.; Sohn, J.I.; Hwang, D.-K.; Kwon, S.-S.; Jo, G.; Song, S.; Kim, S.-M.; Ko, H.-J.; Park, S.-J.; Welland, M.E.; et al. Tunable Electronic Transport Characteristics of Surface-Architecture-Controlled ZnO Nanowire Field Effect Transistors. Nano Lett. 2008, 8, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Soudi, A.; Dhakal, P.; Gu, Y. Diameter dependence of the minority carrier diffusion length in individual ZnO nanowires. Appl. Phys. Lett. 2010, 96, 253115. [Google Scholar] [CrossRef]
- Soudi, A.; Hsu, C.-H.; Gu, Y. Diameter-Dependent Surface Photovoltage and Surface State Density in Single Semiconductor Nanowires. Nano Lett. 2012, 12, 5111–5116. [Google Scholar] [CrossRef]
- Tsai, L.-T.; Chiu, S.-P.; Lu, J.G.; Lin, J.-J. Electrical conduction mechanisms in natively doped ZnO nanowires (II). Nanotechnology 2010, 21, 145202. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Donatini, F.; Bugallo, A.D.L.; Tchoulfian, P.; Chicot, G.; Sartel, C.; Sallet, V.; Pernot, J. Comparison of Three E-Beam Techniques for Electric Field Imaging and Carrier Diffusion Length Measurement on the Same Nanowires. Nano Lett. 2016, 16, 2938–2944. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Yang, L.L.; Willander, M.; Sernelius, B.E.; Holtz, P.-O. Surface recombination in ZnO nanorods grown by chemical bath deposition. J. Appl. Phys. 2008, 104, 073526. [Google Scholar] [CrossRef]
- Serairi, L.; Yu, D.; Leprince-Wang, Y. Numerical modeling and simulation of ZnO nanowire devices for energy harvesting. Phys. Status Solidi C 2016, 13, 683–687. [Google Scholar] [CrossRef]
- Hinchet, R.; Lee, S.; Ardila, G.; Montès, L.; Mouis, M.; Wang, Z.L. Performance Optimization of Vertical Nanowire-based Piezoelectric Nanogenerators. Adv. Funct. Mater. 2013, 24, 971–977. [Google Scholar] [CrossRef]
- Min Kim, S.; Kim, H.; Nam, Y.; Kim, S. Effects of external surface charges on the enhanced piezoelectric potential of ZnO and AlN nanowires and nanotubes. AIP Adv. 2012, 2, 042174. [Google Scholar] [CrossRef]
- Romano, G.; Mantini, G.; Di Carlo, A.; D’Amico, A.; Falconi, C.; Wang, Z.L. Piezoelectric potential in vertically aligned nanowires for high output nanogenerators. Nanotechnology 2011, 22, 465401. [Google Scholar] [CrossRef] [PubMed]
- Fathi, S.; Sheikholeslami, T.F. Investigation of External Charges Effects on Piezoelectric ZnO Nanogenerator. J. Nano Electron. Phys. 2016, 8, 2047. [Google Scholar] [CrossRef]
- Wang, C.-H.; Liao, W.; Lin, Z.; Ku, N.; Li, Y.; Chen, Y.; Wang, Z.; Liu, C. Optimization of the Output Efficiency of GaN Nanowire Piezoelectric Nanogenerators by Tuning the Free Carrier Concentration. Adv. Energy Mater. 2014, 4, 1400392. [Google Scholar] [CrossRef]
- Ebert, P.; Schaafhausen, S.; Lenz, A.; Sabitova, A.; Ivanova, L.; Dähne, M.; Hong, Y.L.; Gwo, S.; Eisele, H. Direct measurement of the band gap and Fermi level position at InN (112̄0). Appl. Phys. Lett. 2011, 98, 062103. [Google Scholar] [CrossRef]
- Sabitova, A.; Ebert, P.; Lenz, A.; Schaafhausen, S.; Ivanova, L.; Dähne, M.; Hoffmann, A.; Dunin-Borkowski, R.E.; Förster, A.; Grandidier, B.; et al. Intrinsic bandgap of cleaved ZnO (1120) surfaces. Appl. Phys. Lett. 2013, 102, 021608. [Google Scholar] [CrossRef]
- Ivanova, L.; Borisova, S.; Eisele, H.; Dähne, M.; Laubsch, A.; Ebert, P. Surface states and origin of the Fermi level pinning on nonpolar GaN (11-̄00) surfaces. Appl. Phys. Lett. 2008, 93, 192110. [Google Scholar] [CrossRef]
- Dumont, J.; Hackens, B.; Faniel, S.; Mouthuy, P.O.; Sporken, R.; Melinte, S. ZnO(0001) surfaces probed by scanning tun-neling spectroscopy: Evidence for an inhomogeneous electronic structure. Appl. Phys. Lett. 2009, 95, 132102. [Google Scholar] [CrossRef]
- Lord, A.M.; Maffeis, T.G.; Allen, M.W.; Morgan, D.; Davies, P.R.; Jones, D.R.; Evans, J.E.; Smith, N.A.; Wilks, S.P. Surface state modulation through wet chemical treatment as a route to controlling the electrical properties of ZnO nanowire arrays investigated with XPS. Appl. Surf. Sci. 2014, 320, 664–669. [Google Scholar] [CrossRef]
- Lausecker, C.; Salem, B.; Baillin, X.; Consonni, V. Modeling the Elongation of Nanowires Grown by Chemical Bath Depo-sition Using a Predictive Approach. J. Phys. Chem. C 2019, 123, 29476–29483. [Google Scholar] [CrossRef]
- Consonni, V.; Sarigiannidou, E.; Appert, E.; Bocheux, A.; Guillemin, S.; Donatini, F.; Robin, I.-C.; Kioseoglou, J.; Robaut, F. Selective Area Growth of Well-Ordered ZnO Nanowire Arrays with Controllable Polarity. ACS Nano 2014, 8, 4761–4770. [Google Scholar] [CrossRef] [PubMed]
- Perillat-Merceroz, G.; Thierry, R.; Jouneau, P.-H.; Ferret, P.; Feuillet, G. Compared growth mechanisms of Zn-polar ZnO nanowires on O-polar ZnO and on sapphire. Nanotechnology 2012, 23, 125702. [Google Scholar] [CrossRef] [PubMed]
- Consonni, V.; Lord, A.M. Polarity in ZnO nanowires: A critical issue for piezotronic and piezoelectric devices. Nano Energy 2021, 83, 105789. [Google Scholar] [CrossRef]
- Mantini, G.; Gao, Y.; D’Amico, A.; Falconi, C.; Wang, Z.L. Equilibrium piezoelectric potential distribution in a deformed ZnO nanowire. Nano Res. 2009, 2, 624–629. [Google Scholar] [CrossRef]
- Araneo, R.; Lovat, G.; Burghignoli, P.; Falconi, C. Piezo-semiconductive quasi-1D nanodevices with or without an-ti-symmetry. Adv. Mater. 2012, 24, 4719–4724. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wang, Z.L. Equilibrium Potential of Free Charge Carriers in a Bent Piezoelectric Semiconductive Nanowire. Nano Lett. 2009, 9, 1103–1110. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, R.; Espinosa, H.D. Giant Piezoelectric Size Effects in Zinc Oxide and Gallium Nitride Nanowires. A First Principles Investigation. Nano Lett. 2011, 11, 786–790. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, V.; Senz, S.; Gösele, U. Influence of the Si/SiO2 interface on the charge carrier density of Si nanowires. Appl. Phys. A 2006, 86, 187–191. [Google Scholar] [CrossRef]
- Chia, A.C.E.; Lapierre, R.R. Analytical model of surface depletion in GaAs nanowires. J. Appl. Phys. 2012, 112, 063705. [Google Scholar] [CrossRef]
- Xu, C.; Shin, P.; Cao, L.; Gao, D. Preferential Growth of Long ZnO Nanowire Array and Its Application in Dye-Sensitized Solar Cells. J. Phys. Chem. C 2009, 114, 125–129. [Google Scholar] [CrossRef]
- Bui, Q.C.; Ardila, G.; Sarigiannidou, E.; Roussel, H.; Jiménez, C.; Chaix-Pluchery, O.; Guerfi, Y.; Bassani, F.; Donatini, F.; Mescot, X.; et al. Morphology Transition of ZnO from Thin Film to Nanowires on Silicon and its Correlated Enhanced Zinc Polarity Uniformity and Piezoelectric Responses. ACS Appl. Mater. Interfaces 2020, 12, 29583–29593. [Google Scholar] [CrossRef] [PubMed]
- Montenegro, D.; Souissi, A.; Martínez-Tomás, C.; Muñoz-Sanjose, V.; Sallet, V.; Martinez-Tomas, M.C. Morphology transitions in ZnO nanorods grown by MOCVD. J. Cryst. Growth 2012, 359, 122–128. [Google Scholar] [CrossRef]
- Willander, M.; Nur, O.; Zhao, Q.X.; Yang, L.L.; Lorenz, M.; Cao, B.Q.; Pérez, J.Z.; Czekalla, C.; Zimmermann, G.; Grundmann, M.; et al. Zinc oxide nanorod based photonic devices: Recent progress in growth, light emitting diodes and lasers. Nanotechnology 2009, 20, 332001. [Google Scholar] [CrossRef] [PubMed]
- Parize, R.; Garnier, J.D.; Chaix-Pluchery, O.; Verrier, C.; Appert, E.; Consonni, V. Effects of Hexamethylenetetramine on the Nucleation and Radial Growth of ZnO Nanowires by Chemical Bath Deposition. J. Phys. Chem. C 2016, 120, 5242–5250. [Google Scholar] [CrossRef]
- Govender, K.; Boyle, D.S.; Kenway, P.B.; O’Brien, P. Understanding the factors that govern the deposition and morphology of thin films of ZnO from aqueous solution. J. Mater. Chem. 2004, 14, 2575–2591. [Google Scholar] [CrossRef]
- Lord, A.M.; Consonni, V.; Cossuet, T.; Donatini, F.; Wilks, S.P. Schottky Contacts on Polarity-Controlled Vertical ZnO Nanorods. ACS Appl. Mater. Interfaces 2020, 12, 13217–13228. [Google Scholar] [CrossRef] [PubMed]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doğan, S.; Avrutin, V.; Cho, S.J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301. [Google Scholar] [CrossRef]
- McCluskey, M.D.; Jokela, S.J. Defects in ZnO. J. Appl. Phys. 2009, 106, 071101. [Google Scholar] [CrossRef]
- Joo, J.; Chow, B.Y.; Prakash, M.; Boyden, E.S.; Jacobson, J.M. Face-selective electrostatic control of hydrothermal zinc oxide nanowire synthesis. Nat. Mater. 2011, 10, 596–601. [Google Scholar] [CrossRef] [PubMed]
- Verrier, C.; Appert, E.; Chaix-Pluchery, O.; Rapenne, L.; Rafhay, Q.; Kaminski-Cachopo, A.; Consonni, V. Effects of the pH on the Formation and Doping Mechanisms of ZnO Nanowires Using Aluminum Nitrate and Ammonia. Inorg. Chem. 2017, 56, 13111–13122. [Google Scholar] [CrossRef] [PubMed]
- Gaffuri, P.; Appert, E.; Chaix-Pluchery, O.; Rapenne, L.; Salaün, M.; Consonni, V. The Path of Gallium from Chemical Bath into ZnO Nanowires: Mechanisms of Formation and Incorporation. Inorg. Chem. 2019, 58, 10269–10279. [Google Scholar] [CrossRef] [PubMed]
- McNeill, A.R.; Bell, K.J.; Hyndman, A.R.; Gazoni, R.M.; Reeves, R.J.; Downard, A.J.; Allen, M.W. Synchrotron X-ray Photoelectron Spectroscopy Study of Electronic Changes at the ZnO Surface Following Aryldiazonium Ion Grafting: A Metal-to-Insulator Transition. J. Phys. Chem. C 2018, 122, 12681–12693. [Google Scholar] [CrossRef]
- McNeill, A.R.; Hyndman, A.R.; Reeves, R.J.; Downard, A.J.; Allen, M.W. Tuning the Band Bending and Controlling the Surface Reactivity at Polar and Nonpolar Surfaces of ZnO through Phosphonic Acid Binding. ACS Appl. Mater. Interfaces 2016, 8, 31392–31402. [Google Scholar] [CrossRef] [PubMed]

 ) to 1 (
) to 1 ( ) × 1018 cm−3 is considered, which is typical in the CVD method, (b) a range of doping level (Nd) from 1 (
) × 1018 cm−3 is considered, which is typical in the CVD method, (b) a range of doping level (Nd) from 1 ( ) to 5 (
) to 5 ( ) × 1018 cm−3
is considered, which is typical in MOCVD method. A trap density Nit = 1 × 1012 eV−1 cm−2 was considered in the simulations.
) × 1018 cm−3
is considered, which is typical in MOCVD method. A trap density Nit = 1 × 1012 eV−1 cm−2 was considered in the simulations.
 ) to 1 (
) to 1 ( ) × 1018 cm−3 is considered, which is typical in the CVD method, (b) a range of doping level (Nd) from 1 (
) × 1018 cm−3 is considered, which is typical in the CVD method, (b) a range of doping level (Nd) from 1 ( ) to 5 (
) to 5 ( ) × 1018 cm−3
is considered, which is typical in MOCVD method. A trap density Nit = 1 × 1012 eV−1 cm−2 was considered in the simulations.
) × 1018 cm−3
is considered, which is typical in MOCVD method. A trap density Nit = 1 × 1012 eV−1 cm−2 was considered in the simulations.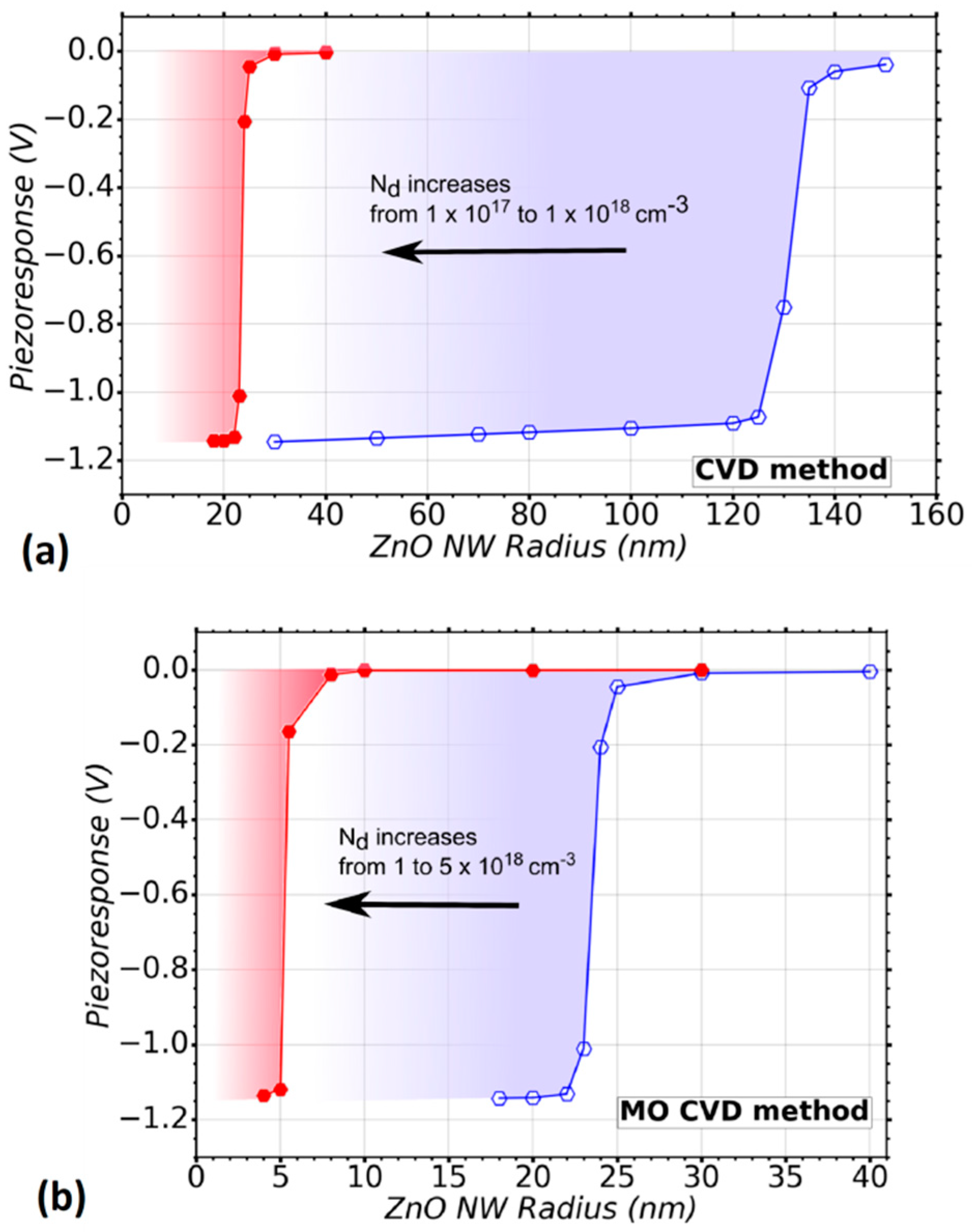
 ) to 5 (
) to 5 ( ) × 1018 cm−3 is considered, which is typical in CBD (O), (b) a range of doping level Nd from 5 × 1018 (○) to 1 (●) × 1019 cm−3 is considered, which is typical in CBD (Zn) method. A trap density Nit = 1 × 1013 eV−1 cm−2 was considered in the simulations.
) × 1018 cm−3 is considered, which is typical in CBD (O), (b) a range of doping level Nd from 5 × 1018 (○) to 1 (●) × 1019 cm−3 is considered, which is typical in CBD (Zn) method. A trap density Nit = 1 × 1013 eV−1 cm−2 was considered in the simulations.
 ) to 5 (
) to 5 ( ) × 1018 cm−3 is considered, which is typical in CBD (O), (b) a range of doping level Nd from 5 × 1018 (○) to 1 (●) × 1019 cm−3 is considered, which is typical in CBD (Zn) method. A trap density Nit = 1 × 1013 eV−1 cm−2 was considered in the simulations.
) × 1018 cm−3 is considered, which is typical in CBD (O), (b) a range of doping level Nd from 5 × 1018 (○) to 1 (●) × 1019 cm−3 is considered, which is typical in CBD (Zn) method. A trap density Nit = 1 × 1013 eV−1 cm−2 was considered in the simulations.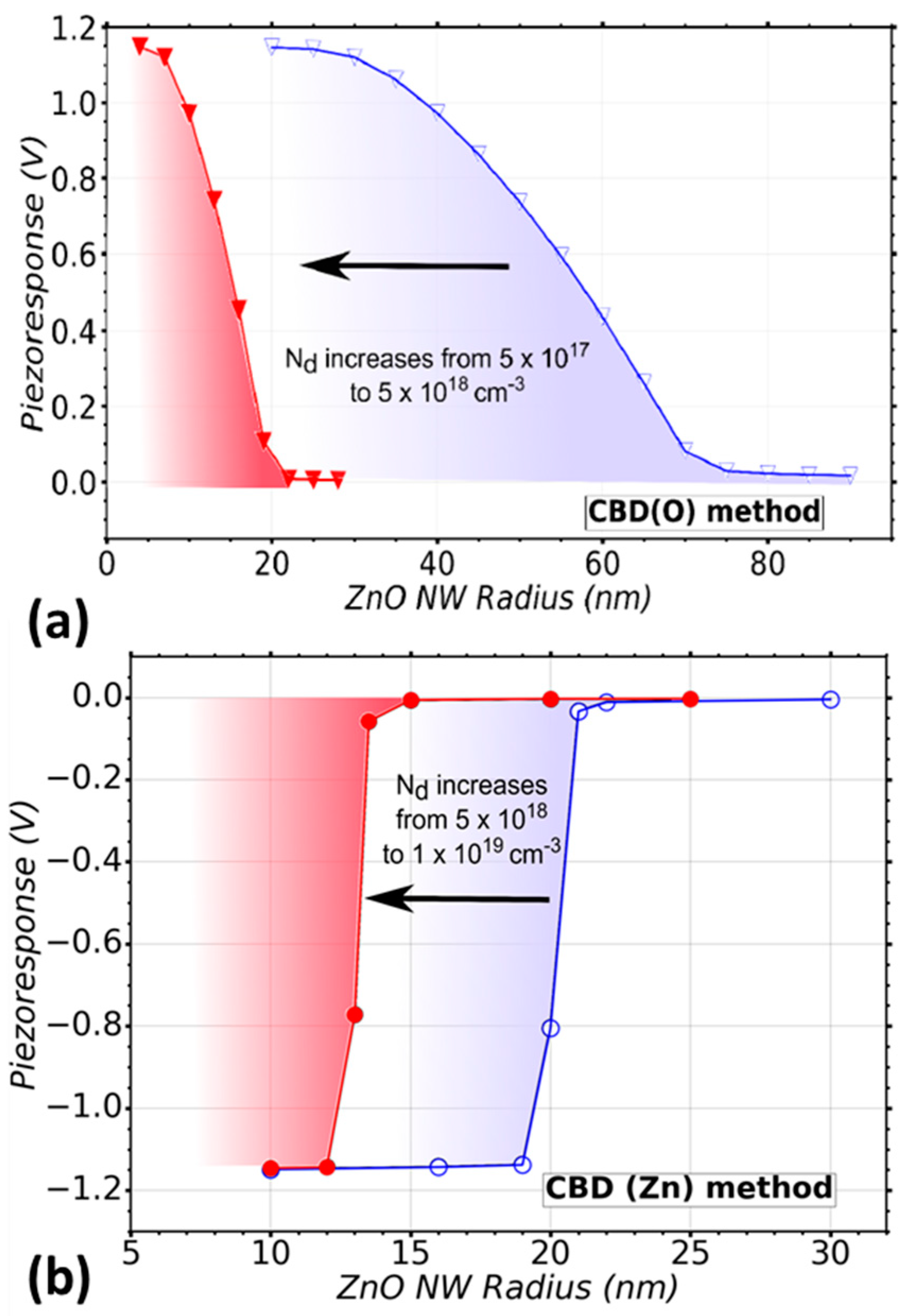
 ) corresponds to the TE method, (
) corresponds to the TE method, ( ) to the CBD (Zn) method, (
) to the CBD (Zn) method, ( ) to the CBD (O) method, (
) to the CBD (O) method, ( ) to the CVD method and (
) to the CVD method and ( ) to the MOCVD method. The blue and magenta arrows indicate the limiting value of Nd for Nit = 1012 eV−1 cm−2 and 1013 eV−1 cm−2. Beyond this value of doping, the critical radius goes below 5nm and we consider that surface effects could modify piezoelectric coefficients. The mark (
) to the MOCVD method. The blue and magenta arrows indicate the limiting value of Nd for Nit = 1012 eV−1 cm−2 and 1013 eV−1 cm−2. Beyond this value of doping, the critical radius goes below 5nm and we consider that surface effects could modify piezoelectric coefficients. The mark ( ) corresponds to the conditions of NWs grown by the electron-deposition method, which was not simulated with FlexPDE.
) corresponds to the conditions of NWs grown by the electron-deposition method, which was not simulated with FlexPDE.
 ) corresponds to the TE method, (
) corresponds to the TE method, ( ) to the CBD (Zn) method, (
) to the CBD (Zn) method, ( ) to the CBD (O) method, (
) to the CBD (O) method, ( ) to the CVD method and (
) to the CVD method and ( ) to the MOCVD method. The blue and magenta arrows indicate the limiting value of Nd for Nit = 1012 eV−1 cm−2 and 1013 eV−1 cm−2. Beyond this value of doping, the critical radius goes below 5nm and we consider that surface effects could modify piezoelectric coefficients. The mark (
) to the MOCVD method. The blue and magenta arrows indicate the limiting value of Nd for Nit = 1012 eV−1 cm−2 and 1013 eV−1 cm−2. Beyond this value of doping, the critical radius goes below 5nm and we consider that surface effects could modify piezoelectric coefficients. The mark ( ) corresponds to the conditions of NWs grown by the electron-deposition method, which was not simulated with FlexPDE.
) corresponds to the conditions of NWs grown by the electron-deposition method, which was not simulated with FlexPDE.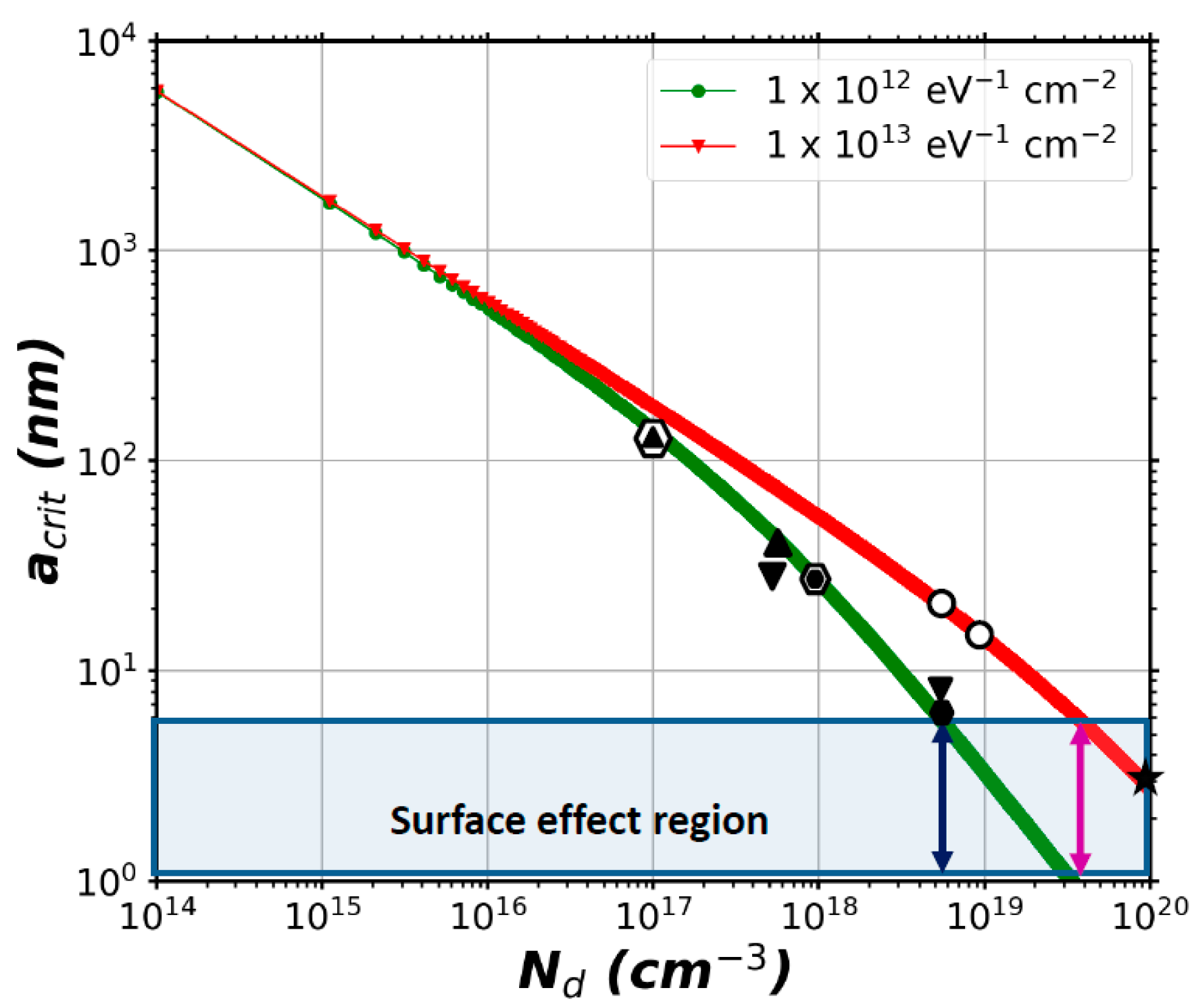
| Growth Method | ZnO NW Radius for Full Depletion | |
|---|---|---|
| TE | <120 | <40 |
| CVD | <120 | <20 |
| MOCVD | <22 | <5 |
| CBD (O) | <55 | <15 |
| CBD (Zn) | <18 | <12 |
| Electrodeposition | Not simulated (estimated < 4) | Not simulated (estimated < 4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez Garcia, A.J.; Mouis, M.; Consonni, V.; Ardila, G. Dimensional Roadmap for Maximizing the Piezoelectrical Response of ZnO Nanowire-Based Transducers: Impact of Growth Method. Nanomaterials 2021, 11, 941. https://doi.org/10.3390/nano11040941
Lopez Garcia AJ, Mouis M, Consonni V, Ardila G. Dimensional Roadmap for Maximizing the Piezoelectrical Response of ZnO Nanowire-Based Transducers: Impact of Growth Method. Nanomaterials. 2021; 11(4):941. https://doi.org/10.3390/nano11040941
Chicago/Turabian StyleLopez Garcia, Andrés Jenaro, Mireille Mouis, Vincent Consonni, and Gustavo Ardila. 2021. "Dimensional Roadmap for Maximizing the Piezoelectrical Response of ZnO Nanowire-Based Transducers: Impact of Growth Method" Nanomaterials 11, no. 4: 941. https://doi.org/10.3390/nano11040941
APA StyleLopez Garcia, A. J., Mouis, M., Consonni, V., & Ardila, G. (2021). Dimensional Roadmap for Maximizing the Piezoelectrical Response of ZnO Nanowire-Based Transducers: Impact of Growth Method. Nanomaterials, 11(4), 941. https://doi.org/10.3390/nano11040941