3.1. Nanorod- and Core–Shell-Mediated Near-Field Amplification: NF-c-Type Nanoresonators
According to the objective function that was defined to achieve the largest average near-field enhancement, the optimized nanorod (NF-NR-c) of a 59.38 nm long axis and 23.39 nm short axis (corresponding to aspect ratio of AR = 2.54) with a gain-coating of 18.13 nm thickness is significantly smaller in all dimensions than its FF-NR-c counterpart, which shows that it is better suited to absorb the incoming probe light than to scatter it (
Figure 1a to
Figure 2a insets and
Table S1). The ratio of the internal local and external pump fields (
) at the population saturation reveals an ~54-fold near-field enhancement (
Figure S1a,
Table S1). The dielectric–metal–gain multilayer composition optimization with the same objective function resulted in a core of 18.99 nm radius, a metal shell of 5 nm and a gain medium of 24.62 nm thickness in NF-CS-c. All are significantly smaller than the corresponding parameters in the FF-CS-c counterpart (
Figure 1a to
Figure 2a insets and
Table S1). The ratio of the local and pump fields (
) at the population saturation reveals an ~32-fold near-field enhancement (
Figure S1a,
Table S1). The near-field enhancement at the pump wavelength extracted from the ratio of saturation thresholds is smaller for NF-CS-c than for NF-NR-c.
The achieved gain effects on n(ω
a), ε
imag(ω
a) and κ(ω
a), were noticeable and significant with respect to the host medium at the pump wavelength, respectively (
Figure S1b,d).
Already at the small pump, positive imaginary values are taken on; accordingly, there is a non-zero absorptance at the pump wavelength, which decreases and converges to zero by increasing the pump. The intervals where the n(ω
a), ε
imag(ω
a) and κ(ω
a) values are taken on are slightly larger for NF-CS-c than for NF-NR-c (
Figure S1b,d and
Table S1).
There is a considerable deviation in both the real and imaginary parts from the passive system permittivity and refractive index at the probe wavelength (
Figure S1c,e). In the case of a weak pump, the small, positive ε
imag(ω
e) and κ(ω
e) values indicate that the gain medium is still weakly absorbing, but above a certain pump threshold, the switching in sign proves that a gain is settled on; then, the imaginary parts gradually decrease. The intervals where the imaginary part of permittivity and refractive index values are taken on are slightly larger for NF-CS-c (
Figure S1c,e and
Table S1).
In NF-NR-c, after a transitional small slope region, the local probe
E-fields linearly increase throughout
: 0.31–2.63) and then saturate (2.63 <
) (
Figure 1a,
Table S1). The extrapolated lasing threshold in the internal local (external) pump
E-field normalized to the
Esat is
: 0.30 (
: 0.007). The (2.16 × 10
5 V/m) slope in the average probe
E-field is considerably smaller than that (8.52 × 10
5 V/m) in the maximal probe
E-field. In NF-CS-c, after the extrapolated threshold value of
: 0.43 (
: 0.013) in the internal local (external) pump
E-field normalized to
Esat, the near-field increases linearly in the interval of (
: 0.48–3.16) with a slope of 9.8 × 10
4 V/m in the average probe
E-field and with a slope of 4.97 × 10
5 V/m in the maximal probe
E-field.
In NF-CS-c, the linear region is wider and the lasing threshold is larger, whereas all of the slope efficiency and the achieved average and maximal probe
E-field values are smaller than those in NF-NR-c. In NF-NR-c, the gain absorptance is positive at small pump rates and then becomes negative at the gain threshold value of
: 0.32 (
: 0.006). In comparison, in NF-CS-c, the threshold of negative gain absorptance is
: 0.31 (
: 0.01). The threshold of negative gain is slightly smaller (larger) in the internal local (external) pump
E-field in NF-CS-c, similarly to the saturation threshold. The positive metal absorptance overrides the negative gain absorptance throughout the complete inspected pump interval; as a consequence, there is no far-field enhancement in NF-NR-c and in NF-CS-c (
Figure 1b). The absorptances in NF-CS-c are slightly smaller, whereas the power outflow values are almost the same in the two optimized NF-c-type systems.
Accordingly, in both NF-c-type nanoresonators, the absorption cross-section (ACS) gradually increases and remains positive, which indicates an uncompensated loss (
Figure 1c). In NF-NR-c, the gradually increasing scattering cross-section (SCS) becomes commensurate with the absorption cross-section; as a result, the extinction cross-section (ECS) increases more rapidly. In contrast, in NF-CS-c, the scattering cross-section remains very small throughout the inspected pump intensity interval; hence, the slowly and monotonously increasing absorption and extinction cross-sections are close to each other. As a result, all optical cross-sections are larger in NF-NR-c than in NF-CS-c.
By increasing the pump intensity, the peak on the spectrum of the average
E-field around the passive resonance is slightly blue-shifted and becomes more intense, and its FWHM decreases (
Figure 1d). The near-field spectra of NF-CS-c and NF-NR-c are similar but more than two-times less intense in NF-CS-c. In the case of NF-NR-c, in the near-field spectrum, there is no linewidth narrowing at small pump intensities; then, as a result of a 3.4-fold decrease, a 13.8 nm linewidth is reached. A monotonously decreasing tendency is observable in NF-CS-c; as a result, a slightly larger (3.6-fold) decrease is achieved with a slightly smaller rate from a smaller FWHM of the passive nanoresonator to a smaller 12.4 nm linewidth of the active nanoresonator (
Figure 1d,
Table S1,
Figure S1f).
At the same time, the dip in the power outflow spectrum around the passive resonance deepens and undergoes linewidth narrowing by increasing the pump intensity for both NF-c-type nanoresonators (
Figure 1e). In the case of NF-NR-c, beside the primary linewidth narrowing at the larger pump, a secondary dip appears at a smaller wavelength, which reveals the existence of coupled modes (
Figure 1e, turquoise). In contrast, in the spectrum of NF-CS-c, there is still no sign of mode competition in the inspected pump interval (
Figure 1e, blue). For further details, see
Section 3.3. about NF-NR-c*-type systems. The peaks in the power outflow spectra of the passive systems are significantly narrower than the near-field peaks. They undergo a similar (1.4- and 1.6-fold) decrease with a smaller rate to considerably larger remaining linewidths (19 and 19.2 nm) in NF-NR and NF-CS-c active systems. This is in accordance with the fact that the NF-c-type nanoresonators are optimized to improve near-field properties (
Figure 1f,
Table S1,
Figure S1f).
The polar diagram of far-field radiation shows that there is no radiation enhancement in the direction of probe propagation (90°). In the complementary polar angle regions, the NF-NR-c amplifies the radiation by redistributing it in four distinct directions. In comparison, the NF-CS-c enhances the radiation similarly, but with a considerably smaller intensity (
Figure 1f).
3.2. Nanorod- and Core–Shell-Mediated Lasing: FF-c-Type Nanoresonators
In the case of the nanorod, when the optimization was performed to enhance the far-field stimulated emission (FF-NR-c), a 97.33 nm long axis and 47.39 nm short axis, corresponding to a smaller aspect ratio of 2.05, were determined, with a much thicker 41.33 nm gain layer coating. This indicates that the FF-NR-c is more sphere-like, and the significantly larger size of both axes shows that both the gold nanorod and the gain volume are an order of magnitude larger compared to the NF-NR-c (
Figure 2a to
Figure 1a insets and
Table S1).
The dielectric–metal–gain multilayer composition optimization realized with the same objective function resulted in a larger core of 28.47 nm radius and a metal shell and a gain medium of 8.85 and 47.45 nm in thickness, respectively (FF-CS-c) (
Figure 2a to
Figure 1a insets and
Table S1). These parameters correspond to a five-fold larger gain and two-fold larger metal volume compared to the NF-CS-c counterpart.
The larger size proves that both the FF-NR-c and the FF-CS-c are capable of promoting far-field scattering, rather than near-field enhancement.
In FF-NR-c, the population inversion exhibits a slower saturation at
: 3.89 (
: 0.09), and the ratio of the internal local (external) pump
E-field strength reveals a 43.22-fold near-field enhancement, which is smaller than in case of NF-NR-c (
Figure S1a,
Table S1). The
: 4.11 (
: 0.11) internal local (external) pump field strength corresponding to saturation indicates a 37.36-fold near-field enhancement in the FF-CS-c system that is larger than that in NF-CS-c (
Figure S1a,
Table S1). Both the internal local and external pump field strength values corresponding to saturation are larger, but the near-field enhancement at the pump wavelength extracted from the ratio of saturation thresholds is smaller in the case of FF-CS-c compared to FF-NR-c. This indicates that the pump process is less promoted in the FF-CS-c nanoresonator than via FF-NR-c, similarly to counterpart NF-c-type nanoresonators.
A similar permittivity and index of refraction are achieved in FF-NR-c and FF-CS-c, after a (faster to slower and faster) slightly faster saturation (of imaginary and real parts in FF-NR-c) in FF-CS-c compared to their NF-c-type counterparts, respectively (
Figure S2b,e). Only the ε
imag(ω
a) and ε
imag(ω
e) values are modified in slightly smaller and larger intervals in the FF-NR-c than in the FF-CS-c (
Figure S2b,c,
Table S1). The near-field and far-field efficiencies are slightly larger in FF-NR-c than in FF-CS-c.
However, there is a significant enhancement in efficiencies of the FF-c-type nanoresonators according to their different objective functions, when the volume fraction ratio of absorbing materials is also considered, especially for the FF-NR-c (
Table S1).
In FF-NR-c, the
: 0.32 (
: 0.007) lasing thresholds are just slightly larger, and the 6.83 × 10
4 V/m (3.57 × 10
4 V/m) slope efficiency in the linear region of the average (maximal) probe
E-field is (almost) ~3-times smaller than that in NF-NR-c, indicating a weaker near-field confinement. The achieved maximal and average probe
E-fields are approximately and more than two-times lower, respectively (
Figure 2a to
Figure 1a and
Table S1). In FF-CS-c, the
: 0.34 (
: 0.009) lasing thresholds are considerably smaller, and the 4.5 × 10
4 V/m (2.9 × 10
5 V/m) slope efficiency in the linear region is more than (almost) two-times smaller. The achieved maximal and average probe
E-fields are more than and almost two-times smaller than those in NF-CS-c (
Figure 2a to
Figure 1a and
Table S1). The FF-NR-c allows a smaller lasing threshold, larger slope efficiency and larger near-field enhancement at the probe wavelength than FF-CS-c does. However, the relation between FF-NR-c and FF-CS-c is similar to that of their NF-c-type counterparts in all these quantities.
Despite the significantly smaller near-field enhancement and the larger volume of FF-NR-c, the NF-c-type and FF-c-type optimized nanorod absorptance values are surprisingly close to each other at the emission (
Figure 2b to
Figure 1b). In FF-NR-c, the gain absorptance becomes negative at the gain threshold value of
: 0.32 (
: 0.007), whereas in NF-CS-c, the threshold of negative gain absorptance is
: 0.33 (
: 0.009). In FF-c-type nanoresonators, the gain threshold values are very similar to those in NF-c-type nanoresonators; however, the thresholds of negative gain become slightly larger in NF-CS-c, similarly to the saturation thresholds. Even if the ohmic loss is similar in the NF-c-type and FF-c-type nanorods, in FF-NR-c, the larger gain makes possible a larger power outflow than that in the passive system above the outflow threshold of
= 2.42. As a result, significant pump energy is converted into far-field radiation. In contrast, the absorptance value in FF-CS-c is more enhanced with respect to its NF-CS-c counterpart, but the larger gain promotes a power outflow enhancement at the larger
= 6.1 power outflow threshold (
Figure 2b to
Figure 1b,
Table S1). The more rapidly increasing and significantly larger gain in FF-NR-c makes it possible to better enhance the far-field radiation; moreover, the power outflow threshold shows up at a significantly smaller pump than in FF-CS-c.
In FF-NR-c, the effect of the overcompensated absorption is observable in the pump-dependent cross-section tendency as well, since the absorption cross-section changes from positive to negative values at the ACS threshold of
: 2.48, with increasing absolute values as the pump increases (
Figure 2c,
Table S1). However, due to the large scattering cross-section, the extinction remains positive and even monotonously increases throughout the inspected pump range, similarly to the NF-NR-c system. The larger cross-section values show that considerably more dynamic energy transitions occur in FF-NR-c than in NF-NR-c, again demonstrating a significant difference between the optimal NF-c-type and FF-c-type systems (
Figure 2c to
Figure 1c).
The initial cross-sections are significantly larger in FF-CS-c than in NF-CS-c. However, while the scattering cross-section monotonously increases and remains higher throughout the inspected pump interval, the absorption and extinction cross-sections exhibit a global maximum and then rapidly decrease. As a result, the absorption cross-section becomes negative, although at a considerably greater local pump field strength (ACS threshold of
: 5.77) than that in FF-NR-c (
Figure 2c,
Table S1). In FF-CS-c, the negative absorption cross-section almost compensates the positive contribution of the scattering cross-section, and the extinction cross-section approaches zero. As a result, all optical cross-sections except the absorption cross-section are larger in NF-NR-c than in NF-CS-c. These results indicate that while the FF-NR-c system is far from the spaser operation region, the FF-CS-c approximates it close to the upper bound of the inspected pump interval (
Figure 2c to
Figure 1c).
By increasing the pump, gradually, a more intense near-field is reached, and on the spectrum, linewidth narrowing is observable on a slightly blue-shifting peak in both FF-NR-c and FF-CS-c (
Figure 2d).
The amplitude of the near-field spectral peak around the passive resonance is significantly larger in FF-NR-c than in FF-CS-c. The near-field spectra of FF-NR-c and FF-CS-c show linewidth broadening at small pumps, and then, the FWHMs start to gradually decrease with increasing pump intensity (
Figure 2d). The 6.1-fold decrease is much larger than that in NF-NR-c and results in a smaller FWHM (12 nm), despite the wider passive spectrum (
Table S1,
Figure S2f). In FF-CS-c, the 4.1-fold decrease is still considerably larger than that in NF-CS-c; however, the linewidth remains slightly larger (12.9 nm) at the largest inspected pump intensity (
Table S1,
Figure S2f). Accordingly, the linewidth of the near-field spectrum of FF-NR-c is always larger than that of FF-CS-c, except at the largest pump, where they are comparable.
The far-field spectrum of FF-NR-c and FF-CS-c exhibits a peak instead of a dip at two consecutive pump intensities and at the highest applied pump intensity, respectively (
Figure 2e). While both the near-field and power outflow spectra are similar in FF-NR-c and FF-CS-c, a dip-to-peak switching in the power outflow spectrum can be seen at smaller pump values in FF-NR-c. The FWHM of the power outflow spectrum gradually and rapidly decreases in FF-NR-c; the large 8.2-fold decrease results in a 6.7 nm linewidth, which is three-times smaller than that in NF-NR-c (
Figure 2e,
Figure S2f). In contrast, in the case of FF-CS-c, sudden narrowing occurs at the largest pump intensity; however, due to the largest 10.9-fold decrease from an intermediate passive linewidth, the reached 3.9 nm FWHM is five-times smaller than that in NF-CS-c, which is the smallest among the inspected systems (
Table S1,
Figure S2f). The FF-c-type nanoresonators show a larger bandwidth compared to their NF-c-type counterparts at small pumps, but this relation is reserved at the largest inspected pump intensity, proving the advantage of these systems in far-field enhancement. The probe signal is not only amplified but it is redistributed in polar angles as well (
Figure 2f). The amplification is larger in FF-c-type than in NF-c-type nanoresonators, and the redistribution is spatially more uniform. The difference between FF-NR-c and FF-CS-c intensity is relatively small compared to the NF-c-type optimization.
By comparing NF-c-type and FF-c-type nanoresonators, one can conclude that the population inversion saturation is faster in the NR and CS nanoresonators optimized to maximize near-field enhancement (
Figures S1a and S2a). At the pump wavelength, the ε
real(ω
a) uniformly is not modified, and ε
imag(ω
a), as well as n(ω
a) and κ(ω
a), decreases slightly more rapidly in NF-c-type nanoresonators (
Figures S1b and S2b,d). At the probe wavelength, ε
real(ω
e) and n(ω
e) decrease more rapidly, whereas the decrease in ε
imag(ω
e) and κ(ω
e) is modified, from faster to slower, in the nanoresonators optimized to maximize the near-field enhancement. In comparison, these tendencies are reversed in the nanoresonators optimized for far-field outcoupling (
Figures S1c,e and S2c,e). In NF-NR-c and FF-NR-c, ε
imag(ω
e) and κ(ω
e) zero crossing occurs at
: 0.52 and at
: 0.62, but their relation is modified at
~4 (
Table S1). The ε
imag(ω
e) and κ(ω
e) values are smaller in NF-CS-c throughout the whole inspected interval and cross zero earlier at
: 0.56, whereas in FF-CS-c, zero crossing occurs later at
: 0.73.
The lasing threshold is slightly smaller in NF-NR-c than in FF-NR-c, whereas this relation is reversed in CS-c nanoresonators. The slope efficiency is uniformly larger for NF-c-type nanoresonators; as a result, the local field increases more rapidly to a larger value before saturation than in FF-c-type nanoresonators (
Figure 1a to
Figure 2a).
The absorptance in gold is very similar, but it is smaller in NF-c-type nanoresonators. The absorptance in the gain medium is larger throughout the complete pump interval in FF-c-type nanoresonators (
Figure 1b to
Figure 2b). The threshold in gain is equal for NR-c nanoresonators, whereas it is smaller in NF-CS-c than in FF-CS-c. For NF-c-type systems, the power outflow remains smaller than the total power of the probe beam throughout the complete inspected pump interval, whereas in FF-c-type nanoresonators, the outflow overrides it above a certain outflow threshold of the pump (
Figure 1b to
Figure 2c).
The absorption cross-section of the smaller maximal absolute value remains positive in NF-c-type nanoresonators, whereas it takes on larger absolute values and becomes negative at a certain ACS threshold in FF-c-type nanoresonators.
It is monotonous for NF-CS-c and FF-NR-c, whereas it exhibits an extremum for NF-NR-c and FF-CS-c. The scattering and the extinction cross-section exhibit a significantly slower monotonous increase to smaller values for the NF-NR-c than in the FF-NR-c. Both the scattering and extinction cross-section monotonously increase for NF-CS-c, whereas the scattering cross-section monotonously increases, but the extinction cross-section exhibits a maximum for FF-CS-c (
Figure 1d to
Figure 2d). The average
E-field increase is faster, but the FWHM decreases less rapidly in NF-c-type nanoresonators (
Figure 1d to
Figure 2d,
Figures S1f–S2f). The outflow gradually decreases by increasing the pump, and the FWHM decreases less rapidly in NF-c-type systems.
The power outflow spectrum switches from a dip to a peak above a certain threshold and the FWHM decreases more rapidly in FF-c-type nanoresonators (
Figure 1e to
Figure 2e,
Figures S1f–S2f). The far-field lobes are larger and are less dependent on the nanoresonator composition in the case of FF-c-type nanoresonators (
Figure 1f to
Figure 2f).
3.3. Nanorod- and Core–Shell-Mediated Spasing: NF-c*-Type Nanoresonators
By increasing the concentration in the [3 × 10
25 m
−3, 3 × 10
26 m
−3] interval, the population inversion saturation behavior of NF-NR-c*-type nanoresonators is intermediate in between NF and FF-NR-c, whereas it increases and saturates most rapidly in NF-CS-c* (
Figures S1a–S3a). This already indicates that NF-NR-c* is a kind of intermediate system, whereas NF-CS-c* differs from both NF and FF-CS-c systems. We have selected those concentrations that result in zero crossing of the extinction cross-section in the inspected pump interval, i.e., below the damage threshold of the nanoresonators.
In NF-NR-c*, in the case of a 5 × 10
25 m
−3 dye concentration, saturation occurs at
: 3.67 (
: 0.08), and the comparison of the internal local and external pump
E-field strengths reveals a 45.88-fold near-field enhancement at the pump wavelength, which is intermediate with respect to the enhancements achieved in NF-NR-c and FF-NR-c (
Figure 2a,
Table S1). The NF-NR-c* approximates the saturation dynamics of FF-NR-c at
= 6.
In NF-CS-c*, in the case of a 8 × 10
25 m
−3 dye concentration, saturation occurs at
: 2.79 (
: 0.11), and the comparison of the internal local and external pump
E-field strengths reveals a 25.36-fold near-field enhancement at the pump wavelength, which is smaller than the enhancement reached in either NF-CS-c or FF-CS-c (
Figure 2a,
Table S1). The saturation arises at a significantly smaller
value in NF-CS-c* than in NF-NR-c*; moreover, the saturation process is faster. This relation is similar (reversed) with respect to the counterpart NF-c-type (FF-c-type) nanoresonators.
In both NF-NR-c* and NF-CS-c*, at the pump wavelength, the difference with respect to the passive system becomes significantly larger in ε
imag(ω
a), as well as in n(ω
a) and κ(ω
a) (
Figures S1b,d–S3b,d,
Table S1). Their values become significantly larger and their decrease is considerably faster than in either of the NF-c-type or FF-c-type counterparts. This causes larger detuning and larger absorption as well.
In both NF-NR-c* and NF-CS-c*, at the probe wavelength, the significantly larger difference in the real parts (ε
real(ω
e) and n(ω
e)) results in larger detuning; however, the real parts decrease faster than in either the NF-c-type or FF-c-type nanoresonator counterpart. The more rapidly decreasing imaginary parts (ε
imag(ω
e) and κ(ω
e)) result in a pronounced negative absorption, and the imaginary parts decrease through a wider interval than in either NF-c-type or FF-c-type nanoresonator counterpart (
Figure S3c,e,
Table S1). The values of ε
imag(ω
a), n(ω
a), κ(ω
a), ε
real(ω
e) and n(ω
e) are larger, whereas ε
imag(ω
e) and κ(ω
e) are smaller in NF-CS-c* than in NF-NR-c* (
Figure S1b,e–S3b,e). All optical parameter intervals are wider in the case of NF-CS-c* than in NF-NR-c* (
Table S1). The initial and final deviations of NF-CS-c* are larger in all values and decrease faster than in NF-NR-c* (
Figure S3c,e).
In NF-NR-c*, the [: 0.65–2.07] region of linear near-field enhancement is contracted, and the largest lasing threshold values (: 0.45 (: 0.013)) are reached with the largest (4.84 × 105 V/m (1.88 × 106 V/m)) slope efficiency in the average (maximal) probe E-field among the nanorod-based nanoresonators.
At small and large pumps, an intermediate value of the average probe
E-field is achieved; however, instead of saturation, a rapid monotonous near-field decrease occurs after a global maximum at
= 2.07 (
Figure 3a,
Table S1).
In NF-CS-c*, the [
: 0.30–2.20] region of linear near-field enhancement contracts, but the smallest lasing threshold values
: 0.29 (
: 0.011)) are reached with the largest (1.87 × 10
5 V/m (8.83 × 10
5 V/m)) slope efficiency in the average (maximal) probe
E-field among the CS nanoresonators (
Figure 3a,
Table S1). At small and large pumps, the smallest average
E-field is achieved, but similarly to the NF-NR-c*, instead of saturation, a rapid near-field decrease occurs after a global maximum at
= 2.2.
In near-field enhancement, both systems override the counterpart NF-NR-c and NF-CS-c nanoresonators at their maximum. In comparison, the lasing threshold is larger, but the slope efficiency as well as the achieved maximal and average local probe E-field strengths are also larger in NF-NR-c* than in NF-CS-c*. Another difference is the faster decrease in the near-field in NF-CS-c*, when the pump is further increased.
The onset of gain occurs at a gain threshold of : 0.29 (: 0.006) in NF-NR-c* and : 0.31 (: 0.012) in NF-CS-c*. The onset of gain occurs at smaller and values in the case of NF-NR-c*. Correspondingly, in both NF-NR-c* and NF-CS-c*, the gold absorptance has a similar (smaller) initial value compared to the counterpart NF-c-type (FF-c-type) nanoresonators, but more rapidly increases and exhibits a maximum value that overrides the absorptance in FF-c-type nanoresonators as well, and then starts to decrease.
The gain exhibits a similar tendency as the gold absorptance, but with a slightly larger absolute value, which promotes the far-field power outcoupling. The decrease is more rapid in NF-CS-c* than in NF-NR-c*; however, the reached maximal gain is larger in NF-CS-c* nanoresonator (
Figure 3b).
In the far-field response, an enhanced power outflow appears, which reveals that the energy of the probe can be enhanced and outcoupled as well (
Figure 3b). This is because the smaller gain is accompanied by an even smaller absorptance in the metal rod (shell), and as a result, the loss is moderated as well. However, in NF-NR-c*, this outcoupling occurs at a larger pump than in FF-NR-c, and the outcoupled power remains smaller. In contrast, in NF-CS-c*, the outcoupling arises at a smaller pump than in FF-CS-c, and its amplitude reaches larger values. In NF-NR-c* and NF-CS-c*, the initial values of power outflow are similar, but in the case of NF-CS-c*, it begins to increase earlier and faster. The outcoupling is achieved at a considerably smaller pump (
= 1.24) in NF-CS-c* than in NF-NR-c* (
= 4.29); however, the maximal outcoupled power reached in NF-CS-c* at (
= 2.2) is almost equal to that in NF-NR-c* at
= 7.7 (
Figure 3b,
Table S1).
Based on the pump-dependent cross-section values in both NF-NR-c* and NF-CS-c*, the scattering cross-section is relatively small and exhibits a maximum at
= 2.1 and
= 2.2. In NF-NR-c* (NF-CS-c*), the absorption cross-section also shows a maximum at
= 2.1 (
= 1.0), and then, it becomes negative at
= 4.24 (1.26) as the pump intensity increases (
Figure 3c). The extinction cross-section is governed by the absorption cross-section; hence, in contrast to the NF-NR-c and NF-CS-c, it also exhibits a maximum and then becomes negative at
= 4.53 (1.29).
Both the absorption and extinction cross-sections reach their minimum at pump values corresponding to the maximal power outflow. The comparison of NF-CS-c* to NF-NR-c* shows that the scattering cross-section is similarly small, the initial absorption cross-section is also smaller in NF-CS-c*; moreover, it becomes negative more rapidly and exhibits a narrower dip of a similar negative value than that in NF-NR-c*. The extinction cross-section is analogously determined by the absorption cross-section in NF-c*-type nanoresonators.
The near-field spectra in NF-NR-c* (NF-CS-c*) indicate that the large refractive index shift at smaller pump values makes the optimized system non-resonant around the emission wavelength, i.e., the peak red-shifts to ~715 nm (~720 nm). Compared to counterpart NF-c-type and FF-c-type nanoresonators, the near-field increases most rapidly from an intermediate level and exhibits narrowing but splits at large pump intensities. In the case of very intense pumping, an additional peak emerges again around 705 nm (700 nm), with neighboring dips on the near-field spectra (
Figure 3d). The only difference is that the splitting results in a global maximum at a larger (smaller) wavelength in NF-NR-c* (NF-CS-c*), and the intensity of the spectra is always lower in NF-CS-c*. In NF-NR-c* and NF-CS-c*, the linewidths of the near-field spectra are similar; however, due to the smaller 3.2-fold linewidth narrowing, the final linewidths of 14.6 and 14.3 nm remain larger compared to the values of NF-c-type counterparts (
Figure 3d,
Table S1,
Figure S3f). This indicates that the NF-c*-type systems are not optimal in the near-field. The NF-CS-c* shows no linewidth narrowing at small pump intensities, but at the largest pump, its near-field spectral bandwidth is comparable to that of NF-NR-c*.
The far-field spectrum not only switches from a dip to a peak, but it also exhibits a narrowing; however, the FWHM decrease is slightly (significantly) slower in NF-NR-c* (NF-CS-c*) than in FF-c-type counterparts (
Figure 3e). At the highest inspected pump, the maximum on the far-field spectrum is coincident with 710 nm in NF-NR-c*, whereas it is still shifted to 705 nm in NF-CS-c* and shows asymmetry as a sign of coupled modes’ co-existence. The dips in NF-NR-c* spectra are deeper and are closer, whereas the peak is more intense. In its power outflow spectrum, NF-NR-c* shows significant 1.8-fold narrowing arising only at the largest inspected pump intensity (
Figure 3e,
Table S1,
Figure S3f). Due to the larger rate of FWHM decrease, the obtained 15.5 nm linewidth is smaller than that in NF-NR-c.
Similarly, in NF-CS-c*, the 1.9-fold decrease is larger; as a result, the reached minimal 16.3 nm linewidth is smaller than the values in the NF-CS-c counterpart ((
Figure 3e,
Table S1,
Figure S3f). Despite the larger rate of narrowing in NF-CS-c*, the linewidth remains slightly smaller in NF-NR-c* according to the narrower passive nanoresonator bandwidth.
At a high intensity, the increased concentration becomes advantageous, but spectral bandwidths in NF-c*-type nanoresonators are intermediate with respect to the counterpart NF-c-type and FF-c-type active nanoresonators. This is in accordance with the pump intensity dependence of the power outflow, which can be enhanced with increased concentration throughout a wide band (
Figure 3b).
According to the polar diagram of far-field emission, NF-NR-c* and NF-CS-c* are unique systems in the sense that they are capable of amplifying the probe beam along the direction of propagation; hence, the spatial redistribution in polar angles becomes significantly less inhomogeneous compared to NF-c-type and FF-c-type counterparts. Similar (in contrast) to the NF-c-type and FF-c-type optimized nanoresonators, based on the EQE the outcoupling into the far-field is more efficient in NF-CS-c* than in NF-NR-c*. These unique transitions indicate that by considerably changing one of the configuration parameters—the dye concentration in the present case—the optical response may undergo a significant modification as well.
The near- and far-field spectra at the pump intensities, which result in the maximal outcoupling in NF-NR-c* and NF-CS-c*, indicate that there is a strong interaction between different co-existing modes (
Figure 4a,b). Undoubtedly, the spectra collected by increasing the concentration from 3 × 10
25 m
−3 to 3 × 10
26 m
−3 reveal that at intermediate concentration (5 × 10
25 m
−3 and 8 × 10
25 m
−3), a peak appears in between two dips on the far-field spectral response of NF-NR-c* and NF-CS-c* (
Figure 4a,b).
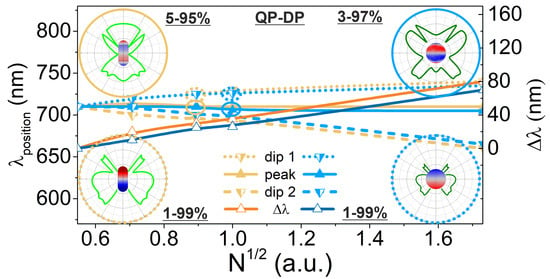
The spectral distance of these dips is proportional to the
at intermediate concentrations, which reveals that two modes are strongly coupled in the active nanoresonator (
Figure 4c). The time evolution of the charge separations at the peak and neighboring dips has been extracted from the steady-state FEM computations, which implicitly comprises full, time-harmonic dynamic data extensions.
The time evolution proves that, although the dipolar mode is dominant at all extrema, at the peak, a quadrupolar charge separation appears in an enhanced fraction of each time cycle (
Figure 4d,
Supplementary Materials). However, this transient phenomenon becomes less dominant by further increasing the concentration. The symmetry of the polar angle distribution of the far-field emission pattern also indicates the co-existence of different modes (
Figure 4e,f).