Characterization and Modeling of Nano Wear for Molybdenum-Based Lubrication Layer Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Manufacture of the Specimens
2.2. Nanotechnical Investigations
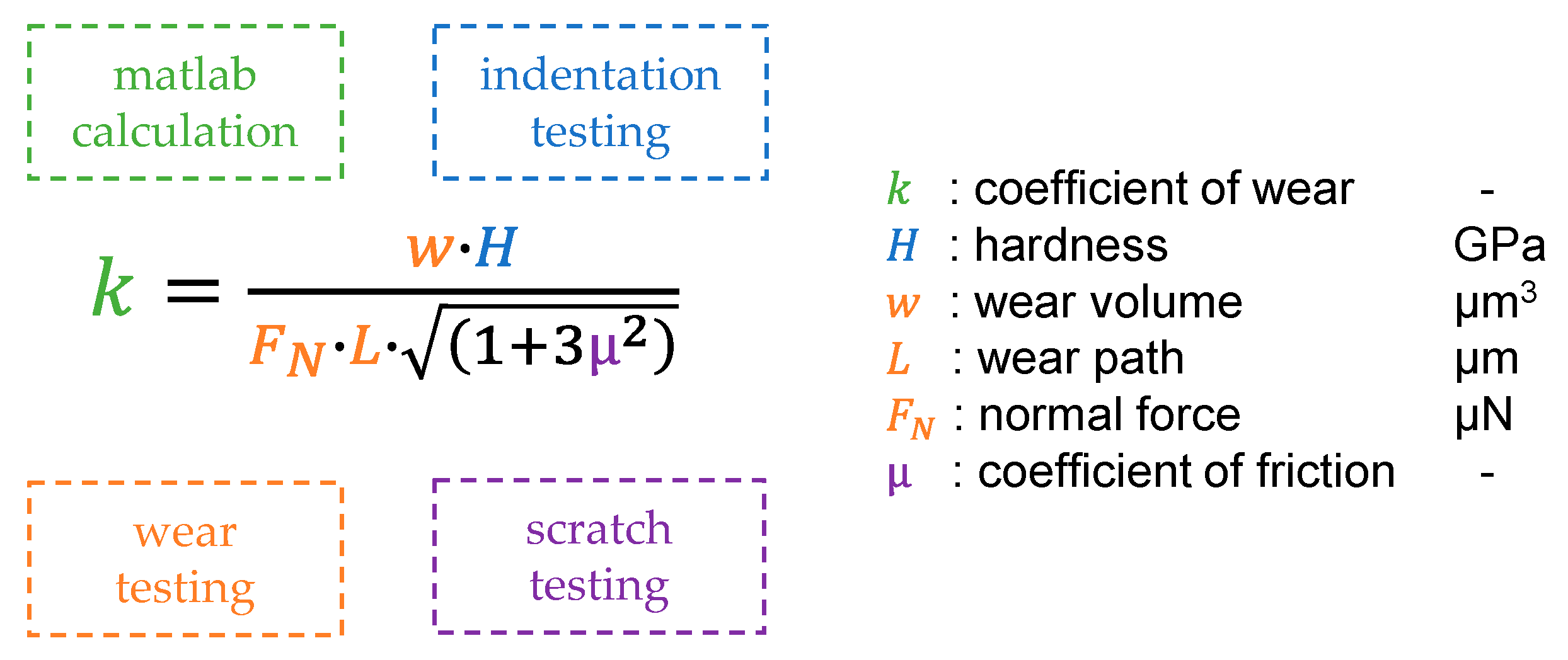
2.3. Wear Modeling
2.4. SEM and Optical Investigations
3. Results and Discussions
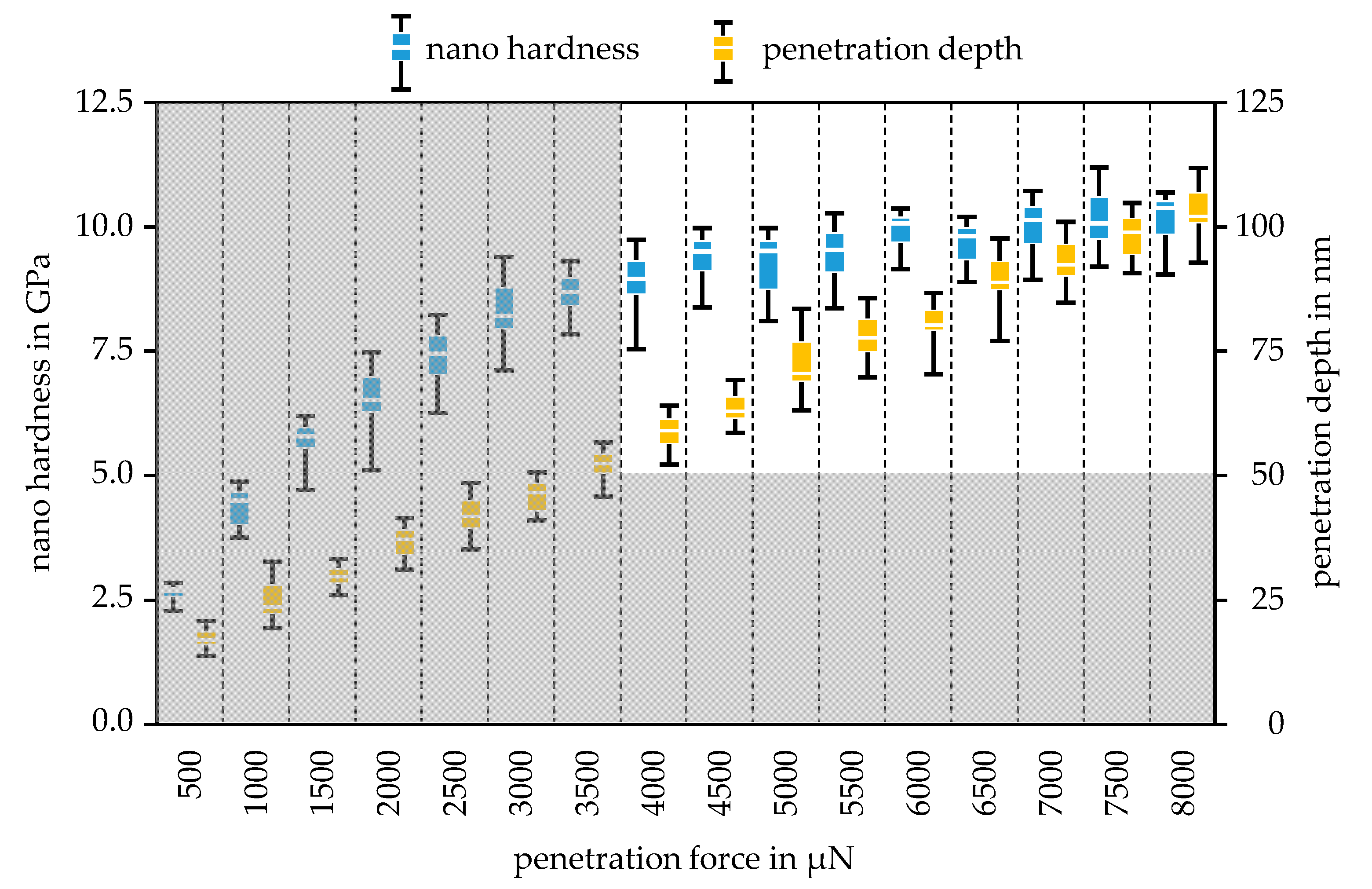
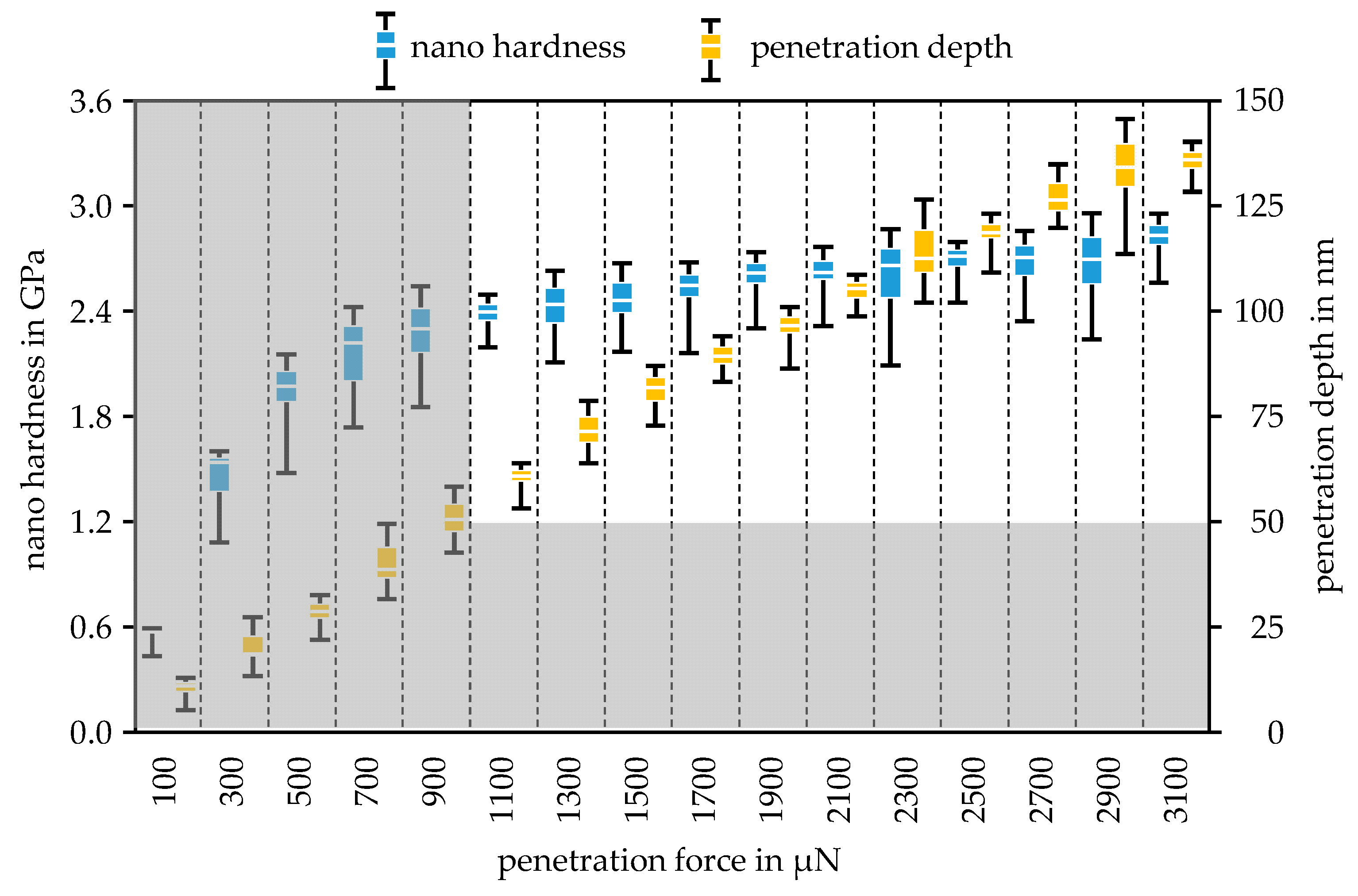
3.1. Nano Indentation and Scratch Test
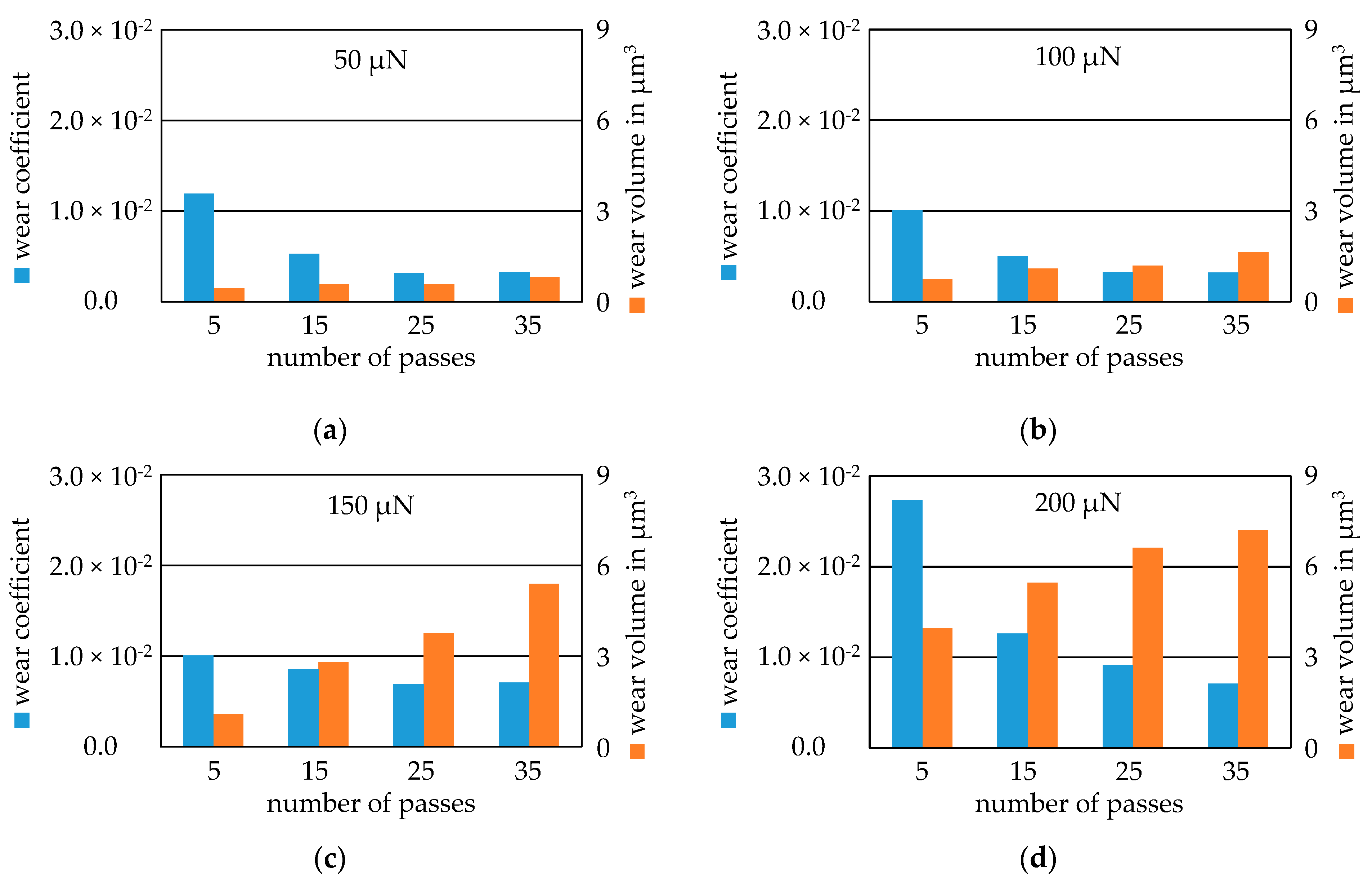
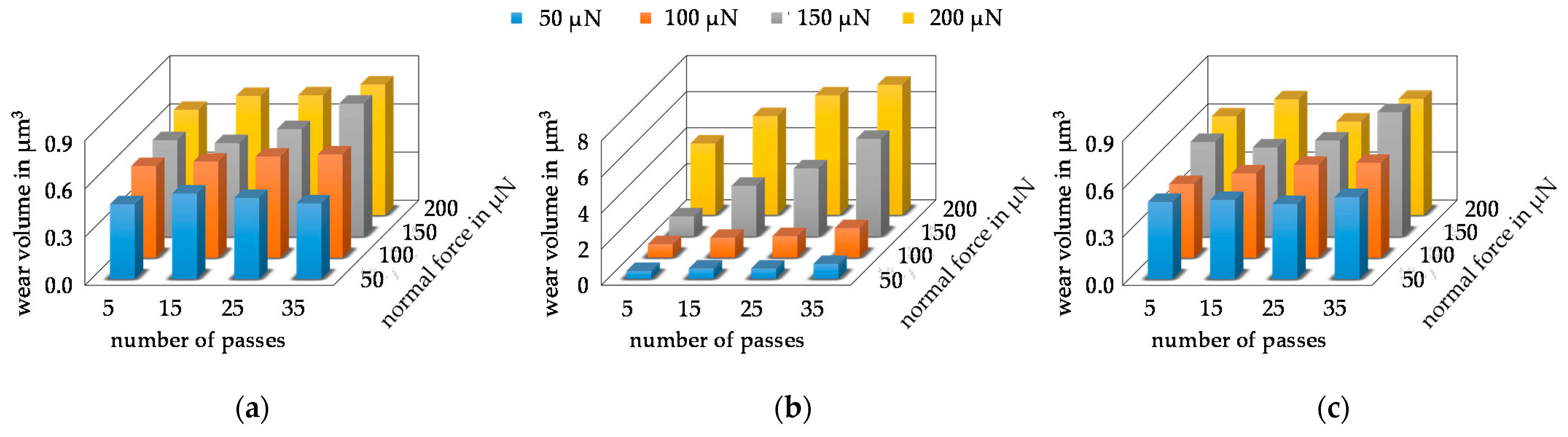
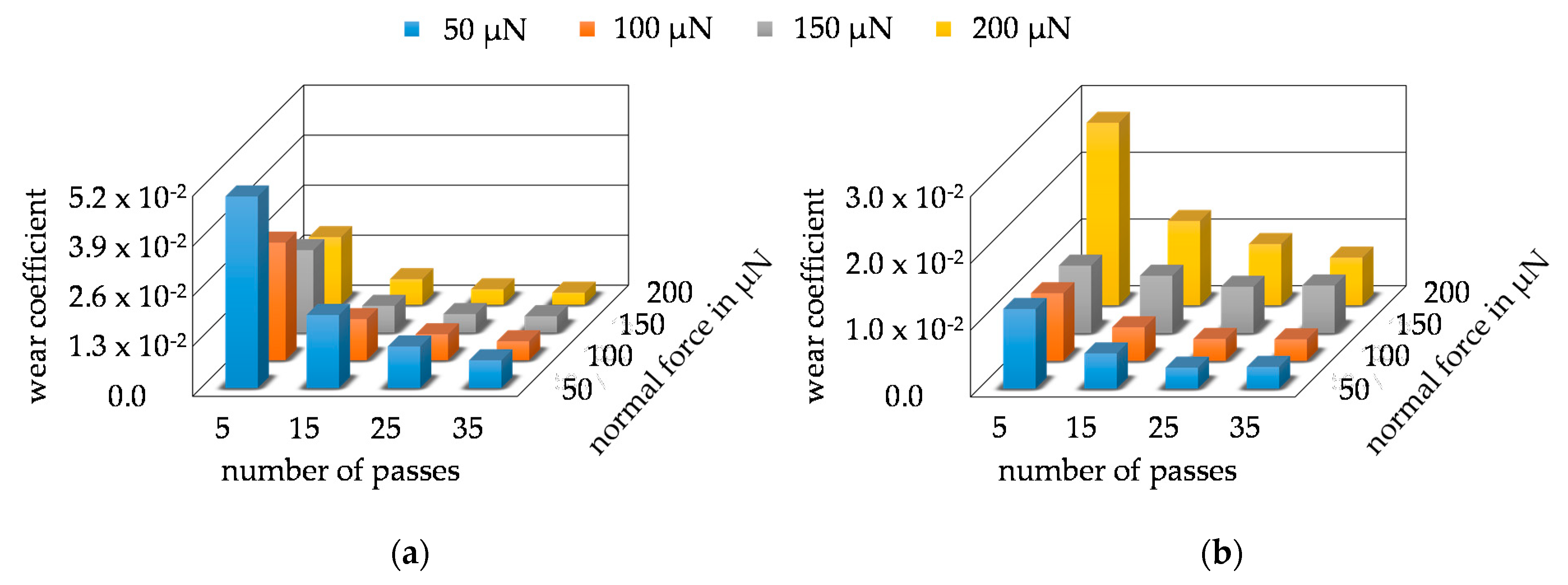
3.2. Wear Tests
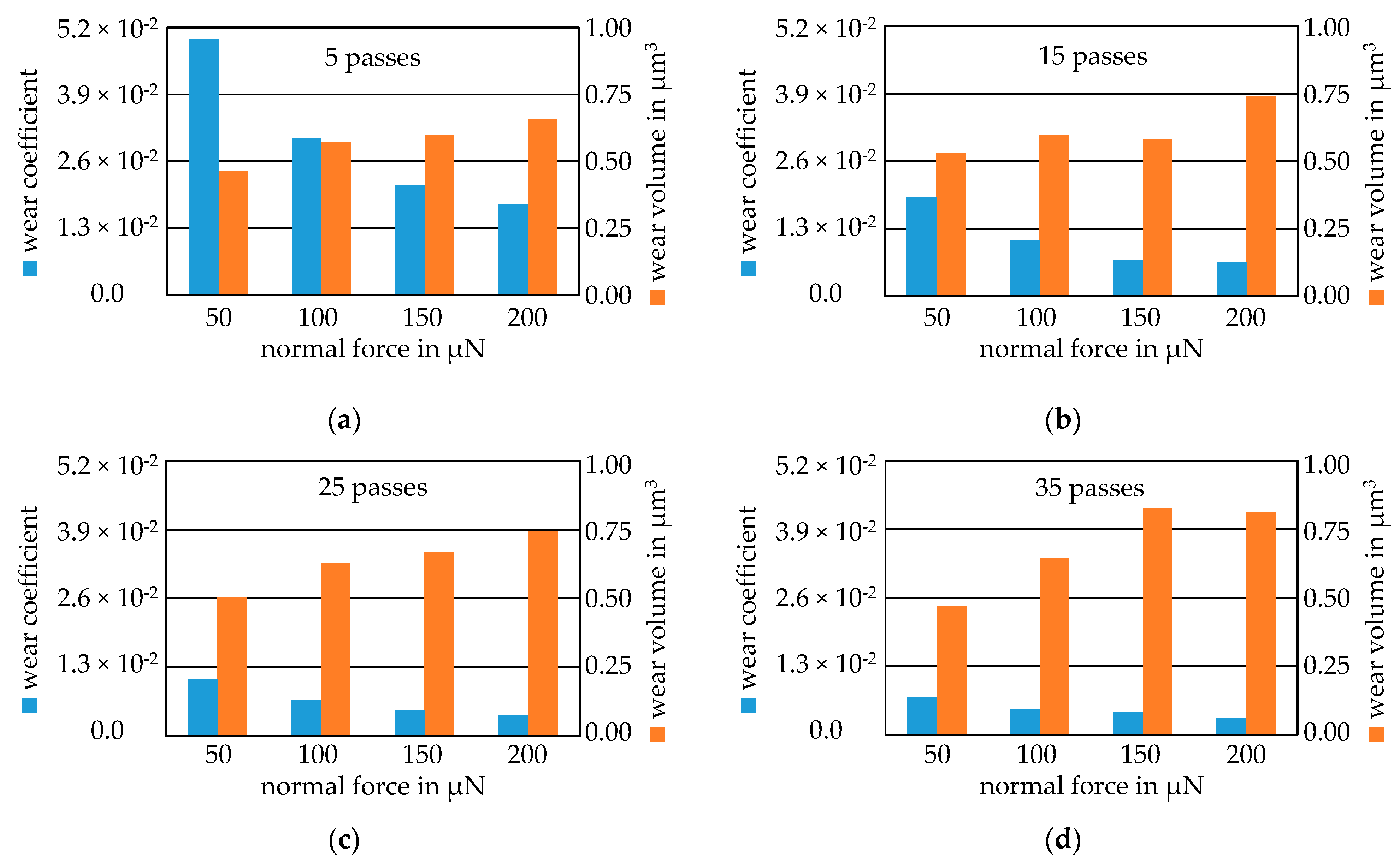
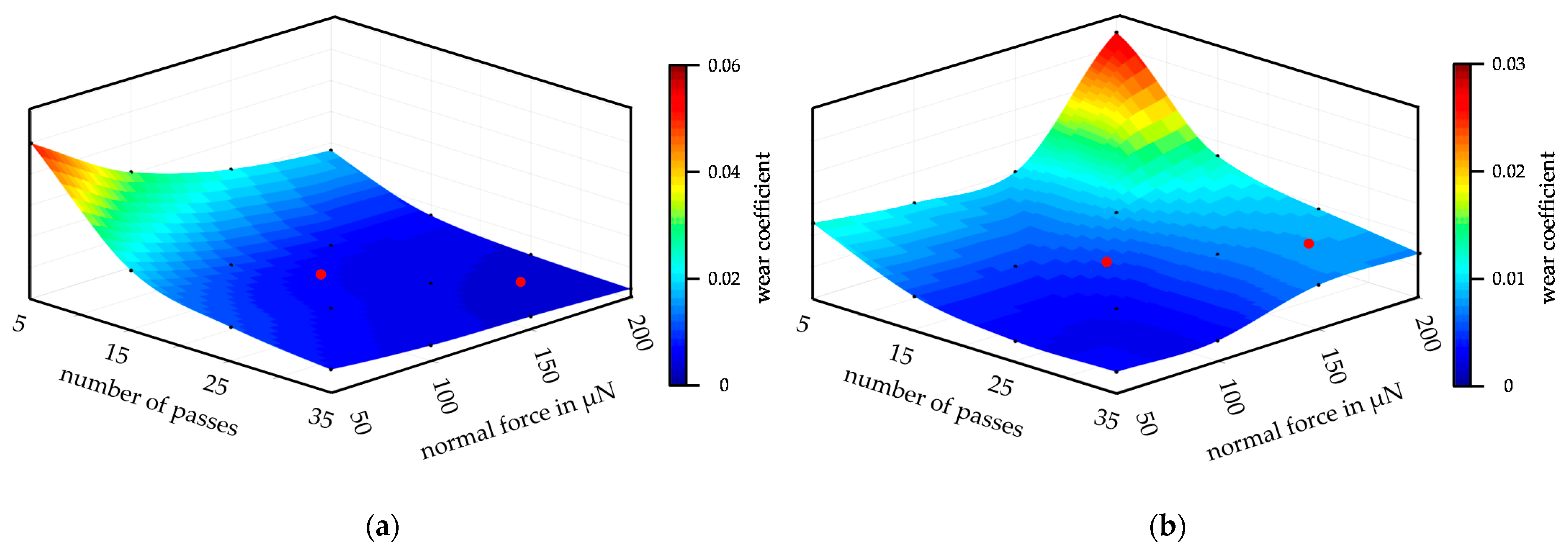
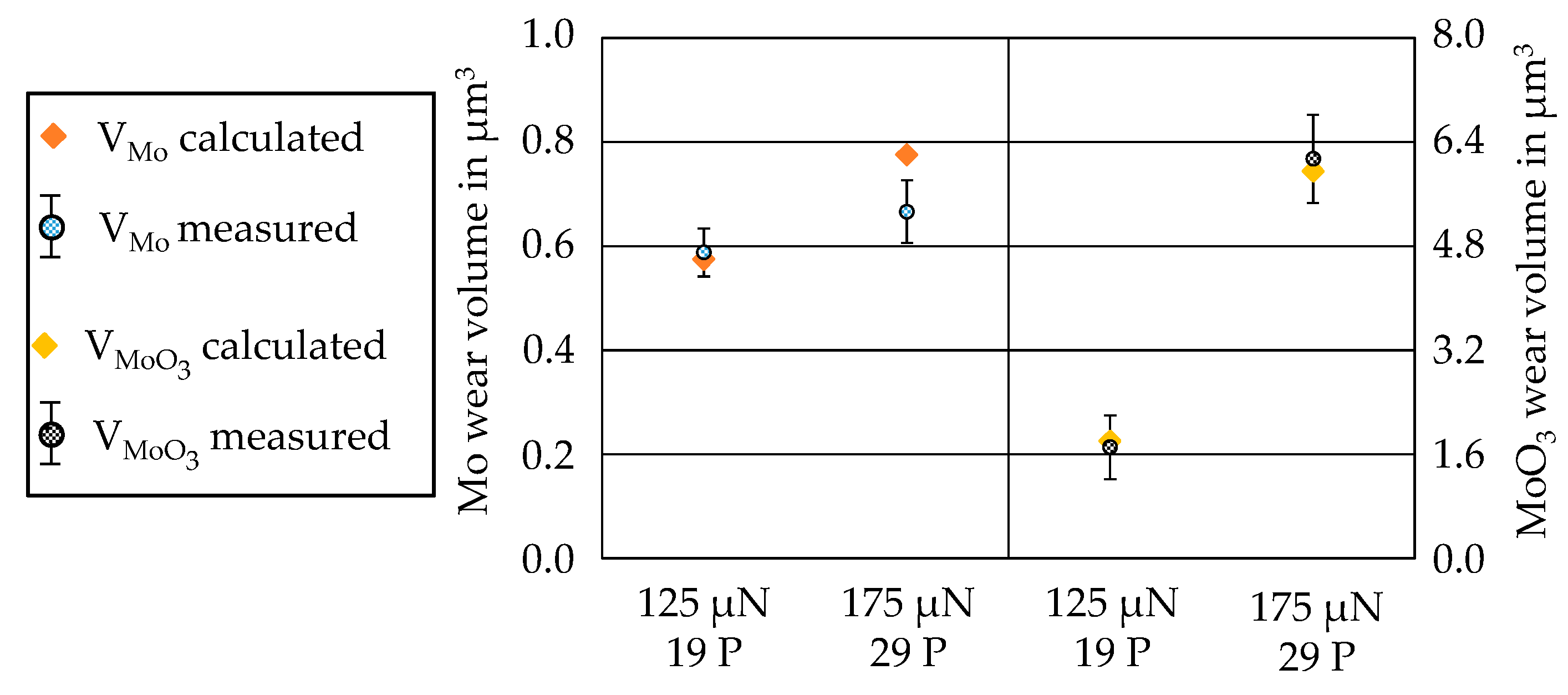
3.3. Wear Modeling and Validation
4. Conclusions
- Rapid abrasion and providing MoO3 in the run-in phase due to the low hardness and exponential wear;
- Wear-resistant Mo reservoir due to the high hardness; and
- Regenerative lubrication, presumably only transfer lubrication, of the wear particles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

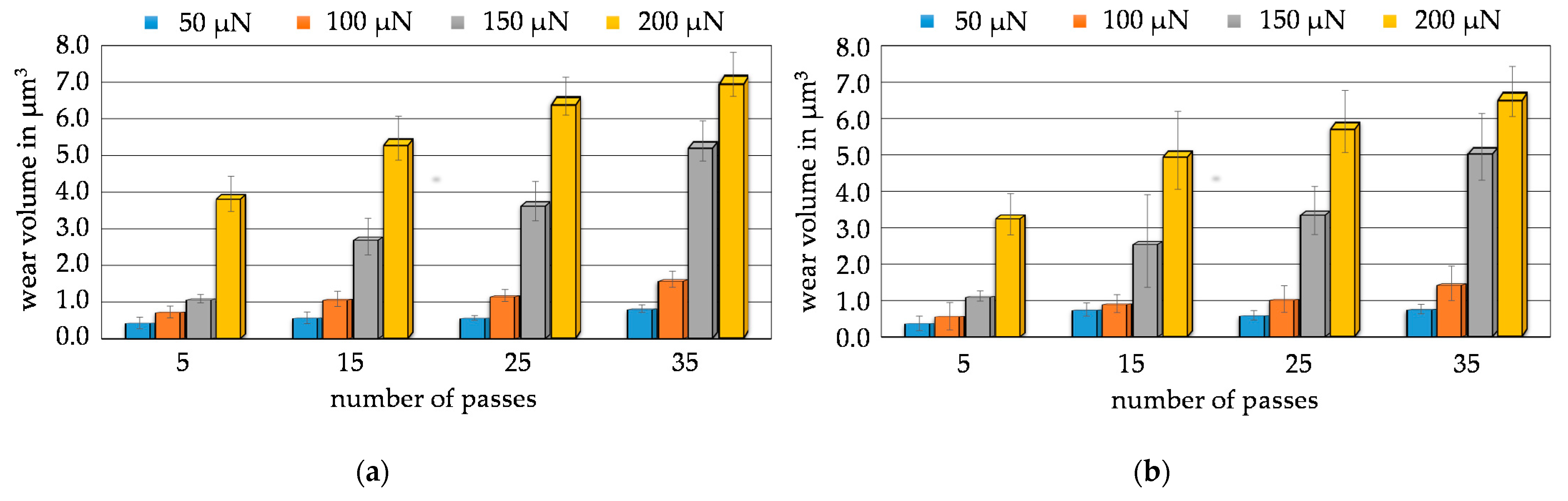
Appendix B
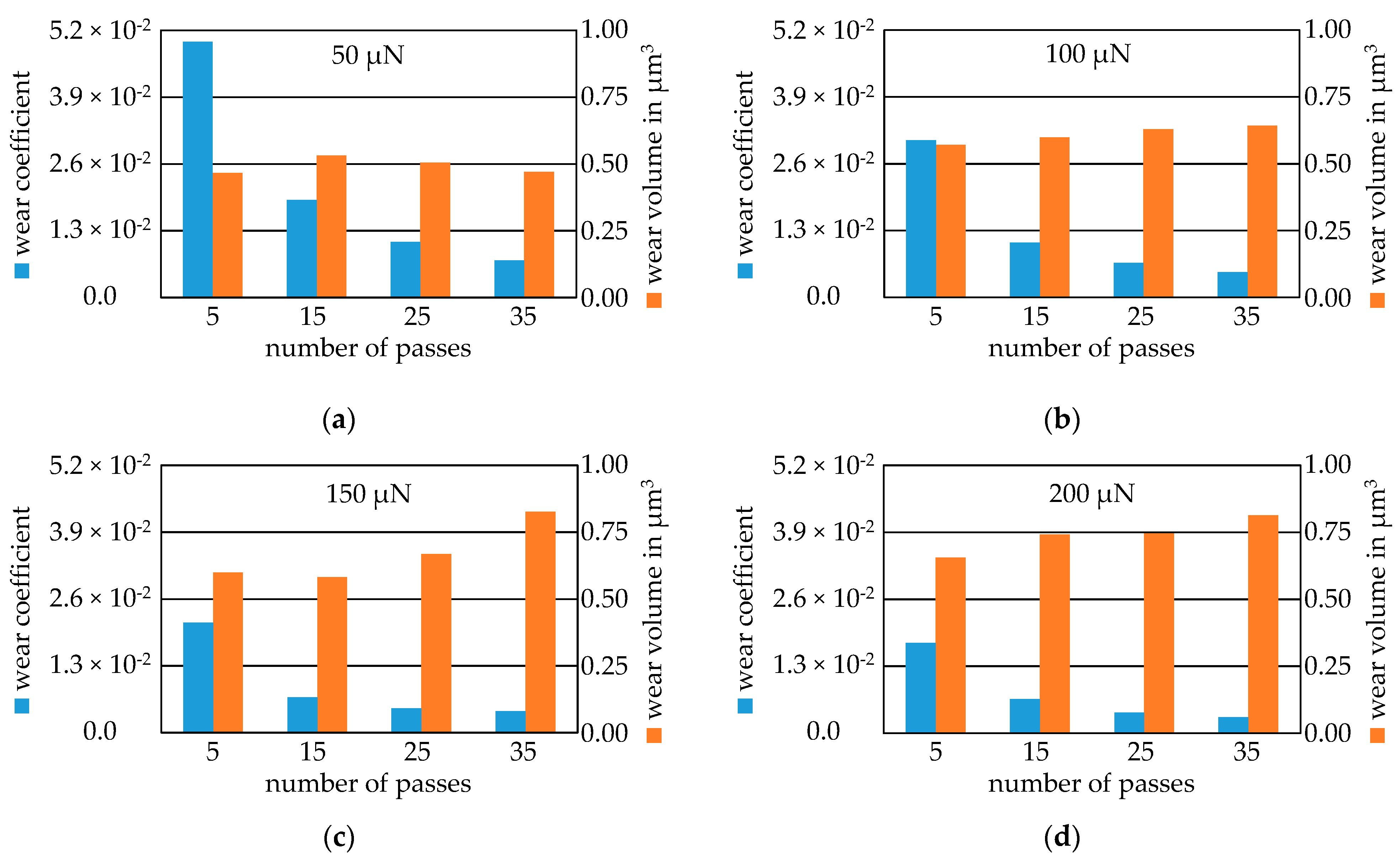
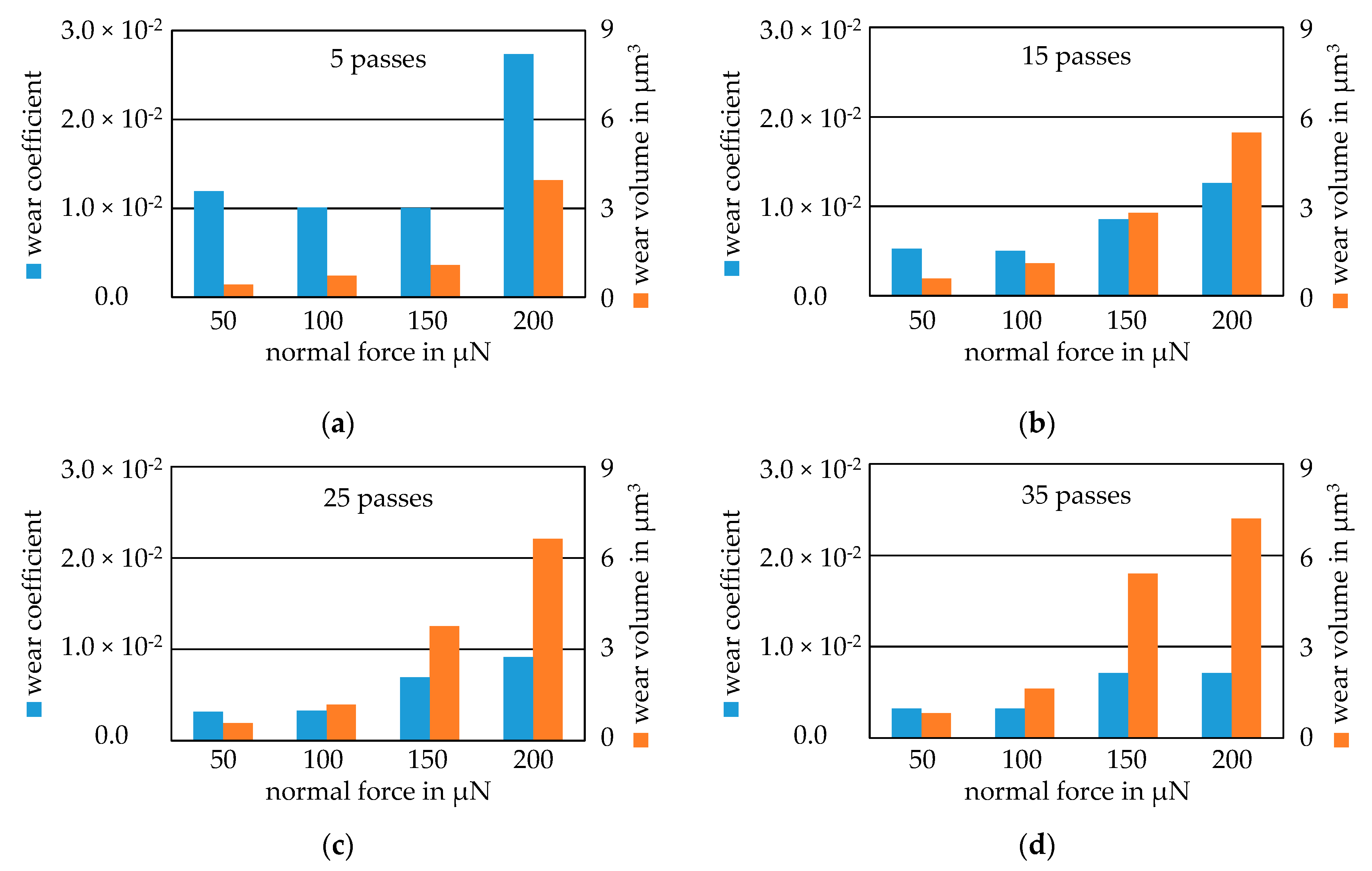
References
- Vazirisereshk, M.R.; Martini, A.; Strubbe, D.A.; Baykara, M.Z. Solid lubrication with MoS2: A review. Lubricants 2019, 7, 57. [Google Scholar] [CrossRef]
- Schöler, S.; Schmieding, M.; Heimes, N.; Pape, F.; Behrens, B.-A.; Poll, G.; Möhwald, K. Characterization of molybdenum based coatings on 100Cr6 bearing steel surfaces. Tribol. Online 2020, 15, 181–185. [Google Scholar] [CrossRef]
- Vashishtha, N.; Sapate, S.G.; Gahlot, J.S.; Bagde, P. Effect of tribo-oxidation on friction and wear behaviour of HVOF sprayed WC–10Co–4Cr coating. Tribol. Lett. 2018, 66. [Google Scholar] [CrossRef]
- Verma, D.K.; Shukla, N.; Kumar, B.; Singh, A.K.; Shahu, K.; Yadav, M.; Rhee, K.Y.; Rastogi, R.B. Synergistic tribo-activity of nanohybrids of zirconia/cerium-doped zirconia nanoparticles with nano lamellar reduced graphene oxide and molybdenum disulfide. Nanomaterials 2020, 10, 707. [Google Scholar] [CrossRef] [PubMed]
- Costa, N.A.; Correa, D.R.N.; Lisboa-Filho, P.N.; Sousa, T.S.P.; Grandini, C.R.; Rocha, L.A. Influence of the molybdenum on characteristics of oxide films produced by micro-arc oxidation on Ti-15Zr-based alloys. Surf. Coat. Technol. 2021, 408, 126856. [Google Scholar] [CrossRef]
- Saravanan, P.; Selyanchyn, R.; Watanabe, M.; Fujikawa, S.; Tanaka, H.; Lyth, S.M.; Sugimura, J. Ultra-low friction of polyethylenimine/molybdenum disulfide (PEI/MoS2)15 thin films in dry nitrogen atmosphere and the effect of heat treatment. Tribol. Int. 2018, 127, 255–263. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Sarkar, A.D. Friction and Wear; Academic Press: London, UK, 1980; ISBN 0-12-619260-X. [Google Scholar]
- Klassen, A.; Bouguecha, A.; Behrens, B.A. Wear prediction for hot forging dies under consideration of structure modification in the surface layer. AMR 2014, 1018, 341–348. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Schaefer, F. Prediction of wear in hot forging tools by means of finite-element-analysis. J. Mater. Process. Technol. 2005, 167, 309–315. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Brunotte, K.; Wester, H.; Rothgänger, M.; Müller, F. Multi-layer wear and tool life calculation for forging applications considering dynamical hardness modeling and nitrided layer degradation. Materials 2020, 14, 104. [Google Scholar] [CrossRef]
- Bhushan, B. Nano- to microscale wear and mechanical characterization using scanning probe microscopy. Wear 2001, 251, 1105–1123. [Google Scholar] [CrossRef]
- Bhushan, B.; Israelachvili, J.N.; Landman, U. Nanotribology: Friction, wear and lubrication at the atomic scale. Nature 1995, 374, 607–616. [Google Scholar] [CrossRef]
- Perry, S.S.; Tysoe, W.T. Frontiers of fundamental tribological research. Tribol. Lett. 2005, 19, 151–161. [Google Scholar] [CrossRef]
- Szlufarska, I.; Chandross, M.; Carpick, R.W. Recent advances in single-asperity nanotribology. J. Phys. D Appl. Phys. 2008, 41, 123001. [Google Scholar] [CrossRef]
- Beake, B.D.; Shipway, P.H.; Leggett, G.J. Influence of mechanical properties on the nanowear of uniaxially oriented poly(ethylene terephthalate) film. Wear 2004, 256, 118–125. [Google Scholar] [CrossRef]
- Fasce, L.; Cura, J.; del Grosso, M.; Bermúdez, G.G.; Frontini, P. Effect of nitrogen ion irradiation on the nano-tribological and surface mechanical properties of ultra-high molecular weight polyethylene. Surf. Coat. Technol. 2010, 204, 3887–3894. [Google Scholar] [CrossRef]
- Vyas, M.K.; Nandan, B.; Schneider, K.; Stamm, M. Nanowear studies in chemically heterogeneous responsive polymeric brushes by surface force microscopy. Eur. Polym. J. 2009, 45, 1367–1376. [Google Scholar] [CrossRef]
- Pihan, S.A.; Emmerling, S.G.J.; Butt, H.-J.; Gutmann, J.S.; Berger, R. Nanowear in a nanocomposite reinforced polymer. Wear 2011, 271, 2852–2856. [Google Scholar] [CrossRef]
- Dinelli, F.; Leggett, G.J.; Alexander, M.R. Nanowear in scanning force microscopy: Information on deposits formed in and downstream of a hexane plasma. J. Appl. Phys. 2002, 91, 3841–3846. [Google Scholar] [CrossRef]
- Berger, R.; Cheng, Y.; Förch, R.; Gotsmann, B.; Gutmann, J.S.; Pakula, T.; Rietzler, U.; Schärtl, W.; Schmidt, M.; Strack, A.; et al. Nanowear on polymer films of different architecture. Langmuir 2007, 23, 3150–3156. [Google Scholar] [CrossRef]
- Sinha, S.K.; Chong, W.L.M.; Lim, S.-C. Scratching of polymers—Modeling abrasive wear. Wear 2007, 262, 1038–1047. [Google Scholar] [CrossRef]
- Jiang, Z.; Lu, C.-J.; Bogy, D.B.; Miyamoto, T. Dependence of nano-friction and nano-wear on loading force for sharp diamond tips sliding on Si, Mn-Zn ferrite, and Au. J. Tribol. 1995, 117, 328–333. [Google Scholar] [CrossRef]
- Degiampietro, K.; Colaço, R. Nanoabrasive wear induced by an AFM diamond tip on stainless steel. Wear 2007, 263, 1579–1584. [Google Scholar] [CrossRef]
- Peng, L.; Lee, H.; Teizer, W.; Liang, H. Nanowear of gold and silver against silicon. Wear 2009, 267, 1177–1180. [Google Scholar] [CrossRef]
- Ali, M.K.A.; Xianjun, H. M50 matrix sintered with nanoscale solid lubricants shows enhanced self-lubricating properties under dry sliding at different temperatures. Tribol. Lett. 2019, 67. [Google Scholar] [CrossRef]
- Mitchell, A.; Shrotriya, P. Onset of nanoscale wear of metallic implant materials: Influence of surface residual stresses and contact loads. Wear 2007, 263, 1117–1123. [Google Scholar] [CrossRef]
- Martinez-Nogues, V.; Nesbitt, J.M.; Wood, R.J.K.; Cook, R.B. Nano-scale wear characterization of CoCrMo biomedical alloys. Tribol. Int. 2016, 93, 563–572. [Google Scholar] [CrossRef]
- Achanta, S.; Drees, D.; Celis, J.-P. Friction and nanowear of hard coatings in reciprocating sliding at milli-Newton loads. Wear 2005, 259, 719–729. [Google Scholar] [CrossRef]
- Stoyanov, P.; Romero, P.A.; Merz, R.; Kopnarski, M.; Stricker, M.; Stemmer, P.; Dienwiebel, M.; Moseler, M. Nanoscale sliding friction phenomena at the interface of diamond-like carbon and tungsten. Acta Mater. 2014, 67, 395–408. [Google Scholar] [CrossRef]
- Machcha, A.R.; Azarian, M.H.; Talke, F.E. An investigation of nano-wear during contact recording. Wear 1996, 197, 211–220. [Google Scholar] [CrossRef]
- Khurshudov, A.G.; Kato, K.; Koide, H. Nano-wear of the diamond AFM probing tip under scratching of silicon, studied by AFM. Tribol. Lett. 1996, 2, 345–354. [Google Scholar] [CrossRef]
- Wang, Z.-Z.; Gu, P.; Wu, X.-P.; Zhang, H.; Zhang, Z.; Chiang, M.Y.M. Micro/nano-wear studies on epoxy/silica nanocomposites. Comp. Sci. Technol. 2013, 79, 49–57. [Google Scholar] [CrossRef]
- Heimes, N.; Pape, F.; Konopka, D.; Schöler, S.; Möhwald, K.; Poll, G.; Behrens, B.-A. Investigation of the scaling of friction coefficients from the nano to the micro level for base materials and coatings. In Production at the Leading Edge of Technology; Behrens, B.-A., Brosius, A., Hintze, W., Ihlenfeldt, S., Wulfsberg, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 161–170. ISBN 978-3-662-62137-0. [Google Scholar]
- Konopka, D.; Pape, F.; Heimes, N.; Matthias, T.; Schöler, S.; Möhwald, K.; Behrens, B.-A.; Poll, G. Micro- and nanotribological characterization of molybdenum oxide based coatings on 100Cr6 bearing steel surfaces. BALTTRIB 2019, 1. [Google Scholar] [CrossRef]
- Dhanasekaran, S.; Gnanamoorthy, R. Microstructure, strength and tribological behavior of Fe-C-Cu-Ni sintered steels prepared with MoS2 addition. J. Mater. Sci. 2007, 42, 4659–4666. [Google Scholar] [CrossRef]
- Malik, I.Y.; Lorenz, U.; Chugreev, A.; Behrens, B.-A. Microstructure and wear behaviour of high alloyed hot-work tool steels 1.2343 and 1.2367 under thermo-mechanical loading. IOP Conf. Ser. Mater. Sci. Eng. 2019, 629, 12011. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation; Springer Science + Business Media LLC: New York, NY, USA, 2011; ISBN 978-1-4419-9872-9. [Google Scholar]
- Behrens, B.-A.; Bouguecha, A.; Vucetic, M.; Peshekhodov, I.; Matthias, T.; Kolbasnikov, N.; Sokolov, S.; Ganin, S. Experimental investigations on the state of the friction-welded joint zone in steel hybrid components after process-relevant thermo-mechanical loadings. AIP Conf. Proc. 2016, 1769, 130013. [Google Scholar] [CrossRef]
- Heimes, N.; Pape, F.; Poll, G.; Konopka, D.; Schöler, S.; Möhwald, K.; Behrens, B.-A. Characterisation of self-regenerative dry lubricated layers on Mo-basis by nano mechanical testing. In Production at the Leading Edge of Technology; Wulfsberg, J.P., Hintze, W., Behrens, B.-A., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 139–148. ISBN 978-3-662-60416-8. [Google Scholar]
- Koinkar, V.N.; Bhushan, B. Effect of scan size and surface roughness on microscale friction measurements. J. Appl. Phys. 1997, 81, 2472–2479. [Google Scholar] [CrossRef]

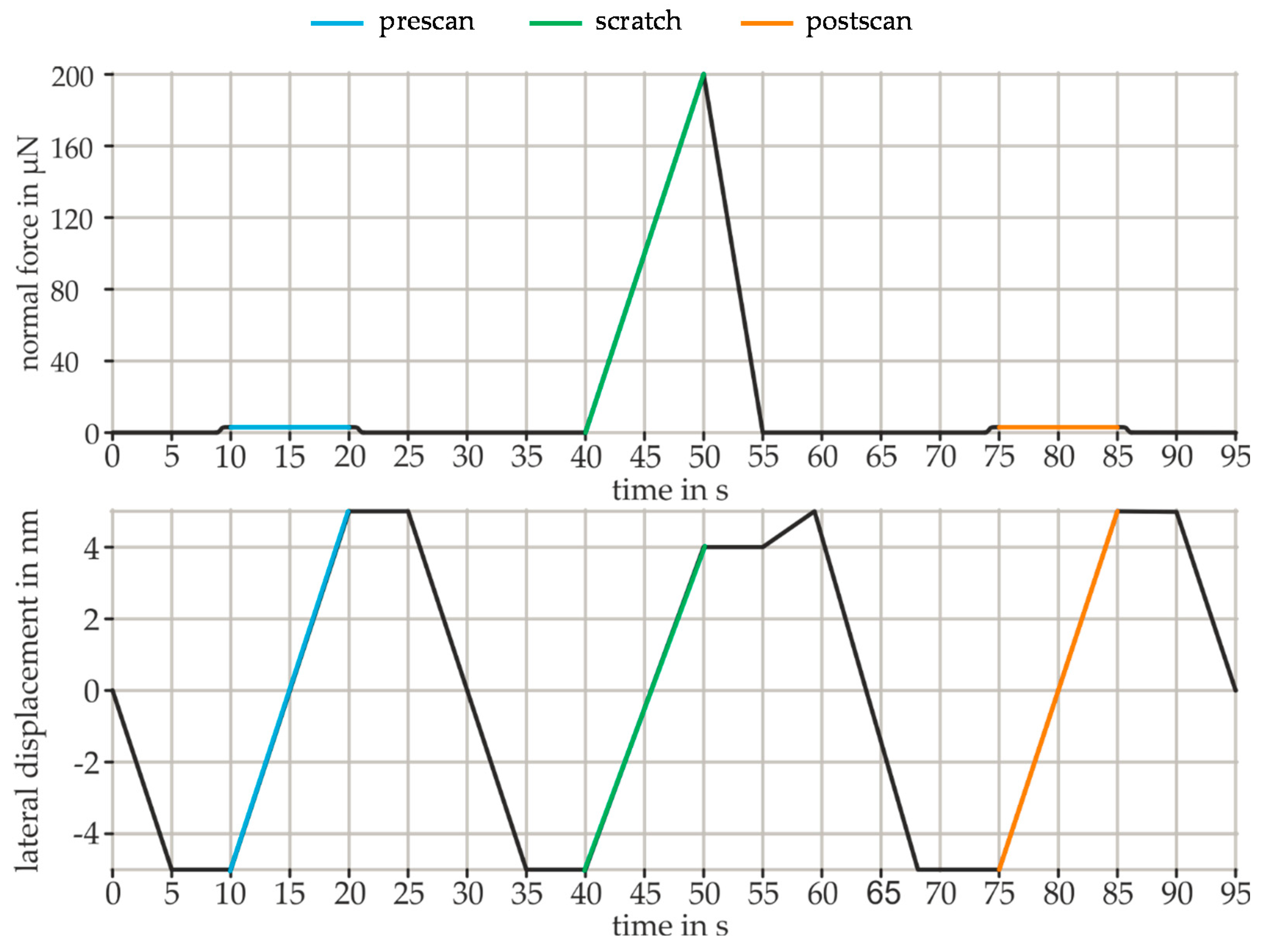
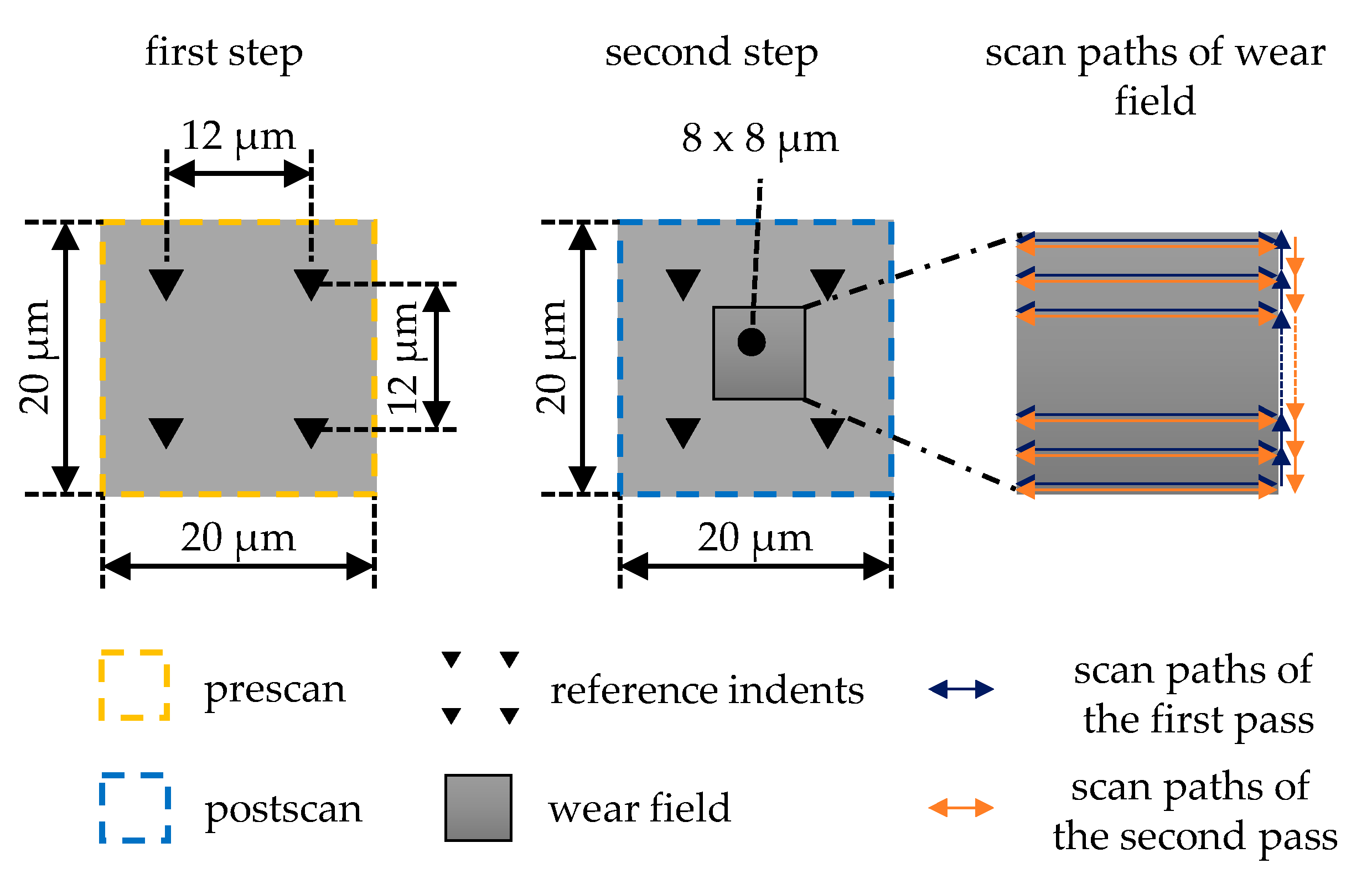






| Scans | Scan Rate in Hz | Scan Size in µm | Scan Direction | Number of Lines | Scanning Force in µN | Number of Passes (P) |
|---|---|---|---|---|---|---|
| Pre-scan | 0.5 | 20 × 20 | horizontal | 512 | 2 | 1 |
| Wear field | 1.0 | 8 × 8 | horizontal | 512 | 50, 100, 125, 150, 175, 200 | 5, 15, 19, 25, 29, 35 |
| Post-scan | 0.5 | 20 × 20 | horizontal | 512 | 2 | 1 |
| Number of Pass (P) | Normal Force in µN | |||||
|---|---|---|---|---|---|---|
| 50 | 100 | 150 | 200 | 125 | 175 | |
| 5 | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | ||
| 15 | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | ||
| 25 | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | ||
| 35 | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | 4 R × 2 MP | ||
| 19 | 4 R × 2 MP | |||||
| 29 | 4 R × 2 MP | |||||
| Specimen | Nano Hardness in GPa | Standard Deviation | Young’s Modulus in GPa | Standard Deviation | CoF | Standard Deviation |
|---|---|---|---|---|---|---|
| Mo | 9.82 | 0.58 | 218.10 | 7.85 | 0.13 | 0.03 |
| MoO3 | 2.62 | 0.17 | 67.26 | 2.40 | 0.20 | 0.04 |
| Steel substrate 1 | 9.30 | 0.30 | 231.00 | 8.00 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behrens, B.-A.; Poll, G.; Möhwald, K.; Schöler, S.; Pape, F.; Konopka, D.; Brunotte, K.; Wester, H.; Richter, S.; Heimes, N. Characterization and Modeling of Nano Wear for Molybdenum-Based Lubrication Layer Systems. Nanomaterials 2021, 11, 1363. https://doi.org/10.3390/nano11061363
Behrens B-A, Poll G, Möhwald K, Schöler S, Pape F, Konopka D, Brunotte K, Wester H, Richter S, Heimes N. Characterization and Modeling of Nano Wear for Molybdenum-Based Lubrication Layer Systems. Nanomaterials. 2021; 11(6):1363. https://doi.org/10.3390/nano11061363
Chicago/Turabian StyleBehrens, Bernd-Arno, Gerhard Poll, Kai Möhwald, Simon Schöler, Florian Pape, Dennis Konopka, Kai Brunotte, Hendrik Wester, Sebastian Richter, and Norman Heimes. 2021. "Characterization and Modeling of Nano Wear for Molybdenum-Based Lubrication Layer Systems" Nanomaterials 11, no. 6: 1363. https://doi.org/10.3390/nano11061363
APA StyleBehrens, B.-A., Poll, G., Möhwald, K., Schöler, S., Pape, F., Konopka, D., Brunotte, K., Wester, H., Richter, S., & Heimes, N. (2021). Characterization and Modeling of Nano Wear for Molybdenum-Based Lubrication Layer Systems. Nanomaterials, 11(6), 1363. https://doi.org/10.3390/nano11061363








